Non-destructive analysis of samples with a complex geometry by NRTA
Received
11th October 2019
, Accepted 2nd December 2019
First published on 3rd December 2019
Abstract
The use of neutron resonance transmission analysis to characterise samples with a complex geometry is discussed. Analytical expressions for such samples have been derived and implemented in the resonance shape analysis code REFIT. They were validated by experiments at the time-of-flight facility GELINA using a set of metallic natural copper samples and pellets made of silver mixed with uranium-oxide powder. The expressions were used to derive sample characteristics by a least squares adjustment to experimental transmission data. In addition, the resonance parameters of 63Cu and 65Cu for energies below 6.5 keV, which are reported in the literature and recommended in evaluated data libraries, were verified.
Introduction
Neutron interaction cross sections show resonance structures that are characteristic for each nuclide. These structures are the basis of Neutron Resonance Analysis (NRA) as a Non Destructive Analysis (NDA) technique to characterise materials.1–3 Neutron resonance structures can be observed by measuring a neutron energy spectrum after a white neutron beam traverses a sample by applying the Time-Of-Flight (TOF) technique. The observed transmission dips are ideal fingerprints to determine both the elemental and isotopic composition of samples simultaneously by Neutron Resonance Transmission Analysis (NRTA).1–3 It is an absolute analytical technique which does not require any calibration. NRTA has already been applied in the seventies to determine the nuclide composition of fresh and spent nuclear fuel plates.4–6 The TOF facility GELINA, installed at the Joint Research Centre in Geel (BE),7 has been extensively used to study objects of archaeological and cultural heritage interest by Neutron Resonance Capture Analysis (NRCA).3 This NRA technique relies on the study of resonance profiles by detecting prompt γ-rays emitted after a neutron capture reaction as a function of the incident neutron energy. NRTA and NRCA are routinely applied at GELINA to characterise reference materials for cross section measurements.8,9 NRTA is also a useful tool to validate nuclear data in the resonance region as demonstrated by Tsuchiya et al.10 and Becker et al.11 Both NRTA and NRCA rely on well-established methodologies that are applied to measure neutron interaction cross section data.12 An extensive overview of NRTA and NRCA applications can be found in ref. 2.
The accident at the Fukushima Daiichi nuclear power plants triggered an interest in NRTA as a NDA technique to determine the composition of complex nuclear materials.13 X-Ray Fluorescence (XRF) has also been proposed for such applications.14 However, X-rays have a limited penetration power. In addition, XRF does not provide information about the isotopic composition. Therefore, only the elemental composition of liquid solutions or the surface layer of solid samples can be investigated by XRF.
An analysis of complex nuclear materials, such as debris of melted fuel or spent nuclear fuel pellets, by NRTA is challenging due to their characteristics: i.e. the presence of matrix materials that do not create low energy resonance structures, the complexity of transmission spectra due to overlapping resonances and the temperature and shape of the samples. Most of those problems have been studied and solved as part of a collaborative effort of the Japan Atomic Energy Agency (JAEA) and the Joint Research Centre (JRC). A method to account for the contribution of strong neutron absorbing light elements that do not have resonances in the low energy region, like structural materials in nuclear fuel, was proposed and validated in ref. 2. The validation was based on transmission measurements at a 25 m station of GELINA using a U3O8 reference sample. To investigate the potential of NRTA for complex nuclear materials with strong overlapping resonances a demonstration experiment was organised at a 10 m station of GELINA.15,16 An inventory of 18 different samples of medium-weight (Cu, Co, Mn, Nb and Rh) and heavy elements (W and Au), in the form of metallic discs were made available to create blind samples. These materials were chosen to mimic the resonance structures of elements present in spent nuclear fuel. The areal densities of the elements present in the blind sample, which was created by participants from external organisations (IAEA, DOE, EURATOM), were predicted within 2%. The potential of NRTA to analyse nuclear materials containing plutonium was shown by transmission measurements at a 10 m station of GELINA using a set of PuO2 reference samples with different isotopic composition.17 For complex samples like debris of melted fuel or cylindrical pellets the thickness of the object in the direction of the neutron beam is not constant. Therefore, the basic Lambert–Beer law cannot be applied and special analysis procedures are required to apply NRTA. An analytical model to describe the transmission through a stochastic medium, such as a sample consisting of a mixture of particle and rock-like debris of melted fuel, has been proposed and validated by experiments at GELINA by Becker et al.18 Harada et al.19 reported analytical expressions for homogeneous samples with a variable thickness in the direction of the neutron beam. In this work other analytical expressions, in particular expressions for cylindrical pellets, are presented and validated by results of experiments that were carried out at GELINA.
Experimental details
Measurement station
The experiments were performed at the TOF facility GELINA,7 with the electron accelerator operating at an 800 Hz frequency. At GELINA neutrons are produced by a pulsed electron beam with an average electron energy of 100 MeV and a pulse width of less than 2 ns.20 The pulsed electron beam bombards a mercury cooled rotating uranium target and produces high-energy photons via the bremsstrahlung process.21 The high-energy photons interact with the uranium target to produce neutrons by (γ, n) and (γ, f) reactions. These neutrons have an energy distribution in the high energy region. To produce a neutron energy spectrum covering also the low energy region, which is of interest to study neutron resonance structured cross sections, the uranium target is surrounded with Be containers filled with water acting as a neutron moderator.
The 50 m transmission station installed at flight path 4 of GELINA was used. A shadow bar made of Cu and Pb was placed close to the uranium target to reduce the γ-ray flash and the fast neutron component. Neutrons scattered from the moderators were collimated into the flight path through evacuated aluminium pipes of 50 cm diameter. Collimators consisting of borated wax, Cu and Pb were placed at regular distances. A combination of Li-carbonate plus resin, Pb and Cu collimators was used to reduce the incident neutron beam to a diameter of about 35 mm at the sample position. The samples were placed in an automatic sample changer at a distance of about 24 m from the neutron source. Close to the sample position a 10B overlap filter, with an areal density of 0.008 at/b, was placed to absorb slow neutrons from a previous burst. The impact of the γ-ray flash was reduced by an 8 mm thick Pb filter. Permanent Co and Na black resonance filters were used to continuously monitor the background at 132 eV and 2850 eV, respectively, and to account for the impact of the sample on the background. Additional black resonance filters made of W and S were mounted on the sample changer to determine the background by the black resonance technique.12 The neutron beam passing through the sample and filters was further collimated and detected by a 6.35 mm thick and 101.6 mm diameter NE912 Li-glass scintillator enriched to 95% in 6Li. The scintillator was connected through a boron-free quartz window to a 127 mm diameter EMI 9823 KQB photomultiplier (PMT). The detector was placed at a distance of 47 m from the facet of the moderator viewing the flight path.
Samples
Three different sample types were used: 1 disk, 2 cylindrical rods (or pellets) and 4 cuboid shaped samples. They were all made of metallic natural copper. The disk sample, with a diameter of 70 mm and thickness of 14.6 mm, was used to verify the accuracy with which the areal density can be derived in ideal conditions, that is, from a measurement in good transmission geometry using a sample with a uniform areal density distribution and a sample diameter larger than the beam diameter. The results obtained with this sample were also used to verify the quality of the resonance parameters of 63Cu and 65Cu. The reference value for the number areal density (or number of atoms per unit area) of 0.123437 (2) at/b was derived from its weight 501.862 (1) g and area 3852.541 (60) mm2. The area was determined by an optical surface inspection with a microscopic based measurement system from Mitutoyo. Two cylindrical rods with a diameter of 4.98 (1) and 10.01 (1) mm were prepared from the same batch of metallic natural Cu. The volume density ρ = 8.913 (40) g cm−3, which was determined from the weight and volume of a representative sample of this batch, is close to the nominal volume density ρ = 8.94 g cm−3 for natural copper. The characteristics of the cuboid samples are summarised in Table 1. The definition of the width and thickness is clarified in Fig. 1. The areal density was derived from the volume density ρ = 8.924 (20) g cm−3 of a representative sample and the thickness of the sample.
Table 1 Characteristics of the cuboid samples made of natural metallic Cu. The weight and geometrical dimensions are given together with the areal density. The latter is derived from the volume density of a representative sample (ρ = 8.924 (20) g cm−3) and the thickness of the sample. Fig. 1 illustrates the definition of the width and thickness. All uncertainties in this paper are given at a 68% confidence limit
| Sample ID |
Length, l (mm) |
Width, w (mm) |
Thickness, t (mm) |
Areal density, n (at/b) |
| C1 |
100.00 (2) |
19.90 (2) |
10.04 (2) |
8.491 (25) × 10−2 |
| C2 |
100.00 (2) |
19.95 (2) |
5.08 (2) |
4.296 (20) × 10−2 |
| C3 |
100.00 (2) |
9.94 (2) |
10.05 (2) |
8.499 (25) × 10−2 |
| C4 |
100.00 (2) |
9.99 (2) |
4.99 (2) |
4.220 (20) × 10−2 |
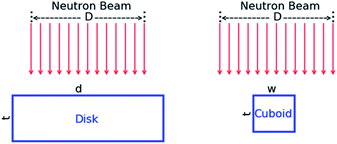 |
| | Fig. 1 Schematic representation of the experimental geometry for the measurements with the disk and cuboid samples to study the impact of the holes fraction. The beam diameter is denoted by D, the disk diameter by d, and the width and thickness of the cuboid sample by w and t, respectively. | |
Note that for the cuboid samples the width is smaller than the beam diameter. The effect of the holes fraction was investigated by placing the cuboid samples perpendicular to the beam direction, as shown in Fig. 1. The analytical expression in case the thickness experienced by the neutron beam is not constant was verified by placing the cuboid sample C3 in three different positions relative to the direction of the incident neutron beam. The angle between the direction of the incident beam and the normal to the facet viewing the neutron beam was 0°, 30° and 45°, as illustrated in Fig. 2.
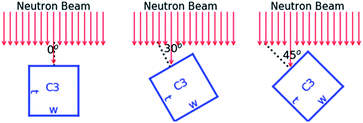 |
| | Fig. 2 Schematic representation of the experimental geometry for the measurements with the cuboid sample C3 to study the impact of a not constant sample thickness in the direction of the incident neutron beam. | |
Data reduction
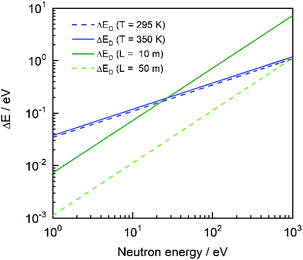
The experimental transmission Texp as a function of TOF was obtained from the ratio of a sample-in measurement Cin and a sample-out measurement Cout, both corrected for their background contributions Bin and Bout, respectively:12| | 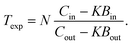 | (1) |
The TOF spectra (Cin, Cout, Bin, Bout) were corrected for losses due to the dead time in the detector and electronics chain. All spectra were normalised to the same TOF-bin width structure and neutron beam intensity. The latter was derived from the counts recorded by BF3 beam monitors that are installed in the ceiling of the neutron producing target hall to monitor the neutron beam intensity.
The observed time-of-flight (tm) of a neutron creating a signal in the neutron detector was determined by the time difference between the stop (Ts) and start signal (T0):
with
t0 a time-offset, which was determined by a measurement of the γ-ray flash. The flight path distance
L = 47.654 (4) m,
i.e. the distance between the centre of the moderator viewing the flight path and the front face of the neutron detector, was derived previously in
ref. 22 from results of transmission measurements with uranium samples based on the energy of
238U resonances.
To avoid systematic effects due to slow variations of both the beam intensity and detector efficiency as a function of time, data were taken by alternating sample-in and sample-out measurements in cycles of about 600 seconds. Such a procedure reduces the uncertainty on the normalisation to the beam intensity to less than 0.25%. This uncertainty was evaluated from the ratio of counts in the 6Li transmission detector and those in the beam monitors. To account for this uncertainty the factor N = 1.0000 (25) is introduced in eqn (1).
The background as a function of TOF was approximated by an analytic expression applying the black resonance technique.12 The background as a function of TOF was parameterised by an analytical expression consisting of a constant and three exponentials:
| | | b(tm) = b0 + b1e−λ1tm + b2e−λ2tm + b3e−λ3(tm + τ0). | (3) |
The time independent contribution is represented by the parameter b0. The first exponential results from the detection of 2.2 MeV γ-rays resulting from neutron capture in hydrogen present in the moderator. This contribution dominates the background in the TOF region below about 80 μs. The second exponential originates predominantly from neutrons scattered inside the detector station. The third one is due to slow neutrons from previous accelerator cycles. The time shift τ0 is the inverse of the accelerator frequency, i.e. τ0 = 1.25 ms for 800 Hz. This contribution was estimated by an extrapolation of the TOF-spectrum at the end of the cycle. The free parameters in the analytical expression were determined by a least squares fit to saturated resonance dips observed in the TOF-spectra resulting from measurements with black resonance filters. The time dependence of the background was derived by dedicated measurements with S, Na, Co and W black resonance filters in the beam. During the regular sample-in and sample-out runs Na and Co black resonance filters were kept in the beam to account for the dependence of the background level on the presence of the sample. The factor K = 1.00 (3) is introduced in eqn (1) to account for systematic effects due to the background model. Its uncertainty was derived in ref. 22 from a statistical analysis of the difference between the observed black resonance dips and the estimated background. This uncertainty is only valid for measurements with at least two fixed black resonance filters in the beam. Fig. 3 shows dead time corrected TOF spectra together with their total background contribution for the sample-in measurements with the disk sample and the cuboid sample C1 in the geometry of Fig. 1. The difference in background level is due to the impact of the sample properties on the amplitude of the background.
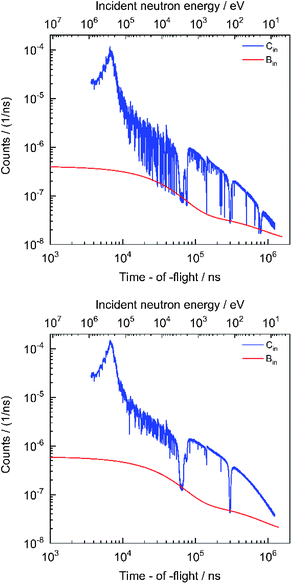 |
| | Fig. 3 TOF spectra for the sample-in measurement with the disk sample (top) and the cuboid sample (C1) in the geometry of Fig. 1 (bottom). The data for the disk sample were obtained from measurements with an additional W black resonance filter placed in the beam. The sample-in spectra are compared with their total background contribution. The spectra are given as a function of time-of-flight (bottom x-axis), which is expressed in nanosecond (1 ns = 10−9 s). The corresponding energies, expressed in electron volt, are given in the top x-axis. | |
The AGS concept23 developed at the JRC Geel was used to derive the experimental transmissions from the TOF spectra. It includes the most important spectra manipulations such as dead time correction, background subtraction and normalisation. It is based on a compact formalism to propagate all uncertainties, both uncorrelated and correlated components, starting from uncorrelated uncertainties due to counting statistics. The code is available at the Nuclear Energy Agency of the OECD.24Fig. 4 shows the experimental transmissions in the energy region from 250 eV to 6500 eV through the disk sample and four cuboid samples placed in the geometry shown in Fig. 1. The impact of the holes fraction is clearly visible in the regions of a strong resonance. For example, the transmission around the 2046 eV resonance is practically zero for the disk sample. This transmission is not zero for the cuboid samples which do not cover the full beam. Evidently, the amplitude of the resonance dip decreases with decreasing sample width.
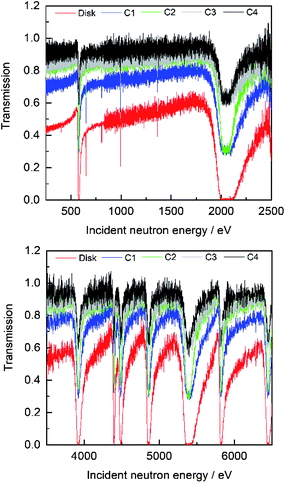 |
| | Fig. 4 Comparison of the experimental transmission through the disk and cuboid shaped samples described in Table 1. The sample position with respect to the neutron beam is shown in Fig. 1. | |
Data analysis and results
The sample composition can be derived from a least squares adjustment to the experimental transmission by minimising the expression:with the residuals r(tm) defined by:| | 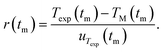 | (5) |
The theoretical (or model) transmission TM(tm) as a function of the observed TOF is obtained from a convolution of the theoretical transmission as a function of energy with the response function of the TOF-spectrometer:
| | 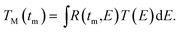 | (6) |
with the theoretical transmission and response function denoted by
T(
E) and
R(
tm,
E), respectively. The quality of the fit is verified by evaluating the chi-square per degree of freedom
χ2/
ν, with
ν the number of degrees of freedom. The resonance shape analysis code REFIT
25 was used to perform the adjustment. This code, which is based on the Reich–Moore
26 approximation of the
R-matrix formalism,
27 accounts for various experimental effects such as Doppler broadening, neutron self-shielding, multiple interaction events and the response function of the neutron detector and TOF-spectrometer.
Verification of resonance parameters
For NRTA applications the resonance parameters are supposed to be known and only sample characteristics are considered as free parameters in the fit.2 Hence, the accuracy of the sample characteristics strongly depends on the quality of the resonance parameters of the nuclides present in the sample, as already demonstrated in ref. 10 and 11. Independent sets of resonance parameters for 63Cu and 65Cu reported in the literature are: the parameters compiled by Mughabghab,28 those resulting from an evaluation carried out at the Oak Ridge National Laboratory (ORNL) by Sobes et al.29 and the parameters reported by Tsuchiya et al.10Table 2 compares their parameters for the resonances at 230 eV, 578 eV, 994 eV, 2046 eV, 3922 eV, 5388 and 6443 eV. Those of Mughabghab28 are based on a compilation of parameters that were derived from experimental data in ref. 30–35. For the radiation widths Mughabghab28 adopted the values of Weigmann and Winter.31 In the ORNL evaluation the radiation width was fixed to Γγ = 500 meV and Γγ = 395 meV for 63Cu and 65Cu, respectively, except for the 230 eV resonance with Γγ = 370 meV. Those of Tsuchiya et al.10 are based on results of transmission experiments at a 50 m station of GELINA combined with the radiation widths of Weigmann and Winter.31 The parameters of Mughabghab28 are the basis of the present versions of BROND, CENDL and JENDL and were used for the previous versions of JEFF and ENDF/B. In the latest JEFF-3.3 library the parameters of Tsuchiya et al.10 were adopted, however, maintaining the external contribution from JEFF-3.2 which is not consistent with the one of Tsuchiya et al.10 The header file of ENDF-BVIII.0 suggests that the parameters for Cu are based on the work of Sobes et al.29 A comparison of the parameters in Table 2 reveals that this is not correct.
Table 2 Resonance parameters for strong s-wave resonance with an energy below 6.5 keV reported by Tsuchiya et al.,10 Mughabghab28 and Sobes et al.29 The resonance energy Er, radiation width Γγ and resonance strength gΓn are compared. The latter is the product of the statistical spin factor g and neutron width Γn. For completeness the assumed spin J is given. The parameters from ENDF/B-VIII.0 were taken from the NEA website36
|
|
E
r (eV) |
Tsuchiya et al.10 |
Mughabghab28 |
Sobes et al.29 |
ENDF/B-VIII.0 |
|
J
|
gΓ
n (meV) |
Γ
γ (meV) |
J
|
gΓ
n (meV) |
Γ
γ (meV) |
J
|
gΓ
n (meV) |
Γ
γ (meV) |
J
|
gΓ
n (meV) |
Γ
γ (meV) |
|
65Cu |
230 |
2 |
8.6 (5) |
240 |
2 |
11.11 (15) |
245.8 (40) |
1 |
10.77 (29) |
178 (1) |
3 |
8.32 |
370 |
|
63Cu |
578 |
2 |
562 (3) |
485 |
2 |
369 (13) |
485 (40) |
2 |
553 (14) |
386 (1) |
2 |
417 |
500 |
|
63Cu |
994 |
2 |
8.3 (3) |
500 |
1 |
8.3 (5) |
260 |
2 |
5.88 (15) |
339 (2) |
2 |
5.88 |
500 |
|
63Cu |
2046 |
1 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 (80) 370 (80) |
570 |
1 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (500) 000 (500) |
500 (70) |
1 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 (397) 525 (397) |
444 (1) |
1 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
500 |
|
65Cu |
3922 |
1 |
8600 (400) |
470 |
1 |
9000 (300) |
620 (40) |
1 |
8896 (242) |
614 (2) |
1 |
8900 |
395 |
|
63Cu |
5388 |
2 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 (500) 700 (500) |
440 |
2 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (750) 500 (750) |
560 (20) |
2 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 409 (598) 409 (598) |
467 (2) |
1 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
500 |
|
65Cu |
6443 |
2 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (880) 500 (880) |
410 |
2 |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (1600) 500 (1600) |
410 (30) |
2 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 (428) 735 (428) |
372 (1) |
2 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
395 |
Measurements in ideal transmission geometry using a homogenous Cu disk with a diameter larger than the beam diameter were carried out to verify the quality of the resonance parameters for 63Cu and 65Cu. Under these conditions the basic Lambert–Beer law is valid and the theoretical transmission T(E) is:
| | 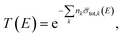 | (7) |
where
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) tot,k
tot,k(
E) is the Doppler broadened total cross section for neutron interactions with nuclide
k and
nk the corresponding number areal density. To account for the Doppler broadening, the free gas model was used with an effective temperature
Teff = 314 K corresponding to a room temperature
T = 293 K and a Debye temperature
θD = 343 K. The latter was taken from
ref. 37. The areal density for Cu was adjusted by fitting simultaneously transmission dips due to resonances in
63Cu and
65Cu and using the isotopic composition of natural Cu recommended in
ref. 38.
Table 3 reports for different energy regions the quality of the fit, i.e. χ2/ν, and the ratio between the adjusted areal density and the reference value. The results obtained with the parameters of Mughabghab28 and Sobes et al.29 suggest that for most of the resonances their parameters are questionable. Table 3 also reveals that the parameters in JEFF-3.3 and ENDF/B-VIII.0 should be reviewed and a new evaluation including the experimental transmission data reported in this work and in the work of Tsuchiya et al.10 is recommended. The best results are obtained by using the parameters of Tsuchiya et al.10 Using their parameters the areal density is reproduced within the uncertainties due to counting statistics, except for the energy regions covering the resonances at 2046 eV and 6443 eV. The χ2/ν indicates that the transmission data in the region of the 2046 eV resonance cannot be fully reproduced. This was also observed by Tsuchiya et al.10 For the regions around the 2046 eV and 6443 eV resonance better results are obtained with the parameters of Sobes et al.29 Considering the results in Table 3 the parameters of Tsuchiya et al.10 were preferred for the analysis of the other data.
Table 3 Results of least squares adjustments to the experimental transmission obtained with a 14.6 mm thick Cu disk. The adjustment is performed in different energy regions using the resonance parameters of Tsuchiya et al.,10 Mughabghab,28 Sobes et al.29 and those recommended in JEFF-3.3 and ENDF/B-VIII.0. The χ2/ν is given together with the ratio nNRTA/n of the fitted areal density and the reference value. The uncertainties are due to propagating only the uncorrelated uncertainties due to counting statistics
| Energy region eV |
Tsuchiya et al.10 |
Mughabghab28 |
Sobes et al.29 |
JEFF-3.3 |
ENDF/B-VIII.0 |
|
χ
2/ν |
n
NRTA/n |
χ
2/ν |
n
NRTA/n |
χ
2/ν |
n
NRTA/n |
χ
2/ν |
n
NRTA/n |
χ
2/ν |
n
NRTA/n |
| 210–240 |
0.74 |
1.020 (13) |
1.05 |
0.910 (16) |
0.64 |
0.804 (52) |
0.52 |
1.108 (16) |
1.69 |
1.028 (13) |
| 540–620 |
1.27 |
1.001 (15) |
16.87 |
1.393 (17) |
7.13 |
1.132 (7) |
1.04 |
0.978 (7) |
12.15 |
1.336 (15) |
| 970–1020 |
0.66 |
0.962 (25) |
0.64 |
0.900 (25) |
0.61 |
1.229 (32) |
0.64 |
0.930 (25) |
0.65 |
1.197 (30) |
| 1800–2400 |
2.12 |
1.049 (5) |
1.96 |
1.059 (6) |
0.63 |
0.985 (5) |
1.81 |
1.103 (6) |
1.61 |
1.170 (7) |
| 3600–4200 |
0.68 |
0.995 (12) |
0.68 |
0.988 (13) |
0.63 |
0.979 (12) |
0.61 |
1.060 (14) |
0.63 |
1.025 (14) |
| 5000–5700 |
0.78 |
1.008 (9) |
0.91 |
1.100 (9) |
0.66 |
0.994 (8) |
0.63 |
1.079 (8) |
2.14 |
1.211 (11) |
| 6300–6650 |
0.58 |
0.939 (13) |
0.57 |
0.949 (13) |
0.99 |
1.004 (14) |
0.67 |
0.933 (13) |
0.59 |
1.016 (13) |
| 200–7000 |
2.50 |
0.995 (2) |
3.92 |
0.992 (2) |
2.17 |
0.984 (4) |
3.16 |
0.992 (2) |
3.75 |
1.103 (2) |
Holes fraction
In case the sample area is smaller than the beam area, a fraction of the incident neutron beam will not traverse the sample and will not be attenuated. Under these conditions the basic Lambert–Beer law (eqn (7)) is not applicable. For a homogeneous sample and a constant sample thickness in the direction of the neutron beam, the theoretical transmission becomes:| | 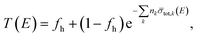 | (8) |
with fh the fraction of the beam that is not covered by the sample. This fraction is also referred to as the holes fraction. Eqn (8) was verified using the cuboid samples in the geometry shown in Fig. 1. In case of a homogeneous sample the holes fraction is related to the beam radius R and sample width w by:| |  | (9) |
In the least squares adjustment both the holes fraction and areal density were adjusted. The result of a fit in the region of the 580 eV resonance for cuboid sample C3 is shown in Fig. 5. The fitted areal densities and holes fractions are given in Table 4. Within the uncertainties due to counting statistics the areal densities derived from the fit are fully consistent with the reference values. The good agreement between the fitted and reference areal density together with the residuals in Fig. 5, confirm that the theoretical transmission of eqn (8) is valid for the transmission through such samples. The holes fractions for the cuboid samples with the same width are within the uncertainties the same. This fraction shows a weak dependence on the width. This can be explained by the neutron beam which is not a perfect parallel uniform neutron beam. The beam diameter derived from the holes fraction deviates slightly from the one derived from a profile obtained with an X-ray photograph. The latter results in a diameter of about 35 mm. Bias effects due to the holes fraction are substantially reduced by having saturated resonance dips in the spectrum due to the presence of a black resonance filter that covers the full neutron beam.
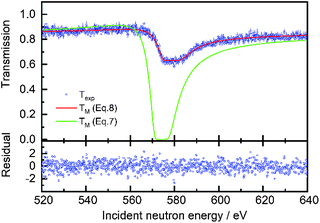 |
| | Fig. 5 Comparison between the experimental Texp and theoretical transmission TM through the cuboid sample C3 as a function of incident neutron energy. The theoretical transmission after adjustment of the areal density and holes fraction (eqn (8)) with REFIT is plotted together with the theoretical transmission neglecting the holes fraction (eqn (7)). The bottom plot shows the residual (eqn (5)) as a function of the incident neutron energy for the fit using eqn (8) for T(E). | |
Table 4 Areal density nNRTA and holes fraction fh derived from a least squares adjustment using the theoretical transmission in eqn (8). The uncertainties on the fitted areal density are due to propagating only the uncorrelated uncertainties due to counting statistics
| ID |
Width (mm) |
Thickness (mm) |
n
NRTA (at/b) |
n
NRTA/n |
f
h
|
Beam diameter (mm) |
| C1 |
19.90 (2) |
10.04 (2) |
8.46 (2) × 10−2 |
0.996 (4) |
0.310 (2) |
34.6 (1) |
| C2 |
19.95 (2) |
5.08 (2) |
4.35 (3) × 10−2 |
1.013 (8) |
0.309 (4) |
34.6 (2) |
| C3 |
9.94 (2) |
10.05 (2) |
8.60 (9) × 10−2 |
1.012 (11) |
0.628 (3) |
33.5 (3) |
| C4 |
9.99 (2) |
4.99 (2) |
4.25 (5) × 10−2 |
1.007 (13) |
0.631 (5) |
34.0 (5) |
Non-uniform geometrical track length in the beam direction
For the geometrical conditions in Fig. 2 and θ ≠ 0°, the sample thickness in the direction of the neutron beam is not constant. An attempt was made to account for the thickness variation by an average effective areal density using the formula:| | 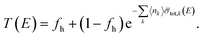 | (10) |
The average effective areal density of nuclide k, which is denoted by 〈nk〉, is related to the areal density nk for θ = 0° by:
| | 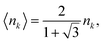 | (11) |
and
| | 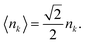 | (12) |
for
θ = 30° and 45°, respectively. The results of fits in the region of the 2046 eV resonance using an average areal density are shown in
Fig. 6 and reported in
Table 5. The results in
Fig. 6 show that the experimental data cannot be reproduced by applying the basic Lambert–Beer law using an average areal density. The average values resulting from the fits are underestimated by about 8.5% and 6.7% compared to those derived from the values in
Table 1.
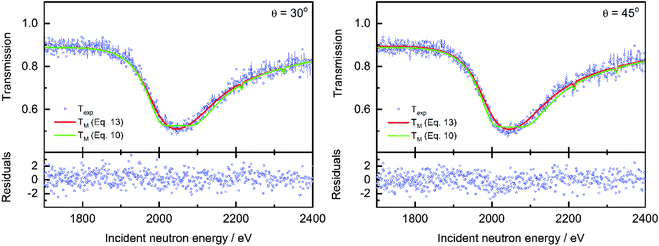 |
| | Fig. 6 Results of a least squares fit to the data obtained from the measurements with the cylindrical rods. The ratios of the values 〈n〉NRTA and 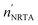 derived from the fit and the corresponding reference values are given together with the holes fraction fh. The uncertainty of the ratio is the combined uncertainty of the fitted value and the one of the reference value. The uncertainties of the fitted values result from propagating only the uncorrelated uncertainties due to counting statistics. derived from the fit and the corresponding reference values are given together with the holes fraction fh. The uncertainty of the ratio is the combined uncertainty of the fitted value and the one of the reference value. The uncertainties of the fitted values result from propagating only the uncorrelated uncertainties due to counting statistics. | |
Table 5 Results of a least squares fit to the data obtained from the measurements in the geometry of Fig. 2. The ratio of the values 〈n〉NRTA and nNRTA derived from the fit and the corresponding reference values are given together with the holes fraction fh. In addition, the fitted angle θ resulting from the fit using eqn (13) for T(E) is reported. The uncertainty of the ratio is the combined uncertainty of the fitted value and the one of the reference value. The uncertainties of the fitted values result from propagating only the uncorrelated uncertainties due to counting statistics
| Angle θ |
Eqn (10)
|
Eqn (13)
|
| 〈n〉NRTA/〈n〉 |
f
h
|
n
NRTA/n |
θ
|
f
h
|
| 0° |
1.012 (11) |
0.632 (3) |
1.017 (17) |
0.2 (3)° |
0.629 (3) |
| 30° |
0.915 (16) |
0.532 (3) |
0.976 (24) |
31 (1)° |
0.501 (2) |
| 45° |
0.933 (15) |
0.527 (2) |
1.003 (40) |
45 (3)° |
0.490 (6) |
The theoretical transmission for the configurations in Fig. 2 can be expressed as:
| | 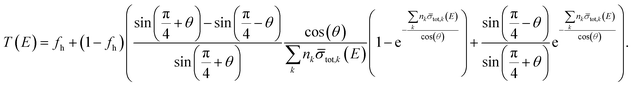 | (13) |
with
nk the areal density for
θ = 0°. Note that for
θ = 0° the expression in
eqn (13) reduces to
eqn (8). The result of a fit using this expression is shown in
Fig. 6 in the region of the 2046 eV resonance.
Table 5 reports the adjusted parameters. Evidently,
eqn (13) is required to avoid bias effects in the abundance derived from the resonance profile. The good agreement between the angle derived from the transmission data and the effective angle suggests that the transmission resonance profiles are sensitive to the geometry of the sample and can be used to provide information about the shape of a sample. Evidently the degree to which such sample characteristics can be derived depends on the resolution of the TOF-spectrometer. A comparison of the holes fraction in
Table 5 reveals that the underestimation of the average areal density is compensated by an overestimation of the holes fraction.
Cylindrical rods
When a cylindrical rod or pellet is placed in a beam with its axis perpendicular to the neutron beam the conditions for a good transmission geometry are not fulfilled and the basic Lambert–Beer law is not applicable. Under these conditions the theoretical transmission is:| | 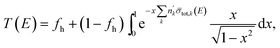 | (14) |
with 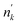 the volume number density of nuclide k multiplied by the rod diameter or the areal number density corresponding to the maximum thickness. Eqn (14) can also be written as:
the volume number density of nuclide k multiplied by the rod diameter or the areal number density corresponding to the maximum thickness. Eqn (14) can also be written as:| | 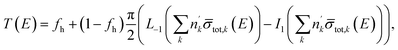 | (15) |
where Ln(z) is the modified Struve function and In(z) the modified Bessel function of the first kind. This expression is different from the one proposed in ref. 39. The procedure in ref. 39 relies on the subtraction of an artificial background. This can only be done when the transmission shows a saturated resonance dip due to an element that is present in the pellet. In addition, the expression of ref. 39 requires the beam radius as an input parameter. Eqn (15) was implemented in REFIT and validated by results of transmission experiments through the cylindrical rods with a nominal diameter of 5 mm and 10 mm. The results of the fit are shown in Fig. 7 and reported in Table 6. The areal density at maximum thickness obtained from a fit to the data are n'NRTA = 0.0429 (8) and n'NRTA = 0.0834 (7) at/b for the rod with a diameter of 5 mm and 10 mm, respectively. These values are within the uncertainties due to counting statistics in very good agreement with the reference values n′ = 0.0421 (2) at/b and n′ = 0.0846 (4) at/b, respectively. These values are derived from the radius of the pellets and the volume density of a sample that was prepared from the same batch of material. Using eqn (10) for the theoretical transmission T(E) results again in an underestimation of the average areal density and an overestimation of the holes fraction. The theoretical average areal density is related to the areal density at maximum thickness by:| | 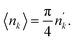 | (16) |
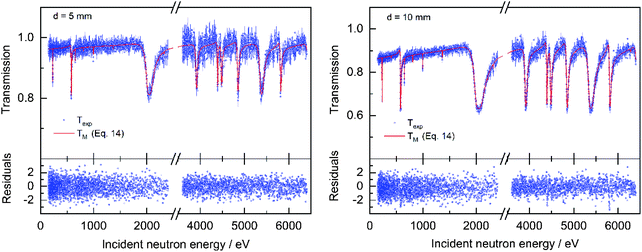 |
| | Fig. 7 Comparison of the experimental Texp and theoretical transmission TM through a pellet sample with a diameter of d = 5 mm (left) and d = 10 mm (right) as a function of incident neutron energy. The theoretical transmission is derived by using eqn (14) for T(E). The bottom plots show the residuals (eqn (5)) as a function of the incident neutron energy for the fit. | |
Table 6 Results of a least squares fit to the data obtained from the measurements with the cylindrical rods. The ratios of the values 〈n〉NRTA and 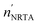 derived from the fit and the corresponding reference values are given together with the holes fraction fh. The uncertainty of the ratio is the combined uncertainty of the fitted value and the one of the reference value. The uncertainties of the fitted values result from propagating only the uncorrelated uncertainties due to counting statistics
derived from the fit and the corresponding reference values are given together with the holes fraction fh. The uncertainty of the ratio is the combined uncertainty of the fitted value and the one of the reference value. The uncertainties of the fitted values result from propagating only the uncorrelated uncertainties due to counting statistics
| Diameter |
Eqn (10)
|
Eqn (14)
|
| 〈n〉NRTA/〈n〉 |
f
h
|
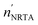
/n′ |
f
h
|
| 5 mm |
0.981 (20) |
0.817 (2) |
1.020 (20) |
0.808 (2) |
| 10 mm |
0.952 (10) |
0.637 (2) |
0.986 (10) |
0.627 (2) |
The analytical expression for cylindrical pellets (eqn (14)) was validated by results of measurements at a 10 m transmission station of GELINA that were carried out by Šalamon et al.39 These experiments were performed to verify the presence of impurities in a set of cylindrical pellets that were used for integral benchmark experiments at the MINERVE reactor of the CEA Cadarache by Gruel et al.40 The samples consisted of a stack of pellets enclosed in two Zircaloy-4 containers. The pellets were produced from a mixture of depleted UO2 powder and silver powder with different enrichments in 109Ag. The transmission resulting from the measurements with one of these pellets is shown in Fig. 8. The experimental transmission is compared with the result of a least squares adjustment in the region between 1 eV and 100 eV using eqn (14). The areal densities of 109Ag, 182,183,186W and 235,238U together with the holes fraction and a normalisation factor were considered as free parameters. The latter accounts for neutron interactions in the Zircaloy-4 cladding material and matrix materials such as oxygen. The results from the fits to the transmission of two pellet samples applying eqn (14) are reported in Table 7. They are compared with the values provided by the manufacturer, which were determined by Inductively Coupled Plasma Mass Spectrometry (ICPMS), and those derived by Šalamon et al.39 Differences between the values obtained in this work and the ones of Šalamon et al.39 are mainly due to the different analysis method. The manufacturer did not specify any amount of tungsten. The results obtained by NRTA reveal the presence of tungsten which is most probably due to the blending process. The differences between the densities for 235U and 238U derived in this work and the values obtained by ICPMS are less than 1%. The areal densities for 109Ag derived in this work are about 4% lower compared to those provided by the manufacturer. A lower 109Ag content is fully consistent with the results of Gruel et al.,40 which suggest an overestimation of the reactivity worth for Ag when using the Ag content derived by ICPMS.
 |
| | Fig. 8 Comparison between the experimental Texp and theoretical transmission TM through a cylindrical pellet sample made from a mixture of silver powder enriched in 109Ag and UO2 powder (sample AGC2 in ref. 39). The experimental data result from measurements carried out by Šalamon et al.39 at GELINA. The theoretical transmission is derived by using eqn (14) for T(E). The bottom plots show the residuals (eqn (5)) as a function of the incident neutron energy. | |
Table 7 Results of least squares fits to data obtained from transmission measurements with cylindrical pellets that were carried out by Šalamon et al.39 at a 10 m station of GELINA. The pellets, referred to as AG9C1 and AG9C2 in ref. 39, were produced from a mixture of UO2 powder with silver powder enriched in 109Ag. The values derived in this work, by ICPMS and by Šalamon et al.39 are compared. The uncertainties of the values derived in this work are due to propagating only uncorrelated uncertainties due to counting statistics. The uncertainties of the ICPMS account only for uncertainty of the pellet diameter, which is 1.2%. Those quoted by Šalamon et al.39 result from propagating systematic components such as uncertainties due to nuclear data and background. The values for 186W are given in ref. 39 without uncertainties
| Nuclide |
n'NRTA |
| AG9C1 |
AG9C2 |
| ICPMS |
This work |
Ref. 39
|
ICPMS |
This work |
Ref. 39
|
|
109Ag |
6.30 (8) × 10−4 |
6.03 (2) × 10−4 |
6.2 (2) × 10−4 |
6.82 (8) × 10−5 |
6.54 (2) × 10−5 |
6.9 (1) × 10−5 |
|
235U |
8.31 (10) × 10−5 |
8.35 (2) × 10−5 |
|
8.39 (10) × 10−5 |
8.45 (20) × 10−6 |
|
|
238U |
1.119 (14) × 10−2 |
1.126 (3) × 10−2 |
1.10 (4) × 10−2 |
1.129 (14) × 10−2 |
1.136 (10) × 10−2 |
1.12 (5) × 10−2 |
|
182W |
|
1.30 (4) × 10−5 |
|
|
6.1 (3) × 10−6 |
|
|
183W |
|
6.6 (2) × 10−6 |
|
|
3.1 (2) × 10−6 |
|
|
186W |
|
1.36 (1) × 10−5 |
1.38 × 10−5 |
|
6.11 (3) × 10−6 |
6.34 × 10−6 |
The results presented in this work, together with the studies mentioned in the introduction, suggest that NRTA is a suitable technique to determine the composition of nuclear spent fuel pellets, in particular to determine the abundance of nuclides that have resonances in the low energy region. Additional complications might be the emission of spontaneous fission neutrons due to the presence of mainly 244Cm and the sample temperature. Spontaneous neutron emission will create a background that is independent of TOF. Such a TOF-independent component can be accurately quantified by using fixed black resonance filters. In any case, a good transmission geometry results in a small solid angle formed by the part of the sample seen by the detector. In addition, the efficiency for fission neutrons compared to the efficiency for 500 eV neutrons is reduced by almost two orders of magnitude when a 6Li glass scintillators is used as neutron detector.
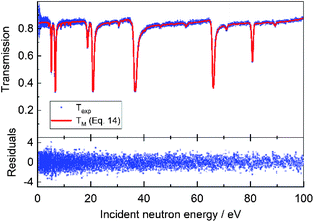
Taking into account transport and safety regulations, only pellets with a cooling time of at least one year can be considered. After such a cooling period the temperature of the pellet will be slightly higher than the room temperature. Evidently to account for the Doppler broadening and to analyse overlapping resonance structures a minimum resolution is required. The resolution depends on the time structure of the pulsed electron beam, the moderator configuration and the flight path length.2,12 The energy resolution, at Full Width Half Maximum (FWHM), for measurements at a 10 m and 50 m transmission station of GELINA is shown in Fig. 9 as a function of neutron energy. This figure includes the FWHM due to Doppler broadening with 238U as target nucleus at 295 K and 350 K. Based on the results obtained in previous works minimum requirements to apply NRA as a NDA technique are described in ref. 41. This study shows that a characterisation of complex materials is feasible at the 10 m station of GELINA where a relative resolution of about ΔE/E ≈ 0.008 is reached. Evidently, the beam intensity should be as high as possible. For the measurements at GELINA the neutron fluence rate at 10 m from the neutron producing target was about 5000 s−1 cm−2 eV−1 at 1 eV.
 |
| | Fig. 9 Comparison of the resolution in FWHM for measurements at a 10 m and 50 m measurement station of GELINA. The total resolution ΔR due to the neutron transport in the moderator and the width of the pulsed electron beam is shown together with the broadening ΔD due to the Doppler effect for a sample at 295 K and 350 K consisting of an element with mass number 238. | |
Conclusions
Transmission experiments were carried out at a 50 m transmission station of the TOF facility GELINA using natural Cu samples. The data obtained with a homogeneous disk in good transmission geometry were used to assess the quality of the resonance parameters for 63Cu and 65Cu in the energy region below 6.5 keV. The best results were obtained using the resonance parameters reported by Tsuchiya et al.10 However, there is still room for improvement to describe the resonance profiles of the 2046 eV and the 6443 eV resonances. The data suggest that some of the parameters recommended by Mughabghab28 and Sobes et al.29 are questionable. Also the parameters recommended in JEFF-3.3 and ENDF/B-VIII.0 should be reviewed.
The importance to account for the holes fraction was demonstrated by measurements with a series of cuboid samples that did not cover the full incident neutron beam. In addition, experiments were carried out to simulate samples with an irregular shape and to validate analytical expressions for the transmission through such samples. The results reveal that sample properties can be derived from resonance transmission profiles without any calibration even when ideal transmission geometry conditions are not fulfilled. This opens perspectives to apply NRTA as an absolute analytical NDA technique to determine the elemental and isotopic composition of complex nuclear material such as spent nuclear fuel pellets.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was performed as part of a collaboration between JAEA and the EURATOM in the field of nuclear material safeguards research and development. This research was implemented under the subsidiary for nuclear security promotion of MEXT. This work was supported by the EUFRAT open access programme of the Joint Research Centre at Geel and partly funded by the European Union's Horizon 2020 Research and Innovation Programme under grant agreement No 847593. We are also indebted to the reviewers of this paper for their constructive remarks.
References
-
H. Postma and P. Schillebeeckx, in Encyclopedia of Analytical Chemistry (chapter a9070), ed. R. A. Meyers, John Wiley & Sons Ltd, 2009 Search PubMed.
-
P. Schillebeeckx, B. Becker, H. Harada and S. Kopecky, JRC Science and Policy Reports, Report EUR 26848 EN, 2014 Search PubMed.
-
H. Postma and P. Schillebeeckx, Neutron Resonance Analysis, in Neutron Methods for Archaeology and Cultural Heritage, ed. N. Kardjilov and G. Festa, Springer Switzerland, 2017, pp. 235–286 Search PubMed.
- H. G. Priesmeyer and U. Harz, Atomkernenergie, 1975, 25, 109–113 CAS.
-
J. W. Behrens, R. A. Schrack, A. D. Carlson and C. D. Bowman, Proc. Conf. Nuclear Cross Sections for Technology, NBS Special Publication, Knoxville, Tennessee, 1980, vol. 594, pp. 436–439 Search PubMed.
- C. D. Bowman, R. A. Schrack, J. W. Behrens and R. G. Johnson, Nucl. Technol., 1984, 67, 162–168 CrossRef.
-
W. Mondelaers and P. Schillebeeckx, Notiziario Neutroni e Luce di Sincrotrone, 2006, vol. 11, pp. 19 – 25 Search PubMed.
- G. Noguere, F. Cserpak, C. Ingelbrecht, A. J. M. Plompen, C. R. Quetel and P. Schillebeeckx, Nucl. Instrum. Methods Phys. Res., Sect. A, 2007, 575, 476–488 CrossRef CAS.
- P. Schillebeeckx, A. Borella, J. C. Drohe, R. Eykens, S. Kopecky, C. Massimi, L. C. Mihailescu, A. Moens, M. Moxon and R. Wynants, Nucl. Instrum. Methods Phys. Res., Sect. A, 2010, 613, 378–385 CrossRef CAS.
- H. Tsuchiya, H. Harada, M. Koizumi, F. Kitatani, J. Takamine, M. Kureta, H. Iimura, A. Kimura, B. Becker, S. Kopecky, K. Kauwenberghs, W. Mondelaers and P. Schillebeeckx, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 767, 364–371 CrossRef CAS.
- B. Becker, S. Kopecky and P. Schillebeeckx, Nucl. Data Sheets, 2015, 113, 171–177 CrossRef.
- P. Schillebeeckx, B. Becker, Y. Danon, K. Guber, H. Harada, J. Heyse, A. R. Junghans, S. Kopecky, C. Massimi, M. Moxon, N. Otuka, I. Sirakov and K. Volev, Nucl. Data Sheets, 2012, 113, 3054–3100 CrossRef CAS.
- H. Harada, F. Kitatani, M. Koizumi, J. Takamine, M. Kureta, H. Tsuchiya, H. Iimura, M. Seya, B. Becker, S. Kopecky and P. Schillebeeckx, Nucl. Data Sheets, 2014, 188, 502 CrossRef.
- K. G. McIntosh, S. D. Reilly and G. J. Havrilla, Spectrochim. Acta, Part B, 2015, 110, 91–95 CrossRef CAS.
-
C. Paradela, G. Alaerts, B. Becker, H. Harada, J. Heyse, F. Kitatani, M. Koizumi, S. Kopecky, W. Mondelaers, A. Moens, P. Schillebeeckx, H. Tsuchiya and R. Wynants, NRD Demonstration Experiments at GELINA, JRC Technical Reports, Report EUR 27507 EN, 2015 Search PubMed.
- C. Paradela, G. Alaerts, B. Becker, J. Heyse, S. Kopecky, A. Moens, W. Mondelaers, P. Schillebeeckx, R. Wynants, H. Harada, F. Kitatani, M. Koizumi and H. Tsuchiya, Characterization of nuclear material by Neutron Resonance Transmission Analysis, Nuovo Cimento, 2015, 38C, 176 Search PubMed.
- C. Paradela, J. Heyse, S. Kopecky, P. Schillebeeckx, H. Harada, F. Kitatani, M. Koizumi and H. Tsuchiya, Neutron resonance analysis for nuclear safeguards and security applications, EPJ Web Conf., 2017, 146, 09002 CrossRef.
- B. Becker, S. Kopecky, H. Harada and P. Schillebeeckx, Eur. Phys. J. Plus, 2014, 129, 1–9 CrossRef.
- H. Harada, A. Kimura, F. Kitatani, M. Koizumi, H. Tsuchiya, B. Becker, S. Kopecky and P. Schillebeeckx, J. Nucl. Sci. Technol., 2015, 52, 837–843 CrossRef CAS.
- D. Tronc, J. M. Salomé and K. H. Böckhoff, Nucl. Instrum. Methods Phys. Res., Sect. A, 1985, 228, 217–227 CrossRef CAS.
- J. M. Salomé and R. Cools, Nucl. Instrum. Methods Phys. Res., Sect. A, 1981, 179, 13–19 CrossRef.
- I. Sirakov, B. Becker, R. Capote, E. Dupont, S. Kopecky, C. Massimi and P. Schillebeeckx, Eur. Phys. J. A, 2013, 49, 144 CrossRef.
- B. Becker, C. Bastian, F. Emiliani, F. Gunsing, J. Heyse, K. Kauwenberghs, S. Kopecky, C. Lampoudis, C. Massimi, N. Otuka, P. Schillebeeckx and I. Sirakov, J. Instrum., 2012, 7, 11002 CrossRef.
-
B. Becker, C. Bastian, J. Heyse, S. Kopecky and P. Schillebeeckx, AGS – Analysis of Geel Spectra User's Manual, NEA/DB/DOC, 2014, vol. 4 Search PubMed.
-
M. C. Moxon and J. B. Brisland, GEEL REFIT, a least squares fitting program for resonance analysis of neutron and capture data computer code, AEA-InTec-0630, AERE-R7864, 1991 Search PubMed.
- C. W. Reich and M. S. Moore, Phys. Rev., 1958, 111, 929–933 CrossRef CAS.
- A. M. Lane and R. G. Thomas, Rev. Mod. Phys., 1958, 30, 257–353 CrossRef.
-
S. F. Mughabghab, Atlas of Neutron Resonances, Elsevier Science, 6th edn, 2018, ISBN: 978-0-444-63769-7 Search PubMed.
-
V. Sobes, PhD thesis, Massachusetts Institute of Technology, February 2014, file retrieved from https://ndclx4.bnl.gov/gf/project/endf/, on 22/05/2014.
- S. V. Kapchigashev and Yu. P. Popov, At. Energy, 1963, 15, 120–126 CAS.
- H. Weigmann and J. Winter, Z. Phys., 1968, 213, 411–419 CrossRef CAS.
- J. Julien, R. Alves, S. D. E. Barros, V. D. Huynh, J. Morgenstern and C. Samour, Nucl. Phys. A, 1969, 132, 129–160 CrossRef CAS.
- R. N. Alves, S. De Barros, P. L. Chevillon, J. Julien, J. Morgenstern and C. Samour, Nucl. Phys. A, 1969, 134, 118–140 CrossRef CAS.
- M. S. Pandey and J. B. Garg, Nucl. Sci. Eng., 1976, 60, 399–404 CrossRef CAS.
- H. A. Mook, J. A. Harvey and N. W. Hill, Phys. Rev. B, 1990, 41, 764–765 CrossRef CAS PubMed.
-
https://www.oecd-nea.org/janis/
.
-
Chronological Scientific Tables 2011, National Astron. Obs. Of Japan, 2011, p. 497 Search PubMed.
- M. Berglund and M. E. Wieser, Pure Appl. Chem., 2011, 83, 397–410 CAS.
- L. Šalamon, B. Geslot, J. Heyse, S. Kopecky, P. Leconte, G. Noguere, C. Paradela, P. Schillebeeckx and L. Snoj, J. Radioanal. Nucl. Chem., 2019, 321, 519–530 CrossRef.
- A. Gruel, P. Leconte, D. Bernard, P. Archier and G. Noguère, Nucl. Sci. Eng., 2011, 169, 229–244 CrossRef CAS.
-
C. Paradela, G. Alaerts, J. Heyse, S. Kopecky, L. Šalamon, P. Schillebeeckx, R. Wynants, H. Harada, F. Kitatani, M. Koizumi, M. Kureta and H. Tsuchiya, Neutron Resonance Analysis System Requirements, JRC Technical Reports, EUR 28239 EN, 2016 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Stefan
Kopecky
b,
Gery
Alaerts
b,
Hideo
Harada
a,
Stefan
Kopecky
b,
Gery
Alaerts
b,
Hideo
Harada
 a,
Jan
Heyse
b,
Fumito
Kitatani
a,
Gilles.
Noguere
c,
Carlos
Paradela
b,
Lino
Šalamon
bcd,
Peter
Schillebeeckx
*b,
Harufumi
Tsuchiya
a,
Jan
Heyse
b,
Fumito
Kitatani
a,
Gilles.
Noguere
c,
Carlos
Paradela
b,
Lino
Šalamon
bcd,
Peter
Schillebeeckx
*b,
Harufumi
Tsuchiya
 *a and
Ruud
Wynants
b
*a and
Ruud
Wynants
b


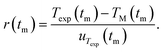
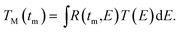
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 370 (80)
370 (80)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (500)
000 (500)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 (397)
525 (397)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 (500)
700 (500)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (750)
500 (750)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 409 (598)
409 (598)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (880)
500 (880)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 (1600)
500 (1600)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 (428)
735 (428)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797
797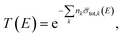
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) tot,k(E) is the Doppler broadened total cross section for neutron interactions with nuclide k and nk the corresponding number areal density. To account for the Doppler broadening, the free gas model was used with an effective temperature Teff = 314 K corresponding to a room temperature T = 293 K and a Debye temperature θD = 343 K. The latter was taken from ref. 37. The areal density for Cu was adjusted by fitting simultaneously transmission dips due to resonances in 63Cu and 65Cu and using the isotopic composition of natural Cu recommended in ref. 38.
tot,k(E) is the Doppler broadened total cross section for neutron interactions with nuclide k and nk the corresponding number areal density. To account for the Doppler broadening, the free gas model was used with an effective temperature Teff = 314 K corresponding to a room temperature T = 293 K and a Debye temperature θD = 343 K. The latter was taken from ref. 37. The areal density for Cu was adjusted by fitting simultaneously transmission dips due to resonances in 63Cu and 65Cu and using the isotopic composition of natural Cu recommended in ref. 38.
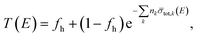


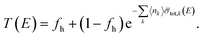
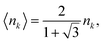
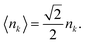
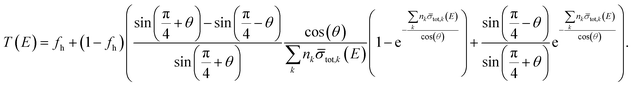
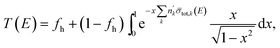
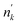 the volume number density of nuclide k multiplied by the rod diameter or the areal number density corresponding to the maximum thickness. Eqn (14) can also be written as:
the volume number density of nuclide k multiplied by the rod diameter or the areal number density corresponding to the maximum thickness. Eqn (14) can also be written as: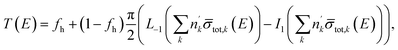
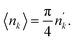

 derived from the fit and the corresponding reference values are given together with the holes fraction fh. The uncertainty of the ratio is the combined uncertainty of the fitted value and the one of the reference value. The uncertainties of the fitted values result from propagating only the uncorrelated uncertainties due to counting statistics
derived from the fit and the corresponding reference values are given together with the holes fraction fh. The uncertainty of the ratio is the combined uncertainty of the fitted value and the one of the reference value. The uncertainties of the fitted values result from propagating only the uncorrelated uncertainties due to counting statistics