 Open Access Article
Open Access ArticleOrganic acids under pressure: elastic properties, negative mechanical phenomena and pressure induced phase transitions in the lactic, maleic, succinic and citric acids†
Francisco
Colmenero

Instituto de Estructura de la Materia (IEM-CSIC), C/Serrano, 113 – 28006 Madrid, Spain. E-mail: francisco.colmenero@iem.cfmac.csic.es
First published on 27th July 2020
Abstract
A detailed study of the behavior under pressure of four important organic acids using the first-principles solid-state methodology is presented. These organic acids are the L-(+)-lactic, maleic, succinic and citric acids. The citric acid monohydrate is also investigated. The computed crystal structures and associated X-ray diffraction patterns are in very good agreement with their experimental counterparts. The elastic tensors of these materials are determined using the finite deformation method and the mechanical stability of their structures is studied. A set of relevant elastic properties is obtained in terms of the computed elastic tensors. This set includes the bulk, shear and Young moduli, the Poisson's ratio, the ductility, hardness and anisotropy indices and the bulk modulus pressure derivatives. In the solid state, these organic acids are shown to be stable, relatively weak and very anisotropic materials and, with the exception of citric acid monohydrate, all of them exhibit the negative Poisson's ratio (NPR) phenomenon. The deformation of the crystal structures under isotropic pressures and anisotropic stresses is then evaluated and analyzed. The organic acids considered display the negative linear compressibility (NLC) phenomenon in several narrow pressure ranges. The presence of large NLC effects in these materials is mainly related to the onset of pressure induced phase transitions or sudden structural rearrangements. The lactic acid exhibits a large NLC effect under the effect of isotropic pressures due to the proximity of a pressure induced phase transition occurring at a pressure of P ∼ 1.0 GPa. The maleic acid shows NLC under isotropic pressures of the order of P ∼ 1.1 GPa but no phase transition is observed. Under anisotropic stresses directed along the minimum Poisson's ratio direction, maleic acid also shows a large NLC effect at small external pressures of P ∼ 0.1 GPa. Succinic acid displays small NLC effects in several pressure ranges under isotropic pressures but large NLC values under anisotropic stresses directed along the minimum NPR direction because it undergoes a pressure induced phase transition near P ∼ 1.5 GPa. Finally, the citric acid shows small NLC values for negative isotropic pressures near −0.5 GPa and a large NLC effect under low anisotropic stresses (P ∼ 0.1 GPa) which is accompanied by the breaking of one intramolecular hydrogen bond present in this material at zero pressure.
1 Introduction
The investigation of the behavior of solid materials under pressure is highly relevant in many scientific research fields such as geoscience,1–16 planetary science and astrophysics,17–28 condensed matter physics29–41 and materials science.42–78 The study of carbon, hydrocarbon, and general organic materials under pressure has played a remarkably important role in these fields and also in biochemistry, biophysics and organic chemistry and physics.2,15,16,18,19,27,28,51,53–55,57–59,67–118 Significant progress has been achieved in the last decades in the field of high pressure crystallography and crystal engineering of organic materials.19,35,87,88,96,97,102–104,116–118 The earlier studies of matter under pressure were an immediate consequence of the fact that most part of the matter in the Earth, solar system and extra-solar solid bodies are subjected to extreme conditions as very high pressures. In geosciences, the influence of pressure is fundamental for understanding the formation and transformation of rocks and minerals. Two fascinating findings at the end of nineteenth century strongly stimulated the research of materials under pressure in materials science and condensed matter physics. The first is the discovery of materials displaying anomalous mechanical behaviors and negative mechanical phenomena such as the negative Poisson's ratio42,44,45 (NPR) and negative linear compressibility52,61,62 (NLC) effects. These materials, showing anomalous variations of their dimensions as a result of the application of pressure, have found an immense range of potential applications as the development of ultrasensitive pressure detectors, robust shock-absorbing composites, pressure-driven actuators, optical telecommunication cables, artificial muscles, next generation body armor and devices for biomedical applications.45,48,50,53,55,60,70 The second is the discovery that compression turns many non-superconductor (and even non-conductor) materials into superconductors.32–34,36,37,40 One of the most important underlying reasons for the wide dissemination of high pressure research is the possibility of exploiting the changes in the chemical nature and structure of solid materials induced by pressure. The pressure induced phase transitions and structural transformations may be advantageously used, for example, in high-pressure synthesis, mechanochemistry and nanotechnology.35,119–133 Mechanically responsible organic crystals showing macroscopic motion as a response to pressure or deformation are very interesting due to their potential applications in nanotechnology as organic actuators.98,130–133The mechanical response of molecular crystals, polymers and organic materials related to living organism physiology is of direct and enormous interest for the human being. The interest in the research of the effect of high pressure on living systems was originated by the discovery of piezophile organisms in the deep marine environments.134–139 The corresponding studies involved not only the investigation of the pressure adaptation mechanisms of these organisms but also the possible role of high pressure in the origin of life.140–142 In the research of organic materials under pressure, the main purpose is generally the study of the modification of the molecular structure and properties of the material under study associated to changes in the noncovalent interactions present in the system, although the production and analysis of drastic structural changes and the detection of phase transitions is also extremely interesting. The effect of pressure in the structure and function of many organic compounds82–115,143–146 including low molecular-weight biomolecules such as peptides, lipids and saccharides and macromolecules such as proteins, nucleic acids and polysaccharides has been investigated at length, as well as the pressure induced modifications of the interactions among many of them (for example the interactions of proteins and lipids in biological membranes143–145,147–153). The mechanical effects of pressure on compounds of biological interest have been utilized in a plethora of applications in biomedicine and biotechnology.79,100,143–146 Very successful applications of the use of high pressure have been achieved in the pharmaceutical103,104,154–157 and food industries89,95,106,158–167 for the manufacturing, decontamination, sterilization, disinfection, sanitization, conservation and low volume storage of chemical products and foods.
Despite of the large amount of effort devoted to the study of the effects of pressure in organic materials, it is surprising to find that detailed studies involving the determination of the mechanical properties together with the study of the mechanical stability and behavior under pressure of a good series of important prototypical organic materials have not been published, saving the cases of the recent studies concerning the cyclic oxocarbon acids70,73 and oxalic acid.71,72 The main purpose of this work is to provide such study for four very important organic acids. These organic acids are one monocarboxylic acid (L-(+)-lactic acid), two dicarboxylic acids (maleic and succinic acids) and one tricarboxylic acid (citric acid). Although the mechanical behavior of many polymers based on these compounds and related systems has been studied, the mechanical properties of these materials are completely unknown. These materials have crucial biological roles, are important reagents in synthetic organic chemistry, have a great number of medical and technological applications and are widely used in the food and pharmaceutical industries. In this work, first-principles solid-state methods based in Density Functional Theory (DFT) employing large plane wave basis sets and pseudopotentials will be employed. In the computations, the representative volume element of the materials considered is the unit cell. Periodic boundary conditions are applied in the calculations.168,169 Thus, the organic acids studied in this paper are modelized as infinite and space unconstrained systems. Theoretical methods of different degree of complexity, ranging from empirical force field approaches to fully featured quantum theory based methods as those used in this work have been employed in the study of the mechanical properties of solid materials.5,8,28,70–78,170–203 The first works concerning the computer modelling of materials displaying negative Poisson's rations (known as auxetic46) were the pioneering papers of Wojciechowski.204 The utilization of large-scale calculations employing state of the art first principles computational modelling techniques for the description of solid-state materials has produced very reliable results and, therefore, this methodology is sufficiently advanced today to predict their mechanical properties in good agreement with experimental measurements. In the first-principles treatment of organic molecular crystals, it is imperative to describe accurately the non-bonding interactions among the atoms forming part of the system205–210 including the dense hydrogen bond network present in the crystal structure of the majority of these materials. In this paper appropriate dispersion corrected energy-density functionals were employed.
In this paper, special care is given to the study of the compressibilities of the considered organic acids. In fact, one of the main reasons for performing this study was to extend the previous studies on the mechanical properties of the oxalic71,72 and cyclic oxocarbon acids.70,73 It was found that these compounds in the solid state exhibit the NPR and NLC phenomena and undergo pressure induced phase transitions for relatively small external pressures. The extremely anomalous mechanical behavior found in these works, raises the question of whether this behavior is a peculiarity of these materials or is a part a more general trend associated to the organic acids. The compressibility is a fundamental material property which measures the variation of the dimensions of a given material with respect to pressure. The isotropic negative linear compressibility (INLC)52,62,70,72,76 phenomenon is an important elastic anomaly in which one dimension of a given material increases upon hydrostatic compression. The anisotropic linear compressibility phenomenon (ANLC),70,71,75–78 however, involves the increase of the dimensions of a given material under the effect of a compressive stress applied along a certain direction. The INLC effect is quantified by means of compressibility associated to a given dimension ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , k
, k![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1/
= 1/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ·(∂
·(∂![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /∂P)P, where P is the external pressure. Conversely, the ANLC phenomenon is measured in terms of the volumetric compressibility along a certain direction, i.e., the directional derivative of the volume with respect to the pressure applied in that direction, kmV = 1/V·(∂V/∂Pm)P. In this case, the pressure is defined in terms of the trace of the stress tensor as
/∂P)P, where P is the external pressure. Conversely, the ANLC phenomenon is measured in terms of the volumetric compressibility along a certain direction, i.e., the directional derivative of the volume with respect to the pressure applied in that direction, kmV = 1/V·(∂V/∂Pm)P. In this case, the pressure is defined in terms of the trace of the stress tensor as 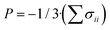 . Since the total volume cannot increase under isotropic compression for thermodynamically and mechanically stable space unconstrained solid materials,43,45,49 the isotropic volumetric compressibility, kV = 1/V·(∂V/∂P)P, must be strictly positive. The positivity of the isotropic volumetric compressibility does not hold for constrained systems43 and in the vicinity of material instabilities as phase transitions45 and appropriate counterexamples have been encountered.211 However, in the case of anisotropic stresses there is not such limitation and the anisotropic volumetric compressibility KmV can be negative.
. Since the total volume cannot increase under isotropic compression for thermodynamically and mechanically stable space unconstrained solid materials,43,45,49 the isotropic volumetric compressibility, kV = 1/V·(∂V/∂P)P, must be strictly positive. The positivity of the isotropic volumetric compressibility does not hold for constrained systems43 and in the vicinity of material instabilities as phase transitions45 and appropriate counterexamples have been encountered.211 However, in the case of anisotropic stresses there is not such limitation and the anisotropic volumetric compressibility KmV can be negative.
This article is organized as follows. The first-principles solid-state methods employed in this work and the precise calculation parameters used are described in Appendix A of the ESI.† The main results obtained for the lactic, maleic, succinic and citric acids are presented and discussed in four separate Subsections of Section 2. The results obtained for citric acid monohydrate are reported in Section 2.5. In each Subsection, the results obtained for the crystal structure of the considered material, its elastic tensor, mechanical stability and mechanical properties are given. The presence of anomalous negative mechanical phenomena and pressure induced phase transitions in these materials and the deformation of the crystal structures under pressure are also studied. Finally, Section 4 contains the main conclusions of this article.
2 Results and discussion
2.1 L-(+)-Lactic acid
The lactic acid, or 2-hydroxypropanoic acid, is a natural monocarboxylic acid which was first isolated from sour milk in 1780 by the Swedish chemist Carl Wilhelm Scheele.212 Berzelius discovered that lactate salts are produced in the muscles during exertion. Wislicenus in 1873 established its molecular structure.212 The participation of Lactobacillus bacteria in the production of lactic acid in fermentation was discovered in 1856, by Louis Pasteur.213 The lactic acid is chiral. The enantiomer studied in this paper is the levogyrous one, L-(+)-lactic acid. It is a product of anaerobic metabolism of sugars in the majority of living organisms and plays a fundamental role as an energy source for neurons in the brain of several mammalian species, including the human one.214–216 Aside of other biological functions, L-lactic acid is the primary endogenous agonist of hydroxycarboxylic acid receptor 1 (HCA1).217 Lactic acid can be produced by fermentation of carbohydrates or synthetically for example from acetaldehyde.212,218,219 Lactic acid is employed in food processing as an additive which is a mild acidulant, as a decontaminant and as a food preservative, and in the pharmaceutical and cosmetic industry. It is also used as a synthetic intermediate in many organic synthesis industries and in various biochemical industries. Lactic acid is an important building block for the production of biodegradable polymers as poly(lactic acid) (PLA) which are among the most frequently used in medical sutures and devices, bioimplants and scaffolds in tissue engineering.220–225 While the mechanical properties of PLA films and many related materials have been studied,226–239 the mechanical properties of solid lactic acid are unknown.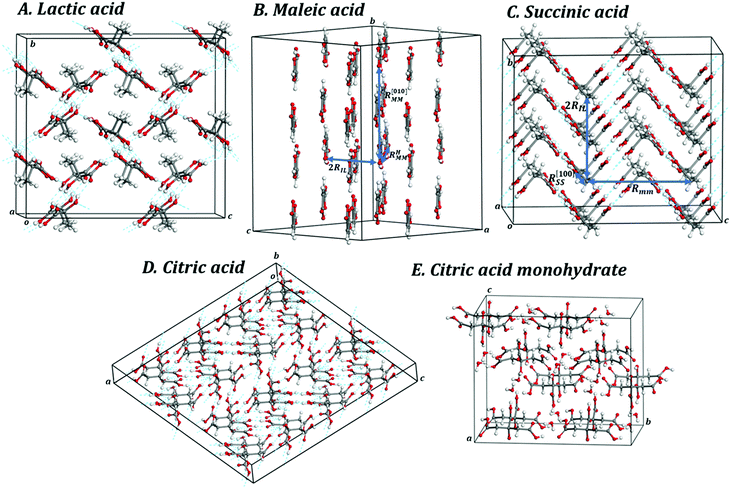 | ||
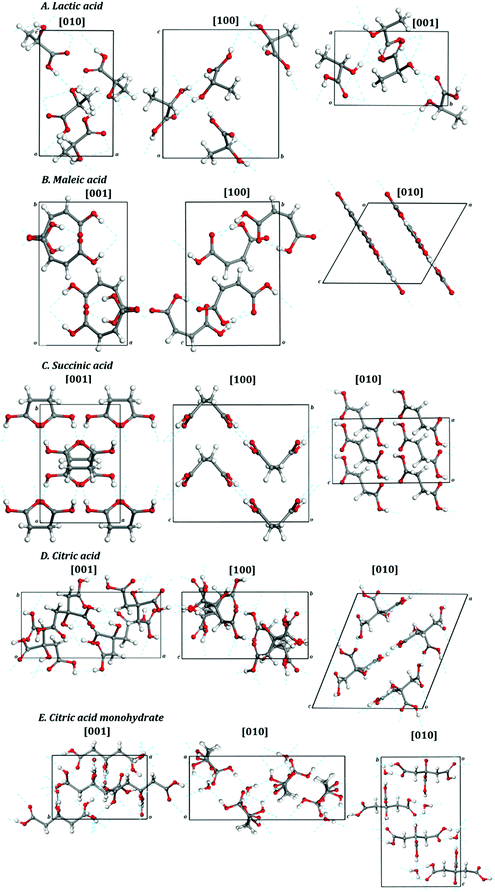
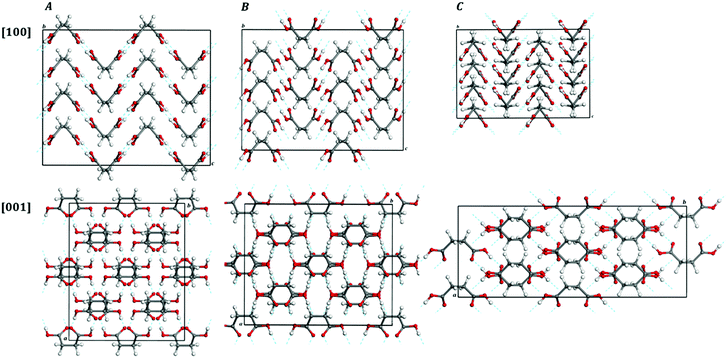
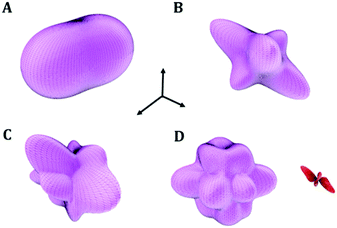
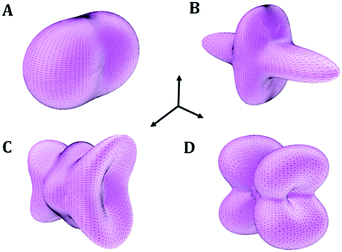
| Fig. 2 Views of 2 × 2 × 2 supercells of (A) L-(+)-lactic acid; (B) maleic acid; (C) succinic acid; (D) citric acid; (E) citric acid monohydrate. Color code: O – red; C – gray; H – white. | ||
| Parameter | a (Å) | b (Å) | c (Å) | α (deg) | β (deg) | γ (deg) | Vol. (Å3) | Dens. (g cm−3) |
|---|---|---|---|---|---|---|---|---|
| L-(+)-Lactic acid240,241 | ||||||||
| PBE | 6.0568 | 8.5894 | 9.6078 | 90.0 | 90.0 | 90.0 | 499.8396 | 1.197 |
| PBE + disp. | 5.4858 | 8.2410 | 9.3290 | 90.0 | 90.0 | 90.0 | 421.7510 | 1.418 |
| Exp.240 | 5.4896(3) | 8.4221(3) | 9.3453(5) | 90.0 | 90.0 | 90.0 | 432.0702 | 1.385 |
| Maleic acid242–245 | ||||||||
| PBE | 8.0760 | 10.5595 | 8.6302 | 90.0 | 126.78 | 90.0 | 589.4946 | 1.308 |
| PBE + disp. | 6.8630 | 10.1247 | 7.3947 | 90.0 | 117.52 | 90.0 | 455.6945 | 1.692 |
| Exp.245 | 7.1511(8) | 10.1107(11) | 7.6405(10) | 90.0 | 119.405(8) | 90.0 | 481.2594 | 1.602 |
| Succinic acid246–251 | ||||||||
| PBE | 6.3299 | 8.8155 | 11.0661 | 90.0 | 97.35 | 90.0 | 612.4274 | 1.281 |
| PBE + disp. | 5.6594 | 8.1169 | 10.3944 | 90.0 | 89.62 | 90.0 | 477.4754 | 1.643 |
| Exp.251 | 5.7015(5) | 8.4154(8) | 10.3538(8) | 90.0 | 90.374(3) | 90.0 | 496.7689 | 1.579 |
| Citric acid252–254 | ||||||||
| PBE | 13.1200 | 5.9182 | 11.76015 | 90.0 | 109.32 | 90.0 | 861.7019 | 1.481 |
| PBE + disp. | 12.8179 | 5.5423 | 11.3389 | 90.0 | 112.13 | 90.0 | 746.1776 | 1.710 |
| Exp.254 | 12.817(16) | 5.628(7) | 11.465(15) | 90.0 | 111.22(10) | 90.0 | 770.9433 | 1.655 |
| Citric acid monohydrate255,256 | ||||||||
| PBE | 6.5500 | 9.4838 | 15.5143 | 90.0 | 90.0 | 90.0 | 963.7298 | 1.448 |
| PBE + disp. | 6.1856 | 9.2915 | 14.9972 | 90.0 | 90.0 | 90.0 | 861.9491 | 1.619 |
| Exp.256 | 6.2343(10) | 9.2882(14) | 15.246(2) | 90.0 | 90.0 | 90.0 | 882.8261 | 1.581 |
A set of interatomic distances and angles in the crystal structure of lactic acid are given in Tables S2 and S3 of the ESI,† compared with the corresponding experimental results.240 The labelling convention used to denote the different atoms in the crystal structure of lactic acid is shown in Fig. S1 of the ESI.† The computed data agrees satisfactorily with the experimental results, despite of the fact that the both set of structural data correspond to different temperatures. The differences in the C–C and C–O distances are smaller than 0.01 Å, except for the C–O double bonds for which the differences are of the order of 0.02 Å. The fact that for the computed C–H, O–H and H⋯O distances, involving hydrogen atoms, there are larger discrepancies with respect to the corresponding experimental values was expected because the experimental structure was determined by refinement from X-ray diffraction data. In general, the experimental hydrogen locations are very unprecise due to the small scattering factor of hydrogen.
As can be observed in Fig. S1 (see also Tables S2 and S3) of the ESI,† there are three non-equivalent hydrogen bonds in lactic acid: O1–H1⋯O3′′′, O3–H3⋯O2′ and O3–H3⋯O3′. In the first one, the donor oxygen atom (O1) is from the OH bond in the carboxylic functional group and the acceptor oxygen atom (O3′′′) is from the OH alcoholic group of a different molecule. In the second and third hydrogen bonds, the donor oxygen atom (O3) is from the alcoholic OH group and the acceptor oxygen atoms are one (O2′) from a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and the other (O3′) from a carboxylic OH group both being located in different molecules.
O bond and the other (O3′) from a carboxylic OH group both being located in different molecules.
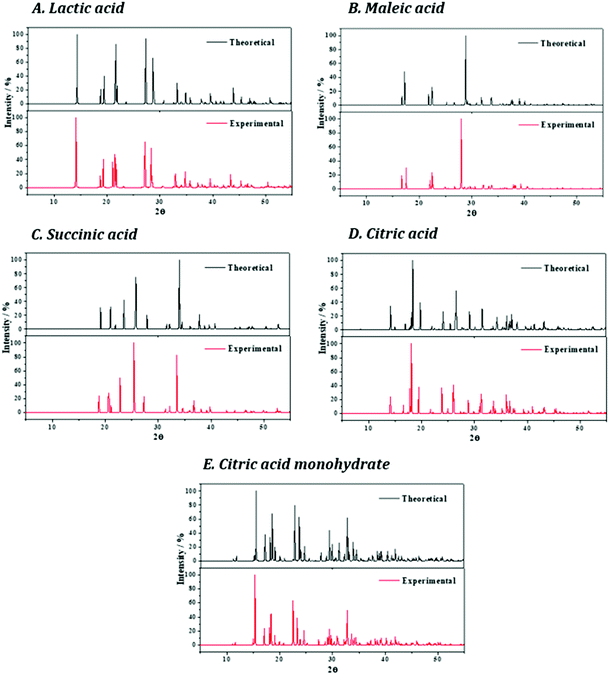
The X-ray powder diffraction pattern of lactic acid was determined from the computed and experimental240 crystal structures. The resulting patterns are given in Fig. 3A and as can be seen, they are in satisfactory agreement as expected from the consistence between the computed and experimental crystal structures.
| ij | C ij | ||||
|---|---|---|---|---|---|
| Lactic acid | Maleic acid | Succinic acid | Citric acid | Citric acid monohydrate | |
| 11 | 13.95 | 38.31 | 23.27 | 21.08 | 22.12 |
| 22 | 18.45 | 35.21 | 19.36 | 30.82 | 52.03 |
| 33 | 16.47 | 13.74 | 21.43 | 25.27 | 31.65 |
| 44 | 8.45 | 7.10 | 13.04 | 13.31 | 4.25 |
| 55 | 9.14 | 20.82 | 13.89 | 10.67 | 11.48 |
| 66 | 15.48 | 11.76 | 6.45 | 13.87 | 7.38 |
| 12 | 7.59 | 9.29 | 10.70 | 6.44 | 6.17 |
| 13 | 5.19 | 19.56 | 12.88 | 7.64 | 7.70 |
| 15 | 0.0 | 22.28 | 2.42 | 3.45 | 0.0 |
| 23 | 9.03 | 4.99 | 14.40 | 12.56 | 4.72 |
| 25 | 0.0 | 6.47 | 6.26 | −4.68 | 0.0 |
| 35 | 0.0 | 7.57 | 8.88 | −3.40 | 0.0 |
| 46 | 0.0 | 6.89 | 0.62 | 8.07 | 0.0 |
The mechanical properties of polycrystalline aggregates of L-(+)-lactic were determined in terms of the elasticity matrix using the Voigt,261 Reuss262 and Hill263 approximations. As in many previous works,70,71,74,76,77,264 the best agreement between the calculated bulk modulus with the single crystal bulk modulus computed from the 4th Birch–Murnaghan equation of state (BM-EOS, see Appendix A in the ESI†) was obtained with the Reuss scheme. The computed mechanical properties in the Reuss approximation together with the bulk modulus and its first two derivatives with respect to pressure extracted from the BM-EOS are reported in Table 3. The calculated bulk modulus, B = 9.82 ± 0.15 GPa, is quite small, a feature common for most organic acid crystals.70,71 Lactic acid in the solid state is a brittle material because the computed ductility index, D = 1.48, is smaller than 1.75.266,267 The calculated Vickers hardness is, H = 0.84 is small and, therefore, lactic acid is a weak material.268 The universal anisotropy index,269AU = 1.38, is quite significant.
| Property | Lactic acid | Maleic acid | Succinic acid | Citric acid | Citric acid monohydrate | |
|---|---|---|---|---|---|---|
| Elastic constants | ||||||
| B (GPa) | Bulk modulus | 9.82 ± 0.15 | 9.16 ± 0.39 | 12.75 ± 0.53 | 13.82 ± 0.41 | 14.56 ± 0.19 |
| G (GPa) | Shear modulus | 6.65 | 1.92 | 5.55 | 8.10 | 8.03 |
| E (GPa) | Young modulus | 16.27 | 5.37 | 14.53 | 20.32 | 20.36 |
| ν | Poisson's ratio | 0.22 | 0.40 | 0.31 | 0.25 | 0.27 |
| D | Ductility index | 1.48 | 4.78 | 2.30 | 1.71 | 1.81 |
| H | Vickers hardness | 0.84 | 0.35 | 0.27 | 0.64 | 0.37 |
| A U | Universal anisotropy index | 1.38 | 25.90 | 2.81 | 1.81 | 1.59 |
| BM-EOS | ||||||
| B (GPa) | Bulk modulus | 12.78 ± 0.56 | 10.35 ± 0.08 | 13.51 ± 0.50 | 13.46 ± 0.36 | 15.66 ± 0.24 |
| B′ | Bulk modulus first derivative | 8.42 ± 1.39 | 3.82 ± 0.07 | 7.78 ± 0.86 | 8.98 ± 0.57 | 8.41 ± 0.34 |
| B′′ (GPa−1) | Bulk modulus second derivative | −1.67 ± 0.23 | −1.86 ± 0.24 | −1.44 ± 0.97 | −2.12 ± 0.78 | 3.12 ± 0.40 |
| χ 2 | χ 2 parameter (fit) | 0.004 | 0.001 | 0.005 | 0.009 | 0.002 |
| ν min | U Lmin | U Tmin | ν max | U Lmin | U Tmin |
|---|---|---|---|---|---|
| Lactic acid | |||||
| −0.27 | (−0.70, −0.71, 0.00) | (0.71, −0.70, 0.00) | 0.59 | (0.61, −0.80, 0.00) | (0.00, 0.00, −1.00) |
| Maleic acid | |||||
| −0.96 | (−0.46, −0.74, −0.49) | (0.00, −0.55, 0.84) | 1.56 | (−0.64, 0.74, −0.22) | (0.00, −0.29, −0.96) |
| Succinic acid | |||||
| −0.26 | (−0.10, −0.69, −0.71) | (0.29, 0.67, −0.69) | 1.07 | (0.63, 0.00, 0.78) | (0.00, 1.00, 0.00) |
| Citric acid | |||||
| −0.23 | (0.46, −0.69, −0.57) | (0.81, 0.59, −0.06) | 0.57 | (0.81, −0.59, −0.02) | (0.36, 0.47, 0.81) |
| Citric acid monohydrate | |||||
| 0.01 | (−0.70, −0.45, 0.55) | (0.71, −0.40, 0.58) | 0.65 | (−0.18, −0.75, 0.63) | (0.11, −0.65, −0.75) |
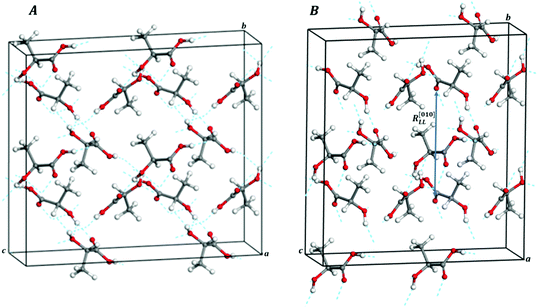 | ||
| Fig. 6 Computed crystal structures of L-(+)-lactic acid under the effect of isotropic pressures: (A) P = 1.026 GPa and (B) P = 1.056 GPa (1 × 2 × 2 supercells). | ||
The b lattice parameter increases again in the pressure range from P = 1.53 to 1.56 GPa. In this case, the increase is much smaller (from 8.60 to 8.64 Å). The estimated compressibility at P = 1.55 GPa is kb ∼ −162.9 TPa−1. The c and a lattice parameters decrease from 7.83 to 7.79 Å and from 5.32 to 5.30 Å, respectively, leading to a decrease of the total volume from 358.98 to 356.69 Å3. Tables S5 and S6 of the ESI† show that the interatomic distances and angles within the lactic molecule units are not altered significantly in this pressure range and that the main bonding change involved is the elongation of the O3–H3⋯O2′ hydrogen bond. However, the change in the H3⋯O2′ distance (0.004 Å) is very small in comparison with the variation in the b lattice parameter, 0.04 Å. The b lattice parameter is equal to the distance between two successive lactic molecules along the [010] crystallographic direction (R[010]LL, see Fig. 6B). The reason for the increase of the b lattice parameter under pressure is, therefore, the enlargement of the non-bonding distances along [010] direction leading to the increase of R[010]LL in the Phase II of solid lactic acid, which is only partially due to the elongation of the O3–H3⋯O2′ hydrogen bond.
2.2 Maleic acid
Maleic acid, or cis-butenedioic acid, is an organic dicarboxylic acid. It is the cis-isomer of butenedioic acid, whereas fumaric acid is the trans-isomer. Maleic acid is habitually derived from the hydrolysis of maleic anhydride which, in turn, is produced synthetically by oxidation of benzene or butane.271 Maleic acid has an exceptionally high ability to form salts with various amino acids (amino acid maleates).178,245 More than 20 salts of this acid with different amino acids have been documented.245 Maleic acid is widely employed in synthetic organic chemistry. For example, it is used industrially for the production of glyoxylic acid by ozonolysis.271 Succinic acid may be produced from maleic acid by hydrogenation. However, its main use is as precursor of fumaric acid. The isomerization may be produced in several ways and must be catalyzed, for example by several chemical reagents, such as mineral acids and thiourea, because the reaction of interconversion, involving a rotation around a double C–C bond, is not spontaneous.271 Maleic acid and polymers based in it, as the polymaleic acid (PMA) and terpolymer of maleic acid (TPMA), are employed in textile industry because are able to establish an esterification reaction with cotton and, at moderate temperatures and in the presence of appropriate catalyzers, can crosslink cotton fibers, leading to a larger durability and improved fabric strength and wash resistance.272,273 While the mechanical properties of polymers formed with maleic acid, materials treated or coated with maleic acid, or related materials have been studied178,245,274,275 the mechanic properties of crystalline maleic acid have not been reported.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–COOH, is shown in Fig. 1B and a picture of a 2 × 2 × 2 supercell of maleic acid is displayed in Fig. 2B. As can be observed in the view from [010] crystallographic direction included in Fig. 1B and in Fig. 2B, the crystal structure of maleic acid is composed of layers formed with hydrogen-bonded maleic acid molecules. Table 1 provides the computed and experimental unit-cell parameters, volume and density. The results are in reasonable agreement with experiment,242–245 the computed unit cell volume being 5.3% smaller than the experimental value given by Rychkov et al.245 As in the case of lactic acid, the main source for this difference must be the fact that the computed crystal structure corresponds to zero temperature and the experimental one to room temperature. The difference could be reduced to a large extent if an experimental determination of the crystal structure at low temperature could be carried out. In fact, volume thermal expansion effects larger than 5% were observed for example for the closely related crystal structure of oxalic acid dihydrate for which low temperature crystal data are available.71 The effect of dispersion interactions in the structure of maleic acid is enormous. As shown in Table 1, the uncorrected PBE functional overestimates the experimental unit-cell volume by nearly 23%.
CH–COOH, is shown in Fig. 1B and a picture of a 2 × 2 × 2 supercell of maleic acid is displayed in Fig. 2B. As can be observed in the view from [010] crystallographic direction included in Fig. 1B and in Fig. 2B, the crystal structure of maleic acid is composed of layers formed with hydrogen-bonded maleic acid molecules. Table 1 provides the computed and experimental unit-cell parameters, volume and density. The results are in reasonable agreement with experiment,242–245 the computed unit cell volume being 5.3% smaller than the experimental value given by Rychkov et al.245 As in the case of lactic acid, the main source for this difference must be the fact that the computed crystal structure corresponds to zero temperature and the experimental one to room temperature. The difference could be reduced to a large extent if an experimental determination of the crystal structure at low temperature could be carried out. In fact, volume thermal expansion effects larger than 5% were observed for example for the closely related crystal structure of oxalic acid dihydrate for which low temperature crystal data are available.71 The effect of dispersion interactions in the structure of maleic acid is enormous. As shown in Table 1, the uncorrected PBE functional overestimates the experimental unit-cell volume by nearly 23%.
The interatomic distances and angles in the computed and experimental245 crystal structures of maleic acid are provided in Tables S8 and S9 of the ESI.† The atom labelling convention employed in these tables is given in Fig. S2 of the ESI.† The calculated distances and angles agree well with the experimental data. The differences in the C–C and C–O distances are smaller than 0.01 Å, except for the C–C and C–O double bonds for which the differences are within 0.02–0.03 Å. There are two non-equivalent hydrogen bonds in the structure of maleic acid, O1–H1⋯O3 and O4–H4⋯O2′′ (Fig. S2, ESI†). The first one is intramolecular, the donor oxygen atom (O1) being from the OH fragment in one of the two carboxylic functional groups and the acceptor oxygen atom (O3) belonging to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of the other carboxylic group. In the second hydrogen bond the donor oxygen atom (O4) is from the OH fragment in the second carboxylic group and the acceptor one (O2′′) is from a C
O bond of the other carboxylic group. In the second hydrogen bond the donor oxygen atom (O4) is from the OH fragment in the second carboxylic group and the acceptor one (O2′′) is from a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in a carboxylic group of other maleic acid molecule.
O bond in a carboxylic group of other maleic acid molecule.
The X-ray powder diffraction patterns of maleic acid determined from the computed and experimental245 crystal structures are shown in Fig. 3B. The agreement between both patterns is very good, providing additional support to the computed crystal structure.
The mechanical properties of polycrystalline maleic acid were obtained using the Voigt,261 Reuss262 and Hill263 approximations. As for lactic acid, the Reuss approximation was chosen as the best because it provided the best agreement between the calculated bulk modulus with the single crystal bulk modulus computed from the 4th Birch–Murnaghan EOS. The mechanical properties obtained with this approximation together with the bulk modulus and its first two derivatives with respect to pressure are provided in Table 3. The calculated bulk modulus, B = 9.16 ± 0.39 GPa, agrees well with the value of B extracted from the BM-EOS, B = 10.35 ± 0.08 GPa. Crystalline maleic acid is ductile because the calculated ductility index, D = 4.8, is greater than 1.75265,266 and is very weak because the computed Vickers hardness, H = 0.35, is very small.267 Maleic acid is very anisotropic mechanically because the associated universal anisotropy index,268AU = 25.90, is extremely large.
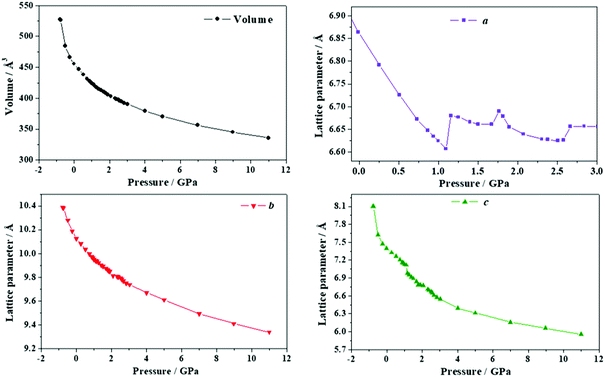 | ||
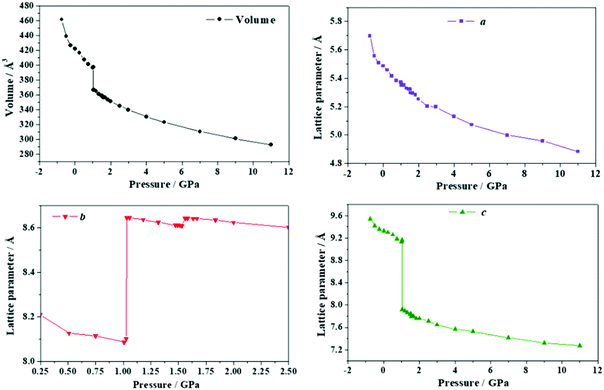
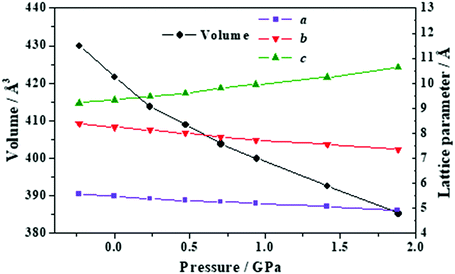
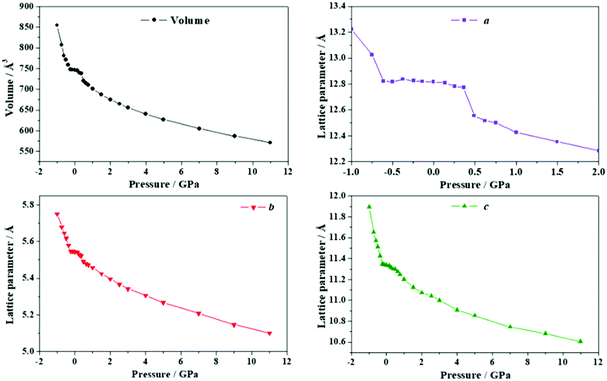
| Fig. 9 Unit cell volume and lattice parameters of maleic acid under the effect of different external isotropic pressures. | ||
The a lattice parameter increases again in the pressure range from P = 1.67 to 1.77 GPa. Its value increases from 6.66 to 6.69 Å and the c lattice parameter decreases from 6.84 to 6.79 Å. In this case, the estimated compressibility at P = 1.73 GPa is ka ∼ −51.8 TPa−1. Finally, from P = 2.58 to 2.84 GPa, the parameter a increases from 6.63 to 6.66 Å (and the c lattice parameter decreases from 6.65 to 6.57 Å). The estimated compressibility at P = 1.61 GPa is kb ∼ −38.2 TPa−1.
The variation of the unit cell structure of maleic acid under increasing external isotropic pressures is displayed in the Animation S2 of the ESI.† As can be seen in the Animation, the maleic acid structural sheets rotate relative to the reference system and the changes are not easily visualizable. However, the variations of the lattice parameters under pressure may be understood from Fig. 2B. The a lattice parameter is identical to twice the interlayer space (RIL) between two sheets in the crystal structure of maleic acid. The b lattice parameter is equal to the distance between two maleic acid molecules belonging to a given sheet along the [010] direction (R[010]MM). Finally, the c lattice parameter is equal to the distance between two maleic acid molecules belonging to a given sheet along the perpendicular (horizontal in Fig. 2B) direction (RHMM). It follows from Table S10 (ESI†) that the INLC in maleic acid arises from the increase of the interlayer space, or equivalently the a lattice parameter, for the three pressure ranges 1.09 to 1.15 GPa, 1.67 to 1.77 GPa and 2.58 to 2.84 GPa. The maleic acid molecule intra-sheet distances decrease consistently under increasing isotropic pressure.
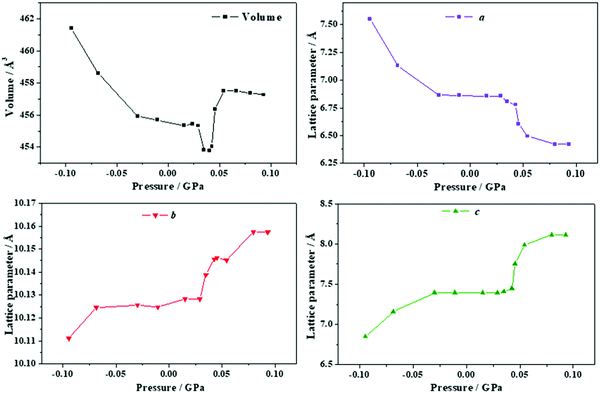 | ||
| Fig. 10 Unit cell volume and lattice parameters of maleic acid under the effect of different stresses applied in the direction of the minimum Poisson's ratio. | ||
The change in the crystal structure of maleic acid under the effect of increasing pressures associated to the anisotropic stresses directed along the minimum Poisson's ratio direction is shown in the Animation S3 of the ESI.† As in the isotropic case, the maleic acid layers rotate relative to the reference system. However, while the rotation in the isotropic case was counterclockwise relative to the b axis, the rotation is clockwise in the present case. The changes in the crystal structure are also opposite to those found for the isotropic case. Now, the interlayer space decreases and the increase in volume is due to the increase of the intrasheet distances between the maleic acid molecule distances. In particular, the distance between two maleic acid molecules belonging to a given sheet along the direction perpendicular to [010] crystallographic direction (referred to as RHMM in the previous section) increases from 7.45 to 7.98 Å while the increase in R[010]MM is insignificantly small.
2.3 Succinic acid
Succinic acid is a dicarboxylic acid276 whose IUPAC name is 1,4-butanedioic acid. Succinic acid has multiple biological roles in living organisms where it takes the form of succinate anion. Succinate has a very important primary biological function as a metabolic intermediate which converts into fumarate by the enzyme succinate dehydrogenase (SDH) in the electron transport chain involved in the process of generation of adenosine triphosphate (ATP).277,278 All metabolic processes which are connected with the tricarboxylic acid cycle (TCA) cycle, including the metabolism of carbohydrates, amino acids, fatty acids, cholesterol, and hemoproteins, depends on the temporary formation of succinate. Succinate also acts as a signaling molecule reflecting the cellular metabolic state. The excess of succinate or fumarate drives the direct or reverse activity of SDH (direct or reverse electron transport) which leads to oxidation or generation of succinate.277,278 Succinate is also a product of the glyoxylate cycle and a re-entry point for the gamma-aminobutyric acid shunt into the TCA cycle.279,280 The biological function of succinic acid is believed to be extremely important and to extend to epigenetics, tumorigenesis, signal transduction, endo- and paracrine modulation and inflammation.277–291 The action of some bacteria as Actinobacillus succinogenes and Anaerobiospirillum succiniciproducens may be exploited to produce succinate in living organisms292 because, under anaerobic conditions, induce the reverse activity of SDH. Succinic acid may be obtained from several synthetic routes276 as the partial hydrogenation of maleic acid but, is mostly produced from biomass via fermentation. Using genetically modified microorganisms, such as Escherichia coli or Saccharomyces cerevisiae, a high-yielding, commercial production of succinic acid from fermentation of glucose has been achieved.293,294 Succinic acid is widely utilized as a safe food additive and as an excipient in pharmaceutical industry.294–296 Succinic acid or succinate salts may be employed to synthesize a large series of organic compounds as 1,4-butanediol, maleic anhydride, succinimide, 2-pyrrolidinone and tetrahydrofuran.276 In the framework of crystal engineering, it has been crystallized with many other molecules in order to develop cocrystals and salts having desirable physicochemical properties.251,296–299 Succinic acid is employed as a precursor of polyesters, as a component of some resins, and to develop biodegradable polymers of interest in tissue engineering.295,300 The characteristics and mechanical properties of many interesting polymers and materials based on, or related to, succinic acid have long been investigated.301–317Tables S12 and S13 of the ESI† give a comparison of the interatomic distances and angles in the computed and experimental251 crystal structures of succinic acid. The atom labelling convention used for succinic acid is shown in Fig. S3 of the ESI.† The computed C–C and C–O bond distances differ from experiment by less than 0.01 Å, except for the C–O double bond in which the difference is about 0.02 Å. For crystalline succinic acid there is only one non-equivalent hydrogen bond, O1–H1⋯O2′ (Fig. S3, ESI†). In the crystal structure of succinic acid, the hydrogen bonding is dual, i.e., each pair of adjacent succinic acid molecules are linked by a pair of symmetry equivalent hydrogen bonds. One hydrogen bond links the oxygen atom of an hydroxyl fragment of a carboxylic group of the first molecule with the oxygen atom in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of a carboxylic group in the second molecule (O1–H1⋯O2′) and the other hydrogen bond relates the oxygen atom of the hydroxyl fragment of the carboxylic group on the second molecule with the oxygen atom in the C
O bond of a carboxylic group in the second molecule (O1–H1⋯O2′) and the other hydrogen bond relates the oxygen atom of the hydroxyl fragment of the carboxylic group on the second molecule with the oxygen atom in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of the carboxylic group in the first molecule (O1′–H1′⋯O2′).
O bond of the carboxylic group in the first molecule (O1′–H1′⋯O2′).
The X-ray powder diffraction patterns of succinic acid obtained in terms of the optimized and experimental251 structures are shown in Fig. 3C and as can be seen they are in good agreement.
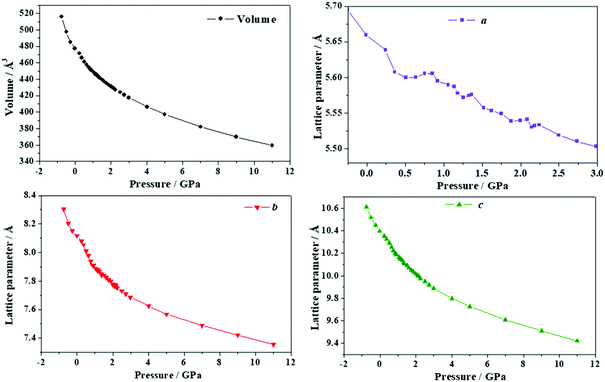 | ||
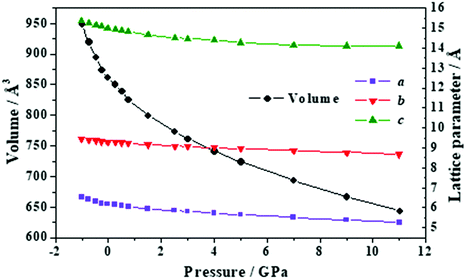
| Fig. 12 Unit cell volume and lattice parameters of succinic acid under the effect of different external isotropic pressures. | ||
The variation of the unit cell structure of succinic acid under increasing external isotropic pressure is displayed in the Animation S4 of the ESI.† The interpretation of the variations of the lattice parameters under pressure may be achieved in a simple way from Fig. 2D. The c lattice parameter is identical to the distance between two successive minima in a given folded sheet (Rmm). According to Table S14 (ESI†), this distance decreases uniformly under pressure and therefore the folds become narrower as pressure increases or, equivalently, the folding angle decreases. The a lattice parameter is equal to the distance between two succinic acid molecules in a given sheet along [100] direction (R[100]SS). Thus, the INLC in succinic acid is related to the increase of this intrasheet distance in the four pressure intervals mentioned in the previous paragraph. The b lattice parameter is twice the space between two consecutive folded sheets or interlayer space (RIL). According Table S14 (ESI†), the interlayer space also decreases when the pressure increases except, as was mentioned in the previous paragraph, in two small pressure regions.
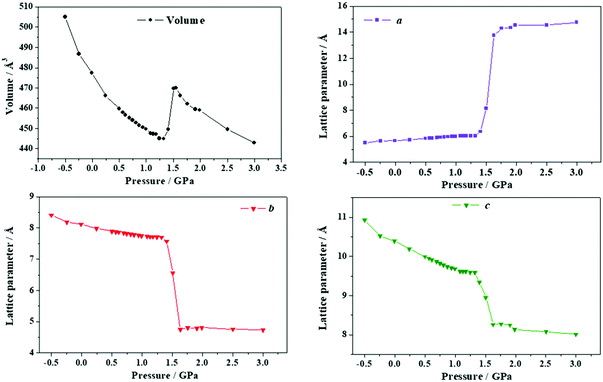 | ||
| Fig. 13 Unit cell volume and lattice parameters of succinic acid under the effect of different stresses applied in the direction of the minimum Poisson's ratio. | ||
2.4 Anhydrous citric acid
Citric acid, or 2-hydroxypropane-1,2,3-tricarboxylic acid, is a weak organic acid.318 His name is due to the fact that it occurs naturally in citrus fruits. It was isolated for the first time from lemon juice in 1784 by the chemist Carl Wilhelm Scheele.319 It can exist either in anhydrous form or as a monohydrate, the last being converted to the first at about 78 °C. Citric acid is present in biologic organisms as the citrate ion and as the mono-hydrogen citrate ion. The citric acid can form diverse citrate salts and may also be esterified at one or more of the carboxylic acid functional groups with different alcohols, to form a variety of mono-, di- and tri-esters. The citrate ion forms chelate complexes with many cations, the alkali metal ones included.318The citric acid is a fundamental intermediate in the tricarboxylic acid cycle279,320 occurring in the metabolism of all aerobic organisms. In this cycle, citrate synthase catalyzes the condensation of oxaloacetate with acetyl coenzyme A (CoA) to form citrate. Then, aconitase catalyses the conversion from citrate to aconitic acid. The series of reactions involved in the TCA to release energy through the oxidation of acetyl-CoA derived from carbohydrates, lipids and proteins, produces nearly two-thirds of the energy derived from food. Citrate can also be transported from the mitochondria into the cytoplasm and transform into acetyl-CoA for fatty acid synthesis. Citrate is a modulator of the conversion regulating allosterically the enzyme acetyl-CoA carboxylase. Large concentrations of citrate in the cytoplasm indicate the presence of enough biosynthetic precursor molecules and inhibits phosphofructokinase and glycolysis.279 Citrate is an essential component of bones, helping to regulate the size of apatite crystals.321 The microbial production of citric acid by several species of fungi as Aspergillus niger from sucrose or glucose is well known from the beginning of nineteenth century and has been exploited widely.318,322 However, citric acid is nowadays also produced synthetically from aconitic or isocitrate salts under high pressure conditions using a reverse nonenzymatic TCA cycle reaction.323 Citric acid is massively produced and used, for instance, as an acidifying, flavoring, cleaning or chelating agent.318,324 It is also used for the development of different materials as biodegradable polymers whose properties including the mechanical ones have been investigated.325–341
Tables S18 and S19 of the ESI† give a comparison of the interatomic distances and angles in the computed and experimental254 crystal structures of citric acid. The atom labelling convention employed ion these tables is displayed in Fig. S4 of the ESI.† The differences of the computed C–C and C–O bond distances with respect to the experimental ones are smaller than 0.01 Å, except for the C–O double bonds for which the differences are about 0.02 Å.
For crystalline citric acid there are six non-equivalent hydrogen bonds (see Tables S18, S19 and Fig. S4 of the ESI†). The hydrogen bonds O1–H5⋯O2′, O3–H6⋯O6′ and O5–H7⋯O4′ link the oxygen atoms of the hydroxyl fragments of the three carboxylic groups with the oxygen atom in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds of carboxylic groups in three different citric acid molecules. The remaining three hydrogen bonds are O7–H8⋯O2, O7–H8⋯O1′ and O7–H8⋯O6 and link the oxygen atom in the OH alcoholic group (O7) with three different oxygen atoms. The O7–H8⋯O2 and O7–H8⋯O6 hydrogen bonds are intramolecular, the acceptor O2 and O6 oxygen atoms belonging to the C
O bonds of carboxylic groups in three different citric acid molecules. The remaining three hydrogen bonds are O7–H8⋯O2, O7–H8⋯O1′ and O7–H8⋯O6 and link the oxygen atom in the OH alcoholic group (O7) with three different oxygen atoms. The O7–H8⋯O2 and O7–H8⋯O6 hydrogen bonds are intramolecular, the acceptor O2 and O6 oxygen atoms belonging to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of carboxylic groups in the same citric acid molecule. The O7–H8⋯O1′ hydrogen bond is intermolecular and the acceptor oxygen atom belongs to the OH fragment of a carboxylic group of a different molecule.
O bond of carboxylic groups in the same citric acid molecule. The O7–H8⋯O1′ hydrogen bond is intermolecular and the acceptor oxygen atom belongs to the OH fragment of a carboxylic group of a different molecule.
Fig. 3D shows that the agreement between the X-ray powder diffraction patterns of citric acid obtained from the optimized and experimental254 structures is very good.
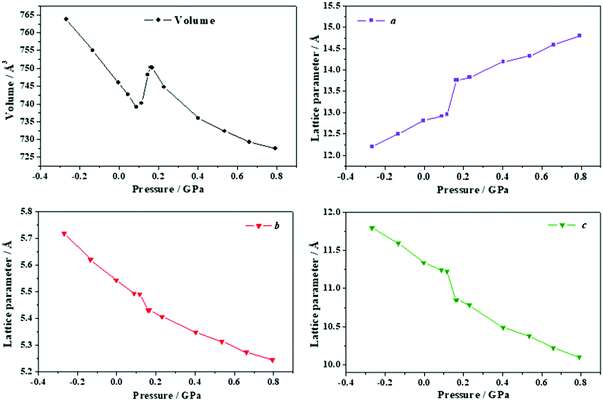 | ||
| Fig. 17 Unit cell volume and lattice parameters of anhydrous citric acid under the effect of different stresses applied in the direction of the minimum Poisson's ratio. | ||
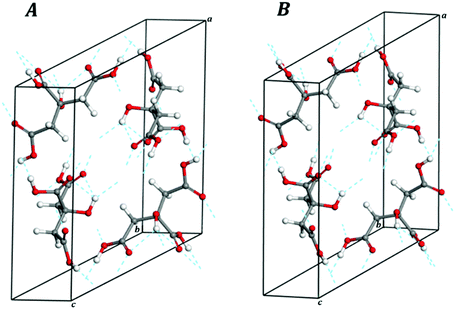 | ||
| Fig. 18 Computed crystal structures of anhydrous citric acid under the effect of external stresses applied along the direction of minimum Poisson's ratio: (A) P = 0.089 GPa and (B) P = 0.168 GPa. | ||
The interatomic distances and angles at P = 0.1163 GPa and P = 0.1613 GPa are given in Tables S22 and S23 of the ESI.† These tables show that the citric acid molecule geometry remains almost the same. The intramolecular hydrogen bond lengths O7⋯O2 and H8⋯O2 in the hydrogen bond O7–H8⋯O2 increase by 0.08 and 0.12 Å, respectively, and the O7–H8⋯O2 angle decreases by nearly 2.3 deg. Thus, the intramolecular hydrogen bond become larger as the pressure increases and finally disappears. However, as in the case of the lactic acid, the increase of the hydrogen bond lengths is very small in comparison with the variation of the lattice parameters and cannot be considered the reason for the large volume increase. Particularly, the a lattice parameter increases by 0.80 Å in passing from 0.10 to 0.16 GPa. The a lattice is identical to the distance between the two citric acid molecules along the [100] crystallographic direction and, therefore, the increase of the unit cell volume under pressure results from the enlargement of the non-bonding distances along [010] which are not compensated by the decrease of the b and c lattice parameters.
Animation S7 of the ESI† displays the variation of the unit cell structure of citric acid under increasing external stresses applied in the direction of minimum Poisson's ratio.
2.5 Citric acid monohydrate
There are seven non-equivalent hydrogen bonds (see Tables S24 and S25 and Fig. S5 of the ESI†) in the crystal structure of citric acid monohydrate. The hydrogen bonds O1–H5⋯Ow′′, O5–H7⋯Ow and O3–H6⋯O2′′ link the oxygen atoms of the hydroxyl fragments of the three carboxylic groups with the oxygen atoms of two water molecules (Ow′′ and Ow) and the oxygen atom from a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of a carboxylic group in another citric acid molecule (O2′′). Two additional hydrogen bonds (O7–H8⋯O2′ and O7–H8⋯O6) link the oxygen atom in the OH alcoholic functional group (O7) with two oxygen atoms from the C
O bond of a carboxylic group in another citric acid molecule (O2′′). Two additional hydrogen bonds (O7–H8⋯O2′ and O7–H8⋯O6) link the oxygen atom in the OH alcoholic functional group (O7) with two oxygen atoms from the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds of two carboxylic groups, the first from a different citric acid molecule (O2′) and the second from the same one (O6). Thus, the second of these hydrogen bonds is intramolecular. The last two hydrogen bonds (Ow–Hw1⋯O7 and Ow-Hw2⋯O4) originate in the oxygen atom of a water molecule (Ow) and end in the oxygen atom of the alcoholic group (O7) and in the oxygen atom of the C
O bonds of two carboxylic groups, the first from a different citric acid molecule (O2′) and the second from the same one (O6). Thus, the second of these hydrogen bonds is intramolecular. The last two hydrogen bonds (Ow–Hw1⋯O7 and Ow-Hw2⋯O4) originate in the oxygen atom of a water molecule (Ow) and end in the oxygen atom of the alcoholic group (O7) and in the oxygen atom of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of a carboxylic group (O4).
O bond of a carboxylic group (O4).
The X-ray powder diffraction patterns of citric acid monohydrate obtained from the optimized and experimental256 structures are highly consistent (see Fig. 3E).
3 Conclusions
The crystal structures and mechanical properties of the L-(+)-lactic, maleic, succinic and anhydrous citric acid and citric acid monohydrated were determined by means of first principles solid-state methods based in density functional theory using large plane wave basis sets and pseudopotential functions. The computed crystal structures were in very good agreement with their experimental counterparts. The calculations were carried out using the PBE energy-density functional supplemented with dispersion corrections to improve the description of the dense network of hydrogen bonds present in the unit cell of these materials. The experimental unit cell volumes of these materials were underestimated by 2.4, 5.3, 3.9, 3.2 and 2.4%, respectively. These results may be compared with those obtained using the uncorrected PBE functional which overestimates the experimental data enormously by 15.7, 22.5, 23.3, 11.8, 9.2%, respectively, due to the inaccurate description of dispersion interactions. The remaining differences with respect to experiment may be attributed mainly to the fact that the experimental structures were determined at room temperature and the first principles results correspond to zero temperature. Low temperature experimental studies of the crystal structures of these materials could reduce to a large extent the differences. For example, very large thermal expansion effects in the crystal structures of related organic materials as oxalic acid have been found.71,345 The good agreement of the X-ray powder diffraction patterns of these materials determined from the optimized and experimental crystal structures provided additional support for the computed structures.The set of organic materials considered includes one mono-, two di- and one tri-carboxylic acids in order to provide diversity and generality to the study of the mechanical behavior of organic acids, thus extending the previous studies of the cyclic oxocarbon acids70,73 and oxalic acid.71,72 These organic acids have extremely important biological functions and are widely utilized in synthetic organic chemistry, crystal and tissue engineering, polymer technology and in the food and pharmaceutical industries. In the majority of these fields, the research on the effects of pressure is growing very fast. However, the lack of very complete studies for a series of prototypical important systems to be used as models is a significant gap in this research. In fact, the mechanical properties and stability and the behavior of these materials under pressure is almost completely unknown. The elastic tensors of these materials were determined using the finite deformation method and the mechanical stability of their structures was studied. A set of relevant elastic properties was derived in terms of the computed elastic tensors. This set includes the bulk, shear and Young moduli, the Poisson's ratio, the ductility, hardness and anisotropy indices and the bulk modulus pressure derivatives. In the solid state, these organic acids are shown to be stable, weak and very anisotropic materials and, with the exception of citric acid monohydrate, all of them exhibit the negative Poisson's ratio (NPR) phenomenon.
Crystalline materials possessing a normal mechanical behavior commonly show decreasing unit cell volumes and lattice parameters under compression and do not present mechanical anomalies. On the other hand, the deltic, squaric, croconic and α- and β-oxalic acids and oxalic acid dihydrate exhibit a rich set of mechanical anomalies, including the NPR and NLC phenomena, as well as pressure induced phase transitions for relatively small external pressures.70–74 This study has demonstrated that the lactic, maleic, succinic and anhydrous citric acids also show negative mechanical phenomena and pressure induced phase transitions. Therefore, it seems that the extremely anomalous mechanical behavior is the norm rather than the exception for the organic acids in the solid state. The mechanical properties of materials belonging to other important organic compound types as alcohols, esters, aldehydes, ketones, amines and amides could be also very interesting and should be investigated in detail.
The NLC effects in these materials are primarily associated to the onset of pressure induced phase transitions or sudden structural rearrangements. L(+)-Lactic acid shows a large NLC effect under isotropic pressures due to the fact that it undergoes a pressure induced phase transition occurring at a pressure of P ∼ 1.0 GPa. The maleic acid exhibits NLC under isotropic pressures of the order of P ∼ 1.1 GPa but no phase transition is observed. Under anisotropic stresses directed along the minimum Poisson's ratio direction, maleic acid also shows a large NLC effect at small external pressures of P ∼ 0.1 GPa. Succinic acid displays small NLC effects under isotropic pressures but large negative compressibilities under anisotropic stresses directed along minimum NPR direction because it undergoes a pressure induced phase transition near P ∼ 1.5 GPa. Finally, the citric acid shows small NLC values for negative isotropic pressures near −0.5 GPa and a large NLC effect under low anisotropic stresses (P ∼ 0.1 GPa) which is accompanied by the breaking of one of the intramolecular hydrogen bonds present in this material at zero pressure.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The supercomputer time provided by the CTI-CSIC center is greatly acknowledged. The author wants to thank the help of Dr V. Timón and A. M. Fernández and for their help and for revising the manuscript.Notes and references
- (a) R. M. Hazen, Am. Mineral., 1977, 62, 286–295 CAS; (b) R. Jeanloz and R. M. Hazen, Nature, 1983, 304, 620–623 CrossRef CAS; (c) R. M. Hazen and L. W. Finger, J. Appl. Phys., 1984, 56, 1838–1840 CrossRef CAS; (d) L. W. Finger, R. M. Hazen and A. M. Hofmeister, Phys. Chem. Miner., 1986, 13, 215–220 CrossRef CAS; (e) R. J. Angel, R. M. Hazen, T. C. McCormick, C. T. Prewitt and J. R. Smyth, Phys. Chem. Miner., 1988, 15, 313–318 CrossRef CAS; (f) N. Ross and R. M. Hazen, Phys. Chem. Miner., 1990, 17, 228–237 CrossRef CAS; (g) R. Jeanloz and R. M. Hazen, Science, 1993, 261, 923–924 CrossRef CAS PubMed; (h) R. M. Hazen, R. T. Downs and L. W. Finger, Science, 1996, 272, 1769–1771 CrossRef CAS PubMed; (i) R. M. Hazen and A. Navrotsky, Am. Mineral., 1996, 81, 1021–1035 CAS; (j) H. Yang, R. M. Hazen, C. T. Prewitt, L. W. Finger, R. Lu and R. J. Hemley, Am. Mineral., 1998, 83, 288–299 CrossRef CAS.
- R. M. Hazen, R. T. Downs, A. P. Jones and L. Kah, Carbon Mineralogy and Crystal Chemistry, Rev. Mineral. Geochem., 2013, 75, 7–46 CrossRef CAS.
- L. G. Liu, Phys. Earth Planet. Int., 1986, 42, 255–262 CrossRef CAS.
- (a) K. J. Kingma, R. E. Cohen, R. J. Hemley and H. K. Mao, Nature, 1995, 374, 243–245 CrossRef CAS; (b) T. S. Duffy, C.-S. Zha, R. T. Downs, H. K. Mao and R. J. Hemley, Nature, 1995, 378, 170–173 CrossRef CAS; (c) H.-R. Wenk, S. Matthies, R. J. Hemley, H. K. Mao and J. Shu, Nature, 2000, 405, 1044–1047 CrossRef CAS PubMed.
- (a) L. Stixrude, R. E. Cohen and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 6442–6445 CrossRef CAS PubMed; (b) R. M. Wentzcovitch and L. Stixrude, Am. Mineral., 1997, 82, 663–671 CAS; (c) B. B. Karki and L. Stixrude, J. Geophys. Res., 1999, 104, 13025–13033 CrossRef CAS; (d) L. Stixrude and C. Lithgow-Bertelloni, J. Geophys. Res., 2005, 110, B03204 CrossRef; (e) L. Stixrude, C. Lithgow-Bertelloni, B. Kiefer and P. Fumagalli, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 024108 CrossRef; (f) P. Fumagalli and L. Stixrude, Earth Plan. Sci. Lett., 2007, 260, 212–226 CrossRef CAS; (g) M. Mookherjee and L. Stixrude, Earth Plan. Sci. Lett., 2009, 279, 11–19 CrossRef CAS; (h) S. Stackhouse, L. Stixrude and B. B. Karki, Earth Plan. Sci. Lett., 2010, 289, 449–456 CrossRef CAS; (i) L. Stixrude, Phys. Rev. Lett., 2012, 108, 055505 CrossRef PubMed; (j) N. de Koker, B. B. Karki and L. Stixrude, Earth Plan. Sci. Lett., 2013, 361, 58–63 CrossRef CAS.
- B. Wunder, R. Wirth and M. Gottschalk, Eur. J. Mineral., 2001, 13, 485–495 CrossRef CAS.
- M. Osako, A. Yoneda and E. Ito, Phys. Earth Planet. Int., 2010, 183, 229–233 CrossRef CAS.
- (a) L. Bezacier, B. Reynard, J. D. Bass, J. Wang and D. Mainprice, Tectonophysics, 2010, 494, 201–210 CrossRef; (b) M. Mookherjee and L. Bezacier, Phys. Earth Planet. Int., 2012, 208–209, 50–58 CrossRef CAS.
- S. Schwartz, S. Guillot, B. Reynard, R. Lafay, B. Debret, C. Nicollet, P. Lanari and A. Line Auzende, Lithos, 2013, 178, 197–210 CrossRef CAS.
- M. O. Schrenk, W. J. Brazelton and S. Q. Lang, Rev. Mineral. Geochem., 2013, 75, 575–606 CrossRef CAS.
- F. Deschamps, M. Godard, S. Guillot and K. Hattori, Lithos, 2013, 178, 96–127 CrossRef CAS.
- B. Li and R. C. Liebermann, Phys. Earth Planet. Int., 2014, 233, 135–153 CrossRef.
- T. Pippinger, R. Miletich, H. Effenberger, G. Hofer, P. Lotti and M. Merlini, Phys. Chem. Miner., 2014, 41, 737–755 CrossRef CAS.
- J. A. Padrón-Navarta, A. Tommasi, C. J. Garrido and D. Mainprice, Contrib. Mineral. Petrol., 2015, 169, 35 CrossRef.
- (a) J. F. Kenney, V. G. Kutcherov, N. A. Bendeliani and V. A. Alekseev, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10976–10981 CrossRef CAS PubMed; (b) V. G. Kutcherov, N. A. Bendiliani, V. A. Alekseev and J. F. Kenney, Dokl. Phys. Chem., 2003, 387, 328–330 CrossRef; (c) V. G. Kutcherov, Abiogenic Deep Origin of Hydrocarbons and Oil and Gas Deposits Formation, InTechOpen, London, 2013, DOI:10.5772/51549.
- T. Al Darouich, F. Behar and C. Largeau, Org. Geochem., 2006, 37, 1155–1169 CrossRef CAS.
- Y. A. Dyadin., E. G. Larionov, E. Y. Aladko, A. Y. Manakov, F. V. Zhurko., T. V. Mikina., V. Yu. Komarov and E. V. Grachev, J. Struct. Chem., 1999, 40, 790–795 CrossRef CAS.
- H. Shimizu, T. Kumazaki, T. Kume and S. Sasaki, J. Phys. Chem. B, 2002, 106, 30–33 CrossRef CAS.
- W. F. Kuhs, in High-Pressure Crystallography, ed. A. Katrusiak and P. F. McMillan, Kluwer Academic Publishers, Dordrecht, 2004, pp. 475–494 Search PubMed.
- (a) A. Pommier, T. L. Grove and B. Charlier, Earth Plan. Sci. Lett., 2012, 333–334, 272–281 CrossRef CAS; (b) B. Charlier, T. L. Grove and M. T. Zuber, Earth Plan. Sci. Lett., 2013, 363, 50–56 CrossRef CAS.
- (a) K. Nishida, Y. Kono, H. Terasaki, S. Takahashi, M. Ishii, Y. Shimoyama, Y. Higo, K. Funakoshi, T. Irifune and E. Ohtani, Earth Plan. Sci. Lett., 2013, 362, 182–186 CrossRef CAS; (b) K. Nishida, A. Suzuki, H. Terasaki, Y. Shibazaki, Y. Higo, S. Kuwabara, Y. Shimoyama, M. Sakurai, M. Ushioda, E. Takahashi, T. Kikegawa, D. Wakabayashi and N. Funamori, Phys. Earth Planet. Inter., 2016, 257, 230–239 CrossRef CAS.
- N. Tsujino, Y. Nishihara, Y. Nakajima, E. Takahashi, K. Funakoshi and Y. Higo, Earth Plan. Sci. Lett., 2013, 375, 244–253 CrossRef CAS.
- N. L. Chabot, E. A. Wollack, R. L. Klima and M. E. Minitti, Earth Plan. Sci. Lett., 2014, 390, 199–208 CrossRef CAS.
- Z. Jing, Y. Wang, Y. Konoc, T. Yu, T. Sakamaki, C. Park, M. Rivers, S. R. Sutton and G. Shen, Earth Plan. Sci. Lett., 2014, 396, 78–87 CrossRef CAS.
- M. Laneuville, M. A. Wieczorek, D. Breuer, J. Aubert, G. Morard and T. Rückriemen, Earth Plan. Sci. Lett., 2014, 400, 251–260 CrossRef.
- J. A. Cartwright, U. Ott, S. Herrmann and C. B. Agee, Earth Plan. Sci. Lett., 2014, 400, 77–87 CrossRef CAS.
- L. J. Conway and A. Hermann, Geoscience, 2019, 9, 227 CAS.
- (a) A. R. Oganov, R. J. Hemley, R. M. Hazen and A. P. Jones, Rev. Mineral. Geochem., 2013, 75, 47–77 CrossRef CAS; (b) G. Saleh and A. Oganov, Sci. Rep., 2016, 6, 32486 CrossRef CAS PubMed; (c) A. S. Naumova, S. V. Lepeshkin and A. R. Oganov, J. Phys. Chem. C, 2019, 123, 20497–20501 CrossRef CAS.
- H. G. Drickamer and C. W. Frank, Electronic Transitions and the High Pressure Chemistry and Physics of Solids, Chapman and Hall, London, 1973 Search PubMed.
- (a) R. M. Hazen and L. W. Finger, J. Appl. Phys., 1979, 50, 6826–6828 CrossRef CAS; (b) H. K. Mao, R. M. Hazen and P. M. Bell, J. Appl. Phys., 1981, 52, 4572–4574 CrossRef CAS; (c) H. K. Mao, A. P. Jephcoat, R. J. Hemley, L. W. Finger, C. S. Zha, R. M. Hazen and D. E. Cox, Science, 1988, 239, 1131–1134 CrossRef CAS PubMed; (d) R. M. Hazen, D. C. Palmer, L. W. Finger, G. D. Stucky, W. T. A. Harrison and T. E. Gier, J. Phys.: Condens. Matter, 1994, 6, 1333 CrossRef CAS.
- P. P. Edwards and F. Hensel, Nature, 1997, 388, 621–622 CrossRef CAS.
- (a) V. V. Struzhkin, R. J. Hemley, H. K. Mao and Y. A. Timofeev, Nature, 1997, 390, 382–384 CrossRef; (b) R. J. Hemley and N. W. Ashcroft, Phys. Today, 1998, 51, 26–32 CrossRef CAS; (c) R. J. Hemley, Science, 1998, 281, 1296–1297 CAS; (d) R. J. Hemley, G. W. Crabtree and M. V. Buchanan, Phys. Today, 2009, 62, 32–37 CrossRef CAS.
- (a) K. Shimizu, K. Suhara, M. Ikumo, M. I. Eremets and K. Amaya, Nature, 1998, 393, 767–768 CrossRef CAS; (b) K. Shimizu, T. Kimura, S. Furomoto, K. Takeda, K. Kontani, Y. Onuki and K. Amaya, Nature, 2001, 412, 316–318 CrossRef CAS PubMed; (c) K. Shimizu, H. Ishikawa, D. Takao, T. Yagi and K. Amaya, Nature, 2002, 419, 597–599 CrossRef CAS PubMed; (d) K. Shimizu, K. Amaya, N. Suzuki and Y. Ōnuki, Phys. B, 2006, 378–380, 632–635 CrossRef CAS.
- N. W. Ashcroft, Nature, 2002, 419, 569–571 CrossRef CAS PubMed.
- H. Huppertz, Z. Kristallograph, 2004, 219, 330–338 CAS.
- A. Gauzzi, E. Gilioli, F. Licci, A. Prodi, F. Bolzoni, M. Marezio, S. Massidda, F. Bernardini, A. Continenza and P. G. Radaelli, in High-Pressure Crystallography, ed. A. Katrusiak and P. F. McMillan, Kluwer Academic Publishers, Dordrecht, 2004, pp. 429–446 Search PubMed.
- T. Oda, K. Sugimori, H. Nagao, I. Hamada, S. Kagayama, M. Geshim, H. Nagara, K. Kusakabe and N. Suzuki, J. Phys.: Condens. Matter, 2007, 19, 365211 CrossRef CAS PubMed.
- E. Kim, T. Pang, W. Utsumi, V. L. Solozhenko and Y. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 184115 CrossRef.
- R. S. Kumar, E. Kim, O. Tschauner, A. L. Cornelius, M. P. Sulic and C. M. Jensen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 174110 CrossRef.
- R. P. Dias, C. S. Yoo, V. V. Struzhkin, M. Kim, T. Muramatsu, T. Matsuoka, Y. Ohishi and S. Sinogeikin, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 11720–11724 CrossRef CAS PubMed.
- M. K. Schmitt, O. Janka, R. Pöttgen and H. Huppertz, Z. Anorg. Allg. Chem., 2017, 643, 1344–1350 CrossRef CAS.
- R. S. Lakes, Science, 1987, 235, 1038–1040 CrossRef CAS PubMed.
- R. S. Lakes and K. W. Wojciechowski, Phys. Status Solidi B, 2008, 245, 545–551 CrossRef CAS.
- G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823–837 CrossRef CAS PubMed.
- R. S. Lakes, Annu. Rev. Mater. Res., 2017, 47, 63–81 CrossRef CAS.
- K. E. Evans, Endeavour, 1991, 15, 170–174 CrossRef CAS.
- J. N. Grima, R. Jackson, A. Alderson and K. E. Evans, Adv. Mater., 2000, 12, 1912–1918 CrossRef CAS.
- K. E. Evans and A. Alderson, Adv. Mater., 2000, 12, 617–628 CrossRef CAS.
- J. N. Grima and R. Caruana-Gauci, Nat. Mater., 2012, 11, 565–566 CrossRef CAS PubMed.
- (a) J. N. Grima, R. Caruana-Gauci, K. W. Wojciechowski and K. E. Evans, Smart Mater. Struct., 2013, 22, 084015 CrossRef; (b) J. N. Grima, R. Caruana-Gauchi, M. R. Dudek, K. W. Wojciechowski and R. Gatt, Smart Mater. Struct., 2013, 22, 084016 CrossRef; (c) R. Gatt, L. Mizzi, J. I. Azzopardi, K. M. Azzopardi, D. Attard, A. Casha, J. Briffa and J. N. Grima, Sci. Rep., 2015, 5, 8395 CrossRef CAS PubMed.
- E. P. Degabriele, D. Attard, J. N. Grima-Cornish, R. Caruana-Gauci, R. Gatt, K. E. Evans and J. N. Grima, Phys. Status Solidi B, 2019, 256, 1800572 CrossRef.
- (a) R. H. Baughman, S. Stafström, S. Cui and S. O. Dantas, Science, 1998, 279, 1522 CrossRef CAS PubMed; (b) J. A. Kornblatt, E. B. Sirota, H. E. King, R. H. Baughman and C. Cui, Science, 1998, 281, 143 CrossRef.
- G. M. Spinks, G. G. Wallace, L. S. Fifield, L. R. Dalton, A. Mazzoldi, D. de Rossi, I. Khayrullin and R. H. Baughman, Adv. Mater., 2002, 14, 1728–1732 CrossRef CAS.
- (a) L. J. Hall, V. R. Coluci, D. S. Galvao, M. E. Koslov, M. Zhang, S. O. Dantas and R. H. Baughman, Science, 2008, 320, 504–507 CrossRef CAS PubMed; (b) V. R. Coluci, L. J. Hall, M. E. Kozlov, M. Zhang, S. O. Dantas, D. S. Galvao and R. H. Baughman, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 115408 CrossRef.
- A. E. Aliev, J. Oh, M. E. Kozlov, A. A. Kuznetsov, S. Fang, A. F. Fonseca, R. Ovalle, M. D. Lima, M. H. Haque, Y. N. Gartstein, M. Zhang, A. A. Zakhidov and R. H. Baughman, Science, 2009, 323, 1575–1578 CrossRef CAS PubMed.
- R. H. Baughman and A. F. Fonseca, Nat. Mater., 2015, 15, 7–8 CrossRef PubMed.
- (a) E. F. Oliveira, P. A. S. Autreto, C. F. Woellner and D. S. Galvao, Carbon, 2018, 139, 782–788 CrossRef CAS; (b) E. F. Oliveira, P. A. S. Autreto, C. F. Woellner and D. S. Galvao, Comput. Mater. Sci., 2019, 161, 190–198 CrossRef CAS; (c) S. M. Sajadi, C. F. Woellner, P. Ramesh, S. L. Eichmann, Q. Sun, P. J. Boul, C. J. Thaemlitz, M. M. Rahman, R. H. Baughman, D. S. Galvao, C. S. Tiwary and P. M. Ajayan, Small, 2019, 15, 1904747 CrossRef CAS PubMed.
- J. Mu, M. Jung de Andrade, S. Fang, X. Wang, E. Gao, N. Li, S. H. Kim, H. Wang, C. Hou and Q. Zhang, et al. , Science, 2019, 365, 150–155 CAS.
- C. N. Weng, K. T. Wang and T. Chen, Adv. Mater. Res., 2008, 33–37, 807–814 CAS.
- H. Abramovitch, M. Burgard, L. Edery-Azulay, K. E. Evans, M. Hoffmeister, W. Miller, F. Scarpa, C. W. Smith and K. F. Tee, Compos. Sci. Technol., 2010, 70, 1072–1079 CrossRef CAS.
- (a) A. B. Cairns, A. L. Thompson, M. G. Tucker, J. Haines and A. L. Goodwin, J. Am. Chem. Soc., 2012, 134, 4454–4456 CrossRef CAS PubMed; (b) A. B. Cairns, J. Catafesta, C. Levelut, J. Rouquette, A. van der Lee, L. Peter, A. L. Thompson, V. Dmitriev, J. Haines and A. L. Goodwin, Nat. Mater., 2013, 12, 212–216 CrossRef CAS PubMed; (c) S. A. Hodgson, L. Adamson, S. L. Hunt, M. J. Cliffe, A. B. Cairns, A. L. Thompson, M. G. Tucker, N. P. Funnella and A. L. Goodwin, Chem. Commun., 2014, 50, 5264–5266 RSC.
- A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 20449–20465 RSC.
- (a) W. Cai and A. Katrusiak, Nat. Commun., 2014, 5, 4337 CrossRef CAS PubMed; (b) W. Cai, A. Gładysiak, M. Anioła, V. J. Smith, L. J. Barbour and A. Katrusiak, J. Am. Chem. Soc., 2015, 137, 9296–9301 CrossRef CAS PubMed.
- L. Chen, W. Liu, W. Zhang, C. Hu and S. Fan, Appl. Phys. Lett., 2009, 94, 253111 CrossRef.
- J. Qu, M. Kadic and M. Wegener, Extreme Mech. Lett., 2018, 22, 165–171 CrossRef.
- L. Francesconi, A. Baldi, X. Liang, F. Aymerich and M. Taylor, Extreme Mech. Lett., 2019, 26, 1–7 CrossRef.
- J. Hou, B. Deng, H. Zhu, Y. Lan, Y. Shi, S. De, L. Liu, P. Chakraborty, F. Gao and Q. Peng, Carbon, 2019, 149, 350–354 CrossRef CAS.
- (a) L. Xie, T. Sun, C. He, H. An, Q. Qin and Q. Peng, Crystals, 2019, 9, 238 CrossRef CAS; (b) W. Wang, C. He, L. Xie and Q. Peng, Nanomaterials, 2019, 9, 487 CrossRef CAS PubMed.
- Y. Wen, E. Gao, Z. Hu, T. Xu, H. Lu, Z. Xu and C. Li, Nat. Commun., 2019, 10, 2446 CrossRef PubMed.
- F. Colmenero, Mater. Res. Express, 2019, 6, 045610 CrossRef.
- F. Colmenero, Phys. Chem. Chem. Phys., 2019, 21, 2673–2690 RSC.
- F. Colmenero, Mater. Lett., 2019, 245, 25–28 CrossRef CAS.
- F. Colmenero, Mater. Res. Express, 2019, 6, 069401 CrossRef CAS.
- F. Colmenero, Appl. Sci., 2019, 8, 2281–2290 CrossRef.
- F. Colmenero, J. Cobos and V. Timón, J. Phys.: Condens. Matter, 2019, 31, 175701 CrossRef CAS PubMed.
- F. Colmenero, Adv. Theor. Simul., 2019, 2, 19000402 Search PubMed.
- F. Colmenero and V. Timón, J. Mater. Sci., 2020, 55, 218–236 CrossRef CAS.
- F. Colmenero, J. Sejkora and J. Plášil, Sci. Rep., 2020, 10, 7510 CrossRef CAS PubMed.
- F. Meersman, I. Daniel, D. H. Bartlett, R. Winter, R. Hazael and P. F. McMillan, Rev. Mineral. Geochem., 2013, 75, 607–648 CrossRef CAS.
- (a) E. C. Pattee and G. G. Brown, Ind. Eng. Chem., 1934, 26, 511–515 CrossRef CAS; (b) J. D. Lindsay and G. G. Brown, Ind. Eng. Chem., 1935, 27, 817–820 CrossRef CAS.
- (a) B. H. Sage and W. N. Lacey, Ind. Eng. Chem., 1934, 26, 1103–1106 Search PubMed; (b) B. H. Sage, W. N. Lacey and J. G. Schaafsma, Ind. Eng. Chem., 1934, 26, 214–217 CrossRef CAS; (c) B. H. Sage, Ind. Eng. Chem., Anal. Ed., 1933, 5, 261–263 CrossRef CAS; (d) B. H. Sage, Studies of Thermal and Physical Properties of Hydrocarbons, PhD thesis, California Institute of Technology, Pasadena, California, 1934.
- K. Suzuki, Y. Taniguchi and Y. Miyosawa, J. Biochem., 1962, 72, 1087–1091 CrossRef PubMed.
- R. K. Williams and C. Shen, Arch. Biochem. Biophys., 1972, 152, 606–612 CrossRef CAS PubMed; U. Sondermann, A. Kutoglu and H. Bässler, J. Phys. Chem., 1985, 89, 1735–1741 CrossRef.
- (a) R. B. Macgregor, R. M. Clegg and T. M. Jovin, Biochemistry, 1985, 24, 5503–5510 CrossRef CAS PubMed; (b) R. B. Macgregor, Biochem. Biophys. Res. Commun., 1990, 170, 775–778 CrossRef CAS PubMed; (c) R. B. Macgregor, Biochim. Biophys. Acta, 1992, 1129, 303–308 CrossRef CAS PubMed; (d) J. Q. Wu and R. B. Macgregor, Biochemistry, 1993, 32, 12531–12537 CrossRef CAS PubMed; (e) J. Q. Wu and R. B. Macgregor, Biopolymers, 1995, 35, 369–376 CrossRef CAS PubMed; (f) R. B. Macgregor, Biopolymers, 1996, 38, 321–327 CrossRef CAS PubMed; (g) R. B. Macgregor, Biopolymers, 1998, 48, 253–263 CrossRef CAS PubMed.
- (a) D. N. Dubins, A. Lee, R. B. Macgregor and T. V. Chalikian, J. Am. Chem. Soc., 2001, 123, 9254–9259 CrossRef CAS PubMed; (b) R. B. Macgregor, Biochim. Biophys. Acta, 2002, 1595, 266–276 CrossRef CAS PubMed; (c) G. Rayan and R. B. Macgregor, J. Phys. Chem. B, 2005, 109, 15558–15565 CrossRef CAS PubMed; (d) T. V. Chalikian and R. B. Macgregor, Phys. Life Rev., 2007, 4, 91–115 CrossRef; (e) G. Rayan and R. B. Macgregor, Biophys. Chem., 2009, 144, 62–66 CrossRef CAS PubMed; (f) G. Rayan, A. D. Tsamaloukas, R. B. Macgregor and H. Heerklotz, J. Phys. Chem. B, 2009, 113, 1738–1742 CrossRef CAS PubMed; (g) A. R. Amiri and R. B. Macgregor, Biophys. Chem., 2011, 156, 88–95 CrossRef CAS PubMed; (h) G. Rayan and R. B. Macgregor, Biophys. Chem., 2015, 199, 34–38 CrossRef CAS PubMed.
- R. M. Hazen, H. K. Mao, L. W. Finger and P. M. Bell, Appl. Phys. Lett., 1980, 37, 288–289 CrossRef CAS.
- C. E. Kundrot and F. M. Richards, J. Appl. Crystallogr., 1986, 19, 208–213 CrossRef CAS.
- (a) A. Katrusiak, Cryst. Res. Technol., 1991, 26, 523–531 CrossRef CAS; (b) A. Katrusiak and Z. Dauter, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1996, 52, 607–608 CrossRef CAS PubMed; (c) A. Katrusiak, High-pressure crystallography, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 135–148 CrossRef CAS PubMed; (d) W. Cai and A. Katrusiak, CrystEngComm, 2012, 14, 4420–4424 RSC; (e) E. Patyk and A. Katrusiak, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, s369 Search PubMed; (f) K. Ostrowska, M. Kropidlowska and A. Katrusiak, Cryst. Growth Des., 2015, 15, 1512–1517 CrossRef CAS.
- (a) R. M. Siegoczynski, High Press Res., 1994, 13, 89–92 CrossRef; (b) R. Kościesza, A. J. Rostocki, A. Kos, D. B. Tefelski, R. M. Siegoczyński and L. Zych, High Pres. Res., 2007, 27, 51–55 CrossRef; (c) D. B. Tefelski, A. J. Rostocki, A. Kos, R. Kościesza and R. M. Siegoczyński, High Pres. Res., 2007, 27, 57–61 CrossRef CAS; (d) R. Kosciesza, R. M. Siegoczynski, A. J. Rostocki, D. B. Tefelski, A. Kos and W. Ejchart, J. Phys.: Conf. Ser., 2008, 121, 142005 CrossRef; (e) D. B. Tefelski, R. M. Siegoczyński, A. J. Rostocki, A. Kos, R. Kościesza and K. Wieja, J. Phys.: Conf. Ser., 2008, 121, 142004 CrossRef; (f) R. Tarakowski, A. Malanowski, R. Kościesza and R. M. Siegoczyński, J. Food Eng., 2014, 122, 28–32 CrossRef CAS.
- (a) C. R. Robinson and S. G. Sligar, Biochemistry, 1994, 33, 3787–3793 CrossRef CAS PubMed; (b) C. R. Robinson and S. G. Sligar, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 3444–3448 CrossRef CAS PubMed.
- H. Kabata, A. Nomura, N. Shimamoto and S. Kunugi, J. Mol. Recognit., 1994, 7, 25–30 CrossRef CAS PubMed.
- (a) L. Erijman and R. M. Clegg, J. Mol. Biol., 1995, 253, 259–265 CrossRef CAS PubMed; (b) L. Erijman and R. M. Clegg, Biophys. J., 1998, 75, 453–462 CrossRef CAS PubMed.
- E. A. Rudd, Biochem. Biophys. Res. Commun., 1997, 230, 140–142 CrossRef CAS PubMed.
- (a) J. Barciszewski, J. Jurczak, S. Porowski, T. Specht and V. A. Erdmann, Eur. J. Biochem., 1999, 260, 293–307 CrossRef CAS PubMed; (b) M. Giel-Pietraszuk and J. Barciszewski, Int. J. Biol. Macromol., 2005, 37, 109–114 CrossRef CAS PubMed; (c) A. Fedoruk-Wyszomirska, E. Wyszko, M. Giel-Pietraszuk, M. Z. Barciszewska and J. Barciszewski, Int. J. Biol. Macromol., 2007, 41, 30–45 CrossRef CAS PubMed.
- P. Tandon, G. Forster, R. Neubert and S. Wartewig, J. Mol. Struct., 2000, 524, 201–215 CrossRef CAS.
- (a) E. V. Boldyreva, J. Mol. Struct., 2003, 647, 159–179 CrossRef CAS; (b) E. V. Boldyreva, Crystal Eng., 2003, 6, 235–254 CrossRef CAS; (c) E. V. Boldyreva, J. Mol. Struct., 2004, 700, 151–155 CrossRef CAS.
- (a) E. V. Boldyreva, H. Sowa, H. Ahsbahs, S. V. Goryainov, V. V. Chernyshev, V. P. Dmitriev, Y. V. Seryotkin, E. N. Kolesnik, T. P. Shakhtshneider, S. N. Ivashevskaya and T. N. Drebushchak, J. Phys.: Conf. Ser., 2008, 121, 022023 CrossRef; (b) E. A. Losev, B. A. Zakharov and E. V. Boldyreva, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, s363 Search PubMed; (c) B. A. Zakharov, Z. Gal, D. Cruickshank and E. V. Boldyreva, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2018, 74, 613–619 CrossRef CAS PubMed; (d) N. Bouvart, R. M. Palix, S. G. Arkhipov, I. A. Tumanov, A. A. L. Michalchuk and E. V. Boldyreva, CrystEngComm, 2018, 20, 1797–1803 RSC; (e) A. A. Gaydamaka, S. G. Arkhipov, B. A. Zakharov, Y. V. Seryotkin and E. V. Boldyreva, CrystEngComm, 2019, 21, 4484–4492 RSC.
- I. T. Desta, S. A. Chizhik, A. A. Sidelnikov, D. P. Karothu, E. V. Boldyreva and P. Naumov, J. Phys. Chem. A, 2020, 124, 300–310 CrossRef CAS PubMed.
- G. Heimel, P. Puschnig, M. Oehzelt, K. Hummer, B. Koppelhuber-Bitschnau, F. Porsch, C. Ambrosch-Draxl and R. Resel, MRS Proc., 2003, 771, L7.22 CrossRef.
- S. M. Gruner, in High-Pressure Crystallography, ed. A. Katrusiak and P. F. McMillan, Kluwer Academic Publishers, Dordrecht, 2004, pp. 543–556 Search PubMed.
- B. Palosz, S. Stelmakh, E. Grzanka, S. Gierlotka, R. Pielaszek, U. Bismayer, S. Werner and W. Palosz, J. Phys.: Condens. Matter, 2004, 16, S353–S377 CrossRef CAS.
- (a) R. Fourme, E. Girard, K. Ascone, M. Mezouar, T. Lin and J. E. Johnson, in High-Pressure Crystallography, ed. A. Katrusiak and P. F. McMillan, Kluwer Academic Publishers, Dordrecht, 2004, pp. 527–542 Search PubMed; (b) E. Girard, A. C. Dhaussy, B. Couzinet, J. C. Chervin, M. Mezouar, R. Kahn, I. Ascone and R. Fourme, J. Appl. Crystallogr., 2007, 40, 912–918 CrossRef CAS; (c) R. Fourme, E. Girard, R. Kahn, T. Prangé, A. C. Dhaussy, M. Mezouar and I. Ascone, High Pressure Res., 2010, 30, 100–103 CrossRef; (d) R. Fourme, I. Ascone, M. Mezouar, A. C. Dhaussy, R. Kahn and E. Girard, in High-Pressure Crystallography, ed. E. V. Boldyreva and P. Dera, NATO Science for Peace and Security Series B: Physics and Biophysics, Springer, Dordrecht, 2010 Search PubMed; (e) R. Fourme, E. Girard, A. C. Dhaussy, K. Medjoubi, T. Prangé, I. Ascone, M. Mezouarf and R. Khan, J. Synchrotron Radiat., 2011, 18, 31–36 CrossRef CAS PubMed.
- F. P. A. Fabbiani and C. R. Pulham, High-pressure studies of pharmaceutical compounds and energetic materials, Chem. Soc. Rev., 2006, 35, 932–942 RSC.
- (a) F. P. A. Fabbiani, D. R. Allan, W. I. F. David, A. J. Davidson, A. R. Lennie, S. Parsons, C. R. Pulham and J. E. Warren, Cryst. Growth Des., 2007, 7, 1115–1124 CrossRef CAS; (b) F. P. A. Fabbiani, G. Buth, B. Dittrich and H. Sowa, CrystEngComm, 2010, 12, 2541–2550 RSC; (c) M. A. Neumann, J. van de Streek, F. P. A. Fabbiani, P. Hidber and O. Grassmann, Nat. Commun., 2015, 6, 7793 CrossRef CAS PubMed.
- C. J. Schaschke, S. Abid and M. J. Heslop, High Press Res., 2007, 27, 33–37 CrossRef CAS.
- W. L. Liu, Z. R. Zheng, R. B. Zhu, Z. G. Liu, D. P. Xu, H. M. Yu, W. Z. Wu, A. H. Li, Y. Q. Yang and W. H. Su, J. Phys. Chem. A, 2007, 111, 10044–10049 CrossRef CAS PubMed.
- M. Zhou, D. P. Xu, T. C. Liu, P. Zhang, S. Q. Gao, Z. W. Li and G. H. Lu, J. Phys. Chem. B, 2008, 112, 15562–15568 CrossRef CAS PubMed.
- (a) F. Ya, Z. Jing, L. Shuang, G. Fu-Ying and X. Da-Peng, Chin. Phys. Lett., 2011, 28, 110702 CrossRef; (b) F. Ya, Z. Jing and X. Da-Peng, Spectrochim. Acta, Part A, 2014, 129, 143–147 CrossRef CAS PubMed.
- S. Fanetti, M. Citroni, L. Malavasi, G. A. Artioli, P. Postorino and R. Bini, J. Phys. Chem. C, 2013, 117, 5343–5351 CrossRef CAS.
- Y. Nishida, IEEE Trans. Plasm. Sci., 2014, 42, 3674–3680 CAS.
- Q. Wang, H. Zhang, Y. Zhang, Ca. Liu, Y. Han, Y. Ma and C. Gao, High Pressure Res., 2014, 34, 355–364 CrossRef CAS.
- A. A. Pribylov, N. A. Skibitskaya and L. A. Zekel, Russ. Chem. Bull., Int. Ed., 2015, 64, 841–845 CrossRef CAS.
- C. M. da Silva, J. G. Silva Filhoa, G. S. Pinheiro, R. C. Vilelac, F. E. A. Meloa, J. A. Lima and P. T. C. Freirea, Vibr. Spectrosc., 2017, 92, 162–168 CrossRef CAS.
- W. Cai, R. Zhang, Y. Yao and S. Deemyad, Phys. Chem. Chem. Phys., 2017, 19, 6216–6223 RSC.
- Q. Wang, D. Sang, S. Guo, X. Wang, W. Wang, B. Zhang, H. Hu, Q. Fan and C. Liu, CrystEngComm, 2019, 21, 4507–4512 RSC.
- R. J. Hemley and P. Dera, Rev. Mineral. Geochem., 2000, 41, 335–419 CrossRef.
- G. R. Desiraju, J. Am. Chem. Soc., 2013, 135, 9952–9967 CrossRef CAS PubMed.
- C. Hejny and V. S. Minkov, IUCrJ, 2015, 2, 218–229 CrossRef CAS PubMed.
- M. K. Beyer and H. C. Schaumann, Chem. Rev., 2005, 105, 2921–2948 CrossRef CAS PubMed.
- E. Horvath-Bordon, R. Riedel, P. McMillan, P. Kroll, G. Miehe, P. van Aken, A. Zerr, P. Hoppe, O. Shebanova and I. McLaren, et al. , Angew. Chem., Int. Ed., 2007, 46, 1476–1480 CrossRef CAS PubMed.
- X. Yue, H. Wang, S. Wang, F. Zhang and R. Zhang, J. Alloys Compd., 2010, 505, 286–290 CrossRef CAS.
- Z. G. Zhang, S. F. Zhang, H. Wang, J. W. Liu and M. Zhu, J. Alloys Compd., 2010, 505, 717–721 CrossRef CAS.
- (a) G. Ligios, A. M. Bertetto and F. Delogu, J. Alloys Compd., 2013, 554, 426–431 CrossRef CAS; (b) F. Delogu and L. Takacs, Acta Mater., 2014, 80, 435–444 CrossRef CAS; (c) F. Delogu, Acta Mater., 2014, 66, 388–395 CrossRef CAS.
- H. Kulla, S. Greiser, S. Benemann, K. Rademann and F. Emmerling, Molecules, 2016, 21, 917 CrossRef PubMed.
- (a) A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, J. Mater. Sci., 2018, 53, 13380–13389 CrossRef CAS PubMed; (b) A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, CrystEngComm, 2019, 21, 2174–2179 RSC.
- G. Ayoub, B. Karadeniz, A. J. Howarth, O. K. Farha, I. Đilović, L. S. Germann, R. E. Dinnebier, K. Užarević and T. Friščić, Chem. Mater., 2019, 31, 5494–5501 CrossRef CAS.
- M. Bykov, S. Chariton, H. Fei, T. Fedotenko, G. Aprilis, A. V. Ponomareva, F. Tasnádi, I. A. Abrikosov, B. Merle and P. Feldner, et al. , Nat. Commun., 2019, 10, 2994 CrossRef PubMed.
- E. Y. Mora, A. Sarmiento, E. Vera López, V. Drozd, A. Durygin, J. Chen and S. K. Saxena, Processes, 2019, 7, 735 CrossRef.
- A. San-Miguel, Chem. Soc. Rev., 2006, 35, 876–889 RSC.
- P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Chem. Rev., 2015, 115, 12440–12490 CrossRef CAS PubMed.
- J. M. Abendroth, O. S. Bushuyev, P. S. Weiss and C. J. Barrett, ACS Nano, 2015, 9, 7746–7768 CrossRef CAS PubMed.
- M. D. Manrique-Juárez, S. Rat, L. Salmon, G. Molnár, C. M. Quintero, L. Nicu, H. J. Shepherd and A. Bousseksou, Coord. Chem. Rev., 2016, 308, 395–408 CrossRef.
- O. Sato, Nat. Chem., 2016, 8, 644–656 CrossRef CAS PubMed.
- E. F. Delong and A. A. Yayanos, Science, 1985, 228, 1101–1103 CrossRef CAS PubMed.
- (a) D. H. Bartlett, M. Wright, A. A. Yayanos and M. Silverman, Nature, 1989, 342, 572–574 CrossRef CAS PubMed; (b) D. H. Bartlett, Res. Microbiol., 1991, 142, 923–925 CrossRef CAS PubMed; (c) E. Chi and D. H. Bartlett, J. Bacteriol., 1993, 175, 7533–7540 CrossRef CAS PubMed; (d) T. J. Welch and D. H. Bartlett, J. Bacteriol., 1996, 178, 5027–5031 CrossRef CAS PubMed.
- G. Bernhardt, R. Jaenicke, H. D. Ludemann, H. Konig and K. O. Stetter, Appl. Environ. Microbiol., 1988, 54, 1258–1261 CrossRef CAS PubMed.
- P. M. Oger and M. Jebbar, Res. Microbiol., 2010, 161, 799–809 CrossRef PubMed.
- M. K. Behan, A. G. Macdonald, G. R. Jones and A. R. Cossins, Biochim. Biophys. Acta, 1992, 1103, 317–323 CrossRef CAS.
- M. L. Porter, N. W. Roberts and J. C. Partridge, Mol. Phylogen. Evol., 2016, 105, 160–165 CrossRef PubMed.
- R. M. Hazen, N. Boctor, J. Brandes, G. D. Cody, R. J. Hemley, A. Sharma and H. S. Yoder, J. Phys.: Condens. Matter, 2002, 14, 11489–11494 CrossRef CAS.
- I. Daniel, P. Oger and R. Winter, Chem. Soc. Rev., 2006, 35, 858–875 RSC.
- F. Pradillon and F. Gaill, Rev. Environ. Sci. Biotechnol., 2007, 6, 181–195 CrossRef.
- V. V. Mozhaev, K. Heremans, J. Frank, P. Masson and C. Balny, Trends Biotechnol., 1994, 12, 493–501 CrossRef CAS.
- V. V. Mozhaev, K. Heremans, J. Frank, P. Masson and C. Balny, Proteins: Struct., Funct., Genet., 1996, 24, 81–91 CrossRef CAS.
- N. Rivalain, J. Roquain and G. Demazeau, Biotechnol. Adv., 2010, 28, 659–672 CrossRef CAS PubMed.
- J. L. Silva, A. C. Oliveira, T. C. R. G. Vieira, G. A. P. de Oliveira, M. C. Suarez and D. Foguel, Chem. Rev., 2014, 114, 7239–7267 CrossRef CAS PubMed.
- K. Heremans, Annu. Rev. Biophys. Bioeng., 1982, 11, 1–21 CrossRef CAS PubMed.
- M. Deckmann, R. Haimovitz and M. Shinitzky, Biochim. Biophys. Acta, 1985, 821, 334–340 CrossRef CAS.
- L. F. Braganza and D. L. Worcester, Biochemistry, 1986, 25, 7484–7488 CrossRef CAS PubMed.
- D. S. Lester, J. Neurochem., 1989, 52, 1950–1953 CrossRef CAS PubMed.
- N. Orr, E. Yavin, M. Shinitzky and D. S. Lester, Anal. Biochem., 1990, 191, 80–85 CrossRef CAS PubMed.
- D. A. Plager and G. L. Nelsestuen, Protein Sci., 1992, 530–539 CAS.
- J. Jonas and A. Jonas, Annu. Rev. Biophys. Biomol. Struct., 1994, 23, 287–318 CrossRef CAS PubMed.
- (a) P. Masson, Ann. Pharm. Fr., 1999, 57, 49–55 CAS; (b) P. Masson, C. Tonello and C. Balny, J. Biomed. Biotechnol., 2001, 1, 85–88 CrossRef CAS PubMed.
- (a) Y. Rigaldie and G. Demazeau, Ann. Pharm. Fr., 2004, 62, 116–127 CrossRef CAS PubMed; (b) Y. Rigaldie, G. Lemagnen, A. Largeteau, D. Larrouture, M. Abba and C. Durandeau, et al. , Eur. J. Parenteral Sci., 2001, 6, 73–77 Search PubMed.
- J. L. Silva, D. Foguel, M. Suarez, A. M. O. Gomes and A. C. Oliveira, J. Phys.: Condens. Matter, 2004, 16, S929–S944 CrossRef CAS.
- T. Elshaarani, H. Yu, L. Wang, R. S. Ullah, S. Fahad, K. U. Rahman, A. Khan, A. Nazir, M. Usman, R. U. Khan, F. Haq, R. Liang, X. Chen and M. Haroon, J. Mater. Sci., 2019, 54, 10009–10023 CrossRef CAS.
- D. F. Keenan, N. P. Brunton, R. Gormley, F. Butler, B. K. Tiwari and A. Patras, Innov. Food Sci. Emerg. Technol., 2010, 11, 551–556 CrossRef CAS.
- (a) G. Ferrari, P. Maresca and R. Ciccaron, J. Food Eng., 2010, 100, 245–253 CrossRef CAS; (b) G. Ferrari, P. Maresca and R. Ciccarone, Proc. Food Sci., 2011, 1, 847–853 CrossRef CAS.
- V. Briones-Labarca, G. Venegas-Cubillos, S. Ortiz-Portilla, M. Chacana-Ojeda and H. Maureira, Food Chem., 2011, 128, 520–529 CrossRef CAS PubMed.
- Z. A. Kruk, H. Y. D. L. Rutley, E. J. Lee, Y. J. Kim and C. Jo, Food Control, 2011, 22, 6–12 CrossRef.
- W. Li, F. Zhang, P. Liu, Y. Bai, L. Gao and Q. Shen, J. Food Eng., 2011, 103, 388–393 CrossRef CAS.
- F. J. Barba, H. Jäger, N. Meneses, M. J. Esteve, A. Frígola and D. Knorr, Innov. Food Sci. Emerg. Technol., 2012, 14, 18–24 CrossRef CAS.
- H. Li, K. Zhu, H. Zhou and W. Peng, Food Chem., 2012, 132, 808–814 CrossRef CAS.
- M. Bashari, M. H. Abdelhai, S. Abbas, A. Eibaid, X. Xu and Z. Jin, Ultrason. Sonochem., 2014, 21, 76–83 CrossRef CAS PubMed.
- Y. Zhang, X. C. Liu, Y. Wang, F. Zhao, Z. Sun and X. Liao, Innov. Food Sci. Emerg. Technol., 2016, 33, 135–144 CrossRef CAS.
- F. Liu, X. Zhang, L. Zhao, Y. Wang and X. Liao, Innov. Food Sci. Emerg. Technol., 2016, 34, 51–58 CrossRef CAS.
- T. von Kármán and M. Born, Phys. Z., 1913, 14, 15–19 Search PubMed ; 1913, 14, 65–71.
- R. Dovesi, in Quantum Mechanical Ab Initio Calculation of the Properties of Crystalline Materials, ed. C. Pisani, Lecture Notes in Chemistry, Springer, Berlin, vol. 67, 1996, pp. 31–46 Search PubMed.
- (a) T. Oxby, W. F. Perger, J. Zhao, J. M. Winey and Y. M. Gupta, AIP Conf. Proc., 2004, 706, 247–250 CrossRef CAS; (b) J. Zhao, J. M. Winey, Y. M. Gupta and W. F. Perger, AIP Conf. Proc., 2004, 706, 429–432 CrossRef CAS; (c) A. Brillante, R. Della Valle, L. Farina, E. Venuti, C. Cavazzoni, A. P. Emerson and K. Syassen, J. Am. Chem. Soc., 2005, 127, 3038 CrossRef CAS PubMed; (d) E. Venuti, R. Della Valle, L. Farina, A. Brillante, M. Masino and A. Girlando, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 104106 CrossRef.
- (a) E. V. Boldyreva, H. Ahsbahs, V. V. Chernyshev, S. N. Ivashevskaya and A. R. Oganov, Z. Kristallogr., 2006, 221, 186–197 CAS; (b) D. A. Rychkov, J. Stare and E. V. Boldyreva, Phys. Chem. Chem. Phys., 2017, 19, 6671–6676 RSC.
- (a) J. C. Tan, B. Civalleri, L. Chung-Cherng, L. Valenzano, R. Galvelis, C. Po Fei, T. D. Bennett, C. Mellot-Draznieks, C. M. Zicovich-Wilson and A. K. Cheetham, Phys. Rev. Lett., 2012, 108, 095502 CrossRef PubMed; (b) M. R. Ryder, B. Civalleri and J. C. Tan, Phys. Chem. Chem. Phys., 2016, 18, 9079–9087 RSC.
- T. P. Rupasinghe, K. M. Hutchins, B. S. Bandaranayake, S. Ghorai, C. Karunatilake, D. K. Bučar, D. C. Swenson, M. A. Arnold, L. R. MacGillivray and A. V. Tivanski, J. Am. Chem. Soc., 2015, 137, 12768–12771 CrossRef CAS PubMed.
- M. J. Turner, S. P. Thomas, M. W. Shi, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2015, 51, 3735–3738 RSC.
- I. Azuri, E. Meirzadeh, D. Ehre, S. R. Cohen, A. M. Rappe, M. Lahav, I. Lubomirsky and L. Kronik, Angew. Chem., Int. Ed., 2015, 127, 13770–13774 CrossRef.
- M. R. Mohamed, M. K. Mishra, L. M. Al Harbi, M. S. Al Ghamdic and U. Ramamurty, RSC Adv., 2015, 5, 64156–64162 RSC.
- I. A. Fedorov, E. S. Rubtsova, N. S. Khaydukova and Y. N. Zhuravlev, IOP Conf. Ser.: Mater. Sci. Eng., 2015, 81, 012120 CrossRef.
- Y. V. Matveychuk, E. V. Bartashevich and V. G. Tsirelson, Cryst. Growth Des., 2018, 18, 3366–3375 CrossRef CAS.
- N. R. Keskar and J. R. Chelikowsky, Nature, 1992, 358, 222–224 CrossRef CAS.
- (a) J. N. Grima, R. Gatt, A. Alderson and K. E. Evans, Mater. Sci. Eng., A, 2006, 423, 219–224 CrossRef; (b) J. N. Grima, R. Gatt, V. Zammit, J. J. Williams, K. E. Evans, A. Alderson and R. I. Walton, J. Appl. Phys., 2007, 101, 086102 CrossRef.
- (a) F. X. Coudert, Phys. Chem. Chem. Phys., 2013, 15, 1602–16018 RSC; (b) F. X. Coudert, Chem. Mater., 2017, 29, 7833–7839 CrossRef.
- Y. T. Yao, K. L. Alderson and A. Alderson, Cellulose, 2016, 23, 3429–3448 CrossRef CAS.
- (a) J. C. Tan, B. Civalleri, A. Erba and E. Albanese, CrystEngComm, 2015, 17, 375–382 RSC; (b) M. R. Ryder and J. C. Tan, Dalton Trans., 2016, 45, 4154–4161 RSC.
- H. Sun, S. Mukherjee and C. V. Singh, Phys. Chem. Chem. Phys., 2016, 18, 26736–26742 RSC.
- Y. Du, J. Maassen, W. Wu, Z. Luo, X. Xu and P. D. Ye, Nano Lett., 2016, 16, 6701–6708 CrossRef CAS PubMed.
- W. Li, M. R. Probert, M. Kosa, M. T. D. Bennett, A. Thirumurugan, R. P. Burwood, M. Parinello, J. A. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2012, 134, 11940–11943 CrossRef CAS PubMed.
- Y. Qiao, K. Wang, H. Yuan, K. Yang and B. Zou, J. Phys. Chem. Lett., 2015, 6, 2755–2760 CrossRef CAS PubMed.
- C. S. Coates, J. W. Makepeace, A. G. Seel, M. Baise, B. Slater, A. L. Goodwin and A. L. Synthesis, Dalton Trans., 2018, 47, 7263–7271 RSC.
- A. Marmier, P. S. Ntoahae, P. E. Ngoepe, D. G. Pettifor and S. C. Parker, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 172102 CrossRef.
- L. Kang, X. Jiang, S. Luo, P. Gong, W. Li, X. Wu, Y. Li, X. Li, C. Chen and Z. Lin, Sci. Rep., 2016, 5, 13432 CrossRef PubMed.
- J. Dagdelen, J. Montoya, M. De Jong and K. Persson, Nat. Commun., 2017, 8, 323 CrossRef PubMed.
- D. T. Ho, S. D. Park, S. Y. Kwon, K. Park and S. Y. Kim, Nat. Commun., 2014, 5, 3255 CrossRef PubMed.
- D. Wu, S. Wang, S. Zhan, S. J. Yuan, B. Yang and H. Chen, Phys. Chem. Chem. Phys., 2018, 20, 18924–18930 RSC.
- F. Hao, X. Liao, M. Li, H. Xiao and X. Chen, J. Phys.: Condens. Matter, 2018, 30, 315302 CrossRef PubMed.
- H. Wang, Q. Li, Y. Gao, F. Miao, X. Zhou and X. G. Wan, New J. Phys., 2016, 18, 073016 CrossRef.
- H. Wang, Z. D. Zhang, R. Q. Wu and L. Z. Sun, Acta Mater., 2013, 61, 2919–2925 CrossRef CAS.
- H. Wang, X. Li, P. Li and J. Yang, Nanoscale, 2017, 9, 850–855 RSC.
- X. F. Wang, T. E. Jones, W. Li and Y. C. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 134108 CrossRef.
- S. Yalameha and A. Vaez, Ab-initio thermodynamic and elastic properties of AlNi and AlNi3 intermetallic compounds, Int. J. Mod. Phys. B, 2018, 32, 1850129 CrossRef CAS.
- H. Hsueh, C. Lee, C. W. Wang and J. Crain, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3851–3856 CrossRef CAS.
- W. Ren, J. Ye, W. Shi, Z. K. Tang, C. T. Chan and P. Sheng, New J. Phys., 2009, 11, 103014 CrossRef.
- (a) D. V. Korabel’nikov and Y. N. Zhuravlev, Phys. Chem. Chem. Phys., 2016, 18, 33126–33133 RSC; (b) D. V. Korabel’nikov and Y. N. Zhuravlev, Phys. Solid State, 2016, 58, 1166–1171 CrossRef; (c) D. V. Korabel’nikov and Y. N. Zhuravlev, J. Phys. Chem. A, 2017, 121, 6481–6490 CrossRef PubMed.
- (a) D. T. Ho, C. T. Nguyen, S. Y. Kwon and S. Y. Kim, Phys. Status Solidi B, 2019, 256, 1800122 CrossRef; (b) C. T. Nguyen, D. T. Ho, S. T. Choi, D. M. Chun and S. Y. Kim, Comput. Mater. Sci., 2019, 157, 17–24 CrossRef CAS.
- (a) K. W. Wojciechowski, Mol. Phys., 1987, 61, 1247–1258 CrossRef CAS; (b) K. W. Wojciechowski, Phys. Lett. A, 1989, 137, 60–64 CrossRef.
- (a) S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS; (b) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed; (c) S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS; (d) J. G. Brandenburg and S. Grimme, J. Phys. Chem. Lett., 2014, 5, 1785–1789 CrossRef CAS PubMed.
- (a) A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed; (b) B. Schatschneider, S. Monaco, A. Tkatchenko and A. J. Liang, J. Phys. Chem. A, 2014, 117, 8323–8331 CrossRef PubMed.
- M. Abdulla, K. Refson, R. H. Friend and P. D. Haynes, J. Phys.: Condens. Matter, 2015, 27, 375402 CrossRef PubMed.
- J. Hoja, A. M. Reilly and A. Tkatchenko, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1294 Search PubMed.
- P. L. Silvestrelli and A. Ambrosetti, J. Chem. Phys., 2019, 150, 164109 CrossRef.
- D. Geatches, I. Rosbottom, R. L. M. Robinson, P. Byrne, P. Hasnip, M. I. J. Probert, D. Jochym, A. Maloney and K. J. Roberts, J. Chem. Phys., 2019, 151, 044106 CrossRef PubMed.
- K. W. Wojciechowski, P. Pieranski and J. Malecki, J. Phys. A, 1983, 16, 2197–2203 CrossRef.
- G. Westhoff and J. N. Starr, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 2014 Search PubMed.
- L. Pasteur, C. R. Chim., 1857, 45, 913–916 Search PubMed.
- M. T. Wyss, R. Jolivet, A. Buck, P. J. Magistretti and B. Weber, J. Neurosci., 2011, 31, 7477–7485 CrossRef CAS PubMed.
- L. B. Gladden, J. Physiol., 2004, 558, 5–30 CrossRef CAS PubMed.
- K. Kasischke, Front. Neuroenerg., 2011, 3, 4 CAS.
- S. Offermanns, S. L. Colletti, T. W. Lovenberg, G. Semple, A. Wise and A. P. Ijzerman, Pharmacol. Rev., 2011, 63, 269–290 CrossRef CAS PubMed.
- H. Benninga, A History of Lactic Acid Making: A Chapter in the History of Biotechnology, Chemists and Chemistry, Springer, Berlin, 1990, vol. 11 Search PubMed.
- I. A. Shuklov, N. V. Dubrovina, K. Kühlein and A. Börner, Adv. Synth. Catal., 2016, 358, 3910–3931 CrossRef CAS.
- A. Stout, B. Basu and T. J. Webster, Acta Biomater., 2011, 7, 3101–3112 CrossRef PubMed.
- H. Liu and T. J. Webster, Biomaterials, 2007, 28, 354–365 CrossRef CAS PubMed.
- T. W. J. Steele, C. L. Huang, E. Widjaja, F. Y. C. Boey, J. S. C. Loo and S. S. Venkatraman, Acta Biomater., 2011, 7, 1973–1983 CrossRef CAS.
- S. C. J. Loo, Z. Y. S. Tan and S. L. I. Lin, J. Pharm. Sci., 2010, 99, 3060–3071 CrossRef CAS PubMed.
- H. K. Makadia and J. Siegel, Polymers, 2011, 3, 1377–1397 CrossRef CAS PubMed.
- A. Basu, K. R. Kunduru, S. Doppalapudi, A. J. Domb and W. Khan, Adv. Drug Delivery Rev., 2016, 107, 192–205 CrossRef CAS PubMed.
- J. Chick and Z. Ustunol, J. Food Sci., 1998, 63, 1024–1027 CrossRef CAS.
- M. E. Broz, D. L. VanderHart and N. R. Washburn, Biomaterials, 2003, 24, 4181–4190 CrossRef CAS.
- J. F. Zhang and X. Sun, Biomacromolecules, 2004, 54, 1446–1451 CrossRef PubMed.
- F. Carrasco, P. Pages, J. Gamez-Perez, O. O. Santana and M. L. Maspoch, Polym. Degrad. Stab., 2010, 95, 116–125 CrossRef CAS.
- G. Perego and G. D. Cella, in Poly(lactic acid): Synthesis, Structures, Properties, Processing, and Applications, ed. R. F. Grossman, D. Nwabunma, R. Auras, L. Lim, S. E. Selke and H. Tsuji, Wiley, New York, 2010 Search PubMed.
- S. W. Hwang, S. B. Lee, C. K. Lee, J. Y. Lee, J. K. Shim, S. E. M. Selke, H. Soto-Valdez, L. Matuana, M. Rubino and R. Auras, Polym. Test., 2012, 31, 333–344 CrossRef CAS.
- V. S. G. Silverajah, N. A. Ibrahim, N. Zainuddin, W. M. Z. W. Yunus and H. A. Hassan, Molecules, 2012, 17, 11729–11747 CrossRef CAS PubMed.
- P. Sennan and J. Pumchusak, Malaysian J. Anal. Sci., 2014, 18, 669–675 Search PubMed.
- S. Farah, D. G. Anderson and R. Langer, Adv. Drug Delivery Rev., 2016, 107, 367–392 CrossRef CAS PubMed.
- J. L. Orellana, D. Wichhart and C. L. Kitchens, J. Nanomater., 2018, 2018, 7124260 Search PubMed.
- M. S. Nasab, M. Tabari and M. H. Azizi, Nanomed. Res. J., 2018, 3, 96–101 CAS.
- Z. Wang, Z. Yao, J. Zhou, M. He, Q. Jiang, A. Li, S. Li, M. Liu, S. Luo and D. Zhang, Int. J. Biol. Macromol., 2019, 29, 878–886 CrossRef PubMed.
- Y. Zhang, L. Cui, H. Xua, X. Feng, B. Wang, B. Pukanszky, Z. Mao and X. Sui, Int. J. Biol. Macromol., 2019, 29, 197–204 CrossRef PubMed.
- K. Lertphirun and K. Srikulkit, Int. J. Polym. Sci., 2019, 2019, 7835172 Search PubMed.
- A. Schouten, J. A. Kanters and J. van Krieken, J. Mol. Struc., 1994, 323, 165–168 CrossRef CAS.
- A. Borba, A. Gómez-Zavaglia, L. Lapinskic and R. Fausto, Phys. Chem. Chem. Phys., 2004, 6, 2101–2108 RSC.
- M. Shahat, Acta Crystallogr., 1952, 5, 763–768 CrossRef CAS.
- M. N. G. James and G. J. B. Williams, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1249–1257 CrossRef CAS.
- G. M. Day, A. V. Trask, W. D. S. Motherwell and W. Jones, Chem. Commun., 2006, 54–56 RSC.
- D. Rychkov, S. Arkhipov and E. Boldyreva, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 160–163 CrossRef CAS PubMed.
- G. D. Rieck, Rec. Trav. Chim. Des Pays-Bas, 1944, 63, 170–180 CrossRef CAS.
- J. D. Morrison and J. M. Robertson, J. Chem. Soc., 1949, 1949, 980–986 RSC.
- J. L. Leviel, G. Auvert and J. M. Savariault, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1981, 37, 2185–2189 CrossRef.
- I. M. Dodd, S. J. Maginn, M. M. Harding and R. J. Davey, CSD Commun., CCDC 1263474, 1998, https://www.drugbank.ca/drugs/DB00139.
- R. S. Gopalan, P. Kumaradhas, G. U. Kulkarni and C. N. R. Rao, J. Mol. Struct., 2000, 521, 97–106 CrossRef.
- P. Lucaioli, E. Nauha, I. Gimondi, L. S. Price, R. Guo, L. Iuzzolino, I. Singh, M. Salvalaglio, S. L. Price and N. Blagden, CrystEngComm, 2018, 20, 3971–3977 RSC.
- J. P. Glusker, J. A. Minkin and A. L. Patterson, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 1066–1072 CrossRef CAS PubMed.
- A. V. Churakov, CSD Commun., CCDC 635772, 2007, DOI: 10.5517/ccpbksb.
- A. Rammohan and J. A. Kaduk, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 239–252 CrossRef CAS PubMed.
- A. G. Roelofsen and J. A. Kanters, Cryst. Struct. Commun., 1972, 1, 23–26 Search PubMed.
- M. D. King, E. A. Davis, T. M. Smith and T. M. Korter, J. Phys. Chem. A, 2011, 115, 11039–11044 CrossRef CAS PubMed.
- J. F. Nye, The Physical Properties of Crystals: Their Representation by Tensors and Matrices, Oxford University Press, New York, 1985 Search PubMed.
- P. F. Weck, E. Kim and E. C. Buck, RSC Adv., 2015, 5, 79090–79097 RSC.
- M. Born, Math. Proc. Camb. Phil. Soc., 1940, 36, 160–172 CrossRef CAS.
- F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- W. Voigt, Lehrbuch der Kristallphysik, Teubner, Leipzig, 1962.
- A. Z. Reuss, Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- R. Hill, Proc. Phys. Soc. London A, 1952, 65, 349–354 CrossRef.
- (a) F. Colmenero, L. J. Bonales, J. Cobos and V. Timón, J. Phys. Chem. C, 2017, 121, 5994–6001 CrossRef CAS; (b) F. Colmenero, L. J. Bonales, J. Cobos and V. Timón, J. Solid State Chem., 2017, 253, 249–257 CrossRef CAS; (c) F. Colmenero, J. Cobos and V. Timón, Inorg. Chem., 2018, 57, 4470–4481 CrossRef CAS PubMed; (d) F. Colmenero, A. M. Fernández, J. Cobos and V. Timón, RSC Adv., 2018, 8, 24599–24616 RSC; (e) F. Colmenero, J. Plášil, J. Cobos, J. Sejkora, V. Timón, J. Čejka and L. J. Bonales, RSC Adv., 2019, 9, 15323–15334 RSC; (f) F. Colmenero, J. Plášil and J. Sejkora, Dalton Trans., 2019, 48, 16722–16736 RSC; (g) F. Colmenero, J. Plášil, J. Cobos, J. Sejkora, V. Timón, J. Čejka, A. M. Fernández and V. Petříček, RSC Adv., 2019, 9, 40708–40726 RSC.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CAS.
- Y. Bouhadda, S. Djella, M. Bououdina, N. Fenineche and Y. Boudouma, J. Alloys Compd., 2012, 534, 20–24 CrossRef CAS.
- H. Niu, P. Wei, Y. Sun, C. X. Chen, C. Franchini, D. Li and Y. Li, Appl. Phys. Lett., 2011, 99, 031901 CrossRef.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed.
- A. Marmier, Z. A. D. Lethbridge, R. I. Walton, C. W. Smith, S. C. Parker and K. E. Evans, Comput. Phys. Commun., 2010, 181, 2102–2115 CrossRef CAS.
- Z. A. D. Lethbridge, R. I. Walton, A. S. H. Marmier, C. W. Smith and K. E. Evans, Acta Mater., 2010, 58, 6444–6451 CrossRef CAS.
- K. Lohbeck, H. Haferkorn, W. Fuhrmann and N. Fedtke, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 2000 Search PubMed.
- M. Vanneste, Principles of Textile Finishing, Woodhead Publishing Series in Textiles, Cambridge, 2015, pp. 227–256 Search PubMed.
- A. Kumar and R. Choudhury, Functional Finishes for Textiles Improving Comfort, Performance and Protection, Woodhead Publishing Series in Textiles, Amsterdam, 2017; pp. 245–284 Search PubMed.
- N. Safari, V. Esfahanian, M. Kolahdoozan and A. Khosravi, J. Dental Mater. Technol., 2019, 8, 143–148 Search PubMed.
- G. Jiang, J. Feng, M. Zhang, M. S. Zhang and H. Huang, RSC Adv., 2016, 6, 107547–107555 RSC.
- B. Cornils and P. Lappe, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 2014 Search PubMed.
- L. Tretter, A. Patocs and C. Chinopoulos, Biochim. Biophys. Acta, 2016, 1857, 1086–1101 CrossRef CAS PubMed.
- R. Haas, D. Cucchi, J. Smith, V. Pucino, C. E. Macdougall and C. Mauro, Trends Biochem. Sci., 2016, 41, 460–471 CrossRef CAS PubMed.
- J. Berg, J. Tymoczko and L. Stryer, Biochemistry, W. H. Freeman, New York, 6th edn, 2006 Search PubMed.
- R. W. Olsen and T. M. DeLorey, in Basic Neurochemistry: Molecular, Cellular and Medical Aspects, ed. G. J. Siegel, B. W. Agranoff and R. W. Albers, Lippincott-Raven, Philadelphia, 6th edn, 1999 Search PubMed.
- A. King, M. A. Selak and E. Gottlieb, Oncogene, 2006, 25, 4675–4682 CrossRef CAS PubMed.
- C. Bardella, P. J. Pollard and I. Tomlinson, Biochim. Biophys. Acta, Bioenerg., 2011, 1807, 1432–1443 CrossRef CAS PubMed.
- S. Drose, Biochim. Biophys. Acta, 2013, 1827, 578–587 CrossRef PubMed.
- M. Yang, T. Soga, P. J. Pollard and J. Patrick, J. Clin. Invest., 2013, 123, 3652–3658 CrossRef CAS PubMed.
- M. Yang and P. J. Pollard, Cancer Cell, 2013, 23, 709–711 CrossRef CAS.
- G. M. Tannahill, A. M. Curtis, J. Adamik, E. M. Palsson-McDermott, A. F. McGettrick, G. Goel, C. Frezza, N. J. Bernard and B. Kelly, Nature, 2013, 496, 238–242 CrossRef CAS PubMed.
- E. Mills and L. A. J. O’Neill, Trends Cell Biol., 2014, 24, 313–320 CrossRef CAS PubMed.
- E. T. Chouchani, V. R. Pell, E. Gaude, D. Aksentijević, S. Y. Sundier, E. L. Robb, A. Logan, S. M. Nadtochiy, E. N. Ord and A. C. Smith, et al. , Nature, 2014, 515, 431–435 CrossRef CAS PubMed.
- V. R. Pell, E. T. Chouchani, C. Frezza, M. P. Murphy and T. Krieg, Cardiovas. Res., 2016, 111, 134–141 CrossRef CAS PubMed.
- J. Gilissen, F. Jouret, B. Pirotte and J. Hanson, Pharmacol. Therap., 2016, 159, 56–65 CrossRef CAS PubMed.
- M. de Castro Fonseca, C. J. Aguiar, J. A. da Rocha Franco, R. Gingold and M. F. Leite, Cell Commun. Signaling, 2016, 14, 3 CrossRef PubMed.
- K. K. Cheng, G. Y. Wang, J. Zeng and J. A. Zhang, BioMed Res. Int., 2013, 2013, 538790 Search PubMed.
- J. M. Otero, D. Cimini, K. R. Patil, S. G. Poulsen, L. Olsson and J. Nielsen, PLoS One, 2013, 8, 541–544 Search PubMed.
- C. Thakker, I. Martínez, K. Y. San and G. N. Bennett, Biotechnol. J., 2017, 7, 213–224 CrossRef PubMed.
- J. G. Zeikus, M. K. Jain and P. Elankovan, Appl. Microbiol. Biotechnol., 1999, 51, 545–552 CrossRef CAS.
- R. D. B. Walsh, M. W. Bradner, S. Fleischman, L. A. Morales, B. Moulton, N. Rodriguez-Hornedo and M. J. Zaworotko, Chem. Commun., 2003, 186–187 RSC.
- N. Blagden, M. de Matas, P. Gavan and P. York, Adv. Drug Delivery Rev., 2007, 59, 617–630 CrossRef CAS.
- Q. Yu, L. Dang, S. Black and H. Wei, J. Cryst. Growth, 2012, 340, 209–215 CrossRef CAS.
- S. Saouane and F. P. A. Fabbiani, Crystals, 2006, 6, 2 CrossRef.
- D. G. Barrett and M. N. Yousaf, Molecules, 2019, 14, 4022–4050 CrossRef PubMed.
- J. Mittal, R. B. Mathur, O. P. Bahl and M. Inagaki, Carbon, 1998, 36, 893–897 CrossRef CAS.
- M. Nagata, H. Goto, W. Sakai and N. Tsutsumi, Polymer, 2000, 41, 4373–4376 CrossRef CAS.
- S. Abele, C. Gauthier, C. Graillat and A. Guyot, Polymer, 2000, 41, 1147–1155 CrossRef CAS.
- J. Vega-Baudrit, R. Pereira, K. Nakayama, T. Masuda and A. Cao, Polym. Polym. Compos., 2004, 12, 63–73 CAS.
- P. Jiang, H. Liu, C. Wang, L. Wu, J. Huang and C. Guo, Mater. Lett., 2006, 60, 919–925 CrossRef CAS.
- N. Elgindy and W. Samy, Int. J. Pharm., 2009, 376, 1–6 CrossRef CAS PubMed.
- M. C. Sweedmana, M. J. Tizzotti, C. Schäfer and R. G. Gilberta, Carbohydr. Polym., 2013, 92, 905–920 CrossRef PubMed.
- S. Tiptipakorn, P. Suwanmala and K. Hemvichian, Adv. Mater. Res., 2013, 747, 253–256 CAS.
- S. L. Li, J. B. Zeng, F. Wu, Y. Yang and Y. Z. Wang, Ind. Eng. Chem. Res., 2014, 53, 1404–1414 CrossRef CAS.
- K. Zhang and O. Ni, J. Dispersion Sci. Technol., 2015, 36, 556–562 CrossRef CAS.
- J. Lu, S. Obara, N. Ioannidis, J. Suwardie, C. Gogos and S. Kikuchi, Adv. Polym. Technol., 2016, 37, 154–166 CrossRef.
- C. Gao, Z. Li, Y. Liu, X. Zhang, J. Wang and Y. Wu, Ind. Eng. Chem. Res., 2017, 56, 3516–3526 CrossRef CAS.
- X. Hu, T. Su, W. Pan, P. Li and Z. Wang, RSC Adv., 2017, 7, 35496–35503 RSC.
- X. L. Xie, Y. Li, J. Z. Xu, Z. Yan, G. J. Zhong and Z. M. Li, J. Mater. Chem. A, 2018, 6, 13373–13385 RSC.
- S. Qiu, K. Zhang, Z. Su and Z. Qiu, Polym. Test., 2018, 66, 64–69 CrossRef CAS.
- Z. Zhu, H. He, B. Xue, Z. Zhan, G. Wang and M. Chen, Materials, 2018, 11, 2422 CrossRef CAS PubMed.
- M. Puchalski, G. Szparaga, T. Biela, A. Gutowska, S. Sztajnowski and I. Krucinska, Polymers, 2018, 10, 251 CrossRef PubMed.
- F. H. Verhoff and H. Bauweleers, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 2014 Search PubMed.
- C. W. Scheele, New Proc. Roy. Acad. Sci., 1874, 5, 105–109 Search PubMed.
- J. Kay and P. D. Weitzman, Krebs’ citric acid cycle: half a century and still turning, Biochemical Society, London, 1987 Search PubMed.
- Y. Y. Hu, A. Rawal and K. Schmidt-Rohr, Proc. Natl. Acad. Sci. U. S. A., 2017, 107, 22425–22429 CrossRef.
- W. A. Lotfy, K. M. Ghanem and E. R. El-Helow, Biores. Technol., 2007, 98, 3470–3477 CrossRef CAS.
- M. Berovic and M. Legisa, Biotechnol. Ann. Rev., 2007, 13, 303–343 CAS.
- H. G. Jo, H. J. Yoon, C. H. Lee and K. B. Lee, Ind. Eng. Chem. Res., 2016, 55, 3833–3839 CrossRef CAS.
- Y. El Ghoul, B. Martel, A. El Achari, C. Campagne, L. Razafimahefa and I. Vroman, Polym. J., 2010, 42, 804–811 CrossRef CAS.
- J. Yang, A. R. Webb and G. A. Ameer, Adv. Mater., 2004, 16, 511–515 CrossRef CAS.
- W. Sridach, S. Jonjankiat and T. Wittaya, J. Adhes. Sci. Technol., 2013, 27, 1727–1738 CrossRef CAS.
- R. T. Tran, Y. Zhang, D. Gyawali and J. Yang, Recent Patents Biomed. Eng., 2009, 2, 216–227 CrossRef CAS.
- L. V. Thomas and P. D. Nair, Biomatter, 2011, 1, 81–90 CrossRef PubMed.
- H. J. Kim, J. M. Koo, S. H. Kim, S. Y. Hwang and S. S. Im, Polym. Degrad. Stab., 2017, 144, 128–136 CrossRef CAS.
- A. Narayanan, R. Kartik, E. Sangeetha and R. Dhamodharan, Carbohydr. Polym., 2018, 191, 152–160 CrossRef CAS PubMed.
- X. Ma, R. Jian, P. R. Chang and J. Yu, Biomacromolecules, 2008, 9, 3314–3320 CrossRef CAS PubMed.
- P. Aruna, M. Marie and P. Iyer, Int. J. Curr. Microbiol. Appl. Sci., 2014, 3, 255–261 CAS.
- N. Reddy and Y. Yang, Food Chem., 2010, 118, 702–711 CrossRef CAS.
- J. M. Halpern, R. Urbanski, A. K. Weinstock, D. F. Iwig, R. T. Mathers and H. von Recum, J. Biomed. Mater. Res., Part A, 2014, 102, 1467–1477 CrossRef PubMed.
- A. Sonseca, O. Sahuquillo, E. J. Foster and E. Gimeneza, RSC Adv., 2015, 5, 55879–55891 RSC.
- L. C. Su, Z. Xie, Y. Zhang, K. Truong Nguyen and J. Yang, Front. Bioeng. Biotechnol., 2014, 2, 23 CrossRef PubMed.
- M. K. Nayunigari, S. K. Gupta, V. Kokkarachedu, K. Kanny and F. Bux, Environ. Technol., 2014, 35, 2903–2909 CrossRef CAS PubMed.
- P. G. Gan, S. T. Sam and A. M. Faiq, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 429, 012042 Search PubMed.
- K. Wilpiszewska, A. K. Antosik and M. Zdanowicz, J. Polym. Environ., 2019, 27, 1379–1387 CrossRef CAS.
- N. Elgindy and W. Samy, Int. J. Pharm., 2009, 376, 1–6 CrossRef CAS PubMed.
- D. H. Boal, U. Seifert and J. C. Shillcock, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 4274–4283 CrossRef CAS PubMed.
- K. W. Wojciechowski, Mol. Phys. Rep., 1995, 10, 129–136 Search PubMed.
- M. C. Rechtsman, F. H. Stillinger and S. Torquato, Phys. Rev. Lett., 2008, 101, 085501 CrossRef PubMed.
- Y. Wang, C. Tsai and W. L. Liu, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 131–135 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: (a) Material data and calculation parameters; (b) atom labelling convention employed; (c) interatomic distances and angles at zero pressure; (d) unit-cell volumes and lattice parameters under isotropic pressures; (d) interatomic distances and angles in Phase II of lactic acid; (e) interatomic distances and angles of succinic and citric acids under several anisotropic stresses; (f) animated sequences of the crystal structures of lactic, maleic, succinic and citric acids under the effect of increasing pressures; (g) computed positions of the atoms in the unit cell of lactic acid under an isotropic pressure of 1.056 GPa (CIF file): CCDC 1945991; (h) computed positions of the atoms in the unit cell of succinic acid under an anisotropic stress with associated pressure of 1.757 GPa (CIF file): CCDC 1945995; (i) computed positions of the atoms in the unit cell of citric acid under an anisotropic stress with associated pressure of 0.168 GPa (CIF file): CCDC 1945994. CCDC 1945991, 1945994 and 1945995. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ma00019a |
| This journal is © The Royal Society of Chemistry 2020 |