Open Access Article
Open Access ArticleIdentifying suitable ionic liquid electrolytes for Al dual-ion batteries: role of electrochemical window, conductivity and voltage†
Surya Sekhar
Manna
 ,
Preeti
Bhauriyal
,
Preeti
Bhauriyal
 and
Biswarup
Pathak
and
Biswarup
Pathak
 *
*
Discipline of Chemistry, Indian Institute of Technology (IIT) Indore, Indore, Madhya Pradesh 453552, India. E-mail: biswarup@iiti.ac.in
First published on 9th July 2020
Abstract
Identifying suitable ionic liquid (IL) electrolytes with the desirable electrochemical properties remains a primary challenge for rechargeable Al dual-ion batteries (DIBs). Furthermore, it is also important to investigate how the size and structure of the cation determine the suitability of IL electrolytes in Al DIBs. In this work, with the help of first principles calculations, we have investigated a series of imidazolium-based room temperature ionic liquids (RTILs) by varying the alkyl substituents along with the pyrrolidinium electrolytes and molten salts such as urea/AlCl3 and acetamide/AlCl3. The suitability of the electrolytes is analyzed on the basis of three criteria: electrochemical window (ECW), ionic conductivity and voltage. The HOMO–LUMO positions of the electrolytes with respect to the Fermi positions of the respective electrodes can determine whether the electrolytes (EMIM-AlCl4, PMIM-AlCl4, BMIM-AlCl4 and urea-AlCl4) can perform as more suitable electrolytes, furnishing higher cationic reduction and anionic oxidation stability. Further, our calculated ionic conductivity data favor the usage of the EMIM-AlCl4 electrolyte as it shows the highest ionic conductivity (14.1 mS cm−1) amongst the considered electrolytes (3.4–12.4 mS cm−1). However, these considered electrolytes do not show drastically different effects on the average voltage, furnishing quite similar values in the range of 2.21–2.46 V, which are in accordance with their corresponding experimentally reported voltages. Overall, from these three criteria, we could certainly validate why EMIM-AlCl4 is the most experimentally used electrolyte in Al DIBs. Moreover, our study also predicts PMIM-AlCl4 to be a suitable ionic liquid electrolyte for Al DIBs, as it shows a higher ECW value (4.7 V), a moderate ionic conductivity (12.4 mS cm−1) and a suitable theoretical voltage (2.28 V) along with exhibiting a higher experimental coulombic efficiency compared to EMIM-AlCl4.
1. Introduction
Renewable energy sources like wind and solar power have been prominently used to fulfill electricity demand as green energy systems. However, the storage of energy from these systems is challenging as the generated electricity is intermittent in nature.1–3 Whereas, efficient electrical energy storage devices must get a constant supply of electricity (power storage backup) and load leveling as well as grid energy storage for future application.4,5 Presently, owing to their high voltage and outstanding power density, Li-ion batteries are the most popular amongst metal-ion batteries, but the main concerns that limit their application are the excessive cost and associated safety concerns mainly coming from thermal runaway events.6,7 Therefore, initialization of new battery systems using more abundant natural resources, such as Na-ion,8–10 Mg-ion11–13 and Al-ion14–17 batteries, is urgently needed in the field of stationary batteries for achieving uninterrupted electricity. Among these emerging trends of batteries, the Al battery is the most predominant one owing to: (i) its low-cost, low-flammability and high abundance of Al metal, and (ii) the involvement of the three electron redox couple that provides a high gravimetric capacity.18–21 For the Al battery systems, the usage of aqueous electrolyte is accompanied by the hydrogen evolution reaction as the standard reduction potential of Al3+ (−1.68 V vs. standard hydrogen electrode) is lower than that of H2O, thus making it difficult for use in a closed system.22,23 In this respect, the non-aqueous Al batteries with ionic liquid (IL) electrolytes with Al salts and organic moieties have emerged as important alternatives.24 These room temperature ionic liquids (RTILs)25 are used as potential electrolytes in secondary batteries owing to their wide electrochemical window, good thermal and chemical stability, low melting point, negligible volatility (thus low flammability) and high ionic conductivity.26 These are salts that exist in a liquid state below 100 °C and many are liquids at room temperature as a consequence of weak electrostatic interactions between cations and anions because of a greater number of alkyl groups present on the cation such that charge is prevented from transferring towards the anion. At present, various ionic liquid electrolytes have been explored and most of them have imidazolium cation moieties,27,28 whereas a few are pyrrolidinium-29 or pyridinium-based ionic liquids. And among these electrolytes, imidazolium organic moieties are more favored as they offer a higher voltage and conductivity (due to their lower viscosity at room temperature). As a result, the AlCl3:EMIM-Cl (1-ethyl-3-methylimidazolium chloride) ionic liquid has become the most widely used electrolyte in aluminium batteries, where Al can be reversibly stripped and deposited with >90% coulombic efficiency, without any dendrite formation.30–33 However, the research on rechargeable Al DIBs with the RTIL electrolyte is in the primary stage and most of the published reports are experimental, which provide promising results, but further understanding is required to choose better ionic liquid electrolytes on the basis of their electrochemical window, relative interaction of electrolytes with the corresponding cathodes and anodes, and interatomic characteristics such as conductivity. In a recent study by Peljo et al., it was observed that the electrochemical window of electrolytes is not dependent upon their highest occupied molecular orbital (HOMO) or lowest unoccupied molecular orbital (LUMO) energy positions, but it is more related to the potential of electrolyte reduction at negative potentials, and the potential of electrolyte oxidation at positive potentials. However, they explored very limited systems including the water oxidation/reduction and Fe(III)/Fe(II) couple in aqueous solution34 and the results cannot be generalized for each system at present. For IL electrolyte systems, one similar study has been conducted by Wang et al., where the electrochemical window (ECW) was calculated for three different halogenated imidazolium salts, 1-butyl-3-methyl imidazolium halide (BMIM-X) (X = Cl, Br, and I) with AlCl3 systems.35 They observed that the ECW of the IL electrolyte decreases as anion size increases from AlCl4 → AlCl3Br → AlCl3I, with a maximum value of 4.7 V obtained for BMIM-Cl/AlCl3. However, this study is also limited to the variation of the anions and does not consider the effect of cation selection. Therefore, it has further become necessary to investigate this concept of electrochemical stability for cation variation as well. As discussed earlier, various IL electrolytes have already been reported experimentally for Al DIBs and other metal ion batteries, but a more systematic approach is required to choose among these ILs to get a higher conductivity and high voltage for overall improved battery performance.Therefore, in this work, we have carried out a systematic study to identify the potential ionic liquid electrolytes for Al DIBs using first principles calculations. We have considered a series of imidazolium organic moiety-based RTILs, such as 1-alkyl-3-methyl imidazolium chloride (Cnmim-Cl, where n = 2, 3, 4, 6, and 8) with AlCl3 salts along with other molten salt-based electrolytes, such as, urea/AlCl3 and acetamide/AlCl3. The suitability is explored based on the ECW of the IL electrolytes with respect to their individual HOMO–LUMO energy levels. Moreover, the corresponding ionic conductivity and voltage calculations are also included to choose the efficient IL electrolytes for Al DIBs.
2. Computational details
First principles calculations are performed using the projected augmented wave (PAW) method as implemented in the Vienna ab initio simulation package (VASP) for calculating the ion core and valence electron interaction.36–38 The exchange–correlation potential is described by using the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE).39 An energy cutoff of 470 eV is used for the plane waves. All the optimized structures are obtained by fully relaxing both the atomic and lattice positions until the Hellmann–Feynman forces of all the atoms are smaller than 0.01 eV Å−1. The Brilliouin zone is chosen with a Gamma centered k-point grid of 21 × 21 × 7 for the unit cell and 3 × 3 × 1 for supercell calculations. All the systems are fully converged for the total energy set at 10−5 eV. The van der Waals interactions play a crucial role in layered systems and in individual ionic liquids; therefore, we have used the DFT-D3 approach for correction of the van der Waals interactions, which adds the vdW correction for the potential energy and interaction forces.40 Our optimized interlayer spacing of graphite (3.34 Å) is in close accordance with the experimentally reported value (3.33 Å).41For the calculations of the HOMO and LUMO energies of the solvation model system, the SMD solvation model42 has been used for geometry optimization for all ILs (dielectric constant 12) using the B3LYP/6-31++G(d,p)43,44 level of theory as implemented in Gaussian 09.45
3. Results and discussion
3.1. Consideration of various AlCl3-based IL electrolytes
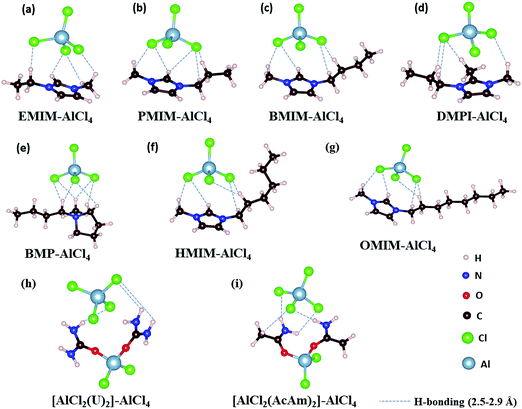
The IL electrolytes examined in our study to understand the ECW and electrochemical properties are categorized into two groups: (i) RTILs having identical active imidazolium cation units with a variation in substituents, and (ii) molten ILs with different active cation ring moieties. These considered systems are represented in Fig. 1. The first category deals with the substituent effect on imidazolium-based ILs, where we vary the alkyl group of the imidazolium ring. This substituent effect by virtue of the steric hindrance could change the intermolecular forces between the imidazolium cation and chloroaluminate anion (AlCl4−). This can also lead to a variation in the physical and chemical properties, such as conductivity, electrodeposition/stripping of Al3+ at the anode, voltage variation and the reversibility of AlCl4− intercalation/deintercalation, and thus influences the overall capability of the electrolyte. In this category, we have studied seven ionic liquid electrolyte systems, 1-ethyl-3-methyl imidazolium chloride ([EMIM]Cl), 1-propyl-3-methyl imidazolium chloride ([PMIM]Cl), 1-butyl-3-methyl imidazolium chloride ([BMIM]Cl), 1,2-dimethyl-3-propyl imidazolium chloride ([DMPI]Cl), 1-hexyl-3-methyl imidazolium chloride ([HMIM]Cl), and 1-methyl-3-octyl imidazolium chloride ([OMIM]Cl) with AlCl3, along with N-butyl-N-methyl pyrrolidinium chloride ([BMP]Cl). The second category of ionic liquids involves two molten salts, urea (U) and acetamide (AcAm) with AlCl3, where the most stable isomerase structures ([AlCl2(U)2]/AlCl4) and ([AlCl2(AcAm)2]/AlCl4) are considered.46 For each IL electrolyte system, we have examined at least four thermodynamically accessible configurations (Fig. S1, ESI†), and the thus obtained most stable orientations (Fig. 1) are considered for further study. The most stable orientations have Cl atoms forming the maximum number of H-bonding interaction (within 2.5–2.9 Å bond distances) with the nearest methylene hydrogens and N–H containing hydrogens in imidazolium salts and molten salts, respectively.47,48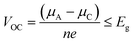 , where e is the electronic charge, n is the number of electrons being transferred and Eg is the gap between the HOMO and LUMO. If in an electrolyte system, μA is located above the LUMO, then the electrolyte undergoes reduction to form a solid electrolyte interface (SEI), which on excessive formation can block further anode electrolyte reaction; similarly, if the position of μC is located below the HOMO, then the electrolyte is oxidized with the formation of the SEI, which will blocked further cathodic reaction.49 Therefore, the thermodynamic stability of the electrolyte requires location of the electrode electrochemical potentials μC and μA within the HOMO and LUMO of the electrolyte. This is the fundamental criterion of an electrolyte to form a stable battery system. However, at present, there is some misconception between the positions of the energy gap (HOMO and LUMO) and ECW of an electrolyte, as shown in Fig. 2b.34 There is no exact relation between the energy gap (HOMO and LUMO) and ECW, and the actual position of the ECW is observed to lie in the HOMO–LUMO energy gap, however not necessarily at the exact position of the HOMO and LUMO values, as shown in Fig. 2c.
, where e is the electronic charge, n is the number of electrons being transferred and Eg is the gap between the HOMO and LUMO. If in an electrolyte system, μA is located above the LUMO, then the electrolyte undergoes reduction to form a solid electrolyte interface (SEI), which on excessive formation can block further anode electrolyte reaction; similarly, if the position of μC is located below the HOMO, then the electrolyte is oxidized with the formation of the SEI, which will blocked further cathodic reaction.49 Therefore, the thermodynamic stability of the electrolyte requires location of the electrode electrochemical potentials μC and μA within the HOMO and LUMO of the electrolyte. This is the fundamental criterion of an electrolyte to form a stable battery system. However, at present, there is some misconception between the positions of the energy gap (HOMO and LUMO) and ECW of an electrolyte, as shown in Fig. 2b.34 There is no exact relation between the energy gap (HOMO and LUMO) and ECW, and the actual position of the ECW is observed to lie in the HOMO–LUMO energy gap, however not necessarily at the exact position of the HOMO and LUMO values, as shown in Fig. 2c.
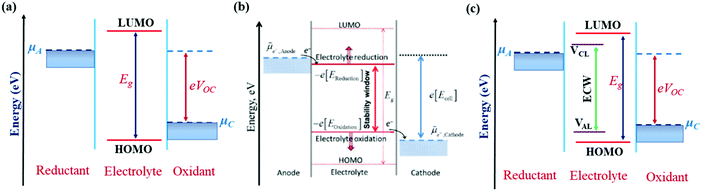 | ||
| Fig. 2 Schematic diagrams of electrode position with respect to the corresponding HOMO–LUMO energy levels of electrolyte where: (a) both electrode Fermi energies (μA & μC) are placed within the HOMO–LUMO gap, and (b) correct notation for the negative and positive potential limits for the electrolyte stability, and the energy levels of the HOMO and LUMO.34 Reproduced from Ref. 34 with permission from Royal Society of Chemistry, Copyright 2018. (c) Stable energy profile of the electrochemical system, where cathodic limiting potential (VCL) is situated above the anode Fermi energy level and anodic limiting potential (VAL) situated below the cathode Fermi energy level to avoid the unwanted oxidation and reduction of the electrolyte. | ||
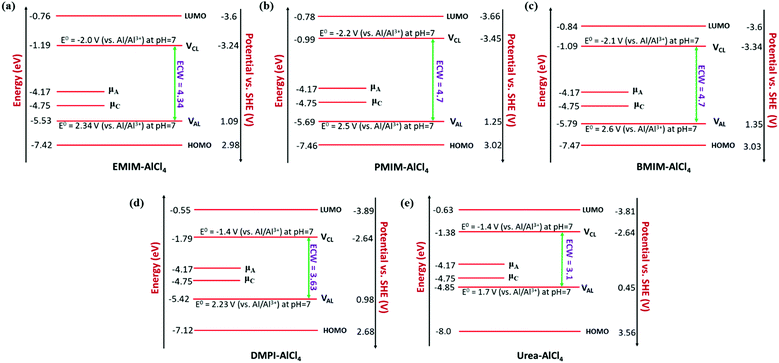
In our study, we have also tried to understand the above-discussed relation between the HOMO–LUMO energy gap and ECW for the considered IL electrolytes to determine suitable electrolyte systems for more efficient Al DIBs. In order to understand the underlying mechanism, we have considered the experimentally reported work functions of both the graphite cathode and Al anode in a vacuum medium.50,51 In this regard, we can define the standard redox potential on the absolute vacuum scale (AVS) by considering the virtual redox reaction between an oxidized species in solution (S) and an electron at rest in a vacuum (V): OxS + e−,V ↔ RedS. In an absolute vacuum, the scale standard hydrogen potential 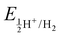 is 4.44 V instead of 0.0 V.52 So, now we can express the limiting Al/Al3+ potential values (Table S1, ESI†) of all the ionic liquids in terms of the absolute vacuum scale at pH = 7. This approach has also been successful in understanding the molecular level arrangement of the HOMO–LUMO positions of the electrolyte with respect to the Fermi positions of respective electrodes.34 Hence, we have studied the considered electrolytes in a schematic way (Fig. 3), where we have considered the two simultaneous potential scales, one being the absolute vacuum scale energy (eV) and the other being the standard hydrogen electrode (SHE) for different types of electrolytes.
is 4.44 V instead of 0.0 V.52 So, now we can express the limiting Al/Al3+ potential values (Table S1, ESI†) of all the ionic liquids in terms of the absolute vacuum scale at pH = 7. This approach has also been successful in understanding the molecular level arrangement of the HOMO–LUMO positions of the electrolyte with respect to the Fermi positions of respective electrodes.34 Hence, we have studied the considered electrolytes in a schematic way (Fig. 3), where we have considered the two simultaneous potential scales, one being the absolute vacuum scale energy (eV) and the other being the standard hydrogen electrode (SHE) for different types of electrolytes.
For the case of the EMIM-AlCl4 electrolyte, as shown in Fig. 3a, both cathodic (VCL) and anodic (VAL) limiting potentials are situated between the HOMO (−7.42 eV) and LUMO (−0.76 eV) of the electrolyte along with the electrode work functions of the cathode (μC = −4.75 eV)50 and anode (μA = −4.17 eV)51 thus it behaves as a stable system, as shown in Fig. 2c. According to this energy profile, if the anodic limiting potential (VAL) is more than 2.34 V vs. (Al/Al3+), AlCl4− undergoes oxidation to Cl2 gas (4AlCl4−− 2e → Cl2 + 2Al2Cl7−),35 and similarly, EMIM+ would undergo reduction (EMIM+ + e → EMIM)53 if the cathodic limiting potential (VCL) is more than −2.0 V vs. (Al/Al3+). This results in the breakdown of reversibility of conversion reactions in Al DIBs. A similar explanation is also applicable for all imidazolium moiety-based electrolytes, such as PMIM-AlCl4, BMIM-AlCl4 and DMPI-AlCl4 (Fig. 3b–d), varying with different ECW values of 4.7 V, 4.7 V and 3.63 V, respectively, which are experimentally verified by the reported results.35,54,55 These observations explain why the imidazolium IL electrolytes behave as stable electrolytes and, particularly, why EMIM-AlCl4 with a broad electrochemical window (4.34 V) is the most preferred electrolyte in Al ion batteries.14–16,56 The ECW is not discussed for HMIM-AlCl4 and OMIM-AlCl4 electrolytes due to the non-availabilty of their experimental oxidation and reduction limiting potential values. The reduction of urea-AlCl4 is a little different due to the existence of isomeric cationic species [AlCl2(U)2] + with AlCl4−. It involves a relatively lower energy barrier (0.1 eV) of electron transfer from the oxidation limiting (VAL) potential to the cathode, making urea-AlCl4 susceptible to oxidation along with having a narrow electrochemical window (3.1 V) compared to the imidazolium-based ionic liquid electrolytes (3.6–4.7 V). However, the higher availability and low cost of urea still make the urea-AlCl4 electrolyte a fairly suitable option in Al DIBs.
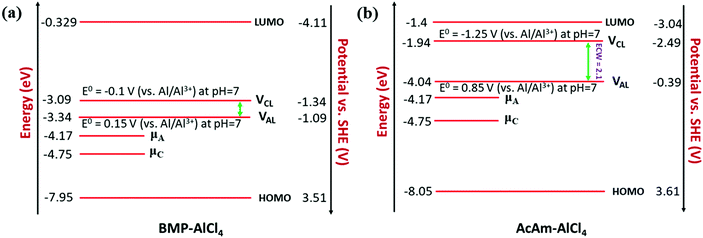
We observe an altogether different behaviour of the ECW for BMP-AlCl4 and the molten salt AcAm-AlCl4, as shown in Fig. 4. For both systems, VCL and VAL are found to be placed above the work functions of the cathode and anode in their respective electrochemical window. This can lead to both oxidation of AlCl4− and reduction of the BMP/AcAm cation in a simultaneous way, which could lead to the formation of a SEI layer, restricting the battery efficiency. As a result, the concentration of ionic salt is not maintained constantly throughout the reaction, leading to a breakdown of the overall reversibility of the electrolyte in the system. The reason behind both the reduction and oxidation can be explained by the charge analysis of the BMP+ ring and AlCl4−. The stability of imidazolium ring-based systems can be correlated with the delocalization of charge through the cation ring. Moreover, based on natural bond orbital (NBO) charge analysis,57 we have observed that two of the nitrogen atoms of EMIM+ have higher charges (−0.353 |e| and −0.350 |e|) compared to the charge on the single nitrogen atom (−0.346 |e|) in the BMP ring (Fig. S2, ESI†). This indicates a stronger interaction between cation and anion in the EMIM-AlCl4 system compared to that of BMP-AlCl4. This strong interaction reflects the less tendency of the respective cations and anions to undergo reduction and oxidation in the EMIM-AlCl4 electrolyte compared to the BMP-AlCl4 electrolyte. Overall, the BMP-AlCl4 electrolyte is an unsuitable electrolyte in the Al ion battery on the basis of both stability and window potential (0.25 V). However, experimentally, the electrochemical properties of the AcAm-AlCl4 system are found to improve as a result of a solvent effect by dichloromethane (DCM) addition.58 The solvation effect is shown to drastically change the properties such as stability and potential window and discharge capacity due to the dilution of the electrolyte. Overall, from the electrochemical window study, we can confirm that the EMIM-AlCl4, PMIM-AlCl4, BMIM-AlCl4, DMPI-AlCl4 and urea-AlCl4 electrolytes are more suitable for Al DIBs compared to the BMP-AlCl4 and AcAm-AlCl4 electrolytes. This potential window concept can be helpful in designing stable electrolytes with wide electrochemical windows for Al DIBs.
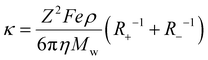 , proposed by Abbott et al.59 to calculate the ionic conductivities. The detailed derivation of this revised expression of the Stokes–Einstein equation can be understood as follows along with the discussion of important approximations/limitations:
, proposed by Abbott et al.59 to calculate the ionic conductivities. The detailed derivation of this revised expression of the Stokes–Einstein equation can be understood as follows along with the discussion of important approximations/limitations:
The conductivity of a liquid salt can be described as60
| κ = F(C+′u++ C−′u−) | (1) |
Therefore,
| κ = yFC(u+ + u−) | (2) |
Eqn (2) represents a modified form of the Stokes–Einstein relation. Here, y represents the degree of dissociation varying between 0 and 1. The approximation associated with eqn (2) was noted in a previous study by Harris et al.61 and it assumes that the IL behaves as an infinitely diluted solution. This approximation does not consider the ion–solvent interactions and assumes that the ion–ion interactions are limited to the association to form neutral species.
A more accurate modified form of the Stokes–Einstein relation correlates ionic transport to viscosity of the medium,
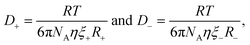 | (3) |
Further,
| u+ = D+F/RT and u− = D−F/RT | (4) |
Combining eqn (2)–(4) derives a form of the Stokes–Einstein equation as obtained by Bonhôte et al.,60 which expresses the specific conductivity of charge in an ambient temperature IL as follows,
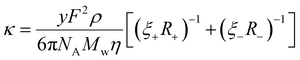 | (5) |
Abbott et al. further derived the above-mentioned Stokes–Einstein eqn (5) by applying hole theory.59 Hole theory is applicable to both ionic and molecular fluids to account for viscosity,62 which is limited by the availability of the holes. Since the fraction of suitably sized holes in ambient-temperature ionic liquids is very low (about 10−6), the holes are assumed at infinite dilution. And as the migration of holes is independent of each other, they can be described by the Stokes–Einstein equation as
| λ+ = Z2Fe/6πηR+ | (6) |
| Λ = λ+ + λ− | (7) |
Therefore, the net equation of conductivity can be written as eqn (8), which has been used in our study to determine the ionic conductivities of the ionic liquids.
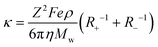 | (8) |
The corresponding ionic radii are obtained by calculating the volumes of spherical structures of both cation and anion and are in accordance with the experimental values (Table S3, ESI†).
The above conductivity equation is basically derived for noninteracting ions, as in an infinitely diluted electrolyte solution. However, in reality, mass, charge, momentum, and energy transport processes in the ionic liquids and molten salts involve correlated interionic collisions, caging, and vortex motions. Therefore, the calculated conductivities cannot be expected to exactly match with the measured conductivities but do provide qualitative values. Here, we consider the molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (AlCl3
1 (AlCl3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) salt) of the IL electrolyte. This is because for an IL ratio higher than 1
salt) of the IL electrolyte. This is because for an IL ratio higher than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the deviation from the Stokes–Einstein equation is more prominent due to the stronger ion–solvent interactions, which are difficult to ignore.61
1, the deviation from the Stokes–Einstein equation is more prominent due to the stronger ion–solvent interactions, which are difficult to ignore.61
The calculated ionic conductivities for the IL electrolytes under investigation are plotted in Fig. 5.
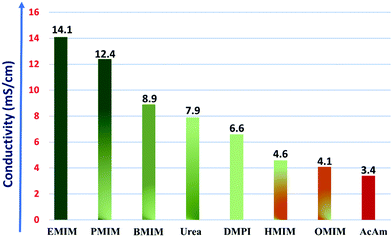 | ||
| Fig. 5 Variation of ionic conductivity of the considered IL electrolytes. Here, the dark green and red colors represent the higher and lower ionic conductivity values, respectively. | ||
We observe that for the case of the imidazolium cation moiety-based RTIL electrolytes, as the size of the alkyl chain (R+) increases from ethyl (EMIM) to octyl (OMIM), the conductivity of the IL electrolyte gradually diminishes with a maximum conductivity of 14.1 mS cm−1 for EMIM-AlCl4, and this trend is in accordance with that of a previously reported study.63 From eqn (8), we can clearly observe that the resultant conductivity mainly varies with the density, viscosity, molecular weight and the ionic radii of the considered ionic salts. And, for the imidazolium cation-based room temperature IL electrolytes, the decrease of the conductivity with the alkyl chain length is the result of the decreasing density of the ionic liquids from ethyl (EMIM) to octyl (OMIM), while the opposite trend is observed for viscosity, because of the longer aliphatic chain resulting in increased viscosity. The variation in density can be correlated with the packing efficiency of the molecules, which decreases with the increase in the size of the alkyl substitution of the imidazolium ring and thus results in an overall decrease in ionic conductivity. On the other hand, the origin of the viscosity trend is likely to be more complex, as it is measured by the internal friction in the system, however a number of parameters contribute to it, such as molecular shape, size, molar mass, temperature and the forces between the ions. In this case, the increase in viscosity could be the resultant combination of the increase in the alkyl chain length, which can restrict their movement in electrolyte, and the increase in dispersion forces due to an overall increase of the molar volume of the electrolyte system. As a result, there is a gradual decrease in the ionic mobility of the ions and the overall ionic conductivity.
In the case of the BMP-AlCl4 electrolyte, due to the non-availability of the physical terms such as density and viscosity, we could not calculate the conductivity, however its conductivity is expected to be much smaller (having a larger size) than that of the EMIM-AlCl4 system.64
However, for the case of the molten salt systems such as urea-AlCl4 (7.9 mS cm−1) and AcAm-AlCl4 (3.4 mS cm−1), the observed conductivities are lower than those of the room temperature IL electrolytes, even though they operate at higher temperatures and generally have lower viscosities. In the case of both urea and AcAm, the larger cation size (R+) and molecular weight are the predominant factors, which reduce the overall conductivities compared to the contribution of the lower viscosity values at higher temperatures. The conductivity of the urea-AlCl4 system is much higher than that of the AcAm-AlCl4 system due to the lower molecular weight, higher density and small cation size. Moreover, in a recent report, Michael Angell et al. have also shown that AlCl3 containing urea derivatives such as N-methyl urea and its salts act as preferential electrolytes having higher ionic conductivities in Al-DIBs due to their lower viscosities.65
Overall, from the ionic conductivity calculations, we conclude that the RTIL electrolytes with smaller alkyl substituents and higher conductivity are superior choices for rechargeable battery electrolytes. Especially, the highest ionic conductivity of EMIM-AlCl4 could be one of the reasons for its selective choice in most of the experimental studies of Al DIBs.14–17,66 However, in a recent study of Al DIBs by Yang et al., it was observed that the PMIM-AlCl4 system behaves as a more suitable electrolyte with 100% coulombic efficiency compared to the EMIM-AlCl4 (95%) system.14,63 And, our study also shows that the ionic conductivity of the PMIM-AlCl4 system is quite high (12.4 mS cm−1). Therefore, we believe that PMIM-AlCl4 can also be utilized as a suitable next generation electrolyte instead of EMIM-AlCl4 in Al DIBs.
3.2. Voltage characteristics
Unlike the metal-ion batteries, the electrolyte in Al DIBs determines the voltage, not only in terms of deciding the electrochemical window, but also by actively participating in the net electrochemical reaction of charging and discharging. Therefore, the potential applicability of the IL electrolytes can also be concluded on the basis of the overall voltage. In the voltage calculation, we have considered the AlCl3/cation for ionic liquid electrolytes with a molar ratio >1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to have extra AlCl3 for generation of the Al2Cl7 ion, which takes part in the charge/discharge reaction mechanism.
1 to have extra AlCl3 for generation of the Al2Cl7 ion, which takes part in the charge/discharge reaction mechanism.
The reaction mechanism of Al DIBs involves the intercalation/deintercalation of AlCl4− at the cathode and electrodeposition/stripping of Al metal at the anode during the charge/discharge process. The net charge/discharge reaction involving the conversion reactions between AlCl4− and Al2Cl7− is given below.
| Al + 7AlCl4− ↔ 4Al2Cl7− + 3e− (anode) | (9) |
| Cn[AlCl4] + e− ↔ Cn + AlCl4− (cathode) | (10) |
For previously studied Al DIBs, the voltage eqn (11) was successfully observed to give quite accurate voltage values in accordance with the corresponding experimental voltage range. Therefore, for the comparative study of the IL electrolytes, we also used the following equation to calculate the voltage.
 | (11) |
In this study, to compare the voltage of the considered IL electrolytes, we have studied a stage-1 AlCl4− intercalated graphite system with the C18[AlCl4] formula unit,68 constructed using a 3 × 3 × 1 supercell of graphite. We observe that for the imidazolium-based IL electrolytes, the voltage does not vary in a monotonic fashion when increasing the alkyl chain length, as shown in Table 1, where the highest voltage of 2.46 V is calculated for HMIM-AlCl4. Further, the calculated voltages for the widely used electrolytes, EMIM-AlCl4, BMIM-AlCl4 and DMPI-AlCl4, for Al dual-ion batteries are 2.25 V, 2.40 V and 2.24 V, respectively, which are also in close accordance with the experimentally reported voltage ranges of 2.25–2.0 V, 2.3–1.98 V and 2.0–1.7 V, respectively.14,55,67 On the other hand, the molten salt electrolytes, urea-AlCl4 and AcAm-AlCl4, are also observed to have similar ranges to that of the RTIL electrolytes with the voltage values of 2.35 V and 2.21 V, respectively, which closely resemble their experimentally reported values of 2.3–1.9 V and 2.3–2.0 V, respectively.58,65
The voltage analysis shows that all the considered IL electrolytes provide similar voltages ranging from 2.21 to 2.46 V and the suitability of the electrolyte cannot be directly concluded from the voltage alone as other factors such as conductivity and electrochemical stability also have an equal deciding role. For example, even though HMIM-AlCl4 has a high voltage value of 2.46 V, it cannot be used as a preferential electrolyte in Al DIBs as its ionic conductivity value (4.6 mS cm−1) is very low.
Based on all three properties, electrochemical window, conductivity and voltage analyzed in this report, we can conclude that EMIM-AlCl4, PMIM-AlCl4, BMIM-AlCl4, DMPI-AlCl4 and urea-AlCl4 have desirable characteristics for use as an electrolyte in Al DIBs possessing a suitably large electrochemical window (4.38 V, 4.7 V, 4.7 V, 3.63 V, and 3.1 V) and high conductivities (14.1, 12.4, 8.9, 6.6, and 7.9 mS cm−1) as well as reasonably high voltages (2.25 V, 2.38 V, 2.40 V, 2.24 V, and 2.35 V), respectively. Our study also provides a reason for the preferential use of the EMIM-AlCl4 electrolyte in various experimental Al DIBs. Moreover, another important IL electrolyte, which can be further used in Al DIBs, is PMIM-AlCl4, which offers a sufficiently high voltage (2.38 V), electrochemical window (4.7 V) and reasonably high conductivity (12.4 mS cm−1) like EMIM-AlCl4 and was also observed to show better coulombic efficiency than EMIM-AlCl4 in a recent experimental report.63
4. Conclusion and outlook
In conclusion, we have systematically identified suitable ionic liquid and molten salt electrolytes for Al dual-ion batteries (DIBs) by analyzing the characteristics, such as electrochemical window, ionic conductivities and voltages. Here, we study a series of imidazolium-based AlCl3 salt electrolytes by varying the alkyl substituent in the imidazolium ring cation and molten salt electrolytes, such as urea/AlCl3, and acetamide/AlCl3. We initiated the study by analyzing the misconception of the relation between the HOMO–LUMO energy gap and the electrochemical window (ECW) of electrolytes, which states that the ECW values are not the same as the energy positions of the HOMO–LUMO, but in actuality they reside inside the HOMO–LUMO gap. In our considered systems, the imidazolium moiety-based ionic liquids such as EMIM-AlCl4 (4.34 V), PMIM-AlCl4 (4.7 V), BMIM-AlCl4 (4.7 V), and DMPI-AlCl4 (3.63 V) are observed to have high ECW values indicating their higher stability towards both cation reduction and anion oxidation. On the other hand, the pyrrolidinium moiety-based BMP-AlCl4 furnishes a small ECW (0.25 V) and is more susceptible to both oxidation of AlCl4− and reduction of BMP+, which could obstruct further reaction on the electrode through SEI formation. In the case of the molten salt electrolytes, urea-AlCl4 can be considered as a suitable electrolyte for Al DIBs with a broad ECW (3.1 V) compared to a smaller ECW (2.1 V) of the AcAm-AlCl4 electrolyte. The second characteristic, the ionic conductivity, which is governed by factors such as viscosity, temperature and cation–anion size of the IL electrolyte, also shows varying values for the considered IL electrolytes. In the case of the imidazolium-based ionic liquids, the ionic conductivity decreases from EMIM-AlCl4 (14.1 mS cm−1) to OMIM-AlCl4 (4.1 mS cm−1) with the increase in the alkyl chain length of the cation due to an abrupt increase of the cation size, which is in good agreement with a previous report.63 We observe that the ionic conductivity also favors the urea-AlCl4 molten salt with higher conductivity (7.9 mS cm−1) compared to AcAm-AlCl4 (3.4 mS cm−1) as a result of the higher density and lower molecular weight and lower cationic size of the urea+ ion. The third characteristic is the average voltage, which is observed to show very similar output values for all the studied IL electrolytes within the range of 2.4–2.2 V, showing good agreement with the experimentally reported voltages (2.3–1.7 V). Our results clearly explain the preferential usage of EMIM-AlCl4 in Al DIB technology as it furnishes a large ECW, higher conductivity and increased voltage. Other than that, we believe that PMIM-AlCl4 could also be a preferable choice as it not only shows a higher ECW value (4.7 V) and high ionic conductivity (12.4 mS cm−1) but also provides a higher coulombic efficiency compared to that of EMIM-AlCl4 as observed in a recent experimental study.56 Additionally, the molten salt (specially the urea containing salt) ionic liquid could also be useful in Al DIBs in terms of practical applications compared to the costly imidazolium-based ionic liquids. Overall, these results provide an in-depth understanding to design an efficient electrolyte with suitable electrochemical properties for Al DIBs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank IIT Indore for the lab and computing facilities. This work is supported by DST-SERB (Project Number CRG/2018/001131) and SPARC (Project Number SPARC/2018-2019/P116/SL), New Delhi. S. S. M. thanks CSIR and P. B. thanks MHRD for research fellowships. We would like to thank Sandeep Das for his valuable suggestion.References
- S. Linic, P. Christopher and D. B. Ingram, Nat. Mater., 2011, 10, 911–921 CrossRef CAS PubMed.
- Y. Zhou, P. Luckow, S. J. Smith and L. Clarke, Environ. Sci. Technol., 2012, 46, 7857–7864 CrossRef CAS PubMed.
- M. Kaltenbrunner, M. S. White, E. D. Glowacki, T. Sekitani, T. Someya, N. S. Sariciftci and S. Bauer, Nat. Commun., 2012, 3, 770 CrossRef PubMed.
- G. Dennler, M. C. Scharber and C. J. Brabec, Adv. Mater., 2009, 21, 1323–1338 CrossRef CAS.
- T. Ackermann and L. Soder, Renewable Sustainable Energy Rev., 2002, 6, 67–128 CrossRef.
- J. Wen, Y. Yu and C. Chen, Mater. Express, 2012, 2, 197–212 CrossRef CAS.
- K. Liu, Y. Liu, D. Lin, A. Pei and Y. Cui, Sci. Adv., 2018, 4, eaas9820 CrossRef PubMed.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-Gonzalez and T. Rojo, Energy Environ. Sci., 2012, 5, 5884–5901 RSC.
- L. O. Vogt, C. Marino and C. Villevieille, Chimia, 2015, 69, 729–733 CrossRef CAS PubMed.
- J. Billaud, R. J. Clément, A. R. Armstrong, J. Canales-Vázquez, P. Rozier, C. P. Grey and P. G. Bruce, J. Am. Chem. Soc., 2014, 136, 17243–17248 CrossRef CAS PubMed.
- G. Singh, N. Tapia-Ruiz, J. M. Lopez del Amo, U. Maitra, J. W. Somerville, A. R. Armstrong, J. Martinez de Ilarduya, T. Rojo and P. G. Bruce, Chem. Mater., 2016, 28, 5087–5094 CrossRef.
- J. Muldoon, C. B. Bucur and T. Gregory, Chem. Rev., 2014, 114, 11683–11720 CrossRef CAS PubMed.
- B. Pan, J. Huang, Z. Feng, L. Zeng, M. He, L. Zhang, J. T. Vaughey, M. J. Bedzyk, P. Fenter, Z. Zhang, A. K. Burrell and C. Liao, Adv. Energy Mater., 2016, 6, 1600140 CrossRef.
- M.-C. Lin, M. Gong, B. Lu, Y. Wu, D.-Y. Wang, M. Guan, M. Angell, C. Chen, J. Yang, B.-J. Hwang and H. Dai, Nature, 2015, 520, 324–328 CrossRef CAS PubMed.
- N. Jayaprakash, S. K. Das and L. A. Archer, Chem. Commun., 2011, 47, 12610–12612 RSC.
- J. V. Rani, V. Kanakaiah, T. Dadmal, M. S. Rao and S. Bhavanarushi, J. Electrochem. Soc., 2013, 160, A1781–A1784 CrossRef CAS.
- S. C. Jung, Y.-J. Kang, D.-J. Yoo, J. W. Choi and Y.-K. Han, J. Phys. Chem. C, 2016, 120, 13384–13389 CrossRef CAS.
- Z. A. Zafar, S. Imtiaz, R. Razaq, S. Ji, T. Huang, Z. Zhang, Y. Huang and J. A. Anderson, J. Mater. Chem. A, 2017, 5, 5646 RSC.
- L. Fu, N. Li, Y. Liu, W. Wang, Y. Zhu and Y. Wu, Chin. J. Chem., 2017, 35, 13–20 CrossRef CAS.
- G. A. Elia, K. Marquardt, K. Hoeppner, S. Fantini, R. Lin, E. Knipping, W. Peters, J.-F. Drillet, S. Passerini and R. Hahn, Adv. Mater., 2016, 28, 7564–7579 CrossRef CAS PubMed.
- Y. Wang, R. Chen, T. Chen, H. Lv, G. Zhu, L. Ma, C. Wang, Z. Jin and J. Liu, Energy Storage Mater., 2016, 4, 103–129 CrossRef.
- S. Liu, J. J. Hu, N. F. Yan, G. L. Pan, G. R. Li and X. P. Gao, Energy Environ. Sci., 2012, 5, 9743–9746 RSC.
- Y. J. He, J. F. Peng, W. Chu, Y. Z. Lia and D. G. Tong, J. Mater. Chem. A, 2014, 2, 1721–1731 RSC.
- Q. Li and N. J. Bjerrum, J. Power Sources, 2002, 110, 1–10 CrossRef CAS.
- E. W. Castner and J. F. Wishart, J. Chem. Phys., 2010, 132, 120901 CrossRef PubMed.
- H. Weingaertner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef CAS PubMed.
- H. Srour, L. Chancelier, E. Bolimowska, T. Gute, S. Mailley, H. Rouault and C. C. Santini, J. Appl. Electrochem., 2016, 46, 149–155 CrossRef CAS.
- J.-K. Kima, A. Matic, J.-H. Ahnb and P. Jacobsson, J. Power Sources, 2010, 195, 7639–7643 CrossRef.
- (a) G. B. Appetecchi, G.-T. Kima, M. Montaninoa, M. Carewskaa, R. Marcilla, D. Mecerreyes and I. D. Meatza, J. Power Sources, 2010, 195, 3668–3675 CrossRef CAS; (b) R. A. DiLeo, A. C. Marschilok, K. J. Takeuchi and E. S. Takeuchi, J. Electrochem. Soc., 2013, 160, A1399–A1405 CrossRef CAS.
- T. Jiang, M. J. Chollier Brym, G. Dubé, A. Lasia and G. M. Brisard, Surf. Coat. Technol., 2006, 201, 1–9 CrossRef CAS.
- T. Jiang, M. J. Chollier Brym, G. Dubé, A. Lasia and G. M. Brisard, Surf. Coat. Technol., 2006, 201, 10–18 CrossRef CAS.
- J. J. Auborn and Y. L. Barberio, J. Electrochem. Soc., 1985, 132, 598–601 CrossRef CAS.
- P. K. Lai and M. Skyllas-Kazacos, J. Electroanal. Chem. Interfacial Electrochem., 1988, 248, 431–440 CrossRef CAS.
- P. Peljo and H. H. Girault, Energy Environ. Sci., 2018, 11, 2306–2309 RSC.
- H. Wang, S. Gu, Y. Bai, S. Chen, N. Zhu, C. Wu and F. Wu, J. Mater. Chem. A, 2015, 3, 22677–22686 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- Y. Chen, F. Peng, Y. Yan, Z. Wang, C. Sun and Y. Ma, J. Phys. Chem. C, 2013, 117, 13879 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- Y. Baskin and L. Meyer, Phys. Rev., 1955, 100, 544 CrossRef CAS.
- V. S. Bernales, A. V. Marenich, R. Contreras, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2012, 116, 9122–9129 CrossRef CAS PubMed.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- H. M. A. Abood, A. P. Abbott, A. D. Ballantyne and K. S. Ryder, Chem. Commun., 2011, 47, 3523–3525 RSC.
- H. Li, Y. Chang, W. Zhu, W. Jiang, M. Zhang, J. Xia, S. Yin and H. Li, J. Phys. Chem. B, 2015, 119, 5995–6009 CrossRef CAS PubMed.
- Y. Zheng, K. Dong, Q. Wang, J. Zhang and X. Lu, J. Chem. Eng. Data, 2013, 58, 32–42 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- G. Baysinger, Lev I. Berger, R. N. Goldberg, H. V. Kehiaian, K. Kuchitsu, G. Rosenblatt, D. L. Roth and D. Zwillinger, CRC Handbook of Chemistry & Physics, CRC Press, London, 73rd edn, 1992–1993 Search PubMed.
- J. Hölzl and F. K. Schulte, Springer Tracts in Modern Physics, Springer, Berlin, Heidelberg, 2006, vol. 85 DOI:10.1007/BFb0048919.
- S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966 CAS.
- B. Vestergaard, N. J. Bjerrum, I. Petrushina, H. A. Hiuler, R. W. Berg and M. Begtrup, J. Electrochem. Soc., 1993, 140, 3108–3113 CrossRef CAS.
- G. E. Gray, J. Winnick and P. A. Kohl, J. Electrochem. Soc., 1996, 143, 3820 CrossRef CAS.
- Z. Lv, M. Han, J. Sun, L. Hou, H. Chen, Y. Li and M.-C. Lin, J. Power Sources, 2019, 418, 233–240 CrossRef CAS.
- H. Sun, W. Wang, Z. Yu, Y. Yuan, S. Wang and S. Jiao, Chem. Commun., 2015, 51, 11892–11895 RSC.
- F. Weinhold and C. Landis, Chem. Educ. Res. Pract., 2001, 2, 91–104 RSC.
- N. Canever, N. Bertrand and T. Nann, Chem. Commun., 2018, 54, 11725–11728 RSC.
- A. P. Abbott, ChemPhysChem, 2005, 6, 2502–2505 CrossRef CAS PubMed.
- P. Bonhôte, A.-P. Dias, N. Papageorgiou, K. Kalyanasundaram and M. Gra1tzel, Inorg. Chem., 1996, 35, 1168–1178 CrossRef PubMed.
- K. R. Harris, J. Phys. Chem. B, 2018, 122, 10964–10967 CrossRef CAS PubMed.
- A. P. Abbott, ChemPhysChem, 2004, 5, 1242–1246 CrossRef CAS PubMed.
- C. Yang, S. Wang, X. Zhang, Q. Zhang, W. Ma, S. Yu and G. Sun, J. Phys. Chem. C, 2019, 123, 11522–11528 CrossRef CAS.
- G. Zhu, M. Angell, C.-J. Pan, M.-C. Lin, H. Chen, C.-J. Huang, J. Lin, A. J. Achazi, P. Kaghazchi, B.-J. Hwang and H. Dai, RSC Adv., 2019, 9, 11322–11330 RSC.
- M. Angell, G. Zhu, M.-C. Lin, Y. Rong and H. Dai, Adv. Funct. Mater., 2020, 30, 1901928 CrossRef CAS.
- K. V. Kravchyk, S. Wang, L. Piveteau and M. V. Kovalenko, Chem. Mater., 2017, 29, 4484–4492 CrossRef CAS.
- Z. Yu, J. Tu, C. Wang and S. A. Jiao, ChemistrySelect, 2019, 4, 3018–3024 CrossRef CAS.
- P. Bhauriyal, A. Mahata and B. Pathak, Phys. Chem. Chem. Phys., 2017, 19, 7980–7989 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The supporting information file contents are different orientation structures of imidazolium-based electrolytes, cathodic and anodic limiting potentials of the considered electrolytes, NBO charge analysis of the EMIM-AlCl4 and BMP-AlCl4 electrolytes, physical properties (density and viscosity) of the considered electrolytes and ionic radii of cations and anions of all the electrolytes. See DOI: 10.1039/d0ma00292e |
| This journal is © The Royal Society of Chemistry 2020 |