Open Access Article
Open Access ArticleMagnetic properties of synthetic fluorophlogopite mica crystals
Zheng
Ma
a,
Vassil
Skumryev
bc and
Martí
Gich
 *a
*a
aInstitut de Ciència de Materials de Barcelona (ICMAB-CSIC), Campus UAB, 08193 Bellaterra, Barcelona, Spain. E-mail: mgich@icmab.es
bDepartament de Física, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Spain
cInstitució Catalana de Recerca i Estudis Avançats (ICREA), 08010 Barcelona, Spain
First published on 27th July 2020
Abstract
Micas have recently attracted the interest of materials scientists to be used as flexible substrates for the growth of nanomaterials. Synthetic fluorophlogopite is particularly appealing due to its high thermal stability and a significantly lower level of impurities compared to natural mica. Perhaps because of such high purity, little attention has been given to its magnetic properties, assumed to be diamagnetic. Herein, we report an in-depth study of the magnetic properties of commercial fluorophlogopite mica crystals as a function of magnetic field and temperature. Our study shows that the magnetic response of mica comprises diamagnetic and paramagnetic components. The latter is quite significant at low temperatures and can be analyzed within the framework of Curie's law and the Langevin theory, which indicate that it originates from isolated magnetic cations. Hence, special care must be taken to study the magnetic properties of mica-supported nanostructures. We propose a protocol to correct the magnetic contributions of mica substrates which can be useful in future developments of flexible magnetic devices.
Introduction
Mica is one of the most common phyllosilicates and is yearly mined in hundreds of thousands of tons1 for multiple applications from building materials and electronic components2 to cosmetics.3 These applications exploit its optical and infrared transparency, a remarkable chemical inertness and thermal stability combined with elasticity and flexibility and a high dielectric strength and electrical resistance. But what makes mica unique is its layered structure (see Fig. 1). It is made up from negatively charged aluminosilicate layers consisting of two tetrahedral sheets with their apical oxygen atoms sandwiching an internal octahedral sheet and their basal oxygens defining six-membered rings of corner sharing tetrahedra on the layer surfaces.4 Neighbouring layers are held together thanks to the weak bonding with 12-coordinated potassium ions accommodated at these ring cavities and which is responsible for an easy cleavage parallel to the {001} basal plane which results in atomically flat surfaces.5 These surfaces were soon recognized as particularly appealing playgrounds for surface science studies on gases, liquids6,7 and also as a substrate for the deposition thin films.8–10 More recently, with the growing interest for flexible electronics and two-dimensional (2D) materials, mica has attracted renewed attention. This is reflected by new discoveries of prospective mica applications such as that of proton conductors for fuel cells11 and in the ever-increasing examples of integration on mica of nanometre-sized functional materials, such as graphene,12 transition metal dichalcogenides,13–15 topological insulators16,17 and oxides.18,19 It is believed that mica could have a remarkable impact on future high-performance flexible electronics.20 For instance, ferroelectric Pb(Zr,Ti)O3 thin films have been deposited on mica via van der Waals epitaxy for flexible non-volatile memory applications.21 Another interesting example is the mica-supported lead-free perovskite based on Na0.5Bi0.5TiO3 with a dual electrocaloric cooling and energy-harvesting functionality.22 In this context, the integration of magnetic materials on mica is also gaining importance.23–26 In parallel, the interest in magnetic 2D materials has been spurred by the recent discovery of this property, either intrinsic or associated to defects, in some of this low dimensional systems.27,28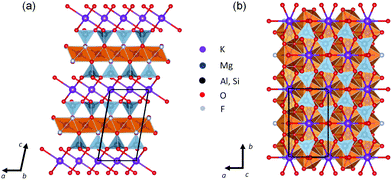 | ||
| Fig. 1 Crystal structure of fluorophlogopite projected along the (a) [010] and (b) [001] crystallographic directions. One representative unit cell is outlined by black solid lines. | ||
Despite the relevance of mica as substrate for growing magnetic materials, not enough attention has been paid to the magnetic properties of mica itself. We can find in the recent literature examples in which the magnetic contribution of mica substrates is simply ignored19,25 or others in which the issue of the substrate contribution to the overall magnetic response is bypassed by transferring it to another substrate more easy to deal with from the magnetic point of view.29 A prior knowledge of the magnetic characteristics of mica substrate appears as imperative before undertaking the magnetic characterization of the nanostructures grown on top of it. Most commercially available substrates are diamagnetic. This means that their magnetic responses are weak (with susceptibilities in the order of −10−6), independent of temperature and vary linearly with applied field. Thus, to obtain the magnetic response of a film, one can readily offset the contribution of a diamagnetic substrate. This is done by compensating the signal obtained from the linear fitting of the magnetization versus magnetic field curve at high enough fields so that the ferri-/ferromagnetic film is already saturated, and the diamagnetic substrate signal dominates the magnetic response. In principle, pure mica should be diamagnetic as other conventional substrates. However, it has been shown that impurities of iron, the most abundant magnetic element in the Earth's crust, are responsible for paramagnetic and/or ferromagnetic contributions in the measured minerals.30,31 Coey et al. investigated the magnetic anomalies of natural micas at various temperatures and at high magnetic fields.32,33 The observed magnetic anisotropy of trioctahedral micas was ascribed to iron incorporation in their crystal structures.32 It is worth noting that unlike the diamagnetic contribution the paramagnetic one is both temperature and field dependent, which makes the above-mentioned correction method inappropriate for iron-bearing mica substrates. Thus, the correction of the magnetic response of iron- or other elements with unpaired spins contained in mica becomes nontrivial, since it can potentially screen intrinsic magnetic response of the nanoscale objects with small magnetic moments grown on it. In this case, the method by Schmidt et al.34 to separate diamagnetic and paramagnetic components, which is based on high field torque measurements, is not convenient because it is not sensitive at low fields and requires samples with oblate or prolate shapes and subtracting the measuring holder contribution.
Among the members of the mica group, phlogopite (KMg3(AlSi3O10)(OH)2) is one of the most common rock-forming minerals. In synthetic fluorophlogopite, the apical hydroxyl groups of phlogopite are substituted by fluorine ions (F−), resulting in an ideal formula KMg3(AlSi3O10)F2. Thanks to the presence of F− this mica has an enhanced thermal stability (up to 1100 °C) and can withstand larger stresses in tension and compression. The fluorophlogopite structure (see Fig. 1) possesses monoclinic space group C2/m, with a = 5.308(2) Å, b = 9.183(3) Å, and c = 10.139(1) Å, β = 100.07(2)°, and Z = 2.35 Fluorophlogopite mica sheets can be produced by solid state reaction or melting methods from suitable oxides and fluorides, and are commercially available.36 Compared to natural micas, synthetic fluorophlogopite has enhanced crystallinity and higher purity.36 Besides, due to its well-controlled chemistry, it features a highly ordered atomically smooth surface, high transparency, chemical durability, and high working temperature. As a result, it has increasingly been the substrate of choice for the development of new functional materials.26,37–39 Yet, the fundamental understanding of this fluorine-rich silicate is far from complete. This is particularly true concerning the magnetic properties which, to our knowledge, were only qualitatively studied by Tsui et al.40 on the fluoromica samples prepared in their laboratory to be used as substrates to grow rare earth films. Their work reports the fluorophlogopite magnetic response as that of a paramagnet and diamagnet mixture and speculate that can be due to the presence of ferromagnetic clusters.
Here we report the magnetic characterization of commercial fluorophlogopite mica sheets, showing how to separate their diamagnetic and paramagnetic responses to temperature and external magnetic field and providing a method for correcting these contributions in the measurements of magnetic films grown on it. Moreover, our study reveals that the paramagnetic signal of fluorophlogopite mica under study originates form isolated magnetic cations rather than from superparamagnetic clusters.
Experimental
The (001)-cut synthetic fluorophlogopite mica sheets of 5 by 5 mm in lateral size and 0.2 μm in thickness were purchased from Changchun Taiyuan Co., Ltd, China. To avoid possible residual contaminations from sample handling, the as received substrates were cut to the appropriate shape for magnetic measurement using a non-magnetic (antiferromagnetic) blade. Then, the top and bottom surfaces of the mica were freshly exfoliated by a scotch tape prior to the measurements. The preferred (001) out-of-plane orientation of the crystal was confirmed by X-ray diffraction (XRD) theta–2theta (θ–2θ) scan conducted in a Siemens D-5000 diffractometer using Cu Kα radiation. The crystallographic configurations in the basal plane were analysed by XRD phi scan (φ scan) in a Bruker D8 Discover X-ray diffractometer using Cu Kα radiation. The transmittance spectrum of fluorophlogopite was collected using a Jasco V-570 spectrometer in the 200–1000 nm region. The topographic images of the freshly exfoliated sheet of mica were acquired with an Agilent 5100 atomic force microscope (AFM) in tapping mode using FORT Si tips from Applied NanoStructures Inc. To determine the chemical composition of the fluorophlogopite plate, inductively coupled plasma mass spectrometry (ICP-MS) analysis was employed to detect trace metal elements. To this end, the specimen was digested in concentrated acid mixture of 4 mL HNO3 (Aldrich), 2 mL HCl (Aldrich), 4 mL H3PO4 (Aldrich), and 0.5 mL HF (Aldrich) at 260 °C using a Milestone UltraWAVE microwave digestion system. The magnetic measurements were conducted by a MPMS-XL superconducting quantum interference magnetometer device (SQUID, Quantum Design Inc.) magnetometer with applied dc magnetic fields either parallel or perpendicular to the mica sheets. Both isothermal magnetisation curves (temperatures ranging from 2 to 360 K) and thermal scans in constant magnetic field (up to 70 kOe) were measured. For the specimen mounting, to minimize the background contribution and signal distortion, a freshly exfoliated fluorophlogopite sheet with mass of 13.81 mg, was well centred in a clear drinking straw by clamping it in-between the walls of the straw without using any additional supporting pieces. The mounting of the sample perpendicular to the magnetic field was made thanks to two transversal cuts on each side of the straw, slightly shorter than the straw diameter, through which the sample was inserted to be placed perpendicular to the straw axis. In order to avoid damaging the sample by the tight contact with the slots cut in the straw, it was covered with a clear commercial PVC film used to wrap food. All the precautions to avoid magnetic contaminations (such as using nonmagnetic tweezers and avoiding textmarker labelling) were taken seriously throughout the sample handling process. Measurements were performed in RSO (Reciprocating Sample Option) operating mode.Results and discussion
Fig. 2(a) shows the out-of-plane XRD θ–2θ scan of the tape-exfoliated mica plate. The observation of only the strong (00l) diffraction peaks indicates a highly textured structure with crystallographic (00l) planes preferentially oriented perpendicular to the out of plane direction of mica sheets. Six (202) reflection peaks found at 60° intervals are observed in the in-plane XRD φ scan pattern (Fig. 2(b)). This implies the presence of twinning in the mica crystals. The (202) axis presents a two-fold symmetry with the basal plane as a mirror plane owing to the monoclinic tilting between a and c axes (β ∼ 100°) in a C2/m space group. It is well-known that twinning can add symmetry to the crystal. Consequently, the observed six peaks in φ scan might be the results of six different configurations corresponding to an alternating stacking sequence of crystals. Given the six-fold rotational symmetry around an axis perpendicular to the basal plane, the periodic stacking sequence is understandable. Next, the elemental composition of fluorophlogopite was determined via ICP-MS. The results presented in Table 1 show that the relative molar fractions of the fluorophlogopite cations are in agreement with the ideal composition (12.5% K, 37.5% Mg, 12.5% Al, and 37.5% Si) except for a significant substitution of Si by Al in the tetrahedral sites. It is worth noting that in 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 layered phyllosilicates both the tetrahedrally and octahedrally coordinated cations are prone to considerable substitution by other metal ions. In particular, this concerns the interchangeable Al3+ and Si4+ cations in the tetrahedral sites and the substitutions by Fe2+ and Ti4+ of octahedral Mg2+,31,41–43 and the resulting charges can be eventually balanced by the cations in the interlayer positions (see Fig. 1). Therefore, the above-observed non-stoichiometry in fluorophlogopite is reasonable. In addition, as shown in Table 1, the ICP-MS analysis reveals the presence of low-concentration traces of Ti [0.5(1) × 10−3 wt%], Fe [0.30(6) × 10−3 wt%], and Ni [0.40(8) × 10−4 wt%], the total of which only accounts for less than 0.1 wt% of the sample. It has been reported that, in Ti-rich trioctahedral mica the incorporated Ti cation mostly adopts the 4+ oxidation state,44,45 which does not carry any magnetic moment. In contrast, iron and nickel cations have large magnetic moments (Fe2+: 5.4 μB, Fe3+: 5.9 μB, and Ni2+: 3.2 μB), which can dominate the magnetic properties even when only present in small amounts. Considering that the magnetic moments of iron cations are about two times that of nickel and that iron content in our sample is nearly one order of magnitude higher than that of nickel, we can anticipate the significant impact of iron impurities on the magnetic properties of our mica crystals.
1 layered phyllosilicates both the tetrahedrally and octahedrally coordinated cations are prone to considerable substitution by other metal ions. In particular, this concerns the interchangeable Al3+ and Si4+ cations in the tetrahedral sites and the substitutions by Fe2+ and Ti4+ of octahedral Mg2+,31,41–43 and the resulting charges can be eventually balanced by the cations in the interlayer positions (see Fig. 1). Therefore, the above-observed non-stoichiometry in fluorophlogopite is reasonable. In addition, as shown in Table 1, the ICP-MS analysis reveals the presence of low-concentration traces of Ti [0.5(1) × 10−3 wt%], Fe [0.30(6) × 10−3 wt%], and Ni [0.40(8) × 10−4 wt%], the total of which only accounts for less than 0.1 wt% of the sample. It has been reported that, in Ti-rich trioctahedral mica the incorporated Ti cation mostly adopts the 4+ oxidation state,44,45 which does not carry any magnetic moment. In contrast, iron and nickel cations have large magnetic moments (Fe2+: 5.4 μB, Fe3+: 5.9 μB, and Ni2+: 3.2 μB), which can dominate the magnetic properties even when only present in small amounts. Considering that the magnetic moments of iron cations are about two times that of nickel and that iron content in our sample is nearly one order of magnitude higher than that of nickel, we can anticipate the significant impact of iron impurities on the magnetic properties of our mica crystals.
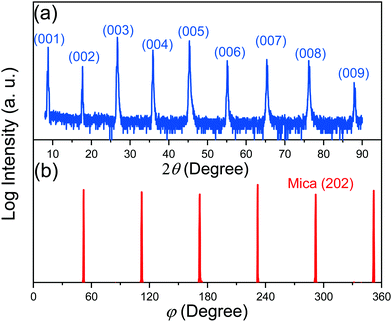 | ||
| Fig. 2 (a) XRD θ–2θ scan indicating (001) out-of-plane texture of the mica plate, and (b) in-plane φ scan of the mica crystals, showing six (202) reflections at 60° intervals. | ||
| Major elements | Concentration (mg g−1) | Molar fraction (mol%) | Trace elements | Concentration (mg g−1) | Mass fraction (wt%) |
|---|---|---|---|---|---|
| K | 79 ± 16 | 16 ± 3 | Ti | 0.5(1) | 0.05(1) |
| Mg | 122 ± 24 | 39 ± 8 | Fe | 0.30(6) | 0.030(6) |
| Al | 68 ± 14 | 19 ± 4 | Ni | 0.040(8) | 0.0040(8) |
| Si | 96 ± 19 | 26 ± 5 | Total | 0.8(1) | <0.1% |
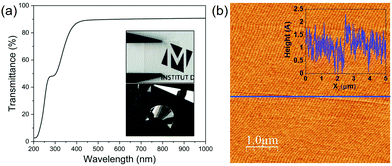
The transmittance spectrum of fluorophlogopite in the region of 200–1000 nm is shown in Fig. 3(a). Firstly, in the UV region, the sample experiences a strong absorbance from 200 to 320 nm with an acute increase of the transmittance, which is followed by another sharp transmittance enhancement to reach 90% as wavelength increases up to ∼400 nm. Further, it is evident that fluorophlogopite mica has an excellent optical transmittance throughout the total visible range (from 400 to 800 nm) with ∼90% transmittance, which preserves up to the infrared region of the spectrum with no sign of decreasing at 1000 nm wavelength (the maximum wavelength examined). The high optical transmittance confirms the high quality of the mica crystals. This high visible transmittance is also indicative of the low iron content of synthetic mica compared to natural micas.46,47 Indeed, the presence of iron decreases both the transmittance in the visible and the UV cut-off frequency and the absorption coefficient was reported to be proportional to the concentration of iron.46 Thus, the measurement of the UV-vis spectra is a simple and fast technique to assess the level of iron impurities in mica. The images presented in the inset of Fig. 3(a) show both high optical transparency and good mechanical flexibility of the exfoliated mica sheets. The mica surface morphology was investigated by AFM, and one representative topographic image is shown in Fig. 3(b). The height profile, as depicted in the inset, shows a small height variability within the range of ∼2 Å. The measured average root mean square (rms) roughness is 3.5 Å, which is much smaller than the thickness of a single unit cell layer (∼10 Å). The atomically flat surface of the crystals is thus confirmed.
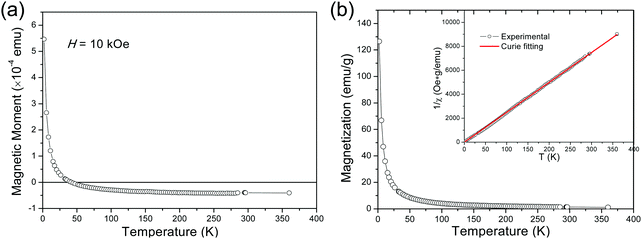
In the following, we report the magnetic characterization of the mica crystals. Magnetic measurements as a function of temperature (T) were carried out with the magnetic field (H) applied along the out-of-plane direction. The obtained evolution of the magnetic moment m as a function of temperature (m–T) curve is presented in Fig. 4(a). It is seen that, after an initial sharp decrease with increasing T to about 20 K, the moment m continues to decrease less and less steeply with further heating, then changes sign, finally tends to level-off at negative moment values at the high-temperature end. A magnetic moment with very small negative values and almost no temperature dependence is the typical diamagnetic response to external magnetic field. In contrast, the paramagnetic response is positive, and the paramagnetic susceptibility is typically inversely proportional to temperature. Therefore, the observed rapid increase of m at the low-temperature end unambiguously evidences the existence of a paramagnetic contribution, which dominates the magnetic response at low temperatures. On the other hand, the levelling off at the high-temperature end is a manifestation of the mica intrinsic diamagnetism, as the contribution to m coming from the paramagnetic component tends to become negligibly small. The observed paramagnetic behaviour is not unexpected taking into account the presence of traces of magnetic elements (iron and nickel) revealed by the elemental analysis of our fluoromica. In fact, other research groups have ascribed the paramagnetic behaviour of natural micas to the random incorporation of iron into the parent mica lattice.30–32 Unlike diamagnetism, the paramagnetic response is typically a function of both, temperature and applied field. Consequently, the prevailing paramagnetic contribution at low temperatures poses an extra challenge for accurate magnetic characterizations of nanometre-sized objects of interest grown on top of mica.
In a next step, we explored the paramagnetic contribution of magnetic impurities by separating it from the diamagnetic one. The subtraction of the diamagnetic signal was achieved by proper vertical translations of the raw m–T curves above the horizontal axis of zero magnetic moment, i.e., by subtracting the value measured at the high-temperature end. Fig. 4(b) presents the resulting magnetization M as a function of temperature (M–T) curve. Note that the magnetic moment has been normalized to the weight of the magnetic cations (namely, Fe and Ni) based on the mass fraction from the ICP-MS elemental analysis. Then, the inverse mass susceptibility versus temperature (χ−1–T) curve can be constructed, as illustrated in the inset of Fig. 4(b), where magnetic susceptibility is defined as χ = M/H. According to the Curie's law, the susceptibility of a paramagnet should obey the relation:
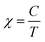 | (1) |
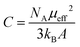 | (2) |
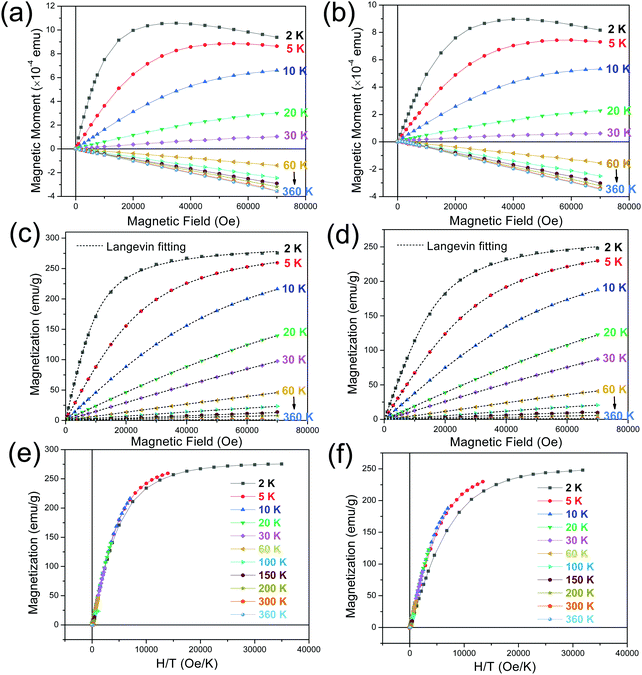
To shed more light on the characteristics of the mica crystals, we present the measured magnetic moment versus applied field (m–H) curves recorded under isothermal condition with the in-plane (Fig. 5(a)) and out-of-plane (Fig. 5(b)) applied fields. No direction was specified for the in-plane geometry due to the multiple in-plane configurations in the crystals. From the in-plane m–H curves (see Fig. 5(a)), one can make the following observations. Firstly, for the isothermal scan acquired at 2 K, m undergoes a steep increase with the field H increasing to about 1 kOe, where it slows down its increase until a maximum moment is reached at H ∼ 30 kOe. This is accompanied by a final almost linear decrease of m as the H further increases. A similar tendency can be observed for the isothermal curve recorded at 5 K, but m peaks at a much larger H ∼ 50 kOe and the linear variation in the high-field region becomes less obvious. Secondly, a typical paramagnetic-like behavior is presented for the curves obtained in the 10–30 K temperature interval. Finally, a linear relationship between m and H is evident for the curves acquired at temperatures above 30 K, for which the m becomes negative. In this temperature regime, the curves tend to converge toward the curve measured at 360 K, which is the highest temperature in this study. These observations and those made above from the thermomagnetic curves allow us concluding that a competition exists between the intrinsic diamagnetic (negative) response of mica and the paramagnetic (positive) response from the impurities to the applied field, which becomes dominant at temperatures below 30 K. It is important to point out that all the M(H) isotherms go through the origin at H = 0 and thereby no magnetic hysteresis is observed. This is in line with what is expected for diamagnetic and/or paramagnetic phases in absence of applied field. The above observation also rules out the possible existence of ferro- or ferri-magnetic phases.
Further insights into the paramagnetic phase can be made by separating the diamagnetic–paramagnetic components from the m–H curves. To this end, the m–H curve at 360 K was used as the baseline of the diamagnetic background, since the paramagnetic component has a negligibly small contribution to it. This baseline curve was subtracted from the isothermal m–H curves, which were subsequently normalized to the weight of the magnetic elements contained in the mica. The resulting magnetic field dependence of magnetization (M–H) curves of the paramagnetic phase are presented in Fig. 5(c and d), for the H along the in-plane and out-of-plane directions, respectively. According to the Langevin theory of paramagnetism, magnetization M can be expressed by the Langevin function
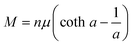 | (3) |
Finally, it is well-known that, from the Langevin theory, when the magnetization of a (super)paramagnet is plotted against H/T for different temperatures, all the curves overlap. The panels (e) and (f) of Fig. 5 show the M versus H/T plots, corresponding to the in-plane and out-of-plane applied field geometries, respectively. The expected overlapping is observed for all the temperatures except for the curve at the lowest temperature (2 K), for which the deviation is might be related to some magnetic interactions at such low temperature.
Summary and conclusion
To summarize, the effective moment μeff determined from the temperature dependence of magnetic susceptibility and magnetization curves, the size of the hypothetic clusters, the absence of coercivity and the fact that no difference between thermomagnetic curves measured after field- and zero-field cooling was observed at any field value, they all strongly support that the magnetic response of impurities in our mica crystals originates from isolated paramagnetic atoms. No evidence of blocked/unblocked superparamagnetic clusters or simply from magnetically ordered contaminations was found.The way to separate and analyse the competing diamagnetic and paramagnetic responses to temperature and external magnetic field in fluorophlogopite mica has been demonstrated. It should be applicable to other diamagnetic materials containing paramagnetic impurities and could be useful when assessing the magnetic properties of nanoobjects grown on substrates of such materials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Michael Mikhov for his useful comments regarding the analysis of the data. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. [819623]). We also acknowledge financial support from the Spanish Ministerio de Ciencia, Innovación y Universidades (MINCIU), through Project No. RTI2018-098537-B-C21, cofunded by ERDF from EU, and “Severo Ochoa” Programme for Centres of Excellence in R&D (Grant No. SEV-2015-0496) and from Generalitat de Catalunya through the projects 2017SGR00765 and 2017SGR1632. The authors also acknowledge Bernat Bozzo, Maite Simón, Vega Lloveras, Francisco Javier Campos and Anna Crespi from the Scientific Services at ICMAB-CSIC and Ignasi Villarroya from the Chemical Analysis Service at UAB. Z. M. was financially supported by China Scholarship Council (CSC) with No. 201606070094. Z. M.'s work was done as a part of the PhD program in Materials Science at Universitat Autònoma de Barcelona.References
- U.S. Geological Survey, Mineral Commodity Summaries 2020, 2020 DOI:10.3133/mcs2020.
- R. J. Benbow, B. H. W. S. De Jong and J. W. Adams, Mica, Ullmann's Encyclopedia of Industrial Chemistry, 2000 DOI:10.1002/14356007.a16_551.
- S.-I. Ohta, Synthetic Mica and Its Applications, Clay Sci., 2006, 12, 119–124, DOI:10.11362/jcssjclayscience1960.12.Supplement2_119.
- S. W. Bailey, Structures of Layer Silicates, Crystal Structure of Clay Minerals and their X-ray identification, Mineralogical Society of Great Britain and Ireland, 2015, pp. 1–124 DOI:10.1180/mono-5.1.
- W. de Poel, S. Pintea, J. Drnec, F. Carla, R. Felici, P. Mulder, J. A. A. W. Elemans, W. J. P. van Enckevort, A. E. Rowan and E. Vlieg, Muscovite mica: Flatter than a pancake, Surf. Sci., 2014, 619, 19–24, DOI:10.1016/j.susc.2013.10.008.
- I. Langmuir, The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 1918, 40, 1361–1403, DOI:10.1021/ja02242a004.
- B. Drake, C. Prater, A. Weisenhorn, S. Gould, T. Albrecht, C. Quate, D. Cannell, H. Hansma and P. Hansma, Imaging crystals, polymers, and processes in water with the atomic force microscope, Science, 1989, 243, 1586–1589, DOI:10.1126/science.2928794.
- J. W. Matthews, Defects in silver films prepared by evaporation of the metal onto mica, Philos. Mag., 1962, 7, 915–932, DOI:10.1080/14786436208212889.
- J. L. Parker and H. K. Christenson, Measurements of the forces between a metal surface and mica across liquids, J. Chem. Phys., 1988, 88, 8013–8014, DOI:10.1063/1.454260.
- C. E. D. Chidsey, D. N. Loiacono, T. Sleator and S. Nakahara, STM study of the surface morphology of gold on mica, Surf. Sci., 1988, 200, 45–66, DOI:10.1016/0039-6028(88)90432-3.
- L. Mogg, G. P. Hao, S. Zhang, C. Bacaksiz, Y. C. Zou, S. J. Haigh, F. M. Peeters, A. K. Geim and M. Lozada-Hidalgo, Atomically thin micas as proton-conducting membranes, Nat. Nanotechnol., 2019, 14, 962–966, DOI:10.1038/s41565-019-0536-5.
- G. Lippert, J. Dabrowski, Y. Yamamoto, F. Herziger, J. Maultzsch, M. C. Lemme, W. Mehr and G. Lupina, Molecular beam growth of micrometer-size graphene on mica, Carbon, 2013, 52, 40–48, DOI:10.1016/j.carbon.2012.09.001.
- K. Ueno, K. Saiki, T. Shimada and A. Koma, Epitaxial growth of transition metal dichalcogenides on cleaved faces of mica, J. Vac. Sci. Technol., A, 1990, 8, 68–72, DOI:10.1116/1.576983.
- Q. Ji, Y. Zhang, T. Gao, Y. Zhang, D. Ma, M. Liu, Y. Chen, X. Qiao, P. H. Tan, M. Kan, J. Feng, Q. Sun and Z. Liu, Epitaxial monolayer MoS2 on mica with novel photoluminescence, Nano Lett., 2013, 13, 3870–3877, DOI:10.1021/nl401938t.
- M. Mattinen, P. J. King, G. Popov, J. Hämäläinen, M. J. Heikkilä, M. Leskelä and M. Ritala, Van der Waals epitaxy of continuous thin films of 2D materials using atomic layer deposition in low temperature and low vacuum conditions, 2D Mater., 2020, 7, 011003, DOI:10.1088/2053-1583/ab4c09.
- H. Peng, W. Dang, J. Cao, Y. Chen, D. Wu, W. Zheng, H. Li, Z. X. Shen and Z. Liu, Topological insulator nanostructures for near-infrared transparent flexible electrodes, Nat. Chem., 2012, 4, 281–286, DOI:10.1038/nchem.1277.
- H. Li, J. Cao, W. Zheng, Y. Chen, D. Wu, W. Dang, K. Wang, H. Peng and Z. Liu, Controlled synthesis of topological insulator nanoplate arrays on mica, J. Am. Chem. Soc., 2012, 134, 6132–6135, DOI:10.1021/ja3021395.
- T. Amrillah, Y. Bitla, K. Shin, T. Yang, Y.-H. Hsieh, Y.-Y. Chiou, H.-J. Liu, T. H. Do, D. Su, Y.-C. Chen, S.-U. Jen, L.-Q. Chen, K. H. Kim, J.-Y. Juang and Y.-H. Chu, Flexible Multiferroic Bulk Heterojunction with Giant Magnetoelectric Coupling via van der Waals Epitaxy, ACS Nano, 2017, 11, 6122–6130, DOI:10.1021/acsnano.7b02102.
- J. Huang, H. Wang, X. Sun, X. Zhang and H. Wang, Multifunctional La0.67Sr0.33MnO3 (LSMO) Thin Films Integrated on Mica Substrates toward Flexible Spintronics and Electronics, ACS Appl. Mater. Interfaces, 2018, 10, 42698–42705, DOI:10.1021/acsami.8b16626.
- Y. Bitla and Y. H. Chu, MICAtronics: a new platform for flexible X-tronics, FlatChem, 2017, 3, 26–42, DOI:10.1016/j.flatc.2017.06.003.
- J. Jiang, Y. Bitla, C. W. Huang, T. H. Do, H. J. Liu, Y. H. Hsieh, C. H. Ma, C. Y. Jang, Y. H. Lai, P. W. Chiu, W. W. Wu, Y. C. Chen, Y. C. Zhou and Y. H. Chu, Flexible ferroelectric element based on van der Waals heteroepitaxy, Sci. Adv., 2017, 3, e1700121, DOI:10.1126/sciadv.1700121.
- C. Yang, Y. Han, C. Feng, X. Lin, S. Huang, X. Cheng and Z. Cheng, Toward Multifunctional Electronics: Flexible NBT-Based Film with a Large Electrocaloric Effect and High Energy Storage Property, ACS Appl. Mater. Interfaces, 2020, 12, 6082–6089, DOI:10.1021/acsami.9b21105.
- H. J. Liu, C. K. Wang, D. Su, T. Amrillah, Y. H. Hsieh, K. H. Wu, Y. C. Chen, J. Y. Juang, L. M. Eng, S. U. Jen and Y. H. Chu, Flexible Heteroepitaxy of CoFe2O4/Muscovite Bimorph with Large Magnetostriction, ACS Appl. Mater. Interfaces, 2017, 9, 7297–7304, DOI:10.1021/acsami.6b16485.
- G. Lan, L. Shen, L. Lu, C. Cao, C. Jiang, H. Fu, C. You, X. Lu, C. Ma, M. Liu and C. L. Jia, Flexible Lithium Ferrite Nanopillar Arrays for Bending Stable Microwave Magnetism, ACS Appl. Mater. Interfaces, 2018, 10, 39422–39427, DOI:10.1021/acsami.8b12954.
- J. Liu, Y. Feng, R. Tang, R. Zhao, J. Gao, D. Shi and H. Yang, Mechanically Tunable Magnetic Properties of Flexible SrRuO3 Epitaxial Thin Films on Mica Substrates, Adv. Electron. Mater., 2018, 4, 1–9, DOI:10.1002/aelm.201700522.
- W. Liu, M. Liu, R. Ma, R. Zhang, W. Zhang, D. Yu, Q. Wang, J. Wang and H. Wang, Mechanical Strain-Tunable Microwave Magnetism in Flexible CuFe2O4 Epitaxial Thin Film for Wearable Sensors, Adv. Funct. Mater., 2018, 28, 1–7, DOI:10.1002/adfm.201705928.
- M. Gibertini, M. Koperski, A. F. Morpurgo and K. S. Novoselov, Magnetic 2D materials and heterostructures, Nat. Nanotechnol., 2019, 14, 408–419, DOI:10.1038/s41565-019-0438-6.
- J. Xu, W. Li and Y. Hou, Two-Dimensional Magnetic Nanostructures, Trends Chem., 2020, 2, 163–173, DOI:10.1016/j.trechm.2019.11.007.
- M. T. Dau, C. Vergnaud, M. Gay, C. J. Alvarez, A. Marty, C. Beigné, D. Jalabert, J. F. Jacquot, O. Renault, H. Okuno and M. Jamet, Van der Waals epitaxy of Mn-doped MoSe2 on mica, APL Mater., 2019, 7, 051111, DOI:10.1063/1.5093384.
- J. T. Kendall and D. Yeo, Magnetic Susceptibility and Anisotropy of Mica, Proc. Phys. Soc., London, Sect. B, 1951, 64, 135–142, DOI:10.1088/0370-1301/64/2/306.
- A. R. Biedermann, C. Bender Koch, W. E. A. Lorenz and A. M. Hirt, Low-temperature magnetic anisotropy in micas and chlorite, Tectonophysics, 2014, 629, 63–74, DOI:10.1016/j.tecto.2014.01.015.
- O. Ballet and J. M. D. Coey, Magnetic properties of sheet silicates; 2:1 layer minerals, Phys. Chem. Miner., 1982, 8, 218–229, DOI:10.1007/BF00309481.
- J. M. D. Coey and S. Ghose, Magnetic Ordering and Thermodynamics in Silicates, Physical Properties and Thermodynamic Behaviour of Minerals, Springer Netherlands, 1988, pp. 459–499 DOI:10.1007/978-94-009-2891-6_14.
- V. Schmidt, A. M. Hirt, P. Rosselli and F. Martín-Hernández, Separation of diamagnetic and paramagnetic anisotropy by high-field, low-temperature torque measurements, Geophys. J. Int., 2007, 168, 40–47, DOI:10.1111/j.1365-246X.2006.03202.x.
- J. W. McCauley, R. E. Newnham and G. V. Gibbs, Crystal Structure Analysis of Synthetic Fluorophlogopite, Am. Mineral., 1973, 58, 249–254 CAS.
- H. R. Shelll and K. H. Ivey, Fluorine Micas, Bulletin 667 of the Bureau of Mines of the United States Department of the interior, Washington, DC, 1969. https://digital.library.unt.edu/ark:/67531/metadc12796/ Search PubMed.
- M. Zheng, H. Sun and K. W. Kwok, Mechanically controlled reversible photoluminescence response in all-inorganic flexible transparent ferroelectric/mica heterostructures, NPG Asia Mater., 2019, 11, 1–8, DOI:10.1038/s41427-019-0153-7.
- J. Yuan, A. Balk, H. Guo, Q. Fang, S. Patel, X. Zhao, T. Terlier, D. Natelson, S. Crooker and J. Lou, Room-Temperature Magnetic Order in Air-Stable Ultrathin Iron Oxide, Nano Lett., 2019, 19, 3777–3781, DOI:10.1021/acs.nanolett.9b00905.
- M. Zheng, X. Y. Li, H. Ni, X. M. Li and J. Gao, van der Waals epitaxy for highly tunable all-inorganic transparent flexible ferroelectric luminescent films, J. Mater. Chem. C, 2019, 7, 8310–8315, 10.1039/c9tc01684h.
- F. Tsui, P. D. Han and C. P. Flynn, Growth of rare-earth monolayers on synthetic fluorine mica, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13648–13652 CrossRef CAS PubMed.
- S. Pini, M. F. Brigatti, M. Affronte, D. Malferrari and A. Marcelli, Magnetic behavior of trioctahedral micas with different octahedral Fe ordering, Phys. Chem. Miner., 2012, 39, 665–674, DOI:10.1007/s00269-012-0520-1.
- Q. Wang, C. Zhu, J. Yun and G. Yang, Isomorphic Substitutions in Clay Materials and Adsorption of Metal Ions onto External Surfaces: A DFT Investigation, J. Phys. Chem. C, 2017, 121, 26722–26732, DOI:10.1021/acs.jpcc.7b03488.
- A. Ibhi, H. Nachitand and H. El Abia, Titanium and barium incorporation into the phyllosilicate phases: The example of phlogopite-kinoshitalite solid solution, J. Phys. IV, 2004, 123, 331–335, DOI:10.1051/jp4:2005123060.
- E. Schingaro, F. Scordari, E. Mesto, M. F. Brigatti and G. Pedrazzi, Cation-site partitioning in Ti-rich micas from Black Hill (Australia): A multi-technical approach, Clays Clay Miner., 2005, 53, 179–189, DOI:10.1346/CCMN.2005.0530208.
- A. Gianfagna, F. Scordari, S. Mazziotti-Tagliani, G. Ventruti and L. Ottolini, Fluorophlogopite from Biancavilla (Mt. Etna, Sicily, Italy): Crystal structure and crystal chemistry of a new F-dominant analog of phlogopite, Am. Mineral., 2007, 92, 1601–1609, DOI:10.2138/am.2007.2502.
- P. Popper, Transmission of Natural and Synthetic Mica in the Ultraviolet, Nature, 1951, 168, 1119–1120 CrossRef CAS.
- R. N. Dhar and S. R. Das, Transmission of Indian Mica between 300 and 1,000 mμ and its Visual Classification, Nature, 1966, 209, 185–186, DOI:10.1038/209185a0.
- A. Slawska-Waniewska, M. Gutowski, H. K. Lachowicz, T. Kulik and H. Matyja, Superparamagnetism in a nanocrystalline Fe-based metallic glass, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 14594–14597, DOI:10.1103/PhysRevB.46.14594.
| This journal is © The Royal Society of Chemistry 2020 |