Open Access Article
Open Access ArticleHigh thermal conductivity polymer chains with reactive groups: a step towards true application†
Anqi
Chen‡
 ab,
Yanyan
Wu‡
abc,
Shaoxin
Zhou‡
d,
Wenxue
Xu
e,
Wenlong
Jiang
b,
You
Lv
b,
Wei
Guo
ab,
Keyu
Chi
f,
Qi
Sun
f,
Tingting
Fu
ab,
Tingting
Xie
a,
Yuan
Zhu
*abg and
Xin-gang
Liang
e
ab,
Yanyan
Wu‡
abc,
Shaoxin
Zhou‡
d,
Wenxue
Xu
e,
Wenlong
Jiang
b,
You
Lv
b,
Wei
Guo
ab,
Keyu
Chi
f,
Qi
Sun
f,
Tingting
Fu
ab,
Tingting
Xie
a,
Yuan
Zhu
*abg and
Xin-gang
Liang
e
aSchool of Microelectronics, Southern University of Science and Technology, Shenzhen 518055, Guangdong, China. E-mail: zhuy3@sustech.edu.cn
bSchool of Innovation and Entrepreneurship, Southern University of Science and Technology, Shenzhen 518055, Guangdong, China
cSchool of Materials Science and Engineering National Institute for Advanced Materials, Nankai University, Tianjin 300071, China
dCollege of Engineering, Yantai Nanshan University, Yantai 265713, Shandong, China
eSchool of Aerospace Engineering, Tsinghua University, Beijing 100084, China
fFoshan (Southern) New Material Research Institute, Foshan 528000, Guangdong, China
gKey Laboratory of Energy Conversion and Storage Technologies, Ministry of Education, Southern University of Science and Technology, Shenzhen 518055, Guangdong, China
First published on 5th August 2020
Abstract
Nanostructured polyethylene (PE, [–CH2–CH2–]n) films with metal-like thermal conductivity have opened up opportunities for polymers in advanced thermal management. However, in practice, polymers used in thermal management are either thermosets or at least stable at high temperature, for which 150–180 °C is typical. Thus PE as a thermoplastic polymer, whose softening temperature is ∼120 °C, is not applicable in real use. Thus here we introduce a simple reactive group –OH to each segment of the PE chain [–CH2–CH2–]n, which turns the polymer into polyvinyl alcohol (PVA), as a step towards the thermo stable system. Our calculations show that for aligned PVA chains, the thermal conductivity can reach 8.49 W m−1 K−1 (infinite chains), and experiments verify this by achieving a thermal conductivity of 8.51 W m−1 K−1 in a PVA film consisting of chain-aligned nanofibers. The alignment degrees of the PVA chains in the nanofibers are especially investigated to elucidate the nanostructure of the film, and the phonon dispersion and transport are also discussed. This work is intended to stimulate a further trial into the development of high thermal conductivity polymer materials towards real uses and true application scenarios.
Introduction
Polymers of good flexibility and moldability are widely used in heat conductive materials as the matrix for metal and ceramic powders.1–3 However, polymers with low thermal conductivity (∼0.2 W m−1 K−1) are also considered as the main conductive bottleneck in applications such as thermal interface materials (TIMs),4,5 moulding compounds,6 printed circuit boards (PCBs)7,8, etc.Although bulk polymer materials are generally regarded as poor heat conductors, an individual polymer chain or a chain-aligned polymer fiber is believed to have very high thermal conductivity.9,10 Researchers believe that excellent thermal conductivity can be realized by assembling the polymer chains in order.11 To date, most of the theoretical and practical interest has focused on polyethylene (PE) due to its model simplicity and its C–C bond similarity to diamond, one of the most thermally conductive (above 1000 W m−1 K−1) materials in nature.12 The long carbon chain of PE serves as an efficient phonon transport path along the axis. Theoretically, the numerical predictions for the thermal conductivities of a PE single polymer chain and for a PE single-crystal are >100 W m−1 K−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 and 273 W m−1 K−1.13 Practically, the thermal conductivities of PE fibers and films can achieve respectively 104 W m−1 K−1
7 and 273 W m−1 K−1.13 Practically, the thermal conductivities of PE fibers and films can achieve respectively 104 W m−1 K−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 and 62 W m−1 K−1.15
14 and 62 W m−1 K−1.15
However, this exceptionally high thermal conductivity will not qualify PE for real thermal management applications, because its softening point is ∼120 °C,16 lower than the aging condition of most application scenarios (150–180 °C). Therefore, research interest should move to the search for thermostable polymers. There are two routes to achieve this in state-of-the-art applications. One is to use thermoset materials (with a reactive group), e.g. epoxy or rubber. The other is to use non-reactive but thermally stable polymers, e.g. dimethyl silicone oil (>200 °C stable). For carbon chain polymers, a thermoset seems to be the only option. Thus our research started here.
The first candidate that came to mind was poly(vinyl alcohol) (PVA, [–CH2–CHOH–]n), because its melting point is above 200 °C17,18 and it introduces only a minor change in the carbon chain of PE ([–CH2–CH2–]n) by replacing a hydrogen (–H) with a hydroxyl (–OH)19 in each segment. The literature20,21 shows that this replacement should result in the evolution of a phonon dispersion curve (Fig. 1a). In the low-frequency range, the group velocity of PVA drops dramatically compared to PE, which could be mainly attributed to the strong phonon-scattering effect by the heavy –OH branches.20 Thus we can expect a drop in thermal conductivity by introducing –OH. But how large the drop is and how this would threaten the prospects of the high thermal conductivity polymer in true applications are yet to be clarified.
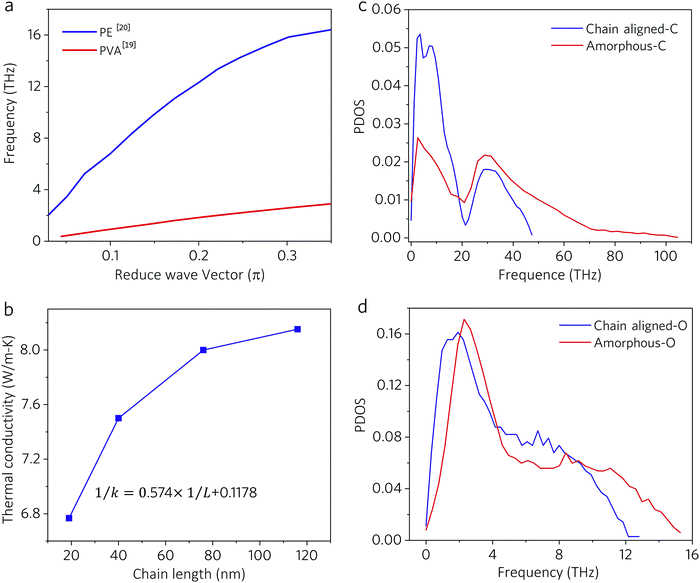 | ||
| Fig. 1 (a) Phonon dispersion curves of PVA20 and PE21 in the orthorhombic lattice. (b) Effect of chain length (L) on thermal conductivity (k). (c) PDOS of carbon atoms in chain-aligned and amorphous PVA. (d) PDOS of oxygen atoms in chain-aligned and amorphous PVA. | ||
Here, we report a consistent result of the PVA thermal conductivity from both theoretical and experimental studies. For aligned PVA chains (infinite length), the theoretical thermal conductivity is calculated as 8.49 W m−1 K−1, while the thermal conductivity of the as-fabricated nanostructured film is measured as 8.51 W m−1 K−1, over one order of magnitude larger than the reported ∼0.3 W m−1 K−1 of the amorphous PVA material.22 Since the chain alignment is crucial to explain the structure–property relationship, we have also investigated the phonon densities of states (PDOS) of aligned polymer chains in theory and developed the polarized Fourier transform infrared (FTIR) method to measure the chain alignment in the experiment. This method is a good complement to the wide-angle X-ray scattering (WAXS) method at low chain orderness or crystallinity. We understand that the –OH groups (at a near-right angle to the C–C main chain) in PVA break the symmetry of PE chains. This enables the polarized FTIR method to discern alignment degree differences at even low orderness, for which, the WAXS signal is not distinct. Moreover, for nanofiber alignment characterization, we have developed a laser diffraction (LD) method to monitor the film quality on-line. This work shows promising progress in high thermal conductivity polymers with reactive groups, which is a step towards true applications, particularly when thermal stability is required.
Results and discussion
Simulation of PVA thermal conductivity
Here we used the non-equilibrium molecular dynamics method (NEMD)23,24 to calculate the thermal conductivity (k) of amorphous PVA and chain-aligned PVA. For amorphous PVA, the thermal conductivity is 0.253 W m−1 K−1, while for chain-aligned PVA, the thermal conductivity increases as the chain length (L) increases (Fig. 1b) and finally converges to 8.49 W m−1 K−1 at infinity. To shed some light on this contrast, phonon DOS (PDOS) of C atoms and O atoms in amorphous PVA and chain-aligned PVA were calculated by Green's function-based molecular dynamics (GFMD)25 method and the results are demonstrated in Fig. 1c and d. The PDOS of C atoms in the aligned PVA chains is much greater than that in the amorphous PVA chains at a lower frequency, while the PDOS of O atoms shows a similar phenomenon but much less significant. Since low-frequency phonons transport further and thus are more important contributors to thermal conductivity, this PDOS evolution accounts well for the enhancement of thermal conductivity by chain alignment.Fabrication of PVA nanofibrous films
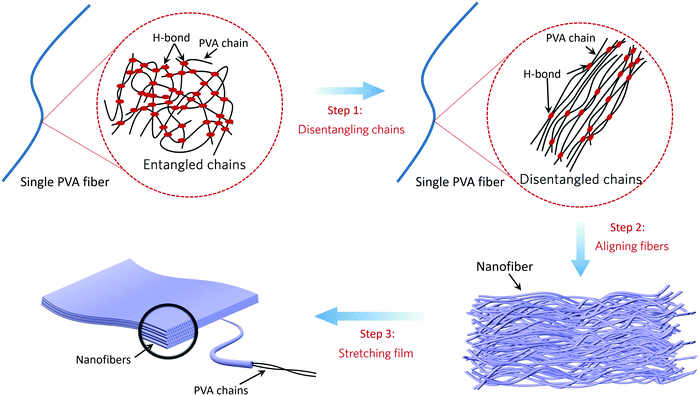
Motived by the theoretical results, we fabricated nanostructured polymer films using a 3-step method (Fig. 2): (1) disentangling chains: ultrasonic pretreatment was used to disentangle the chains in the spinning solution and thus help align the chains during electrospinning; (2) aligning fibers: modified electrode collectors were used to align continuous nanofibers during the film-forming process; and (3) stretching films: hot-stretching was applied to the nanostructured polymer films for a further increase of the chain and fiber alignment.Characterization of chain alignment
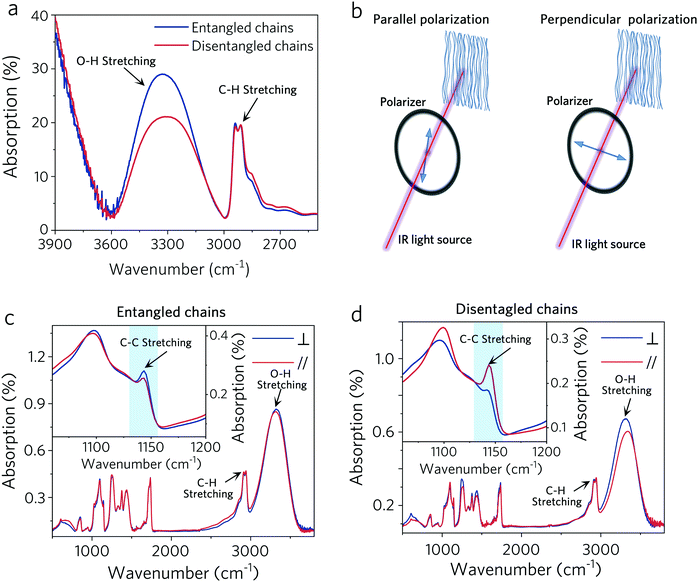
When the sample orderness is low, ordinary crystallinity measurement like WAXS cannot discern the chain alignment details (Fig. S5, ESI†), which is a technical gap we need to fill. Considering that the –OH groups (at a near-right angle to the carbon chain) in PVA break the symmetry that PE preserves, which might bring about interesting changes in the FTIR spectra especially when the incident light is polarized, we used the polarized FTIR to study the structural differences between entangled and disentangled chains. We luckily found some distinct changes in the spectra. We believe that this method can be extended to carbon chain polymers with other unsymmetrical branches and thus is a powerful tool for chain alignment study when the sample orderness is far from crystalline.Fig. 3 presents the structural information of the PVA nanostructured film with entangled and disentangled chains fabricated by electrospinning. The –OH branches introduce lots of hydrogen bonds into the system,26 which cause severe chain entanglement and restrain chains from aligning during the electrospinning process. In step 1, we used high power ultrasonic pretreatment to break the hydrogen bonds and disentangle the polymer chains in the spinning solution. Fig. 3a shows the FTIR spectra of the PVA nanostructured film with and without the disentanglment process. We set the C–H stretching band (2912 cm−1) as the benchmark, whose intensity barely changes during the disentanglement process. The large band observed between 3000 and 3600 cm−1 is linked to the O–H stretching of hydrogen bonds.27,28 The intensity of this band decreases greatly after the ultrasonic pretreatment, indicating the decrease of hydrogen bonds. This may result in a better chain alignment in the following electrospinning process, which could be further confirmed by the polarized FTIR. Fig. 3b demonstrates the configuration of polarized FTIR and Fig. 3c and d give the results. In Fig. 3d, the C–C stretching band (1143 cm−1)29 of the disentangled sample presents a distinct anisotropic feature: the perpendicular (⊥) polarized band intensity is much lower than the parallel polarized (‖) one (Fig. 3d), which is not observed in the entangled film (Fig. 3c). Therefore, the disentangling pretreatment in polymer spinning solution should significantly enhance the chain-aligning efficacy of electrospinning.
On-line monitoring of fiber alignment
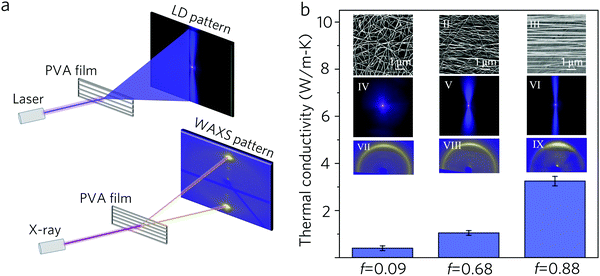
Besides the chain alignment, the fiber alignment is also crucial to the thermal conductivity of the nanofibrous film. Thus during the electrospinning process, a pair of parallel electrode collectors were used to align the fibrous film layer by layer, and a laser diffraction (LD) system (Fig. 4a) was set up for the on-line monitoring of the fiber alignment. The diffraction patterns mathematically are equal to the Fourier transform of the fiber arrangement patterns. In diffraction patterns, the orientation information is mainly reflected by the azimuthal intensity distribution. The alignment degree f, which is also called Herman's Orientation Factor (HOF), can be calculated accordingly30,31 (Supplementary Note 3, ESI†). The f value ranges from 0 to 1, representing random to perfect alignment. For films of different f (Fig. 4b, insets I–III), the LD diffraction patterns (Fig. 4b, insets IV–VI) agree well with the WAXS patterns (Fig. 4b, insets VII–IX) and the Fourier transform patterns of the SEM images (Fig. S6, ESI†), yet this method is low-cost, time-saving and on-line. The real-time feedback of alignment information provided by this system helps the on-line adjustment of experimental parameters.Thermal conductivity measurement
Fig. 4b also exhibits the structure–property relationship of different f values. The highly aligned PVA nanostructured film with f = 0.88 has the highest thermal conductivity (3.42 W m−1 K−1), about eight times higher than that of the randomly aligned nanostructured film (0.41 W m−1 K−1, f = 0.09). This is much less than that expected (∼8.49 W m−1 K−1). The reason is given by the WAXS pattern (Fig. 4b, inset IX), that although the fiber alignment is well controlled, the chain alignment is not as good. To achieve a higher chain alignment degree, hot stretching is thus conducted. The nanostructured film with f = 0.88 was stretched at 200 °C in air. SEM images (Fig. S4, ESI†) present that after hot stretching, the fibers became slimmer while their alignment was enhanced. The measured thermal conductivity as a function of the draw ratio (λ) is depicted in Fig. 5. The thermal conductivity increases as the draw ratios increase, from 3.71 W m−1 K−1 (λ = 1) to 8.51 W m−1 K−1 (λ = 12). The corresponding WAXS patterns are also presented in the left column in Fig. 5 The pattern transition from discontinuous rings (λ = 1) to discrete long arcs (λ = 4) to short arcs (λ = 12) indicates that the chain alignment is improving continuously. And the orientation distribution functions (ODF, value from 0–1)32 calculated from WAXS patterns (method see Supplementary Note 3, ESI†) are also depicted in Fig. 5. The ODF changes greatly from 0.40 to 0.93, verifying a great enhancement of crystal quality. It is noteworthy that here the ODF accounts for two origins of orientation. One is the chain orientation within each fiber; the other is the fiber orientation itself. Since the fibrous film we chose had a known fiber orientation as high as 0.88, and was merely enhanced to ∼0.92 after the hot stretching (calculated from the Fourier transformation of the SEM image in Fig. S4, ESI†), the large change in ODF mainly comes from the chain orientation improvement. We also notice that the increasing trend of thermal conductivity seems unsynchronized with the increase in orientation. When the ODF increases from 0.4 to 0.84, the thermal conductivity increases mildly from 3.42 W m−1 K−1 to 5.69 W m−1 K−1. In contrast, the last increase of ODF from 0.84 to 0.93 leads to a leap of thermal conductivity from 5.69 W m−1 K−1 to 8.51 W m−1 K−1, implying that the phonon excitation and transport are significantly boosted due to the final effort of orientation.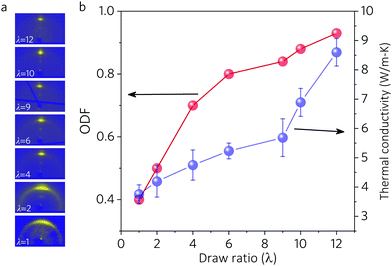 | ||
| Fig. 5 (a) WAXS patterns of nanostructured films at different draw ratios. (b) Thermal conductivity and orientation distribution functions (ODF) as a function of draw ratio (λ). | ||
Discussion and prospect
The thermal conductivity of polymers can be obtained from the Debye equation,33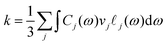 | (1) |
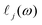 is the phonon mean free path, generally decreasing with ω and very sensitive to any phonon-scattering effect. Compared with PE, the PDOS of PVA drops in the low frequency range (Fig. S2, ESI†). Fig. 1a shows a decrease in νj of PVA. Moreover,
is the phonon mean free path, generally decreasing with ω and very sensitive to any phonon-scattering effect. Compared with PE, the PDOS of PVA drops in the low frequency range (Fig. S2, ESI†). Fig. 1a shows a decrease in νj of PVA. Moreover, 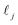 in PVA should be significantly shortened since the large amount of side –OH branches and the resulting hydrogen bonds are both strong phonon-scattering sources. Based on the above three reasons, a decrease in thermal conductivity is destined after the introduction of –OH. But according to our work, the thermal conductivity for aligned PVA chains remains a relatively high value as ∼8.49 W m−1 K−1, which is comparable with most thermal interface composites. Also the as-fabricated PVA film can withstand 180 °C high temperature, which promises its future in thermal management applications.
in PVA should be significantly shortened since the large amount of side –OH branches and the resulting hydrogen bonds are both strong phonon-scattering sources. Based on the above three reasons, a decrease in thermal conductivity is destined after the introduction of –OH. But according to our work, the thermal conductivity for aligned PVA chains remains a relatively high value as ∼8.49 W m−1 K−1, which is comparable with most thermal interface composites. Also the as-fabricated PVA film can withstand 180 °C high temperature, which promises its future in thermal management applications.
Moreover in real applications, fillers are usually incorporated into the polymer matrix to reduce the coefficient of thermal expansion (CTE) and enhance the thermal conductivity.34 In this situation, the presence of reactive group –OH may not only help enhance the thermostability but also help couple the polymer and the inorganic filler surface to reduce the interfacial thermal resistance.35 For chain-aligned PVA-based composite materials, the filler influence on the thermal conductivity, thermal expansion, interfacial problems, and chain orientation awaits more systematic investigation.
Conclusions
In summary, we have completed pioneering joint theoretical and experimental work on high thermal conductivity polymer chains with reactive groups, which is a step forwards towards true application in thermal management. The PVA ([–CH2–CHOH–]n) nanostructured film with a thermal conductivity of 8.51 W m−1 K−1 was achieved by a 3-step method. The phonon density and transport behavior of PVA were studied in detail. A combination of polarized FTIR, WAXS and real-time LD was developed to determine the alignment degree of chains and fibers, which may provide a full solution on alignment characterization for other polymer systems. This work is intended to stimulate a further trial into the development of highly thermal conductive polymer materials towards true thermal management application scenarios.Experimental section
Calculation of thermal conductivity and PDOS
NEMD23 was used to predict the thermal conductivity of PVA. NEMD requires the use of a temperature gradient, which was realized by fixing different temperatures at two ends of the calculated system. The heat flux driven by the temperature gradient was then acquired. The thermal conductivity was calculated accordingly based on Fourier's law.36,37 The GFMD simulation25 was used to calculate the PDOS of crystalline and amorphous PVA based on the fluctuation–dissipation theory in this article. Green's functions in reciprocal space can be obtained from the Fourier transform of the lattice displacements using molecular dynamics (MD).38 Then the force constant matrix and dynamical matrix were obtained. The eigenvalues of the dynamical matrix were used to compute the PDOS. See Supplementary Note 1 (ESI†) for more details.Fabrication of thermally conductive PVA nanostructured films
The films were fabricated by a 3-step method. The steps are (1) disentangling chains: high-power ultrasonic pre-treatment was applied to the 10 wt% PVA (Mw ∼ 145![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, L ∼ 1000 nm) solution; (2) aligning fibers: aligned continuous nanofibers were produced by electrospinning (ET-2535H, Ucalery) and collected using two parallel electrodes; and (3) stretching films: the nanostructured polymer films were mechanically stretched at ∼200 °C (infrared heating chamber, 300 W) and the stretching rate is about 1 cm min−1. See Supplementary Note 2 (ESI†) for more details.
000, L ∼ 1000 nm) solution; (2) aligning fibers: aligned continuous nanofibers were produced by electrospinning (ET-2535H, Ucalery) and collected using two parallel electrodes; and (3) stretching films: the nanostructured polymer films were mechanically stretched at ∼200 °C (infrared heating chamber, 300 W) and the stretching rate is about 1 cm min−1. See Supplementary Note 2 (ESI†) for more details.
Alignment measurement
Polarized FTIR spectroscopy (Nicolet IS50) was used to study the optical anisotropy of the polymer sample at the molecular level to evaluate the chain alignment. WAXS (Rigaku with a 2-D detector Pilatus 200 K) measurements were used to determine the crystallite orientation and crystallinity of films. A laser diffraction (LD) system was set up for the on-line monitoring of the fiber alignment degree. See Supplementary Note 3 (ESI†) for more details including light parameters used and orientation factor calculation.Thermal conductivity measurements
The thermal conductivities k (k = ρCρα)39 of PVA fibers were obtained by separately measuring the diffusivity α, density ρ, and heat capacity Cρ. Here α was measured by the Angstrom method, ρ was measured by using the draining method (ME204, Mettler Toledo), and Cρ was measured using a Differential Scanning Calorimeter (DSC3, Mettler Toledo). The measurement platform for the Angstrom method is homemade. See Supplementary Note 4 (ESI†) for more details on its setup and calibration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the National Key Research and Development Program of China (Grant No. 2017YFE0120800), the National Natural Science Foundation of China (Grant No. 51872132, No. 51702277 and No. 51802144), the Science and Technology Development Fund of the Macao Special Administrative Region (Grant No. FDCT/013/2017/AMJ) and the Science and Technology Innovation Commission of Shenzhen (Grant No. JCYJ20180504165648211). The authors thank Dr Zhaobo Tian (Tsinghua University) for the analysis of the hot stretched sample and Su Qin (Southern University of Science and Technology) for the technical support in WAXS measurements.References
- M. Peplow, The plastics revolution: how chemists are pushing polymers to new limits, Nature, 2016, 536, 7616 CrossRef.
- A. J. Heeger, Semiconducting and Metallic Polymers: The Fourth Generation of Polymeric Materials (Nobel Lecture), Angew. Chem., Int. Ed., 2001, 40(14), 2591–2611 CrossRef CAS.
- X. Zeng, J. Sun, Y. Yao, R. Sun, J.-B. Xu and C.-P. Wong, A Combination of Boron Nitride Nanotubes and Cellulose Nanofibers for the Preparation of a Nanocomposite with High Thermal Conductivity, ACS Nano, 2017, 11(5), 5167–5178 CrossRef CAS PubMed.
- Y.-F. Zhang, D. Han, Y.-H. Zhao and S.-L. Bai, High-performance thermal interface materials consisting of vertically aligned graphene film and polymer, Carbon, 2016, 109, 552–557 CrossRef CAS.
- Y. Sun, Y. He, B. Tang, C. Tao, J. Ban and L. Jiang, Influence from the types of surface functional groups of RGO on the performances of thermal interface materials, RSC Adv., 2017, 7(88), 55790–55795 RSC.
- N. Saba, M. T. Paridah and M. Jawaid, Mechanical properties of kenaf fibre reinforced polymer composite: a review, Constr. Build. Mater., 2015, 76, 87–96 CrossRef.
- C. A. Smith, Thermochemical and physical properties of printed circuit board laminates and other polymers used in the electronics industry, Polym. Test., 2016, 52, 234–245 CrossRef CAS.
- T. Wang, D. Ou, H. Liu, S. Jiang, W. Huang, X. Fang, X. Chen and M. Lu, Thermally Conductive Boron Nitride Nanosheet Composite Paper as a Flexible Printed Circuit Board, ACS Appl. Nano Mater., 2018, 1(4), 1705–1712 CrossRef CAS.
- A. Henry and G. Chen, High Thermal Conductivity of Single Polyethylene Chains Using Molecular Dynamics Simulations, Phys. Rev. Lett., 2008, 101(23), 235502 CrossRef.
- D.-G. Kang, H. Ko, J. Koo, S.-I. Lim, J. S. Kim, Y.-T. Yu, C.-R. Lee, N. Kim and K.-U. Jeong, Anisotropic Thermal Interface Materials: Directional Heat Transfer in Uniaxially Oriented Liquid Crystal Networks, ACS Appl. Mater. Interfaces, 2018, 10(41), 35557–35562, DOI:10.1021/acsami.8b09982.
- K. Chen and L. Li, Ordered Structures with Functional Units as a Paradigm of Material Design, Adv. Mater., 2019, 31(32), 1901115 CrossRef PubMed.
- A. A. Balandin, Thermal properties of graphene and nanostructured carbon materials, Nat. Mater., 2011, 10(8), 569–581 CrossRef CAS PubMed.
- X. Wang, M. Kaviany and B. Huang, Phonon coupling and transport in individual polyethylene chains: a comparison study with the bulk crystal, Nanoscale, 2017, 9(45), 18022–18031 RSC.
- S. Shen, A. Henry, J. Tong, R. Zheng and G. Chen, Polyethylene nanofibres with very high thermal conductivities, Nat. Nanotechnol., 2010, 5(4), 251 CrossRef CAS PubMed.
- Y. Xu, D. Kraemer, B. Song, Z. Jiang, J. Zhou, J. Loomis, J. Wang, M. Li, H. Ghasemi and X. Huang, Nanostructured polymer films with metal-like thermal conductivity, Nat. Commun., 2019, 10(1), 1–8 CrossRef.
- H. Khonakdar, J. Morshedian, U. Wagenknecht and S. Jafari, An investigation of chemical crosslinking effect on properties of high-density polyethylene, Polymer, 2003, 44(15), 4301–4309 CrossRef CAS.
- S. Sudhamani, M. Prasad and K. U. Sankar, DSC and FTIR studies on gellan and polyvinyl alcohol (PVA) blend films, Food Hydrocolloids, 2003, 17(3), 245–250 CrossRef CAS.
- S. Morimune, T. Nishino and T. Goto, Poly(vinyl alcohol)/graphene oxide nanocomposites prepared by a simple eco-process, Polym. J., 2012, 44(10), 1056–1063 CrossRef CAS.
- L. Zhang and L. Liu, Hierarchically hydrogen-bonded graphene/polymer interfaces with drastically enhanced interfacial thermal conductance, Nanoscale, 2019, 11(8), 3656–3664 RSC.
- S. D. Dabhi and P. K. Jha, Stability, phonon dispersion and specific heat of solid poly(vinyl alcohol) using density functional theory, Polymer, 2015, 81, 45–49 CrossRef CAS.
- J. Barnes and B. Fanconi, Review of vibrational data and force field constants for polyethylene, J. Phys. Chem. Ref. Data, 1978, 7(4), 1309–1322 CrossRef CAS.
- X. Xie, D. Li, T.-H. Tsai, J. Liu, P. V. Braun and D. G. Cahill, Thermal conductivity, heat capacity, and elastic constants of water-soluble polymers and polymer blends, Macromolecules, 2016, 49(3), 972–978 CrossRef CAS.
- E. A. Algaer and F. Müller-Plathe, Molecular dynamics calculations of the thermal conductivity of molecular liquids, polymers, and carbon nanotubes, Soft Mater., 2012, 10(1–3), 42–80 CrossRef CAS.
- Y. Hong, J. Zhang, X. Huang and X. C. Zeng, Thermal conductivity of a two-dimensional phosphorene sheet: a comparative study with graphene, Nanoscale, 2015, 7(44), 18716–18724 RSC.
- L. T. Kong, Phonon dispersion measured directly from molecular dynamics simulations, Comput. Phys. Commun., 2011, 182(10), 2201–2207 CrossRef CAS.
- Q. Tang, A molecular dynamics simulation: the effect of finite size on the thermal conductivity in a single crystal silicon, Mol. Phys., 2004, 102(18), 1959–1964 CrossRef CAS.
- Z. Xu, Y. Lu and Q. Guo, Bioinspired strategy for tuning thermal stability of PVA via hydrogen-bond crosslink, Compos. Sci. Technol., 2015, 118, 16–22 CrossRef.
- Y. Gan, S. Bai, S. Hu, X. Zhao and Y. Li, Reaction mechanism of thermally-induced electric conduction of poly(vinyl alcohol)–silver nitrate hybrid films, RSC Adv., 2016, 6(61), 56728–56737, 10.1039/C6RA08994A.
- H. S. Mansur, R. L. Oréfice and A. A. Mansur, Characterization of poly (vinyl alcohol)/poly (ethylene glycol) hydrogels and PVA-derived hybrids by small-angle X-ray scattering and FTIR spectroscopy, Polymer, 2004, 45(21), 7193–7202 CrossRef CAS.
- M. Xu, D. N. Futaba, M. Yumura and K. Hata, Alignment control of carbon nanotube forest from random to nearly perfectly aligned by utilizing the crowding effect, ACS Nano, 2012, 6(7), 5837–5844 CrossRef CAS PubMed.
- K. Young, F. M. Blighe, J. J. Vilatela, A. H. Windle, I. A. Kinloch, L. Deng, R. J. Young and J. N. Coleman, Strong Dependence of Mechanical Properties on Fiber Diameter for Polymer−Nanotube Composite Fibers: Differentiating Defect from Orientation Effects, ACS Nano, 2010, 4(11), 6989–6997 CrossRef CAS PubMed.
- L. S. Tóth and P. Van Houtte, Discretization techniques for orientation distribution functions, Texture, Stress, Microstruct., 1992, 19(4), 229–244 CrossRef.
- C. Choy, Thermal conductivity of polymers, Polymer, 1977, 18(10), 984–1004 CrossRef CAS.
- L. Ren, K. Pashayi, H. R. Fard, S. P. Kotha, T. Borca-Tasciuc and R. Ozisik, Engineering the coefficient of thermal expansion and thermal conductivity of polymers filled with high aspect ratio silica nanofibers, Composites, Part B, 2014, 58, 228–234 CrossRef CAS.
- J. Li, L. Shao, X. Zhou and Y. Wang, Fabrication of high strength PVA/rGO composite fibers by gel spinning, RSC Adv., 2014, 4(82), 43612–43618 RSC.
- T. Terao, E. Lussetti and F. Müller-Plathe, Nonequilibrium molecular dynamics methods for computing the thermal conductivity: application to amorphous polymers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75(5), 057701 CrossRef.
- P. L. Garrido, P. I. Hurtado and B. Nadrowski, Simple one-dimensional model of heat conduction which obeys Fourier's law, Phys. Rev. Lett., 2001, 86(24), 5486 CrossRef CAS PubMed.
- C. Campaná and M. H. Müser, Practical Green's function approach to the simulation of elastic semi-infinite solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(7), 075420 CrossRef.
- Y. Zhu, Heat-loss modified Angstrom method for simultaneous measurements of thermal diffusivity and conductivity of graphite sheets: the origins of heat loss in Angstrom method, Int. J. Heat Mass Transfer, 2016, 92, 784–791 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: The theoretical calculation, fabrication of thermally conductive PVA nanostructured films, alignment measurement and thermal diffusivity measurements. See DOI: 10.1039/d0ma00346h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |