High performance photocatalytic and thermoelectric two-dimensional asymmetrically ordered Janus-like MXene alloys

Abstract

MXenes are two-dimensional transition metal carbides, nitrides, and/or carbonitrides which display extensive versatility in their elemental composition for tuning and optimization of their functional properties. In this work, by using a multiscale approach of density functional theory calculations, cluster expansion method, and Monte Carlo simulations, we systematically investigate the Ti_2(1−x)Mo_2xCO₂ alloy system of two-dimensional Ti₂CO₂ and Mo₂CO₂ MXenes with 0 < x < 1. From the alloy formation energies, we identify the stable ground-state and report the possible existence of an asymmetrically ordered Janus-like MXene alloy TiMoCO₂. This alloy is theoretically validated to be stable thermodynamically, mechanically, and thermally, with a high order–disorder phase transition temperature of ∼640 K. Importantly, TiMoCO₂ is a semiconductor with a band gap of 0.60 eV and its valence band maximum and conduction band minimum are located on opposite sides of the MXene monolayer. As such, the asymmetric configuration generates an intrinsic dipole moment, which realigns the conduction and valence band edges, permitting photocatalytic redox water-splitting to favorably occur with a higher solar absorption efficiency in the visible-infrared region due to the smaller band gap. From the transport calculations, we propose the TiMoCO₂ MXene alloy to exhibit high room temperature n- and p-type power factors of 49.8 μW cm⁻¹ K⁻² and 15 μW cm⁻¹ K⁻², respectively, outperforming other related experimentally synthesized Ti–Mo based MXene alloys and even similar to that of p-doped SnSe which is one of the best performing thermoelectric materials. All these indicate the stable asymmetrically ordered Janus-like TiMoCO₂ MXene alloy to be a promising high performance water-splitting photocatalyst and thermoelectric material, paving the way for more stable Janus-like MXenes with interesting and outstanding functional properties to be discovered.

---

1. Introduction

MXenes are a large family of two-dimensional (2D) layered transition metal carbides, nitrides, and/or carbonitrides discovered in 2011, with the structural formula M_n+1X_n (where M is transition metal, and X is C and/or N, with n = 1, 2, 3, or 4).^1–3 They are typically derived from their MAX phase precursors by the selective chemical etching of the A-group elements such as Al or Ge,⁴ although other synthesis approaches are feasible as well.^5,6 Although post-chemical etching results in MXenes to be mostly terminated with a mixture of functional groups, e.g., O, OH, and F, a recent study has shown that exclusively O-terminated MXenes, i.e., M_n+1X_nO₂, can be attainable via post-treatment under vacuum and subsequent exposure to O₂ gas at slightly elevated temperatures.⁷ Owing to the compositional tunability, elemental flexibility, 2D crystallinity, excellent electrical conductivity, and hydrophilicity, MXenes have been under the spotlight for a wide spectrum of research spanning from energy,³ environment,⁸ and even biomedical applications.⁹ This rich chemistry exhibits the versatility of MXenes in the design of materials.

As the world becomes increasingly conscious towards climate change and sustainability, alternative green energy sources such as hydrogen production from photocatalytic water-splitting have become heavily sought for as a clean fuel. As such, MXenes have been garnering intense research interest in photocatalytic water-splitting.^10–12 Typically, a practical water-splitting photocatalyst has to fulfill 3 main requirements: (1) band gap > 1.23 eV such that the band edges straddle water redox potentials; (2) high solar photon absorption; and (3) a low electron–hole recombination rate.^13,14 Moreover, 2D materials like MXenes display high specific reaction surface and the low dimensionality minimizes the distances that photogenerated electrons and holes have to migrate to the reaction interface, reducing the possibility of electron–hole recombination and enhancing the photocatalytic performance. Currently, only a handful of MXenes are theoretically identified to exhibit semiconducting behaviors, e.g., Ti₂CO₂, Zr₂CO₂, Hf₂CO₂, and Sc₂CT₂ (where T = O, F, OH).¹⁵ Unfortunately, these MXenes possess either insufficient band gaps, misaligned band edges, or weak solar absorption, which compromise their photocatalytic performance.¹⁶ Our previous work has suggested stoichiometric engineering of the disordered alloy of Ti₂CO₂ and Zr₂CO₂, i.e., Ti_2(1−x)Zr_2xCO₂ where x = 0.2778, to show enhanced photocatalytic capabilities.¹⁷ However, it is possible that the random distribution of Ti and Zr in the M-sites could lead to disorder-based scatterings which may impede the mobility of the photogenerated electrons and holes.¹⁸ Therefore, ordered semiconductor MXene alloys with reduced disorder-based scatterings would be desirable.

Likewise, another abundant but inefficiently utilized energy source is waste thermal energy, for which, thermoelectric (TE) materials can be exploited for conversion into useful electrical energy. The efficiency of thermoelectric materials can be evaluated using a dimensionless figure-of-merit, defined as 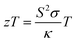, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the total thermal conductivity, and T is the temperature. As such, a good performing thermoelectric material should possess a high power factor S²σ and low κ, although these two parameters are usually negatively correlated.¹⁹ Recently, a few Mo-based MXene flexible thin films, e.g., Mo₂C, Mo₂TiC₂, and Mo₂Ti₂C₃, have been experimentally investigated for their thermoelectric performance.²⁰ The Mo₂TiC₂ film displays the highest S²σ of ∼3.09 μW cm⁻¹ K⁻² at 800 K (and ∼0.5 μW cm⁻¹ K⁻² at 300 K) among these thin films. While these values are not exceptional, one can exploit the compositional versatility of MXenes to further optimize, tune, and create a better thermoelectric material.

As such, we wonder whether it is possible to surpass these limitations to discover a novel alloying approach to make MXene photocatalysis and thermoelectric properties better for sustainability applications. Herein, we investigate the substitutional alloy MXene Ti_2(1−x)Mo_2xCO₂ and attempt to predict its synthesizability, noting that its thicker counterparts, Mo₂TiC₂ and Mo₂Ti₂C₃, have been successfully synthesized and are well-studied.^20–22 Using a multiscale approach of density functional theory (DFT) calculations, cluster expansion (CE) method, and Monte Carlo (MC) simulations,^23–27 we screened through a total of more than 9 million different Ti_2(1−x)Mo_2xCO₂ MXene alloy configurations with the 3 different types of O-termination. We then systematically map out their structure–stability relationship by validating the thermodynamically stable alloy ground-state(s), followed by the assessment of their suitability as water-splitting photocatalysts and thermoelectric materials, using their respective figure-of-merit derived from electronic, optical, and thermal calculations. Thus, for the first time, we report the possible existence of an asymmetrically ordered Janus-like (or 2-faced) MXene alloy TiMoCO₂. This alloy is thermodynamically, mechanically, and thermally stable with a high order–disorder phase transition temperature of ∼640 K. In essence, the TiMoCO₂ MXene alloy is a semiconductor with a band gap of 0.60 eV. The asymmetric structure gives rise to an intrinsic dipole moment leading to band edge realignment due to the valence band maximum (VBM) and conduction band minimum (CBM) situating on the opposite surfaces of the MXene monolayer, which in turn straddles water redox potentials. Photocatalytic redox water-splitting can therefore occur with a much higher solar absorption efficiency, reaching above 10⁴–10⁵ cm⁻¹ in the visible-infrared region. Its room temperature intrinsic hole and electron mobilities are evaluated to be 133.61–142.39 cm² V⁻¹ s⁻¹ and 19.65–29.99 cm² V⁻¹ s⁻¹, respectively, surpassing some 2D monolayer transition metal dichalcogenides (TMDs). Moreover, we determine the TiMoCO₂ MXene alloy to exhibit high room temperature n- and p-type power factors of 33.7–49.8 μW cm⁻¹ K⁻² and ∼15 μW cm⁻¹ K⁻², respectively, which outperform other related experimentally synthesized Ti–Mo based MXene alloys and are even comparable to that of p-doped SnSe, which is one of the best performing thermoelectric materials. All these indicate the stable asymmetrically ordered Janus-like TiMoCO₂ MXene alloy to be a promising high performance water-splitting photocatalyst and thermoelectric material. Our work paves the way for more Janus-like MXenes with interesting and outstanding properties to be discovered.

2. Methodology

2.1 Cluster expansion (CE) method and Monte Carlo (MC) simulations

According to the CE formalism,^28–30 a particular alloy configuration, ϱ, on a fixed lattice, can be described using a set of occupational variables. For this work, a pseudo-binary Ti_2(1−x)Mo_2xCO₂ substitutional MXene alloy is generated on the metallic sublattice with Ti and Mo, while ensuring the composition of C and O on the anion sublattice to remain unvaried. As such, for a given ϱ, its respective formation energy E_f corresponds its stability at 0 K to its most stable O-terminated MXene constituents, fcc-Ti₂CO₂ and hcp-Mo₂CO₂:

E_f(Ti_2(1−x)Mo_2xCO₂,ϱ) = E(Ti_2(1−x)Mo_2xCO₂,ϱ) − (1 − x)E(Ti₂CO₂) − xE(Mo₂CO₂) (1)

where E(Ti₂CO₂), E(Mo₂CO₂), and E(Ti_2(1−x)Mo_2xCO₂,ϱ) are the total energies per atom of Ti₂CO₂, Mo₂CO₂, and a particular ϱ of the Ti_2(1−x)Mo_2xCO₂ alloy, respectively. This configuration-dependent E_f is described via the CE formalism^31–33 where we can obtain the effective cluster interactions (ECIs) between the alloyants, Ti and Mo. To perform CE, we utilize the Thermodynamic Tool-Kit (TTK) code,^{17,22,23,30,32–41} the fundamental principles of which have been methodically elaborated in our previous works for other MXene alloys.^17,40,41 In essence, for each alloy configuration (of each fcc, hcp, and fcc + hcp O-terminated MXene, i.e., 3 “different” systems), we construct an initial CE Hamiltonian by fitting the ECIs from a learning set of DFT-calculated E_f of ∼100 configurations comprising up to 20-atom Ti_2(1−x)Mo_2xCO₂ MXene supercells. This is followed by screening of over 3 million alloy structures with unique configurations (up to 70-atom supercells) to obtain their corresponding CE energies. Alloy configurations with E_f close to or at the ground-state hull would be verified via DFT and added to the learning set to generate an updated CE Hamiltonian for the ensuing iteration(s). The iterative process is ended and the CE is considered to be properly truncated when either no new ground-states are predicted and/or the CE E_f values are reproduced precisely within <0.003 eV atom⁻¹.

Utilizing the properly truncated CE, we perform MC simulations via the TTK code to survey the equilibrium Ti–Mo distribution in the alloys at the ground-state hull composition across different temperatures. A simulation cell of 24 × 24 × 1 times the size of the primitive unit cell of Ti₂CO₂ and Mo₂CO₂ is used. As such, a series of canonical (fixed chemical potential and temperature) MC runs with 30 000 sampling steps per run is conducted to assess the Ti–Mo distribution, and to predict the order–disorder phase transition temperature of the alloy at ground-state hull composition.

2.2 First-principles calculations

Density functional theory (DFT) calculations⁴² are performed using the Perdew–Burke–Ernzerhof (PBE) exchange correlation based on the generalized gradient approximation (GGA)^43,44 as implemented in the Vienna ab initio Simulation Package (VASP).^45,46 Electron-ion interactions are described via the projector augmented-wave (PAW) method.⁴⁷ The plane-wave cut-off energy is set to 500 eV. During structural relaxation, the volume of the unit cell is fixed while the cell shape is allowed to change. A vacuum spacing of ∼15 Å is ensured in the out-of-plane direction to minimize spurious interactions between periodic images. All atomic coordinates are therefore fully relaxed until the Hellmann–Feynman forces on each atom are <0.001 eV Å⁻¹. A dipole correction in the direction normal to the MXene plane is included for all the calculations.⁴⁸ Monkhorst–Pack k-point meshes⁴⁹ with a density of ∼40 k-points per Å⁻¹ inclusive of the Γ-point are used during structural optimizations, whereas finer meshes of ∼160 k-points per Å⁻¹ are utilized for detailed electronic density-of-states (DOS) and electronic band structure calculations. To achieve an accurate description of the band gaps, the band-edge positions, and the dielectric functions of the ground-state alloy, the Heyd–Scuseria–Ernzerhof (HSE06)^50,51 hybrid functional is utilized. The effective electron and hole masses are determined by the parabolic fitting of the conduction band minimum (CBM) and valence band maximum (VBM), respectively, along selected k-point paths in the in-plane directions.⁵²

To investigate the elastic properties, the elastic tensor is determined using the stress–strain relationship via six finite distortions of the lattice to derive the elastic constants.⁵³ The ionic contributions are determined from the inversion of the ionic Hessian matrix which is evaluated from finite differences and multiplied with the internal strain tensor.⁵⁴

Ab initio molecular dynamics (AIMD) simulations are employed to evaluate the stability of the ground-state MXene alloy at finite temperatures; the simulations are carried out with a 5 × 5 × 1 supercell at 300 K and 600 K with the Nosé–Hoover thermostat^55,56 for 20 ps with a time step of 1 fs.

The elucidation of the phonon dispersions and the electron–phonon couplings is performed using density functional perturbation theory (DFPT)^57,58 under PBE-GGA as implemented in the PHONON package of QUANTUM ESPRESSO.^59,60 Here, a set of optimized norm-conserving Vanderbilt (ONCV) pseudopotentials from PseudoDojo⁶¹ are used to replace core electrons, along with a plane-wave cut-off energy of 100 Ry and a well-converged and uniform 12 × 12 × 1 k-point mesh for the Brillouin zone sampling, followed by the interpolation of the phonon dispersion and electron–phonon matrix elements into well-converged ultrafine 240 × 240 × 1 k-point and 400 × 400 × 1 q-point meshes with maximally localized Wannier functions^62,63 as implemented in Electron–Phonon coupling using the Wannier function (EPW)⁶⁴ code for the evaluation of the transport properties for an accurate description of the carrier mobilities and thermoelectric performance via the self-energy relaxation time approximation (SERTA)⁶⁵ within the framework of the Boltzmann transport equation (BTE). On the basis of the BTE, we evaluate the electron velocity matrix using first-order k-derivatives of the Hamiltonian via EPW, followed by the subsequent determination of the electrical conductivity σ and Seebeck coefficient S as elaborated according to published works.^66,67

3. Results and discussion

3.1 Alloy screening and formation stability

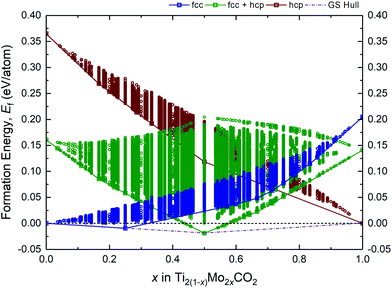
A fully O-terminated MXene M₂CO₂ can adopt 1 of the 3 possible geometries of O atoms, i.e., fcc, hcp, or fcc + hcp (fcc on one surface, and hcp on the other) (Fig. S1, ESI†). While our previous and other published works have shown Ti₂CO₂ and Mo₂CO₂ to preferentially adopt the fcc and hcp geometry, respectively,^15,17,41 we have considered all 3 geometries in our screening of alloys lest there are thermodynamically MXene alloys with any of these 3 possible geometries. As such, Fig. 1 illustrates the formation energies E_f of more than 9 million different alloy configurations derived from eqn (1) for the fcc, hcp, and fcc + hcp O-termination geometries, using the constructed ECIs by the CE method. The most stable configurations (at 0 K) are known as ground-states, which form a ground-state hull (dashed–dotted line) across compositions, implying the theoretical lower bound of E_f for the Ti_2(1−x)Mo_2xCO₂ alloy. On the other hand, states or configurations above the ground-state hull are accessible only at finite temperatures. Accordingly, from Fig. 1, only 2 stable alloy ground-states at x = 0.25 (Ti_1.5Mo_0.5CO₂) and x = 0.5 (TiMoCO₂) can be observed, of which Ti_1.5Mo_0.5CO₂ and TiMoCO₂ occur as fcc and fcc + hcp O-terminated MXenes, respectively. On the grounds that only TiMoCO₂ displays semiconducting character which is crucial for photocatalytic water-splitting and will be revealed later, whereas Ti_1.5Mo_0.5CO₂ is metallic, we focus on the in-depth investigations of the TiMoCO₂ MXene alloy in the following sections.

Fig. 1 Plot of formation energy E_fversus composition for Ti_2(1−x)Mo_2xCO₂ MXene. Each point represents a particular alloy configuration whose relative stability is indicated by its E_f with respect to its most energetically stable fcc O-terminated Ti₂CO₂ and hcp O-terminated Mo₂CO₂ constituent MXenes. Alloys with fcc, hcp, and fcc + hcp O-termination geometry are indicated in blue, red, and green, respectively. The solid line refers to the local ‘ground-state’ hull which joins the lowest energy structures across compositions for each corresponding O-termination geometry; whereas the dashed–dotted line is the overall ground-state (GS) hull which joins the lowest energy structures across compositions regardless of the geometry of O-termination.

3.2 Asymmetrically ordered Janus-like TiMoCO₂ MXene alloy

3.2.1 Structural properties and stability. TiMoCO₂ possesses an asymmetrically ordered Janus-like structure in which the atomic layers are stacked in the sequence O(fcc)–Ti–C–Mo–O(hcp) as illustrated in Fig. 2a. Due to this asymmetric structure, the TiMoCO₂ MXene alloy has the space group P3m1 (no. 156) (instead of P3̄m1 (no. 164) like most other M₂CO₂ MXenes) and possesses no inversion symmetry. The configuration of the M-sites (M–C–M′) in this MXene alloy is rather intriguing because from our previous works on other Ti-based MXene alloy systems (Ti_2(1−x)M_2xCO₂, where M = Zr, Hf, V, Nb, and Ta),^17,41 alloys with such a Janus-like configuration typically possess the most positive E_f and if ground-states with x = 0.5 exist, it would likely occur with in-plane ordering. Analogously, even experimentally synthesized 2D TMD MoSSe alloys with a Janus-like configuration (S–Mo–Se)^68,69 have been theoretically evaluated to be energetically less favorable than the disordered counterpart.^70–72 The origin of this stability in TiMoCO₂ can be attributed to the appropriate O-termination geometries for the respective Ti (fcc) and Mo (hcp) sides resulting in Bader charges to be similar to those of O, Ti, and Mo in their thermodynamically stable constituent MXenes Ti₂CO₂ (fcc) and Mo₂CO₂ (hcp) (Table S1, ESI†). Moreover, we have further verified that even the bare TiMoC MXene alloy without O-terminations is stable by 81.8 meV per atom with respect to the constituent Ti₂C and Mo₂C MXenes (Table S2, ESI†). Accordingly, our TiMoCO₂ MXene alloy with its favorable E_f and thermodynamic stability would have enhanced synthesizability.

Fig. 2 (a) Side and top views of the Janus-like ground-state TiMoCO₂ MXene alloy. The red, green, blue, and grey spheres correspond to O, Ti, Mo, and C, respectively. Plots of the (b) average energy U_avg and (c) heat capacity C_v, both versus the temperature T for the TiMoCO₂ MXene alloy. (d) Plot showing the variations in the free energy of the ordered Janus-like ground-state TiMoCO₂ MXene alloy at 300 K and 600 K with respect to the AIMD simulation time. The insets show the side and top views of the final crystal structure of the TiMoCO₂ MXene alloy at 300 K and 600 K after 20 ps. (e) Phonon dispersion along the high-symmetry path of (f) the hexagonal Brillouin zone for the Janus-like ground-state TiMoCO₂ MXene alloy.

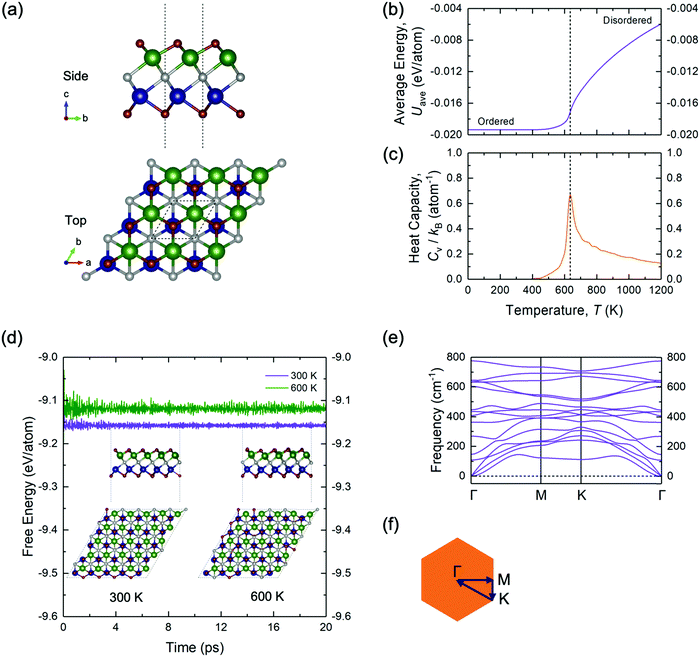
To further validate the stability of the ground-state configuration of TiMoCO₂, a series of canonical MC runs, AIMD simulations, and phonon calculations are performed. Fig. 2b and c show, respectively, a plot of average energy U_avg (of the MC simulation cell) and another plot of heat capacity C_v, both versus temperature T. The ordered configuration at the end of the MC runs corresponds exactly to the configuration of the DFT- and CE-determined ground-state TiMoCO₂ MXene alloy (Fig. 2a). Moreover, the order–disorder phase transition temperature, which is the peak in the plot of C_vversus T, is determined to be ∼640 K, implying that the ordered configuration is thermodynamically stable under room conditions (∼300 K). Besides, AIMD simulations in Fig. 2d carried out at 300 K and 600 K (below its order–disorder phase transition temperature) show the energies to fluctuate about constant values, with negligible structural deviations and no structural reconstructions after annealing for 20 ps. In addition, the phonon dispersion in Fig. 2e along the high-symmetry path of the Brillouin zone exhibits no negative (imaginary) frequencies, suggesting the dynamic stability of the TiMoCO₂ ground-state configuration.

Likewise, the mechanical stability of the TiMoCO₂ MXene alloy is also examined. A (hexagonal) 2D MXene possesses 3 independent non-zero elastic constants which are calculated to be: C₁₁ = 322.22 N m⁻¹, C₁₂ = 103.06 N m⁻¹, and C₆₆ = 109.58 N m⁻¹. These elastic constants fulfill the Born stability criteria according to Born–Huang's lattice dynamical theory for hexagonal 2D structures,^73,74i.e., C₁₁ > 0, C₁₁ − C₁₂ > 0, and 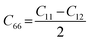, indicating that the TiMoCO₂ MXene alloy is mechanically stable. Using these elastic constants, we evaluate the in-plane Young's modulus Y_s and the Poisson's ratio ν according to the following expressions:^75,76 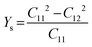and 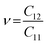, which give 289.26 N m⁻¹ and 0.32, respectively. We note that using the same approach, we obtain Y_s values of 243.02 N m⁻¹ and 241.04 N m⁻¹ for the constituent MXenes Ti₂CO₂ and Mo₂CO₂, indicating that the alloying would produce a mechanically stronger material. Moreover, this value of Y_s is much higher than those of 2D TMDs such as monolayer MoS₂ (171 ± 11 N m⁻¹)⁷⁷ and WS₂ (177 ± 12 N m⁻¹),⁷⁷ and slightly lower than that of graphene (324 ± 13 N m⁻¹)⁷⁸ which is the strongest 2D material. This implies the TiMoCO₂ MXene alloy to overall possess high mechanical strength as well. With the thermodynamically favorable E_f, dynamically stable phonon dispersion, thermally stable MC and AIMD simulations, and favorable elastic constants, we believe that the experimental realization of this material is highly feasible.

3.2.2 Photocatalytic properties. Fig. 3a illustrates the electronic band structure of the TiMoCO₂ ground-state configuration with a band gap of 0.60 eV. The band gap is indirect with the valence band maximum (VBM) located on the Γ point, whereas the conduction band minimum (CBM) resides on the K–Γ valley. At first glance, this value of the band gap appears to fall short of the ‘1.23 eV band gap’ prerequisite for typical redox water-splitting photocatalysis to be thermodynamically feasible. However, for TiMoCO₂ MXene alloys, this requirement can be overcome for reasons explained in the following paragraph. While a thicker absorption layer is typically required for an indirect band gap material, this indirect gap impedes the rate of electron–hole recombination, thereby increasing the probability for the holes and electrons to partake in the water-splitting redox reactions.⁷⁹

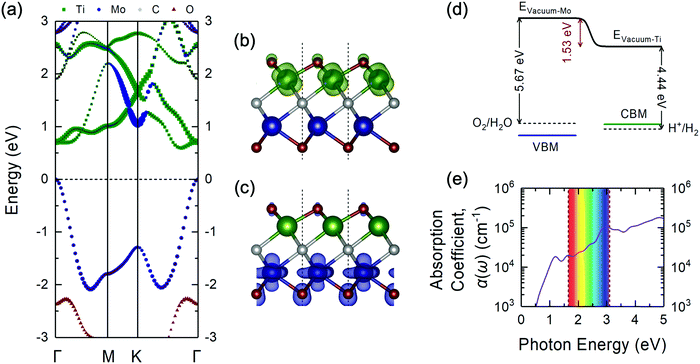Fig. 3 (a) Projected electronic band structure of the Janus-like ground-state TiMoCO₂ MXene alloy via the HSE06 functional plotted along the high-symmetry path of the hexagonal Brillouin zone (see Fig. 2f). The size of each point corresponds to the relative magnitude of the respective elemental contribution to the band. The Fermi level is set to 0 eV at the VBM. The side view of the partial charge density of the (b) CBM (in green) and (c) VBM (in blue) of the TiMoCO₂ MXene alloy. The value of the isosurfaces is 0.02 e Å⁻³. The red, green, blue, and grey spheres correspond to O, Ti, Mo, and C, respectively. (d) Band edge alignments of the VBM and CBM in blue and green solid lines, respectively, with regard to the water redox potentials in dashed lines, and their corresponding vacuum levels. The potential difference between the two sides of the TiMoCO₂ MXene alloy induced by the intrinsic dipole moment is denoted in red. For the actual electrostatic potential profile, please refer to Fig. S2 (ESI†). (e) Plot of the in-plane optical absorption coefficient α(ω) versus photon energy for the TiMoCO₂ MXene alloy. The visible wavelength region (1.65 to 3.10 eV) is shown as an iridescent rectangle for guide.

From the atomic projections of the electronic band structure and the charge density isosurface distributions (Fig. 3a–c), it can be observed that the VBM state is mainly composed of Mo-d_z² and O-p_z (at Mo side) orbitals, whereas the CBM state mainly originated from Ti-d_xz orbitals. This distinction in the orbital contributions for both sides of TiMoCO₂ is the key factor for allowing photocatalytic redox water-splitting to be thermodynamically feasible even with a small band gap. Due to the difference in the electronegativity between Ti (1.54) and Mo (2.16),⁸⁰ and consequent Bader charge of Ti (+1.92e), Mo (+1.60e), and the fcc-terminated and hcp-terminated O (−1.08e and −0.93e, respectively), an intrinsic dipole moment of 0.232 D is generated with the electric field pointing from the Ti to Mo side. This dipole moment-induced electric field promotes photogenerated electron–hole separation and localizes the electrons and holes on Ti and Mo sides, respectively. As such, there exists an electrostatic potential difference of 1.53 eV as shown in Fig. S2 (ESI†) and Fig. 3d. Moreover, by aligning the band edge positions relative to the respective water redox potentials, i.e., the VBM to water oxidation potential (5.67 eV) w.r.t. the Mo side's vacuum level and the CBM to water reduction potential (4.44 eV) w.r.t. the Ti side's vacuum level, we observe in Fig. 3d that both the VBM and CBM straddle the water redox potentials, indicating that redox water-splitting photocatalysis is thermodynamically feasible albeit there is a band gap of 0.60 eV. The bending of the vacuum level along the direction of the internal electric field permits the reduction of the band gap requirement, i.e., difference between oxidation and reduction potentials of water, from 1.23 eV to 1.23 eV minus the value of the electrostatic potential difference between the two surfaces.⁸¹ Intriguingly, for our TiMoCO₂ MXene alloy with an electrostatic potential difference of 1.53 eV, the band gap requirement would therefore be 0 eV, indicating that so long as the VBM and CBM are located on the opposite sides of the MXene, the size of its band gap would not affect the thermodynamic feasibility of photocatalytic redox water-splitting.

With the omission of the band gap prerequisite, the absorption properties of the TiMoCO₂ MXene alloy is investigated to elucidate its efficiency in solar conversion. Fig. 3e shows the absorption coefficient α(ω) derived from the calculated frequency-dependent complex dielectric function ε(ω) = ε₁(ω) + iε₂(ω) according to the relation:⁸²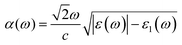, with c being the speed of light in vacuum. It can be observed that the TiMoCO₂ MXene alloy exhibits strong absorption of a wide wavelength range from ultraviolet to visible to infrared with α(ω) reaching above 10⁴–10⁵ cm⁻¹ in the visible-infrared region. Since this region accounts for majority of the incident solar energy, by implementation of the metric which integrates the product of the incident solar photon flux according to the AM1.5G solar spectrum with the absorbance of the material up to its band gap's equivalent wavelength, as elaborated comprehensively in our previous work as well as other literature,^17,36,83 we obtain its maximum short-circuit current of 4.2 mA cm⁻². This value is much larger than those of conventional photovoltaic materials such as Si, and also those of 2D materials like MoS₂ and WS₂, with maximum short-circuit currents ranging from 0.1 to 3.6 mA cm⁻² (Table 1), which suggests TiMoCO₂ to be a potential photovoltaic material, in addition to its desirable visible-infrared absorbance for efficient photocatalysis.

Table 1 Figures-of-merit of the maximum short-circuit currents for photocatalytic water-splitting and power factors at 300 K for thermoelectric applications for TiMoCO₂ and other representative water-splitting photocatalytic and thermoelectric materials

Material	Maximum short-circuit current^a (mA cm^−2)	Thermoelectric power factor (μW cm^−1 K^−2)
		n-doping	p-doping
a This work.
TiMoCO2	4.2	33.7–49.8^a	16.0^a
MoS2	3.6	35.0^88	—
WS2	2.7	—	2.8^89
Si	0.1	—	—
Mo2TiC2	—	0.5^20	—
Mo2Ti2C3	—	0.1^20	—
SnSe	—	—	10.0–40.0^90

---

Other than the appropriate band and promising absorption characteristics, the electron and hole mobilities of the TiMoCO₂ MXene alloy are also investigated to elucidate its efficacy in photocatalytic water-splitting. Herein, using the SERTA approach and accounting for electron–phonon scattering of all the phonon modes,⁶⁵ we obtain the room temperature intrinsic hole mobility μ_p to be 142.39 and 133.61 cm² V⁻¹ s⁻¹ along the x- and y-direction, respectively. These values show high isotropy in both x- and y-directions, which are consistent with the VBM being comprised of Mo-d_z² and O-p_z orbitals, and the consequent isotropic effective hole mass of 0.23m₀ along both x- and y-directions, indicating in-plane orientation-independent hole transport in either direction of TiMoCO₂. In contrast, the room temperature intrinsic electron mobility μ_n is anisotropic with 29.99 and 19.65 cm² V⁻¹ s⁻¹ along the corresponding x- and y-directions, in accord with the contribution of the in-plane anisotropic Ti-d_xz orbitals to the CBM with anisotropic effective electron masses of 0.81m₀ and 1.31m₀ along the respective x- and y-directions. It is evident that μ_p is larger than μ_n as a result of lighter effective mass. Besides, the ∼1 order of magnitude difference between μ_p and μ_n promotes the effective spatial separation of the holes and electrons, which decreases the probability of photogenerated electron–hole recombination.^35,38 To estimate the reliability of the calculated carrier mobilities with our approach, μ_p and μ_n values of widely investigated 2D MoS₂ are analogously calculated to be 29.22 and 121.58 cm² V⁻¹ s⁻¹, respectively, which are close to their corresponding experimental measurements of ∼40–76 and ∼60–150 cm² V⁻¹ s⁻¹.^84–86 Evidently, TiMoCO₂ possesses a higher μ_p than that of MoS₂, suggesting its potential application as a hole transport material. Accordingly, the indirect band gap, dipole-induced electric field, appropriate band edge positions, high absorbance, and decent mobilities would favor photogeneration of the electrons and holes while bolstering effective spatial and charge separation of these photoelectrons and holes for effective water redox reactions, establishing the TiMoCO₂ MXene alloy to be an efficient water-splitting photocatalyst.

3.2.3 Thermoelectric properties. Meanwhile, from the calculated transport properties of the TiMoCO₂ MXene alloy, we are able to further utilize these data to assess its potential thermoelectric performance. In the simulation of the doping effects, we achieve n- or p-type doping by assuming a shift of the position of the Fermi level into the conduction or valence bands, respectively, within the rigid band approximation. Fig. 4 shows the various thermoelectric quantities at room temperature, i.e., Seebeck coefficient S, electrical conductivity σ, and power factor S²σ with respect to carrier concentration N, which suggest n-doping of the TiMoCO₂ ground-state configuration to produce a better thermoelectric material with higher peak S²σ than p-doping. These peak S²σ values show varying degrees of isotropy corresponding to their band character, similar to their respective mobilities as described above. Moreover, compared with other representative thermoelectric materials as tabulated in Table 1, the peak n-doped S²σ is ∼2 orders of magnitude larger than those of symmetrical Ti–Mo MXene alloys Mo₂TiC₂ and Mo₂Ti₂C₃ and ∼1 to 1.5 times larger than that of the MoS₂ monolayer. However, the peak p-doped S²σ is comparable to that of p-doped SnSe which is one of the best performing thermoelectric materials. It is important to also note that the peak n- and p-doped S²σ can be achieved at reasonably decent optimal doping concentrations of 4.0 × 10²⁰ cm⁻³ and 2.5 × 10¹⁹ cm⁻³, respectively, assuming an effective monolayer thickness of 7.2 Å. On top of that, the softer ZA phonon mode (lowest phonon band in Fig. 2e) and the absence of inversion symmetry could potentially reduce thermal conductivity⁸⁷ which is crucial for maximizing thermoelectric figure-of-merit zT; and hence, entailing the TiMoCO₂ MXene alloy to be a potential thermoelectric material upon optimal n- or p-type doping.

Fig. 4 Plots of thermoelectric quantities such as (a) power factor S²σ, (b) Seebeck coefficient S, and (c) conductivity σ as a function of carrier density N, assuming an effective monolayer thickness of 7.2 Å, for the n- and p-doped Janus-like ground-state TiMoCO₂ MXene alloy at room temperature. Due to isotropy, the plots for p-doped thermoelectric properties for x- and y-directions are almost equal to and overlap with each other.

3.2.4 Further exploration in the design of functional materials. In addition, before concluding this work, it is imperative for us to propose possible approaches and alloying formulations to set a direction for further optimization and tuning of the functional properties of asymmetrically ordered Janus-like MXenes. As such, we consider permutations between elements in the same respective group as Ti or Mo in the periodic table, i.e., ZrMoCO₂, HfMoCO₂, TiCrCO₂, and TiWCO₂, since their valency is maintained albeit at different electron energy levels. Some preliminary results with regard to their electronic band structures are illustrated in Fig. S3 and their electronic properties are tabulated in Table S3 (ESI†). Upon Ti replacement with Zr or Hf, while the band gaps vary mildly and the effective hole masses increase slightly down the group, the main contribution to the CBM has transformed to Mo-d_z² orbitals, indicating that since both the CBM and VBM are on the Mo's side, the photocatalytic water-splitting redox potential would not be realigned and the band gap would no longer permit redox water-splitting to occur simultaneously. In spite of this, the drastic reduction in the effective electron masses would suggest increased electron mobilities, potentially improving their n-type thermoelectric transport properties. On the other hand, substitution of Mo with Cr or W has resulted in significant decreases in the band gaps, for TiCrCO₂ due to the CBM and VBM being on the Cr's side analogous to the situation described for ZrMoCO₂ and HfMoCO₂, implying photocatalytic redox water-splitting to be thermodynamically unfavorable. However, the VBM and CBM of TiWCO₂ still reside on the opposing sides of the MXene layer, which, coupled with the larger solar absorption from the reduced band gap and also a higher degree of photogenerated electron–hole separation due to larger effective mass variation between holes and electrons, could synergistically further enhance the photocatalytic performance. It is important to note that a caveat for these conjectural ZrMoCO₂, HfMoCO₂, TiCrCO₂, and TiWCO₂ MXene alloys is that their stability evaluation involving CE and DFT calculations is yet to be implemented and more meticulous investigations have to be made to validate their formation stabilities, synthesizability, and their photocatalytic water-splitting and thermoelectric performance. Regardless, we have showcased that such Janus-like asymmetrically ordered MXene alloys can give rise to intriguing and even contrasting properties, signifying that this would be a promising direction for tuning and optimization of MXenes for tailored functional properties.

4. Conclusions

In summary, through a systematic first-principles multiscale approach using DFT calculations, CE method, and MC simulations, we are able to identify a novel asymmetrical ordered Janus-like TiMoCO₂ MXene alloy ground-state by screening through the formation energies of more than 9 million different configurations of Ti_2(1−x)Mo_2xCO₂ substitutional alloy system with consideration of all 3 possible types of O-termination. This alloy is thermodynamically, mechanically, and thermally stable with a high order–disorder phase transition temperature of ∼640 K. Importantly, TiMoCO₂ is semiconducting with a band gap of 0.60 eV. It possesses an intrinsic dipole moment as a consequence of the asymmetric structure which realigns the conduction and valence band edges located on opposite sides of the MXene, permitting photocatalytic redox water-splitting to be thermodynamically favorable with enhanced solar absorption efficiency above 10⁴–10⁵ cm⁻¹ in the visible-infrared region. As a thermoelectric material, it is found that TiMoCO₂ exhibits high room temperature n- and p-type power factors of 33.7–49.8 μW cm⁻¹ K⁻² and ∼15 μW cm⁻¹ K⁻², respectively, surpassing other related experimentally synthesized Ti–Mo based MXene alloys and are even similar to that of p-doped SnSe which is one of the best performing thermoelectric materials. All these demonstrate the asymmetrically ordered Janus-like TiMoCO₂ MXene alloy to be a promising high performance water-splitting photocatalyst and thermoelectric material, paving the way for more stable Janus-like MXenes with interesting and outstanding properties awaiting to be discovered.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This work is supported by the Agency for Science, Technology and Research (A*STAR) of Singapore (1527200024). TLT acknowledges the Advanced Manufacturing and Engineering Young Individual Research Grant (AME YIRG) of Agency for Science, Technology and Research (A*STAR) of Singapore (A1884c0016) for support in furthering the development of the cluster expansion code (TTK) used in this work. Computational resources are provided by the National Supercomputing Centre Singapore (NSCC) and A*STAR Computational Resource Centre (A*CRC).

References

1. M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331.
2. M. Naguib, N. Mochalin Vadym, W. Barsoum Michel and Y. Gogotsi, Adv. Mater., 2013, 26, 992–1005.
3. B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 16098.
4. O. Mashtalir, M. Naguib, V. N. Mochalin, Y. Dall’Agnese, M. Heon, M. W. Barsoum and Y. Gogotsi, Nat. Commun., 2013, 4, 1716.
5. Y. Gogotsi, Nat. Mater., 2015, 14, 1079.
6. J. Zhou, X. Zha, Y. Chen Fan, Q. Ye, P. Eklund, S. Du and Q. Huang, Angew. Chem., Int. Ed., 2016, 55, 5008–5013.
7. I. Persson, J. Halim, T. W. Hansen, J. B. Wagner, V. Darakchieva, J. Palisaitis, J. Rosen and P. O. Å. Persson, Adv. Funct. Mater., 2020, 1909005.
8. K. Rasool, R. P. Pandey, P. A. Rasheed, G. R. Berdiyorov and K. A. Mahmoud, in 2D Metal Carbides and Nitrides (MXenes): Structure, Properties and Applications, ed. B. Anasori and Y. Gogotsi, Springer International Publishing, Cham, 2019, pp. 417–444,  DOI:10.1007/978-3-030-19026-2_22.
9. H. Lin, Y. Chen and J. Shi, Adv. Sci., 2018, 5, 1800518.
10. Y. Sun, X. Meng, Y. Dall’Agnese, C. Dall’Agnese, S. Duan, Y. Gao, G. Chen and X.-F. Wang, Nano-Micro Lett., 2019, 11, 79.
11. Z. Guo, J. Zhou, L. Zhu and Z. Sun, J. Mater. Chem. A, 2016, 4, 11446–11452.
12. L. Cheng, X. Li, H. Zhang and Q. Xiang, J. Phys. Chem. Lett., 2019, 10, 3488–3494.
13. A. K. Singh, K. Mathew, H. L. Zhuang and R. G. Hennig, J. Phys. Chem. Lett., 2015, 6, 1087–1098.
14. X. Zhang, Z. Zhang, D. Wu, X. Zhang, X. Zhao and Z. Zhou, Small Methods, 2018, 2, 1700359.
15. M. Khazaei, M. Arai, T. Sasaki, C. Y. Chung, S. Venkataramanan Natarajan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2012, 23, 2185–2192.
16. H. Zhang, G. Yang, X. Zuo, H. Tang, Q. Yang and G. Li, J. Mater. Chem. A, 2016, 4, 12913–12920.
17. Z. M. Wong, T. L. Tan, S.-W. Yang and G. Q. Xu, ACS Appl. Mater. Interfaces, 2018, 10, 39879–39889.
18. V. K. Sangwan and M. C. Hersam, Annu. Rev. Phys. Chem., 2018, 69, 299–325.
19. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
20. H. Kim, B. Anasori, Y. Gogotsi and H. N. Alshareef, Chem. Mater., 2017, 29, 6472–6479.
21. B. Anasori, Y. Xie, M. Beidaghi, J. Lu, B. C. Hosler, L. Hultman, P. R. C. Kent, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2015, 9, 9507–9516.
22. T. L. Tan, H. M. Jin, M. B. Sullivan, B. Anasori and Y. Gogotsi, ACS Nano, 2017, 11, 4407–4418.
23. N. A. Zarkevich, T. L. Tan, L. L. Wang and D. D. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 144208.
24. G. Ceder, A. V. d. Ven, C. Marianetti and D. Morgan, Modell. Simul. Mater. Sci. Eng., 2000, 8, 311.
25. W. Chen, D. Schmidt, W. F. Schneider and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 075415.
26. V. Ozoliņš, C. Wolverton and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 6427–6443.
27. L. Cao, C. Li and T. Mueller, J. Chem. Inf. Model., 2018, 58, 2401–2413.
28. J. W. D. Connolly and A. R. Williams, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 5169–5172.
29. J. M. Sanchez, F. Ducastelle and D. Gratias, Phys. A, 1984, 128, 334–350.
30. N. A. Zarkevich and D. D. Johnson, Phys. Rev. Lett., 2004, 92, 255702.
31. A. van de Walle, Nat. Mater., 2008, 7, 455.
32. T. L. Tan, L.-L. Wang, D. D. Johnson and K. Bai, Nano Lett., 2012, 12, 4875–4880.
33. T. L. Tan, L.-L. Wang, J. Zhang, D. D. Johnson and K. Bai, ACS Catal., 2015, 5, 2376–2383.
34. N. A. Zarkevich, T. L. Tan and D. D. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104203.
35. M.-F. Ng and T. L. Tan, Nano Lett., 2013, 13, 4951–4956.
36. T. L. Tan, M.-F. Ng and G. Eda, J. Phys. Chem. C, 2016, 120, 2501–2508.
37. Z. M. Wong, H. Cheng, S.-W. Yang, T. L. Tan and G. Q. Xu, J. Phys. Chem. C, 2017, 121, 26446–26456.
38. T. L. Tan and M.-F. Ng, Phys. Chem. Chem. Phys., 2015, 17, 20391–20397.
39. T. L. Tan, L.-L. Wang, D. D. Johnson and K. Bai, J. Phys. Chem. C, 2013, 117, 22696–22704.
40. Z. M. Wong, T. L. Tan, S.-W. Yang and G. Q. Xu, J. Phys.: Condens. Matter, 2018, 30, 485402.
41. Z. M. Wong, T. L. Tan, A. J. K. Tieu, S.-W. Yang and G. Q. Xu, Chem. Mater., 2019, 31, 4124–4132.
42. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
45. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
46. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
47. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
48. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080.
49. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
50. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
51. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
52. C. Hamaguchi, in Basic Semiconductor Physics, ed. C. Hamaguchi, Springer International Publishing, Cham, 2017, pp. 125–151,  DOI:10.1007/978-3-319-66860-4_3.
53. Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104.
54. X. Wu, D. Vanderbilt and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035105.
55. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
56. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
57. X. Gonze, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 1096–1114.
58. S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562.
59. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
60. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
61. M. J. van Setten, M. Giantomassi, E. Bousquet, M. J. Verstraete, D. R. Hamann, X. Gonze and G. M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54.
62. F. Giustino, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165108.
63. F. Giustino, Rev. Mod. Phys., 2017, 89, 015003.
64. S. Poncé, E. R. Margine, C. Verdi and F. Giustino, Comput. Phys. Commun., 2016, 209, 116–133.
65. S. Poncé, E. R. Margine and F. Giustino, Phys. Rev. B, 2018, 97, 121201.
66. G. D. Mahan and J. O. Sofo, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 7436.
67. T. Deng, X. Yong, W. Shi, Z. M. Wong, G. Wu, H. Pan, J.-S. Wang and S.-W. Yang, J. Mater. Chem. A, 2020, 8, 4257–4262.
68. A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744–749.
69. J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192–8198.
70. H.-P. Komsa and A. V. Krasheninnikov, J. Phys. Chem. Lett., 2012, 3, 3652–3656.
71. J. Kang, S. Tongay, J. Li and J. Wu, J. Appl. Phys., 2013, 113, 143703.
72. J. Wang, H. Shu, T. Zhao, P. Liang, N. Wang, D. Cao and X. Chen, Phys. Chem. Chem. Phys., 2018, 20, 18571–18578.
73. M. Born and K. Huang, Dynamical theory of crystal lattices, Clarendon Press, 1954.
74. R. John and B. Merlin, Crystal Structure Theory and Applications, 2016, vol. 05, No. 03, 13.
75. X. Wei, B. Fragneaud, C. A. Marianetti and J. W. Kysar, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205407.
76. J. Zhou and R. Huang, J. Mech. Phys. Solids, 2008, 56, 1609–1623.
77. K. Liu, Q. Yan, M. Chen, W. Fan, Y. Sun, J. Suh, D. Fu, S. Lee, J. Zhou, S. Tongay, J. Ji, J. B. Neaton and J. Wu, Nano Lett., 2014, 14, 5097–5103.
78. G.-H. Lee, R. C. Cooper, S. J. An, S. Lee, A. van der Zande, N. Petrone, A. G. Hammerberg, C. Lee, B. Crawford, W. Oliver, J. W. Kysar and J. Hone, Science, 2013, 340, 1073.
79. T. Luttrell, S. Halpegamage, J. Tao, A. Kramer, E. Sutter and M. Batzill, Sci. Rep., 2014, 4, 4043.
80. A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221.
81. X. Li, Z. Li and J. Yang, Phys. Rev. Lett., 2014, 112, 018301.
82. G. Dresselhaus and M. S. Dresselhaus, Proceedings of the International School of Physics, ed. E. Fermi and J. Tauc, Academic Press, NY, 1966.
83. M. Bernardi, M. Palummo and J. C. Grossman, Nano Lett., 2013, 13, 3664–3670.
84. D. Lembke, A. Allain and A. Kis, Nanoscale, 2015, 7, 6255–6260.
85. M.-W. Lin, L. Liu, Q. Lan, X. Tan, K. S. Dhindsa, P. Zeng, V. M. Naik, M. M.-C. Cheng and Z. Zhou, J. Phys. D: Appl. Phys., 2012, 45, 345102.
86. T. Momose, A. Nakamura, M. Daniel and M. Shimomura, AIP Adv., 2018, 8, 025009.
87. S. Sarikurt, D. Çakır, M. Keçeli and C. Sevik, Nanoscale, 2018, 10, 8859–8868.
88. K. Hippalgaonkar, Y. Wang, Y. Ye, D. Y. Qiu, H. Zhu, Y. Wang, J. Moore, S. G. Louie and X. Zhang, Phys. Rev. B, 2017, 95, 115407.
89. G. E. Yakovleva, A. I. Romanenko, A. S. Berdinsky, V. A. Kuznetsov, A. Y. Ledneva, S. B. Artemkina and V. E. Fedorov, Semiconductors, 2017, 51, 725–728.
90. L.-D. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141.

---

Footnote

† Electronic supplementary information (ESI) available: Structures of the 3 different fully O-terminated MXenes; electrostatic potential profile for the Janus-like ground-state TiMoCO₂ MXene alloy; projected electronic band structures of the Janus-like ground-state TiMoCO₂, and its analogous conjectural ZrMoCO₂, HfMoCO₂, TiCrCO₂, and TiWCO₂ MXene alloys; table of structures of various TiMoCO₂ MXene alloys with different O-sites and their constituent MXenes Ti₂CO₂ and Mo₂CO₂, their relative energies with respect to the constituents obtained via density functional theory, and the Bader charges of the respective elements; table of calculated DFT and alloy formation energies of bare TiMoC MXene with respect to its constituent Ti₂C and Mo₂C MXenes; and table of band gap and the respective contributions and directional effective hole and electron masses of the valence band maximum and conduction band minimum for Janus-like ground-state TiMoCO₂, and its analogous conjectural ZrMoCO₂, HfMoCO₂, TiCrCO₂, and TiWCO₂ MXene alloys. See DOI: 10.1039/d0ma00391c

---