Microgel organocatalysts: modulation of reaction rates at liquid–liquid interfaces

Abstract

Controlling the catalytic activity via the use of smart and responsive carriers is a major challenge in research concerning supported catalysis. In homogeneous reactions, responsive polymeric carriers are often used to switch on/off reagent supply by controlled shielding of embedded catalysts. However, reactions on liquid interfaces are rare subjects of these kinds of studies. As an example of colloidal microgel-catalysts based on poly(N-isopropylacrylamide) (PNIPAM) containing covalently bound L-proline, we herein present how temperature and the effect of cononsolvency can be used as triggers to modulate reaction rates in a homogenous phase and on liquid–liquid interfaces. In particular, the aldol reaction of cyclohexanone with 4-nitrobenzaldehyde in water, methanol and water–methanol mixtures was the focus of our study. The swelling degree of the microgels evaluated by dynamic and static light scattering (DLS and SLS) was adjusted to demonstrate the effect of swelling on the rate of the aldol reaction. Combining our experimental results with computer simulations, based on dissipative particle dynamics (DPD), we could relate significant differences in reaction rates to the temperature-responsive swelling of the microgels. The simulations show that in aqueous reaction mixtures, the microgel-catalysts are adsorbed at the liquid–liquid interface between water and the hydrophobic reagents. Increasing the temperature causes the microgel-catalysts to immerse more into the reagent phase due to the temperature-responsiveness of PNIPAM. As a result, the average number of contacts between the L-proline catalyst and the reagents increases drastically resulting in a more than 5-fold increase of the catalytic rate observed in the experiments. On the contrary, the simulations of the reaction in methanol confirm that reagents form a homogeneous mixture in which the defined average number of contacts changes negligibly with the increasing temperature as PNIPAM does not possess a temperature-responsive behaviour in this solvent.

---

Introduction

Due to their fascinating properties and diverse application possibilities, aqueous microgels have become an important class of materials in the recent studies of polymer science.^1–3 In general, microgels are usually spherical, crosslinked, polymeric colloids with a size between 100 nm and 10 μm.^4,5 In appropriate solvents, such as water or methanol, microgels form stable solutions and due to their porous and soft structure the solvents can permeate into them. Microgels based on the lower critical solution temperature-responsive polymer (LCST-type) poly(N-isopropylacrylamide) (PNIPAM) undergo an entropy-driven volume phase transition by changing from a swollen to a collapsed state when their aqueous solution is heated above the volume phase transition temperature (VPTT).^4,6 For PNIPAM-based microgels the VPTT is 32 °C, and is independent of the molecular weight of the polymer or the concentration of the solution.^7,8 Beyond this type of responsiveness, PNIPAM-based microgels also show sensitivity towards the solvent composition.⁹ For instance, they are fully swollen in pure water and pure methanol whereas in a mixture with a molar fraction of x(methanol) = 0.2 the microgels de-swell to a collapsed state. This phenomenon is called cononsolvency and is based on the interplay of different molecular interactions between the polymer chains and the two solvents.^10–17

Due to their versatile properties, microgels find various applications in drug delivery, as biomaterials or in the field of catalysis.^18–20 In the last-named application, microgels enable the exploration and control of chemical reactions in compartments, opening new platforms for bio-inspired catalysts. Here, microgels have been investigated as responsive carrier colloids for catalytically active materials, namely metal nanoparticles, metallic complexes, organocatalysts and enzymes.^21–26 In particular, the most explored catalytic systems are the LCST-type microgel hydrides containing metallic nanoparticles.^21,22,27 A more recent report focuses on exploring upper critical solution temperature type microgels (UCST-type) as nanocatalyst platforms for silver nanoparticles.²³ In this work, silver nanoparticles were applied for catalysing the reduction of 4-nitrophenol whereas the temperature induced UCST-type collapse of the microgel network was used to control the velocity of this reaction. Recently, Landfester et al. reported a dual-responsive polymer photocatalyst in the form of a nanogel consisting of a crosslinked poly(N-isopropylacrylamide) nanogel, copolymerized with an organic, photocatalytically active monomer.²⁶ The nanogel undergoes a decrease in diameter with increasing temperature, which shields the photo-catalytic sites, thus decreasing its catalytic activity. In a recent study, we showed the successful incorporation of the organocatalyst L-proline into microgels based on PNIPAM.²⁸ It was demonstrated that the microgels show high activity and selectivity for catalysing the enantioselective aldol reaction of 4-nitrobenzaldehyde and cyclohexanone in water in which free L-proline is not active. Additionally, by following the kinetics of the aldol reaction, we were able to relate the reaction rates to the structure of the microgel-catalysts. In particular, it was found that the microgel-catalysts are more active in water when the L-proline sides are located in the core of the microgels. This is because the core of the microgels provides a suitable environment around the L-proline catalysts which can serve as a host for the hydrophobic reagents. It has been demonstrated that the reagents are preferentially concentrated in the core to minimize unfavourable contacts with water. These contacts are shielded by a polymer layer, formed at the microgel periphery. In contrast, for using methanol as the solvent, corona-located L-proline side groups are more favourable for the reaction rate as diffusion is the essential rate-determining factor in this case. However, in the previous study the microgels only served as passive carriers.

The purpose of the current work is to demonstrate the adaptability of the microgel-catalysts by varying their swelling degree using different triggers and performing catalytic reactions in homogeneous solutions and in heterogeneous mixtures. We will investigate the way in which the collapse of the microgels induced by temperature on the one hand and the cononsolvency on the other hand interfere with the reaction rate of the mentioned aldol reaction. In particular, we will focus on the question of whether the microgel collapse accelerates the reaction due to a more favourable reaction environment or closing the pores inhibits reagent supply and therewith decelerates the reaction. In addition, we will use computer simulations, based on dissipative particle dynamics (DPD), to relate significant differences in reaction rates to the temperature-responsive swelling of the microgels. For the heterogeneous reaction mixture, we will focus on the temperature-dependent adsorption behaviour of the microgels at the liquid–liquid interface between water and the hydrophobic reagents. Calculating the average number of contacts between the L-proline catalyst and the reagents in this mixture, we will validate our results with molecular explanations. As a reference, we will present equivalent simulations for the homogeneous reaction in methanol in which PNIPAM does not possess the temperature-responsive behaviour.

Results and discussion

In the present work, microgel-catalysts were synthesized on the basis of NIPAM and a polymerisable form of protecting-group-free L-proline. Therefore, the catalyst precursor trans-4-hydroxy-L-proline was transformed in a first step via a Williamson ether synthesis type reaction using acryloyl chloride. The yield of this reaction is 32%, which is in accordance with the literature.²⁹ The microgel-catalysts were synthesized via free radical precipitation polymerisation of NIPAM, L-proline monomer and N,N′-methylenebis(acrylamide) (BIS) as a crosslinker in aqueous solution. The polymerisation reaction displayed a good yield of 92% (see also Fig. S1, ESI†).

For further analysis and tests of the catalytic performance, the microgel-catalysts were freeze-dried using lyophilization. This method is a classical and reliable tool for water removal. However, residual moisture adsorbed onto the porous network of the microgel-catalysts is difficult to remove. Since the purpose of a part of this work is to study the influence of the water–methanol mixture on the catalytic performance of the microgel-catalysts, an accurate description of this factor is needed. For this reason, the water content of the synthesized microgel-catalysts was determined by TGA measurements of the freeze-dried samples. The loss of weight corresponds to the mass of water adsorbed on the microgel-network. The corresponding TGA curve can be found in the ESI.† The curve reveals a mass loss of 11.47% up to a temperature of 175 °C. Since any other residue from synthesis was removed via dialysis, this mass can be assigned to water. Primarily, 11.47% appears to be a significant value, which should have a tremendous effect on the catalytic performance. If the weight of the sample of one catalytic test is considered, this 11.47% responds to a mass of about 4.2 mg corresponding to 36.4 mg microgel-catalysts and 0.12 ml water–methanol mixture. As a result, the additional amount of water is about 3.5% with reference to the solvent mixture. This value is not negligible, but it is probably below the accuracy of the syringes used for adjusting the total solvent volume of the catalytic testing. Additionally, this work does not try to picture the universal mole fraction of the solvent–microgel-catalyst mixtures but rather defines the mole fractions of the solvent added to the reaction mixtures.

The number of effectively incorporated L-proline groups in the microgel-catalysts was determined using ATR-FTIR spectroscopy. In combination with a calibration method it is possible to calculate the fraction of catalytic groups in a quantitative manner.²⁸ For the microgel-catalysts used in this work a weight fraction of 10.1 wt% corresponding to a molar fraction of 6.69 mol% was determined. The corresponding FTIR spectra can be found in the ESI (see Fig. S3, ESI†).

In order to correlate the swelling properties of the microgel-catalysts with their catalytic performance, temperature-resolved dynamic light scattering (DLS) experiments were performed. Thereby, the hydrodynamic radius R_h of the microgel-catalysts in the two pure solvents, water and methanol, and in the most unfavourable mixture of 20 mol% methanol was determined under variton of the temperature (Fig. 1a). Additionally, a comparison with the temperature-dependent radii of pure PNIPAM microgels (5 mol% crosslinker) in the same solvents is presented (Fig. 1b). Here, for easier comparison, R_h was normalized to the respective value in the fully collapsed state.

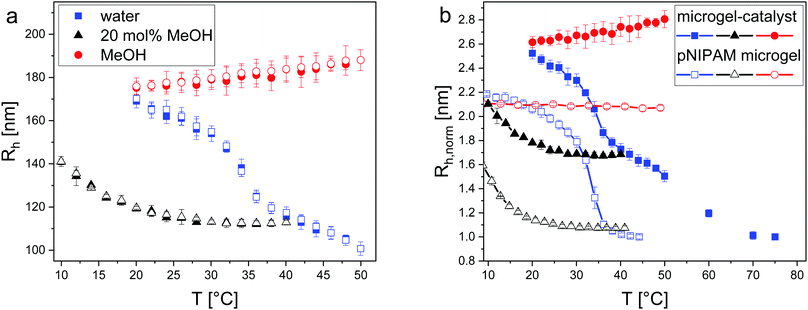Fig. 1 (a) Plot of the hydrodynamic radius R_h of microgel-catalysts in water (blue), methanol (red) and 20 mol% methanol (black) depending on the adjusted temperature. The full symbols represent the heating cycle and the open symbols the cooling cycle. At 25 °C the microgel-catalysts have a size of R_h = 167 ± 2 nm (water), R_h = 175 ± 7 nm (methanol) and R_h = 116 ± 2 nm (20 mol% methanol). For the aqueous system, the VPTT was determined at the inflection point of the curve (35.0 ± 0.5 °C). (b) Comparison of the normalized radius (normalized to R_h in water in the fully collapsed state) of the microgel-catalysts (full symbols) and a pure PNIPAM microgel (open symbols) in water (blue), methanol (red) and 20 mol% methanol (black). The data of the pure PNIPAM microgels were previously shown.¹¹

The microgel-catalysts (similar to PNIPAM microgels) show a reversible temperature-dependent phase transition in water as depicted by the symmetrical S-shaped curve. At 25 °C, the microgel-catalysts are swollen in water with a hydrodynamic radius of 167 ± 2 nm. By increasing the temperature, the microgel-catalysts start collapsing and the VPTT is reached at around 35.0 ± 0.5 °C. This value was extrapolated from the inflection point of the graph. After crossing the VPTT, the collapse proceeds further until a value of R_h = 110 ± 1 nm is obtained at 45 °C. In this mainly collapsed state, the microgel-catalysts have lost about 34% of their size compared to the value at 25 °C (compare Fig. 1). However, no plateau of the radius in water is observed up to 50 °C. The smallest size, and thus of the fully collapsed state, was measured at the synthesis temperature of 70 °C with a hydrodynamic radius of about 68 nm corresponding to a decrease in size of about 60%. This observation deviates strongly from the behaviour of pure PNIPAM microgels, where the fully collapsed size has already reached at around 45 °C.

The DLS measurements performed in methanol suggest that the microgel-catalysts do not show a distinct temperature-responsive volume phase transition in this solvent. Here, R_h = 175 ± 7 nm is slightly larger than the value in water at 25 °C. The slight increase of Rh at higher temperatures which can be identified in Fig. 1 suggests that methanol becomes a better solvent for the L-proline modified microgels with increasing temperature. In contrast, the pure PNIPAM microgels show no temperature dependence in methanol at all.

In the 20 mol% methanol–water mixture an increase in size is observed below room temperature. Additionally, the microgel-catalysts are less collapsed in the mixture than in water at high temperatures. These findings are true for both the microgel-catalysts and the pure PNIPAM microgels. However, the difference between the radius of the fully collapsed state in water at high temperature and the 20 mol% mixture is significantly higher in the case of the microgel-catalysts.

In addition to DLS measurements, the swelling behaviour was characterized using SLS (details and data are shown in the ESI† Fig. S5 and Table S1). In general, R_g exhibits comparable trends to R_h concerning the swelling state of the microgel-catalysts as described above. The ratios of R_g/R_h close to 0.78 indicate a less fuzzy and more homogeneous structure of the microgel-catalysts compared to pure PNIPAM microgels. For comparison, studies by Senff et al. documented ratios between 0.55 and 0.6 for PNIPAM microgels in the swollen state in water.³⁰

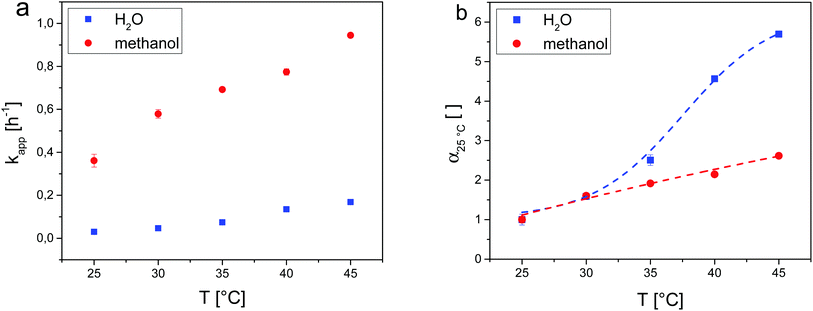
Aligning the results of DLS, the temperature-resolved catalytic activity of the microgel-catalysts was investigated in the temperature range of 25–45 °C in steps of 5 °C in water and additionally in methanol for reference. The intervals were chosen based on the accuracy of the apertures. For each temperature, the conversion of the time-resolved aldol reaction of 4-nitrobenzaldehyde and cyclohexanone was followed using ¹H-NMR spectroscopy of the raw reaction mixture. For both solvents, the apparent reaction rate constant k_app was at repeat determination (see Fig. 2a) and normalized to the corresponding values at 25 °C in the following manner:

k_app,T/k_app,25°C = α_25°C

Fig. 2 (a) Apparent reaction rate constant k_app and (b) normalized constants α_25°C of the aldol reaction catalysed by microgel-catalysts in water (blue) and methanol (red) corresponding to the adjusted temperature. The normalization was applied to show the relative change of reaction rate to the value at 25 °C and therewith the influence of the microgel collapse.

In this way the influence of the microgel collapse in water could be directly compared to the non-responsive system in methanol as both curves give the relative change of reaction rate in comparison with the value at 25 °C. The values for α_25°C were plotted in relation to the adjusted temperature (see Fig. 2b).

For both solvents, α_25°C increases upon increasing the reaction temperature. However, the course of the two curves differs significantly. For methanol, α_25°C seems to follow a linear function. It can be assumed that this acceleration of the reaction rate is mainly due to the increase of reaction temperature since methanol as the solvent does not induce a collapse of the microgel network (compare Fig. 1). For water as reaction medium, the behaviour of α_25°C is completely different. The reaction rate increases slowly up to 30 °C followed by a stronger increase above 30 °C, which flattens regardless of the temperature towards the end of the curve.

However, a distinct plateau was not observed in the investigated temperature range. These observations can be correlated with the results from DLS measurements presented above: it is known that the target aldol reaction in water requires a certain hydrophobic environment close to the catalytic active L-proline sites.^28,29 In general, a polymer network of PNIPAM microgels contains hydrophobic and hydrophilic chain segments and the temperature-induced collapse above the LCST causes changes in the local environment around the hydrophobic isopropyl domains.³¹ As a consequence of this process, water is displaced and more hydrophobic guest molecules, like the reagents of the aldol reaction, can enter the network. This effect is a good explanation for the behaviour of α_25°C in aqueous solution.

At 35 °C, the VPTT of the microgel-catalysts is reached correlated with the temperature with the strongest network collapse. On increasing the temperature further to 45 °C, α_25°C is about 5.5 times higher than at 25 °C. In between these points, α_25°C runs along the S-shaped curve mentioned above. Apparently, the collapse of the microgel-catalysts is the predominant factor in this system. Other temperature-dependent effects like reagent solvability or diffusion could not be verified. As the copolymerized L-proline derivative influences the swelling behaviour of the microgel-catalysts in water, the microgel-catalysts are not fully collapsed at 45 °C but at the synthesis temperature. This might explain why there was no hint of diffusion limitation during the catalysis at 45 °C.

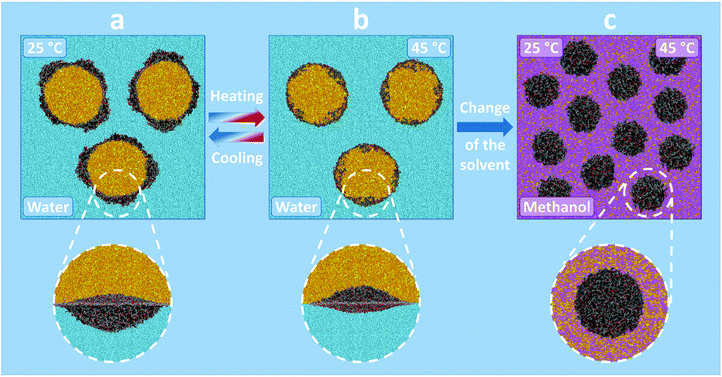
On the contrary, system (II) demonstrates substantially different behaviour. Since the reagents are miscible with methanol (Table S2 in the ESI†), a homogeneous mixture is formed, where the microgels retain their spherical shape, which is demonstrated in Fig. 4c and Fig. S5 (ESI†). The radial concentration profiles (lower row in Fig. S7, ESI†) indicate the uniform distribution of both methanol and reagents inside the microgel. However, unlike in the case of system (I), PNIPAM is not temperature-responsive in the methanol environment (the solvent always acts as a good one, Table S2 in the ESI†), and therefore the increase of the temperature does not cause the visible changes in the concentration profiles (Fig. S7a and S7b, ESI†). Thus, in this case the temperature has low influence on the probability of interaction (contacts) between the catalyst and the reagents.

To study the activitiy of the microgel-catalysts in water (I) and methanol–water mixtures (II) and to confirm the aforementioned assumptions, DPD simulations of the corresponding systems were performed at different temperatures. Fig. 3 illustrates the studied systems. Since the reagents (“oil”) are immiscible with water (Table S2 in the ESI†) and the compositions of water and “oil” are nearly symmetric, we can expect the formation of an oil–water emulsion for system (I), in which the microgels are adsorbed at the oil–water interfaces reducing the interfacial tension and providing the stability of the emulsion droplets (Fig. 3a and b).^32–34

Fig. 3 Schematic illustration of the catalytic systems studied in this work: (a and b) oil-in-water emulsion, stabilized by thermo-sensitive microgels, which are protruded into water (a) and reagent (b) phase at low and high temperatures, respectively; and (c) homogeneous mixture of reagents, methanol and microgels.

It has to be mentioned that uptake of “oil” by the microgels and the colloidal stability of the microgels can be realized either for a small fraction of “oil” in water or at a very high concentration of the microgels (in both cases all the “oil” is adsorbed). We do not consider this regime in the current paper.

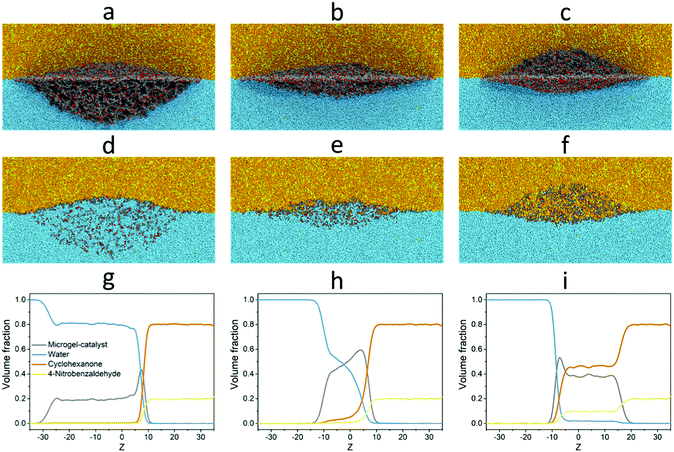
Thus, for system I we have studied the behaviour of a single microgel adsorbed at the liquid–liquid interface. Fig. 4 demonstrates the simulation snapshots of the microgel modified with L-proline groups. Different columns correspond to the different temperatures (the whole set of the snapshots is shown in Fig. S6 in the ESI†). Here, we can observe the deformation of the adsorbed microgels, which is caused by the effective shielding of unfavourable water–reagent contacts. The deformation degree is determined by the interplay between the surface energy of the liquid interface and the elastic energy of the network of the microgel.^3,32–34 Moreover, since PNIPAM is temperature-responsive in aqueous medium, the temperature also influences the overall shape of the microgel as well as the degree of immersion into water and oil. At room temperature, the microgels are mostly immersed into the water (Fig. 4a). The increase of the temperature to the value above VPTT causes the quasi-1D collapse of the microgel (Fig. 4b) which results in a more symmetric shape of the microgel at the interface. Further increase of the temperature leads to the preferential immersion of the microgel into the reagent (oil) phase. The physical reason for such behaviour is related to the change of the solvent quality of the water for the PNIPAM-proline microgel. At low temperatures, water acts as a good solvent for the microgel while the reagents act as moderately poor (or theta-) solvents (Table S2 in the ESI†). At high temperatures, water becomes a poor solvent whereas the reagents remain better solvents for the microgel. This leads to the transfer of a significant volume of the microgel from the water to “oil”. The cross-section of the microgel (Fig. 4d–f) demonstrates that the interior of the microgels remains permeable to both liquids (water and reagents) while the ratio of the liquids is different for different temperatures. This visual picture is quantified by concentration profiles (Fig. 4g–i) in the central part of the microgel plotted in the direction normal to the interface (along the z-axis).^32,34 Thus, the probability of interaction (contacts) between the catalyst and reagents grows with the increase of the temperature.

Fig. 4 Results of computer simulations of microgels adsorbed at the water–reagent interface: (a–c) side-viewed snapshots of the adsorbed microgels, (d–f) cross-section of the microgels through the centre of mass and visualization of PNIPAM (grey), L-proline (red), 4-nitrobenzaldehyde (yellow), cyclohexanone (orange) and water (blue) beads, (g–i) concentration profiles inside the microgel along the normal to the interface, z-axis, respectively. The lines of different colours correspond to the concentrations of respective types of beads. Different columns correspond to different temperatures: T = 25 °C (a, d, g), T = 35 °C (b, e, h), and T = 45 °C (c, f, i).

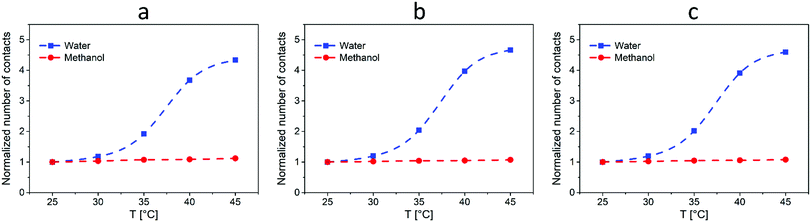
To further quantify the intensity of interactions between L-proline and both 4-nitrobenzaldehyde and cyclohexanone, we calculated the average number of contacts between the corresponding simulation beads.³² As a result, we plotted the values (normalized to the number of contacts at T = 25 °C) as a function of temperature for both systems (I) and (II) (Fig. 5). Here, it can be seen that for system (I) the number of contacts between catalyst and reagent beads grows significantly with the increase of the temperature. Surprisingly, an excellent correlation was found between the simulation results and the corresponding α_25°C plot in Fig. 2b, namely, the S-shape of the curves together with the values at different temperatures (more than two-fold increase of the number of contacts at T = 35 °C and almost 5-fold increase of the number of contacts at T = 45 °C). Therefore, the increase of probability of interactions (contacts) between the catalyst and the reagents can be considered as the driving force for the increase of the reaction rate with the temperature in system (I). In turn, the number of contacts reveals almost no changes with the temperature for the system (II), which is also in agreement with the results in Fig. 2b. Overall, such a good correlation between the experimental data and the simulations can serve as the direct proof of the conclusions made from the results presented in Fig. 2.

Fig. 5 Normalized average number of contacts between the beads of L-proline and 4-nitrobenzaldehyde (a), cyclohexanone (b), and both reagents (c) as a function of temperature. The blue curves correspond to the case of the water–reagent system while the red curves correspond to the case of the methanol–reagent system. The error bars are of the size of the points.

As stated before, PNIPAM based microgels are swollen in water and methanol, forming colloidally stable solutions. However, in certain mixtures of the two they undergo a volume phase transition resulting in a collapse of the polymeric network. In addition to the temperature sensitive behaviour, this transition is subject to influence the performance of the microgel-catalysts.

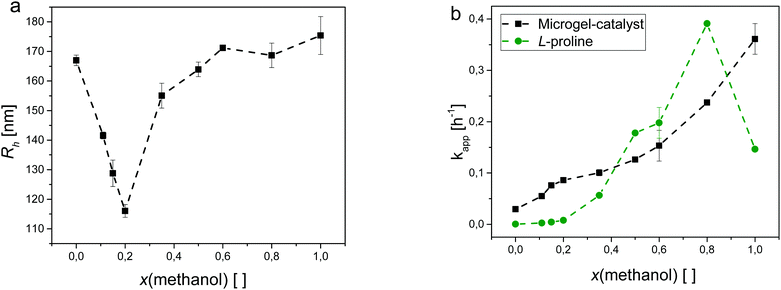
To quantify this effect, the hydrodynamic radius of the microgel-catalysts was determined in a first step performing DLS experiments under variation of the fraction of methanol (see Fig. 6a). As catalytic testing in this part was exclusively performed at 25 °C, the values for R_h were measured at this temperature.

Fig. 6 (a) Plot of the hydrodynamic radius R_h of the microgel-catalysts as a function of the methanol fraction x(methanol) at 25 °C. The cononsolvency point showing the minimal value for R_h (116 ± 2 nm) was found at x(methanol) = 0.2. (b) This is in accordance with the literature. In comparison the plots of apparent reaction rate constants k_app in relation to the methanol fraction x(methanol) of the corresponding methanol–water mixtures for microgel-catalysts (black) and L-proline reference (green) (measured at 25 °C) are shown.

The microgel-catalysts show a solvent-composition dependent swelling. At a temperature of 25 °C, they are swollen in pure water and in pure methanol. As mentioned above, their hydrodynamic radius in pure water is 167 ± 2 nm, whereas pure methanol as the solvent gives rise to an even higher value for R_h of 175 ± 7 nm. From the literature, it is known that the phase transition of PNIPAM induced by cononsolvency is more continuous than the temperature induced phase transition in pure water.¹⁰ Here, the minimal value of R_h can be found at x(methanol) = 0.2. At this solvent composition, the microgel-catalysts are in their collapsed state displaying a hydrodynamic radius of 116 ± 2 nm. This value is slightly higher than the one at 45 °C for the temperature-induced phase transition. Additionally surprising is that the incorporation of the catalyst as a co-monomer does not seem to affect the position of this minimum as the literature shows the same result for pure PNIPAM microgels.¹⁰ In contrast, for temperature-induced phase transitions the VPTT depends on the hydrophily of incorporated co-monomers.^31,35

In the region between the minimal and the maximal values of R_h, the microgel-catalysts are in a partially collapsed state. However, starting from the minimum, this partial collapse is not symmetrical. This is due to the fact that the collapse of the network is determined by competitive molecular interactions. In aqueous solution predominant H-bonds between the carbonyl groups of NIPAM units and water molecules are destroyed when the share of methanol increases within the solvent mixture. The resulting destabilization of the polymer solution can neither be compensated for by the formation of H-bonds between the carbonyl group and methanol nor by the solvation of the isopropyl group. As a consequence, a reduction of the total coverage of the chains by solvent molecules and collapse of the polymer network occur.^10,12,17,36 Additionally, recent literature states a preferential adsorption of methanol molecules on PNIPAM chains. This results in an enriched methanol fraction within the polymer network in solvent mixtures causing the cononsolvency-induced collapse (15–30 mol% methanol).³⁷

From the DLS results, suitable water–methanol mixtures were identified for catalytic testing of the microgel-catalysts. For those mixtures, the apparent reaction rate constant k_app was detected in the repeat determination. The values for k_app were plotted in relation to the methanol fraction x(methanol) (see Fig. 6b). Complementary, k_app values for unbound L-proline are given as well. From the chosen designation, a high value for k_app correlates with a fast and a small k_app with a slow rate of reaction, respectively.

The plot of k_app shows a consistent picture for both catalytic systems: for free L-proline as well as for the microgel-catalysts a higher methanol fraction results in a higher rate of reaction.

Starting from pure water, k_app of free L-proline increases slowly until x(methanol) = 0.2. From this point on it increases rapidly reaching its maximum at a methanol fraction of 0.8. However, going to pure methanol, k_app decreases again by about 60% in comparison to the value at x(methanol) = 0.8. An explanation for this observation lies in the mechanism of the aldol reaction. A series of studies showed that water plays an ambivalent role in the enamine type reaction mechanism.^38–41 On the one hand, the intrinsic kinetic effect of water within the catalytic cycle is a suppression of the reaction rate as the presence of water suppresses the formation of key intermediates within the cycle. On the other hand, reversibly and irreversibly formed spectator species, such as oxazolidinones and oxapyrrolizidines, are suppressed as well, resulting in an acceleration of the reaction. Thus, the net effect on the observed productivity of the reaction will depend on the balance between these two effects. It is interesting to note that for the microgel-catalysts this effect does not seem to matter, as with the increasing fraction of methanol k_app also increases steadily. Additionally, here the route of k_app follows a different trend in comparison to the unbound L-proline. Starting from pure water again, k_app increases strongly up to a methanol fraction of 0.2. At this point the development of k_app changes its growth to a steady increase similar to the development of k_app for free L-proline. The route of k_app is probably the result of a combination of multiple overlapping effects. It is known that the reaction in methanol is faster than in water due to the better solubility of the reagents in the solvent media. Thus, the aforementioned enrichment of methanol in the collapsed polymeric network is favourable for the aldol reaction. For this reason, k_app increases with increasing methanol fraction. A counterpart is formed by the swelling and collapsing of the microgel network. Going from pure water to x(methanol) = 0.2 the microgels collapse, creating a more hydrophobic environment in their core where the catalyst sites are located. As mentioned above, this environment enables the aldol reaction to take place more easily in this region where the solvent composition is still mainly water-based. As a result, the rate of reaction increases intensely.

Crossing the methanol fraction of x(methanol) = 0.2 the microgels swell again increasing the hydrophily of the network at the same time. However, increasing the share of methanol in the solvent composition also decreases the need for a hydrophobic environment because of a better solvability of the reagents. Here, the diffusion of the reagents is the dominant factor.

Experimental

Materials

N-Isopropylacrylamide (NIPAM, 98%; Sigma-Aldrich) was purified and destabilized by recrystallization in n-hexane. Crosslinker N,N′-methylenebisacrylamide (BIS, 99%; Sigma-Aldrich) and initiator 2,2′-azobis(2-methylpropionamidine) dihydrochloride (AMPA, 97%, Sigma-Aldrich) were used as received without further purification. A polymerisable form of the L-proline organocatalyst was prepared according to the literature.²⁹ For the synthesis procedure trifluoroacetic acid (CF₃CO₂H, 99%, Alfa Aesar), trans-4-hydroxy-L-proline (99+%, Alfa Aesar), trifluoromethanesulfonic acid (CF₃SO₃H, 98+%, Alfa Aesar) and acryloyl chloride (97+%, Sigma-Aldrich) were utilized. Reagents for catalysis were 4-nitrobenzaldehyde (99%, Alfa Aesar) and cyclohexanone (ACS, 99+%, Alfa Aesar). The corresponding solvents were water (LiChrosolv®, Merck) and anhydrous methanol (max. 0.002% water, VWR Chemicals, stored under argon on the molecular sieve A3). The solvent mixtures of water and methanol were prepared prior to catalytic testing and stored in centrifuge tubes. For the determination of reaction conversion, the analysis using ¹H-NMR spectroscopy was executed in deuterated chloroform (CDCl₃, 99.8%, deutero). For reference values of the molecular catalysis, L-proline (99%, Alfa Aesar) was used as the catalyst.

Microgel-catalyst synthesis

The L-proline-modified NIPAM microgels used as microgel-catalysts were synthesized in a free radical precipitation polymerisation according to a previous report (see also Fig. S1, ESI†).²⁸ In a double-wall glass reactor equipped with a glass-stirrer, a solution of NIPAM (4.0738 g, 90 mol%), the polymerisable form of L-proline (0.6680 g, 10 mol%) and BIS (0.1232 g) dissolved in 399 ml of distilled water was purged with argon for 20 min while stirring (400 rpm) and heating up to 70 °C. The reaction was started by injecting AMPA (0.1084 g), dissolved in 2 ml distilled water, purged with argon and run for 1.5 h under argon atmosphere. Purification of the microgel ensued by dialysis (regenerated cellulose tube MWCO 12 000–14 000 Da) against distilled water and freeze-drying. For uniform adjustment of the water content within the microgel-catalysts to atmospheric humidity, the dried microgels were exposed to the laboratory air for two days.

Thermogravimetric analysis (TGA)

Determination of the water content in the microgel-catalysts was implemented using thermogravimetric analysis. The measurements were performed on a NETZSCH TG 209 C using the controlling device NETZSCH TASC 414/4. About 10 mg of dried microgel was placed into an aluminum oxide crucible. For each measurement, a temperature program from 20 to 250 °C was executed with a linear heating rate of 10 °C min⁻¹. The final temperature of 250 °C was maintained for 10 min.

Attenuated total reflection Fourier-transform infrared spectroscopy (ATR-FTIR-spectroscopy)

For the determination of the actual catalyst content, freeze-dried microgel-catalysts were measured on a FT-IR Nexus from Thermo Nicolett using an ATR-unit SMART SPLIPEA (spectral resolution 4.4 cm⁻¹, Si crystal) from Thermo Electron Corporation in combination with calibration.²⁸

Nuclear magnetic resonance spectroscopy (NMR spectroscopy)

The ¹H-NMR spectroscopy of freeze dried microgel-catalysts was carried out in D₂O using a Bruker Avance 400 High-Resolution Liquid-State NMR. The spectrum was used for qualitative analysis and can be found in Fig. S4 of the ESI.†

Dynamic light scattering (DLS)

The microgel sizes in various solvents were measured using dynamic light scattering experiments. For performing the measurements an ALV setup connected to a goniometer equipped with a HeNe laser (λ = 633 nm) was used. The temperature of the index-match-bath filled with toluene was controlled by a programmable thermostat (Julabo F32). Highly diluted samples of the freeze-dried microgel-catalysts were investigated to avoid multiple scattering. The solutions were filtered using cellulose acetate (CA) filters (Minisart®, pore size 0.8 μm). For temperature-resolved measurements in water and methanol the value of the temperature was adjusted between 20 and 50 °C in steps of 2 °C. In the case of the sample in 20 mol% methanol the temperature was varied between 10 and 40 °C. According to the literature scattering angles between 40° and 110° in steps of 10° were evaluated for each temperature.⁴² Additionally, individual q-dependent measurements were performed at 25 °C in all solvents and in water at 60, 70 and 75 °C. Here, the scattering angle was varied in steps of 5°. For measurements in various water–methanol mixtures, solely q-dependent measurements at 25 °C between 40° and 110° in steps of 5° were performed. The corresponding values of refractive indices and viscosities of the water–methanol mixtures were taken from the literature (Table 1).^43,44 The average diffusion coefficient was determined from the second order cumulant. The Stokes–Einstein equation was applied to determine the corresponding hydrodynamic radius R_h. Samples were prepared several times. The error bars were then obtained by averaging over several q-dependent measurements and the deviation within the results of the q-dependence.

Table 1 Refractive indices and viscosities of the binary water–methanol mixtures used for DLS measurements.^43,44

x(methanol) [—]	Refractive index [—]	Viscosity [mP]
0.11	1.3365	13.45
0.15	1.3375	14.40
0.20	1.3388	15.50
0.35	1.3396	15.49
0.50	1.3389	13.30
0.60	1.3380	10.69
0.80	1.3334	8.30

---

Static light scattering (SLS)

Highly diluted samples of the microgel-catalysts were investigated to prevent multiple scattering and the influence of the structure factor. After redispersion, all samples were filtered with CA filters (Minisart®, pore size 0.8 μm). All experiments were performed on a closed goniometer from SLS-Systemtechnik GmbH with two laser wavelengths of 407 and 640 nm. In total, a q-range between 0.003 nm⁻¹ and 0.04 nm⁻¹ was covered. The temperature of the toluene bath was controlled via a thermostat (Julabo CF40). Before each measurement, the temperature was equilibrated for at least 10 min. The scattering intensity was corrected by subtracting the respective solvent scattering. Due to an increase in the scattering intensity of the solvent background at low q, q-values below 0.0056 nm⁻¹ were excluded for the evaluation of the radius of gyration. The radius of gyration, R_g, was determined from the Guinier plot at small q-values for the microgel-catalysts in water (25, 45 °C), methanol (25 °C) and 20 mol% methanol (10, 25 °C).

Catalytic testing

Conversion analysis of the reactions catalysed by microgel-catalysts or L-proline, respectively, was executed in glass tubes equipped with stirring magnets and sealed with rubber plugs. For each run of the reaction with microgel-catalysts, 0.0302 g (0.2 mmol, 1 equiv.) 4-nitrobenzaldehyde and 36.4 mg microgel-catalyst (0.02 mmol L-proline-groups, 0.1 equiv.) were placed in a glass tube and dissolved in 0.12 ml solvent-mixture. The amount of microgel-catalyst was calculated from FTIR-analysis. To start the reaction, 0.103 ml (1.0 mmol, 5 equiv.) cyclohexanone was added. For the reference measurements with L-proline, the amounts of reagents were adjusted to 0.1511 g (1.0 mmol, 1 equiv.) 4-nitrobenzaldehyde, 11.6 mg L-proline (0.1 mmol, 0.1 equiv.), 0.60 ml solvent-mixture and 0.515 ml (5.0 mmol, 5 equiv.) cyclohexanone. With variation of the reaction time, all reaction runs were processed at room temperature (25 °C). After each run the reaction was terminated by separation of the catalysts, performing extraction with ethyl acetate and brine followed by drying of the organic phase with magnesium sulfate. After removal of the solvent, the conversion of the reaction run was determined using ¹H-NMR spectroscopy of the raw reaction mixture dissolved in CDCl₃. For this a Bruker AV III 400 MHz spectrometer was used.

Computer simulations

Dissipative particle dynamics (DPD) simulations were performed to study the microgels in water–reagent and methanol–reagent environments.^45,46 Within the standard DPD framework, all polymer segments and solvent molecules are represented in terms of spherical beads of equal mass m, and each bead usually represents a group of atoms. The interactions between the beads are mainly determined by a conservative force, F_ij, which is responsible for the repulsion between them via a soft potential characterized by the parameters a_ij: the bigger the value of a_ij, the stronger the repulsion between the ith and the jth beads.⁴⁵F_ij acts only within a certain cut-off radius, r_c, which serves as the characteristic length scale unit.⁴⁵ By setting the standard value of the number density as 3 (in dimensionless units), the interaction parameters a_ij (in units of k_BT/r_c) can be mapped onto the Flory–Huggins (FH) parameters χ_ij using the linear relation a_ij = a_ii + 3.27χ_ij, where a_ii = 25 for any two beads of the same type. A more detailed description can be found in the literature.⁴⁶

The implementation of the DPD approach lies in the explicit representation of all modelling species. Our systems contain the beads of the following types: P, L, N, C, W and M. The first two types correspond to PNIPAM and L-proline; the second pair corresponds to 4-nitrobenzaldehyde and cyclohexanone; and the last pair corresponds to water and methanol, respectively. The interactions between the beads were estimated through the FH parameters χ_ij. While most of the interaction parameters were estimated using the Hansen solubility parameter⁴⁷ with chosen length scale r_c = 0.81 nm (see the details²⁸), the water–PNIPAM interactions at different temperatures were determined using the approach proposed by Yong et al.⁴⁸ Thus, the value of a_WP ranged from a_WP = 25.6 at T = 25 °C to a_WP = 28.7 at T = 45 °C, which corresponds to the transition from the good to the poor solvent conditions for the microgel with the continuous change of χ_WP from 0.18 to 1.13. Finally, the L-proline–water and PNIPAM–methanol interaction parameters were fixed as a_LW = a_PM = 25 which reflects the facts that the catalyst is highly soluble in water and that PNIPAM swells a bit more in methanol than in water at the same temperature. The total set of the interaction parameters at T = 25 °C can be found in Table S2 in the ESI.†

The microgel model was constructed from an ideal diamond-like network as reported in our previous publications.^29,30,49 The resulting microgel network has a total number of the beads of type P ∼ 100000 (including both sub-chains and dangling chains) with the subchain length equal to N_sub = 10 beads. To obtain the microgel-catalyst model, the beads of type L were uniformly distributed throughout the network and randomly grafted onto the subchain beads. The fraction of the L beads was 10% with respect to the P beads. While this value is similar to that of L-proline monomers used in the synthesis (10 mol%, or ∼13% by mass), the amount of cross-links in the model (∼4.7%) was slightly higher than the amount of BIS used in this synthesis (2.5% mol, or ∼2.7% by mass). This was done in order to avoid a strong flattening of microgels at the liquid interface³³ and provide better correlation with the shape of a real microgel whose size (mass) exceeds the size of the model microgel in computer simulations.

The behaviour of the microgels in a water–reagent mixture was modelled using an orthogonal simulation box with imposed periodic boundary conditions and dimensions of L_x × L_y × L_z = 140r_c × 140r_c × 70r_c. In turn, the behaviour of the microgels in a methanol–reagent mixture was modelled in a cubic box with dimensions of L_x × L_y × L_z = 110r_c × 110r_c × 110r_c. The fraction of the reagent beads in both cases was 50% of all the liquid beads while the proportion between C and N beads was taken as 4 : 1 similar to that in the experimental conditions. In each case the total number of the beads was about 4 million. The simulations were carried out at different temperatures (different sets of the interaction parameters a_ij) from T = 25 °C to T = 45 °C with the temperature step of 5 °C using the open source software LAMMPS⁴⁹ with an integration time step of Δt = 0.03τ. Initially, the systems were equilibrated over 4 × 10⁶ steps, and then the statistics were gathered during the subsequent 2 × 10⁶ steps by taking snapshots of each 25 × 10³ steps.

Conclusions

Responsive microgel-catalysts based on PNIPAM with the covalently bound organocatalyst L-proline can be used for catalysing the enantioselective aldol reaction of 4-nitrobenzaldehyde and cyclohexanone. We demonstrated that the activity of the catalysts can be modulated by the variation of the swelling degree of the microgel-network and localization of microgels in the reaction mixture. In this work, the modulation of the swelling degree of the microgels was induced by temperature in water and by the principles of cononsolvency in mixtures of water and methanol.

For the temperature induced switching of the network, we showed a change of reaction rate correlated with the swelling degree of the microgel-catalysts in water. As the microgel-network provides a suitable environment around the L-proline catalysts, it can serve as a host for the hydrophobic reagents. As collapsing of the microgel-catalysts is driven by enhanced hydrophobicity of the network, an acceleration of the aldol reaction could be observed. The detailed mechanism behind this phenomenon is demonstrated on the molecular level with computer simulations based on dissipative particle dynamics (DPD). We demonstrated that in the heterogeneous reaction mixture, the microgels adsorb at the liquid–liquid interface between water and the hydrophobic reagents (depicted here as the oil phase). Further temperature increase forces the microgels to immerse more into the hydrophobic reagent phase due to the temperature-responsiveness of PNIPAM and consequently increasing the number of contacts between the L-proline catalyst and the reagents. Due to this, the catalytic reaction rate increases to about five times its initial value, as shown in the experiments.

By picturing comparative measurements in methanol in which the microgels do not show temperature-induced switching, the influence of the increase of temperature could be considered as being negligible. Additionally, the computer simulations confirm that the reagents form a homogeneous mixture in which the defined average number of contacts changes negligibly with the increasing temperature.

In the case of cononsolvency-induced switching, overlapping effects could be identified. Increasing the methanol fraction of the water–methanol mixtures up to x(methanol) = 0.2, at which the microgels are in collapsed state, resulted in a higher reaction rate. However, as methanol is a better solvent for the aldol reaction than water, increasing the share of methanol in general leads to a faster reaction. This effect is supported, as in the cononsolvency region the microgel-catalysts create a methanol enriched solvent fraction in their polymeric network, which is favourable for the aldol reaction, especially in mainly water-based media.

In summary, our experimental data demonstrate that microgel-catalysts are unique adaptive and switchable catalytic systems which are able to modulate the reaction rates and operate in homogeneous solutions and hetero-phased systems (emulsions). This behaviour is unique and opens new possibilities for the development of sustainable and highly efficient catalysts based on stimuli-responsive microgels.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Sonderforschungsbereich SFB 985 “Functional Microgels and Microgel Systems” of the Deutsche Forschungsgemeinschaft, Volkswagen Foundation, the Government of the Russian Federation within Act 211, Contract No. 02.A03.21.0011, and the Ministry of Science and Higher Education of the Russian Federation, Grant No. 13.1902.21.0011, for financial support. The authors gratefully acknowledge the computing time granted by the John von Neumann Institute for Computing (NIC) provided on the supercomputer JURECA at the Jülich Supercomputing Centre (JSC) and acknowledge the Moscow State University Supercomputer Center for providing the computational resources.⁵⁰

References

1. F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140.
2. A. J. D. Krüger, J. Köhler, S. Cichosz, J. C. Rose, D. B. Gehlen, T. Haraszti, M. Möller and L. De Laporte, Chem. Commun., 2018, 54, 6943–6949.
3. M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Langmuir, 2019, 35, 6231–6255.
4. A. Pich and W. Richtering, Chemical Design of Responsive Microgels, Springer, Berlin, 2011, vol. 234.
5. W. O. Baker, Ind. Eng. Chem., 1949, 41, 511–520.
6. F. Natalia, G. Stoychev, N. Puretskiy, I. Leonid and V. Dmitry, Eur. Polym. J., 2015, 68, 650–656.
7. H. G. Schild, Prog. Polym. Sci., 1992, 17, 163–249.
8. J. Seuring and S. Agarwal, ACS Macro Lett., 2013, 2, 597–600.
9. H. G. Schild, M. Muthukumar and D. A. Tirrell, Macromolecules, 1991, 24, 948–952.
10. C. Scherzinger, P. Lindner, M. Keerl and W. Richtering, Macromolecules, 2010, 43, 6829–6833.
11. H. Kojima, F. Tanaka, C. Scherzinger and W. Richtering, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 1100–1111.
12. C. Scherzinger, A. Schwarz, A. Bardow, K. Leonhard and W. Richtering, Curr. Opin. Colloid Interface Sci., 2014, 19, 84–94.
13. C. H. Hofmann, F. A. Plamper, C. Scherzinger, S. Hietala and W. Richtering, Macromolecules, 2013, 46, 523–532.
14. F. M. Winnik, M. F. Ottaviani, S. H. Bossmann, M. Garcia-Garibay and N. J. Turro, Macromolecules, 1992, 25, 6007–6017.
15. F. M. Winnik, H. Ringsdorf and J. Venzmer, Macromolecules, 1990, 23, 2415–2416.
16. N. F. A. Van Der Vegt and D. Nayar, J. Phys. Chem. B, 2017, 121, 9986–9998.
17. C. Dalgicdir, F. Rodríguez-Ropero and N. F. A. Van Der Vegt, J. Phys. Chem. B, 2017, 121, 7741–7748.
18. A. Melle, A. Balaceanu, M. Kather, Y. Wu, E. Gau, W. Sun, X. Huang, X. Shi, M. Karperien and A. Pich, J. Mater. Chem. B, 2016, 4, 5127–5137.
19. S. Engel, H. Höck, M. Bocola, H. Keul, U. Schwaneberg and M. Möller, Polymers, 2016, 8, 1–16.
20. R. Borrmann, V. Palchyk, A. Pich and M. Rueping, ACS Catal., 2018, 8, 7991–7996.
21. T. Brändel, V. Sabadasch, Y. Hannappel and T. Hellweg, ACS Omega, 2019, 4, 4636–4649.
22. Y. Lu, S. Proch, M. Schrinner, M. Drechsler, R. Kempe and M. Ballauff, J. Mater. Chem., 2009, 19, 3955–3961.
23. D. Yang, M. Viitasuo, F. Pooch, H. Tenhu and S. Hietala, Polym. Chem., 2018, 9, 517–524.
24. T. Terashima, M. Ouchi, T. Ando and M. Sawamoto, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 1061–1069.
25. B. Sharma, J. B. Pickens, S. Striegler and J. D. Barnett, ACS Catal., 2018, 8, 8788–8795.
26. C. T. J. Ferguson, N. Huber, K. Landfester and K. A. I. Zhang, Angew. Chem., Int. Ed., 2019, 10677–10681.
27. Y. Mei, Y. Lu, F. Polzer, M. Ballauff and M. Drechsler, Chem. Mater., 2007, 19, 1062–1069.
28. D. Kleinschmidt, M. Sofia Fernandes, M. Mork, A. Astrid Meyer, J. Krischel, M. V. Anakhov, R. A. Gumerov, I. I. Potemkin, M. Rueping and A. Pich, J. Colloid Interface Sci., 2019, 559, 76–87.
29. T. E. Kristensen, K. Vestli, K. A. Fredriksen, F. K. Hansen and T. Hansen, Org. Lett., 2009, 11, 2968–2971.
30. H. Senff and W. Richtering, Colloid Polym. Sci., 2000, 278, 830–840.
31. A. Burmistrova, M. Richter, M. Eisele, C. Üzüm and R. von Klitzing, Polymers, 2011, 3, 1575–1590.
32. R. A. Gumerov, S. A. Filippov, W. Richtering, A. Pich and I. I. Potemkin, Soft Matter, 2019, 15, 3978–3986.
33. K. Geisel, A. A. Rudov, I. I. Potemkin and W. Richtering, Langmuir, 2015, 31, 13145–13154.
34. A. M. Rumyantsev, R. A. Gumerov and I. I. Potemkin, Soft Matter, 2016, 12, 6799–6811.
35. M. Rey, X. Hou, J. S. J. Tang and N. Vogel, Soft Matter, 2017, 13, 8717–8727.
36. F. Tanaka, T. Koga and F. M. Winnik, Phys. Rev. Lett., 2008, 101, 1–4.
37. K. Nothdurft, D. H. Müller, T. Brands, A. Bardow and W. Richtering, Phys. Chem. Chem. Phys., 2019, 21, 22811–22818.
38. N. Zotova, A. Franzke, A. Armstrong and D. G. Blackmond, J. Am. Chem. Soc., 2007, 129, 15100–15101.
39. P. M. Pihko, K. M. Laurikainen, A. Usano, A. I. Nyberg and J. A. Kaavi, Tetrahedron, 2006, 62, 317–328.
40. B. List, R. A. Lerner and C. F. Barbas, J. Am. Chem. Soc., 2000, 122, 2395–2396.
41. D. G. Blackmond, A. Armstrong, V. Coombe and A. Wells, Angew. Chem., Int. Ed., 2007, 46, 3798–3800.
42. P. Štěpánek and R. M. Johnsen, Collect. Czechoslov. Chem. Commun., 1995, 60, 1941–1949.
43. C. Wohlfarth, Optical Constants, Refractive Indices of Pure Liquids and Binary Liquid Mixtures (Supplement to III/38), Springer, Berlin, 2008, p. 570.
44. S. Z. Mikhail and W. R. Kimel, J. Chem. Eng. Data, 1961, 6, 533–537.
45. P. Espanol and P. Warren, Europhys. Lett., 1995, 30, 191–196.
46. R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435.
47. C. M. Hansen, Hansen Solubility Parameters: A User's Handbook, CRC Press, Boca Raton, 2nd edn, 2007.
48. X. Yong, O. Kuksenok, K. Matyjaszewski and A. C. Balazs, Nano Lett., 2013, 13, 6269–6274.
49. LAMMPS Molecular Dynamics Simulator, http://lammps.sandia.gov/.
50. V. V. Voevodin, A. S. Antonov, D. A. Nikitenko, P. A. Shvets, S. I. Sobolev, I. Y. Sidorov, V. V. Stefanov, K. S. Voevodin and S. A. Zhumatiy, Supercomput. Front. Innov., 2019, 6, 4–11.

---

Footnote

† Electronic supplementary information (ESI) available: Primary data of thermogravimetric analysis, ATR-FTIR-spectroscopy and static light scattering; details on dissipative particle dynamics simulations. See DOI: 10.1039/d0ma00407c

---