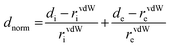A new antiferromagnetic Dy₆ oxido-material as a multifunctional aqueous phase sensor for picric acid as well as Fe³⁺ ions

Abstract

Owing to the continuous significance of high nuclearity clusters as sensory materials, an attempt is made to develop a new octahedron like Dy₆ cluster as a promising agent to detect picric acid (PA) and Fe³⁺ in the aqueous phase. A novel oxido-metal (OM)-based inorganic compound was synthesized using a green approach. Single crystal X-ray data ascertained the bonding modes and geometry composition of the cluster [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆](NO₃)₂(H₂O)₂ (1) containing a distorted octahedral oxido ion (O²⁻) at the center of the hexanuclear cage. The complex was further characterized by spectral and magnetic studies. The variable temperature magnetic susceptibility data indicate an antiferromagnetic interaction existing between Dy^III⋯Dy^III ions with Curie constant 79.55 cm³ K mol⁻¹ and Weiss constant −7.65 K. The cluster displayed intermolecular O–H⋯O and O–N⋯O interactions forming a supramolecular framework. These interactions have been verified by Hirshfeld surface analyses. The Ln discrete material is disclosed as the first aqueous phase dual sensor for picric acid (PA) and Fe³⁺. The complex shows highly sensitive, discriminative and selective sensing behavior for the said species. The sensing mechanism is investigated by spectral titration, time decay and DFT (B3LYP/def2-SVP) studies. The detection limit has been discovered for the present OM towards the sensing of PA and Fe³⁺ ions to be ∼0.03 and ∼0.09 ppb, respectively, and therefore this becomes the first cage as a dual-sensor for an explosive and a metal ion.

---

1. Introduction

High nuclearity metal-oxido and -hydroxido complexes are of great interest not only because of their promising applications as advanced materials (e.g. magnets, optical materials and catalysts¹) but also due to their potential biological applications. However, generally applicable synthetic procedures towards defined lanthanide oxido/hydroxido cluster compounds are limited. Simple hydrolysis of lanthanide ions is commonly believed to be of limited synthetic quality because it leads to unpredictable, serendipitous, and ill-defined lanthanide hydroxides and oxido/hydroxidos,² as a result of the inherent properties of the lanthanide cations. The high charge and the polarizing power result in an utmost tendency to readily hydrolyse in aqueous solutions. Additionally, trivalent rare-earth ions, being large cations, show variable coordination numbers and geometries with small energy differences. Thus, it is generally difficult to control the oligomerization of rare-earth centres.³ The most successful synthetic route to lanthanide hydroxide clusters is the ligand-controlled hydrolytic approach.⁴ In such a method, an ancillary ligand pre-occupies part of the coordination sphere of a lanthanide ion, leaving only a limited number of sites for hydroxyl coordination. The hydroxyl group, being unsaturated both coordinatively and electrically, has a proclivity to bridge one or more lanthanide ions, leading ultimately to the assembly of finite-size and structurally well-defined lanthanide clusters.^4,5 Ln oxido-clusters, though rare, are very promising species due to their versatile applications as inexpensive and green photocatalysts for eliminating organic pollutants from water,^6,7 and in optical, electronic, and magnetic materials.⁸ Currently, organic dyes and metal cations (like Fe³⁺) have been given marvellous attention for their crucial effects on human health and the environment.^9–20

With ever-increasing worry for public health and water quality, there is now a much greater demand for the detection of pollutants in water.

Moreover, nitroaromatic compounds (NACs) also constitute an important class of organic pollutants. The constituents used in most industrial explosives are based on nitroaromatics, nitroaliphatics, and organic peroxide compounds, such as 2,4,6-trinitrotoluene (TNT), 3-nitrophenol (MNP), 2,4-dinitrotoluene (2,4-DNT), 2,4,6-trinitrophenol (TNP) or picric acid (PA), 1,3,5-trinitro-1,3,5-triazacyclohexane (RDX), 4-nitrophenol (PNP), 2,3-dimethyl-2,3-dinitrobutane (DMNB), nitrobenzene and nitromethane (NM).^24,25 Amongst these nitro complexes, TNT or picric acid (PA), with remarkable explosive power (7350 m s⁻¹), is generally used in matches, fireworks, glass, dyes, and the leather industry.²⁶ TNT disengages into the environment during commercial production and use, leading to the adulteration of soil and aquatic systems.²⁷ Not only organic substituents but also inorganic ones cause the adulteration of soil or aquatic systems through mining, ore processing, etc. Many metal ions, such as Cu²⁺ and Fe³⁺ ions, play crucial roles in several metabolic processes and have extensive applications in industry.^16,17 Typically, Fe³⁺ ions play a vital role in plenty of biochemical processes at the cellular level, such as oxygen storage and transport, and electron transfer processes in DNA/RNA synthesis.¹⁸ But excessive Fe³⁺ in a living cell does harm to nucleic acids and proteins through catalysing the production of reactive oxygen species.¹⁹ Fe³⁺ was diagnosed as one of the main pathogenetic factors in Alzheimer's disease.¹⁹ Therefore, it is urgent to develop highly efficient methods for quick, reliable and robust detection of NACs and Fe³⁺ ions for human health and environmental concerns. Thus, the rapid, selective and sensitive detection of organic molecules along with Fe³⁺ ions present in soil and in ground water is very significant for human life, tracing buried explosives and environmental monitoring of surrounding industrial areas. The rapid and precise detection of explosives could also be achieved through their fluorescent probe properties as it become a major concern in the view of the hurriedly growing use of explosives in international terrorist attacks,^22–24 and for security operations, environmental protection, mine field analysis and forensic research.²⁸ However, selective and sensitive detection of TNT in the presence of other nitro compounds in the aqueous phase is a challenge due to their strong electron affinities, leading to false responses.²⁹ Therefore, the development of portable, reliable, and inexpensive methods/technologies for the detection of nitroaromatics and metal ion pollutants simultaneously has been a matter of great concern to researchers.

Keeping the diverse applications of Ln-based clusters in mind, we have synthesized and characterized a low cost, easy to prepare, simple Dy₆ oxido-cluster having an octahedron shape. This oxido-metal (OM) cluster has been explored as a luminescent dual-sensor for PA and Fe³⁺ for the first time in the category of discrete cages.

2. Experimental

2.1 Materials and methods

All reagents of analytical grade were obtained from commercial sources and used without further purification. Dy(NO₃)₃·5H₂O, 3-amino-1-propanol (ampH), triethylamine (NEt₃), all the nitroaromatic compounds, and metal salts were obtained from the Sigma-Aldrich Chemical Co. India.

Caution! Picric acid is highly explosive and should be handled carefully and in small amounts.

2.2 Physical methods

The FTIR spectra of the compounds were recorded within the range 4000–400 cm⁻¹ using KBr pellets on a PerkinElmer Model spectrum GX spectrophotometer. Melting points were determined by the open capillary method and were uncorrected. The electronic spectrum of 10⁻³ M solution in H₂O was recorded using a PerkinElmer λ-45 UV visible spectrophotometer with cuvettes of 1 cm path length. Fluorescence measurements were made on a Hitachi F-2700 spectrophotometer. Solid state fluorescence spectra were recorded on a Jobin Yvon Horiba Fluorolog-3 spectrofluorimeter at room temperature. PXRD patterns have been recorded using a Miniflex II X-ray diffractometer with Cu-Kα radiation. Time-resolved fluorescence spectra were measured using a time-resolved single photon counting setup on an FL920 spectrometer (Edinburgh Instruments, UK). The instrument response function (IRF) was obtained using LudoxTM suspension. The emission decay data were analysed using FAST software available freely online. Thermal gravimetric analysis (TGA) data were recorded from room temperature up to 700 °C at a heating rate of 20 °C min⁻¹. The data were obtained using a Shimadzu TGA-50H instrument. X-ray photoelectron spectra (XPS) were obtained on a PHI 5000 Versa Probe II system equipped with A1 Kα radiation as the source (hν = 1486.6 eV).

2.3 X-ray crystal structure determination and refinements

Single crystal X-ray diffraction of 1 was performed at 296 K on a Bruker SMART APEX CCD diffractometer; X-ray data were collected using graphite monochromated Mo-Kα radiation (λ = 0.71073 Å). The linear absorption coefficients, scattering factors for the atoms, and the anomalous dispersion corrections were taken from the International Tables for X-ray Crystallography.³⁰ The data integration and reduction were processed using SAINT software.³¹ An empirical absorption correction was applied to the collected reflections using SADABS³² and the space group was determined using XPREP.³³ The structure was solved by direct methods using SIR-97³⁴ and refined on F² by full matrix least squares using the SHELXL-97 program package.³⁵ All non-hydrogen atoms were refined with anisotropic displacement parameters. A summary of the crystallographic data and the structure refinement for the complex is given in Table 1. The CCDC reference number for 1 is 1571865.†

Table 1 Crystal and structure refinement data for 1

Compound	1
a R 1 = ∑||Fo| − |Fc||/∑|Fo| with Fo^2 > 2σ(Fo^2). b wR2 = [∑w(|Fo^2| − |Fc^2|)^2/∑|Fo^2|^2]^1/2.
Empirical formula	Dy6N8O47
Formula weight	1839.08
Crystal system	Monoclinic
Space group	P21/n
Color	Colorless
a, Å	12.5852(3)
b, Å	10.2029(3)
c, Å	15.6621(4)
α	90
β	97.381(3)
γ	90
h	−14 ≤ h ≤ 14
k	−7 ≤ k ≤ 12
l	−10 ≤ l ≤ 18
V, Å^3	1994.44(9)
Z	2
ρ calcd (g cm^−3)	3.062
λ, Å	0.71073
T, K	293
μ, mm^−1	11.240
F(000)	1656
Reflections collected	3505
Independent reflections	3026
R indices [I > 2σ(I)]	R 1 = 0.0431, wR2 = 0.1314
R indices (all data)	R 1 = 0.0508, wR2 = 0.1432
Goodness-of-fit on F^2	1.090

---

2.4 Magnetic measurements

All the magnetic measurements have been performed in a Quantum Design made vibrating sample magnetometer (VSM) (PPMS, Quantum Design). All the magnetic susceptibility data were collected at a 0.1 Tesla field in the temperature range of 1.8–300 K on a crystalline solid sample of 1. To avoid torquing, the samples were fixed in vaseline. Pascal's constant was used for the diamagnetic data correction. Magnetic relaxation measurements were performed by cooling the sample in the presence of a DC field and measuring the magnetization as a function of time after removal of the DC field.

2.5 Fluorescence experiments

In a typical experimental setup, a 1 mM solution of 1 was prepared in H₂O. In a 1 cm quartz cuvette, 3 mL of the solution of 1 in water was placed and the fluorescence response upon excitation of 1 at 290 nm was measured in situ after incremental addition of freshly prepared nitro analyte solutions in the range of 300–700 nm, while keeping a 2 nm slit width for both the source and detector.

2.6 DFT studies

The density functional theory (DFT) calculations were done with the ORCA 3.0.3 computational package.³⁶ The geometry optimization was carried out using the hybrid B3LYP functional³⁷ and Aldrich's def2-SVP basis set for C, H, O, and N atoms.³⁸ The optimized structure was further re-calculated using the def2-TZVP basis set for all atoms to calculate the HOMO and LUMO energies. To accelerate the calculations, we utilized the resolution of identity (RI) approximation with the decontracted auxiliary def2-SVP/J coulomb fitting basis set and the chain-of-spheres (RIJCOSX) approximation of the exact exchange as implemented in ORCA.³⁹ Frontier molecular orbitals (HOMO and LUMO) play an important role to exemplify the chemical reactivity, kinetic stability and electrical transport properties of a molecule. Systems having high E_HOMO are good electron donors, while those having low E_LUMO are good electron acceptors.

2.7 Hirshfeld surface analysis

Hirshfeld surfaces⁴⁰ mapped with various properties and 2D fingerprint plots⁴¹ were generated using Crystal Explorer 3.0.⁴² This has been proven to be a useful visualization tool for the analysis of intermolecular interactions in crystal packing.⁴¹ The Hirshfeld surface can be defined in a crystal as the region around a molecule where the ratio of the electron distribution of a sum of spherical atoms for the molecule (the promolecule) to the corresponding sum over the crystal (the procrystal) equals 0.5. The shape and nature of the surface are directly influenced by the surrounding environment of the molecule in the crystal. For each point on the Hirshfeld isosurface, two distances d_e, the distance from the point to the nearest nucleus external to the surface, and d_i, the distance to the nearest nucleus internal to the surface, are defined. The normalized contact distance (d_norm) based on d_e and d_i is given by
where r^vdW_i and r^vdW_e are the van der Waals radii of the atoms. The value of d_norm may be negative or positive depending on the intermolecular contacts being shorter or longer than the van der Waals separations.⁴¹ The parameter d_norm displays a surface with a red-white-blue colour scheme, where bright red spots highlight shorter contacts, white colour areas represent contacts around the van der Waals separation, and blue colour regions are devoid of close contacts.

2.8 Synthesis of [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆](NO₃)₂(H₂O)₂ (1)

A mixture containing Dy(NO₃)₃·5H₂O (2 mmol; 0.88 mg) and 3-aminophenol (ampH) (8 mmol; 0.62 mL) was dissolved in 20 mL MeOH/H₂O (4 : 6 v/v) and stirred for 40 min, and then NEt₃ (2 mmol; 0.28 mL) was added and refluxed for 1 h at 90 °C. After cooling down to room temperature it was allowed to undergo slow evaporation in the dark for 32 days, and white transparent X-ray quality crystals of 1 were obtained. The complex decomposes at 280 °C. Yield 74%, anal. calcd for Dy₆N₈O₄₇H₃₆: H = 1.93, N = 5.97; found: H = 1.97, N = 5.89. IR spectra (KBr pellets, cm⁻¹): ν(NO₂): 1342–1486 cm⁻¹, ν(Dy–O₂NO): 1100–1650 cm⁻¹, ν(Dy–O–Dy): 800 cm⁻¹.

3. Results and discussion

3.1 Synthesis

Our initial synthetic strategy was to follow the methodology proposed by Anja-verena et al.⁴³ to synthesize an oxido material with dysprosium based cluster type OM (oxido-metal) complexes using green synthetic methods. In this case, we modified the synthetic procedure to obtain the maximum number of free basic sites on the cluster surface in order to facilitate binding with analytes to explore its sensing abilities. The cluster-type basic lanthanide nitrate [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆](NO₃)₂(H₂O)₂, denoted in the rest of the paper as Dy₆(μ₆-O), can be easily obtained via direct hydrolysis of a lanthanide nitrate in the presence of mild acidic conditions. The additional use of ampH may provide mild acidic conditions during the synthesis, as it doesn’t appear in the final product. Lanthanide based oxido/hydroxido cluster compounds are rare,⁴³ and the reaction yielded block shaped white/transparent crystals which are stable in the reaction solution as well as in the open atmosphere (Fig. 6b). X-ray diffraction data have been collected on the same crystal.

3.2 Crystal structure investigations of [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆](NO₃)₂(H₂O)₂ (1)

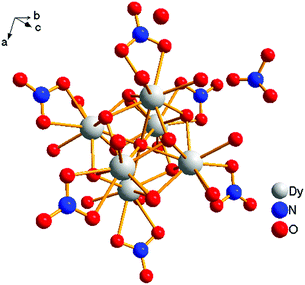
[Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆](NO₃)₂(H₂O)₂ crystallizes in the monoclinic space group P21/n with one formula unit in the unit cell. The structure of the basic lanthanide nitrate is characterized by (slightly distorted) nona-coordinated Dy³⁺, which has at the center an oxygen anion O²⁻ (μ₆-bridging) lying on an inversion centre (Fig. 2).

Fig. 1 Structural unit of [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆](NO₃)₂(H₂O)₂.

Fig. 2 Core of the molecule.

The protonation sites and charge on O atoms are ascertained by BVS calculations (Table S1, ESI†). Since the μ₆-O atom is located on an inversion centre and binds to six Dy³⁺ cations, a slightly distorted anion-centred [ODy₆] octahedron results (Fig. 3). Above each face of the {ODy₆} octahedron is located a hydroxide anion, OH⁻. The hydroxide anions themselves thus build up a (slightly distorted) cube, the inverse platonic polyhedron of an octahedron. Each lanthanide cation carries two additional water molecules in terminal positions. The Dy^III ions lie in a spherical capped square antiprism coordination environment (Fig. 4a and b), which is confirmed by SHAPE analysis (Table S7, ESI†). Altogether, for the lanthanide, a 4 + 4 + 1 coordination of Dy³⁺ by oxygen is achieved. The [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆]²⁺ cluster units arrange themselves in a body-centered fashion, connected three dimensionally by nitrate anions that are located above the octahedral faces of two neighbouring units (Fig. 1).

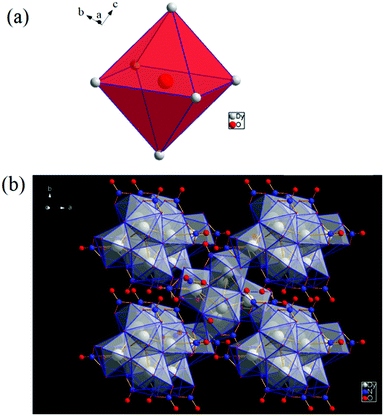Fig. 3 (a) Polyhedral representation of the distorted octahedral O²⁻ at the centre of the molecule, and (b) polyhedral representation of the molecule.

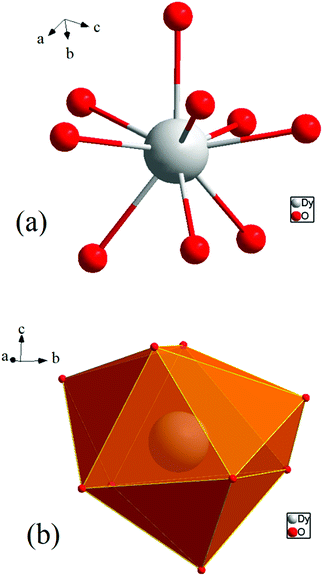Fig. 4 (a) Spherical capped square antiprism environment around Dy³⁺. (b) Polyhedral representation of the coordinating environment.

The observed interatomic distances in [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆]²⁺ are in agreement with the contraction of the ionic radii along the row of trivalent lanthanide cations.⁴⁴ Not only do the mean metal–metal distances decrease [d(Dy1–Dy2) 3.5114(7), d(Dy1–Dy3) 3.5258(7) pm], but the metal–oxygen distances do too.^50,51 Although such a type of cluster unit has been reported previously for basic perchlorates and iodides as in [Nd₆(μ₆-O)(μ₃-OH)₈(H₂O)24](ClO₄)₈(H₂O)₈,⁴⁵ [Gd6(μ₆-O)-(μ₃-OH)₈(H₂O)₂₄](ClO₄)₈(H₂O)₈,^45,46 and [Dy₆(μ₆-O)(μ₃-OH)₈-(H₂O)₂₄]I₈(H₂O)₈,⁴³1 is the first example of a dysprosium compound with this cluster unit. It seems that for the formation of the [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆]²⁺ cluster unit, the oxido anion works as a template to induce the self-assembly of dysprosium ions.

The structure directing effect of a “central spherical negative charge density” such as for product formation has already been assumed in another context.³

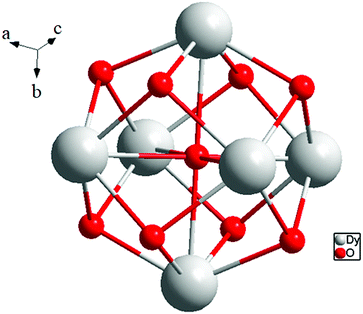
The presence of lattice water and nitrate ions along with coordinated water molecules leads to the formation of a supramolecular network through O–H⋯O and O–N⋯O interactions (Fig. 5).

Fig. 5 3D supramolecular network due to O–H⋯O and O–N⋯O interactions.

Selected bond lengths and bond angles are given in Table S3, ESI.†

The pH conditions exert a crucial influence on the generation of the central oxido anion. If one allows the pH value to decrease by evaporation of the solution, the formation of [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆]²⁺ is observed as the final product of hydrolysis.

3.3 FT-IR spectra, PXRD analyses and TGA

The vibrational spectrum of Dy₆(μ₆-O) shows a number of characteristic vibrations owing to the presence of coordinated water molecules, metal oxygen bonding and lattice water and nitrate molecules. It provides ample information about the nature of nitrate binding and its coordination modes (Fig. 6d). The peaks in the region 400–1000 cm⁻¹ correspond to the fingerprint region of the hexanuclear Dy₆(μ₆-O) cation and the peaks in the range 1100–1650 cm⁻¹ are characteristic of the (Dy–O₂NO) moieties. The shift of the O=N absorption band from 1325–1432 cm⁻¹ in O₂NO to 1342–1486 cm⁻¹ for the hybrid materials is due to the coordination of nitrogen associated oxygen with dysprosium as confirmed from the crystal structure. The absorption band at 800 cm⁻¹ is a significant peak attributed to the stretching vibration of Dy=O, which correlates with the number of hydrogen bonds in which terminal O atoms are involved. One strong band is observed at 800 cm⁻¹ in Dy₆(μ₆-O). This gives some insight into the protonation sites of this bridging O atom.

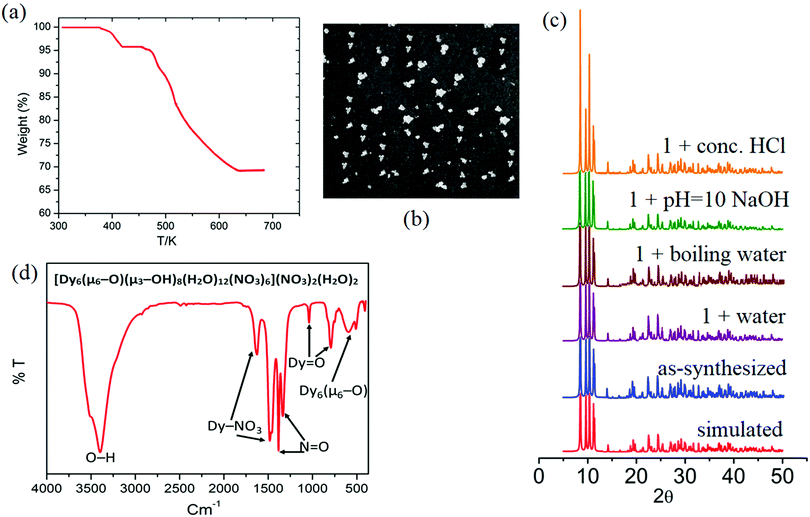Fig. 6 (a) Thermogram, (b) white transparent cube-shaped crystals, (c) PXRD patterns, and (d) FT-IR of the hybrid material Dy₆(μ₆-O).

The protonation is much lower as indicated by the predominantly strong peak.^47–50 The hydrogen bonds to the terminal O atoms diminish the force constants of the Dy=O bonds and hence the intensity reduction occurs. Therefore, these regions in the IR spectra of the oxido-cluster system can be regarded as fingerprint regions for characterizing the protonated [Dy₆(μ₆-O)(μ₃-OH)₈(H₂O)₁₂(NO₃)₆]²⁺ polycation.⁴⁸

The shift of the Dy–O–Dy stretching vibration band to a higher energy region (800–406 cm⁻¹ region) is formally due to the increase in the bond strength during the formation of the oxido-cluster. Also, one additional weak band was observed for the hybrid Dy₆(μ₆-O) below 500 cm⁻¹ due to the vibration of the Dy³⁺–O central bond, which has a large bond length in this polyhedron.⁵¹ A single broad peak at 3406 cm⁻¹ clearly indicates the presence of lattice and coordinate water molecules.

In order to determine the chemical stability of Dy₆(μ₆-O), and the phase purity of the sample, the cluster was checked in water, conc. HCl solution, and NaOH solution at room temperature, as well as in boiling water. After being immersed in these different solutions for 24 h, the measured PXRD patterns show retained crystallinity and unchanged structures, demonstrating their excellent stability (Fig. 6c). The PXRD patterns of 1 before and after immersing in different solvents for 24 h are identical and in good agreement with the simulated ones, confirming the structural integrity and phase purity of sample 1. It should be pointed out that there are limited MOFs/clusters showing good stability in boiling water, as well as in aqueous solutions with such a wide pH range.⁷ The thermal stability of compound Dy₆(μ₆–O) was investigated using TGA analysis as shown in Fig. 6a.

The TGA curves of the complex exhibit one weight loss step between 378 and 434 K. The weight loss measured for compound Dy₆(μ₆-O) was 3.9% (calc 4.26%). This can be attributed to the loss of unbound lattice H₂O and NO₃⁻ (in the form of some neutral species). The number of water and nitrate ions in the molecular formula of compound Dy₆(μ₆-O) is two each. The decomposition of water and nitrate starts from 460 K and the OM starts from 520 K for compound Dy₆(μ₆-O). Dy₆(μ₆-O) was found to be completely decomposed at 685 K after which a flat plateau followed. The stability of the OM framework in the solution state is confirmed by the identical patterns of the solid-state and solution UV-visible spectra even at high temperatures (Fig. S7, ESI†).⁵²

3.4 Study of non-covalent interactions

The Hirshfeld surfaces⁵³ of 1 are illustrated in Fig. 6, revealing surfaces mapped over a d_norm range of −0.234 to 1.439 Å. These surfaces are transparently shown to visualize the moieties around which these were calculated. The deep red depressions⁵³ visible on the d_norm surfaces are indicative of hydrogen bonding contacts. The dominant interactions viz. O–H⋯O and O–N⋯O are shown in the Hirshfeld surface plots as the red-shaded area in Fig. 7.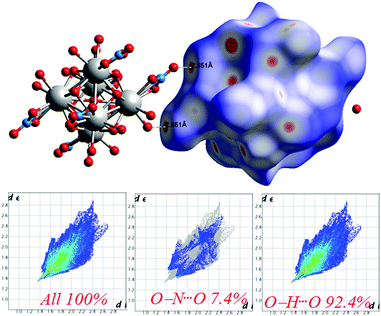

Fig. 7 Intermolecular O⋯H interactions in 1 through red spots shown by Hirshfeld surface mapping over d_norm with 2D-fingerprint plots.

The 2D-fingerprint plots provide quantitative information about the decomposition of the Hirshfeld surfaces into contributions from the various intermolecular interactions present in the crystal structures.⁵³ The fingerprint plots are presented in Fig. 7. The intermolecular O–H⋯O interactions appear as one long sharp broad spike, and the O–N⋯O interactions appear as two broad small side peaks of the 2D fingerprint plots in the region 2.76 Å < (d_e + d_i) < 5.53 Å shown as a light sky-blue pattern.

3.5 Magnetic studies

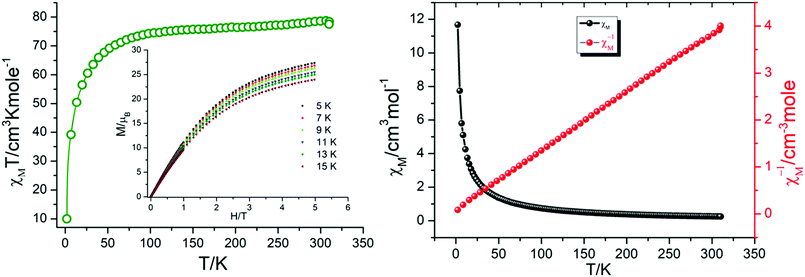
Magnetic susceptibility measurements were carried out under direct current (dc) for 1 in an applied magnetic field of 0.1 T between 300 and 1.8 K (Fig. 8). The complex follows the Curie–Weiss law, χ_M = C/(T − θ) (χ_M = molar magnetic susceptibility), with a Curie constant of C = 79.55 cm³ K mol⁻¹ and Weiss constant of θ = −7.65 K, and an observed χ_MT value at 300 K of 78.61 cm³ K mol⁻¹, which is in agreement with the expected value of 85.02 cm³ K mol⁻¹ for six uncoupled Dy^III ions (S = 5/2, L = 5, ⁶H_15/2, g = 4/3, and χ_MT free ion = 14.17 cm³ K mol⁻¹)^61,62 and previously reported Dy₆ systems (Table 2). Upon cooling, the χ_MT value for the compound gradually decreases from 300 to 50 K due to the depopulation of the excited sublevels of the ground multiplets and/or significant magnetic anisotropy present in Dy systems.

Fig. 8 χ _M T vs. T plot (left), and χ_Mvs. T and χ_M⁻¹vs. T plots (right) for 1.

Table 2 Observed χ_MT values of Dy(III) complexes with high nuclearity (Ln_n, n > 5)

S. no.	Compound^a	Structural feature	χ M T at 300 K	Ref.
a Abbreviations: HL^1, o-vanillin; H2L^2, 2-hydroxymethyl-6-methoxyphenol; ovnH, o-vanillin; avnH2, aldol-vanillin; H3L^3, 2,6-bis((2-hydroxyethylimino)methyl)-4-methylphenol; H3L^4, 1,3-bis(salicylideneamino)-2-propanol; L^5H3, N′-(2-hydroxy-3-methoxybenzylidene)-6-(hydroxymethyl)picolinohydrazide; H2L^6, 6,6′-((1E,1′E)-(2,2′-(pyrimidine-4,6-diyl)bis(hydrazin-2-yl-1-ylidene))bis(methanylylidene))bis(2-methoxyphenol); H2L^7, (E)-N′-(2-hydroxybenzylidene)pyrazine-2-carbohydrazide; H2L^8, (E)-N′-(2-hydroxy-3-methoxybenzylidene)pyrazine-2-carbohydrazide; H2ovph, o-vanillin picolinoylhydrazone; H2apovh, (N'-(amino(pyridin-2-yl) methylene)-ovanilloylhydrazine); L^9H, pivalic acid; L^10H, 3,5-dinitrobenzoic acid; L^11H, 2,6-dimethoxyphenol; thmeH3, tris(hydroxymethyl)ethane; tpaH, triphenylacetic acid; H2EDDC, (N',N′′,E,N',N′′,E)-N',N′′-(ethane-1,2-diylidene)dipyrazine-2-carbohydrazide; H2opch (E)-N'-(2-hydroxy-3-methoxybenzylidene)pyrazine-2-carbohydrazide; H2L^12, 3-(pyridin-2-yl)-N′-((pyridin-2-yl)methylene)-1H-pyrazole-5-carbohydrazide; H3L^13, N′-(2-hydroxybenzylidene)-3-(pyridin-2-yl)-1H-pyrazole-5-carbohydrazide; L^14H3, (E)-2-((2-hydroxyethylimino)methyl)-6-(hydroxymethyl)-4-methylphenol.
1	[Dy6(μ3-OH)4(L^1)4(L^2)2(H2O)9Cl]Cl5·15H2O	By two alkoxide oxygen atoms of (L^2)^2− in a vertex-to-vertex manner	82.3	69
2	[Dy6(μ3- OH)4(ovn)4(avn)2(NO3)4(H2O)4](NO3)2·(H2O)·3(CH3)2CO	By two alkoxide oxygen atoms of avn^2− in a vertex-to-vertex manner	86.6	70
3	[Dy6(L^3)4(μ4-O)(NO3)4(CH3OH)]·CH3OH	By four phenoxo groups of (L^3)^3− and one μ4-O^2− in an edge-to-edge manner	85.5	71
4	[Dy6(L^4)4(μ3-OH)4(CH3OH)2(NO3)2]·6CH3CN	By four alkoxide oxygen atoms of (L^4)^3− and two μ3-OH^− in an edge-to-edge manner	83.6	72
5	[{Dy6(L^5)2(L^5H)2}(μ3-H)4][MeOH]2[H2O]6[Cl]4·8H2O·4CH3OH	Two Dy3 triangles in a edge-to-edge fashion	84.2	73
6	[Dy6(L^5)2(μ3-OH)4(μ2-OH)2(SCN)8(H2O)4]·6CH3CN·2CH3OH ·H2O	By two pyrimidine groups of (L^5)^2− in a planar Dy3 + Dy3 manner	78.3	74
7	[Dy6(L^5)2(μ3-OH)4(μ2-OH)2(NO3)6(H2O)6]·2NO3·10H2O		80.9	74
8	[Dy8L6(μ3-OH)4(μ2-CH3O)2(CH3OH)6(H2O)2]·6H2O·10CH3OH· 2CH3CN	By a paramagnetic [Dy(μ2-CH3O)2Dy]^4+ linker	116.1	55
9	[Dy6(μ3-OH)3(μ3-CO3)(μ-OMe)(HL^7)6(MeOH)4(H2O)2]3·3MeOH·2H2O	Vertex- and edge-sharing Dy3 triangles	84.8	75
10	[Dy6(μ3-CO3)2(L^8)5(HL^8)(MeOH)2]·4H2O·5MeOH·EtOH	Trigonal prism	85.78	76
11	[Dy6(ovph)4(Hpvph)2Cl4(H2O)2(CO3)2]·CH3OH·H2O·CH3CN	Trigonal prism	82.1	77
12	[Dy6(apovh)4(Hapovh)4(CO3)2(SCN)2]·6CH3CN·8CH3OH·2H2O	Covalently linked by two Hapovh-ligands (Dy3 molecular cluster pair)	88.3	78
13	[Dy6(L^9)6(L^11)6(OCH3)6·2CH3OH]	Dy6 wheels	82.45	54
14	[Dy6(L^10)6(L^11)6(OCH3)6·2CH3OH]		80.32
15	[Dy7(OH)6(thmeH2)5(thmeH)(tpa)6(MeCN)2](NO3)2	Centred-hexagonal Dy7 core	98.0	79
16	[Dy8(μ3-CO3)4(L^8)8(H2O)8]·10MeOH·2H2O	Quadruple-CO3^2− bridged Dy8	106.4	80
17	Dy8(μ3-OH)4(L12)4(DEA)4Cl4	Butterfly-shaped Dy8	105.95	81
18	Dy8(μ3-OH)4(L13)6(DMF)4(H2O)8	Dy8 core in a staircase-type arrangement	103.13
19	[Dy7(EDDC)(opch)4(O3PC10H7)3(OAc)5(MeOH)2]·4MeOH	Cyclic Dy7	102.89	82
20	[Dy14(EDDC)4(opch)4(O3PC10H7)10(OAc)6(H2O)4]·xH2O	Dimer of cyclic Dy7	204.29
21	[Dy10(L^14H)10(κ^2-Piv)10]·9CHCl3·4CH3CN	Dy10 wheels	141.30	83
22	[Dy6(μ6-O)(μ3-OH)8(H2O)12(NO3)6](NO3)2(H2O)2	Dy6 octahedron ball	78.61	This work

---

However, upon a further decrease in temperature (below 50 K), these compounds exhibit different thermal behaviour and quite a significant difference from other Dy₆ wheels’ magnetic moment.⁵⁴

In compound 1, χ_MT further decreases rapidly to reach 10.95 cm³ K mol⁻¹ at 1.8 K. This thermal evolution may be ascribed to very weak antiferromagnetic magnetic interactions between Dy^III ions.

These behaviours are consistent with the field dependence of the magnetization at 1.8 K. The magnetic moment for the 4f system could be calculated by 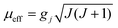. Using the 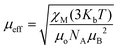equation, the value at 300 K is found to be 25.03 μ_B. Magnetization (M) data for 1 were collected in the 0–6 T field range below 15 K.

The field dependence of M shows that M increases smoothly with increasing applied dc field without saturation even at 6 T, which is ascribed to the anisotropy and the crystal-field effect.^54,56 The non-superimposed M versus H/T plot (Fig. 8) indicates the presence of significant magnetic anisotropy and/or low-lying excited states.

3.6 Luminescent property and detection of PA and Fe³⁺

Since Dy₆(μ₆-O) exhibits luminescent properties, the emission of the complex is investigated in different solvents (Fig. S1, ESI†). Among them intense emission is observed in water compared to the others. As water is a green solvent, so we decided to investigate the luminescent and sensing properties of OM in water. Emission maxima of 345 nm was observed for 1 in water at excitation wavelength of 296 nm. The quantum yield is found to be 0.72.

The bright-blue luminescence of 1 prompts us to investigate its potential application in selective sensing of explosive nitroaromatics (NACs) and some essential metal ions.

3.6.1 Nitroaromatic sensing. The photoluminescence spectra of 1 dispersed in water possess a strong fluorescence band at 345 nm. To examine the sensing ability of 1 for different nitroaromatics, fluorescence titration experiments were carried out by gradual addition of 2 mM stock solutions of various NACs, viz. NB (nitrobenzene), MNP (3-nitrophenol), PNP (4-nitrophenol), 2,4-DNP (2,4-dinitrophenylhydrazine) and PA (2,4,6-trinitrophenol). Incremental addition of NB, MNP and PNP had a minor effect on the fluorescence intensity of 1 (Fig. S2–S6, ESI†).

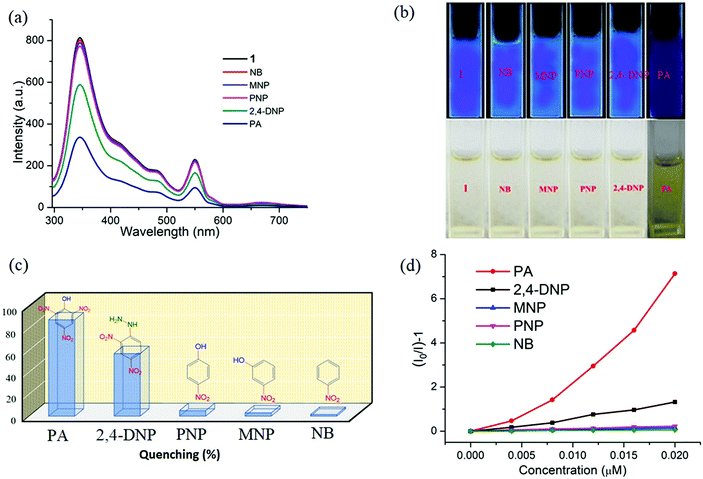
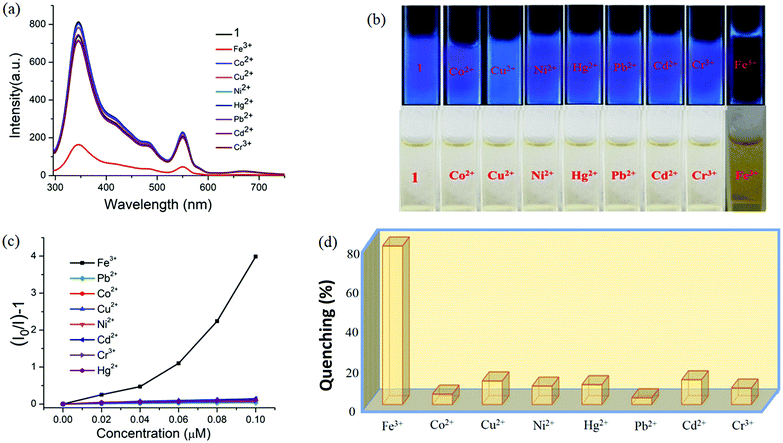
Interestingly, 1 shows marvellous sensing behaviour towards PA by quenching the initial fluorescence intensity by 58.6%, after adding 0.91 ppb of PA in the aqueous phase (Fig. 9).

Fig. 9 (a) The change in fluorescence intensity of 1 (λ_ex = 296 nm) on addition of 0.91 ppb of different NACs. (b) Digital photographs of solutions of 1 in the presence of different nitroaromatic analytes under portable UV light (top) and under normal light (bottom). (c) Quenching efficiency of different analytes. (d) Stern–Volmer plot for various nitro analytes.

Appreciable fluorescence quenching of 87.6% could be clearly observed even at a very low concentration of PA with 2.29 ppb in the aqueous phase (details in the ESI†). The quenching efficiency of 1 is amongst the highest values reported for polyoxometalates (POMs), oxido-metal clusters (OM) and MOFs,^6,28,57,58 and 1 is most sensitive among them (Fig. 9a).

To confirm the fluorescence response of the OM towards other NACs, we also performed the sensing experiments with NB, MNP, PNP, and 2,4-DNP. Negligible quenching was observed with NB, MNP and PNP, whereas 2,4-DNP showed some interference (Fig. 9a and c). This clearly suggests that there is a strong interaction between PA and 1, which helps show the highly selective sensing behaviour towards PA with a record low, to the best of our knowledge, detection limit of 0.03 ppb in the aqueous phase. To explore the reason behind the quenching mechanism for selective sensing of PA, we analysed the quenching efficiencies of all the analytes by using the Stern–Volmer equation²⁸ (details in the ESI†). The plot with PA shows a linear increase at low concentrations, which deviates from linearity and turns upwards with increasing concentration, whereas the other nitro analytes showed only linear trends in the S–V plots (Fig. 9d).

A 3D representation of the Stern–Volmer (SV) plots of 1 for various nitro analytes in the aqueous phase is shown in Fig. S8, ESI.† From the linear fitting of the plot, the quenching constant for PA was found to be 3.5 × 10⁸, which indicates the super quenching ability of 1 towards PA in water. To the best of our knowledge, this is one of the highest quenching constant values for any OM among the reported POMs as well as MOFs for selective sensing of PA to date.^6,21,59

The behaviour of the interaction (whether static or dynamic) between the OM and analytes can be anticipated by (i) analysing the absorption spectral changes of the OM on the addition of analytes, and (ii) time-resolved measurements of the photoluminescence decay of the OM after addition of analytes. To explore the mechanism, we measured the fluorescence lifetime of 1 with and without addition of PA. The average lifetime remained unchanged even after the addition of PA, suggesting that the quenching process follows a static mechanism (Fig. S9, ESI†). To get deeper insight, we recorded the UV-vis spectrum of 1 in the presence of PA (Fig. S10, ESI†) and found that, upon gradual addition, a new band at 352 nm appears, which ascertained the formation of a non-emissive ground state complex and also supports the static mechanism.⁷⁰

With the other NACs tested, no considerable change was observed in the spectral pattern except for 2,4-DNP, which shows a small peak at 361 nm (Fig. S11, ESI†). From the above spectroscopic results, it is confirmed that there is a strong interaction between PA and 1 in the ground state. As PA possesses two types of functional groups, and to verify whether the hydroxyl group plays any role in sensing, we performed some experiments with hydroxyl substituted aromatic and aliphatic molecules without nitro groups like catechol, 2,6-bis(hydroxymethyl) p-cresol, di(trimethylolpropane), and 1,1,1-tris(hydroxymethyl)propane.

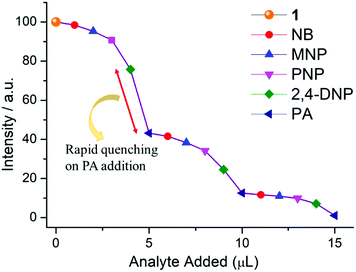
From Fig. S12, ESI,† it is observed that no considerable quenching was observed in the emission spectrum with gradual addition of analytes, which confirms that the whole PA molecule is responsible for sensing. To gain more insight into the discriminative sensing behaviour of 1 towards PA in the presence of other interfering NACs, we performed some competition experiments by sequential addition of different NACs followed by PA into 1 and the corresponding emission spectra were recorded (Fig. 10). The initial addition of different NACs showed negligible intensity quenching but effective quenching was observed after addition of the PA solution (Fig. S13–S16, ESI†), even in high concentrations, which demonstrates the exceptional selectivity of compound 1 for PA. Further, from the crystal structure, it can be seen the pores are almost occupied and there is no chance of encapsulation of the nitro analytes into the pores. The mechanism behind the fluorescence quenching might also be photo induced electron transfer between the electron rich framework and the electron deficient analyte adsorbed on the surface⁶¹ as 1 has an electron rich framework of an oxido-metal cluster.

Fig. 10 Fluorescence quenching of 1 upon successive addition of aqueous solutions of different nitro compounds (1 μL each, 2 mM stock solution) in the mixture. Maximum quenching is observed for PA even in the presence of other nitro analytes.

Generally, OM structures possess a band structure and exhibit a definite band gap energy.^6,7,57,58,60

As demonstrated by Li and co-workers,⁶² calculation of the electronic band structure is much more suitable compared to molecular orbital (MO) calculations. Indeed, the valence band (VB) and conduction band (CB) energies can be defined in a similar manner to the MOs of discrete molecules. One can envisage that electron-deficient NACs will quench the luminescence of OMs if the lowest unoccupied MOs (LUMOs) of the analytes, which are π*-type orbitals, reside between the VB and CB of the luminescent OM. Upon excitation, effective charge transfer can take place from the CB of the OM to the LUMO of the NACs, thereby quenching the fluorescence intensity. Hence, for more electron-deficient analytes with more stable LUMOs, electron transfer from the CB of the OM to the LUMOs of the analytes becomes thermodynamically more favourable.

However, with electron-rich analytes, for which the LUMO is located above the CB of the OM, excited-state electrons from the LUMO of the analytes will be transferred to the CB of the OM, leading to enhancement of the luminescence intensity.

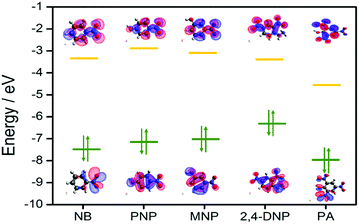
To gain deeper insight into this mechanism, we calculated the HOMO–LUMO energies of the employed NACs by DFT at the B3LYP/6-31G* level, as shown in Fig. 11, and from the results it is ascertained that the observed maximum fluorescence intensity quenching is due to easy electron transfer from the framework to the lowest LUMO energy level of PA compared to the other NACs (Table S2, ESI†).^28,57,58 However, the observed order of the quenching efficiency is not in full agreement with the corresponding LUMO energies of the other nitro analytes, which indicates that electron transfer is not the sole mechanism for the intensity quenching.^57–60 To explore this, we recorded the UV-vis spectra for all the NACs. Only PA showed the maximum spectral overlap with the emission spectrum of 1, whereas it was negligible for the other nitro analytes (Fig. 12), which confirms that the resonance energy transfer mechanism along with the electron transfer mechanism is responsible for the selective fluorescence quenching with PA, while for the other NACs fluorescence quenching happens only through the electron transfer mechanism.^28,63 Since energy transfer is a long-range process, the emission quenching can pass on to the neighbouring fluorophores.⁶⁴

Fig. 11 HOMO and LUMO energy levels of the molecular orbitals considered for nitro analytes.

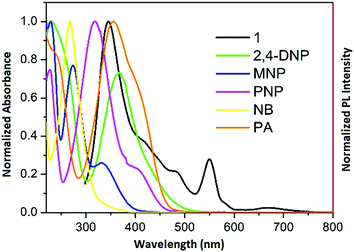Fig. 12 Spectral overlap between the normalized emission spectra of 1 (λ_ex = 296 nm) and normalized absorbance spectra of the nitro analytes.

Hence, when the energy-transfer process gets involved in quenching, the quenching efficiency could undergo a radical upsurge, amplifying the detection sensitivity range, as well as the selectivity limit.

3.6.2 Metal ion sensing. Moreover, the sensing ability of the present OM was also examined for some transition metal ions in water. Fe³⁺ has been found to be detected selectively by 1. In a typical experiment, the fluorescence spectrum of 1 was recorded upon gradual addition of Fe³⁺ in water solution (1 mM). As expected, the gradual addition of Fe³⁺ solution into 1 resulted in fast and high fluorescence quenching (80%) with significant spectroscopic variation upon addition of 5.58 ppb of Fe³⁺ (Fig. 13). 1 also displays selective chromogenic behaviour towards Fe³⁺ with a colour change from colourless to light orange, which was observed by the naked eye (Fig. 13b).

Fig. 13 (a) The change in fluorescence intensity of 1 (λ_ex = 296 nm) with addition of different cations. (b) Digital photographs of solutions of 1 in the presence of different metal ions under portable UV light (top) and normal light (bottom). (c) Stern–Volmer plot for various analytes. (d) The fluorescence quenching efficiencies upon addition of different analytes (5.58 ppb).

Specifically, 1 could detect Fe³⁺ even at concentrations as low as 0.09 ppb. To check the selective sensing behaviour of 1 towards Fe³⁺, we performed fluorescence experiments with some metal ions, such as Co²⁺, Cu²⁺, Ni²⁺, Pb²⁺, Cd²⁺, Cr³⁺ and Hg²⁺ (Fig. S17–S24, ESI†). All these metal ions had no significant effect on the fluorescence intensity under identical experimental conditions (Fig. 13d), which suggests the selective sensing behaviour of 1 towards Fe³⁺ (Fig. 13a). To examine the selectivity of Fe³⁺ in the presence of other metal ions, we also performed some competition experiments. When we added different metal ions to 1, the fluorescence intensities were not affected much, even at high concentrations, but impressive quenching was observed after adding Fe³⁺ solution, which confirms the remarkable selectivity (Fig. 14 and Fig. S25, ESI†). The Stern–Volmer plot (Stern–Volmer constant, K_SV = 3.79 × 10⁷ M⁻¹; details in the ESI†) obtained from the fluorescence quenching of 1 with increasing Fe³⁺ concentration showed a good linear response at low concentrations (Fig. 13c). As the concentration increased, the plot deviates from linearity, demonstrating the simultaneous presence of both static and dynamic mechanisms. The 3D representation of the Stern–Volmer (SV) plots of 1 for various analytes in the aqueous phase is shown in Fig. S26, ESI.†

Fig. 14 Fluorescence quenching of 1 upon successive addition of aqueous solutions of different metal ions (20 μL each, 1 mM stock solution) in the mixture. The maximum quenching is observed for Fe³⁺ even in the presence of other ions.

According to a literature survey, the majority of MOFs, POMs and OMs selectively detect Fe³⁺ through interactions between their functional sites and Fe³⁺ as a result of cationic exchange⁶⁵ or a strong interaction between the frameworks and the introduced Fe³⁺, such as diffusion into the MOF channels or attachment to the MOF surface.^66–68

In the present case diffusion is not possible because of the absence of porosity, while the coordinated water or bridged hydroxide ions could facilitate the interaction with Fe³⁺. To elucidate the sensing mechanism, fluorescence lifetime measurements were initially performed which indicate the existence of static quenching (Fig. S27, ESI†). Then, UV-vis spectra of all the metal ions used were recorded which shows that Fe³⁺ ions exhibit maximum overlap with emission of 1 (Fig. S28, ESI†) signifying the possible role of energy transfer in quenching mechanism. Since, the outer electronic structure of Fe³⁺ is 3d⁵ with five half-filled orbitals, there is also a great possibility of electron transfer from the conduction band of OM to half-filled 3d orbital of Fe³⁺. Additionally, X-ray photoelectron spectroscopy confirmed the presence of hard Fe³⁺ in complex, thus demonstrating the binding of Fe³⁺ onto the surface of 1 (Fig. S29, ESI†) probably with hard oxygen of coordinated hydroxide (OH⁻) following hard and soft acid–base (HSAB) principle.

Since the cluster also showed selective sensing behaviour to Fe³⁺ ions as well as picric acid, the interference of transition metal ions with the performance of picric acid sensing should also be checked. Excellent sensors usually possess ultrahigh selectivity against other competing species.²⁸ To eliminate the interference of transition metals, the phosphate ion could be utilized since it has high affinity specifically for metals like Fe³⁺, Cu²⁺etc.²⁸ On addition of phosphate ions, Fe³⁺ ions could be displaced from cluster 1 in solution unlike picric acid.

3.6.3 Recyclability test. The detection ability of the present OM can be restored and it can be recycled for a significant number of cycles by centrifuging the dispersed solution after use (Fig. S30, ESI†). Remarkably, the initial fluorescence intensity was almost regained even after four cycles, suggesting high photostability and reversibility of 1 for detection applications.

3.6.4 Detection limit. For calculating the detection limit, PA (0.5–3 μL, 2 mM stock solution) and Fe³⁺ (20–100 μL, 1 mM stock solution) were added to 1, and the corresponding fluorescence intensities were recorded. By plotting the fluorescence intensity with increasing concentration of the analyte, the slope (m) of the respective graph was calculated (Fig. S31 and S32, ESI†). The standard deviation (σ) was calculated from five blank measurements of 1 (Table S4, ESI†). The detection limit is calculated according to the formula: detection limit = (3σ/m). The detection limit of 1 was found to be ∼0.03 for PA and ∼0.09 ppb for Fe³⁺ (Tables S5 and S6, ESI†).

4. Conclusion

Fulfilling the requirement of an aqueous phase multisensor, a new oxido cluster of dysprosium (Dy₆) is designed. This oxido metal (OM) based material is characterized by single crystal X-ray, spectral and magnetic studies. The magnetic data support the presence of anti-ferromagnetic exchange interactions in the molecule. The Dy₆ oxido material is disclosed as a wonderful sensor for picric acid (PA) as well as Fe³⁺ ions in aqueous medium, and is the best dual-sensor with detection limits of ∼0.03 and ∼0.09 ppb, respectively, for the said analytes. Spectral titrations, time decay measurements and DFT analysis reveal that the pathway of sensing is via photo-induced electron and energy transfer. The present material thus opens new doors to discover fascinating materials with desired multifunctional properties in future endeavours by manipulating the structural core of the cluster.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to the Chairperson, Department of Chemistry, Aligarh Muslim University, Aligarh, for providing the necessary research facilities. M. R. thanks UGC, New Delhi, for providing a Non-NET Fellowship. M. S. acknowledges the financial support from SERB-DST, New Delhi (EMR/2016/005808/IPC). Sameer Hussain gratefully acknowledges financial support from China Postdoctoral Science Foundation (No. 2020M673368) and the Fundamental Research Funds for the Central Universities (No. xjh012020001).

Notes and references

1. Z. Zheng, Chem. Commun., 2001, 2521; Z. Zheng, in Inorganic Synthesis, ed. J. R. Shapley, Wiley-Interscience, New York, 2004, p. 184.
2. S. A. Cotton, Lanthanides and Actinides, Macmillan, London, 1991.
3. R. Anwander, Angew. Chem., 1998, 110, 619 ( Angew. Chem., Int. Ed. , 1998 , 37 , 599 ).
4. (a) R. Wang and Z. Zheng, Comments Inorg. Chem., 2000, 22, 1; (b) Z. Zheng, Chem. Commun., 2001, 2521.
5. R. Anwander, Angew. Chem., Int. Ed., 1998, 37, 599.
6. H. Zhang, J. Yang, W. Kan, Y. Liu and J. Ma, Cryst. Growth Des., 2016, 16, 265–276.
7. B. Wang, X. Lv, D. Feng, L. Xie, J. Zhang, M. Li, Y. Xie, J. Lie and H. Zhou, J. Am. Chem. Soc., 2016, 138(19), 6216.
8. E. M. Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S. Jiang, D. Collison, J. Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243,  DOI:10.1038/ncomms6243.
9. E. Tahmasebi, M. Y. Masoomi, Y. Yamini and A. Morsali, Inorg. Chem., 2015, 54, 425–433.
10. S. Heng, A. M. Mak, D. B. Stubing, T. M. Monro and A. d. Abell, Anal. Chem., 2014, 86, 3268–3272.
11. Y. Shiraishi, Y. Matsunaga, P. Hongpitakpong and T. Hirai, Chem. Commun., 2013, 49, 3434–3436.
12. Y.-C. He, J. Yang, W.-Q. Kan, H.-M. Zhang, Y.-Y. Liu and J.-F. Ma, J. Mater. Chem. A, 2015, 3, 1675–1681.
13. B. Liu, J. Yang, G.-C. Yang and J.-F. Ma, Inorg. Chem., 2013, 52, 84–94.
14. Y.-X. Tan, Y. Zhang, Y.-P. He, Y.-J. Zheng and J. Zhang, Inorg. Chem., 2014, 53, 12973–12976.
15. G. He, H. Peng, T. Liu, M. Yang, Y. Zhang and Y. Fang, J. Mater. Chem., 2009, 19, 7347.
16. X.-Y. Xu and B. Yan, ACS Appl. Mater. Interfaces, 2015, 7, 721–729.
17. J. L. Bricks, A. Kovalchuk, C. Trieflinger, M. Nofz, M. Buschel, A. I. Tolmachev, J. Daub and K. Rurack, J. Am. Chem. Soc., 2005, 127, 13522–13529.
18. A. Barba-Bon, A. M. Costero, S. Gil, M. Parra, J. Soto, R. Martinez-Manez and F. Sancenon, Chem. Commun., 2012, 48, 3000–3002.
19. Z. Chen, Y. Sun, L. Zhang, D. Sun, F. Liu, Q. Meng, R. Wang and D. Sun, Chem. Commun., 2013, 49, 11557–11559.
20. Approaches for the Remediation of Federal Facility Sites Contaminated with Explosive or Radioactive Wastes, US Environmental Protection Agency, Washington DC, 1993.
21. M. Han, G. Wen, W. Dong, Z. Zhou, Y. Wu, J. Zhao, D. Li, L. Ma and X. Bu, J. Mater. Chem. C, 2017, 5, 8469–8474.
22. M. D. Allendorf, C. A. Bauer, R. K. Bhakta and R. J. T. Houk, Chem. Soc. Rev., 2009, 38, 1330–1352.
23. B. Chen, S. Xiang and G. Qian, Acc. Chem. Res., 2010, 43, 1115–1124.
24. (a) M. E. Germain and M. J. Knapp, Chem. Soc. Rev., 2009, 38, 2543–2555; (b) Y. Salinas, R. M. Manez, M. D. Marcos, F. Sancenon, A. M. Castero, M. Parra and S. Gil, Chem. Soc. Rev., 2012, 41, 1261–1296; (c) S. Shanmugaraju and P. S. Mukherjee, Chem. – Eur. J., 2015, 21, 6656–6666; (d) A. Chowdhury and P. S. Mukherjee, J. Org. Chem., 2015, 80, 4064–4075.
25. (a) S. J. Toal and W. C. Trogler, J. Mater. Chem., 2006, 16, 2871–2883; (b) M. S. Meaney and V. L. McGuffin, Anal. Bioanal. Chem., 2008, 391, 2557–2576; (c) B. Gole, A. K. Bar and P. S. Mukherjee, Chem. – Eur. J., 2014, 20, 2276–2291.
26. X. Hu, C. Qin, X. Wang, K. Shao and Z. Su, New J. Chem., 2015, 39, 7858–7862.
27. G. He, H. Peng, T. Liu, M. Yang, Y. Zhang and Y. Fang, J. Mater. Chem., 2009, 19, 7347.
28. (a) A. K. Dwivedi, G. Saikia and P. K. Iyer, J. Mater. Chem., 2011, 21, 2502; (b) A. H. Malik, S. Hussain, A. S. Tanvar, S. Layek, V. Trivedi and P. K. Iyer, Analyst, 2015, 140, 4388; (c) B. Zhao, T. Liu, Y. Fang, L. Wang, W. Kan, Q. Deng and B. Song, Sens. Actuators, 2017, 246, 370.
29. B. Xu, X. Wu, H. Li, H. Tong and L. Wang, Macromolecules, 2011, 44, 5089.
30. J. A. Ibers and W. C. Hamilton, International Tables for X-ray Crystallography, Kynoch Press, Birmingham, England, 1974, vol. IV.
31. SMART & SAINT Software Reference manuals, Version 6.45, Bruker Analytical X-ray Systems, Inc., Madison, WI, 2003.
32. G. M. Sheldrick, SADABS, software for empirical absorption correction, Ver. 2.05, University of Göttingen, Göttingen, Germany, 2002.
33. XPREP, version 5.1, Siemens Industrial Automation Inc.,Madison, WI, 1995.
34. G. M. Sheldrick, SHELXL97, Program for Crystal Structure Refinement, University of Göttingen, Göttingen, Germany, 2008.
35. A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. G. Moliterni, G. Polidori and R. J. Spagna, J. Appl. Crystallogr., 1999, 32, 115–119.
36. (a) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73; (b) F. Neese, Orca. An ab initio, density functional and semiempirical Program Package version, 2009.
37. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
38. (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297; (b) A. Schaefer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829; (c) A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571.
39. (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104; (b) C. Steffen, K. Thomas, U. Huniar, A. Hellweg, O. Rubner and A. Schroer, J. Comput. Chem., 2010, 31, 2967.
40. (a) M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19; (b) S. K. Seth, D. Sarkar, A. Royd and T. Kar, CrystEngComm, 2011, 13, 6728–6741; (c) S. K. Seth, D. Sarkar and T. Kar, CrystEngComm, 2011, 13, 4528–4535.
41. (a) S. K. Seth, V. S. Lee, J. Yana, S. M. Zain, A. C. Cunha, V. F. Ferreira, A. K. Jordao, M. C. B. V. de Souza, S. M. S. V. Wardell, J. L. Wardellf and E. R. T. Tiekink, CrystEngComm, 2015, 17, 2255–2266; (b) S. K. Seth, J. Mol. Struct., 2014, 1070, 65–74; (c) T. Dey, P. Chatterjee, A. Bhattacharya, S. Pal and A. K. Mukherjee, Cryst. Growth Des., 2016, 16, 1442.
42. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer, Version 3.0, University of Western Australia, 2012.
43. A. Mudring, T. Timofte and A. Babai, Inorg. Chem., 2006, 45, 5162.
44. (a) R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 925; (b) R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751; (c) G. Meyer and P. Linzmeier, Rev. Chim. Miner., 1977, 14, 52.
45. D.-S. Zhang, B.-Q. Ma, T.-Z. Jin, S. Gao, Ch.-H. Yan and T. C. W. Mak, New J. Chem., 2000, 24, 61.
46. R. Wang, M. D. Carducci and Z. Zheng, Inorg. Chem., 2000, 39, 1836–1837.
47. A. S. J. Wery, J. M. Gutierrez-Zorrila, A. Luque, P. Roman and M. Martinez-Ripoll, Polyhedron, 1996, 15, 4555–4564.
48. W. P. Griffith and P. J. B. Lesniak, J. Chem. Soc. A, 1969, 1066–1071.
49. F. Corigliano and S. di Pasquale, Inorg. Chim. Acta, 1975, 12, 99–101.
50. J. Fuchs, S. Mahjour and R. Palm, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1976, 31, 544.
51. S. Onodera and Y. Ikegami, Inorg. Chem., 1980, 19, 615–618.
52. F. Sama, A. K. Dhara, M. N. Akhtar, Y. Chen, M. Tong, I. A. Ansari, M. Raizada, M. Ahmad, M. Shahid and Z. A. Siddiqi, Dalton Trans., 2017, 46, 9801.
53. (a) F. Sama, I. A. Ansari, M. Raizada, M. Ahmad, C. M. Nagaraja, M. Shahid, A. Kumar, K. Khan and Z. A. Siddiqi, New J. Chem., 2017, 41, 1959–1972; (b) I. A. Ansari, F. Sama, M. Raizada, M. Shahid, M. Ahmad and Z. A. Siddiqi, New J. Chem., 2016, 40, 9840–9852.
54. B. Joarder, S. Mukherjee, S. Xue, J. Tang and S. K. Ghosh, Inorg. Chem., 2014, 53(14), 7554.
55. (a) A. K. Mondal, S. Goswami and S. Konar, Dalton Trans., 2015, 44, 5086; (b) L. Zhang, P. Zhang, L. Zhao, J. Wu, M. Guo and J. Tang, Dalton Trans., 2016, 45, 10556.
56. J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733.
57. C. J. O'Connor, Prog. Inorg. Chem., 1982, 29, 203.
58. Y. Cui, Y. Yue, G. Qian and B. Chen, Chem. Rev., 2012, 112, 1126–1162.
59. J. Ye, L. Zhao, R. F. Bogale, Y. Gao, X. Wang, X. Qian, S. Guo, J. Zhao and G. Ning, Chem. – Eur. J., 2015, 21, 2029.
60. (a) W. Wu, S. Ye, G. Yu, Y. Liu, J. Qin and Z. Li, Macromol. Rapid Commun., 2012, 33, 164; (b) B. Gole, W. Song, M. Lackinger and P. S. Mukherjee, Chem. – Eur. J., 2014, 20, 13662; (c) Y. Salinas, R. M. Manez, M. D. Marcos, F. Sancenon, A. M. Costero, M. Parra and S. Gil, Chem. Soc. Rev., 2012, 41, 1261.
61. W.-C. Chen, C. Qin, X.-L. Wang, Y.-G. Li, H.-Y. Zang, Y.-Q. Jiao, P. Huang, K.-Z. Shao, Z.-M. Su and E.-B. Wang, Chem. Commun., 2014, 50, 13265–13267.
62. S. Pramanik, C. Zheng, X. Zhang, T. J. Emge and J. Li, J. Am. Chem. Soc., 2011, 133, 4153–4155.
63. (a) C.-K. Lin, D. Zhao, W.-Y. Gao, Z. Yang, J. Ye, T. Xu, Q. Ge, S. Ma and D.-J. Liu, Inorg. Chem., 2012, 51, 9039; (b) C. H. Hendon, D. Tiana, M. Fontecave, C. Sanchez, L. D'arras, C. Sassoye, L. Rozes, C. Mellot-Draznieks and A. Walsh, J. Am. Chem. Soc., 2013, 135, 10942.
64. B. Wang, X.-L. Lv, D. Feng, L.-H. Xie, J. Zhang, M. Li, Y. Xie, J.-R. Li and H.-C. Zhou, J. Am. Chem. Soc., 2016, 138, 6204.
65. L.-H. Cao, F. Shi, W.-M. Zhang, S.-Q. Zang and T. C. W. Mak, Chem. – Eur. J., 2015, 21, 15705–15712.
66. A. Barba-Bon, A. M. Costero, S. Gil, M. Parra, J. Soto, R. Martinez-Manez and F. Sancenon, Chem. Commun., 2012, 48, 3000–3002.
67. R. Feyisa Bogale, J. Ye, Y. Sun, T. Sun, S. Zhang, A. Rauf, C. Hang, P. Tian and G. Ning, Dalton Trans., 2016, 45, 11137–11144.
68. H. Xu, H.-C. Hu, C.-S. Cao and B. Zhao, Inorg. Chem., 2015, 54, 4585–4587.
69. I. J. Hewitt, J. Tang, N. T. Madhu, C. E. Anson, Y. Lan, J. Luzon, M. Etienne, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 6352–6356.
70. (a) T. Wang, N. Zhang, R. Bai and Y. Bao, J. Mater. Chem. C, 2018, 6, 266–270; (b) T. Wang, N. Zhang, W. Baic and Y. Bao, Polym. Chem., 2020, 11, 3095–3114; (c) B. Hussain, D. Savard, T. J. Burchell, W. Wernsdorfer and M. Murugesu, Chem. Commun., 2009, 1100–1102.
71. S.-Y. Lin, W. Wernsdorfer, L. Ungur, A. K. Powell, Y.-N. Guo, J. Tang, L. Zhao, L. F. Chibotaru and H.-J. Zhang, Angew. Chem., Int. Ed., 2012, 51, 12767–12771.
72. H. Ke, L. Zhao, Y. Guo and J. Tang, Eur. J. Inorg. Chem., 2011, 4153–4156.
73. S. Das, S. Hossain, A. Dey, S. Biswas, J.-P. Sutter and V. Chandrasekhar, Inorg. Chem., 2014, 53, 5020–5028.
74. X.-L. Li, H. Li, D.-M. Chen, C. Wang, J. Wu, J. Tang, W. Shi and P. Cheng, Dalton Trans., 2015, 44, 20316–20320.
75. H. Tian, Y.-N. Guo, L. Zhao, J. Tang and Z. Liu, Inorg. Chem., 2011, 50, 8688–8690.
76. H. Tian, M. Wang, L. Zhao, Y.-N. Guo, Y. Guo, J. Tang and Z. Liu, Chem. – Eur. J., 2012, 18, 442–445.
77. Y.-N. Guo, X.-H. Chen, S. Xue and J. Tang, Inorg. Chem., 2012, 51, 4035–4042.
78. S. Xue, L. Zhao, Y.-N. Guo, P. Zhang and J. Tang, Chem. Commun., 2012, 48, 8946–8948.
79. J. W. Sharples, Y.-Z. Zheng, F. Tuna, E. J. L. McInnes and D. Collison, Chem. Commun., 2011, 47, 7650–7652.
80. H. Tian, L. Zhao, Y.-N. Guo, Y. Guo, J. Tang and Z. Liu, Chem. Commun., 2012, 48, 708–710.
81. S. Bala, M. S. Bishwas, B. Pramanik, S. Khanra, K. M. Fromm, P. Poddar and R. Mondal, Inorg. Chem., 2015, 54, 8197–8206.
82. H. Tian, S.-S. Bao and L.-M. Zheng, Chem. Commun., 2016, 52, 2314–2317.
83. S. Das, A. Dey, S. Kundu, S. Biswas, R. S. Narayanan, S. Titos-Padilla, G. Lorusso, M. Evangelisti, E. Colacio and V. Chandrasekhar, Chem. – Eur. J., 2015, 21, 16955–16967.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthetic procedure, PXRD pattern, magnetic plots, fluorescence plots, CIF files, and additional figures. CCDC 1571865. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ma00648c

‡ Current address: Molecular Magnetism Lab, Department of Chemistry, IISER, Bhopal, India.

---