Negative thermal expansion in (Sc,Ti)Fe₂ induced by an unconventional magnetovolume effect

Abstract

Negative thermal expansion (NTE) has been found in some magnetic functional materials due to the magnetovolume effect (MVE), in which an order-to-disorder magnetic transition occurs. Here, we report an unconventional MVE which can induce the crossover from the common positive thermal expansion of the end members of ScFe₂ and TiFe₂ to the NTE in the solid solution of (Sc_1−xTi_x)Fe₂ (x = 0.6, α_V = −28.36 × 10⁻⁶ K⁻¹, 125–205 K). The direct evidence of neutron powder diffraction and first-principles calculations discloses that the decrease of intrinsic magnetic moments at the Fe(2a) site results in the ferromagnetic transition from one to another, which causes a stronger negative contribution to thermal expansion than the conventional MVE. The pair distribution function analysis verifies that the decrease in the nearest distance of Fe(6h)–Fe(6h) lying in the ab plane results in the shrinkage of the a(b) axis. The analysis of anisotropic atomic displacement parameters excludes the phonon induced NTE mechanism. Furthermore, an intriguing zero thermal expansion has been found in Sc_0.55Ti_0.45Fe₂ (10–250 K). The present study provides an approach to achieve NTE or controllable thermal expansion, which may be used to enhance other magnetic-related effects, such as the magnetocaloric and barocaloric effect.

---

New concepts

Negative thermal expansion (NTE) is a novel physical property of materials, which plays a critical role in understanding the nature of thermal expansion and controlling the thermal expansion property. It has been widely known that the abnormal thermal expansion of Invar alloys is a result of the magnetovolume effect (MVE). Based on the theory of MVE, there has been great progress in finding new NTE or zero thermal expansion (ZTE) materials. Here, we report an unconventional MVE, which can induce a crossover from a normal PTE of ScFe₂ and TiFe₂ to an intriguing NTE and ZTE in (Sc,Ti)Fe₂ solid solutions. In such a case, almost no change happens in the direction order of the spin alignment, but in the magnitude of the magnetic spin, which can be regarded as an unconventional MVE. It has been known that the previous studies on MVE are all correlated to ferromagnetic-to-paramagnetic, ferromagnetic-to-antiferromagnetic or antiferromagnetic-to-paramagnetic transitions. The (Sc,Ti)Fe₂ material is a first example that shows an unconventional MVE caused by the new type of ferromagnetic-to-ferromagnetic transition.

Introduction

Negative thermal expansion (NTE) materials, whose unit cell volume unusually contracts on heating, have attracted much attention to compensate the normal positive thermal expansion (PTE) of materials.^1,2 In 1996, the study on the novel NTE property of cubic ZrW₂O₈ marked the beginning of worldwide efforts to investigate NTE materials.³ In essence, on the basis of two fundamental mechanisms,^2,4–6 NTE materials can be divided into two classes, i.e. the phonon induced type, such as the tension effect,^7–14 and the electronic transition induced one, such as magnetic, ferroelectric, or charge order.^15–21

The studies on NTE materials can be actually traced to the discovery of magnetic Invar alloys (Fe₆₅Ni₃₅) in 1897 by the scientist C. É. Guillaume.²² The abnormal thermal expansion of Invar alloys is a result of the magnetovolume effect (MVE), i.e., an ordered magnetic structure with larger volume transforms to a disordered magnetic configuration with smaller volume, which causes a negative contribution to thermal expansion.²³ Based to the theory of MVE, there has been great progress in finding NTE materials in magnetic compounds, such as antiperovskite Mn₃AN,^19,21 Invar alloys,^1,22,24 La(Fe,Si,Co)₁₃,²⁵ Mn₃Ge,²⁶ R₂Fe₁₇ (R = rare earth elements),²⁷ and Tb(Co,Fe)₂.²⁸ It should be noted that the present NTE materials induced by MVE are due to the order-to-disorder magnetic configuration transformation, which means a change in the direction of the spin alignment. For example, the NTE of magnetic Mn₃Cu_1−xGe_xN results from the transformation of the ordered Γ^5g antiferromagnetic (AFM) spin structure to the disordered paramagnetic (PM) one.²⁹ The zero thermal expansion (ZTE) of Invar alloys is caused by the spin alignment changing from the parallel alignment (ferromagnetic) to the disordered PM state.²³

It has been well known that the two conventional physical properties of ferroelectricity and ferromagnetism (FM) have comparability. NTE can be formed in strong ferroelectricity due to the decrease in the magnitude of spontaneous polarization (P_S).¹⁸ In magnetics, if spontaneous magnetization (the total of intrinsic atomic magnetic moments) can be reduced with increasing temperature, NTE can occur. In such a case, no change happens in the order of spin alignment, but in the magnitude of magnetic spin, which can be regarded as an unconventional MVE (UMVE).

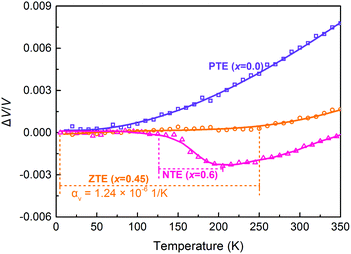
Here, we report the crossover from positive to negative thermal expansion in (Sc,Ti)Fe₂ intermetallics induced by UMVE. Intriguingly, a strong NTE property is found in the (Sc_0.4Ti_0.6)Fe₂ solid solution. The average volume coefficient of thermal expansion (CTE) is −28.36 × 10⁻⁶ K⁻¹ in the temperature range of 125–205 K. Furthermore, the ZTE property has been achieved in Sc_0.55Ti_0.45Fe₂. The direct experimental evidence from neutron powder diffraction (NPD) and the pair distribution function (PDF) have revealed that the anomalous thermal expansion of (Sc,Ti)Fe₂ is due to the decrease of intrinsic atomic magnetic moments, which is different from the order-to-disorder magnetic transition. The present work not only proposes a method to achieve NTE materials, but also provides a good example of ZTE materials.

Results and discussion

In the vicinity of phase boundaries, the moderate change of external fields (magnetic, pressure, temperature, or electric field) can induce a giant response on various physical properties, such as superconductivity, magnetoresistance, magnetostriction, thermal expansion, and piezoelectricity.³⁰ It has been known that ScFe₂ and TiFe₂ crystallize in the same MgZn₂-type hexagonal structure,³¹ but different magnetic structure (FM in ScFe₂ while AFM in TiFe₂). The solid solutions of (Sc,Ti)Fe₂ formed by the end members with opposite magnetic properties may bring novel physical capabilities in a possible magnetic phase boundary. Therefore, a series of polycrystalline ingots of (Sc_1−xTi_x)Fe₂ (x = 0, 0.45, 0.6, 1.0) have been prepared by arc melting. It is interesting to find that the solid solutions of (Sc,Ti)Fe₂ remain in a single phase with the same hexagonal structure (space group: P6₃/mmc), but with a much different magnetic structure (Fig. S1, ESI†), which will be discussed in detail in the following sections.

Variable temperature NPD has been analyzed to study the thermal expansion property of (Sc_1−xTi_x)Fe₂ (Fig. S2, ESI†). The two end members of ScFe₂ and TiFe₂ exhibit normal PTE in the whole temperature range (Fig. 1 and Fig. S3, ESI†). As a general rule, PTE should be expected in any chemical compositions of (Sc,Ti)Fe₂ solid solutions, when both the end members exhibit PTE. However, an intriguing PTE-to-NTE crossover is found in the solid solutions of (Sc_1−xTi_x)Fe₂. A strong NTE is found in the composition of x = 0.6. The CTE value of (Sc_0.4Ti_0.6)Fe₂ is α_V = −28.36 × 10⁻⁶ K⁻¹ (125–205 K). As a comparison, the NTE magnitude of (Sc_0.4Ti_0.6)Fe₂ is well approaching that of the magnetic materials of Mn₃(Cu_0.5Ge_0.5)N (α_V = −36 × 10⁻⁶ K⁻¹, 280–365 K)³² and La(Fe,Si,Co)₁₃ (α_V = −26.1 × 10⁻⁶ 1 K⁻¹, 240–350 K).²⁵ Furthermore, by adjusting the chemical composition of Ti in (Sc_1−xTi_x)Fe₂, an excellent ZTE property is found in Sc_0.55Ti_0.45Fe₂ (α_V = 1.24 × 10⁻⁶ K⁻¹, 10–250 K). It should be noted that most ZTE or NTE materials resulting from electronic transitions are typified by a fairly narrow temperature range.⁴ It is rare that the ZTE of Sc_0.55Ti_0.45Fe₂ is over a relatively broad temperature range in electronic-transition-type ZTE materials. Meanwhile, the macroscopic thermal expansion of (Sc,Ti)Fe₂ has been investigated by thermo-dilatometer (Fig. S4, ESI†). Obviously, the thermal expansion property measured from the macroscopic dilatometer measurement is in good agreement with the result of intrinsic unit cell volume, which reveals the reliability of the PTE-to-NTE crossover in (Sc,Ti)Fe₂. It should be noted that the temperature dependence of the unit cell volume was previously reported in Sc_0.35Ti_0.65Fe_1.95.³¹ It has been known that the thermal expansion property of magnetic materials can be influenced by MVE. The present phenomenon of the PTE-to-NTE crossover certifies that this is a complicated magnetic property in the solid solutions of (Sc,Ti)Fe₂.

Fig. 1 The controllable thermal expansion in (Sc,Ti)Fe₂ solid solutions. The relative change of unit cell volume of (Sc_1−xTi_x)Fe₂ solid solutions at x = 0 (PTE), x = 0.45 (ZTE) and x = 0.6 (NTE) as a function of temperature.

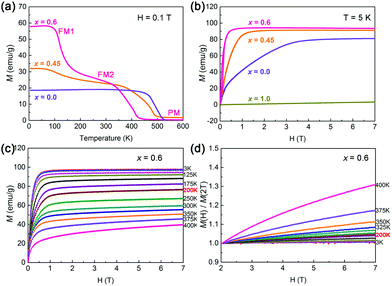
To reveal the reason for the PTE-to-NTE crossover in the (Sc,Ti)Fe₂ solid solutions, the macroscopic magnetism has been investigated. Firstly, the temperature dependence of magnetization (M–T) at a magnetic field 0.1 T has been measured for x = 0, 0.45, 0.6, and 1.0 (Fig. 2a and Fig. S5, ESI†). According to the character of M–T curves, both the end members of ScFe₂ and TiFe₂ show a typical magnetic property of ferromagnetism and antiferromagnetism, respectively. However, the solid solutions of x = 0.45 and 0.6 have unambiguous two ferromagnetic transitions, which is verified by two pronounced steps before reaching T_C. The first transition (FM1-to-FM2) at a lower temperature appears more sharply at x = 0.6 (Fig. 2a). The M–T curves in both FC (field cooling, cooling with magnetic field) and ZFC (zero field cooling, cooling without magnetic field) modes under 1 T for (Sc_1−xTi_x)Fe₂ (x = 0, 0.45 and 0.6) have also been measured (Fig. S6, ESI†). Clearly, the FC and ZFC curves mostly overlap for all compositions, which means little thermal hysteresis caused by the magnetic-structural interplay in (Sc_1−xTi_x)Fe₂. To study the evolution details of magnetic properties, the temperature dependence of magnetization under different magnetic fields (0.01, 0.05, 0.1, 0.5, and 1 T) was studied on (Sc_0.4Ti_0.6)Fe₂ (Fig. S7, ESI†). The initial and the saturated magnetizations (H = 1 T) of (Sc_0.4Ti_0.6)Fe₂ are different. With an increasing external magnetic field, the magnetization is increased in the whole temperature range, and the magnetic transition temperature is gradually enhanced to a higher temperature for both FM1–FM2 and FM2–PM transitions. This means that the ferromagnetic order is more stable in a magnetic field.

Fig. 2 The macroscopic magnetic behavior of (Sc,Ti)Fe₂. (a) Temperature dependence of magnetization (M–T) at a magnetic field 0.1 T for (Sc_1−xTi_x)Fe₂ (x = 0, 0.45, and 0.6). (b) Magnetization curves (M–H) of (Sc_1−xTi_x)Fe₂ (x = 0, 0.45, 0.6, and 1.0) at 5 K. (c) A set of magnetization curves (M–H) of (Sc_0.4Ti_0.6)Fe₂ at various temperatures. (d) The magnetization curves (2 T to 7 T) of (Sc_0.4Ti_0.6)Fe₂ are normalized to the data at 2 T.

To further verify the two transitions, a set of magnetization curves (M–H) of x = 0.6 are measured at selected temperatures. As shown in Fig. 2c, the M–H curves show a typical ferromagnetic character at 3–200 K, i.e., the magnetization can reach saturation easily by applying a magnetic field. For better estimating the saturation of magnetization at a high magnetic field, the magnetization curves at various temperatures are normalized based on the data of 2 T (Fig. 2d). Obviously, the normalized magnetization curves at 3–200 K are almost saturated (parallel to the horizontal axis). This means the order of spin alignment changes a little from 3 K to 200 K. The magnetic state basically remains in the ferromagnetic order. However, the magnetization magnitude sharply reduces from 3 K to 200 K for the x = 0.6 compound (Fig. 2a). It is known that both the order of spin alignment and the local magnetic moment size can change the magnetization. Therefore, it indicates that the first transition of FM1-to-FM2 consists of two ferromagnetic states with different local moments. On the contrary, when the temperature exceeds 200 K, the spins gradually depart from the parallel alignment, resulting in the disordered spin direction. Due to the disordered spin alignment, the magnetization curves can hardly reach saturation by applying a magnetic field, which can be reflected from the inclined magnetization curves. It corresponds to the second transition of the ordered ferromagnetic state to a disordered paramagnetic one (FM2-to-PM). Fig. 2b shows the magnetization curves of different components at 5 K, which not only shows the FM and AFM character of (Sc_1−xTi_x)Fe₂ (x = 0, 0.45 and 0.6) and TiFe₂ at low temperature, but also reveals the value of saturation magnetization (M_S) in the order of M_S (x = 0.6) > M_S (x = 0.45) > M_S (x = 0.0) for (Sc_1−xTi_x)Fe₂. The two ferromagnetic states in (Sc,Ti)Fe₂ with different degrees of localization have also been proved in the previous macroscopic magnetic measurements.³¹ It should be noted that such a transition between the two ferromagnetic states is rare in magnetic materials, which is different from the order-to-disorder magnetic transition, such as in Invar alloys (FM–PM)²³ and antiperovskite (AFM–PM).²⁹

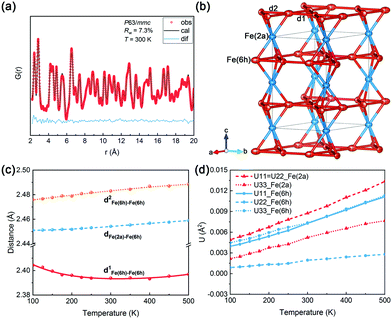
Intuitively, the temperature range of the FM1-to-FM2 transition overlaps with that of NTE at x = 0.6 (Fig. 1 and 2a), indicating that the anomalous thermal expansion property of (Sc,Ti)Fe₂ is entangled with the magnetic behavior. It is well known that NPD is a powerful tool to reveal the microcosmic magnetic structure of magnetic materials. Therefore, variable temperature high-intensity NPD was carried out to study the spin–lattice coupling of (Sc,Ti)Fe₂ (Fig. S8, ESI†). Firstly, the lattice parameters are extracted from the NPD data (Fig. S11, ESI†). One can see that the abnormal thermal expansion of (Sc_0.4Ti_0.6)Fe₂ mainly comes from the shrinkage of the a(b) axis. To further study the reason for the shrinking character in the a(b) axis, it is necessary to observe the change of distance between the magnetic Fe–Fe atoms.

Due to the constraint of crystallographic symmetry, the NPD analysis only gets the “apparent” bond length. In order to directly observe the “true” distance between the Fe–Fe atoms, experiments of PDF analysis of synchrotron radiation X-ray total scattering were carried out in NTE (Sc_0.4Ti_0.6)Fe₂. As shown in Fig. 3a, the hexagonal model (P6₃/mmc) can be well reconciled with the experimental PDF data in the temperature range of 100–500 K. Temperature dependence of the pair distance of Fe–Fe obtained from PDF analysis is shown in Fig. 3c, which is similar to that obtained from the NPD data (Fig. S12, ESI†). Therefore, the local structure is consistent with the average structure in the present (Sc,Ti)Fe₂ alloys. It is interesting to find that only the nearest distance of Fe(6h)–Fe(6h) (d¹) lying in the ab plane shrinks in the NTE temperature range (Fig. 3b), while the other ones expand. This phenomenon may be on account of that the nearest distance of Fe(6h)–Fe(6h) controls the magnetic interaction of (Sc,Ti)Fe₂. The fact that the distance of the magnetic atoms controls magnetism has been found in other magnetic materials, such as the pressure dependence of magnetism in Mn₃Ga_0.95N_0.94.³³ Furthermore, anisotropic atomic displacement parameters (ADPs) of Fe atoms are extracted from the PDF analysis (Fig. 3b and d). Obviously, the ADPs along the a(b) and c axis have little difference, which means the thermal vibration of Fe atoms is nearly isotropic. Therefore, the PDF analysis can exclude the phonon induced type NTE mechanism, and further reveal that the abnormal thermal expansion of (Sc,Ti)Fe₂ is related with the magnetic interaction.

Fig. 3 The local structure analysis for (Sc_0.4Ti_0.6)Fe₂. (a) Pair distribution function (PDF) fit of synchrotron radiation X-ray total scattering obtained at room temperature for the NTE (Sc_0.4Ti_0.6)Fe₂. (b) The anisotropic atomic displacement ellipsoids of Fe atoms in (Sc,Ti)Fe₂. (c) Temperature dependence of the pair distance of Fe–Fe obtained from the PDF analysis. (d) Temperature dependence of anisotropic atomic displacement parameters of Fe atoms of the NTE (Sc_0.4Ti_0.6)Fe₂.

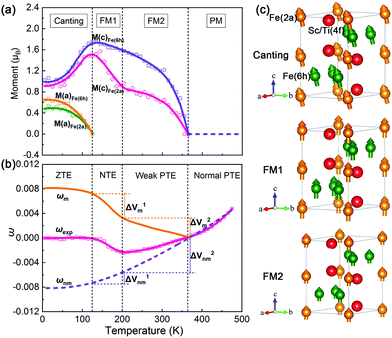
Fig. 4 shows the spin–lattice coupling effect of (Sc,Ti)Fe₂, which is revealed by the variable temperature high-intensity NPD. The details of the magnetic structure analysis of (Sc,Ti)Fe₂ can be found in the ESI.† For the NTE compound of x = 0.6, it has four magnetic configurations in the investigated temperatures (Fig. 4): canting, FM1, FM2, and PM. The magnetic moments of the Fe element can be calculated from the structure refinements of the NPD patterns, which are not obtained from the macroscopic magnetic measurements. These magnetic moments stand for the average atomic moments or ordered moments. As shown in Fig. 4a, the average magnetic moments of x = 0.6 are shown along the a and c axis for different Fe sites, which can be divided into four pronounced regions. In the canting region (T < 125 K), the Fe magnetic moments gradually turn from the canting spin alignment to the c-axis paralleled one with increasing temperature. It also means that the Fe moments increase to the maximum value along the c axis at 125 K, while gradually going down to zero along the a axis. The total local moments at Fe(2a) and Fe(6h) change little in the canting region (Fig. S13, ESI†). It needs to be noted that it is the first time that a canting magnetic structure has been observed in the x = 0.6 compound.³¹ In the FM1 region (125 K < T < 205 K), the decrease of average moments is mainly caused by the reduction in the intrinsic atom magnetic moments, since the degree of FM order has little changes (Fig. 2). Intriguingly, there is a sharp reduction in the ferromagnetic moments at Fe(2a) from 1.49 to 0.96 μ_B, but it remains nearly constant at Fe(6h). Therefore, the FM1-to-FM2 transition of (Sc,Ti)Fe₂ is mainly attributed to the decrease of the Fe(2a) ferromagnetic moment, which is similar to the previous studies.³⁴ In the FM2 region (205 K < T < 365 K), the average moments gradually decrease to zero when reaching T_C, due to the magnetic structure configuration transition from the ordered spin (FM2) to the disordered one (PM). Such transition is often observed in ferromagnetic materials, such as Invar alloys.²²

Fig. 4 The spin–lattice coupling effect of (Sc,Ti)Fe₂. (a) The average ferromagnetic moments of x = 0.6 along the a and c axis for different Fe sites. (b) Thermal expansion of x = 0.6. The spontaneous volume magnetostriction (ω_m) is calculated by subtracting the contribution of nonmagnetic phase (ω_nm) to thermal expansion from the experiment one (ω_exp). ΔV_m and ΔV_nm denote the contributions from MVE and nonmagnetic phase, respectively. (c) The magnetic structure of canting, FM1, and FM2.

To better observe the lattice's response to the change of average magnetic moment in (Sc_0.4Ti_0.6)Fe₂, its thermal expansion can be divided into four types on the basis of the magnitude of CTE (Fig. 4b), i.e., ZTE (α_V = −0.87 × 10⁻⁶ K⁻¹, 5–125 K), NTE (α_V = −28.36 × 10⁻⁶ K⁻¹, 125–205 K), weak PTE (α_V = 15.33 × 10⁻⁶ K⁻¹, 205–365 K), and normal PTE (α_V = 43.15 × 10⁻⁶ K⁻¹, 365–475 K). When compared with Fig. 4a and b, the four regions of thermal expansion are almost consistent with that of magnetic moments, which indicates that the thermal expansion of (Sc_0.4Ti_0.6)Fe₂ is determined by the change of Fe magnetic moments.

To quantitatively describe the contribution of the magnetic moment to the thermal expansion, the spontaneous volume magnetostriction (ω_m) can be calculated by subtracting thermal expansion of the nonmagnetic phase (ω_nm) from the experimental (ω_exp) one (Fig. 4b). It can be regarded that MVE has little influence on the thermal expansion of ScFe₂ below 365 K, since its magnetization hardly changes (Fig. 2a). Therefore, the ω_nm value of (Sc_0.4Ti_0.6)Fe₂ can approximately be identical to the experimental thermal expansion of ScFe₂. Intuitively, ω_m almost remains constant in the ZTE region, and gently decreases in the weak PTE region, but sharply decreases in the NTE region. For explaining this phenomenon, the change of the Fe moments is combined with thermal expansion. Firstly, for better describing MVE, ΔV_m and △V_nm denote the negative contribution from MVE and the positive contribution from nonmagnetic phase to thermal expansion, respectively. Thermal expansion of (Sc_0.4Ti_0.6)Fe₂ is a result of the balance of ΔV_m and ΔV_nm. In the ZTE region of 5–125 K, the total local moments at Fe(2a) nearly have no change (Fig. S13, ESI†), and ZTE occurs due to little changes in both ΔV_m and ΔV_nm. In the NTE region, a sharp decrease of intrinsic moments at Fe(2a) makes ΔV_m¹ exceed ΔV_nm¹, so NTE occurs (125–205 K). It is not difficult to understand the weak PTE in 205–365 K, since the contribution from ΔV_m² cannot completely counteract the role of ΔV_nm².

It is to be noted that the FM2-to-PM transition in (Sc,Ti)Fe₂ is a conventional order-to-disorder transition, while the FM1-to-FM2 one can be regarded as the UMVE in which an intrinsic moment decrease happens. As shown in Fig. 4b, the negative contribution to thermal expansion from the UMVE (ΔV_m¹) is stronger than that from the conventional MVE (CMVE) (ΔV_m²). Therefore, it may be easier to induce NTE from the decrease of intrinsic moments. Similarly, the previous study has found that the decrease of intrinsic moments can enhance other magnetic effects; for example, the decrease of Mn intrinsic moments has been reported to enhance the barocaloric effect in Mn₃GaN.³⁵

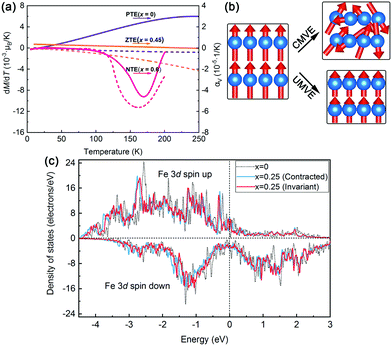
To more clearly find the mechanism determining the PTE-to-NTE crossover in (Sc,Ti)Fe₂, the rate of the Fe(2a) magnetic moments (M_Fe(2a), dM/dT) and the value of α_V are compared for three representative compositions (x = 0.0, 0.45, and 0.6) as shown in Fig. 5a. Obviously, there is a strong correlation in both dM/dT and α_V. For example, when M_Fe(2a) decreases sharply, NTE occurs (x = 0.6); however, when M_Fe(2a) remains almost constant, a normal PTE occurs (x = 0.0). This means that the thermal expansion can be tuned by controlling the decrease of intrinsic magnetic moment in the FM1-to-FM2 transition. For example, a ZTE property can be achieved in Sc_0.55Ti_0.45Fe₂ (α_V = 1.24 × 10⁻⁶ K⁻¹, 10–250 K) by adjusting the chemical composition of Ti, since the M_Fe(2a) decreases slightly.

Fig. 5 (a) Temperature dependence of the rate of the magnetic moments (dM/dT) at Fe(2a), and the volume coefficient of thermal expansion (α_V) for x = 0 (PTE), x = 0.45 (ZTE), and x = 0.6 (NTE). (b) The schematic diagrams of CMVE and UMVE. In the UMVE, no change happens in the direction order of spin alignment, but in the reduction of magnitude of magnetic spins; while for the CMVE, an inverse phenomenon happens. (c) Calculated electron density of states of Fe 3d for both ScFe₂ and Sc_0.75Ti_0.25Fe₂. Two conditions are calculated for the Ti-substituted Sc_0.75Ti_0.25Fe₂. One is for constant volume the same as ScFe₂ (invariant) and the other is a contracted one (contracted).

It has been known that with increasing Ti concentration, the magnetic structure of (Sc,Ti)Fe₂ changes from FM to AFM (Fig. 2 and Fig. S5, ESI†). Therefore, the positive magnetic exchange interaction of (Sc,Ti)Fe₂ should be weakened, and the magnetic moments of Fe should decrease. However, there is an unusual phenomenon occurring in the Fe moments. The total magnetic moments for one chemical formula of (Sc,Ti)Fe₂ are calculated by 3/2M_Fe(6h) + 1/2M_Fe(2a) (Fig. S15, ESI†). Obviously, the magnetic moments of (Sc,Ti)Fe₂ increase after a certain content of Ti-substitution (0 ≤ x ≤ 0.6). Such an increase is in good accordance with the above macroscopic magnetic measurement (Fig. 2).

The first-principles calculations are carried out to further explain the interesting phenomenon due to the UMVE. Firstly, the schematic diagrams of the CMVE and UMVE are depicted in Fig. 5b, which clearly shows the difference between both MVEs. The cell volumes of three different magnetic configurations: FM, PM and nonmagnetic (NM) are calculated by DFT for three representative compositions of ScFe₂, Sc_0.75Ti_0.25Fe₂, and Sc_0.5Ti_0.5Fe₂ (Table S1, ESI†). In our calculations, it is interesting to find that the volume contraction between FM and NM is larger than that of FM and PM for all compositions. It means that the reduction in the magnitude of the magnetic spin, i.e. UMVE, can induce more NTE.

Secondly, the electronic structure of ScFe₂ and one Ti substitution (25% Ti) are calculated to explain the change of Fe magnetic moments by Ti substitution. Fig. 5c shows the electron density of states of (Sc_1−xTi_x)Fe₂. To study how the electron doping influences the magnetic moment, the lattice dimension of ScFe₂ is kept invariant, and only one Ti atom substitution is carried out (x = 0.25, Invariant). It is found that the Fermi level moves toward higher energy, i.e., the density of states of Fe d in spin up increase (Fig. 5c). The density of states of Fe d in spin up should be all occupied, but due to the exchange effect, a small part of the electrons in the crystal go to the empty d-orbit of the adjacent atoms, which makes Fe d in spin up lose part of the electrons. The d-orbit of Sc is the emptiest, so the transfer of Fe d electrons in spin up is most obvious, which results in the decrease of Fe magnetic moment. As the Ti substitution for Sc, the d electrons increase, and the transfer of Fe d electrons in spin up becomes difficult. As a result, the Fe magnetic moment is unusually increased. On the other hand, the Ti substitution shrinks the lattice (x = 0.25, Contracted), and the Fermi level moves toward lower energy than that of the invariant lattice, resulting in the reduced magnetic moment of Fe (Fig. 5c). Comparing the above opposite effects, if the former overwhelms the latter, the magnetic moment of Fe can be unusually enhanced after a certain content of Ti-substitution (Fig. 2b and Fig. S15, ESI†).

It has been known that the previous studies on MVE are mostly correlated to the order-to-disorder magnetic transition of FM-to-PM or AFM-to-PM. For example, thermal expansion can be controlled by changing the order-to-disorder magnetic transition for the CMVE, such as Ho₂(Fe,Cr)₁₇,³⁶ antiperovskite manganese nitrides³⁷ and La(Fe,Si,Co)₁₃.²⁵ The ZTE property has also been found in the antiperovskite manganese nitrides (α_V < 1.5 × 10⁻⁶ K⁻¹, 190–272 K),³⁸ Ho₂Fe₁₆Cr (α_V = 1.3 × 10⁻⁶ K⁻¹, 13–330 K),³⁶ and La(Fe,Si)₁₃ (α_V = 1.5 × 10⁻⁶ K⁻¹, 20–275 K).³⁹ The present study on (Sc,Ti)Fe₂ is the first example to show that NTE is caused by a new type of ferromagnetic transition, i.e. FM1-to-FM2.

Conclusions

In summary, an UMVE has been found in the (Sc,Ti)Fe₂ solid solutions, which induces a crossover from the normal PTE of ScFe₂ and TiFe₂ to intriguing NTE and ZTE of (Sc,Ti)Fe₂. A strong NTE property is found in the x = 0.6 compound (α_V = −28.36 × 10⁻⁶ K⁻¹, 125–205 K). Furthermore, a negligible volume coefficient of thermal expansion (α_V = 1.24 × 10⁻⁶ K⁻¹) has been found in Sc_0.55Ti_0.45Fe₂ within a broad temperature range (10–250 K). The PDF analysis verifies that the decrease of the nearest distance of Fe(6h)–Fe(6h) lying in the ab plane results in the shrinkage of the a(b) axis, and excludes the phonon induced type NTE mechanism. The spin–lattice coupling of (Sc,Ti)Fe₂ has been revealed by both variable temperature NPD and macroscopic magnetic measurements. The direct experimental evidence reveals the NTE mechanism that the decrease of intrinsic magnetic moments at Fe(2a) results in the FM1–FM2 transition, which causes a stronger negative contribution to the thermal expansion than the CMVE. By adjusting the chemical composition of Ti in (Sc,Ti)Fe₂, the thermal expansion can be tuned from PTE to NTE or ZTE due to the change in the rate of the FM1–FM2 transition. The first-principles calculations reveal that the UMVE can induce more NTE than CMVE, and explain the abnormal phenomenon of the increased magnetic moment after the Ti-substitution.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (grant no. 21825102, 21731001 and 21590793), and the Fundamental Research Funds for the Central Universities, China (FRF-TP-18-001C2). This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. We thank Dr Chinwei Wang for collecting neutron powder diffraction data at the high-intensity diffractometer Wombat of the Australian Nuclear Science and Technology Organisation (ANSTO).

Notes and references

1. P. Mohn, Nature, 1999, 400, 18.
2. J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522–3567.
3. T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90.
4. C. S. Coates and A. L. Goodwin, Mater. Horiz., 2019, 6, 211–218.
5. J. P. Attfield, Front. Chem., 2018, 6, 1–6.
6. K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001.
7. J. S. O. Evans, P. A. Hanson, R. M. Ibberson, N. Duan, U. Kameswari and A. W. Sleight, J. Am. Chem. Soc., 2000, 122, 8694–8699.
8. X. Su, N. Zhao, S. Hao, C. C. Stoumpos, M. Liu, H. Chen and M. G. Kanatzidis, Adv. Funct. Mater., 2019, 29, 1806534.
9. B. K. Greve, K. L. Martin, P. L. Lee, P. J. Chupas, K. W. Chapman and A. P. Wilkinson, J. Am. Chem. Soc., 2010, 132, 15496–15498.
10. L. Hu, J. Chen, A. Sanson, H. Wu, C. Guglieri Rodriguez, L. Olivi and X. Xing, J. Am. Chem. Soc., 2016, 138, 8320–8323.
11. J. P. Attfield, Nature, 2011, 480, 465–466.
12. A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. Evans, D. A. Keen and M. G. Tucker, Science, 2008, 319, 794–797.
13. M. T. Dove and H. Fang, Rep. Prog. Phys., 2016, 79, 066503.
14. A. Sanson, Chem. Mater., 2014, 26, 3716–3720.
15. M. Azuma, W. T. Chen, H. Seki, M. Czapski, S. Olga, K. Oka and S. Ishiwata, Nat. Commun., 2011, 2, 347.
16. K. Oka, K. Nabetani, C. Sakaguchi, H. Seki, M. Czapski, Y. Shimakawa and M. Azuma, Appl. Phys. Lett., 2013, 103, 061909.
17. P. J. Saines, P. T. Barton, M. Jura, K. S. Knight and A. K. Cheetham, Mater. Horiz., 2014, 1, 332–337.
18. J. Chen, K. Nittala, J. S. Forrester, J. L. Jones, J. Deng, R. Yu and X. Xing, J. Am. Chem. Soc., 2011, 133, 11114–11117.
19. S. Iikubo, K. Kodama, K. Takenaka, H. Takagi, M. Takigawa and S. Shamoto, Phys. Rev. Lett., 2008, 101, 205901.
20. T. Yokoyama and K. Eguchi, Phys. Rev. Lett., 2011, 107, 065901.
21. C. Wang, L. Chu, Q. Yao, Y. Sun, M. Wu, L. Ding, J. Yan, Y. Na, W. Tang, G. Li, Q. Huang and J. W. Lynn, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 220103.
22. C. É. Guillaume, CR. Acad. Sci., 1897, 125, 18.
23. M. van Schilfgaarde, I. A. Abrikosov and B. Johansson, Nature, 1999, 400, 46.
24. T. Yokoyama and K. Eguchi, Phys. Rev. Lett., 2013, 110, 075901.
25. R. Huang, Y. Liu, W. Fan, J. Tan, F. Xiao, L. Qian and L. Li, J. Am. Chem. Soc., 2013, 135, 11469–11472.
26. Y. Song, Y. Qiao, Q. Huang, C. Wang, X. Liu, Q. Li, J. Chen and X. Xing, Chem. Mater., 2018, 30, 6236–6241.
27. P. Álvarez-Alonso, P. Gorria, J. A. Blanco, J. Sánchez-Marcos, G. J. Cuello, I. Puente-Orench, J. A. Rodriguez-Velamazan, G. Garbarino, I. dePedro, J. R. Fernandez and J. L. Sanchez-Llamazares, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 184411.
28. Y. Song, J. Chen, X. Liu, C. Wang, J. Zhang, H. Liu and X. Xing, J. Am. Chem. Soc., 2018, 140, 602–605.
29. S. Iikubo, K. Kodama, K. Takenaka, H. Takagi and S. Shamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 020409.
30. E. Dagotto, Science, 2005, 309, 257–262.
31. Y. Nishihara and Y. Yamaguchi, J. Phys. Soc. Jpn., 1986, 55, 920–935.
32. K. Takenaka and H. Takagi, Appl. Phys. Lett., 2005, 87, 261902.
33. K. Shi, Y. Sun, J. Yan, S. Deng, L. Wang, H. Wu and C. Wang, Adv. Mater., 2016, 28, 3761–3767.
34. M. Saoudi, J. Déportes and B. Ouladdiaf, J. Magn. Magn. Mater., 2001, 231, 265–272.
35. D. Matsunami, A. Fujita, K. Takenaka and M. Kano, Nat. Mater., 2015, 14, 73.
36. S. Dan, S. Mukherjee, C. Mazumdar and R. Ranganathan, RSC Adv., 2016, 6, 94809–94814.
37. K. Takenaka, M. Ichigo, T. Hamada, A. Ozawa, T. Shibayama, T. Inagaki and K. Asano, Sci. Technol. Adv. Mater., 2014, 15, 015009.
38. K. Takenaka and H. Takagi, Appl. Phys. Lett., 2009, 94, 131904.
39. S. Li, R. Huang, Y. Zhao, W. Wang, Y. Han and L. Li, Adv. Funct. Mater., 2017, 27, 1604195.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental methods, computational method and model, magnetic structure analysis and supplementary figures. See DOI: 10.1039/c9mh01025d

---