Design and fabrication of a three-dimensional meso-sized robotic metamaterial with actively controlled properties†
Chenyang
Luo
a,
Yuanping
Song
b,
Chang
Zhao
a,
Sridharan
Thirumalai
a,
Ian
Ladner
a,
Michael A.
Cullinan
a and
Jonathan B.
Hopkins
 *b
*b
aWalker Department of Mechanical Engineering, The University of Texas at Austin, Austin, TX 78712, USA
bDepartment of Mechanical and Aerospace Engineering, University of California, Los Angeles, CA 90095, USA. E-mail: hopkins@seas.ucla.edu
First published on 3rd September 2019
Abstract
Metamaterials can achieve naturally unobtainable properties according to how their microarchitectures are engineered. By incorporating robot-inspired actuators, sensors, and microprocessors within their microarchitectures, still more extreme properties and diverse combinations of properties can be achieved; and their properties can be actively tuned in real time according to uploaded control instructions. Despite the enormous potential of such robotic metamaterials, no three-dimensional designs have been demonstrated because such designs are difficult to make using existing fabrication approaches. Making them with constituent cells small enough to be considered a material instead of a collection of macro-sized robots is even more difficult. Here we demonstrate the first fabricated three-dimensional robotic metamaterial that achieves actively controlled properties. It's cells are meso-sized (5 mm), which make them the smallest robots to date among those intended to work together within a lattice for achieving any objective. We optimize the design's geometry and demonstrate its ability to tune its stiffness as desired using closed-loop control.
New conceptsThis work introduces a robotic metamaterial that consists of meso-sized compliant cells that interact with each other using embedded actuators and sensors to achieve desired system-level properties via active closed-loop control. Each cell possesses a microprocessor at its core that can receive uploaded control instructions, which dictate how the cell responds to the loads and relative displacements of neighboring cells. Using this swarm control approach, desired bulk properties emerge from the metamaterial in response to external loads regardless of how the cells are arranged within the material's lattice. Such materials can achieve unprecedented properties and combinations of properties that are not possible to achieve using natural homogenous materials, composites, or even passive architected materials. Additionally, these properties can be adjusted on demand as rapidly as new instructions can be uploaded to the microprocessors within their lattices. Although, in theory, such materials could be used to satisfy the property requirements of almost any application, they are difficult to fabricate, particularly with cells small enough to be considered a material rather than a collection of macro-sized robots. Here we introduce the first three-dimensional property-controlled robotic metamaterial ever fabricated. Its cells are 5 mm in size and successfully achieve properties via closed-loop control. |
Introduction
Traditional mechanical metamaterials (a.k.a. architected materials) passively achieve desired system-level behaviors primarily from their engineered microarchitecture instead of their composition.1 Robotic metamaterials2 also consist of engineered microarchitectures but these architectures additionally possess embedded actuators and sometimes sensors and micro-processors that enable more advanced system-level behaviors primarily via active control. Such materials require batteries or other external power sources that enable them to achieve extreme behaviors that are not possible using passive materials. Moreover, robotic metamaterials can achieve unprecedented combinations of properties that are either strongly coupled or not compatible within other passive materials. And robotic metamaterials can decouple their properties by independently altering each property in real-time according to uploaded control instructions. Thus, such materials can enable demanding material applications that are currently not possible. Examples include (i) the frames of vehicles that must alter their stiffness and damping properties according to changing ambient conditions to increase speed, fuel efficiency, and comfort during transit, (ii) stabilization tables that adjust their natural frequency to optimally eliminate ambient vibrations, and (iii) endoscopic tools that become appropriately compliant when maneuvering inside a body but become sufficiently stiff when they must cut or separate tissue. Numerous other applications are detailed in Song et al.3 and McEvoy and Correll.2The concept underlying robotic metamaterials originated from the idea of “programmable matter,” proposed by Goldstein et al.,4 where many small robots constitute a large lattice that changes its overall shape when its cell robots change their locations within the lattice. Although numerous programmable-matter-inspired designs have been proposed5–12 many are not structurally practical and do not exhibit repeatable properties because the robots must detach and then reattach to their neighboring cells to change shape and this process produces friction, which is not repeatable. Thus, more recently proposed designs consist of compliant robots that remained permanently joined to one another within a more traditional metamaterial-like lattice, but that are individually controlled to deform in specific ways to produce the desired material shape.13–18
Others have simplified the concept of robotic metamaterials by pursuing designs that use control to alter their system-level properties (e.g., Young's modulus, Poisson's ratio, damping ratio, etc.) instead of changing their bulk shape. Shape-changing robotic metamaterials are more complex because the microprocessors within each robot need to communicate with all the other microprocessors in the lattice to determine the unique commands that need to be sent to corresponding actuators for achieving the desired bulk material shape. Such communication issues are eliminated if the material properties are all that is desired to be control. To successfully control properties only, a common set of command instructions can be uploaded to all of the micro-processors regardless of where their corresponding robots are located within the lattice. When each robot obeys those instructions in response to unique loads imparted on them by their neighbors when the material is externally loaded, the desired system-level properties collectively emerge according to principles of swarm control.19 Although this concept has been proposed for a variety of robotic metamaterial designs,3,20 most such designs have not been demonstrated and those that have been were demonstrated using single macro-sized (>8 cm) two-dimensional (2D) robot cells.3
Despite how promising property-controlled robotic metamaterials are for enabling applications that could not be achieved any other way, fabricating three-dimensional (3D) designs with cell robots that are sub-macro sized has not been demonstrated previously because it is difficult to fabricate such materials with integrated actuators and sensors. Thus, different approaches that are easier to fabricate have been pursued for enabling limited property control within materials for specific applications. For example, temperature is commonly used to change the stiffness of properties of ceramics,21 polymers,22 metal oxides,23 and shape memory alloys.24,25 In more advanced materials, external magnetic,26–28 electrostatic,29,30 or pressure31–33 fields have been used to change the effective stiffness of structures that are filled with particles that react to those fields. Recent metamaterial designs have also utilized electromagnetic locks to change the effective stiffness of the material structure.34
The work proposed here is the first successful attempt at fabricating a 3D meso-robotic metamaterial that achieves its properties via control. The original robotic metamaterial design3 that was proposed to achieve actively controlled properties is not yet possible to fabricate as a functioning material on any scale. As such, a simplified 2D version of the design's cell was fabricated and tested in a previous publication.3 In contrast, the design introduced here uses a new compliant topology that leverages different micro-actuators and sensors to enable the fabrication of the design's cells such that they are not only 3D but are >16× smaller than the 2D version fabricated from the previous publication. Thus, this paper provides the advances necessary to make materials that achieve controllable properties a practical reality instead of a theoretical fascination.
Design and optimization
Design
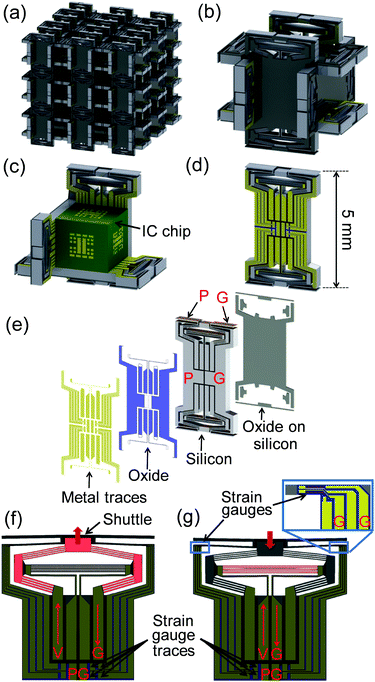
Here we introduce the design of a 3D robotic metamaterial, which can be fabricated with 5 mm-sized robot cells that use integrated actuators and sensors to control the material's mechanical properties. A 3 × 3 × 3 lattice of the design is shown in Fig. 1a and one of its robot cells is shown in Fig. 1b. The envisioned final embodyment of the robotic metamaterial includes an integrated circuit (IC) chip microprocessor (Fig. 1c) located at the center of each cell, which attaches to six actuators (Fig. 1d) using a flip-chip assembly process. Each actuator consists of four primary layers (Fig. 1e)—(1) a silicon handle layer that is coated in a nonconductive oxide (dark grey), (2) a conductive silicon layer (light grey), (3) a nonconductive oxide layer (blue), and (4) a conductive metal trace layer (yellow). The detailed steps for fabricating these actuators is provided in Part A of ESI.† All the IC chips within the lattice are redundantly wired to receive power as long as one power (P) and one ground (G) line are externally attached to any cell actuator within the lattice at the locations labeled P and G in Fig. 1e. This redundant wiring will permit the lattice to function regardless of broken or defective cells. Once powered, each IC chip can obey its uploaded control commands by interacting with its neighboring cells to exhibit desired system-level properties. Two pairs of piezoresistive strain gauges, shown as tiny red traces in Fig. 1f and g, are deposited on opposing sides of the base of the flexures that guide the shuttles of each actuator so that the deformation displacement induced on each cell from its neighbors can be sensed in real time. The strain gauges are wired with traces that route their signals back to the IC chip where a Wheatstone bridge circuit35 processes the displacement of the shuttle. The IC chip can then actuate neighboring cells in response to the measured shuttle displacements. If the IC chip imparts a voltage on the trace labeled V in Fig. 1f, a current will flow through the double-chevron thermal actuator36 (pink) to the ground trace, labeled G, causing the shuttle to push outward on its neighboring cell as the beams within the actuator heat up and expand. If, however, the IC chip imparts a voltage on the trace labeled V in Fig. 1g, current will flow through the other thermal actuator (also pink) to the ground trace, labeled G, causing the shuttle to pull inward on its neighboring cell. Thus, if a high stiffness lattice property is desired, the robot cells within the lattice can resist externally applied loads via control. Or if a low, zero, or even negative stiffness lattice property is desired, the cells can apply a load in the same direction as the externally applied load. Moreover, since actuators oriented in all three orthogonal directions are connected to the same IC chip within any one robot, they can communicate with one another and produce a desired system-level Poisson's ratio. And although thermal actuators typically require a significant time to heat up and cool down, the proposed design could also enable demanding time dependent behaviors such as lattice vibration amplification or damping because the response speeds of the design's actuators approach a kilohertz due to their small size.37 Thus, almost any combination of desired mechanical properties can be achieved via closed-loop control. Note also that fabrication defects or broken features caused by wear will be compensated for by this closed-loop control approach. If the overall lattice is cut or reshaped, it will still be able to exhibit its desired properties similar to other materials with properties that are not dependent on their bulk shape despite the fact that the robot cells along the cut surfaces will no longer function.Optimization
The geometry of the metamaterial design of Fig. 1 was optimized to achieve the largest range of desired programmable properties. The metamaterial's actuators were defined by 11 independent geometric parameters specified in Part B of ESI.† By bounding these parameters to sweep from the smallest feature size that is possible to fabricate to the largest geometrically compatible feature size using sufficiently small resolution increments detailed in Part B of ESI,† the full design space was searched to identify optimal designs. After assigning the correct material properties to the various layers that constitute each actuator as detailed in Part B of ESI,† a finite element analysis (FEA) of each design considered within the parameter sweep was conducted to calculate each actuator design's load capacity and stroke capabilities. COMSOL's structural mechanics, heat transfer, and AC/DC modules were all used to perform the FEA calculations.Specifically, each design's shuttle was held fixed with respect to the central body of its actuator and the maximum voltage was applied to the trace labeled V in Fig. 1f so that the maximum compressive load that the actuator can resist could be calculated. The maximum voltage was found by identifying the highest voltage that could be imparted on the design without causing any of its constituent flexures to yield or buckle or without causing any of its internal elements to exceed a temperature of 750 °C, which would cause thermal degradation of the layers. The maximum compressive load calculated was then multiplied by two (since each robot cell possesses two parallel actuators oriented along each of the three orthogonal directions) and divided by the cross-sectional area of the cell, i.e., (5 mm)2 = 25 mm2, to convert the load into the maximum compressive stress that the lattice can resist with infinite stiffness. The same procedure was used to calculate the maximum tensile stress that the lattice can resist with infinite stiffness except that the maximum voltage was applied to the trace labeled V in Fig. 1g instead of Fig. 1f for each actuator design considered in the parameter sweep. The boundary learning optimization tool (BLOT)38 was then used to identify the design's performance boundary (colored orange in Fig. 2a), which circumscribes the maximum compressive and tensile stresses that all the geometric versions of the metamaterial can resist with infinite stiffness. Note that each blue dot in the plot represents a single geometric version of the design of Fig. 1 generated from the parameter sweep performed. As long as each design version is loaded with stresses between its corresponding maximum compressive and tensile stresses plotted in Fig. 2a, the material can be controlled to achieve any Young's modulus desired including negative values. If a design is loaded with stresses outside of its maximum compressive and tensile stress range, its corresponding Young's modulus can still be controlled but within finite bounds that shrink as the material is loaded with larger compressive or tensile stresses.
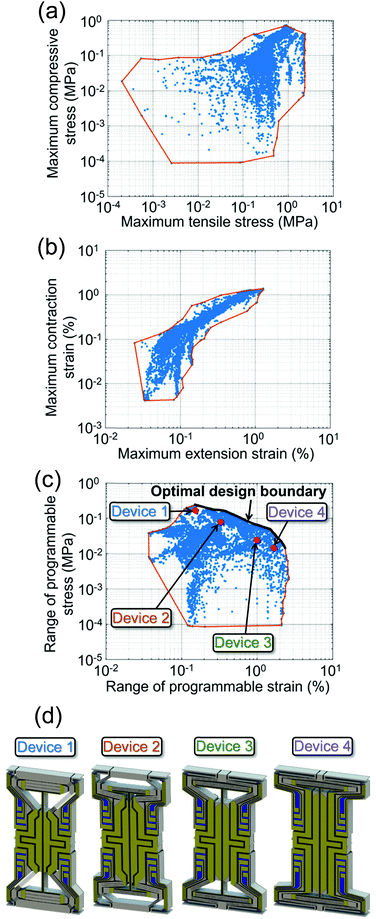 | ||
| Fig. 2 Performance boundary plots generated from a parameter sweep of the design of Fig. 1 showing (a) maximum compressive and tensile stresses, (b) maximum contraction and extension strains, and (c) the ranges of programmable stress and strain for each design version considered in the sweep; (d) four design versions (i.e., devices) that are close to and parallel the optimal design boundary. | ||
The maximum contraction displacement of each design's shuttle was also calculated by subjecting the trace labeled V in Fig. 1g to the largest possible voltage that did not cause any constituent flexures to yield or buckle and did not cause any of the internal elements to exceed a temperature of 750 °C. This maximum contraction displacement was then multiplied by two (since each actuator has two shuttles at either end) and divided by the cell size (i.e., 5 mm) to convert the calculated displacement into the maximum contraction strain that the lattice design can achieve. The same procedure was used to calculate the maximum extension strain that each lattice design can achieve except that the maximum voltage was applied to the trace labeled V in Fig. 1f instead of Fig. 1g for each actuator design considered in the parameter sweep. BLOT was again used to identify the design's performance boundary (colored orange in Fig. 2b), which circumscribes the maximum contraction and extension strains that all the geometric versions of the metamaterial can achieve.
Optimal designs were identified by plotting the range of programmable stress of each design in the parameter sweep versus their range of programmable strain as shown in Fig. 2c. The range of programmable stress of each design was calculated by adding its corresponding maximum tensile stress plotted in Fig. 2a with its corresponding maximum compressive stress in the same figure. Note that both values are shown as being positive. The range of programmable strain of each design was calculated by adding its corresponding maximum extension strain plotted in Fig. 2b with its corresponding maximum contraction strain in the same figure. All optimal designs lie on the portion of the orange boundary that is shown black and labeled in Fig. 2c. Metamaterial designs that achieve larger ranges of programmable strain at the expense of their range of programmable stress lie on the right side of this black boundary while designs that achieve larger ranges of programmable stress at the expense of their range of programmable strain lie on the left side of the same boundary. Since most of the optimal designs along this boundary possess geometric features that challenged the limits of our fabrication approach, four different design examples (shown as red dots and labeled as devices 1 through 4 in Fig. 3c) were selected that lie along a line that is close to and parallels the black optimal design boundary, but that were more likely to survive the fabrication process. Computer-aided design (CAD) models of the four designs are shown in Fig. 2d. Their geometric parameters are provided in Part C of ESI.†
Fabrication and testing
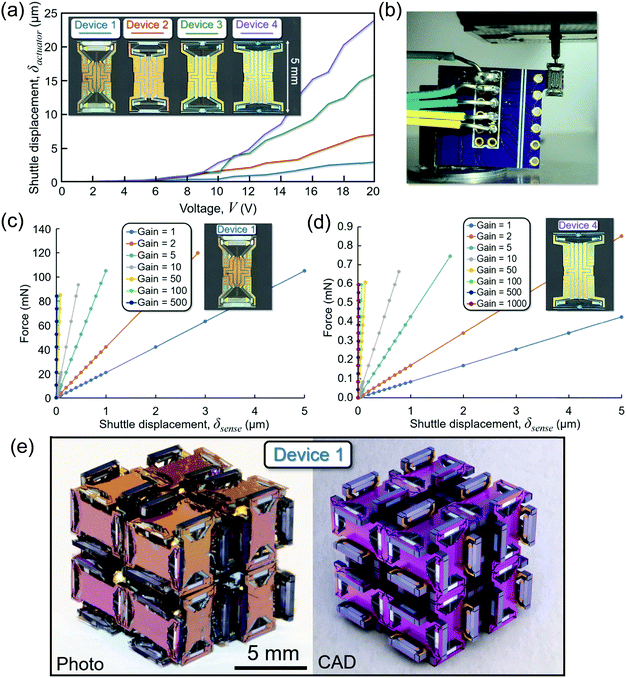
Photographs of each of the four devices fabricated using the approach detailed in Part A of ESI† are provided in Fig. 3a. A plot of applied voltage versus the resulting displacement measured for the four fabricated devices’ actuator shuttles is provided in the same figure. The data in the plot was collected using digital image correlation with a Basler acA4024 CMOS camera mounted on a Cascade Microtech MPS150 probe station. Note from Fig. 3a that device 1 achieves the smallest stroke (i.e., shuttle displacement capability) while device 4 achieves the largest stroke as expected from the plot of Fig. 2c. The remainder of the measured results focus on devices 1 and 4 since those devices achieve the smallest and largest ranges of programmable strain respectively but also achieve the largest and smallest ranges of programmable stress respectively. The results of Fig. 3a and| δactuator = CV2, | (1) |
Force versus displacement plots of the actuator shuttles of devices 1 and 4 were then measured using a Hysitron TI 950 Tribolndenter (Fig. 3b) to determine the natural stiffness, ko, of each device with no voltage applied. The natural stiffness of devices 1 and 4 were measured to be 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013 N m−1 and 85.2 N m−1 respectively. Using these measurements, eqn (1), and
013 N m−1 and 85.2 N m−1 respectively. Using these measurements, eqn (1), and
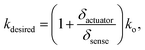 | (2) |
The test setup of Fig. 3b was then used to characterize the open-loop stiffness tunability of devices 1 and 4. This was done by applying a force on the actuator shuttles using the Tribolndenter and then measuring the resulting displacement of the shuttle, δsense. The voltage, V, was then identified using eqn (1) and (2) that allowed the actuator to achieve desired stiffness values by changing the applied force load to achieve any desired displacement. Only individual devices were tested rather than entire cells due to the limited space in the Tribolndenter setup, but the cells should work the same as the individual devices due to the fact that each device is running its own independent control loop with its own sensors and actuators. Fig. 3c and d show the ability of devices 1 and 4 to tune their stiffnesses over a range of gains where the gain, Ga, is the ratio of the desired stiffness to the natural stiffness of the device according to
| Ga = kdesired/ko. | (3) |
For all cases, the total voltage applied to the actuators was limited to 12 V in order to avoid thermal damage.
As demonstrated by Fig. 3c, device 1 can achieve an infinite stiffness of up to a total applied force of 87 mN. In other words, the actuator is able to push back on the indenter with enough force that total displacement of the indenter is zero up to a force of 87 mN. When the force is increased above 87 mN, the maximum achievable gain drops. For example, for a force of 100 mN the maximum achievable gain is about seven which means that the stiffness of the structure can only be tuned up to seven times its natural stiffness at this force level. For gains greater than 3, the maximum force limit of the nanointentor of 120 mN is reached, which prevents additional testing beyond this range.
The natural stiffness of device 4 is ∼250 times less than device 1 so the maximum force over which the device can achieve infinite stiffness is only ∼600 μN. But since device 4 is much less stiff than device 1, it can achieve much higher shuttle displacements. For example, with a gain that produces 5 times the stiffness, device 4 can achieve a displacement of 1.75 μm while device 1 can only achieve a displacement of 1 μm (Fig. 3d). Unfortunately, the Tribolndenter of Fig. 3b is only capable of testing up to a displacement of 5 μm so for gains less than ∼2.4, the full range of possible strains cannot be tested. However, these results demonstrate the ability to optimize and test different metamaterial versions of the design of Fig. 1 with various tradeoffs between their ranges of programmable stress and strain.
Conclusions
Fig. 3e provides a photograph and a computer-aided design (CAD) model rendering of a fabricated 2 × 2 × 2 robot-cell lattice consisting of device 1 actuators, which demonstrate that any arbitrarily large lattice could be fabricated using these base devices. Details pertaining to the envisioned production assembly of large lattices of such actuator devices is provided in Part D of ESI.† With the photograph of Fig. 3e and the data collected in Fig. 3, we have shown that traditional microfabrication approaches can be used to produce 3D meso-robotic metamaterials consisting of sub-macro-sized cell robots with programmable mechanical properties that can be tuned over large ranges using uploaded control instructions. These results provide a key breakthrough toward enabling true robotic metamaterials with small enough cell sizes to more accurately justify their classification as materials rather than as collections of discrete macro-scale robots.Conflicts of interest
There are no conflicts of interest.Acknowledgements
This work was supported by AFOSR award number FA9550-18-1-0459 and based on work accomplished at Texas Nanofabrication Facilities supported in part by the National Science Foundation under The National Nanotechnology Coordinated Infrastructure (grant EECS-1542159). The authors acknowledge program officer Byung “Les” Lee. Author contributions: C. L. did most of the fabrication and testing of the devices. Y. S. performed all FEA optimizations and generated the plots of Fig. 2. C. Z. helped finalize the device designs for fabrication. S. T. aided in testing the devices. I. L. aided with the design and testing of the devices. M. A. C., advised his students and helped to draft the manuscript. J. B. H. generated the concept for the paper, designed the initial device of Fig. 1, managed the project, made the figures, and helped to draft the manuscript.References
- N. A. Fleck, V. S. Deshpande and M. F. Ashby, Proc. R. Soc. London, Ser. A, 2010, 466, 2495–2516 CrossRef CAS.
- M. A. McEvoy and N. Correll, Science, 2015, 347, 1261689 CrossRef CAS.
- Y. Song, P. C. Dohm, B. Haghpanah, A. Vaziri and J. B. Hopkins, Adv. Eng. Mater., 2016, 18, 1113–1117 CrossRef.
- S. C. Goldstein, J. D. Campbell and T. C. Mowry, Computer, 2005, 38, 99–101 Search PubMed.
- D. Rus and M. Vona, Proceedings 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), IEEE, vol. 4, pp. 2513–2520.
- J. W. Suh, S. B. Homans and M. Yim, in Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), IEEE, vol. 4, pp. 4095–4101.
- S. Vassilvitskii, J. Kubica, E. Rieffel, J. Suh and M. Yim, in Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), IEEE, vol. 1, pp. 801–808.
- P. J. White and M. Yim, in 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, 2007, pp. 2773–2778.
- S. Murata, H. Kurokawa, E. Yoshida, K. Tomita and S. Kokaji, in Proceedings. 1998 IEEE International Conference on Robotics and Automation (Cat. No. 98CH36146), IEEE, vol. 1, pp. 432–439.
- J. Bishop, S. Burden, E. Klavins, R. Kreisberg, W. Malone, N. Napp and T. Nguyen, in 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, 2005, pp. 3684–3691.
- P. White, V. Zykov, J. Bongard and H. Lipson, in Robotics: Science and Systems I, Robotics: Science and Systems Foundation, 2005.
- K. Gilpin, A. Knaian and D. Rus, in 2010 IEEE International Conference on Robotics and Automation, IEEE, 2010, pp. 2485–2492.
- E. Hawkes, B. An, N. M. Benbernou, H. Tanaka, S. Kim, E. D. Demaine, D. Rus and R. J. Wood, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 12441–12445 CrossRef CAS.
- A. I. Nawroj, J. P. Swensen and A. M. Dollar, IEEE Trans. Robot., 2017, 33, 796–806 Search PubMed.
- A. I. Nawroj and A. M. Dollar, IEEE Robot. Autom. Lett., 2017, 2(4), 1878–1881 Search PubMed.
- L. A. Shaw and J. B. Hopkins, J. Mech. Robot., 2015, 8, 021019 CrossRef.
- Z. Lou, L. Wang, K. Jiang and G. Shen, Nano Today, 2019, 26, 176–198 CrossRef CAS.
- M. A. McEvoy and N. Correll, Soft Robot., 2018, 5, 6 Search PubMed.
- M. Brambilla, E. Ferrante, M. Birattari and M. Dorigo, Swarm Intell., 2013, 7, 1–41 CrossRef.
- J. B. Hopkins, Proc. 30th Annu. Meet. Am. Soc. Precis. Eng, Austin, TX, 2015.
- W. Li, R. Wang, D. Li and D. Fang, Phys. Res. Int., 2011, 2011, 1–3 CrossRef.
- R. S. Li and J. Jiao, Int. Microelectron. Packag. Soc, 2000.
- J. B. Wachtman, W. E. Tefft, D. G. Lam and C. S. Apstein, Phys. Rev., 1961, 122, 1754–1759 CrossRef CAS.
- J. Rossiter, K. Takashima, F. Scarpa, P. Walters and T. Mukai, Smart Mater. Struct., 2014, 23, 045007 CrossRef.
- M. R. Hassan, F. Scarpa, M. Ruzzene and N. A. Mohammed, Mater. Sci. Eng., A, 2008, 481–482, 654–657 CrossRef.
- Z. Varga, G. Filipcsei and M. Zrínyi, Polymer, 2006, 47, 227–233 CrossRef CAS.
- S. Abramchuk, E. Kramarenko, D. Grishin, G. Stepanov, L. V. Nikitin, G. Filipcsei, A. R. Khokhlov and M. Zrínyi, Polym. Adv. Technol., 2007, 18, 513–518 CrossRef CAS.
- C. Majidi and R. J. Wood, Appl. Phys. Lett., 2010, 97, 164104 CrossRef.
- A. Bergamini, R. Christen, B. Maag and M. Motavalli, Smart Mater. Struct., 2006, 15, 678–686 CrossRef CAS.
- M. Henke, J. Sorber and G. Gerlach, in Electroactive Polymer Actuators and Devices, ed. Y. Bar-Cohen, 2012, vol. 8340, p. 83401P Search PubMed.
- Y. Shan, M. Philen, A. Lotfi, S. Li, C. E. Bakis, C. D. Rahn and K. W. Wang, J. Intell. Mater. Syst. Struct., 2009, 20, 443–456 CrossRef.
- E. Brown, N. Rodenberg, J. Amend, A. Mozeika, E. Steltz, M. R. Zakin, H. Lipson and H. M. Jaeger, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 18809–18814 CrossRef CAS.
- V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre and D. A. Weitz, Nature, 2001, 411, 772–775 CrossRef CAS.
- B. Haghpanah, H. Ebrahimi, D. Mousanezhad, J. Hopkins and A. Vaziri, Adv. Eng. Mater., 2016, 18, 643–649 CrossRef.
- R. M. Panas, M. A. Cullinan and M. L. Culpepper, Precis. Eng., 2012, 36, 44–54 CrossRef.
- C. Zhao, I. S. Ladner, A. Song, J. B. Hopkins and M. A. Cullinan, Proc. – 32nd ASPE Annu. Meet, Charlotte, NC, 2017.
- S.-C. Chen and M. L. Culpepper, J. Microelectromech. Syst., 2014, 23, 500 Search PubMed.
- A. Hatamizadeh, Y. Song and J. B. Hopkins, Math. Probl. Eng., 2018, 2018, 1058732 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Metamaterial actuator fabrication details, parameter sweep details, and final device parameters. See DOI: 10.1039/c9mh01368g |
| This journal is © The Royal Society of Chemistry 2020 |