Thermally assisted delayed fluorescence (TADF): fluorescence delayed is fluorescence denied†
Daniel Sylvinson Muthiah
Ravinson
 and
Mark E.
Thompson
and
Mark E.
Thompson
 *
*
Department of Chemistry, University of Southern California, Los Angeles, CA 90089, USA. E-mail: met@usc.edu
First published on 5th March 2020
Abstract
High luminescence efficiency is a prerequisite for achieving an electroluminescence (EL) efficiency approaching 100% (photons/electrons). Since the EL process involves the formation of both singlet (S1) and triplet (T1) excitons, this requirement can be further refined to be high luminescence efficiency from both singlet and triplet states, or rapid interconversion between them coupled with high luminescence efficiency from either the singlet or triplet states. A common approach to harvesting S1 and T1 excitons in EL is to use a heavy metal-based emitter, relying on the high spin orbit coupling of a metal ion, such as Ir3+, to promote rapid intersystem crossing and mixing of the S1 and T1 states. An alternative to the use of rare elements like Ir to achieve high EL efficiency involves the use of emitters that harvest S1 and T1 excitons via thermally assisted delayed fluorescence (TADF). In this report, we introduce the routes for efficient radiative decay from S1 and T1 states and describe the TADF process in some depth. The kinetics and efficiency of TADF are analyzed as a function of the energy difference between the S1 and T1 and the rates of emission from each state.
I. Introduction
Molecular materials are important in a wide range of optoelectronic applications, including organic LEDs (OLEDs), photovoltaics and sensors to name a few, with OLEDs having advanced to a significant commercial level, being used in both high performance mobile displays and televisions. In these applications, controlling the interplay between singlet and triplet excited states is critical to maintain high luminescence efficiency (nonradiative decay rate ≪ radiative decay rate). In this paper, we will focus on processes most relevant to OLEDs where high luminescence efficiency and high radiative rate are both important to achieving efficient electroluminescence.Electroluminescence in OLEDs involves hole–electron recombination creating a mixture of singlet (S1) and triplet (T1) excitons or excited states. Spin statistics during recombination leads to formation of S1 and T1 states in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio. The first efficient OLEDs utilized only the singlet excitons, whereas later devices harvested both singlet and triplet excitons.1–4 Understanding how the S1 and T1 states emit and interconvert is important in achieving a high electroluminescence efficiency, ηEL. For the purposes of this paper, we will consider only internal electroluminescence efficiencies, thus ηEL here has a maximum efficiency of 100% (photons/electrons), noting that the external efficiency is less than the internal efficiency by up to a factor of 5, depending on the outcoupling optics used in the device.5–8
3 ratio. The first efficient OLEDs utilized only the singlet excitons, whereas later devices harvested both singlet and triplet excitons.1–4 Understanding how the S1 and T1 states emit and interconvert is important in achieving a high electroluminescence efficiency, ηEL. For the purposes of this paper, we will consider only internal electroluminescence efficiencies, thus ηEL here has a maximum efficiency of 100% (photons/electrons), noting that the external efficiency is less than the internal efficiency by up to a factor of 5, depending on the outcoupling optics used in the device.5–8
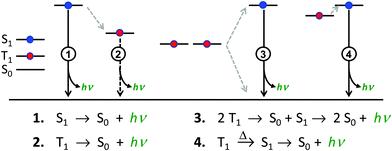
There are four basic processes that give rise to light emission from S1 and T1 states that have been used in efficient OLEDs, illustrated in Fig. 1. The first process, Type 1, involves radiative decay of the S1 state and is commonly referred to as fluorescence. In the absence of a symmetry mismatch between the S0 and S1 states, this process is an allowed transition and typically takes place with a lifetime <10 ns. The second process involves emission from the T1 state (Type 2) and is called phosphorescence. In this case, the direct radiative relaxation from T1 to S0 is spin forbidden, requiring spin–orbit coupling (SOC) or other means to promote radiative decay to the ground state, leading to emission lifetimes of 1 μs–minutes.‡ Phosphorescent lifetimes on μs timescale are typically the result of significant SOC in the luminophore, brought about by heavy atoms such as iridium or platinum.9 In this case, SOC of the heavy metal atom mixes the singlet and triplet states such that the emitting triplet is a linear combination of singlet and triplet states: ϕT1 = C1ϕT + C2ϕS where C1 ≫ C2, leading to μs luminescence. Two other processes illustrated in (Fig. 1) can lead to relatively efficient emission. The Type 3 process is a bimolecular process, involving Triplet–Triplet Annihilation (TTA) to promote one molecule to the S1 state while the other relaxes to S0. This can be thought of as two concerted electron transfers such that spin is conserved: 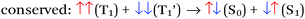 . The S1 state formed in this process then emits as in Type 1. The timescale for emission here is not related to the S1 lifetime, but instead to the rate of diffusion and recombination of the two triplets, often giving measured emission lifetimes in the 10–100 μs range or longer. The last process, Type 4, is a unimolecular process, involving both the S1 and T1 states. Here, the T1 and S1 energies are very close and ambient thermal energy is sufficient to promote the intersystem crossing (ISC) from T1 to S1, which then emits via S1 → S0 (Type 1). This process is most often referred to as Thermally Assisted Delayed Fluorescence (TADF), and typically takes place on the 1–100 μs timescale. The kinetics of this process will be discussed in the third section of this paper. TADF and TTA were both first described by Parker and Hatchard, the former in 196110 and the latter in 1962.11
. The S1 state formed in this process then emits as in Type 1. The timescale for emission here is not related to the S1 lifetime, but instead to the rate of diffusion and recombination of the two triplets, often giving measured emission lifetimes in the 10–100 μs range or longer. The last process, Type 4, is a unimolecular process, involving both the S1 and T1 states. Here, the T1 and S1 energies are very close and ambient thermal energy is sufficient to promote the intersystem crossing (ISC) from T1 to S1, which then emits via S1 → S0 (Type 1). This process is most often referred to as Thermally Assisted Delayed Fluorescence (TADF), and typically takes place on the 1–100 μs timescale. The kinetics of this process will be discussed in the third section of this paper. TADF and TTA were both first described by Parker and Hatchard, the former in 196110 and the latter in 1962.11
Considering that spin statistics of the electroluminescent process gives S1 and T1 excitons in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio, only two of the emission processes outlined above can give rise to OLEDs with ηEL ∼ 100%. OLEDs based on only fluorescence have a limiting efficiency of 25%.1,2,4,12 Similarly, OLEDs based on TTA emission have been reported, but suffer a 50% loss in triplet excitons, severely limiting their theoretical efficiencies.13 Phosphorescence-based OLEDs (Type 2) with efficient ISC from S1 to T1 can give efficiencies of 100%4,14 and are used in virtually every commercial OLED display produced today. The other process that has been demonstrated to give rise to ca. 100% efficient OLEDs involves TADF emitters, Type 4. These materials show tremendous promise.15,16 Phosphorescence from heavy metal based emitters (Type 2) has been well covered in previous reports4,17 and will not be discussed in depth here. Although TADF has also been discussed in some depth elsewhere,18–20 this perspective piece will focus on that process, aiming to discuss TADF in terms that will be useful for any researcher working with luminescent and electroluminescent materials.
3 ratio, only two of the emission processes outlined above can give rise to OLEDs with ηEL ∼ 100%. OLEDs based on only fluorescence have a limiting efficiency of 25%.1,2,4,12 Similarly, OLEDs based on TTA emission have been reported, but suffer a 50% loss in triplet excitons, severely limiting their theoretical efficiencies.13 Phosphorescence-based OLEDs (Type 2) with efficient ISC from S1 to T1 can give efficiencies of 100%4,14 and are used in virtually every commercial OLED display produced today. The other process that has been demonstrated to give rise to ca. 100% efficient OLEDs involves TADF emitters, Type 4. These materials show tremendous promise.15,16 Phosphorescence from heavy metal based emitters (Type 2) has been well covered in previous reports4,17 and will not be discussed in depth here. Although TADF has also been discussed in some depth elsewhere,18–20 this perspective piece will focus on that process, aiming to discuss TADF in terms that will be useful for any researcher working with luminescent and electroluminescent materials.
II. What is and is not fluorescence?
The original definitions of fluorescence and phosphorescence are phenomenological, tied to the time scale of emission. Phosphorescence was discovered in the seventeenth century in inorganic solids and later in molecular materials and characterized as having significantly delayed emission,21 with some on the time scale of minutes. The discovery of fluorescence came much later and was characterized as immediate or nearly immediate emission,21–23 often referred to as prompt emission as opposed to the delayed emission from phosphorescence. Thus, the emission decay rate was initially used as the discriminator of fluorescence and phosphorescence. With a better understanding of the photophysical processes, a more precise set of mechanistically based definitions were proposed to characterize fluorescence as originating from an allowed transition, giving a fast or ultrafast emission rate, and phosphorescence as being the result of a forbidden transition, leading to a very slow radiative rate or delayed emission.21,24 Sometime later another definition became popular, stating that fluorescence involves emission from singlet excited states and that phosphorescence involves emission from triplet states (or other excited states with higher spin multiplicity than the ground state). However, classifying all emission from singlet excited states as fluorescence misses the fact that some S1 → S0 transitions are symmetry forbidden, leading to very long emission lifetimes. For example, the natural radiative lifetime of the S1 state of pyrene is >0.5 μs,25 hardly something that should be referred to as fluorescence from either a phenomenological or mechanistic standpoint. Therefore, definitions of fluorescence and phosphorescence based on the nature of the transition, i.e. allowed or forbidden, offer the “cleanest” way to classify emitters as being fluorescent or phosphorescent, respectively.Considering the definitions given above, Type 2 emission is clearly phosphorescence. Although the SOC of a heavy metal ion imparts some singlet character into the nominally triplet excited state to relax the forbidden nature of the emission, radiative lifetimes of 1–100 μs or longer are common and clearly indicative of a phosphorescent process. A question arises as to whether TADF (Type 4) is fluorescence or phosphorescence. The emitter spends the lion's share of its time in the T1 state (vide infra) and requires ISC to enable spin-forbidden promotion to the S1 state, suggesting that phosphorescence is the best label. However, luminescence in TADF comes primarily from the S1 → S0 transition, thus this step in the emission process is typically an allowed process and could be aptly referred to as fluorescence. It is important to note that organic TADF based emitters have emission lifetimes in the 1–100 μs regime, consistent with the forbidden nature of the prerequisite T1 → S1 ISC process. Therefore, while luminescence in the final step can be classified as fluorescence, it is important to recognize that the emission process is controlled largely by the long-lived T1 state, and the prerequisite ISC process between the T1 and S1 states. Thus, even though TADF carries the name fluorescence within its acronym, the process itself is actually phosphorescence.
III. “Simple” kinetic picture of TADF
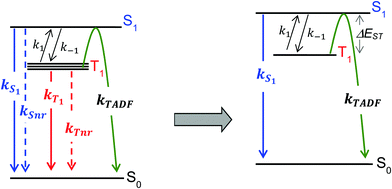
For the purposes of the discussion here, only the kinetics of TADF emitters with the potential to achieve an ηEL of 100% will be considered. A luminescence efficiency near 100% is a prerequisite for achieving a near-unity value for ηEL. This requires that the emission efficiency from T1 and S1 be ∼100%, allowing us to simplify the kinetic scheme significantly by ignoring the nonradiative channels, which by definition are much slower than the radiative rates, as illustrated in Fig. 2. The triplet sublevels in the simplified picture are considered to be degenerate, consistent with the zero field splitting (ZFS) of these levels being markedly lower than the energy difference between the singlet and triplet, ΔEST. It is important to include the rate constants for ISC between the T1 and S1 states. These rate constants are often referred to as reverse ISC (kRISC) for endergonic ISC (T1 → S1) and kISC for exergonic ISC (S1 → T1)26,27 but the simpler labels of k1 for T1 → S1 and k−1 for S1 → T1 will be used here. Using k1 and k−1 eliminates the need for a “reverse” ISC to promote a “forward” TADF. The phosphorescent channel (from T1) can be neglected since kT1 is much smaller than kS1, kISC, and kTADF for TADF emitters. For to outcompete phosphorescence or nonradiative decay from the T1 state, a small exchange energy (ΔEST < 2000 cm−1, 0.25 eV) is required, which becomes an upper limit for the efficient TADF emitters. A common signature of TADF is emission spectra that redshift upon cooling due to the lower T1 energy. Emission due to TADF originates from the S1 state at room temperature, whereas at 77 K, there is insufficient thermal energy to promote the T1 → S1 ISC process and thus emission is from the T1 state, i.e. phosphorescence, albeit with a much longer lifetime. Therefore, estimates of ΔEST are often made by comparing emission spectra measured at room temperature and at 77 K. While this simple approach is a good qualitative measure, temperature effects on the line shape and rigidochromic solvent shifts make this method of estimating ΔEST unreliable. Thus, the best method to determine ΔEST and directly measure the energy difference between the two states is to perform variable temperature photophysical measurements (vide infra).18,28–32
to outcompete phosphorescence or nonradiative decay from the T1 state, a small exchange energy (ΔEST < 2000 cm−1, 0.25 eV) is required, which becomes an upper limit for the efficient TADF emitters. A common signature of TADF is emission spectra that redshift upon cooling due to the lower T1 energy. Emission due to TADF originates from the S1 state at room temperature, whereas at 77 K, there is insufficient thermal energy to promote the T1 → S1 ISC process and thus emission is from the T1 state, i.e. phosphorescence, albeit with a much longer lifetime. Therefore, estimates of ΔEST are often made by comparing emission spectra measured at room temperature and at 77 K. While this simple approach is a good qualitative measure, temperature effects on the line shape and rigidochromic solvent shifts make this method of estimating ΔEST unreliable. Thus, the best method to determine ΔEST and directly measure the energy difference between the two states is to perform variable temperature photophysical measurements (vide infra).18,28–32
Using the simplified three level model of Fig. 2, one only needs to consider three rate constants to evaluate the rate constant and radiative lifetime for TADF, i.e. k1, k−1 and kS1. As we will show below, the relative values of k1 and k−1 can be determined from the energy difference between S1 and T1, ΔEST. Using this simple model gives the kinetic scheme in eqn (1) and the rate expression in eqn (2).
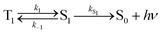 | (1) |
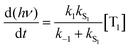 | (2) |
Here, we will consider three cases: kS1 ≫ kISC, kS1 ≪ kISC and kS1 ∼ kISC, where kISC = k1, k−1. Compounds whose kinetics correspond to each of these cases will henceforth be referred to as Class 1, 2 and 3 materials, respectively.
Case 1: kS1 ≫ kISC
This is the simplest case to consider. If we assume that k1 is slower than phosphorescence (kT1), there will be no interconversion between singlet and triplet channels prior to radiative or nonradiative decay, thus both states will relax independently. Emission will be from fluorescence (with the lifetime given by τS1 = 1/kS1) and the T1 will decay nonradiatively. This is the situation found in fluorescence-based OLEDs, and for devices optimized to harvest triplet excitons by TTA.13 Highly efficient fluorescent dyes are designed to have very slow ISC rates since this process can be an efficient nonradiative channel for excited state decay. In fluorescent OLEDs, the dopant gives rise to singlet emission (Type 1) while the triplets nonradiatively decay to the ground state. Thus, in this case, the OLED efficiency is 25% if the triplets do not lead to net emission and 62.5% for fluorescence plus TTA collection of the triplets.13 An alternative is to use two different emitting materials, one that fluoresces with high efficiency and the other phosphoresces at high efficiency, collecting the S1 excitons exclusively at the fluorophore and the T1 excitons at the phosphor. This approach allows for highly efficient, parallel Type 1 and Type 2 processes.33–36Case 2: kISC ≫ kS1
Rapid ISC is the common situation for TADF based emitters that include transition metal ions, particularly those with monovalent group 11 metals. There has been a great deal of recent interest in monovalent copper, silver and gold complexes for TADF.29,30,37–39 Their d10 configuration prevents the nonradiative decay though ligand field states that is prevalent for complexes with metal ions with d1–d9 configurations. The closed shell configuration for the d10 ions does not preclude strong SOC in these complexes, leading to fast ISC rates. TADF emitters built around group 11 metal ions have achieved τTADF as short as 0.5 μs and ΦPL ∼ 1.0.30 If k1 and k−1 are both ≫kS1, a rapid preequilibrium approximation can be used to simplify the rate law given in eqn (2), giving eqn (3), where Keq is the equilibrium constant for T1 ⇄ S1. It is important to stress that once the ISC rate exceeds kS1 by a factor of 50 or more, no further benefit accrues from increasing this rate; i.e. making a rapid preequilibrium even more rapid does not change the kinetics of the overall process.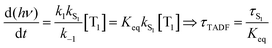 | (3) |
It is important to stress that the individual values of k1 and k−1 are unimportant in this rapid preequilibrium limit, all that matters is their ratio, which gives Keq. This feature leads to an interesting conclusion: if the TADF efficiency is 100%, it becomes possible to determine Keq from time-resolved emission data at short lifetimes. Large SOC constants of the central ion in metal complexes typically push k−1 values into the 1–200 ps regime, allowing for a direct measure of this rate constant from the initial emission decay times. After a few hundred ps, the emission rate settles to the rate given by eqn (3), which is on the 0.5–5 μs time scale. Thus, the ratio of the emission intensity at earliest time (pure S1 emission) to the intensity at long time (>500 ps) is equal to Keq.30 Note that this situation is only true in cases where ΦPL ∼ 1.0, so nonradiative decay can be neglected. Thus, with Keq and τTADF in hand one can easily determine kS1. One can also use the value of Keq to calculate ΔEST as given in eqn (4). The factor of 1/3 in this equation accounts for the three-fold degeneracy of the triplet state.40Fig. 3 shows the luminescence decay traces for two TADF emitters, one with a silver ion and the other a copper ion. These decay traces were generated using time correlated single photon counting methods with a 20 ps excitation source. The two complexes have similar k−1 values (160 and 220 ps, respectively), but very different Keq values (0.13 and 0.02, respectively). These Keq values correspond to ΔEST values of 190 cm−1 for the silver complex and 570 cm−1 for the copper complex (both at 300 K). The ΔEST values obtained this way are comparable to values found using a detailed variable temperature kinetic analysis of the photoemission lifetimes.30
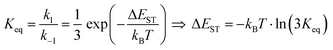 | (4) |
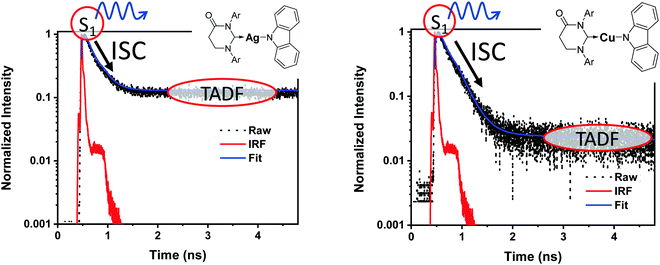 | ||
| Fig. 3 Emission decay traces are shown for silver (left) and copper (right) based TADF emitters.30 The initial decay is due to ISC (S1 → T1). The τTADF values for the two compounds are 500 and 1400 ns, respectively, well outside of the window shown here. | ||
The emission behavior of heavy metal phosphorescent materials, such as those commonly used in OLEDs, can also be treated by a similar analysis to the one given here for Case 2. The emission is well fit to an equation similar to eqn (3), where k1 and k−1 are rates of internal conversion between triplet sublevels, and kS1 is replaced with kTIII, the decay rate constant for the highest lying triplet sublevel (see the ESI† for details).
Case 3: kISC ∼ kS1
When kISC and kS1 are comparable, the situation is more complicated than the two previous cases. The S1 and T1 states cannot be treated independently (Case 1) and cannot be simplified to eqn (2) using a preequilibrium approximation (Case 2). This situation is common for organic TADF emitters, where there are no metal atoms to provide strong SOC. The principal approach that has been used to enhance the ISC rate in these compounds (and move closer to Case 2) is to make the energy difference between the S1 and T1 states very small. A small ΔEST is typically achieved in organic TADF materials by decoupling the donor and acceptor groups involved in a charge transfer excited state.16,18–20 This decoupling is accomplished by designing molecules where the donor and acceptor moieties are oriented orthogonal to each other,41 connected by a nonconjugated linkage42,43 or are on separate molecules (i.e. an exciplex)44,45 The idea of using a small ΔEST to promote ISC makes sense when one considers the parameters that control the TADF rate given in eqn (5) (to a first approximation considering only direct spin–orbit coupling),12,46–49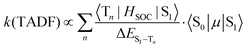 | (5) |
A small value of ΔEST (in eqn (5)) will enhance the rate of TADF; however, there are two other mitigating factors. The spin–orbit coupling operator (HSOC) in organic compounds is typically very small, making the Tn/S1 mixing terms in the numerator small as well. Moreover, the approach that is often used to promote a small ΔEST value is to build electron donor–acceptor luminophores where emission results from a charge transfer transition.16 Minimizing the electronic coupling between the donor and acceptor leads to the desired small ΔEST values, but also markedly decreases the oscillator strength of the S0 → S1 transition, 〈S0|μ|S1〉, and counteracts the effect of a small ΔEST. Therefore, while τTADF values approaching 1 μs have been reported for organic TADF compounds, these lifetimes are rarely achieved and most are longer (τTADF = 5–100 μs).18–20
While the kinetics of emission from Class 3 TADF materials cannot be simplified by a preequilibrium approximation, the kinetics can be simplified by assuming that knr can be neglected (consistent with a high ΦPL) and slow phosphorescence (kT1 can be ignored), leading to eqn (6) following the substitution of k1 according to eqn (4). Emission decay traces for Class 3 emitters are bimodal, with a prompt component for decay from S1 state (ns timescale) and a slower one for TADF (μs timescale). The prompt time constant is often erroneously ascribed to kS1, yet rates for emission from the S1 state (kS1) and ISC from S1 → T1 (k−1) are comparable, so it is not possible to unequivocally determine either rate constant from the prompt luminescence decay.
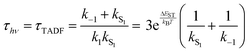 | (6) |
Even the simple treatment in eqn (6) illustrates why decreasing ΔEST has a positive effect on τTADF. Thus, while some approaches to decreasing ΔEST can be counterproductive (vide supra), a small ΔEST is clearly beneficial. Note that while increasing the already fast ISC rate for Class 2 TADF materials does not lead to a smaller τTADF, the same is not true for Class 3 emitters. Increasing k−1 independent of ΔEST will still lead to lower τTADF (as per eqn (6)) until k−1 reaches values much faster than kS1, at which point the emitter will behave like a Class 2 material. The values for k−1 in purely organic molecules generally vary over a wide range spanning 103–1011 s−1.51 However, those molecules that exhibit TADF typically feature rather slow ISC rates (<107 s−1) for reasons outlined below.
Before discussing the strategies being investigated by researchers to boost the ISC rate of organic TADF emitters, it is instructive to offer a brief discussion on the factors that influence ISC. Within the Condon approximation assuming non-dependence of spin orbit coupling (SOC) on vibrational degrees of freedom, the ISC rate (k−1) can be simply expressed according to Fermi's golden rule as:
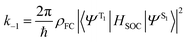 | (7) |
The situation in organic TADF emitters can be improved if energetically close-lying states of different orbital character are introduced that can interact with the 1,3CT states directly via SOC. For such a scenario, the electronic wavefunctions of the S1 and T1 states can now be expressed in terms of the SOC-unperturbed (spin-pure) electronic wavefunctions (ΦSn/Tn) according to first-order perturbation theory in eqn (8).
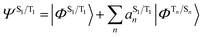 | (8a) |
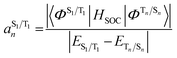 | (8b) |
It is crucial that the new states that couple to the 1,3CT states lie close in energy as the strength of coupling between the states according to eqn (8) is inversely proportional to the energy separation between them. The short-range nature of the HSOC operator indicates that it is beneficial if these states also have significant spatial overlap with the 1,3CT states (for instance, CT or localized excited states featuring one of the molecular orbitals that is also involved in 1,3CT states). This requirement creates a situation again where transition metal ions are advantageous, since they often have degenerate or nearly degenerate d-orbitals that give rise to closely spaced 1,3CT states of differing orbital parentage. It should be noted that the formalism presented above within the Condon approximation assumes that SOC is not dependent on the vibrational degrees of freedom. However, several groups have demonstrated the pivotal role of spin–vibronic coupling mechanisms in facilitating ISC in TADF systems, wherein the S1 and T1 states can couple with each other through spin–orbit and vibronic coupling via close-lying intermediate states (Sn and Tn).55–60
Researchers have sought to improve ISC in organic TADF systems using the mechanisms presented above, with k−1 rates as high as 1011 s−1 thought to be achievable.61 Design strategies have included the introduction of close-lying states capable of coupling with the 1,3CT states through one or a combination of the following approaches: introduction of a manifold of multiple close lying 1,3CT states by attaching multiple donor units to an acceptor core or vice versa,62–64 introduction of LE states (usually 3LE) localized on the donor moieties or the acceptor moieties or both that lie close in energy to 1,3CT states,65–67 and introduction of a functionalized bridging unit between the donor and acceptor units that offers close-lying LE states localized on the bridging unit and CT states (from the donor to bridge and bridge to acceptor).43 Several groups have highlighted the importance of vibrational flexibility of the molecular structure to allow for efficient spin–vibronic coupling between states to boost ISC.56,58,60 Computational tools have been used to identify the specific vibrational modes that are most conducive to ISC among all modes for several systems.58,60 Such studies may aid the rational design of performant TADF chromophores wherein steric interactions along the modes facilitating ISC can be optimally relaxed, while steric blockades along other modes are maintained to minimize non-radiative decay.
Environmental factors also have a significant effect on TADF as ISC rates varying by orders of magnitude across media of different polarity have been reported.61,68,69 This apparent sensitivity to solvent media has been attributed to the fact that the states of different character (e.g., charge transfer vs. π–π*) that couple with each other are affected differently by the polarity of the surrounding matrix, and that the energy separation between them varies accordingly which directly affects the extent of coupling between them (eqn (8)). Therefore, the matrix surrounding the emitter cannot be considered innocuous and can in fact be leveraged as a design parameter to optimize TADF performance.
IV. The not so simple kinetic picture of TADF
In Section III, an important limitation was made and that was that only systems with TADF efficiencies near 100% would be considered. This led to a tremendous simplification of the kinetic equations. It would not be fair to the reader to not show the full kinetic scheme and discuss how this scheme is used to derive the various TADF kinetic parameters, albeit briefly. A number of detailed papers have described the complete kinetic picture of TADF with ϕPL ≤ 100%.18,28–32 Using only the assumption that the three triplet sublevels are degenerate, the TADF rate can be expressed according to eqn (9),70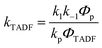 | (9) |
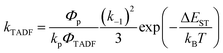 | (10) |
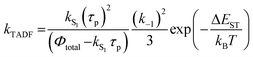 | (11) |
V. Conclusion
High luminescence efficiency is a prerequisite for high electroluminescence efficiency. The electroluminescent process involves the formation of both singlet and triplet excitons, thus high luminescence efficiency from both singlet and triplet states is required, or rapid interconversion between the two states with high luminescence efficiency from either the singlet or triplet state. Careful optimization of OLED structures with emitters that meet the luminescence efficiency prerequisite has enabled internal efficiencies to reach 100% (photons/electrons) and have been subsequently transitioned to commercial applications on a large scale. These high efficiency OLEDs give long operational lifetime for devices emitting light from green to red; however, achieving long operational stability for blue emissive OLEDs remains a challenge. Device lifetime studies have shown that the degradation of blue OLEDs is a consequence of the high energy of the blue exciton and subsequent annihilation events.71–73 TTA can lead to high energy (“hot”) singlet excitons (T1 + T1 → S0 + Sn) whereas triplet–polaron annihilation leads to hot polarons (T1 + H− → S0 + H−*). Both the hot Sn and H−* states formed from blue excitons have sufficient energy to promote bond breaking and decomposition of the emitter and/or host material. Analogous processes take place for singlet excitons; however, the markedly shorter lifetime of the singlet exciton significantly decreases the likelihood of these bimolecular annihilation events. The radiative lifetime of the dopant clearly affects the operational lifetime of the OLED. Iridium based phosphors are the standard for the green and red subpixels of commercial RGB displays. Researchers have worked to decrease the radiative lifetimes of these iridium based emitters, which would be a clear benefit for blue emissive materials; however, achieving lifetimes below 1 μs has proven to be difficult.9 Less research has been performed to date on TADF emitters for OLEDs than for heavy metal complexes, yet their radiative lifetimes show tremendous promise. Although organic TADF materials seem also to be limited to radiative lifetimes ≥1 μs, recent advances in molecular design have the potential to shorten those lifetimes into the nanosecond regime. Notably, radiative lifetimes of 500 ns have been obtained from TADF emitters incorporating group 11 metals (Cu, Ag, Au). The key is to design TADF luminophores that fall in Case 2, so that the ISC rate markedly exceeds the rate of S1 emission. Therefore, while the inorganic photophysical community has focused in the past on heavy metal phosphors, TADF emitters that incorporate transition metal ions may be the answer to achieve short excited state lifetimes, and thus long OLED operational lifetimes.Conflicts of interest
Much of the research referenced above for Case 2 TADF materials was supported by the Universal Display Corporation and one of the authors (M. E. T.) has a financial interest in this company.Acknowledgements
The authors would like to thank Prof. Peter Djurovich for helpful discussion in preparing this manuscript.References
- S. Miyata, Y. Sakuratani and X. T. Tao, Opt. Mater., 2003, 21, 99–107 CrossRef CAS.
- C. W. Tang, S. A. VanSlyke and C. H. Chen, J. Appl. Phys., 1989, 65, 3610–3616 CrossRef CAS.
- A. A. Shoustikov, Y. You and M. E. Thompson, IEEE J. Sel. Top. Quantum Electron., 1998, 4, 3–13 CrossRef CAS.
- M. E. Thompson, P. E. Djurovich, S. Barlow and S. Marder, in Comprehensive Organometallic Chemistry III, ed. D. O’Hare, Elsevier Ltd, Oxford, UK, 1st edn, 2007, ch. 4, vol. 12, pp. 102–194 Search PubMed.
- Y. Qu, J. Kim, C. Coburn and S. R. Forrest, ACS Photonics, 2018, 5, 2453–2458 CrossRef CAS.
- P. Y. Ang, P.-A. Will, S. Lenk, A. Fischer and S. Reineke, Sci. Rep., 2019, 9, 18601 CrossRef CAS PubMed.
- X. Huang, Y. Qu, D. Fan, J. Kim and S. Forrest, Org. Electron., 2019, 69, 297–300 CrossRef CAS.
- M. C. Gather and S. Reineke, J. Photonics Energy, 2015, 5, 57607 CrossRef.
- H. Yersin, A. F. Rausch, R. Czerwieniec, T. Hofbeck and T. Fischer, Coord. Chem. Rev., 2011, 255, 2622–2652 CrossRef CAS.
- C. A. Parker and C. G. Hatchard, Trans. Faraday Soc., 1961, 57, 1894–1904 RSC.
- C. A. Parker and C. G. Harchard, Proc. Chem. Soc., 1962, 147, 10.1039/PS9620000133.
- R. Hamze, P. I. Djurovich and M. E. Thompson, Mater. Energy, 2016, 7, 195–241 CAS.
- D. Y. Kondakov, Philos. Trans. R. Soc., A, 2015, 373, 20140321 CrossRef PubMed.
- C. Adachi, M. A. Baldo, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2001, 90, 5048–5051 CrossRef CAS (citations to date: >3500).
- H. Yersin, Highly Efficient OLEDs, 2018 Search PubMed.
- M. Y. Wong and E. Zysman-Colman, Adv. Mater., 2017, 29, 1605444 CrossRef PubMed.
- H. Yersin, Highly Efficient OLEDs with Phosphorescent Materials, 2007 Search PubMed.
- F. B. Dias, T. J. Penfold and A. P. Monkman, Methods Appl. Fluoresc., 2017, 5, 012001 CrossRef PubMed.
- Y. Liu, C. Li, Z. Ren, S. Yan and M. R. Bryce, Nat. Rev. Mater., 2018, 3, 18020 CrossRef CAS.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- B. Valeur and M. N. Berberan-Santos, Molecular Fluorescence: Principles and Applications, Wiley-VCH Verlag & Co, Weinheim, Germany, 2nd edn, 2013 Search PubMed.
- F. Goppelsröder, J. Prakt. Chem., 1867, 101, 408–414 CrossRef.
- G. G. Stokes, Philos. Trans. R. Soc. London, 1852, 142, 463–562 CrossRef.
- N. J. Turro, Modern Molecular Photochemistry, University Science Books, 1991 Search PubMed.
- K. Hara and W. R. Ware, Chem. Phys., 1980, 51, 61–68 CrossRef CAS.
- S. Xu, Q. Yang, Y. Wan, R. Chen, S. Wang, Y. Si, B. Yang, D. Liu, C. Zheng and W. Huang, J. Mater. Chem. C, 2019, 7, 9523–9530 RSC.
- X. Cai, X. Li, G. Xie, Z. He, K. Gao, K. Liu, D. Chen, Y. Cao and S. J. Su, Chem. Sci., 2016, 7, 4264–4275 RSC.
- T. Palmeira and M. N. Berberan-Santos, J. Phys. Chem. C, 2017, 121, 701–708 CrossRef CAS.
- S. Shi, M. C. Jung, C. Coburn, A. Tadle, M. R. David Sylvinson, P. I. Djurovich, S. R. Forrest and M. E. Thompson, J. Am. Chem. Soc., 2019, 141, 3576–3588 CrossRef CAS PubMed.
- R. Hamze, S. Shi, S. C. Kapper, D. S. Muthiah Ravinson, L. Estergreen, M.-C. Jung, A. C. Tadle, R. Haiges, P. I. Djurovich, J. L. Peltier, R. Jazzar, G. Bertrand, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2019, 141, 8616–8626 CrossRef CAS PubMed.
- C. Baleizao and M. N. Berberan-Santos, J. Chem. Phys., 2007, 126, 204510 CrossRef PubMed.
- T. Hosokai, H. Matsuzaki, H. Nakanotani, K. Tokumaru, T. Tsutsui, A. Furube, K. Nasu, H. Nomura, M. Yahiro and C. Adachi, Sci. Adv., 2017, 3, e1603282 CrossRef PubMed.
- Y. R. Sun, N. C. Giebink, H. Kanno, B. W. Ma, M. E. Thompson and S. R. Forrest, Nature, 2006, 440, 908–912 CrossRef CAS PubMed.
- G. Schwartz, M. Pfeiffer, S. Reineke, K. Walzer and K. Leo, Adv. Mater., 2007, 19, 3672–3676 CrossRef CAS.
- G. Schwartz, S. Reineke, K. Walzer and K. Leo, Appl. Phys. Lett., 2008, 92, 3 CrossRef.
- C. J. Zheng, J. Wang, J. Ye, M. F. Lo, X. K. Liu, M. K. Fung, X. H. Zhang and C. S. Lee, Adv. Mater., 2013, 25, 2205–2211 CrossRef CAS PubMed.
- D. Di, A. S. Romanov, L. Yang, J. M. Richter, J. P. H. Rivett, S. Jones, T. H. Thomas, M. Abdi Jalebi, R. H. Friend, M. Linnolahti, M. Bochmann and D. Credgington, Science, 2017, 356, 159 CrossRef CAS PubMed.
- R. Hamze, J. L. Peltier, D. Sylvinson, M. Jung, J. Cardenas, R. Haiges, M. Soleilhavoup, R. Jazzar, P. I. Djurovich, G. Bertrand and M. E. Thompson, Science, 2019, 363, 601–606 CrossRef CAS PubMed.
- A. S. Romanov, S. T. E. Jones, L. Yang, P. J. Conaghan, D. Di, M. Linnolahti, D. Credgington and M. Bochmann, Adv. Opt. Mater., 2018, 6, 1801347 CrossRef.
- P. F. Jones and A. R. Calloway, Chem. Phys. Lett., 1971, 10, 438–443 CrossRef CAS.
- M. Godumala, S. Choi, M. J. Cho and D. H. Choi, J. Mater. Chem. C, 2016, 4, 11355–11381 RSC.
- Y. Geng, A. D'Aleo, K. Inada, L. S. Cui, J. U. Kim, H. Nakanotani and C. Adachi, Angew. Chem., Int. Ed., 2017, 56, 16536–16540 CrossRef CAS PubMed.
- H. Yersin, L. Mataranga-Popa, R. Czerwieniec and Y. Dovbii, Chem. Mater., 2019, 31, 6110–6116 CrossRef CAS.
- B. Zhang and Z. Xie, Front. Chem., 2019, 7, 306 CrossRef CAS PubMed.
- M. Sarma and K. T. Wong, ACS Appl. Mater. Interfaces, 2018, 10, 19279–19304 CrossRef CAS PubMed.
- J. N. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: An introduction, University Science Book, Sausalito, California, 2009 Search PubMed, ch. 4, section 4.23.
- R. Hamze, P. I. Djurovich and M. E. Thompson, The WSPC Reference on Organic Electronics: Organic Semiconductors, World Scientific, 2016, pp. 195–241 DOI:10.1142/9789813148611_0006.
- R. Baková, M. Chergui, C. Daniel, A. Vlček and S. Záliš, Coord. Chem. Rev., 2011, 255, 975–989 CrossRef.
- A. F. Rausch, H. H. H. Homeier and H. Yersin, in Photophysics of Organometallics, ed. A. J. Lees, Springer Berlin Heidelberg, Berlin, Heidelberg, 2010, pp. 193–235 DOI:10.1007/3418_2009_6.
- M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- J. N. Turro, V. Ramamurthy and J. C. Scaiano, Principles of Molecular Photochemistry: An introduction, University Science Book, Sausalito, California, 2009 Search PubMed.
- M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- B. T. Lim, S. Okajima, A. K. Chandra and E. C. Lim, Chem. Phys. Lett., 1981, 79, 22–27 CrossRef CAS.
- Highly Efficient OLEDs, pp. 257–296 DOI:10.1002/9783527691722.ch8.
- J. Tatchen, N. Gilka and C. M. Marian, Phys. Chem. Chem. Phys., 2007, 9, 5209–5221 RSC.
- J. S. Ward, R. S. Nobuyasu, A. S. Batsanov, P. Data, A. P. Monkman, F. B. Dias and M. R. Bryce, Chem. Commun., 2016, 52, 2612–2615 RSC.
- C. M. Marian, M. Etinski and V. Rai-Constapel, J. Phys. Chem. A, 2014, 118, 6985–6990 CrossRef CAS PubMed.
- C. M. Marian, J. Phys. Chem. C, 2016, 120, 3715–3721 CrossRef CAS.
- M. Etinski, V. Rai-Constapel and C. M. Marian, J. Chem. Phys., 2014, 140, 114104 CrossRef PubMed.
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956–2961 CrossRef CAS PubMed.
- I. Lyskov and C. M. Marian, J. Phys. Chem. C, 2017, 121, 21145–21153 CrossRef CAS.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234 CrossRef CAS PubMed.
- J. Nishide, H. Nakanotani, Y. Hiraga and C. Adachi, Appl. Phys. Lett., 2014, 104, 5 CrossRef.
- D. D. Zhang, M. H. Cai, Y. G. Zhang, D. Q. Zhang and L. Duan, Mater. Horiz., 2016, 3, 145–151 RSC.
- Q. S. Zhang, J. Li, K. Shizu, S. P. Huang, S. Hirata, H. Miyazaki and C. Adachi, J. Am. Chem. Soc., 2012, 134, 14706–14709 CrossRef CAS PubMed.
- F. B. Dias, K. N. Bourdakos, V. Jankus, K. C. Moss, K. T. Kamtekar, V. Bhalla, J. Santos, M. R. Bryce and A. P. Monkman, Adv. Mater., 2013, 25, 3707–3714 CrossRef CAS PubMed.
- F. B. Dias, J. Santos, D. R. Graves, P. Data, R. S. Nobuyasu, M. A. Fox, A. S. Batsanov, T. Palmeira, M. N. Berberan-Santos, M. R. Bryce and A. P. Monkman, Adv. Sci., 2016, 3, 10 Search PubMed.
- R. Ishimatsu, S. Matsunami, K. Shizu, C. Adachi, K. Nakano and T. Imato, J. Phys. Chem. A, 2013, 117, 5607–5612 CrossRef CAS PubMed.
- M. K. Etherington, J. Gibson, H. F. Higginbotham, T. J. Penfold and A. P. Monkman, Nat. Commun., 2016, 7, 7 Search PubMed.
- K. Goushi, K. Yoshida, K. Sato and C. Adachi, Nat. Photonics, 2012, 6, 253–258 CrossRef CAS.
- N. C. Giebink, B. W. D’Andrade, M. S. Weaver, P. B. Mackenzie, J. J. Brown, M. E. Thompson and S. R. Forrest, J. Appl. Phys., 2008, 103, 044509 CrossRef.
- J. Lee, C. Jeong, T. Batagoda, C. Coburn, M. E. Thompson and S. R. Forrest, Nat. Commun., 2017, 8, 15566 CrossRef CAS PubMed.
- S. R. Forrest, Philos. Trans. R. Soc., A, 2015, 373, 20140320 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0mh00276c |
| ‡ Atomic emission from a lanthanide ion is typically a phosphorescent process as well, with a spin mismatch between the ground and excited states making radiative decay a formally spin forbidden process. |
| This journal is © The Royal Society of Chemistry 2020 |