Open Access Article
Open Access ArticleCharge transfer excitons in a donor–acceptor amphidynamic crystal: the role of dipole orientational order†
Joshua W. R.
Macdonald
*a,
Giacomo
Piana
b,
Massimiliano
Comin
 c,
Elizabeth
von Hauff
c,
Elizabeth
von Hauff
 d,
Gabriele
Kociok-Köhn
d,
Gabriele
Kociok-Köhn
 e,
Chris
Bowen
f,
Pavlos
Lagoudakis
bg,
Gabriele
D'Avino
e,
Chris
Bowen
f,
Pavlos
Lagoudakis
bg,
Gabriele
D'Avino
 c and
Enrico
Da Como
c and
Enrico
Da Como
 *a
*a
aCentre for Photonics and Photonic Materials (CPPM) and Department of Physics, University of Bath, Claverton Down, Bath BA2 7AY, UK. E-mail: e.da.como@bath.ac.uk; j.w.r.macdonald@bath.ac.uk
bPhysics and Astronomy, University of Southampton, University Road, Southampton SO17 1BJ, UK
cInstitut Néel CNRS and Université Grenoble Alpes, F-38042 Grenoble, France
dDepartment of Physics and Astronomy, Vrije Universiteit, de Boelelaan 1081, 1081 HV Amsterdam, The Netherlands
eMaterial and Chemical Characterization Facility (MC2), University of Bath, Claverton Down, Bath BA2 7AY, UK
fDepartment of Mechanical Engineering, University of Bath, Claverton Down, Bath BA2 7AY, UK
gSkolkovo Institute of Science and Technology (Skoltech), Skolkovo, Moscow 121205, Russia
First published on 25th August 2020
Abstract
Large amplitude motions in molecular solids are responsible for anomalous electrical characteristics in amphidynamic crystals. We study the effect of orientational dipolar disorder on charge transfer excitons (CTEs) in a donor–acceptor amphidynamic co-crystal of perylene–tetrabromophthalic anhydride (–TBPA). This co-crystal offers long range positional order of alternating donor and acceptor molecular entities arranged in stacks. Further it has a phase transition at 250 K due to progressive freezing of the dipolar orientational motion in the TBPA permanent dipole. The optical absorption band and photoluminescence at the semiconductor gap consists of at least three energetically separated CTE resonances that cover a spectral range of more than 400 meV. As the temperature is lowered below the phase transition the CTE band remains broad, but shows a shift of ∼150 meV to higher energy. On the basis of optical reflectivity, photoluminescence, and model calculations we interpret the room temperature CTE band as a collection of resonances in which at least one the nearest neighbour dipoles to the CTE is flipped from their lowest energy configuration. This first comprehensive optical investigation on an amphidynamic co-crystal demonstrates the importance of understanding the role of permanent dipoles in the CTE photophysics of organic semiconductors.
New conceptsIn donor–acceptor molecular systems the fundamental optical excitations are charge transfer excitons (CTEs). These excitons enter directly into the operation of many optoelectronic devices based on organic semiconductors, for example they determine the power conversion efficiency of solar cells or the light emission colour of light emitting diodes. The common understanding about CTEs is that the HOMO of donors and LUMO of acceptors largely determine the energy of the CTE optical transitions. Commonly those exhibit broad optical signatures in absorption and emission due to structural disorder and molecular vibrations. In this paper we demonstrate that even in a perfectly ordered material system such as a charge transfer single crystal, the CTE absorption and photoluminescence emission is remarkably broad in energy. By using a novel class of materials such as amphidynamic crystals we show how orientational dipolar disorder results in the generation of a series of CTE resonances, all contributing to the observed broad band. By probing the resonances at different temperatures we show how freezing of dynamical disorder still results in residual CTE transition splitting due to electrostatic interactions. Our work provides novel insights into the energetics and photoluminescence efficiency of CTEs and how these crucial parameters could be tuned by a judicious choice of crystalline arrangements of permanent dipoles. |
Introduction
When an electron and a hole straddle over at least two molecules and interact by their mutual Coulomb potential, the most fundamental particle in organic optoelectronics is formed; the charge transfer exciton (CTE). Such excitations dominate the operation of organic light emitting diodes and solar cells,1–3 yet understanding of their underlying physics remains far from being complete. While the role of CTE in electroluminescence is crucially linked to spin dynamics and recombination.4,5 With regard to the photovoltaic effect there is continued debate on the mechanism by which geminate electrons and holes that constitute the CTE are able to spatially separate and escape the coulombic well.6–8 There are a number of factors influencing CTE dissociation in its constituent charged particles which include: electronic delocalization,8–11 interface dipole layers,12 localized dipoles,13 molecular doping,14 entropy,15 and disorder in the local density of states.16,17In addition, the energy of the CTE and its luminescence efficiency are linked to a critically important device parameter; the cell open-circuit-voltage.18 A microscopic understanding of the electrostatic interactions governing the CTE energetics has yet to be addressed in detail, in part due to the chemical diversity of organic semiconductors resulting in a multitude of heterojunctions which can form. These can range from planar two-dimensional interfaces19,20 to molecularly dispersed blends of a donor and an acceptor21 which, while being device relevant, are often microscopically ill defined.11 Furthermore the recent interest in electrostatic phenomena in organic semiconductors22 calls for studies on model structurally defined systems where the effect of dipoles and quadrupoles23 can be controlled.
Here we want to focus on molecularly dispersed systems and clearly the most defined organic material for molecularly dispersed donor–acceptor junctions is a charge transfer co-crystal.24,25 In such solids the electrostatic interactions between two molecules of different electron affinity generate an alternating structure of donor and acceptor molecular entities, thereby building a bulk crystal. It has been firmly established that the photophysics of such co-crystals is dominated by CTEs,26,27 but the role of electronic delocalization, disorder and in particular localized dipoles on the CTE characteristics has remained largely unexplored.27 An opportunity to study the role of localized molecular dipoles has been recently provided by the work of Harada et al.28 Their co-crystal between the donor, perylene, and the acceptor, tetrabromophthalic anhydride (TBPA), is an ideal system to study dipolar effects on CTEs since the acceptor TBPA molecule has a strong permanent dipole, estimated to be 4.5 Debye.28 Interestingly, the TBPA molecules, and thus the dipoles, exhibit a dynamic reorientation by 180° above 250 K, while below this temperature they start to localize in a fixed crystallographic orientation.
Perylene–TBPA can be thus considered an amphidynamic crystal,29–31i.e. a molecular material displaying rapid and large-amplitude molecular motions in the solid state, resulting in unique electrical properties due to the combined effect of electronic structure and dynamic motion. In fact, the decrease in the frequency of TBPA dynamic reorientation leads to a phase transition at 250 K, where the room temperature phase of the co-crystal, that has a relative permittivity of ε = 15, transforms into a low temperature phase (LTP), and is claimed to be anti-ferroelectric.28 In the low temperature anti-ferroelectric phase, TBPA dipoles are fixed and aligned antiparallel within the unit cell. The phase transition leads to a collapse of the relative permittivity to ε = 5 (ref. 28). Thus perylene:TBPA is not only an interesting solid state molecular machine that can be controlled by the application of electric fields, but also a model material system to study the influence of large changes on the dielectric function on the CTE optical properties without modification of the chemical structure.
In this article, we report on the optical properties of perylene–TBPA single crystals as a function of temperature across the phase transition. We show that a broad CTE absorption band, >400 meV, includes several resonances whose energy positions and intensities are sensitive to temperature. The modelling of the optical absorption in the presence of thermal orientational disorder provides an immediate explanation of the HTP broad-band absorption and its features as a direct consequence of the accessible microscopic configurations of TBPA molecules with varying orientations. We also report on the PL which maintains the broad features seen in absorption, but with an increasing intensity of its high energy resonances as the temperature is lowered. The crucial role of dipole disorder on CTE energetics and photophysics is discussed in detail, outlining important implications for next generation materials.
Results
Structure of perylene–TBPA
Fig. 1 shows the crystal structure and unit cell of perylene–TBPA in both its high temperature phase (HTP, Fig. 1a) and low temperature phase (LTP, Fig. 1b). The system is a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal of perylene and TBPA as donor and acceptor, respectively, which are alternately stacked in the unit cell. Donors and acceptors alternate at equal distances and therefore the stack is classified as regular, in contrast to dimerized. In the HTP, the TBPA molecule is seen to reorient 180° in its molecular plane, as indicated by the curved arrows in Fig. 1a. This rotation occurs about a centre of inversion of the unit cell and analysis of the occupation probability from the X-ray experiment shows that the two orientations have the same probability. Conversely, in the LTP the unit cell almost doubles in volume (ESI,† Table S2) and TBPA takes up two opposing orientations in two inequivalent sites of the unit cell. Since TBPA is not a centrosymmetric molecule, the two acceptor molecules per unit cell are oriented with opposite permanent dipoles.
1 co-crystal of perylene and TBPA as donor and acceptor, respectively, which are alternately stacked in the unit cell. Donors and acceptors alternate at equal distances and therefore the stack is classified as regular, in contrast to dimerized. In the HTP, the TBPA molecule is seen to reorient 180° in its molecular plane, as indicated by the curved arrows in Fig. 1a. This rotation occurs about a centre of inversion of the unit cell and analysis of the occupation probability from the X-ray experiment shows that the two orientations have the same probability. Conversely, in the LTP the unit cell almost doubles in volume (ESI,† Table S2) and TBPA takes up two opposing orientations in two inequivalent sites of the unit cell. Since TBPA is not a centrosymmetric molecule, the two acceptor molecules per unit cell are oriented with opposite permanent dipoles.
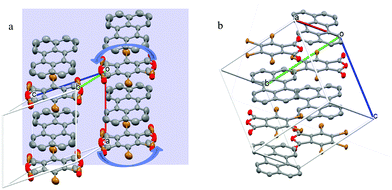 | ||
| Fig. 1 Unit cell of perylene–TBPA in (a) HTP at 290 K and (b) LTP at 150 K. Curved arrows in (a) are included to highlight the TBPA dynamic reorientation. In TBPA the coloured atoms indicate oxygen (red) and bromine (brown). In the HTP of (a) the bromine and oxygen atoms appear superimposed because of the dynamical reorientation. The background plane in (a) represents the crystal face used for optical reflectivity measurements. Unit cell parameters are reported in the ESI.† | ||
A more quantitative examination of the differences between the two phases is shown in Table 1, with a comparison of molecular distances and angles which are relevant for the discussion of optical properties. The smallest distance between the centre of perylene and benzene ring of TBPA reduces by 3–5% between the HTP and LTP, while the maximum distance increases by ∼1%. In the LTP, the TBPA sits at a different angle with respect to each of its neighbouring perylene molecules in its stack (cf.Fig. 1b). Notably, both of these angles are markedly different to the one between the TBPA and perylene in the HTP, which causes the reduction in smallest perylene–TBPA distance measured, while the maximum distance does not change significantly. The difference in angle may also be linked to the dipolar nature of TBPA, where the electron density largely resides on the bromine atoms.28
| Temperature | 290 K (HTP) | 240 K28 (LTP) | 150 K (LTP) |
|---|---|---|---|
| a Distances are calculated as the smallest/largest distance measured between an atom on the central ring of perylene and an atom in the benzene ring of TBPA. Values at 240 K are derived from data collected by Harada et al.28 and deposited on the Cambridge Structure Database. | |||
| Perylene–TBPA minimum distancea | 3.49 Å | 3.39 Å, 3.39 Å | 3.34 Å, 3.36 Å |
| Perylene–TBPA maximum distancea | 5.66 Å | 5.67 Å, 5.74 Å | 5.67 Å, 5.71 Å |
| Perylene–TBPA planar angle | 1.65° | 3.71°, 6.26° | 3.92°, 6.48° |
Optical signatures of CTEs
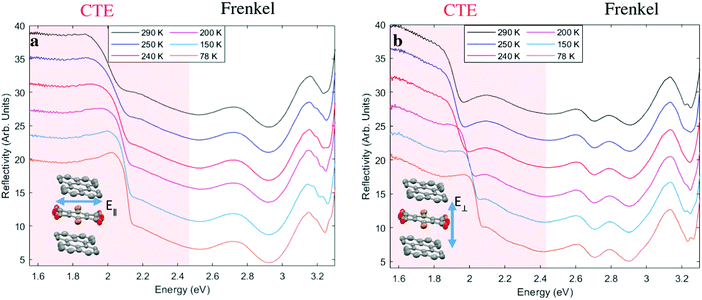
The temperature-dependent optical reflectivity of perylene–TBPA at near-normal incidence is shown in Fig. 2, for polarizations of light parallel and perpendicular to the TBPA long molecular axis as shown in insets. The spectrum can be divided into two regions: the Frenkel exciton region in which excitations are localized on one molecule at photon energies larger than 2.5 eV and the CTE region, involving electron transfer excitations from perylene to TBPA at smaller photon energies. In the Frenkel exciton region, for both polarizations, there is little variation with temperature. The increase in reflectivity at the shortest wavelength edge of our measurement range is due to intramolecular excitations of TBPA, known to absorb in the UV region,28 whereas features between 2.5 eV and 3.1 eV are instead attributed to perylene intramolecular excitations.32In contrast, the CTE region of the spectra reveals distinct temperature-dependent changes in both polarizations. The spectra are dominated by a prominent dip whose edge shifts between 2 eV and 2.15 eV in Fig. 2a, and 1.95 eV to 2.15 eV in Fig. 2b with decreasing temperature. In Fig. 2b, a broad feature is observed in the region 1.6 to 1.85 eV. This weak feature resolves into a more pronounced dip at 1.85 eV as the temperature is lowered.
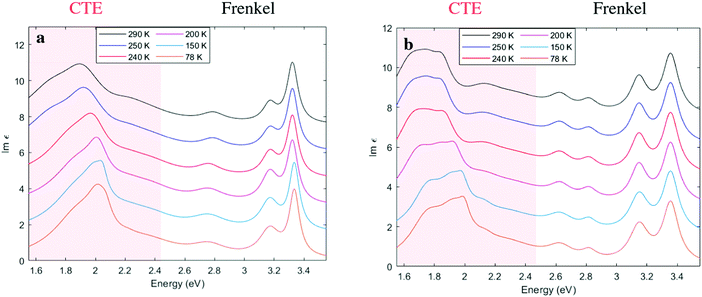
In order to further examine the CTE features from the reflectivity spectra, we performed a Kramers-Kronig consistent transform by fitting a series of Lorentzian oscillators, see Fig. 3. This provides the imaginary part of the dielectric function, Im (ε), in accordance with the procedure in Kuzmenko et al.33 In agreement with the reflectivity data, we can identify in Fig. 3 two regions with different types of excitations: Frenkel excitons and CTEs, the latter delocalized across donor and acceptor. The CTE band is broad, but is also notable for appearing to consist of more than one peak, with a shoulder seen in Fig. 3a and at least three features discernible as the temperature is lowered in Fig. 3b. Below the phase transition at 250 K all the CTE features appear to blue shift without a pronounced spectral narrowing.
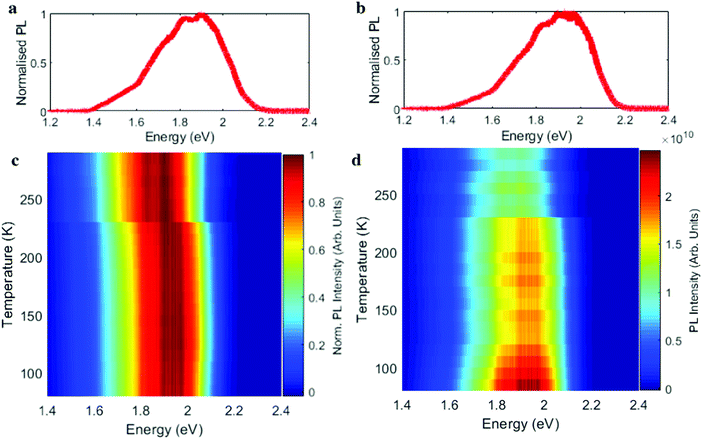
Fig. 4 shows the PL spectrum of perylene–TBPA at different temperatures. The PL at room temperature in Fig. 4a exhibits a peak at 1.9 eV in addition to at least two broad shoulders at 1.7 eV and 1.5 eV, which we attribute to emission from the CTE resonances observed in Fig. 3a. By lowering the temperature to 150 K the dominant PL feature has blue shifted to 1.98 eV, while the shoulders appear reduced in relative intensity; see Fig. 3b. A comprehensive illustration of the temperature dependence is shown by the normalized spectra in Fig. 4c and shows an abrupt blue shift in the PL emission at the phase transition temperature. This behaviour appears in agreement with the absorption characteristics previously seen in Fig. 3a. The PL intensity is instead shown in Fig. 4d and presents an almost step-like increase at the phase transition, together with a further progressive intensity increase below 150 K.
Model and interpretation of spectra
From our optical reflectivity data it appears that the CTE band is composed of at least three excitonic resonances within an energy range from 1.6 eV to 2.0 eV. Such CTE optical resonances appear for light polarized both parallel and perpendicular to the direction of donor–acceptor stack. Such characteristics are rarely seen in other charge transfer co-crystals. The most common optical characteristics in co-crystals with centrosymmetric donor and acceptor pairs is a single CTE transition polarized along the stacking axis and with the only source of band broadening being the coupling to low energy (< 30 meV) phonons.34 Moreover, energetically distinct CTE transitions have been observed only in the presence of an external electric field in Stark effect experiments at cryogenic temperatures.35,36 The explanation for such pioneering experiments resides in the breaking of the centrosymmetric charge distribution of the CTE configuration, which can be D(+)A(−)D or DA(−)D(+) with equal probability. In the presence of an electric field in the stacking direction, the resulting parallel or antiparallel CTE orientations separate at different energies.All the resonances in the CTE band show a strong temperature dependence with clear abrupt changes at the phase transition. On the basis of the very precise X-ray data and the spectroscopic observations we propose a model which is a generalization of the Mulliken trimer model, typically used to describe CTE in donor acceptor co-crystals.34,35,37 Since the reorientation of the permanent dipoles occurs on a microsecond timescale,20 while CTE formation upon light absorption occurs at a much smaller femtosecond timescale, it is safe to consider the dipoles in an instantaneously locked configuration, even in the HTP. However, while in the LTP the orientation of the dipoles is known and can be considered partially frozen, in the HTP it is considered as a collection of thermally accessible configurations.
We rationalize the optical spectra polarized along the stack axis in the framework of a three-state model for an asymmetric D1AD2 trimer (D = perylene, A = TBPA). This picture for low-energy CT excitations, coupled to an electrostatic modelling of the dipolar fields of TBPA molecules provides a simple model to describe the optical spectra, including an account of the effect of orientational disorder. We remark that the model strictly describes CTEs polarized parallel to the stack under the approximation of point-like molecules. However, TD-DFT calculations accounting for the actual shape of the molecules, especially the non-centrosymmetric TBPA, reveal that intra-stack CT transitions present a non-negligible (∼10%) absorption cross section polarized perpendicular to the stack, as further discussed in the ESI.† This, together with the uncertainty associated with the comparison of reflectivity intensities for different polarizations, may rationalize the similar absorption intensities obtained for two light polarization in Fig. 3.
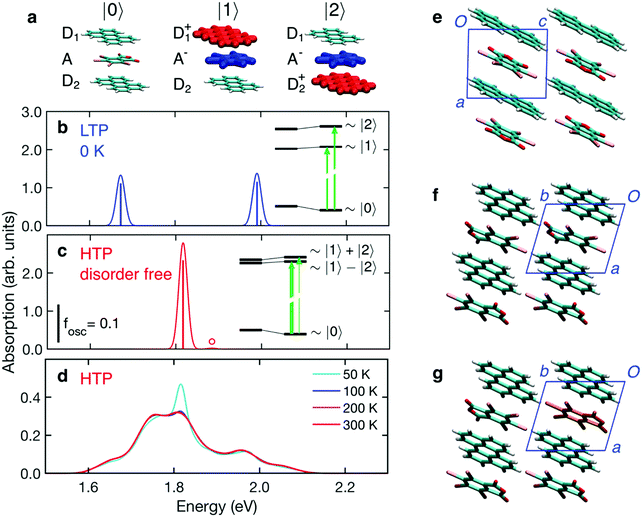
CTE degrees of freedom are described on a minimal basis corresponding to the three lowest-energy charge configurations shown in Fig. 5a, and accounting for intermolecular hopping integrals mixing the basis states. The energies of the CT electronic configurations, |1〉 and |2〉, includes the excitonic electron–hole interaction. Most importantly, these energies are also affected by the electrostatic landscape generated by the molecules surrounding the region where CT takes place. Electrostatic energies are assessed with a simple model where TBPA molecules are described as extended dipoles, which allows calculation of the electrostatic potential at molecular sites retaining the specificities of the crystal packing in the two phases. The model is described in detail in the ESI.†
The LTP crystal structure presents two symmetry inequivalent perylene located on inversion sites. This asymmetry determines different electrostatic potentials, generated by the dipoles of TBPA molecules, at the two D sites, leading to two CT configurations, |1〉 and |2〉, with energies differing by ∼0.3 eV (see inset in Fig. 5b). The absorption spectrum in Fig. 5b is hence characterized by two CT transitions of almost equal oscillator strength, corresponding to an electron transfer from each of the two asymmetric perylenes to the central TBPA. In this calculation we have considered the LTP crystal as a perfect crystalline solid at T = 0 K, i.e. without the possibility of thermal excitations causing the reorientation of any TBPA. The two CTE resonances shown in Fig. 5b are thus the result of the different crystal fields experienced by the two inequivalent perylene, due to the locked dipole of the neighbouring TBPA molecules, with a smaller contribution from intermolecular CT interactions. The inset gives a visual rendering of the two effects.
The structure of the HTP contains only one donor–acceptor pair per unit cell, thus in contrast to the LTP, all perylenes are equivalent. It is, however, characterized by the disorder of TBPA that can be found in two opposite orientations (cf.Fig. 1a). To allow for a microscopic assessment of the dipolar field, we had to resolve the uncertainty in the structure associated with the fractional population of TBPA orientations. We did this by considering that the LTP is the most energetically stable configuration, hence building a hypothetical HTP crystal supercell with TBPA relative orientations analogous to those in the LTP. This hypothetical zero-temperature (disorder-free) HTP crystal structure can be superimposed to the LT one, revealing that, except for the thermal lattice expansion and for small changes in molecular orientations, the two structures are almost identical. We notice that the dipoles of neighbouring TBPA molecules are parallel along the axis b and anti-parallel along a and c (Fig. 5e and f). The resulting nearest-neighbour dipolar interactions are all attractive and stabilize this configuration.
Fig. 5c shows the absorption spectrum calculated for the disorder-free HTP structure. The two perylenes of the trimer are only slightly inequivalent, leading to two CT configurations that differ only by ∼50 meV (see inset in Fig. 5c). In this case, the large majority of the absorption intensity goes to the lowest-energy dipole-allowed excitation, which corresponds to an approximately symmetric electron transfer from the two Ds to the A. The absorption spectrum of this hypothetical disorder-free HTP is hence characterized by a single absorption peak, at an energy in between the two bands calculated for the LTP (cf.Fig. 5b and c).
Having examined the two hypothetical cases above, which do not include disorder in dipole orientations, we turn now on the effect of thermally accessible microscopic configurations, featuring TBPA dipoles that are flipped with respect to the defect-free HTP structure. To achieve this we performed a stochastic sampling of disorder based on our electrostatic model, ultimately enabling the calculation of the absorption spectra at finite temperature, see ESI† for full details on the sampling. The calculated absorption spectrum of the HTP is shown in Fig. 5d and presents a remarkably broad CTE band, extending between 1.6 and 2.1 eV. The band is composed of several peaks and shows a weak dependence on temperature in the relevant temperature window (200–300 K).
The good agreement between the experimental (Fig. 3b) and calculated spectra allows us to ascribe the broad absorption feature to thermal dipolar disorder in the HTP. A closer examination of the calculated and experimental spectra reveals that these are characterized by some partially resolved peaks. Our calculations allow us to assign the most intense band to the absorption of the disorder-free structure (cf.Fig. 5c and d), while other peaks can be assigned to thermally-accessible configurations in which TBPA molecules are flipped with respect to the minimum-energy structure, i.e. “orientational defects”. Fig. 5g shows an example of a single TBPA molecule being rotationally misaligned to its lowest energy configuration. We emphasize that the occurrence of partly-resolved peaks, instead of in a featureless broadening of the main peak, is a specific signature of the discrete nature of dipolar disorder in the HTP, where only two specific molecular orientations of TBPA are possible. A close inspection of the characteristic spectroscopic signature of orientational defects reveals that nearest neighbour dipoles along the a and b crystallographic axis play a major role in contributing to resonances which are 50–150 meV either side of the central 1.8 eV peak. Fig. S3 in ESI† shows a decomposition of the broad spectrum of Fig. 5d, which pinpoints the single TBPA misoriented molecules responsible for each peak.
The clear disagreement between the experimental and calculated absorption spectra of the LPT suggests that residual (quenched) disorder persists below the transition temperature, as also evinced from a careful analysis of X-ray.28 The presence of quenched disorder in the LTP is also consistent with the large activation energy (56 kJ mol−1 = 580 meV) estimated from dielectric measurements,19 which may be associated with energy barriers for TBPA flipping, and with the evidence for a significant relaxation dynamics in the LTP, at least in the proximity of the transition.
Finally, we note the reduced PL intensity in the HTP of Fig. 4b is consistent with having non-radiative channels for CTE recombination. As the rotational motion of TBPA decreases and then ceases with reducing temperature, the structure of Fig. 1b should promote recombination with a decreased number of non-radiative channels. In addition, our estimations of transfer integrals in the two structures show that in the LTP the wave function overlap between perylene and TBPA is higher, thereby promoting radiative recombination. From our experimental data, we see a further increase in PL below ∼150 K, which we believe to correspond with the cessation of the TBPA dynamic motion. This cessation of motion could also explain the CTE peaks of Fig. 3 not shifting further below 150 K and the change in angles presented in Table 1.
Discussion and conclusions
The implications of our studies for the CTE photophysics in systems relevant for organic photovoltaics is immediate. Dipolar interactions at the molecular scale can have dramatic effects on the energy of CTE states. Relative orientations between the dipoles in close proximity to the donor acceptor molecules involved in the CTE determine its energy with shifts up to ∼200 meV. Thus, the CTEs cannot be considered as independent quasiparticles involving only the donor and acceptor, but rather an electron and hole pair interacting with the nearest neighbour permanent dipoles in a complex electrostatic energy landscape. Considering the fundamental link between the CTE energy and the open circuit voltage of organic solar cells, local electrostatics arising from permanent dipoles appears to be a tantalizing opportunity to tune and control the overall efficiency of solar cells. Further work should focus on the supramolecular design of dipolar orientations capable of maximizing high energy CTE resonances with high oscillator strengths and the expenses of low energy non-radiative ones.In conclusion, we have grown perylene–TBPA amphidynamic co-crystals which undergo an order–disorder phase transition with the purpose of studying the effects of dipolar order on the CTEs. We have found that the presence of the dipolar TBPA molecule and its dynamic reorientation in its crystallographic site leads to the splitting of the CTE resonance due to their intertwined electrostatics. As the temperature was lowered below the phase transition and the degree of dipole reorientation reduced, the CTE band shifted to higher energy, but remained intrinsically broad. On the basis of an electrostatic excitonic model we have attributed the broad CTE band to many different resonances arising from misaligned dipoles from their lowest energy configuration. Lastly, PL experiments revealed that the different CTE resonances emit independently over a broad spectrum and with an increased radiative contribution once dipoles cease to reorient. These findings are of importance for the understanding and subsequent design of novel organic and hybrid semiconducting materials, in particular for future organic photovoltaic applications based on supramolecular amphidynamic systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
JM and EDC acknowledge EPSRC and the CDT in New and Sustainable Photovoltaics (project EP/L01551X/1) for funding and support. GP and PL thank the EPSRC for funding (project EP/M025330/1). EDC acknowledges support from the Royal Society for a Wolfson Lab Refurbishment grant (WL120030).References
- K. Vandewal, K. Tvingstedt, A. Gadisa, O. Inganas and J. V. Manca, Nat. Mater., 2009, 8, 904–909 CrossRef CAS PubMed.
- V. Coropceanu, X. K. Chen, T. H. Wang, Z. L. Zheng and J. L. Bredas, Nat. Rev. Mater., 2019, 4, 689–707 CrossRef.
- J. Lee, K. Vandewal, S. R. Yost, M. E. Bahlke, L. Goris, M. A. Baldo, J. V. Manca and T. Van Voorhis, J. Am. Chem. Soc., 2010, 132, 11878–11880 CrossRef CAS PubMed.
- M. Reufer, M. J. Walter, P. G. Lagoudakis, B. Hummel, J. S. Kolb, H. G. Roskos, U. Scherf and J. M. Lupton, Nat. Mater., 2005, 4, 340–346 CrossRef CAS PubMed.
- T. Basel, D. L. Sun, S. Baniya, R. McLaughlin, H. Choi, O. Kwon and Z. V. Vardeny, Adv. Electron. Mater., 2016, 2, 9 Search PubMed.
- H. Bässler and A. Kohler, Phys. Chem. Chem. Phys., 2015, 17, 28451–28462 RSC.
- K. Vandewal, S. Albrecht, E. T. Hoke, K. R. Graham, J. Widmer, J. D. Douglas, M. Schubert, W. R. Mateker, J. T. Bloking, G. F. Burkhard, A. Sellinger, J. M. J. Frechet, A. Amassian, M. K. Riede, M. D. McGehee, D. Neher and A. Salleo, Nat. Mater., 2014, 13, 63–68 CrossRef CAS.
- G. D’Avino, L. Muccioli, Y. Olivier and D. Beljonne, J. Phys. Chem. Lett., 2016, 7, 536–540 CrossRef PubMed.
- M. Hallermann, I. Kriegel, E. Da Como, J. M. Berger, E. von Hauff and J. Feldmann, Adv. Funct. Mater., 2009, 19, 3662–3668 CrossRef CAS.
- A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. Van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 335, 1340–1344 CrossRef CAS.
- D. Fazzi, M. Barbatti and W. Thiel, J. Phys. Chem. Lett., 2017, 8, 4727–4734 CrossRef CAS.
- V. I. Arkhipov, P. Heremans and H. Bassler, Appl. Phys. Lett., 2003, 82, 4605–4607 CrossRef CAS.
- B. Carsten, J. M. Szarko, H. J. Son, W. Wang, L. Y. Lu, F. He, B. S. Rolczynski, S. J. Lou, L. X. Chen and L. P. Yu, J. Am. Chem. Soc., 2011, 133, 20468–20475 CrossRef CAS.
- F. Deschler, E. Da Como, T. Limmer, R. Tautz, T. Godde, M. Bayer, E. von Hauff, S. Yilmaz, S. Allard, U. Scherf and J. Feldmann, Phys. Rev. Lett., 2011, 107, 127402 CrossRef PubMed.
- N. R. Monahan, K. W. Williams, B. Kumar, C. Nuckolls and X. Y. Zhu, Phys. Rev. Lett., 2015, 114, 5 CrossRef PubMed.
- R. A. Street, Adv. Mater., 2016, 28, 3814–3830 CrossRef CAS PubMed.
- K. Tvingstedt, J. Benduhn and K. Vandewal, Mater. Horiz., 2020, 7(7), 1888–1900 RSC.
- D. P. Qian, Z. L. Zheng, H. F. Yao, W. Tress, T. R. Hopper, S. L. Chen, S. S. Li, J. Liu, S. S. Chen, J. B. Zhang, X. K. Liu, B. W. Gao, L. Q. Ouyang, Y. Z. Jin, G. Pozina, I. A. Buyanova, W. M. Chen, O. Inganas, V. Coropceanu, J. L. Bredas, H. Yan, J. H. Hou, F. L. Zhang, A. A. Bakulin and F. Gao, Nat. Mater., 2018, 17, 703–709 CrossRef CAS.
- H. Alves, R. M. Pinto and E. S. Macoas, Nat. Commun., 2013, 4, 7 Search PubMed.
- A. E. Jailaubekov, A. P. Willard, J. R. Tritsch, W. L. Chan, N. Sai, R. Gearba, L. G. Kaake, K. J. Williams, K. Leung, P. J. Rossky and X. Y. Zhu, Nat. Mater., 2013, 12, 66–73 CrossRef CAS.
- V. Belova, P. Beyer, E. Meister, T. Linder, M. U. Halbich, U. Halbich, S. Schmid, T. Zeche, T. Meisel, A. V. Generalov, A. S. Anselmo, R. Scholz, O. Konovalov, A. Gerlach, M. Koch, A. Hinderhofer, A. Opitz, W. Brutting and F. Schreibert, J. Am. Chem. Soc., 2017, 139, 8474–8486 CrossRef CAS.
- G. D’Avino, L. Muccioli, F. Castet, C. Poelking, D. Andrienko, Z. G. Soos, J. Cornil and D. Beljonne, J. Phys.: Condens. Matter, 2016, 28, 433002 CrossRef PubMed.
- M. Schwarze, W. Tress, B. Beyer, F. Gao, R. Scholz, C. Poelking, K. Ortstein, A. A. Günther, D. Kasemann, D. Andrienko and K. Leo, Science, 2016, 352, 1446–1449 CrossRef CAS PubMed.
- M. Pope and C. E. Swenberg, Electronic Processes in Organic Crystals and Polymers, Oxford University Press, Oxford, 1999 Search PubMed.
- K. P. Goetz, D. Vermeulen, M. E. Payne, C. Kloc, L. E. McNeil and O. D. Jurchescu, J. Mater. Chem. C, 2014, 2, 3065–3076 RSC.
- R. J. Dillon and C. J. Bardeen, J. Phys. Chem. A, 2012, 116, 5145–5150 CrossRef CAS PubMed.
- J. Tsutsumi, H. Matsui, T. Yamada, R. Kumai and T. Hasegawa, J. Phys. Chem. C, 2012, 116, 23957–23964 CrossRef CAS.
- J. Harada, M. Ohtani, Y. Takahashi and T. Inabe, J. Am. Chem. Soc., 2015, 137, 4477–4486 CrossRef CAS.
- T. A. V. Khuong, J. E. Nunez, C. E. Godinez and M. A. Garcia-Garibay, Acc. Chem. Res., 2006, 39, 413–422 CrossRef CAS.
- L. Catalano and P. Naumov, CrystEngComm, 2018, 20, 5872–5883 RSC.
- H. Chung, D. Dudenko, F. Zhang, G. D’Avino, C. Ruzié, A. Richard, G. Schweicher, J. Cornil, D. Beljonne, Y. Geerts and Y. Diao, Nat. Commun., 2018, 9, 278 CrossRef PubMed.
- T. Rangel, A. Rinn, S. Sharifzadeh, F. H. da Jornada, A. Pick, S. G. Louie, G. Witte, L. Kronik, J. B. Neaton and S. Chatterjee, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 284 CrossRef CAS PubMed.
- A. B. Kuzmenko, Rev. Sci. Instrum., 2005, 76, 083108 CrossRef.
- A. Brillante and M. R. Philpott, J. Chem. Phys., 1980, 72, 4019–4030 CrossRef CAS.
- D. Haarer, M. R. Philpott and H. Morawitz, J. Chem. Phys., 1975, 63, 5238–5245 CrossRef CAS.
- G. Weiser and A. Elschner, J. Phys. Chem. A, 2009, 113, 6910–6918 CrossRef CAS PubMed.
- A. Painelli and A. Girlando, J. Chem. Phys., 1986, 84, 5655–5671 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1995103 and 1995104. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0mh01044h |
| This journal is © The Royal Society of Chemistry 2020 |