Open Access Article
Open Access ArticleProbing the stability and magnetic properties of magnetosome chains in freeze-dried magnetotactic bacteria
Philipp
Bender
 *a,
Lourdes
Marcano
bc,
Iñaki
Orue
d,
Diego
Alba Venero
*a,
Lourdes
Marcano
bc,
Iñaki
Orue
d,
Diego
Alba Venero
 e,
Dirk
Honecker†
f,
Luis
Fernández Barquín
g,
Alicia
Muela
hi and
M. Luisa
Fdez-Gubieda
jh
e,
Dirk
Honecker†
f,
Luis
Fernández Barquín
g,
Alicia
Muela
hi and
M. Luisa
Fdez-Gubieda
jh
aDepartment of Physics and Materials Science, University of Luxembourg, 1511 Luxembourg, Grand Duchy of Luxembourg. E-mail: philipp.bender@uni.lu; Fax: +352 46 66 44 36521; Tel: +352 46 66 44 6521
bHelmholtz-Zentrum Berlin für Materialien und Energie, 12489 Berlin, Germany
cDpto. Electricidad y Electrónica, Universidad Del País Vasco – UPV/EHU, 48940 Leioa, Spain
dSGIker, Universidad Del País Vasco – UPV/EHU, 48940 Leioa, Spain
eISIS Neutron and Muon Facility, Rutherford Appleton Laboratory, Chilton, OX11 0QX, UK
fLarge Scale Structures Group, Institut Laue-Langevin, 38042 Grenoble, France
gCITIMAC, Universidad de Cantabria, 39005 Santander, Spain
hBCMaterials, Basque Center for Materials, Applications and Nanostructures, UPV/EHU Science, Spain
iDpto. Immunologia, Microbiologia y Parasitologia, Universidad Del País Vasco – UPV/EHU, 48940 Leioa, Spain
jDpto. Electricidad y Electrónica, Universidad Del País Vasco – UPV/EHU, 48940 Leioa, Spain
First published on 27th February 2020
Abstract
Magnetospirillum gryphiswaldense biosynthesize high-quality magnetite nanoparticles, called magnetosomes, and arrange them into a chain that behaves like a magnetic compass. Here we perform magnetometry and polarized small-angle neutron scattering (SANS) experiments on a powder of freeze-dried and immobilized M. gryphiswaldense. We confirm that the individual magnetosomes are single-domain nanoparticles and that an alignment of the particle moments along the magnetic field direction occurs exclusively by an internal, coherent rotation. Our magnetometry results of the bacteria powder indicate an absence of dipolar interactions between the particle chains and a dominant uniaxial magnetic anisotropy. Finally, we can verify by SANS that the chain structure within the immobilized, freeze-dried bacteria is preserved also after application of large magnetic fields up to 1 T.
1 Introduction
Magnetotactic bacteria are microorganisms that are able to align and navigate along geomagnetic fields thanks to the presence of one or more chains of magnetic nanoparticles with high chemical purity synthesized in their interior (i.e., magnetosomes).1,2Magnetospirillum gryphiswaldense for example contains a variable number of cuboctahedral magnetite (Fe3O4) magnetosomes with a mean diameter of 40 nm arranged in a chain.3 This arrangement results from the interplay between the magnetic dipolar interaction, between nearest magnetite crystals, and a complex lipid/protein-based architecture that conform the cytoskeleton.4,5 A previous study of this strain has shown that the magnetosomes arrange in helical-like shaped chains due to the tilting of the individual magnetic moments of the magnetosomes with respect to the chain axis.6 This natural magnetic arrangement can be considered a prototype of a 1D magnetic nanoarchitecture and has motivated various studies to synthesize similar particles7–10 and 1D structures.11–13In general, linear 1D assemblies of magnetic nanoparticles have received considerable interest in various fields including micromechanical sensors,14,15 microfluidics,16 micro-swimmers17 and also fundamental science.18 Different techniques exist to synthesize 1D nanoparticle chains11,12,19–21 however, thanks to the high biological control imposed in the synthesis of the magnetosomes, magnetotactic bacteria produce 1D nanostructures with high reproducibility and quality.22 Due to their exceptional properties magnetotactic bacteria, such as M. gryphiswaldense, remain highly investigated, motivating several experimental studies where their structural23–25 and magnetic properties26–28 were evaluated. In Körnig et al.29 and Blondeau et al.30 it was observed that already small magnetic fields (i.e. small torques) of around 30 mT can be sufficient to break-up the particle chains within alive but immobilized bacteria.
In this work we investigate the response of freeze-dried magnetotactic bacteria to large magnetic fields up to 1 T. We use a combination of DC magnetometry and small-angle neutron scattering (SANS) to determine the magnetic properties of the individual magnetosomes and the chains. From the polarized SANS results we can gain additionally insight into the nanostructure of the 1D chains, enabling us to test their mechanical stability in high fields, i.e. high magnetic torques.
2 Experimental section
M. gryphiswaldense strain MSR-1 (DMSZ 6631) was grown in a flask standard medium (FSM).31 The culture was kept in three-fourths full bottles at 28 °C without agitation. After 120 h, when the magnetosomes were well-formed,3 the bacteria cells were collected and fixed in 2% glutaraldehyde. After repeated washings with distilled water, the bacteria were freeze-dried, resulting in a powder sample with random orientation of the particle chains, i.e., a structurally and magnetically isotropic sample. Additionally, we grew and freeze-dried bacteria without magnetosomes,3 which were measured by SANS as a background sample to subtract from the magnetotactic bacteria signal.To characterize the bacteria, we first performed transmission electron microscopy (TEM, JEOL JEM-1400Plus) on unstained bacteria adsorbed onto carbon-coated copper grids, and used ImageJ32 for the image processing and analysis.
For the magnetization measurements the bacteria powder was introduced in a gelatin capsule and investigated with a superconducting quantum interference device magnetometer (Quantum Design MPMS-3) in DC mode. The bacteria powder was dense enough to prevent rotation or any other physical movement of the bacteria even at large magnetic fields. We collected isothermal remanence magnetization (IRM) and direct current demagnetization (DCD) curves, as well as an isothermal magnetization loop at room-temperature. The IRM curve was obtained by measuring the remanence from the initially demagnetized state by taking the sample through successive minor loops from 0 to 1 T. In a similar manner, the DCD curve was obtained by a progressive demagnetization of the initially saturated sample, and the isothermal magnetization loop was measured between 1 and −1 T in continuous mode. The diamagnetic contributions from the bacteria and sample holder were corrected. Additionally, we measured first-order reversal curves (FORC) with a customized vibrating sample magnetometer between a saturating field of 0.1 T and increasing reversal fields, until reaching finally the major loop. The resulting FORC diagrams were generated from a total of 80 minor loops according to Roberts et al.33
The polarized SANS (SANSPOL) experiment of the bacteria powder was conducted at room temperature with the Larmor instrument at ISIS neutron and muon source, Rutherford Appleton Laboratory. The powder of the randomly oriented bacteria was enclosed in an aluminium sample holder. It can be noted, that we observed no changes between repeated field-dependent measurements under the same conditions, which strongly indicates that the bacteria did not physically move during the experiment. The magnetic field H was applied perpendicular to the incoming neutron beam (k‖ex ⊥ H‖ez). The resulting SANS cross-sections can be written in case of an isotropic magnetization distribution in ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) y as34,35
y as34,35
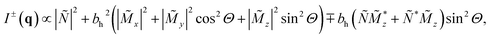 | (1) |
![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) x,y,z(q) denote the Fourier transforms of the nuclear scattering length density and of the magnetization in the x-, y- and z-directions, respectively. From the measured SANSPOL intensities, the nuclear-magnetic cross-terms
x,y,z(q) denote the Fourier transforms of the nuclear scattering length density and of the magnetization in the x-, y- and z-directions, respectively. From the measured SANSPOL intensities, the nuclear-magnetic cross-terms 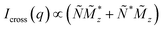 can be determined as a function of the applied field from the sector perpendicular to H of the exclusively polarisation dependent cross section (i.e. the residual scattering pattern) I−(q) − I+(q) = Icross(q)sin2
can be determined as a function of the applied field from the sector perpendicular to H of the exclusively polarisation dependent cross section (i.e. the residual scattering pattern) I−(q) − I+(q) = Icross(q)sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ. Analysis of the cross-term is in particular useful for systems where the nuclear scattering dominates the magnetic scattering, which is usually the case e.g. for iron oxide nanoparticles.23,36–38 Furthermore, we measured the SANS signal of the empty bacteria as background measurement and subtracted it from the SANSPOL intensities I±(q) to be able to determine the nuclear scattering of the magnetosome chains.
Θ. Analysis of the cross-term is in particular useful for systems where the nuclear scattering dominates the magnetic scattering, which is usually the case e.g. for iron oxide nanoparticles.23,36–38 Furthermore, we measured the SANS signal of the empty bacteria as background measurement and subtracted it from the SANSPOL intensities I±(q) to be able to determine the nuclear scattering of the magnetosome chains.
3 Results and discussion
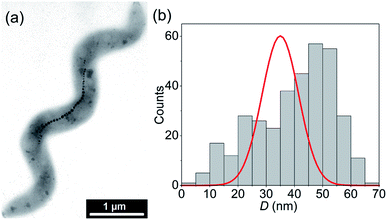
Fig. 1(a) shows a typical TEM image of a M. gryphiswaldense containing a chain of magnetosomes. The observed chain is composed of uniformly-sized nanoparticles except for those at both ends of the chain, which are slightly smaller.6 This results in a broadening of the size histogram (Fig. 1(b)), whose mean value is 〈D〉 = 40 nm. Typically, the number of particles per cell is around 15 to 40, with a center-to-center distance between neighboring particles of about 50–60 nm.6A shown in Fdez-Gubieda et al.,3 the magnetosomes synthesized by M. gryphiswaldense are nearly perfect magnetite. Using the bulk values of magnetite39 for the exchange constant A = 7 pJ m−1, the first-order anisotropy constant K1 = −13 kJ m−3, and the saturation magnetization MS = 0.48 MA m−1, the critical single-domain size 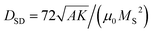 (i.e., the size above which domain formation is energetically favorable40) can be calculated to DSD ≈ 75 nm. This is significantly above the mean size of the magnetosomes and thus we can assume that at first approximation they are single-domain particles.
(i.e., the size above which domain formation is energetically favorable40) can be calculated to DSD ≈ 75 nm. This is significantly above the mean size of the magnetosomes and thus we can assume that at first approximation they are single-domain particles.
Fig. 2(a) displays the isothermal magnetization curve of the powder of the freeze-dried bacteria, normalized to the magnetic moment measured in saturation (mS ≈ 2 × 10−5 A m2). In this powder it is safe to assume that the bacteria and hence the 1D chains were randomly oriented (i.e., isotropic ensemble). The curve is fully saturated at around 0.3 T and exhibits a hysteresis with a coercive field of μ0Hc = 22 mT and a normalized remanence of mr/mS = 0.45. This is close to the expected value of 0.5 for an isotropic ensemble of single-domain nanoparticles with uniaxial anisotropy (i.e., Stoner–Wohlfarth particles).41 The slightly reduced value 0.45 can be attributed to the small particles at the end of the chains which are superparamagnetic.42 The good agreement with the Stoner–Wohlfarth model indicates that during the magnetization process (i) a mechanical particle rotation and (ii) dipolar interactions are negligible, because both would reduce the remanence significantly.43–45
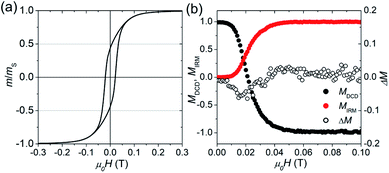 | ||
| Fig. 2 Isothermal, room-temperature magnetization measurements of the freeze-dried bacteria powder: (a) normalized magnetization curve. (b) Normalized remanence curves MDCD and MIRM, and the modified Henkel plot ΔM (eqn (2)). | ||
The fact that the magnetosomes do not physically rotate implies a strong mechanical coupling between the magnetosomes and the surrounding bacteria. At each applied field during the quasi-static magnetization curve the magnetic torque Tmag, and the counteracting mechanical torque Tmech, as well as the torque due to the magnetic anisotropy Tanis, are at equilibrium (Tmag = Tmech = Tanis). The average magnetic torque Tmag = μ0HMS〈V〉sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ exerted on the magnetosomes can be directly estimated from the magnetization curve. Here, Φ is the average angle between the particle moments and the applied field, which is given by m/mS = cos
Φ exerted on the magnetosomes can be directly estimated from the magnetization curve. Here, Φ is the average angle between the particle moments and the applied field, which is given by m/mS = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ.43,44 Using for the saturation magnetization the literature value of magnetite MS = 0.48 MA m−139 and for the mean particle volume 〈V〉 ≈ 1/8π〈D〉3 (with 〈D〉 being the mean size according to TEM, i.e., 40 nm) we get for the maximum of the average torque Tmaxmag ≈ 6.5 × 10−19 N m (at a field strength of around μ0H = 0.1 T). From Tmaxmag we can calculate the corresponding forces applied on the particle surface to Fmaxmag = 2Tmaxmag/〈D〉 ≈ 32.5 pN, which is below the rupture forces (40–80 pN) between actin filaments and actin-binding proteins reported in literature.29,46 Although it has to be considered that we have an isotropic ensemble (i.e., a random orientation distribution) and thus for some magnetosomes, the exerted forces will be higher than 32.5 pN, this explains why a physical rotation of the magnetosomes is inhibited.
Φ.43,44 Using for the saturation magnetization the literature value of magnetite MS = 0.48 MA m−139 and for the mean particle volume 〈V〉 ≈ 1/8π〈D〉3 (with 〈D〉 being the mean size according to TEM, i.e., 40 nm) we get for the maximum of the average torque Tmaxmag ≈ 6.5 × 10−19 N m (at a field strength of around μ0H = 0.1 T). From Tmaxmag we can calculate the corresponding forces applied on the particle surface to Fmaxmag = 2Tmaxmag/〈D〉 ≈ 32.5 pN, which is below the rupture forces (40–80 pN) between actin filaments and actin-binding proteins reported in literature.29,46 Although it has to be considered that we have an isotropic ensemble (i.e., a random orientation distribution) and thus for some magnetosomes, the exerted forces will be higher than 32.5 pN, this explains why a physical rotation of the magnetosomes is inhibited.
To further evaluate the amount of dipolar interactions we performed modified Henkel and FORC measurements. Fig. 2(b) shows the field-dependence of the normalized isothermal remanence magnetization (IRM) and direct current magnetization (DCD) curves, with M = m/mr. Note that MIRM starts in the demagnetized state (m/mr = 0), and saturates at the maximum remanent magnetization with m/mr = 1, while MDCD starts at 1 and finishes at −1. For the ideal case of non-interacting, uniaxial, single-domain nanoparticles the two remanence curves are related according to the Wohlfarth model (MDCD(H) = 1 − 2MIRM(H)).41 However, if inter-particle interactions appear the relation between MIRM and MDCD is expected to deviate from the Wohlfarth relation, which can be tested via the modified Henkel plot:
| ΔM = MDCD − (1 − 2MIRM). | (2) |
The sign of ΔM provides information about the nature of the interactions, and traditionally negative values (ΔM < 0) are interpreted as a sign for the presence of dipolar interactions.47 For the magnetosome chains (see Fig. 2(b)), we find that ΔM is slightly negative around μ0Hc. However, the deviation is small, at least in comparison to strongly interacting systems,45 and could also stem from disordered spins.48
A more sensitive approach to evaluate the magnitude of interactions are FORC measurements.49,50 In these curves, the magnetization M, is recorded as a function of the applied field, μ0H, from the so-called reversal field (μ0HR) up to some positive maximum value (here 100 mT). The complete set of FORCs is obtained by varying the reversal field in discrete steps between the maximum and the minimum field (here −100 mT). Fig. 3(a) shows a group of FORCs (80 curves), measured at room temperature, obtained between 100 and −100 mT in steps of 2.5 mT, that fills the interior of the major hysteresis loop. These measurements give rise to the FORC distribution presented in Fig. 3(b) and (c) (3D representation and contour plot, respectively), which is calculated from the mixed second order derivative of the magnetization33
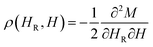 | (3) |
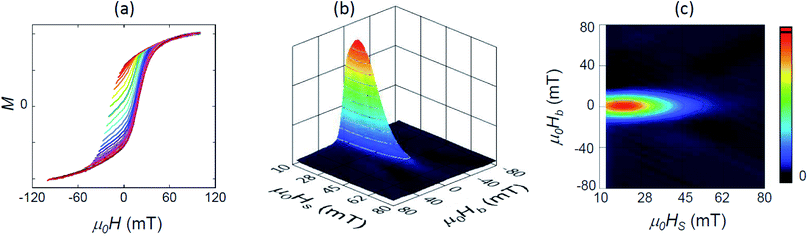 | ||
| Fig. 3 (a) Set of 80 room-temperature FORC measurements in arbitrary units, and (b) the resulting 3D FORC diagram and (c) the contour plot projected in the (HS, HB) plane. | ||
Our magnetometry results are thus in good agreement with previous FORC studies,42,51,52 and indicate a dominance of a uniaxial magnetic anisotropy and an absence of dipolar interactions. However, this does not mean that there are no interactions between the particles within the chains. As shown in Charilaou et al.53 and Koulialias et al.,54 due to the collinear arrangement of the anisotropy axes the dipolar stray fields results in an additional uniaxial anisotropy contribution along the chain axis (i.e. shape anisotropy) which enhances the total anisotropy of the 1D chains along the chain axis compared to the individual particles.
Thus, we can conclude from FORC, that the 1D chains of the freeze-dried bacteria do not interact with each other. Another interesting result we can deduce from magnetometry is that in the freeze-dried bacteria the particles do not mechanically rotate even at high fields (i.e. high magnetic torques), which implies a high mechanical coupling between the magnetosomes and the cytoskeleton. To further evaluate the stability and also the magnetic properties we performed a polarized SANS experiment on the same sample.
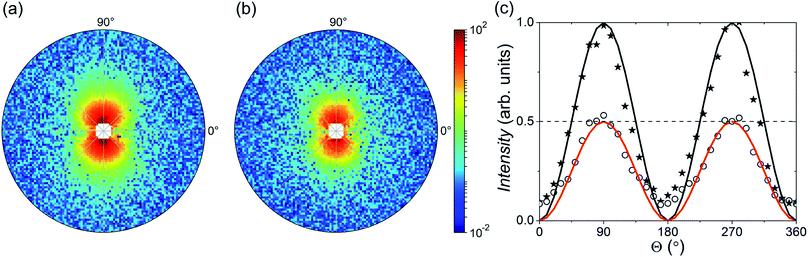
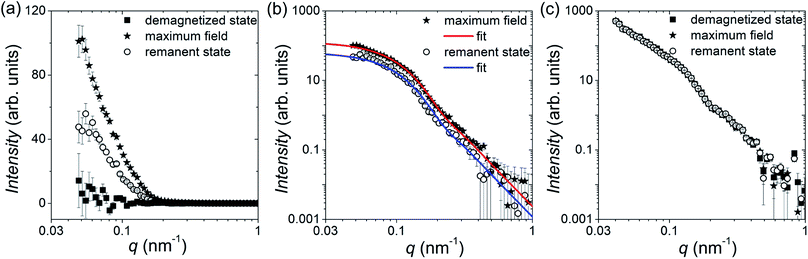
Fig. 4 shows the 2D patterns of the residual SANS cross-section I−(q) − I+(q) = Icross(q)sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ at an applied field of 1 T (Fig. 4(a)) and in the remanent state (Fig. 4(b)). In Fig. 4(c) we plot additionally both scattering intensities integrated over the q-range 0.045–0.5 nm−1 as a function of Θ, which nicely shows the expected sin2-dependency. By azimuthally integrating the intensity in the sector perpendicular to H (Θ = 90°, ΔΘ = 10°), we extracted the 1D nuclear-magnetic cross-term Icross(q). In Fig. 5(a), we plot Icross(q) detected at the maximum field of 1 T, and detected at zero field in the demagnetized state and in the remanent state, respectively. As can be seen, for the demagnetized state Icross(q) ≈ 0 over the whole q-range, which is expected because the cross-term is directly proportional to the sample magnetization in field direction. In the saturated and the remanent state, on the other hand, we detect finite values, whereby the absolute values of the remanent state are by a factor of 2 smaller than in saturation (see also Fig. 4(c)). This implies a reduced remanence of mR/mS = 0.5 (here mR is the remanent moment and mS the measured moment in saturation), which is the expected value for an isotropic ensemble of single-domain particles with uniaxial anisotropy (i.e. Stoner–Wohlfarth particles),41 and in good agreement with our magnetization curve (Fig. 2(a)).
Θ at an applied field of 1 T (Fig. 4(a)) and in the remanent state (Fig. 4(b)). In Fig. 4(c) we plot additionally both scattering intensities integrated over the q-range 0.045–0.5 nm−1 as a function of Θ, which nicely shows the expected sin2-dependency. By azimuthally integrating the intensity in the sector perpendicular to H (Θ = 90°, ΔΘ = 10°), we extracted the 1D nuclear-magnetic cross-term Icross(q). In Fig. 5(a), we plot Icross(q) detected at the maximum field of 1 T, and detected at zero field in the demagnetized state and in the remanent state, respectively. As can be seen, for the demagnetized state Icross(q) ≈ 0 over the whole q-range, which is expected because the cross-term is directly proportional to the sample magnetization in field direction. In the saturated and the remanent state, on the other hand, we detect finite values, whereby the absolute values of the remanent state are by a factor of 2 smaller than in saturation (see also Fig. 4(c)). This implies a reduced remanence of mR/mS = 0.5 (here mR is the remanent moment and mS the measured moment in saturation), which is the expected value for an isotropic ensemble of single-domain particles with uniaxial anisotropy (i.e. Stoner–Wohlfarth particles),41 and in good agreement with our magnetization curve (Fig. 2(a)).
We can assume that the nuclear scattering cross-section Ñ of the bacteria is dominated by the particles. Thus, in case of a homogeneous magnetization, i.e., single-domain particles with Ñ ∝ ![[M with combining tilde]](https://www.rsc.org/images/entities/i_char_004d_0303.gif) z, we can write at first approximation for the cross-term Icross(q) ∝ F2(q), where F2(q) is the particle form factor, for which we will use here the spherical one.55 From Icross(q) we can thus additionally estimate the size of the particles by fitting the 1D cross-sections with the spherical form factor (Fig. 5(b)). We assumed a normal size distribution and determined by a global fit of both data sets (i.e., maximum field and remanent state) for the particle diameter a (number-weighted) mean value of 35(2) nm and a standard deviation of 13(1) nm. Comparison of the obtained number-weighted distribution with the size histogram derived by TEM shows a good agreement (Fig. 1(b)).
z, we can write at first approximation for the cross-term Icross(q) ∝ F2(q), where F2(q) is the particle form factor, for which we will use here the spherical one.55 From Icross(q) we can thus additionally estimate the size of the particles by fitting the 1D cross-sections with the spherical form factor (Fig. 5(b)). We assumed a normal size distribution and determined by a global fit of both data sets (i.e., maximum field and remanent state) for the particle diameter a (number-weighted) mean value of 35(2) nm and a standard deviation of 13(1) nm. Comparison of the obtained number-weighted distribution with the size histogram derived by TEM shows a good agreement (Fig. 1(b)).
The similarity between the functional form of the cross-term detected at saturation and remanence (Fig. 5(b)) shows, that qualitatively the magnetic cross-section and magnetic particle morphology is not altered by applying a magnetic field. This confirms that the particles are in fact (at least at first approximation) single-domain particles and that a rotation of the particle moments into the field direction occurs by an internal, coherent rotation of the atomic magnetic moments inside the individual particles.
Fig. 5(c) shows additionally the 1D cross-sections I(q), which we determined by an azimuthal integration of I+(q) in the sector parallel to H (Θ = 0°, ΔΘ = 10°). The scattering intensity of the bacteria without magnetosomes is subtracted such that we can assume that the SANS signal is dominated by the purely nuclear cross-section of the magnetosomes. We observe that I(q) does not vary with field leading to a perfect overlap of the scattering curves, which shows that I(q) is dominated by the nuclear scattering, and which in turn verifies that the nuclear cross-section is not changed by applying the magnetic fields. Hence we can conclude that the particle chains within the freeze-dried bacteria remain intact and do not rotate, because otherwise we would expect a significant variation between the field-dependent cross-sections. Moreover, the arrangement and separation of the particles composing the magnetosome chains do not vary with field, since no change in the structure factor (i.e., the SANS signal in the low q-range) is observed. Therefore, we can conclude that within the freeze-dried bacteria the internal microstructure is not altered by external fields, which makes them a good system to characterize the magnetic properties of the individual magnetosome chains. This verifies our own observations via TEM, where we could observe no deviations from the chain structure in the probed bacteria, as well as published electron holography studies on similar dried bacteria where also no break-ups were detected.56,57
4 Conclusions
To summarize, we investigate here the magnetic response of a powder of freeze-dried and immobilized M. gryphiswaldense by magnetometry and polarized SANS. The magnetosomes are around 40 nm in size and arranged in linear chains inside the bacteria. We can confirm that the particles are single-domain particles, and that the 1D magnetosome chains inside the bacteria are not magnetically interacting with each other and behave like randomly oriented magnetic nanoparticles with uniaxial anisotropy along the chain axis. Furthermore, we can conclude that the particles inside the freeze-dried bacteria do not physically rotate in field direction also in presence of large magnetic fields (i.e. large magnetic torques), which implies a high mechanical coupling between the magnetosomes and the cytoskeleton. As a result the alignment of the particle moments along the magnetic field-direction occurs exclusively by an internal, coherent rotation. Finally, we can show that the particle chains remain intact also after application of large fields of up to 1 T. This confirms that the freeze-drying of the bacteria results in mechanically stable configurations of the magnetosome chains, and thus the freeze-dried bacteria can be regarded as model samples to study the magnetization behavior of such 1D nanoparticle chains.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank the Science and Technology Facilities Council (STFC) for granting beamtime at the instrument Larmor. P. Bender acknowledges financial support from the National Research Fund of Luxembourg (CORE SANS4NCC grant) and L. Marcano acknowledges the Basque Government for her fellowship (POS_2018_1_0070). This project has received additional funding from the European Commission Framework Programme 7 under grant agreement no 604448 (NanoMag), and the Spanish Government is acknowledged for funding under project MAT2017-83631-C3-R.Notes and references
- D. A. Bazylinski and R. B. Frankel, Nat. Rev. Microbiol., 2004, 2, 217–230 CrossRef CAS PubMed.
- I. S. Khalil, M. P. Pichel, L. Abelmann and S. Misra, Int. J. Robot Res., 2013, 32, 637–649 CrossRef.
- M. L. Fdez-Gubieda, A. Muela, J. Alonso, A. Garcia-Prieto, L. Olivi, R. Fernandez-Pacheco and J. M. Barandiaran, ACS Nano, 2013, 7, 3297–3305 CrossRef CAS PubMed.
- A. Komeili, Z. Li, D. K. Newman and G. J. Jensen, Science, 2006, 311, 242–245 CrossRef CAS PubMed.
- M. Toro-Nahuelpan, G. Giacomelli, O. Raschdorf, S. Borg, J. M. Plitzko, M. Bramkamp, D. Schüler and F.-D. Müller, Nat. Microbiol., 2019, 4, 1978–1989 CrossRef CAS PubMed.
- I. Orue, L. Marcano, P. Bender, A. García-Prieto, S. Valencia, M. A. Mawass, D. Gil-Cartón, D. Alba Venero, D. Honecker, A. García-Arribas, L. Fernández Barquín, A. Muela and M. L. Fdez-Gubieda, Nanoscale, 2018, 10, 7407–7419 RSC.
- N. Lee, H. Kim, S. H. Choi, M. Park, D. Kim, H.-C. Kim, Y. Choi, S. Lin, B. H. Kim and H. S. Jung, et al. , Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 2662–2667 CrossRef CAS PubMed.
- P. Guardia, R. Di Corato, L. Lartigue, C. Wilhelm, A. Espinosa, M. Garcia-Hernandez, F. Gazeau, L. Manna and T. Pellegrino, ACS Nano, 2012, 6, 3080–3091 CrossRef CAS PubMed.
- A. Lak, M. Cassani, B. T. Mai, N. Winckelmans, D. Cabrera, E. Sadrollahi, S. Marras, H. Remmer, S. Fiorito and L. Cremades-Jimeno, et al. , Nano Lett., 2018, 18, 6856–6866 CrossRef CAS PubMed.
- I. Castellanos-Rubio, I. Rodrigo, R. Munshi, O. Arriortua, J. S. Garitaonandia, A. Martinez-Amesti, F. Plazaola, I. Orue, A. Pralle and M. Insausti, Nanoscale, 2019, 11, 16635–16649 RSC.
- C. Martinez-Boubeta, K. Simeonidis, A. Makridis, M. Angelakeris, O. Iglesias, P. Guardia, A. Cabot, L. Yedra, S. Estradé and F. Peiró, et al. , Sci. Rep., 2013, 3, 1652 CrossRef PubMed.
- S. Sturm, M. Siglreitmeier, D. Wolf, K. Vogel, M. Gratz, D. Faivre, A. Lubk, B. Büchner, E. V. Sturm and H. Cölfen, Adv. Funct. Mater., 2019, 29, 1905996 CrossRef CAS.
- I. Andreu, A. Urtizberea and E. Natividad, Nanoscale, 2020, 12, 572–583 RSC.
- J. Yuan, Y. Xu and A. H. Mueller, Chem. Soc. Rev., 2011, 40, 640–655 RSC.
- H. Wang, Y. Yu, Y. Sun and Q. Chen, Nano, 2011, 6, 1–17 CrossRef.
- A. Cebers, Curr. Opin. Colloid Interface Sci., 2005, 10, 167–175 CrossRef CAS.
- R. Dreyfus, J. Baudry, M. L. Roper, M. Fermigier, H. A. Stone and J. Bibette, Nature, 2005, 437, 862 CrossRef CAS PubMed.
- B. Kiani, D. Faivre and S. Klumpp, New J. Phys., 2015, 17, 043007 CrossRef.
- H. Wolf and R. Birringer, J. Appl. Phys., 2005, 98, 074303 CrossRef.
- B. D. Korth, P. Keng, I. Shim, S. E. Bowles, C. Tang, T. Kowalewski, K. W. Nebesny and J. Pyun, J. Am. Chem. Soc., 2006, 128, 6562–6563 CrossRef CAS PubMed.
- K. Nakata, Y. Hu, O. Uzun, O. Bakr and F. Stellacci, Adv. Mater., 2008, 20, 4294–4299 CrossRef CAS.
- T. Prozorov, D. A. Bazylinski, S. K. Mallapragada and R. Prozorov, Mater. Sci. Eng., R, 2013, 74, 133–172 CrossRef.
- A. Hoell, A. Wiedenmann, U. Heyen and D. Schüler, Phys. B, 2004, 350, E309–E313 CrossRef CAS.
- P. Bender, D. Zákutná, S. Disch, L. Marcano, D. Alba Venero and D. Honecker, Acta Crystallogr., Sect. A: Found. Crystallogr., 2019, 75, 766–771 CrossRef CAS PubMed.
- S. Rosenfeldt, C. N. Riese, F. Mickoleit, D. Schüler and A. S. Schenk, Appl. Environ. Microbiol., 2019, 85, e01513–e01519 CrossRef PubMed.
- L. Marcano, A. García-Prieto, D. Muñoz, L. Fernández Barquín, I. Orue, J. Alonso, A. Muela and M. L. Fdez-Gubieda, Biochim. Biophys. Acta, Gen. Subj., 2017, 1861, 1507–1514 CrossRef CAS PubMed.
- L. Marcano, D. Muñoz, R. Martín-Rodríguez, I. Orue, J. Alonso, A. García-Prieto, A. Serrano, S. Valencia, R. Abrudan, L. Fernández Barquín, A. García-Arribas, A. Muela and M. L. Fdez-Gubieda, J. Phys. Chem. C, 2018, 122, 7541–7550 CrossRef CAS.
- D. Gandia, L. Gandarias, I. Rodrigo, J. Robles-García, R. Das, E. Garaio, J. Á. García, M.-H. Phan, H. Srikanth and I. Orue, et al. , Small, 2019, 15, 1902626 CrossRef CAS PubMed.
- A. Körnig, J. Dong, M. Bennet, M. Widdrat, J. Andert, F. D. Müller, D. Schüler, S. Klumpp and D. Faivre, Nano Lett., 2014, 14, 4653–4659 CrossRef PubMed.
- M. Blondeau, Y. Guyodo, F. Guyot, C. Gatel, N. Menguy, I. Chebbi, B. Haye, M. Durand-Dubief, E. Alphandery, R. Brayner and T. Coradin, Sci. Rep., 2018, 8, 7699 CrossRef PubMed.
- U. Heyen and D. Schüler, Appl. Microbiol. Biotechnol., 2003, 61, 536–544 CrossRef CAS PubMed.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671 CrossRef CAS PubMed.
- A. P. Roberts, C. R. Pike and K. L. Verosub, J. Geophys. Res., 2000, 105, 28461–28475 CrossRef.
- D. Honecker, A. Ferdinand, F. Döbrich, C. D. Dewhurst, A. Wiedenmann, C. Gómez-Polo, K. Suzuki and A. Michels, Eur. Phys. J. B, 2010, 76, 209–213 CrossRef CAS.
- A. Michels, D. Honecker, F. Döbrich, C. Dewhurst, A. Wiedenmann, C. Gómez-Polo and K. Suzuki, Neutron News, 2011, 22, 15–19 CrossRef.
- S. Disch, E. Wetterskog, R. P. Hermann, A. Wiedenmann, U. Vainio, G. Salazar-Alvarez, L. Bergström and T. Brückel, New J. Phys., 2012, 14, 013025 CrossRef.
- P. Bender, J. Fock, C. Frandsen, M. F. Hansen, C. Balceris, F. Ludwig, O. Posth, E. Wetterskog, L. K. Bogart, P. Southern, W. Szczerba, L. Zeng, K. Witte, C. Grüttner, F. Westphal, D. Honecker, D. González-Alonso, L. Fernández Barquín and C. Johansson, J. Phys. Chem. C, 2018, 122, 3068–3077 CrossRef CAS.
- S. Mühlbauer, D. Honecker, É. A. Périgo, F. Bergner, S. Disch, A. Heinemann, S. Erokhin, D. Berkov, C. Leighton, M. R. Eskildsen and A. Michels, Rev. Mod. Phys., 2019, 91, 015004 CrossRef.
- J. M. Coey, Magnetism and Magnetic Materials, Cambridge University Press, 2010 Search PubMed.
- R. Skomski, J. Phys.: Condens. Matter, 2003, 15, R841 CrossRef CAS.
- E. P. Wohlfarth, J. Appl. Phys., 1958, 29, 595–596 CrossRef.
- M. Kumari, M. Widdrat, É. Tompa, R. Uebe, D. Schüler, M. Pósfai, D. Faivre and A. M. Hirt, J. Appl. Phys., 2014, 116, 124304 CrossRef.
- P. Bender, A. Tschöpe and R. Birringer, J. Magn. Magn. Mater., 2013, 346, 152–160 CrossRef CAS.
- P. Bender, A. Tschöpe and R. Birringer, J. Magn. Magn. Mater., 2014, 372, 187–194 CrossRef CAS.
- P. Bender, F. Krämer, A. Tschöpe and R. Birringer, J. Phys. D: Appl. Phys., 2015, 48, 145003 CrossRef.
- J. M. Ferrer, H. Lee, J. Chen, B. Pelz, F. Nakamura, R. D. Kamm and M. J. Lang, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9221–9226 CrossRef CAS PubMed.
- M. Fearon, R. W. Chantrell and E. P. Wohlfarth, J. Magn. Magn. Mater., 1990, 86, 197–206 CrossRef.
- J. A. De Toro, M. Vasilakaki, S. S. Lee, M. S. Andersson, P. S. Normile, N. Yaacoub, P. Murray, E. H. Sánchez, P. Munñiz and D. Peddis, et al. , Chem. Mater., 2017, 29, 8258–8268 CrossRef CAS.
- I. Mayergoyz, IEEE Trans. Magn., 1986, 22, 603–608 CrossRef.
- C. R. Pike, A. P. Roberts and K. L. Verosub, J. Appl. Phys., 1999, 85, 6660–6667 CrossRef CAS.
- H. Fischer, G. Mastrogiacomo, J. F. Löffler, R. J. Warthmann, P. G. Weidler and A. U. Gehring, Earth Planet. Sci. Lett., 2008, 270, 200–208 CrossRef CAS.
- R. Egli, A. P. Chen, M. Winklhofer, K. P. Kodama and C.-S. Horng, Geochem., Geophys., Geosyst., 2010, 11, Q01Z11 CrossRef.
- M. Charilaou, J. Kind, I. García-Rubio, D. Schüler and A. U. Gehring, Appl. Phys. Lett., 2014, 104, 112406 CrossRef.
- D. Koulialias, I. García-Rubio, L. Rahn-Lee, A. Komeili, J. F. Löffler, A. U. Gehring and M. Charilaou, J. Appl. Phys., 2016, 120, 083901 CrossRef.
- J. S. Pedersen, Adv. Colloid Interface Sci., 1997, 70, 171–210 CrossRef CAS.
- R. E. Dunin-Borkowski, M. R. McCartney, R. B. Frankel, D. A. Bazylinski, M. Pósfai and P. R. Buseck, Science, 1998, 282, 1868–1870 CrossRef CAS.
- E. Simpson, T. Kasama, M. Pósfai, P. R. Buseck, R. Harrison and R. E. Dunin-Borkowski, J. Phys.: Conf. Ser., 2005, 108 CrossRef CAS.
Footnote |
| † Present address: Department of Physics and Materials Science, University of Luxembourg, 1511 Luxembourg, Grand Duchy of Luxembourg. |
| This journal is © The Royal Society of Chemistry 2020 |