Open Access Article
Open Access ArticleInfluence of patch size and chemistry on the catalytic activity of patchy hybrid nonwovens†
Christian
Hils
 a,
Martin
Dulle
a,
Martin
Dulle
 b,
Gabriel
Sitaru
c,
Stephan
Gekle
b,
Gabriel
Sitaru
c,
Stephan
Gekle
 c,
Judith
Schöbel
d,
Andreas
Frank
e,
Markus
Drechsler
f,
Andreas
Greiner
ag and
Holger
Schmalz
c,
Judith
Schöbel
d,
Andreas
Frank
e,
Markus
Drechsler
f,
Andreas
Greiner
ag and
Holger
Schmalz
 *ag
*ag
aMacromolecular Chemistry II, University of Bayreuth, Universitätsstraße 30, 95440 Bayreuth, Germany. E-mail: holger.schmalz@unibayreuth.de
bJCNS-1/ICS-1, Forschungszentrum Jülich GmbH, Wilhelm-Johnen-Straße, 52428 Jülich, Germany
cBiofluid Simulation and Modeling, Theoretische Physik VI, University of Bayreuth, Universitätsstraße 30, 95440 Bayreuth, Germany
dMacromolecular Chemistry & New Polymeric Materials, Zernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747 AG, Groningen, The Netherlands
eMacromolecular Chemistry I, University of Bayreuth, Universitätsstraße 30, 95440 Bayreuth, Germany
fBavarian Polymer Institute, Keylab Optical and Electron Microscopy, University of Bayreuth, Universitätsstraße 30, 95440 Bayreuth, Germany
gBavarian Polymer Institute, Keylab Synthesis and Molecular Characterization, University of Bayreuth, Universitätsstraße 30, 95440 Bayreuth, Germany
First published on 26th November 2019
Abstract
In this work, we provide a detailed study on the influence of patch size and chemistry on the catalytic activity of patchy hybrid nonwovens in the gold nanoparticle (Au NP) catalysed alcoholysis of dimethylphenylsilane in n-butanol. The nonwovens were produced by coaxial electrospinning, employing a polystyrene solution as the core and a dispersion of spherical or worm-like patchy micelles with functional, amino group-bearing patches (dimethyl and diisopropyl amino groups as anchor groups for Au NP) as the shell. Subsequent loading by dipping into a dispersion of preformed Au NPs yields the patchy hybrid nonwovens. In terms of NP stabilization, i.e., preventing agglomeration, worm-like micelles with poly(N,N-dimethylaminoethyl methacrylamide) (PDMA) patches are most efficient. Kinetic studies employing an extended 1st order kinetics model, which includes the observed induction periods, revealed a strong dependence on the accessibility of the Au NPs' surface to the reactants. The accessibility is controlled by the swellability of the functional patches in n-butanol, which depends on both patch chemistry and size. As a result, significantly longer induction (tind) and reaction (tR) times were observed for the 1st catalysis cycles in comparison to the 10th cycles and nonwovens with more polar PDMA patches show a significantly lower tR in the 1st catalysis cycle. Thus, the unique patchy surface structure allows tailoring the properties of this “tea-bag”-like catalyst system in terms of NP stabilization and catalytic performance, which resulted in a significant reduction of tR to about 4 h for an optimized system.
Introduction
Noble metal nanoparticles, especially gold nanoparticles (Au NPs), are gaining increasing attention due to their excellent performance in heterogeneous catalysis, ascribed to their extremely high specific surface area.1–5 For decades, gold has been considered as a poor catalyst since bulk gold is chemically inert. However, when gold is present in the form of small particles with diameters in the nanometer range it becomes surprisingly active.2,5 First reports on the catalytic activity of Au NPs date back to the 1970s, describing the hydrogenation of alkenes and alkynes with supported Au NPs,6 followed by the discovery that Au NPs show a high catalytic activity for CO oxidation even at temperatures below 0 °C in 1987.7 Since then, a plethora of reactions catalysed by Au NPs have been identified, e.g. oxophilic activation of epoxides and carbonyl compounds, hydrosilylation reactions, hydrolysis/alcoholysis of silanes, hydrogenation reactions, reduction of aromatic nitro compounds and C–C coupling reactions.5In general, an inherent problem involved in heterogeneous catalysis with NPs is their high specific surface area. On one hand, it is indispensable for a good catalytic performance, but on the other hand it makes the NPs prone to aggregation, which in turn will result in a decreased activity. Thus, efficient strategies have to be developed that can prevent NP agglomeration while preserving their excellent catalytic activity. One common way is the use of low molecular weight or polymeric ligands for NP stabilization. But one has to keep in mind that the ligands can influence the catalytic activity of the NPs as well as the selectivity and the ligands can fade away from the NP surface with time, resulting in destabilization and, thus, agglomeration.8,9 Moreover, the complete separation of ligand-stabilized NPs after catalysis is rather difficult, leading to a limited recyclability of the NPs.10 One strategy to overcome these issues is the immobilization of NPs on a solid inorganic support, like (porous) metal oxides and silica,11–15 nano-tubes and -rods,16–18 or two-dimensional layered materials like graphene or graphitic carbon nitride.19–21 An interesting approach is the use of magnetic iron oxide NPs as a support, facilitating an easy recovery of the catalyst by applying a magnetic field.22 In addition, metal–organic frameworks (MOFs) have been employed as versatile hosts for metal NPs.23–25 Besides these examples polymeric supports, like nanocellulose,26 micro- or nano-porous polymers,27–31 microgels,32,33 polyelectrolyte brushes,34–36 dendrimers and unimolecular micelles,37,38 as well as polymer micelles,39–44 are highly attractive for NP stabilization, as their properties can be easily tailored to the demands of a specific catalytic application (NP stabilization, selectivity, and responsivity). In a different approach, polymer nanofibers produced by electrospinning45,46 or using polyelectrolyte brushes47 can be used as a sacrificial support for NPs, which can be removed by subsequent calcination. Here, sintering of the NPs occurs during calcination, resulting in porous, mesostructured catalysts that can be easily removed from the reaction media, allowing a good reusability/recyclability. However, due to the sintering of the NPs the catalytically active surface area is partially reduced.
Crystallization-driven self-assembly (CDSA) is increasingly gaining importance for the production of defined cylindrical micelles with tailored functionality for NP stabilization.48,49 This field was pioneered by the inspiring work of Manners and Winnik on the CDSA of diblock copolymers with a crystallizable poly(ferrocenyl dimethylsilane) (PFS) block. In analogy to living polymerization, CDSA can be conducted in a living manner, using small micellar fragments as seeds for the addition of unimers (molecularly dissolved block copolymers bearing a crystallizable block).50,51 This seeded-growth protocol paves the way to a precise length control of cylindrical micelles and to a variety of different micellar architectures, like patchy micelles and block comicelles (in analogy to BCPs),52–55 branched and platelet-like micelles,56 and hierarchical self-assemblies.57–59 In addition to PFS-containing BCPs, a variety of other semi-crystalline polymers were reported to undergo CDSA, e.g. polyethylene (PE),60,61 poly(L-lactide),62,63 poly(3-hexylthiophene),64 oligo(p-phenylenevinylene),65 polycarbonates,66 or poly(ε-caprolactone).67
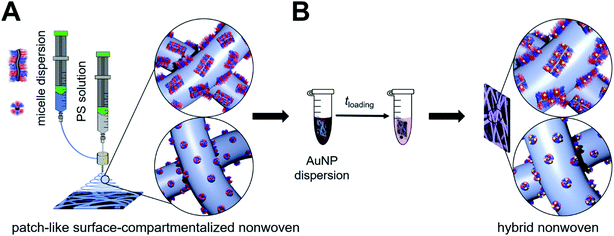
We have recently shown that Au NP-loaded patchy nonwovens with functional, nanometer-sized patches on the nonwoven's surface are efficient, “tea-bag”-like catalyst systems.68 The patchy nonwovens were prepared by combining coaxial electrospinning46,69 as a versatile “top-down” method with CDSA (“bottom-up” approach), employing a polystyrene (PS) solution as the core and a dispersion of functional, patchy worm-like crystalline-core micelles (wCCMs) as the shell (Fig. 1). The patchy wCCMs were produced by CDSA and consist of a semi-crystalline polyethylene (PE) core and a corona made of alternating nanometer-sized PS and functional, amino group-containing patches. To this end, the poly(methyl methacrylate) (PMMA)-block of a polystyrene-block-polyethylene-block-poly(methyl methacrylate) (PS-b-PE-b-PMMA) triblock terpolymer was functionalized by post-polymerization amidation with N,N-diisopropylethylenediamine (DiPA) at 130 °C in DMSO.44 The patchy nonwovens were loaded with catalytically active Au NPs via a simple dipping process and showed excellent performance and reusability in the catalytic alcoholysis of dimethylphenylsilane with n-butanol. However, due to the comparably harsh conditions used for the amidation of the PS-b-PE-b-PMMA triblock terpolymer a significant fraction of imide units (amide/imide ≈ 50/50) was formed, leading to a limited solubility of the functionalized triblock terpolymer in THF, the solvent employed for CDSA. Thus, the degree of functionalization of the amidated patches could not be increased above f ≈ 55%, as for higher degrees of functionalization the amidated patches were insoluble in THF and CDSA to defined wCCMs was not possible. However, with respect to the efficient stabilization of Au NPs a higher degree of functionalization would be beneficial. In the meantime, we have developed a more efficient amidation method, which will be used in this study. In this approach, the amine is activated with n-butyllithium, allowing an almost quantitative amidation without the formation of undesired imide units.43
Here, we present a comprehensive study on the influence of micelle geometry as well as patch size and chemistry on the catalytic activity of Au NP-loaded patchy nonwovens, prepared by coaxial electrospinning and subsequent loading with Au NPs via a facile dipping process (Fig. 1). Patchy micelles with different shapes (worm-like and spherical), employed as the shell in coaxial electrospinning, were prepared by CDSA of polystyrene-block-polyethylene-block-poly(N,N-dialkylaminoethyl methacrylamide) (SEDxA) triblock terpolymers in THF for wCCMs and dioxane for sCCMs (spherical crystalline-core micelles),60 respectively. The chemistry/polarity of the amidated patches was tuned by using N,N-diisopropylethylenediamine and N,N-dimethylethylenediamine for post-polymerization amidation of PS-b-PE-b-PMMA triblock terpolymers, whereby the size of the patches was altered by using PS-b-PE-b-PMMA triblock terpolymers with different PS and PMMA weight fractions. The morphology of the neat and Au NP-loaded patchy nonwovens was studied by scanning electron microscopy (SEM) and small-angle X-ray scattering (SAXS). As this study focuses on the influence of the patchy surface structure of the support on the catalytic activity of the embedded Au NPs we have chosen the alcoholysis of dimethylphenylsilane with n-butanol as an established model reaction. This allows comparison to our previous results and to literature data.68,70
Experimental
Materials
All chemicals were used as received unless otherwise noted. Deionized water (filtered through a Millipore Milli-Q Plus system, QPAK® 2 purification cartridge, conductivity: 18.2 MΩ cm), tetrachloroauric(III) acid trihydrate (HAuCl4·3H2O, 99.99%, Alfa Aesar), sodium borohydride (NaBH4, ≥96%, Fluka), trisodium citrate dihydrate (99% for analytical purposes, Grüssing), dimethylphenylsilane (≥97%, TCI Europe), n-butanol (99.9%, anhydrous, Alfa Aesar), undecane (≥99%, Sigma-Aldrich), n-butyllithium (2.5 mol L−1 in hexane, Acros Organics), n-pentane (purified by distillation prior to use), deuterated chloroform (CDCl3, 99.8%, Deutero), calcium hydride (CaH2, Merck), N,N-dimethylethylenediamine (DMEDA, ≥98%, Sigma-Aldrich, dried over CaH2 and purified by distillation), N,N-diisopropylethylenediamine (DiPEDA, 97%, Acros Organics, dried over CaH2 and purified by distillation), dry ice, hydrochloric acid (37 wt% in water, VWR), nitric acid (>65 wt% in water, Sigma-Aldrich), ruthenium(III) chloride hydrate (ReagentPlus®, Sigma-Aldrich), sodium hypochlorite solution (NaOCl, 10–15 wt% in water, Sigma-Aldrich), N,N-dimethylformamide (DMF, 99%, Acros Organics), tetrahydrofuran (THF, ≥99.9%, Sigma-Aldrich, dried by successive distillation over CaH2 and potassium and stored under nitrogen until use), acetone (99.9%, Acros Organics), dioxane (p.a., AppliChem) and polystyrene (synthesized by anionic polymerization in THF, Mn = 1.8 106 g mol−1, Đ = 1.08). Special care was taken for handling CaH2, as it strongly reacts with alcohols and water under the formation of hydrogen.Synthesis of citrate-stabilized Au NPs
The citrate-stabilized Au NPs were prepared according to the procedure reported by Schaal et al.71 To 100 mL of an aqueous HAuCl4 solution (c = 0.50 × 10−3 mol L−1), 9 mL of a NaBH4 solution in water (c = 4.85 × 10−2 mol L−1) were added dropwise followed by stirring for 5 min. The reaction mixture changed colour from yellow to red, indicating the formation of Au NPs. Subsequently, 5 mL of an aqueous sodium citrate solution (c = 0.05 mol L−1) were added and the mixture was stirred for another 5 min. Au NPs (cAu = 0.50 × 10−3 mol L−1, determined by inductively coupled plasma-optical emission spectrometry (ICP-OES)) with a mean diameter of DTEM = 9.5 ± 2.4 nm, as determined by transmission electron microscopy (TEM), were obtained (Fig. S1A and B†). The Au NP dispersion showed a localized surface plasmon resonance at λmax = 529 nm (Fig. S1C†).Synthesis of the PS-b-PE-b-PMMA triblock terpolymers
The PS-b-PE-b-PMMA triblock terpolymers were synthesized by a combination of living anionic polymerization and catalytic hydrogenation, as published elsewhere.60 The composition of the employed PS-b-PE-b-PMMA triblock terpolymers is S40E21M39108 and S48E27M25141. In this notation, the subscripts describe the mass fraction of the corresponding block in wt% and the superscript denotes the overall number – average molecular weight in kg mol−1. The number-average molecular weight in kg mol−1 was determined by a combination of MALDI-ToF MS (matrix-assisted laser desorption/ionization – time of flight mass spectrometry) and 1H NMR (nuclear magnetic resonance) spectroscopy.Synthesis of SEDxA triblock terpolymers
For the post-polymerization modification of the PS-b-PE-b-PMMA triblock terpolymers, the PMMA block was amidated with the corresponding N,N-dialkylethylenediamine (DMEDA, DiPEDA) under an inert argon atmosphere, as published elsewhere.43 The amidation resulted in quantitative functionalization of the PMMA block, as determined by 1H NMR and FT-IR (Fourier transform-infrared) spectroscopy (Fig. S2 and S3†). The following polystyrene-block-polyethylene-block-poly(N,N-dialkylaminoethyl methacrylamide) (SEDxA) triblock terpolymers were prepared: S28E15DiPA58156 (s-SEDiPA), S48E21DiPA41181 (as-SEDiPA) and S33E17DMA50132 (s-SEDMA).Formation of patchy micelles60
The functional, patchy sCCMs of the amidated SEDxA triblock terpolymers were prepared by dissolving the triblock terpolymers in dioxane (c = 10 g L−1) at 95 °C for 30 min, followed by cooling to room temperature. The patchy wCCMs were prepared by crystallization-driven self-assembly (CDSA) of the amidated SEDxA triblock terpolymers in THF. To this end, the triblock terpolymers were dissolved in THF (c = 10 g L−1) at 65 °C for 30 min and subsequently cooled to the crystallization temperature (Tc, Table S1 and Fig. S4†) of the polyethylene middle block, using a thermostated shaker unit (HLC-MKR 13, Ditabis). The self-assembly process was allowed to proceed for 24 h at a shaking rate of 200 rpm.Preparation of patchy nonwovens by coaxial electrospinning
For the preparation of patchy nonwovens by coaxial electrospinning, different solutions were prepared. For the core a 7 wt% PS (Mn = 1.8 106 g mol−1) solution in DMF and for the shell dispersions of SEDxA sCCMs or wCCMs in dioxane or THF (c = 10 g L−1), respectively, were employed. The fibres were spun on a rotating disk collector (D = 20 cm, 800 rpm) placed at a distance of 5 cm from the coaxial needle (COAX_2DISP sealed coaxial needles, LINARI NanoTech, dcore = 0.51 mm and dshell = 1.37 mm) at a temperature of 20.8 °C and a relative humidity of ca. 30%. For electrospinning, a high voltage of 11.4 kV at the needle and −1.0 kV at the collector were applied. The feed rate of the PS core solution was 1.2 mL h−1 and for the micellar shell dispersion it was 1.0 mL h−1.Loading of patchy nonwovens with citrate-stabilized Au NPs (dipping process)
For each system, the loading of the nonwovens was done in an Eppendorf vial by dipping a piece of nonwoven (surface area: S = 1 cm2 and thickness: d ≈ 400 μm) fixed in a cage made of a stainless-steel mesh (1.4432 V4A/316L, mesh size: 400 mesh, and wire thickness: 30 μm) into 1 mL of an aqueous, citrate-stabilized Au NP dispersion (cAu = 0.50 × 10−3 mol L−1 and DTEM = 9.5 ± 2.4 nm) for 24 h. After incorporation of the Au NPs, the nonwovens were subsequently washed with a sodium citrate solution (c = 5 × 10−3 mol L−1) and water (2 × 5 mL each). The hybrid nonwovens were dried in a vacuum oven (<5 mbar, 40 °C) for 15 h. The amount of Au in the patchy nonwovens was determined by inductively coupled plasma-optical emission spectrometry (ICP-OES, triple determination) and UV-vis measurements (for details see the ESI, eqn (S1) and Fig. S5†) from the respective Au contents of the dispersions before and after loading (difference method).Catalytic alcoholysis of dimethylphenylsilane
In a typical synthesis, 32 mg of dimethylphenylsilane (0.23 mmol) and 36.7 mg of undecane (0.23 mmol, internal standard for gas chromatography) were dissolved in 4 g of dry n-butanol, as published elsewhere.68 An Au NP-loaded nonwoven (S = 1 cm2, d ≈ 400 μm, pre-swollen for 24 h in pure n-butanol) was placed in the reaction solution. The reaction was shaken at 400 rpm (Heidolph Multi Reax Shaker) for 24 h and aliquots of 10 μL of the reaction solution were taken after different periods of time for kinetic studies. The aliquots were diluted with 1 mL of acetone for gas chromatography measurements. This procedure was repeated 9 times using the same hybrid nonwoven and a freshly prepared reaction mixture, whereby kinetics were followed for the 1st and 10th cycles only. Before reuse, the Au NP nonwovens were washed with n-butanol and dried by placing on a piece of filter paper. The determination of conversion (xp) via gas chromatography was based on the ratio of the integrals of the reactant (dimethylphenylsilane) to the internal standard (undecane, 0.23 mmol) and was referenced to the respective zero measurement.Instruments
Results and discussion
Table 1 summarizes the molecular characteristics of the employed SEDxA triblock terpolymers, which were prepared by post-polymerization amidation of the PMMA block of the corresponding PS-b-PE-b-PMMA triblock terpolymers using N,N-dimethylethylenediamine and N,N-diisopropylethylenediamine, respectively.43 Quantitative functionalization of the obtained SEDMA (polystyrene-block-polyethylene-block-poly(N,N-dimethylaminoethyl methacrylamide)) and SEDiPA (polystyrene-block-polyethylene-block-poly(N,N-diisopropylaminoethyl methacrylamide)) triblock terpolymers was confirmed by 1H NMR (nuclear magnetic resonance) and FT-IR (Fourier transform-infrared) spectroscopy (Fig. S2 and S3†). The polarity of the amidated PDxA block was tuned by employing different amines for functionalization, whereas the patch sizes in the corona of the self-assembled crystalline-core micelles (CCMs) were altered using PS/PDxA blocks of different lengths. Consequently, triblock terpolymers with comparable block lengths of the PS and PDxA corona blocks are termed symmetric, i.e., s-SEDiPA and s-SEDMA, and the triblock terpolymer with unequal block lengths is termed asymmetric, i.e., as-SEDiPA.| Sample code | Compositiona | Block length PS/PDxA | PDxA corona [wt%] | R h (sCCMs)b [nm] | l (wCCMs)c [nm] | Patch size PS/PDxAc [nm] |
|---|---|---|---|---|---|---|
| a Subscripts denote the content of the respective polymer block in wt% and superscript denotes the number-average molecular weight in kg mol−1 determined by a combination of MALDI-ToF MS (matrix-assisted laser desorption/ionization – time of flight mass spectrometry) and 1H NMR. b Hydrodynamic radii of the sCCMs determined by DLS. c Average sizes ± standard deviation as determined by TEM image analysis of at least 100 micelles/patches. | ||||||
| s-SEDiPA | S28E15DiPA58156 | 420/430 | 67 | 31.4 ± 0.3 | 260 ± 100 | 12 ± 2/10 ± 3 |
| as-SEDiPA | S38E21DiPA41181 | 660/350 | 52 | 35.8 ± 0.3 | 480 ± 240 | 18 ± 4/9 ± 2 |
| s-SEDMA | S33E17DMA50131 | 420/430 | 60 | — | 510 ± 310 | 18 ± 5/17 ± 5 |
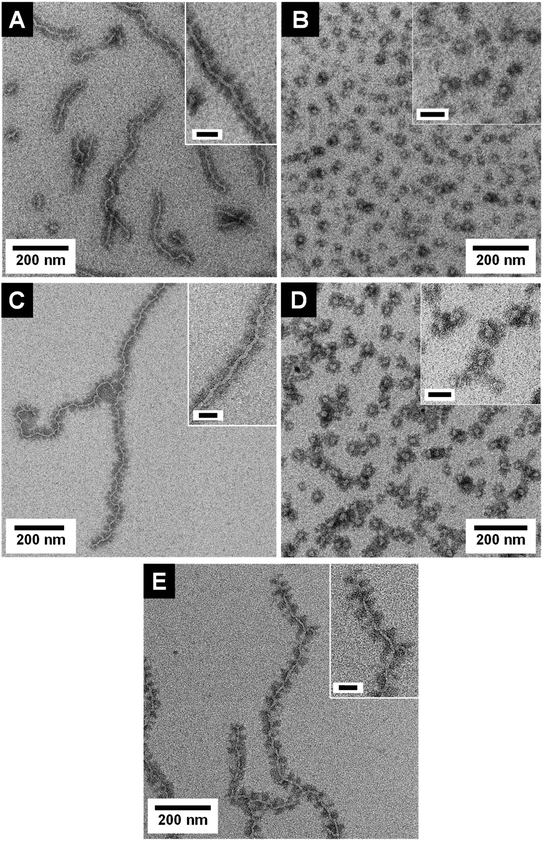
The patchy CCMs with different shapes (worm-like and spherical) were obtained by CDSA of the functionalized triblock terpolymers.60 First, the triblock terpolymers were dissolved above the melting point (Tm) of the polyethylene (PE) middle block using a selective (non-)solvent for the PE block, and then cooled down to the respective crystallization temperature (Tc) and, finally, crystallized at Tc for 24 h. Worm-like CCMs (wCCMs) are formed when a good solvent for the PE middle block (THF) is chosen, whereas a bad solvent for the PE block (1,4-dioxane) leads to the formation of spherical CCMs (sCCMs). The employed crystallization temperatures and respective μDSC (micro-differential scanning calorimetry) traces are given in the ESI (Table S1, Fig. S4†).
The transmission electron microscopy (TEM) micrographs shown in Fig. 2 as well as dynamic light scattering (DLS) results (Table 1, Fig. S8†) prove the successful formation of both micelle shapes, i.e., patchy wCCMs and sCCMs. The sCCMs exhibit apparent hydrodynamic radii of Rh ≈ 31–37 nm and the wCCMs show average lengths of l ≈ 260–510 nm. Selective staining of the PS block with RuO4 reveals the patchy structure of the corona for both micelle shapes. However, the patchy corona of the sCCMs is less defined compared to the well-ordered corona of the wCCMs, which shows an almost alternating arrangement of the PS (dark) and PDxA (bright) patches (Fig. 2). This is in agreement with our previous results on the corona structure of patchy PS-b-PE-b-PMMA triblock terpolymer micelles.60 The size of the corona patches varies with the block length of the PS and PDxA corona blocks (Table 1), i.e., the widths of both corona patches are similar for a symmetric composition of the corona in terms of PS and PDxA block lengths (≈18 nm for s-SEDMA and ≈11 nm for s-SEDiPA wCCMs, respectively), but show a significant difference for an asymmetric block length ratio (≈18 nm for PS and ≈9 nm for PDiPA in the case of as-SEDiPA wCCMs).
The functional patchy micelles were then used in a coaxial electrospinning process to generate nonwovens with a patch-like surface structure (Fig. 1A), employing a PS solution (Mn = 1.8 106 g mol−1, c = 7 wt% in DMF) as the core-forming material and a dispersion of the patchy micelles as the shell (c = 10 g L−1 in THF (wCCMs) or dioxane (sCCMs)). The patchy nonwovens are termed according to the micelle type employed as the shell material, i.e., NW_s-SEDiPA(w) stands for a nonwoven with s-SEDiPA wCCMs on the surface. The resulting fibres show an uniform thickness of 1.27 ± 0.15 μm and a homogeneous coating of the surface with the functionalized CCMs (Fig. 3A–C, 8A and S9†), as revealed by scanning electron microscopy (SEM). This is promoted by the PS patches of the micelles, which are adsorbed onto the surface of the PS nonwoven. The characteristic shape of the sCCMs (Fig. 3A and S9B†) as well as wCCMs (Fig. 3B, 8A and S9A†) was preserved after electrospinning, as indicated by spherical and elongated structures observable on the fibres' surface. In order to exclude any effect arising from the sample preparation for SEM, i.e., coating with a thin Pt layer (d ≈ 1.3 nm), we have measured one uncoated patchy nonwoven based on s-SEDiPA wCCMs (NW_s-SEDiPA(w), Fig. 3C). Here, the so-called beam deceleration mode was employed (for details see the Experimental section) and again worm-like structures arising from the decoration of the PS fibres with wCCMs are visible, showing that coating with Pt has no impact on the observed fibre morphology.
In the next step, Au NP-containing hybrid nonwovens were produced via a facile ligand exchange process (Fig. 1B), i.e., the patchy nonwovens (surface area: S = 1 cm2 and thickness: d ≈ 400 μm) were dipped in an aqueous dispersion of preformed, citrate-stabilized Au NPs for 24 h and subsequently washed with sodium citrate solution and water to remove unbound Au NPs. The employed Au NPs showed a rather broad size distribution with a number average diameter of DTEM = 9.5 ± 2.4 nm, as determined by TEM (Fig. S1A and B†). This was also confirmed by asymmetric flow field-flow fractionation (AF4), revealing a tailing of the size distribution toward larger particle sizes (Fig. S1D†). The obtained average diameter of gyration of Dg = 17.9 ± 2 nm agrees with the size determined by TEM (DTEM = 9.5 ± 2.4 nm), taking the rather broad size distribution and the fact that light scattering overestimates the content of larger particles (scattering intensity is proportional to D6) into account. It is noted that we intentionally did not aim for the production of narrowly distributed Au NPs, as for catalytic applications a simple and fast NP synthesis is preferred.
The successful incorporation of Au NPs within the functional surface of the patchy nonwovens could be easily followed by the discoloration of the Au NP dispersion and the resulting purple colour of the produced hybrid nonwovens. The strong binding of the Au NPs within the functional surface patches can be attributed to a replacement of the citrate ligands by the multidentate, amino-group containing patches (gain in entropy by release of citrate molecules). Electrostatic interactions with the amino groups (pKa ≈ 7) in the functional patches can be neglected as the Au NP dispersion shows a pH of 8 and under these conditions the amino groups are uncharged.68 The Au content of the hybrid nonwovens was calculated from the respective Au content of the Au NP dispersions after loading, as determined by UV-vis (ultraviolet-visible) spectroscopy. Here, the Au content of the initial Au NP dispersion determined by ICP-OES (inductively coupled plasma-optical emission spectrometry) was used as the reference (difference method). A detailed description of this method is given in the ESI (Fig. S5†). The Au contents of the hybrid nonwovens and the overall surface area (SAuNP) of the embedded Au NPs, as determined from the respective Au content and the average diameter of DTEM = 9.5 ± 2.4 nm, are given in Table 2. The Au NP-loaded hybrid nonwovens are termed according to the employed patchy nonwoven template, i.e., NW_s-SEDiPA(w)/Au stands for a patchy NW_s-SEDiPA(w) nonwoven loaded with Au NPs.
| Hybrid nonwoven | m Au,calibration , [μg cm−2] | m Au,UV-vis 400 nm , [μg cm−2] | S AuNP [m2] |
|---|---|---|---|
| a Relative to the area of the nonwoven (S = 1 cm2) under the assumption of an equal thickness (d ≈ 400 μm). b The amount of Au in the dispersions was calculated according to Fig. S5, using a calibration based on the employed Au NP dispersion. c Determined from the absorbance at λ = 400 nm according to eqn (S1). d Overall surface area of the embedded Au NPs calculated from the NP diameter obtained by TEM (DTEM = 9.5 ± 2.4 nm) and the Au content in the hybrid nonwovens (mAu,UV-vis 400 nm), assuming a perfect spherical shape (eqn (S7–S10)). Given errors were calculated based on error propagation (eqn (S11)). | |||
| NW_s-SEDiPA(s)/Au | 69 | 70 | (2.29 ± 0.58) × 10−3 |
| NW_s-SEDiPA(w)/Au | 52 | 57 | (1.86 ± 0.47) × 10−3 |
| NW_as-SEDiPA(s)/Au | 77 | 77 | (2.52 ± 0.64) × 10−3 |
| NW_as-SEDiPA(w)/Au | 82 | 82 | (2.68 ± 0.68) × 10−3 |
| NW_s-SEDMA(w)/Au | 76 | 77 | (2.52 ± 0.64) × 10−3 |
An important issue in heterogeneous catalysis with supported NPs is the efficient immobilization and stabilization of the NPs in order to avoid agglomeration and, thus, a loss in the catalytically active surface area, while preserving the catalytic activity of the NPs. The latter might be strongly influenced by the type of stabilizing ligand, i.e., their binding strength to the Au NPs' surface. Accordingly, the performance of the patchy nonwovens as a support for the efficient stabilization of Au NPs was analysed by SEM and SAXS (small-angle X-ray scattering), and the catalytic activity of the immobilized NPs was probed employing the alcoholysis of dimethylphenylsilane. In the following, the impact of the micelle morphology and patch size as well as patch chemistry will be discussed in detail.
Effect of micelle morphology and patch size
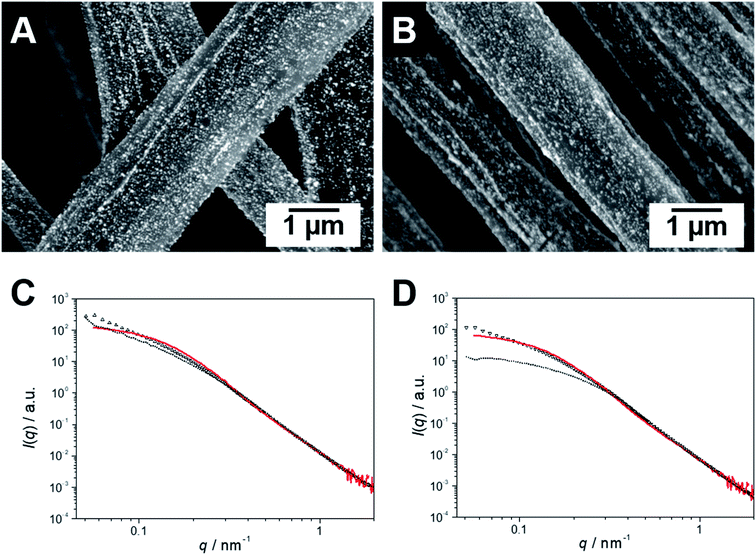
SEM coupled with a backscattered electron (BSE) detector confirms the homogeneous loading of the patchy nonwovens based on spherical and worm-like s-SEDiPA CCMs with Au NPs (Fig. 4A and B). NP agglomerates, which would be discernible as large, bright appearing domains, are hardly detectable. The absence of larger NP agglomerates is also supported by the SAXS results shown in Fig. 4C (NW_s-SEDiPA(w)/Au) and Fig. 4D (NW_s-SEDiPA(s)/Au), which compare the scattering profiles of the Au NPs within the hybrid nonwovens (open triangles) with that of the Au NP dispersion (coloured in red) used in the loading process. The scattering profiles of the embedded Au NPs were determined by subtracting the scattering intensity of the Au NP-loaded hybrid nonwovens from that of the corresponding neat nonwovens, as described in our previous work.68 For both hybrid nonwovens, the scattering profile of the embedded Au NPs is similar to that of the neat Au NP dispersion for scattering vectors q > 0.1 nm−1. Only for smaller q-values, the scattering profiles do not reach a plateau but show a slight increase with decreasing q-values. This might point to a weak, partial agglomeration of the incorporated Au NPs or to an additional structure factor contribution due to the close vicinity of the embedded Au NPs in the corona of the patchy micelles located on the nonwovens' surface.We have also studied whether agglomeration or a loss of the embedded Au NPs might occur during catalysis. For the hybrid nonwoven based on s-SEDiPA wCCMs (Fig. 4C, NW_s-SEDiPA(w)/Au) the scattering profiles prior to (open triangles) and after 10 catalysis cycles (dotted profile) are nearly identical, i.e., neither a loss of Au NPs (scattering intensity would decrease) nor a significant agglomeration (steeper increase of scattering intensity for low q-values would be expected) takes place during catalysis. In contrast, for the hybrid nonwoven based on s-SEDiPA sCCMs (Fig. 4D, NW_s-SEDiPA(s)/Au) a significantly lower scattering intensity and a pronounced plateau for low q-values were observed after 10 catalysis cycles. This points to a partial loss of larger Au NPs during catalysis, revealing that patchy nonwovens based on spherical s-SEDiPA CCMs are less efficient in NP stabilization with respect to s-SEDiPA wCCMs. This might be attributed to the less defined patchy corona of the sCCMs (Fig. 2).
Fig. 5 displays the scattering profiles of the embedded Au NPs for hybrid nonwovens based on spherical (NW_as-SEDiPA(s)/Au, filled squares) and worm-like (NW_as-SEDiPA(w)/Au, open triangles) as-SEDiPA CCMs, which exhibit a highly asymmetric corona, i.e., different PS and PDiPA patch sizes (Table 1). Here, the scattering intensity for NW_as-SEDiPA(w)/Au shows only a comparably weak increase for low q-values and tends to form a plateau, unlike the behaviour of NW_s-SEDiPA(w)/Au (symmetric corona). Moreover, the scattering profile of the embedded Au NPs is now almost identical to that of the Au NPs in the initial Au NP dispersion (red profile). This points to a more efficient stabilization of the Au NPs embedded within the asymmetric patchy corona of as-SEDiPA wCCMs against agglomeration. Again, for the NW_as-SEDiPA(s)/Au hybrid nonwoven a steeper increase in scattering intensity for low q-values is observed, which points to a partial agglomeration and underpins the conclusion that patchy sCCMs are less efficient in NP stabilization compared to wCCMs. The enhanced stabilization of Au NPs against agglomeration for as-SEDiPA wCCMs might be attributed to the slightly smaller size of the functional PDiPA patches (9 ± 2 nm for as-SEDiPA(w) and 10 ± 3 nm for s-SEDiPA(w)) in combination with the increased size of the PS patches (18 ± 4 nm for as-SEDiPA(w) and 12 ± 2 nm for s-SEDiPA(w)), which separate the PDiPA patches from each other (Table 1). Accordingly, there is less space for the Au NPs in the PDiPA patches and the spatial separation of the PDiPA patches by the PS patches is stronger, leading to a reduced possibility to form NP agglomerates.
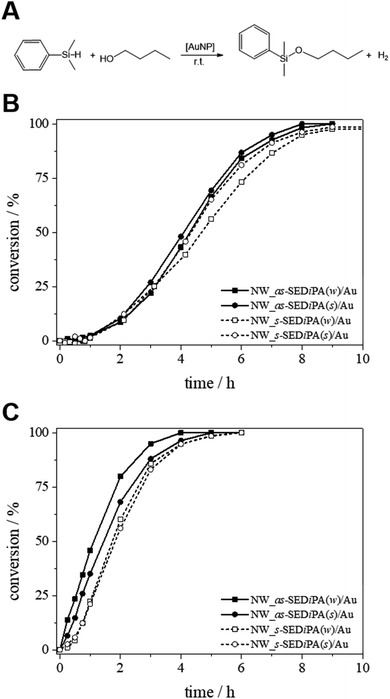
Next, we studied the impact of the micelle shape and patch size on the catalytic activity of the patchy hybrid nonwovens, employing the alcoholysis of dimethylphenylsilane in n-butanol (n-BuOH) as an established model reaction (Fig. 6A).68 We ran 10 consecutive cycles and the kinetics were followed for the 1st and 10th cycles in order to address the effect of swelling of the PDxA patches in n-BuOH on the catalytic performance and to probe the reusability of our catalyst system. Detailed information on the Au content of the nonwovens is given in Table 2, and the used molar ratio of Au to dimethylphenylsilane and other kinetic parameters are summarized in Table 3.
| Hybrid nonwovens | Aua mol% | k app [h−1] | r [h−1] | t ind [min] | t R [h] | k [L m−2 mol−1 s−1] |
|---|---|---|---|---|---|---|
| a Relative to dimethylphenylsilane (0.23 mmol). b Apparent rate constant (kapp) and accessibility rate (r) determined according to eqn (5). c Time at 3% conversion was taken as the induction time (tind) and calculated using eqn (5). d Reaction time (tR) at 99% conversion, calculated using eqn (5). e Rate constant normalized to the overall surface area of the embedded Au NPs (SAuNP, Table 2) and the concentration of n-BuOH (cn-BuOH = 10.93 mol L−1); given errors were calculated based on error propagation (eqn (S12)). | ||||||
| NW_s-SEDiPA(s)/Au | 0.15 | 1.77 ± 0.10 | 0.29 ± 0.02 | 21 | 5.29 | (1.97 ± 0.51) × 10−2 |
| NW_s-SEDiPA(w)/Au | 0.12 | 1.54 ± 0.11 | 0.38 ± 0.05 | 20 | 5.25 | (2.10 ± 0.55) × 10−2 |
| NW_as-SEDiPA(s)/Au | 0.17 | 1.18 ± 0.10 | 0.79 ± 0.15 | 16 | 5.16 | (1.19 ± 0.31) × 10−2 |
| NW_as-SEDiPA(w)/Au | 0.18 | 1.27 ± 0.11 | 1.43 ± 0.38 | 11 | 4.32 | (1.20 ± 0.32) × 10−2 |
| NW_s-SEDMA(w)/Au | 0.17 | 1.55 ± 0.26 | 0.54 ± 0.16 | 17 | 4.68 | (1.56 ± 0.47) × 10−2 |
Fig. 6B shows the conversion vs. time (xp/t) plots of the 1st catalysis cycles for hybrid nonwovens based on s- and as-SEDiPA CCMs. Irrespective of the micelle morphology and patch sizes of the CCMs employed for surface decoration, the hybrid nonwovens showed an induction time of tind ≈ 1 h. Full conversion is reached in about 8–9 h for all hybrid nonwovens, while the s-SEDiPA based systems show slightly longer reaction times. The latter might be attributed to the higher PDiPA content in the corona of the s-SEDiPA micelles in combination with a higher PDiPA block length (Table 1), resulting in a slightly higher diffusion barrier for the reactants in the swollen PDiPA patches with respect to as-SEDiPA based hybrid nonwovens. However, one has to take the slightly different Au contents of the hybrid nonwovens into account (Table 2). This point will be addressed in detail later on in the discussion of the kinetics of the 10th catalysis cycles. Interestingly, the induction times are significantly decreased for the 10th catalysis cycles (tind ≈ 10–20 min, Table 3) and, in addition, full conversion is already reached in about 4–6 h. This shows that the higher induction and reaction times observed in the 1st catalysis cycles are most likely related to an initial period, where the PDiPA patches swell in n-BuOH and, thus, enable the reactants to access the embedded Au NPs. This is also in contrast to our previous work, where we have observed that the 1st and 10th catalysis cycles were almost identical with comparable induction times.68 This discrepancy can be attributed to the different degrees of functionalization (f) of the PDiPA blocks (f = 55% vs. quantitative functionalization in this study) and the fact that the previously employed amidation method resulted in about 50 mol% imide units, which show only limited solubility in n-BuOH. Hence, the swelling of the PDiPA patches clearly affects the accessibility of the catalytically active Au NP surface and, as a consequence, the duration of the induction period and the overall reaction time.
In order to get a deeper insight into the kinetics of the reaction and, hence, the influence of the micelle shape and patch size, we have evaluated the kinetics of the 10th catalysis cycles. We have purposely chosen the 10th catalysis cycles to rule out the effect of initial swelling from the dry state, manifested by the long induction times observed for the 1st catalysis cycles. Despite the large excess of n-BuOH compared to silane, Fig. S10† shows that a classical pseudo 1st order kinetics model cannot reproduce the experimental data over the full time range. We therefore developed a theoretical model, which extends the classical pseudo 1st order kinetics with an additional induction period to address the influence of patch swelling. We consider the reaction of dimethylphenylsilane (reactant E) with n-BuOH, which acts as both the solvent and the reactant, employing the rate law
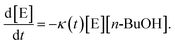 | (1) |
In order to model the induction period, i.e., the swelling of the patches, the two reactants (dimethylphenylsilane and n-BuOH) are considered to become available for the embedded catalytically active Au NPs with a certain accessibility rate r. The specialty of our model is that the reaction rate κ(t) is increasing over time according to
| κ(t) = κ0(1 − e−rt), | (2) |
Replacing (2) in (1) yields the rate law for our model
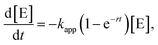 | (3) |
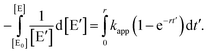 | (4) |
The natural logarithm form of the power law expression is finally obtained as
 | (5) |
We note that for the immediate availability of the reactants, i.e., r → ∞, the classic equation describing the kinetics of a pseudo 1st order reaction (eqn (S5)†) is recovered from eqn (5).
Accordingly, the experimental data were fitted with eqn (5) to yield the apparent rate constants (kapp) and the accessibility rates (r) (Fig. 7 and S11†). To facilitate comparison between the different catalyst systems the apparent rate constants were normalized to the concentration of n-BuOH (cn-BuOH = 10.93 mol L−1) and the overall surface area (SAuNP) of the embedded Au NPs, yielding the rate constants k for the Au NP-catalysed alcoholysis of dimethylphenylsilane (eqn (S6),†Table 3). Using the obtained values for kapp and r, the corresponding induction times (tind) and overall reaction times (tR) can be calculated from eqn (5) and are also given in Table 3.
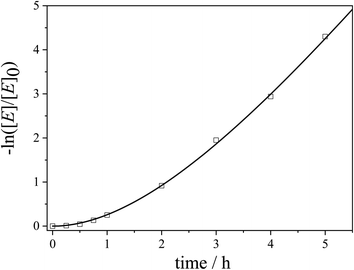 | ||
| Fig. 7 Kinetics plot for the 10th cycle of the catalytic alcoholysis of dimethylphenylsilane with an Au NP-loaded patchy nonwoven based on s-SEDiPA wCCMs (NW_s-SEDiPA(w)/Au) as the catalyst (squares: experimental data and line: fit according to our extended pseudo 1st order kinetics model in eqn (5)). | ||
The normalized rate constants (k) are in a comparable range for the different hybrid nonwovens based on s-SEDiPA and as-SEDiPA CCMs (Table 3). Similar results were obtained by using the classical 1st order kinetics model for the determination of the reaction rate constants (eqn (S5), Fig. S10, Table S2†), although in this case only the second half of the observation period, where the plot exhibits a constant slope, can be fitted by the classical model. Interestingly, the accessibility parameters (r) for the as-SEDiPA based hybrid nonwovens are higher with respect to those of the s-SEDiPA based ones. A possible explanation is the lower steric demand of the PDiPA patches in the as-SEDiPA CCMs (lower PDiPA block length and content in the corona, Table 1). This is also reflected in the shorter induction and reaction times observed for the as-SEDiPA based hybrid nonwovens, despite their slightly lower normalized rate constants compared to s-SEDiPA based nonwovens. Altogether, the induction (tind ≈ 10–20 min) and reaction times (tR ≈ 4–5 h) for the 10th catalysis cycles (Table 3) are significantly shorter in comparison to the 1st catalysis cycles (tind ≈ 1 h and tR ≈ 8–9 h, as estimated from the xp/t plots in Fig. 6B), showing again the importance of patch swelling in n-BuOH for the reaction kinetics. With respect to our previous work a significant reduction of the reaction time from about 7 to 4.3 h could be achieved for the NW_as-SEDiPA(w)/Au hybrid nonwoven.68
Effect of patch chemistry
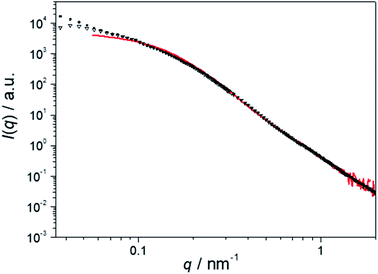
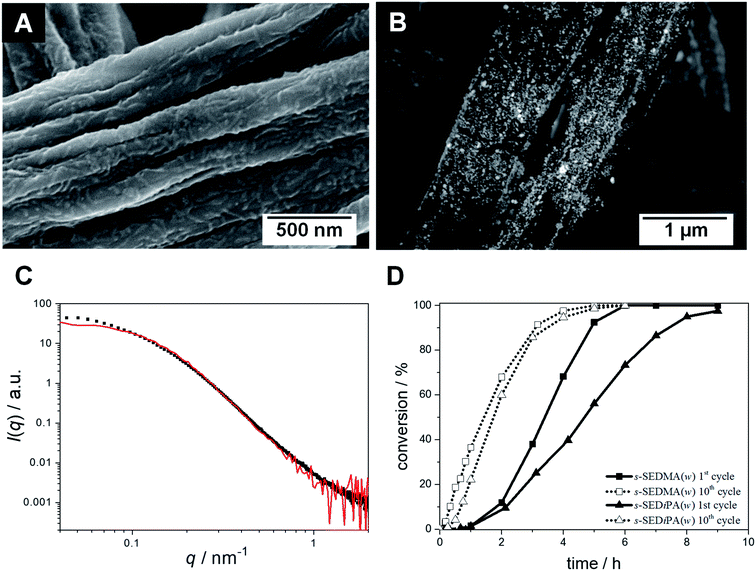
To further study the effect of patch swelling on the catalytic activity of the hybrid nonwovens, we altered the patch chemistry (PDMA vs. PDiPA) and compared nonwovens decorated with s-SEDiPA (Fig. 3B and C) and s-SEDMA (Fig. 8A) wCCMs. If there is any effect of patch chemistry on the reaction kinetics, this effect should be largest for the CCMs with the highest weight fraction of PDxA units in the corona, i.e., s-SEDMA and s-SEDiPA (Table 1). The PDMA patches are more hydrophilic compared to PDiPA and, consequently, are expected to swell faster and to a greater extend in n-BuOH.The SEM image acquired with a BSE detector again shows nicely dispersed, bright appearing Au NPs on the surface of the respective NW_s-SEDMA(w)/Au hybrid nonwoven (Fig. 8B). The SAXS profile of the embedded Au NPs (Fig. 8C, filled squares) shows no sign of agglomeration, in contrast to the weak, partial agglomeration observed for the s-SEDiPA (Fig. 4C and D) and as-SEDiPA (Fig. 5) based hybrid nonwovens. The scattering profile is almost identical to that of the Au NPs in the initial NP dispersion (Fig. 8C, red profile) and the scattering intensity reaches a well-defined plateau for low q-values. This shows that nonwovens decorated with s-SEDMA wCCMs are best suited for Au NP stabilization and efficiently hinder the formation of NP agglomerates.
Fig. 8D compares the xp/t-plots for the 1st and 10th cycles of the catalytic alcoholysis of dimethylphenylsilane with NW_s-SEDiPA(w)/Au and NW_s-SEDMA(w)/Au, respectively. The most obvious difference can be observed in the 1st catalysis cycles. The induction times are comparable (tind ≈ 1 h), but the overall reaction time is significantly lower for the s-SEDMA(w) based hybrid nonwoven (about 6 h compared to 9 h for NW_s-SEDiPA(w)/Au). In addition, for the 10th cycles the accessibility parameter (r) is higher and the induction (tind) as well as overall reaction time (tR) are lower for the s-SEDMA(w) decorated hybrid nonwoven (Table 3). This clearly underlines the influence of patch swelling on the reaction kinetics and supports our assumption that the increased hydrophilicity of the PDMA patches results in a better swelling of the patches in n-BuOH (higher accessibility parameter) and, thus, leads to reduced induction and reaction times.
In summary, concerning the efficiency for Au NP stabilization patchy wCCMs are more efficient compared to sCCMs and the s-SEDMA(w) based nonwoven showed the best performance, i.e., no hints of NP agglomeration could be detected by SEM and SAXS. However, the shortest induction and reaction times for the 10th cycle of the Au NP-catalyzed alcoholysis of dimethylphenylsilane were observed for the as-SEDiPA(w) based hybrid nonwoven. Accordingly, the interplay of the micelle shape, patch size and chemistry influences the stabilization and catalytic activity of the embedded Au NPs. PDMA patches are more efficient for NP stabilization, which might be attributed to a stronger interaction with the NPs' surface (less steric hindrance of methyl groups compared to iso-propyl groups). But in contrast, a stronger interaction with the NPs' surface could lead to reduced reaction rate constants (Table 3: NW_s-SEDMA(w)/Au shows a slightly lower normalized rate constant (k) compared to NW_s-SEDiPA(w)/Au). Besides these parameters, also the accessibility parameter (r) has to be taken into account, which describes the rate at which the reactants (dimethylphenylsilane and n-BuOH) become available for the embedded Au NPs. This parameter is largest for NW_as-SEDiPA(w)/Au and results in the shortest observed induction and reaction times, despite the lower normalized rate constant in comparison to s-SEDMA(w) and s-SEDiPA(w) based hybrid nonwovens (Table 3).
The reaction times for full conversion and the rate constants strongly depend on the Au content and the Au NP size, i.e., the total Au NP surface area. This makes a comparison to other studies difficult, as mostly only reaction times are given and the rate constants are not normalized to the overall Au NP surface area. Nevertheless, the reported reaction times for the Au NP-catalysed alcoholysis of dimethylphenylsilane with n-BuOH at room temperature are in the range of the reaction times found in this study (tR ≈ 4–5 h) or even higher (Table S3†).70,73,74 Shorter reaction times at full conversion were only reported for Au NPs supported on nanosized hydroxyapatite (Au/HAPnano) and were attributed to the high adsorption capacity of the support, which increases locally the concentration of dimethylphenylsilane at the surface of Au/HAPnano.75 However, the employed Au NPs (D = 3 nm) were significantly smaller compared to the Au NPs used in this study (DTEM = 9.5 ± 2.4 nm), which results in an increased catalytically active surface area.
Conclusions
The studied electrospun patchy nonwovens are efficient supports for the stabilization of Au NPs against agglomeration and the corresponding hybrid nonwovens with embedded Au NPs exhibit a high activity and reusability in the catalytic alcoholysis of dimethylphenylsilane. Utilizing an extended pseudo 1st order kinetics model revealed that the catalytic activity is influenced by the patch size and chemistry (PDMA vs. PDiPA patches), which determine the accessibility of the reactants to the surface of the embedded Au NPs. This is also manifested by the observation of longer induction and reaction times in the 1st catalysis cycles in comparison to that of the 10th cycles. This allows tailoring the properties of the patchy hybrid nonwovens in terms of NP stabilization and catalytic performance. Compared to heterogeneous catalysis with Au NPs that are stabilized by particulate supports (MOFs, metal oxides, and 2D materials) our “tea-bag”-like catalyst system can be simply dipped in the reaction mixture and pulled out after catalysis without the need for filtration or centrifugation to separate the catalyst. Electrospinning as a “top-down” approach can be easily upscaled and the synthesis of the PS-b-PE-b-PMMA precursor triblock terpolymers (catalytic hydrogenation of polystyrene-block-polybutadiene-block-poly(methyl methacrylate) triblock terpolymers produced by living anionic polymerization (also commercially available from Arkema)) can be conducted on a kg scale. In addition, the functional, amino group-containing patches are not only efficient stabilizers for Au NPs, but can also be employed for the incorporation of other metal (Ag and Pd) or transition metal oxide (CuO and ZnO) NPs. This opens the way for a variety of applications in heterogeneous catalysis, which will be addressed in future studies. Moreover, the facile loading of the patchy nonwovens by a simple dipping process and the efficient stabilization of the embedded NPs might also be utilized for water purification.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the German Research Foundation through the Collaborative Research Centre SFB 840 (projects A2, A12 and B8) and the Bavarian State Ministry of the Environment and Consumer Protection (TNT01NaT-72524). We thank S. Agarwal for assistance with coaxial electrospinning and H.-W. Schmidt for discussion and support in SEM measurements. We appreciate the support of the Keylab Mesoscale Characterization: Scattering Techniques (S. Rosenfeldt) of the Bavarian Polymer Institute (BPI) for conducting some of the SAXS experiments, Carmen Kunert for SEM and TEM and Rika Schneider for AF4 measurements. C. H. acknowledges support by the Graduate School of the University of Bayreuth. G. S. acknowledges support from the Biological Physics program of the Elite Network of Bavaria and S. G. thanks the Volkswagen Foundation. We appreciate support through the computational resources provided by the Bavarian Polymer Institute.References
- A. Alshammari and V. N. Kalevaru, in Catalytic Application of Nano-Gold Catalysts, ed. N. K. Mishra, InTech, 2016 Search PubMed.
- M. Haruta, Chem. Rec., 2003, 3, 75–87 CrossRef CAS PubMed.
- S. Nishimura and K. Ebitani, ChemCatChem, 2016, 8, 2303–2316 CrossRef CAS.
- C. Burda, X. Chen, R. Narayanan and M. A. El-Sayed, Chem. Rev., 2005, 105, 1025–1102 CrossRef CAS PubMed.
- M. Stratakis and H. Garcia, Chem. Rev., 2012, 112, 4469–4506 CrossRef CAS PubMed.
- G. C. Bond, P. A. Sermon, G. Webb, D. A. Buchanan and P. B. Wells, J. Chem. Soc., Chem. Commun., 1973, 444–445 RSC.
- M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 16, 405–408 CrossRef.
- L. M. Rossi, J. L. Fiorio, M. A. S. Garcia and C. P. Ferraz, Dalton Trans., 2018, 47, 5889–5915 RSC.
- S. Kunz, Top. Catal., 2016, 59, 1671–1685 CrossRef CAS.
- Á. Molnár and A. Papp, Coord. Chem. Rev., 2017, 349, 1–65 CrossRef.
- A. Cao, R. Lu and G. Veser, Phys. Chem. Chem. Phys., 2010, 12, 13499–13510 RSC.
- M. Davidson, Y. Ji, G. J. Leong, N. C. Kovach, B. G. Trewyn and R. M. Richards, ACS Appl. Nano Mater., 2018, 1, 4386–4400 CrossRef CAS.
- I. Ro, J. Resasco and P. Christopher, ACS Catal., 2018, 8, 7368–7387 CrossRef CAS.
- Y. Wang, H. Arandiyan, J. Scott, A. Bagheri, H. Dai and R. Amal, J. Mater. Chem. A, 2017, 5, 8825–8846 RSC.
- G. Zhan and H. C. Zeng, Coord. Chem. Rev., 2016, 320–321, 181–192 CrossRef CAS.
- M. Massaro, C. G. Colletti, G. Lazzara, S. Milioto, R. Noto and S. Riela, J. Mater. Chem. A, 2017, 5, 13276–13293 RSC.
- J. Yuan, H. Schmalz, Y. Xu, N. Miyajima, M. Drechsler, M. W. Möller, F. Schacher and A. H. E. Müller, Adv. Mater., 2008, 20, 947–952 CrossRef CAS.
- J. John, E. Gravel, A. Hagège, H. Li, T. Gacoin and E. Doris, Angew. Chem., Int. Ed., 2011, 50, 7533–7536 CrossRef CAS PubMed.
- Y. Gong, M. Li, H. Li and Y. Wang, Green Chem., 2015, 17, 715–736 RSC.
- A. Kumar and Q. Xu, ChemNanoMat, 2018, 4, 28–40 CrossRef CAS.
- S. Navalon, A. Dhakshinamoorthy, M. Alvaro and H. Garcia, Coord. Chem. Rev., 2016, 312, 99–148 CrossRef CAS.
- R. K. Sharma, S. Dutta, S. Sharma, R. Zboril, R. S. Varma and M. B. Gawande, Green Chem., 2016, 18, 3184–3209 RSC.
- H. R. Moon, D.-W. Lim and M. P. Suh, Chem. Soc. Rev., 2013, 42, 1807–1824 RSC.
- C. R. Kim, T. Uemura and S. Kitagawa, Chem. Soc. Rev., 2016, 45, 3828–3845 RSC.
- A. Dhakshinamoorthy, A. M. Asiri and H. Garcia, ACS Catal., 2017, 7, 2896–2919 CrossRef CAS.
- M. Kaushik and A. Moores, Green Chem., 2016, 18, 622–637 RSC.
- M. Rose, ChemCatChem, 2014, 122, 1166–1182 Search PubMed.
- J. Artz, ChemCatChem, 2018, 10, 1753–1771 CrossRef CAS.
- S. Bhattacharyya, D. Samanta, S. Roy, V. P. Haveri Radhakantha and T. K. Maji, ACS Appl. Mater. Interfaces, 2019, 11, 5455–5461 CrossRef CAS PubMed.
- J. He, S. Razzaque, S. Jin, I. Hussain and B. Tan, ACS Appl. Nano Mater., 2019, 2, 546–553 CrossRef CAS.
- S. K. Dey, D. Dietrich, S. Wegner, B. Gil-Hernández, S. S. Harmalkar, N. de Sousa Amadeu and C. Janiak, ChemistrySelect, 2018, 3, 1365–1370 CrossRef CAS.
- Z. H. Farooqi, S. R. Khan and R. Begum, Mater. Sci. Technol., 2017, 33, 129–137 CrossRef CAS.
- R. Roa, S. Angioletti-Uberti, Y. Lu, J. Dzubiella, F. Piazza and M. Ballauff, Z. Phys. Chem., 2018, 232, 773–803 CAS.
- Y. Lu and M. Ballauff, Prog. Polym. Sci., 2016, 59, 86–104 CrossRef CAS.
- P. Hervés, M. Pérez-Lorenzo, L. M. Liz-Marzán, J. Dzubiella, Y. Lu and M. Ballauff, Chem. Soc. Rev., 2012, 41, 5577–5587 RSC.
- M. Müllner and A. H. E. Müller, Polymer, 2016, 98, 389–401 CrossRef.
- X. Fan, Z. Li and X. J. Loh, Polym. Chem., 2016, 7, 5898–5919 RSC.
- R. Ye, A. V. Zhukhovitskiy, C. V. Deraedt, F. D. Toste and G. A. Somorjai, Acc. Chem. Res., 2017, 50, 1894–1901 CrossRef CAS PubMed.
- T. Rudolph, M. von der Lühe, M. Hartlieb, S. Norsic, U. S. Schubert, C. Boisson, F. D'Agosto and F. H. Schacher, ACS Nano, 2015, 9, 10085–10098 CrossRef CAS PubMed.
- S. H. Jo, H. W. Kim, M. Song, N. J. Je, S.-H. Oh, B.-Y. Chang, J. Yoon, J. H. Kim, B. Chung and S. I. Yoo, ACS Appl. Mater. Interfaces, 2015, 7, 18778–18785 CrossRef CAS PubMed.
- F. H. Schacher, P. A. Rupar and I. Manners, Angew. Chem., Int. Ed., 2012, 51, 7898–7921 CrossRef CAS PubMed.
- E. M. Sulman, V. G. Matveeva, M. G. Sulman, G. N. Demidenko, P. M. Valetsky, B. Stein, T. Mates and L. M. Bronstein, J. Catal., 2009, 262, 150–158 CrossRef CAS.
- J. Schöbel, C. Hils, A. Weckwerth, M. Schlenk, C. Bojer, M. C. A. Stuart, J. Breu, S. Förster, A. Greiner, M. Karg and H. Schmalz, Nanoscale, 2018, 10, 18257–18268 RSC.
- J. Schöbel, M. Karg, D. Rosenbach, G. Krauss, A. Greiner and H. Schmalz, Macromolecules, 2016, 49, 2761–2771 CrossRef.
- C.-L. Zhang and S.-H. Yu, Chem. Soc. Rev., 2014, 43, 4423–4448 RSC.
- S. Agarwal, A. Greiner and J. H. Wendorff, Prog. Polym. Sci., 2013, 38, 963–991 CrossRef CAS.
- C. Bojer, K. Ament, H. Schmalz, J. Breu and T. Lunkenbein, CrystEngComm, 2019, 21, 4840–4850 RSC.
- U. Tritschler, S. Pearce, J. Gwyther, G. R. Whittell and I. Manners, Macromolecules, 2017, 50, 3439–3463 CrossRef CAS.
- R. L. N. Hailes, A. M. Oliver, J. Gwyther, G. R. Whittell and I. Manners, Chem. Soc. Rev., 2016, 45, 5358–5407 RSC.
- X. Wang, G. Guerin, H. Wang, Y. Wang, I. Manners and M. A. Winnik, Science, 2007, 317, 644–647 CrossRef CAS PubMed.
- J. B. Gilroy, T. Gädt, G. R. Whittell, L. Chabanne, J. M. Mitchels, R. M. Richardson, M. A. Winnik and I. Manners, Nat. Chem., 2010, 2, 566–570 CrossRef CAS PubMed.
- P. A. Rupar, L. Chabanne, M. A. Winnik and I. Manners, Science, 2012, 337, 559–562 CrossRef CAS PubMed.
- T. Gädt, N. S. Ieong, G. Cambridge, M. A. Winnik and I. Manners, Nat. Mater., 2009, 8, 144–150 CrossRef PubMed.
- J. Xu, H. Zhou, Q. Yu, G. Guerin, I. Manners and M. A. Winnik, Chem. Sci., 2019, 10, 2280–2284 RSC.
- A. M. Oliver, R. J. Spontak and I. Manners, Polym. Chem., 2019, 43, 3577 Search PubMed.
- Z. M. Hudson, C. E. Boott, M. E. Robinson, P. A. Rupar, M. A. Winnik and I. Manners, Nat. Chem., 2014, 6, 893–898 CrossRef CAS PubMed.
- H. Qiu, Z. M. Hudson, M. A. Winnik and I. Manners, Science, 2015, 347, 1329–1332 CrossRef CAS PubMed.
- X. Li, Y. Gao, C. E. Boott, M. A. Winnik and I. Manners, Nat. Commun., 2015, 6, 8127 CrossRef PubMed.
- H. Dou, M. Li, Y. Qiao, R. Harniman, X. Li, C. E. Boott, S. Mann and I. Manners, Nat. Commun., 2017, 8, 426 CrossRef PubMed.
- J. Schmelz, M. Karg, T. Hellweg and H. Schmalz, ACS Nano, 2011, 5, 9523–9534 CrossRef CAS PubMed.
- B. Fan, L. Liu, J.-H. Li, X.-X. Ke, J.-T. Xu, B.-Y. Du and Z.-Q. Fan, Soft Matter, 2016, 12, 67–76 RSC.
- W. Yu, M. Inam, J. R. Jones, A. P. Dove and R. K. O'Reilly, Polym. Chem., 2017, 8, 5504–5512 RSC.
- M. Inam, G. Cambridge, A. Pitto-Barry, Z. P. L. Laker, N. R. Wilson, R. T. Mathers, A. P. Dove and R. K. O'Reilly, Chem. Sci., 2017, 8, 4223–4230 RSC.
- X. Li, P. J. Wolanin, L. R. MacFarlane, R. L. Harniman, J. Qian, O. E. C. Gould, T. G. Dane, J. Rudin, M. J. Cryan, T. Schmaltz, H. Frauenrath, M. A. Winnik, C. F. J. Faul and I. Manners, Nat. Commun., 2017, 8, 15909 CrossRef CAS PubMed.
- D. Tao, C. Feng, Y. Cui, X. Yang, I. Manners, M. A. Winnik and X. Huang, J. Am. Chem. Soc., 2017, 139, 7136–7139 CrossRef CAS PubMed.
- J. R. Finnegan, X. He, S. T. G. Street, J. D. Garcia-Hernandez, D. W. Hayward, R. L. Harniman, R. M. Richardson, G. R. Whittell and I. Manners, J. Am. Chem. Soc., 2018, 140, 17127–17140 CrossRef CAS PubMed.
- M. C. Arno, M. Inam, Z. Coe, G. Cambridge, L. J. Macdougall, R. Keogh, A. P. Dove and R. K. O'Reilly, J. Am. Chem. Soc., 2017, 139, 16980–16985 CrossRef CAS PubMed.
- J. Schöbel, M. Burgard, C. Hils, R. Dersch, M. Dulle, K. Volk, M. Karg, A. Greiner and H. Schmalz, Angew. Chem., Int. Ed., 2017, 56, 405–408 CrossRef PubMed.
- A. Greiner and J. H. Wendorff, Angew. Chem., Int. Ed., 2007, 46, 5670–5703 CrossRef CAS PubMed.
- F. Mitschang, H. Schmalz, S. Agarwal and A. Greiner, Angew. Chem., Int. Ed., 2014, 53, 4972–4975 CrossRef CAS PubMed.
- P. A. Schaal and U. Simon, Beilstein J. Nanotechnol., 2013, 4, 336–344 CrossRef PubMed.
- W. S. Rasband, ImageJ, U. S. National Institutes of Health, Bethesda, Maryland, USA, 1997–2018 Search PubMed.
- P. Raffa, C. Evangelisti, G. Vitulli and P. Salvadori, Tetrahedron Lett., 2008, 49, 3221–3224 CrossRef CAS.
- T. Taguchi, K. Isozaki and K. Miki, Adv. Mater., 2012, 24, 6462–6467 CrossRef CAS PubMed.
- T. Mitsudome, Y. Yamamoto, A. Noujima, T. Mizugaki, K. Jitsukawa and K. Kaneda, Chem.–Eur. J., 2013, 19, 14398–14402 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Characterization of the AuNP dispersion (TEM, DLS, UV-vis, and AF4), the SEDxA triblock terpolymers (1H NMR, FT-IR, μDSC, DLS and TEM), nonwovens based on as-SEDiPA sCCMs and wCCMs (SEM) and details of determination of the Au content in the patchy nonwovens and of treatment of kinetics data. See DOI: 10.1039/c9na00607a |
| This journal is © The Royal Society of Chemistry 2020 |