Open Access Article
Open Access ArticleMetal oxide decorated porous carbons from controlled calcination of a metal–organic framework†
Gregory S.
Day
ab,
Jialuo
Li
 b,
Elizabeth A.
Joseph
b,
Peter C.
Metz
b,
Elizabeth A.
Joseph
b,
Peter C.
Metz
 a,
Zachary
Perry
b,
Matthew R.
Ryder
a,
Zachary
Perry
b,
Matthew R.
Ryder
 *a,
Katharine
Page
c and
Hong-Cai
Zhou
*a,
Katharine
Page
c and
Hong-Cai
Zhou
 bd
bd
aNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA. E-mail: rydermr@ornl.gov
bDepartment of Chemistry, Texas A&M University, College Station, Texas 77843, USA. E-mail: zhou@chem.tamu.edu
cDepartment of Materials Science and Engineering, University of Tennessee, Knoxville, Tennessee 37916, USA. E-mail: kpage10@utk.edu
dDepartment of Materials Science, Texas A&M University, College Station, Texas 77843, USA
First published on 12th May 2020
Abstract
Thermal decomposition of an iron-based MOF was conducted under controlled gas environments to understand the resulting porous carbon structure. Different phases and crystallite sizes of iron oxide are produced based on the specific gas species. In particular, air resulted in iron(III) oxide, and D2O and CO2 resulted in the mixed valent iron(II,III) oxide. Performing the carbonization under non-oxidative or reducing conditions (N2, He, H2) resulted in the formation of a mixture of both iron(II,III) oxide and iron(III) oxide. Based on in situ and air-free handling experiments, it was observed that this is partially due to the formation of zero-valent iron metal that is rapidly oxidized when exposed to air. Neutron pair distribution function analysis provided insight into the effect of the gas environment on the local structure of the porous carbon, indicating a noticeable change in local order between the D2O and the N2 calcined samples.
Introduction
Porous carbons have long been utilized for adsorption,1 separation,2 and catalytic applications.3 Several different methodologies can be used for the generation of porous carbons, from the direct pyrolysis of an organic precursor such as biological waste products4 or organic polymers,5 to the chemical activation of a carbon precursor using a strong base.6 In particular, metal oxide doped porous carbons have been used for many different catalytic transformations, such as alcohol oxidation,7 the Fischer–Tropsch reaction,8 and oxygen evolution.9 The generation of these metal oxide doped porous carbon species has typically been achieved through post-synthetic growth or incorporation of metal nanoparticles within the carbon structure.10 In these materials, the porosity of the carbon is either the result of a porous biological precursor, which often has a non-uniform range of porosities, or is dependent on the processing step, typically through chemical etching.11Metal–organic frameworks (MOFs) are a class of porous materials comprised of inorganic nodes, often referred to as secondary building units (SBUs), connected by organic linkers.12 One of the main advantages of MOFs is that both their physical and chemical structures and functionalities can be tuned through simple ligand or metal modification. Such features are promising for many next-generation smart applications,13 and have identified MOFs as particularly interesting materials for gas separation14 and catalysis.15 Additionally, the regular geometry of these compounds results in high levels of crystallinity and regularly shaped and organized pores.
Due to their tunable porosity and the presence of metal centers, there has been a growing interest in using MOFs as templates for the generation of porous carbons.16 MOF-derived carbons are typically produced via the direct calcination of MOFs in inert atmospheres like N2,17 Ar,18 or He.19 Carbonization offers many benefits for MOFs, the most obvious benefit being the increased hydrolytic stability compared to the parent MOF, allowing them to be utilized under aqueous conditions.18 This improved stability, alongside their tunable structures, give MOF-derived carbons the potential to be used as a replacement for standard porous carbons in areas such as water remediation20 or chemical warfare agent degradation.21 The ordered structure of MOFs also leads to the relatively facile formation of graphitic carbon, known for its electrical conductivity. This has resulted in many examples of MOF-derived carbons being utilized in electrochemical applications such as the oxygen evolution reaction.22 Additionally, there is an interest in dispersing metallic nanoparticles throughout a carbon scaffold to prevent sintering and maintain high chemical activity,21 which MOF-derived carbons excel at through their pre-dispersed metal SBUs.23
MOFs have long been used as gas storage materials due to their high surface areas, increasing accessible surface for the physisorption of gases.14 The adsorption affinity and capacity are often dependent on the dimensions of the host/guest, such as the size of the gas molecule, pore window,24 or the degree of polarizability.25 As such, the use of different gases during calcination should result in varying degrees of gas adsorption and diffusion. While activation processes have been studied in the formation of activated carbons,26 less research has focused on the effect of different gas environments on the formation of MOF-derived carbons. In particular, it has been noted in the MOF-derived carbon literature that calcination conditions have an impact on the resulting pore structure.27 However, there has yet to be a thorough systematic study of this process.
Results and discussion
In this work, we have focused on a typical iron-containing MOF, PCN-250 (PCN = porous coordination network)28 (also known as MIL-127 (ref. 29)), consisting of Fe3μ3O clusters and the ligand, 3,3′,5,5′-azobenzenetetracarboxylate (ABTC), with the formula C48H28Fe6N6O32, or (Fe3O)2(ABTC)3. This iron-based MOF was of particular interest for carbonization due to the catalytic applications of iron oxide particles,30,31 as well as the ease of separation afforded by the magnetic behavior of iron oxide.18 PCN-250 has been well studied for gas storage and separation applications due to its accessible open metal sites.28,32 Open metal sites are utilized to improve the polarization of gas molecules within the MOF pores, improving the adsorption affinity of the gas species.24 Improved gas adsorption affinity, results in an increased likelihood of adsorption events occurring during calcination, which could result in variations in the pore structure of the final porous carbon.Initial thermogravimetric analysis (TGA) of PCN-250 under air, N2, and water-saturated N2 determined the decomposition temperature of PCN-250 to be between 350 to 450 °C, with partial dependence on the gas flow environment (Fig. S1†). Calcination under air results in the near-complete thermolysis of the ligand (76% of the total theoretical mass), while analysis under N2 only results in a 25% mass loss upon decomposition at 450 °C, with a subsequent mass loss event occurring at 580–620 °C. Interestingly, when PCN-250 is decomposed in the presence of water vapor, the mass loss event at 620 °C results in what appears to be the complete pyrolysis of the ligand, with the final sample mass corresponding to that observed under air oxidation.
Based on the TGA results, we became interested in the gas flow-dependent decomposition of PCN-250 and decided to study the effect of gas environments on the material structure. We hypothesized that the different gas environments should result in highly differentiated pore structures when transformed into a MOF-derived carbon. To prevent complete loss of ligand-derived carbon upon carbonization, the samples were calcined at 500 °C for 4 hours under six different gas environments: air, N2, He, water enriched N2 (utilizing D2O to prevent potential H incorporation for neutron diffraction experiments, 2% D2O by volume), CO2, and H2 (5% in N2).
Brunauer–Emmett–Teller (BET) adsorption analysis of each sample was conducted to confirm the effect the gas environments have on surface area (Fig. 1). In general, the calcined samples have lower BET surface areas compared to uncalcined PCN-250 (approximately 1500 m2 g−1),28 with the air calcined samples showing the smallest BET surface area, 9 m2 g−1, and the He calcined sample showing the highest BET surface area, 265 m2 g−1. In agreement with our initial hypothesis, the surface area has a strong correlation with the residual carbon content in the material (Table S1†). The surface area of the samples was found to correlate linearly with the carbon content, giving a correlation coefficient (R2) value of 0.93129 (Fig. S2†). The R2 value improves to 0.98115 if the data for the D2O sample is removed as an outlier (Fig. S3†).
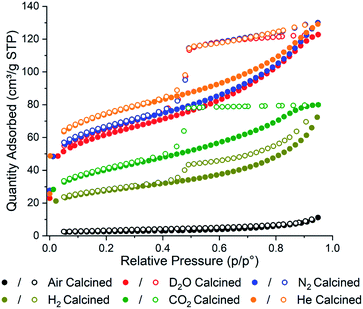 | ||
| Fig. 1 N2 adsorption isotherms of the calcined PCN-250 samples showing alterations in total capacity and pore shapes via calcination gas environment. | ||
The carbon content for the D2O calcined sample is the highest, despite only having the third-highest surface area (221 m2 g−1). This could be due to the D2O labilizing the metal–carboxylate bonds during the heating phase of the calcination, due to a competitive ligand exchange, forming a partially amorphous MOF structure that possesses a lower surface area before carbonization. This pre-carbonization amorphization likely prevents off-gassing during carbonization, causing some of the ligands to become trapped within the structure. The presence of organics is corroborated by the higher hydrogen and nitrogen content in the D2O sample (1.91 and 5.28%, respectively) (Table S1†). The nitrogen contained in the azobenzene bridge of the ligand is well known for readily eliminating N2 well below 500 °C,33 which suggests that the remaining nitrogen content within the MOF-derived carbons is due to poor heat transfer within the porous structure, preventing carbonization of some of the interior ligands. To test this hypothesis, we performed additional experiments looking at the collapse of PCN-250 under water-rich streams at lower temperatures. Compared to heating under N2, there was an increased degree of amorphization under water at 250, 275, and 300 °C (Fig. S4†). When PCN-250 was heated under water at 300 °C for 16 h there was negligible crystallinity remaining in the sample, while heating under N2 still showed characteristic peaks for PCN-250.
The samples of PCN-250 exhibit a large hysteresis at when the relative pressure, p/p0, is greater than 0.4, which is representative of mesoporous structures within the material. The generation of a 38 Å mesopore within PCN-250 has been previously reported,32 which matches the pore size distribution of the calcined PCN-250 samples reported here (Fig. S5 and S6†). The N2 and the He calcined samples show broadly similar isotherms, suggesting a similarity in the environments generated by these gases during calcination. Interestingly, the D2O in N2 calcined sample also shows a similar isotherm to that produced by N2 and He, which suggests that the concentration of D2O in the sample during calcination is low enough to not significantly impact the overall carbon superstructure, despite the differences in total carbon content. However, this same phenomenon is not observed with the sample calcined in the presence of 5% H2 in N2, which shows a significant reduction in the BET surface area, 98 m2 g−1.
Despite the differences in sample porosity, the morphologies of the individual samples are similar, maintaining the relative shape of PCN-250 as seen through scanning electron microscopy (SEM) images (Fig. S7–S13†). The air calcined sample shows the most substantial deviation from the shape of pre-treated PCN-250, with large cracks and channels observed in the material (Fig. S8†). The other samples all show similar contractions on a few of the crystal faces and corresponding concavity to the crystal edges (Fig. S9–S13†). These strains induce the formation of a wave-like pattern on the faces of most of the crystals, with the effect being most evident for the CO2 calcined sample (Fig. S11†).
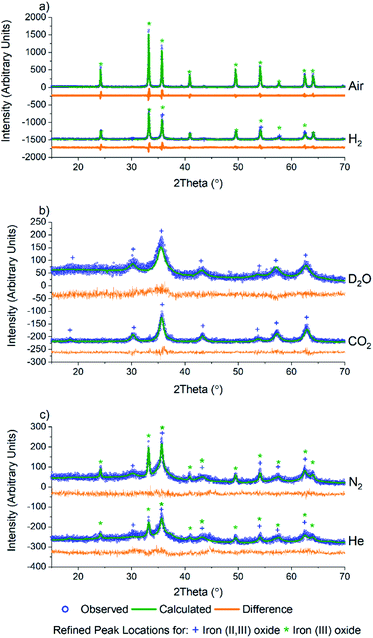
As PCN-250 contains iron-based SBUs, we were interested in probing the presence and phases of the resulting Fe nanoparticles within the samples. Powder X-ray diffraction (PXRD) data were collected using a Bruker D8 diffractometer equipped with Cu Kα radiation. The six samples showed that in addition to altering the porous carbon structure of the material, calcination under different gas environments resulted in the generation of various iron oxide phases and variation in crystallite domain size (Fig. 2). Analysis of the iron oxide domains was performed via Rietveld refinement of the experimental data using known iron oxide structures, and the software package GSAS II.34 The unit cell parameters, the atomic displacement and position parameters of the atoms, and the crystallite size of the iron oxide phases were refined. All samples were initially modeled as a mixed-phase system consisting of both iron(II,III) oxide and iron(III) oxide, with subsequent single-phase fits performed on those data showcasing zero contribution from a second phase. As expected, calcination under air results in the complete formation of the fully oxidized iron(III) oxide, Fe2O3 (Fig. 2a).
Interestingly, Rietveld refinement of the H2 calcined sample (Fig. 2a, bottom) gave an iron(III) oxide phase fraction of 81.5(7)% with a balance of 18.5(14)% being iron(II,III) oxide by mass (Table 1). The sample visibly glowed as it was exposed to air after cooling to room temperature (Video 1†), which suggests that oxide formation does not occur during the calcination process, but only upon exposure to air.
| Atmosphere | BET surface area (m2 g−1) | Pore volume (cm3 g−1) | Iron(II,III) oxide fraction (mass%) | Iron(III) oxide fraction (mass%) | Iron(II,III) oxide size (nm) | Iron(III) oxide size (nm) |
|---|---|---|---|---|---|---|
| Air (X-ray) | 9 | 0.017 | 0 | 100 | N/A | 132.9(19) |
| Air (neutron) | — | — | 0 | 100 | N/A | 99(9) |
| H2 (X-ray) | 98 | 0.112 | 18.5(14) | 81.5(7) | 25(11) | 88.4(20) |
| D2O (X-ray) | 221 | 0.190 | 100 | 0 | 6.2(6) | N/A |
| D2O (neutron) | — | — | 100 | 0 | 19.9(7) | N/A |
| CO2 (X-ray) | 144 | 0.124 | 100 | 0 | 13.5(11) | N/A |
| N2 (X-ray) | 235 | 0.201 | 70.5(20) | 29.5(10) | 5.2(6) | 210(190) |
| N2 (neutron) | — | — | 46.4(14) | 53.6(16) | 15.2(5) | 330(200) |
| He (X-ray) | 265 | 0.200 | 62(4) | 37.7(22) | 19(12) | 70(40) |
Exposure to oxygen atom-containing gases such as D2O and CO2 did not result in iron(III) oxide, but formed the mixed valent iron(II,III) oxide, as confirmed via Rietveld refinement (Fig. 2b). This is likely due to the poorly oxidizing nature of the two molecules, which, while introducing oxygen atoms to the metal clusters of PCN-250, do not have the oxidation potential to produce iron(III) oxide. Initial refinement using standard iron(II,III) oxide resulted in a poor fit, with the intensity ratio of the (113) to (022) peaks (35.8 and 30.3° 2θ) differing significantly from that seen in the bulk material. The fit quality was substantially improved by using a model with cation deficiencies in the structure, with an iron occupancy of 0.982 in the tetrahedral site and 0.974 in the octahedral site.35 The refined iron(II,III) oxide crystallite sizes are less than 20 nm (Table 1), likely due to the conditions invoked through confinement in the MOF-derived graphitic scaffold, and with the milder oxidation preventing the sintering observed with iron(III) oxide.
Meanwhile, after calcination under an inert atmosphere, the resulting material was also observed to oxidize in air at room temperature. Interestingly, while H2 calcined PCN-250 mainly resulted in the formation of iron(III) oxide, the N2 and He calcined samples resulted in a more even mixture of the two iron oxide phases. The N2 calcined sample resulted in 70.5(2)% iron(II,III) oxide and 29.5(10)% iron(III) oxide by mass (Fig. 2c, top), while the He calcined sample resulted in 62(4)% iron(II,III) oxide and 37.7(22)% iron(III) oxide (Fig. 2c, bottom) according to Rietveld refinement of the laboratory PXRD patterns (Table 1).
Rietveld refinement on the PXRD of the six samples also revealed information regarding trends in the crystallite size of the iron oxide phases. In general, the iron(III) oxide phases, when present, appeared to be larger than those of the iron(II,III) oxide. The iron(III) oxide crystallite phases range in size from 70 nm in the He calcined sample to 210 nm in the N2 sample. Both air and N2 calcination resulted in the formation of iron(III) oxide domains greater than 100 nm.
Transmission electron microscopy (TEM) images of both the air calcined (Fig. 3a and S14†) and the N2 calcined (Fig. 3c and S18†) samples both show the presence of bulk iron(III) oxide. Meanwhile, both the He calcined (Fig. S20†) and the H2 calcined (Fig. S15†) samples have poorly discernible features, with no apparent signs of bulk iron oxides, nor nanoparticle oxides. This is suggestive of the highly mixed and intermediate ranged size of the iron oxide nanoparticles, which corresponds with the size values determined by PXRD Rietveld refinement. The iron(III) oxide particles are less than 100 nm (88.4(20) nm and 70(40) nm for H2 and He respectively), and the iron(II,III) oxide particles are greater than 10 nm (25(11) nm and 19(12) nm for H2 and He respectively), corroborating the TEM images.
 | ||
| Fig. 3 High-resolution SEM of (a) air, (b) D2O, and (c) N2 calcined samples. TEM images of (d) air, (e) D2O, and (f) N2 calcined samples. Higher resolution versions of the images are in the ESI.† | ||
Further insight into the bulk carbon structure of the materials was achieved via high magnification images using a high-resolution SEM. The SEM images show the presence of nanoscale features, typically in the form of approximately 20 nm nodules (Fig. 3 and S21–S26†). The nodules are readily apparent alongside the surface wave-like pattern, suggesting that the physical strain introduced during the nodule formation is likely responsible for the bulk wave-like pattern on the surface of the material (Fig. S22†). These nodules are present in all the materials except for the air calcined sample (Fig. 3a and S21†). As the air calcined PCN-250 has limited carbon content, these nodules are likely at least partially due to the residual carbon within the remaining samples. In the air calcined sample, there instead appear to be 20–100 nm holes formed due to the complete pyrolysis of the ligand, which correlates well with the small observed level of mesoporosity in the air calcined sample.
Samples previously calcined under air, D2O, and N2 were studied via neutron diffraction and total scattering at the Nanoscale Ordered Materials Diffractometer (NOMAD)36 beamline of the Spallation Neutron Source (SNS) at Oak Ridge National Laboratory (ORNL) to enable pair distribution function (PDF) analysis. Analysis of the Bragg diffraction peaks in the three samples was performed via the same Rietveld refinement methods described for the laboratory PXRD data (Table 1). Both the air and the D2O calcined samples still only showed the presence of a single iron oxide phase, iron(III) oxide and iron(II,III) oxide, respectively. Similar to the laboratory PXRD data, the D2O data was also best fit to an iron(II,III) oxide structure containing cationic vacancies.35 Both data sets show a similar trend to the lab-scale data, with the iron(III) oxide crystallites being significantly more substantial and the iron(II,III) oxide crystallites tending to be smaller, with some minor variation between the two sets of refinements. Analysis of the Bragg diffraction of both the air and the D2O calcined samples also showed significant magnetic diffraction peaks (Fig. S27–S38†).
The neutron diffraction data of the N2 calcined sample still exhibits a mixture of iron(II,III) oxide and iron(III) oxide. However, the ratio of the two phases differs significantly, with the neutron data refining to 46.4(14)% and 53.6(16)% for iron(II,III) oxide and iron(III) oxide, respectively. Most likely, this is the result of a sampling error, with the sample not being in the same condition for both laboratory PXRD and neutron diffraction analysis. The significant estimated standard deviation in the iron(III) oxide domain size is likely due to the polydisperse distribution of crystallites within the N2 calcined sample, with both bulk and nanoparticle domains observed in the TEM (Fig. S18 and S19†).
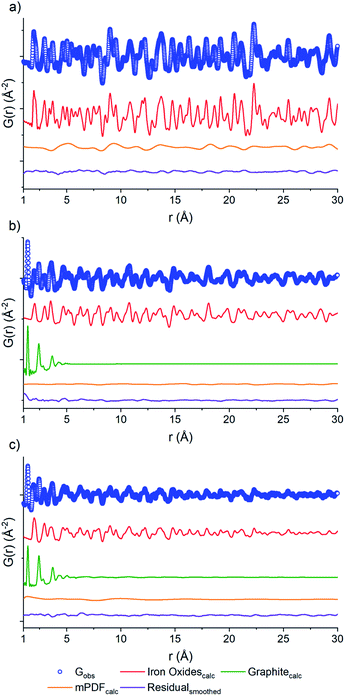
PDF fits of the three samples were performed using PDFgui.37 Each data set (Fig. 4) shows raw data (blue circles), the oxide fit (red line), the graphite fit (green line), the mPDF fit (orange line), with the final difference curve shown below (purple line) the noise present in the data is removed via a 100 point 3rd order polynomial Savitzky–Golay smoothing function performed on the residual curve. All three graphs are shown at different scales for clarity.
The nuclear component of the iron oxide PDF data for the three samples was fit with the unit cell parameters, atomic thermal parameters, the linear atomic correlation factor, and the empirical spherical particle size were refined. The air calcined sample was in reasonable agreement with iron(III) oxide, corroborating Rietveld analysis (Fig. 4). The main component of the difference curve of the air calcined sample appeared to be due to a broadly oscillating curve, which is characteristic of magnetic scattering. To confirm this, we fit the difference PDF using the magnetic pair distribution function (mPDF) method developed by Frandsen and Billinge38,39 in Diffpy-CMI.40 The mPDF was modeled using the known magnetic structure of iron(III) oxide,41 consisting of spins ferromagnetically aligned within the plane, but antiferromagnetically aligned between adjacent planes of the iron sublattice. Both the paramagnetic scale factor and the scale factor for the overall mPDF function were refined. The difference curve after the refinement of both the nuclear and magnetic PDF is minimal (Fig. 4a). This suggests that the residual carbon content of the air calcined sample is low, matching well with the elemental analysis data, with the air calcined sample only containing 0.15% carbon by mass (Table S1†).
The nuclear component of the PDF for the D2O calcined sample (Fig. 4b) was modeled using iron(II,III) oxide and graphite. The residual after fitting the nuclear component is relatively small, but with a periodic oscillation related to the magnetic correlations of iron(II,III) oxide. The inverse spinel structure of iron(II,III) oxide consists of iron(III) in the tetrahedral positions and mixed iron(II) and iron(III) in the octahedral positions. The spins of the tetrahedral sites align antiferromagnetically with the spins of the octahedral sites. The overall imbalance in the spin magnetic moment due to the differences in site numbers and oxidation states account for the ferrimagnetic properties of iron(II,III) oxide.42 The mPDF was again fit against the nuclear difference PDF (Fig. 4b) using a spin configuration determined from the literature.42 As the iron oxide crystallite size is much reduced and the percentage of carbon is vastly increased in the D2O sample compared to the air calcined sample (31.6% versus 0.15%), the overall contribution from magnetic scattering is less apparent.
Meanwhile, the PDF of the N2 calcined sample data (Fig. 4c) was fit to a three-phase mixture of iron(II,III) oxide, iron(III) oxide, and graphite, with the residual consisting of the magnetic scattering from both iron(II,III) oxide as well as iron(III) oxide. The nuclear and the magnetic PDFs were modeled with a mixture of the two iron oxide phases, with the scale factors for the contributing phases refined. The initial analysis does not show any alteration to the two magnetic structures, both the iron(III) oxide and the iron(II,III) oxide spins are the best fit using the antiferromagnetic and ferrimagnetic structures mentioned previously. The current work is not focused on the exact variation between the local magnetic structure and that of the bulk phase materials. Still, this concept will be investigated as part of future work.
The carbon component of the D2O and N2 samples were both fit to graphitic carbon. Previous studies into MOF carbonization have shown that MOF-derived carbons, especially those using aromatic ligand units, tend to have a high degree of graphitization.43 Observation of the PDF of the D2O and N2 samples showed the presence of a large peak at 1.4 Å, which is indicative of the sp2 C–C bond in graphitic carbon,44 further supporting the identification of the carbon phase in these materials as graphitic.
The domain size of the carbon scaffold was modeled in PDFgui using an empirical spherical shape function for the graphite phase.45 Both the D2O and the N2 data only show carbon correlations out to near 5 Å. When refined through the entire range of 1–30 Å, the D2O domain size settles on 5.28 Å while the N2 only refines out to the slightly larger 5.76 Å. However, constraining the domain size and refining the two samples from 5.3 to 15 Å does suggest some minor contribution from the graphite phase in the N2 sample, with the scale factor for graphite being 0.019 as opposed to 0.0023 for the D2O sample. To accurately visualize the longer-range component as well as differences in the degree of order between the two samples, the 1–5 Å and the 5–15 Å fits of both the N2 and the D2O data were graphed together with the N2 data scaled such that the intensity at the 1.4 Å peak matches that of the D2O data (Fig. 5). The image shows the higher relative intensities for the N2 fit at 2.42, 3.7, 4.26, and 5.1 Å, which shows the higher degree of structural order in the N2 sample relative to the D2O sample, which correlates well with the difference in porosity and elemental analysis data. To best illustrate this relationship, we opted to take the difference of the D2O graphitic curve from the scaled N2 graphitic curve (orange line in Fig. 5), which shows some possibility of minor features at distances greater than 5 Å visible as small humps or waves. By comparing the position of these waves to that of the peaks in a calculated bulk graphite PDF, we can observe that the waves of the N2 do correspond in location with the graphite peaks at 7.1, 8.25 and 10.8 Å, suggesting that the N2 data does have a minor amount of larger-scale graphitic components.
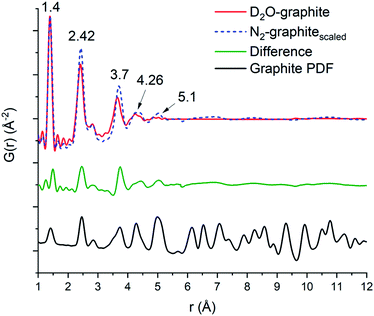 | ||
| Fig. 5 Overlap of the D2O (red line) and N2 (blue dashes) with the N2 scaled so the first peak (1.4 Å) matches that of the D2O, a difference curve (orange) which is taken as the D2O graphitic curve subtracted from the scaled N2 curve is shown below. At the bottom is a calculated PDF for the graphitic carbon phase utilized for the PDF fitting.46 The overall range of the order between the two matches well out to 4.2 Å. The N2 calcined sample has a greater degree of order at the intermediate ranges (2.42 and 3.66 Å) and shows greater order at 5.1 Å, with minor broad features from 6 Å and beyond. | ||
The first three C–C peaks (1.4, 2.42, and 2.84 Å) correspond to standard graphitic carbons.44 The peak at 1.4 Å corresponds to the bond between two sp2 hybridized carbons, the peak at 2.42 Å corresponds to the distances between meta oriented carbon atoms in hexagonal carbon moieties, and the peak at 2.84 Å corresponds to the para–para distance in graphitic carbon.44 In keeping with the general trend of longer-range order observed in the N2 sample, we also observed an increase in relative order in the short-range peaks of the graphitic PDF by observing the alteration in the peak intensity ratio at low r. The D2O calcined sample has an intensity ratio of 2.05 for the 1.4 to 2.42 Å peaks, while the N2 calcined sample has an intensity ratio of 1.57. This suggests that there is a higher degree of simple C–C sp2 hybridized bonds in the D2O calcined structure compared to complete C6 units. This can be visualized by observing the difference in the scaled N2 compared to the D2O at 2.42 Å (Fig. 5), as there is a noticeable peak there, which corresponds to the higher relative number of units in the N2 sample. This result corresponds well with the porosity and surface area of the D2O calcined sample, which is noticeably lower than that of the N2 calcined sample despite having a more substantial carbon content. The increased carbon content is likely due to the amorphous collapse of the carbon domains, which has limited the ability of the material to maintain a porous structure.
Meanwhile, the N2 calcined sample has a higher degree of complete C6 units relative to its carbon content, explaining its higher porosity and surface area. The structural collapse induced by D2O exposure is likely due to the competition between the D2O and the MOF ligand, ABTC, to bind to the iron centers in PCN-250. This competitive delegation could potentially cause an initial loss of order within the D2O structure ahead of carbonization. Results from bulk testing under water vapor conditions have shown that a complete loss of crystallinity does occur before thermal decomposition, which does suggest that small scale nanoscale amorphization could be potentially occurring during standard calcination experiments (Fig. S4†). This partial collapse could also be partially insulating for the interior of the material upon calcination, as the D2O has not only the highest carbon content (31.61% by weight) but also the highest hydrogen content at 1.91% by weight, which is significantly higher than the next highest sample, the N2 calcined sample at 1.47%. This is likely due to incomplete carbonization of the interior structure during calcination, aided by the insulating nature of the pre-amorphized ligand under D2O conditions.
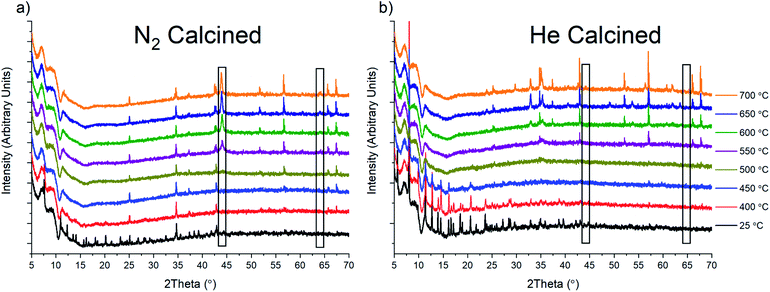
To probe the oxide species that form under inert gas flow, we conducted in situ variable temperature PXRD analysis under He and N2 flow (Fig. 6). Unfortunately, due to safety concerns and instrument limitations, we were unable to conduct the same calcination in the presence of H2. Upon heating to around 450 °C, there is a complete loss of crystallinity in the sample as it appears to lose the last remnants of MOF structural stability. After this loss of stability, the only peaks that are present are due to the alumina sample holder utilized for these experiments. However, in the N2 calcined sample, at 550 °C, a new phase, Fe(0), starts to grow in (marked with a black rectangle in Fig. 6a). This Fe(0) phase grows in intensity as the temperature is ramped to 700 °C. We were also able to observe the Fe(0) phase when the sample was held at 500 °C for 2 h, which is similar to the 4 h calcination condition used for the bulk sample prep (Fig. S43†). For comparison, holding the sample at 500 °C under He for 4 h produced no noticeable growth of Fe(0). However, the eventual increase was observed once the sample reached 700 °C after having been previously held at 500 °C for 4 h and 600 °C for 2 h (Fig. S44†). As a control, we also performed the same variable temperature program under UHP Ar gas. The results show similar behavior to the He calcination, with a small growth of Fe(0), although the intensity of the phase peaks is generally quite low under Ar as well (Figure S45†). Based on these results, we hypothesized that the formation of Fe(0) was due to the presence of N2 and that the formation of Fe(0) under He and Ar could be the result of N2 impurities, with the UHP cylinder utilized having 5 ppm N2. However, the UHP Ar utilized did not list any N2 content, although it cannot be discounted at present. Interestingly, performing the same 200 °C to 700 °C in situ experiments using the isolated Fe3μ3O cluster under both N2 and He did not result in the formation of any crystalline species (Fig. S46†).
To determine if Fe(0) was indeed being formed during tube furnace calcination, an air-free sample collection environment was built (Fig. S47†). Using the cell, the sample could be isolated under N2 during and after calcination and then brought into an Ar filled glove-box. Using an air-free PXRD cell (Fig. S48†), we were able to analyze the sample, showing the presence of Fe(0) (Fig. S49†). The procedure also allowed us to calcine PCN-250 under H2 and isolate the result, which showed the presence of Fe(0) (Fig. S50†). Rietveld refinement of these samples suggests a domain size of 13.9 nm for the N2 sample and a size of 30 nm for the H2 calcined sample.
Additionally, N2 adsorption analysis of the two samples suggests that the post calcination oxidation appears to increase the BET surface area and pore volume, as both air-free samples have lower surface areas and pore volumes compared to their air-exposed counterparts. The N2 calcined sample exhibits a BET surface area of 220 m2 g−1 and a pore volume of 0.188 cm3 g−1 (versus 235 m2 g−1 and 0.201 cm3 g−1 for the air-exposed sample), and the H2 calcined sample exhibits a BET surface area of 84 m2 g−1 and a pore volume of 0.084 cm3 g−1 (versus 98 m2 g−1 and 0.112 cm3 g−1 for the air-exposed sample). Also, the isotherms of the two samples are broadly similar in features to their oxidized counterparts, with some variation in the H2 sample due to a more considerable hysteresis, suggesting a difference in the mesopore shape (Fig. S51†).
Conclusions
The work herein showcases the unique behavior of the iron-based MOF, PCN-250, during calcination under different gas flow environments. While our initial hypothesis proposed that the calcination conditions could change the porosity of the sample, we were surprised by the formation of different phases of iron during the calcination process. These results show that the nanoconfined state of the iron sites within the MOF allows for an unprecedented level of oxidation control, with the atmospheric conditions above the sample being entirely responsible for the formation of the resulting iron oxide phase. The local structure of several of the materials was probed via neutron scattering PDF experiments, which allowed for partial investigation of the magnetic structure of the carbon scaffolded iron oxide materials, which showed that while the size range of the carbon ordering is similar between different samples, the relative ratio of ordering at the molecular level changes significantly with the gas environment. A post-calcination oxidation event was observed for N2, H2, and He calcined samples, which resulted in the formation of mixed oxide phases within the samples. These materials were probed via in situ PXRD and air-free calcination methods, which showed that these post-calcination oxidations are at least partially due to the formation of zero-valent iron under calcination conditions. Future work will focus on elucidating the mechanism of zero-valent iron formation, as well as the effect of the local environment and nanoconfinement of the metal centers on the reduction event. The ability to control the bulk and local structure of metal oxide-containing porous carbons are of great use for potential catalytic applications, with future work focusing on the development of heterogeneous catalysts through the controlled calcination of MOFs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the U.S. Department of Energy (DOE) Office of Science Graduate Student Research (SCGSR) program and the Center for Gas Separations Relevant to Clean Energy Technologies, an Energy Frontier Research Center funded by the DOE Office of Science (Basic Energy Sciences) under Contract Number DE-SC0001015. The SCGSR program is administered by the Oak Ridge Institute for Science and Education (ORISE) for the DOE under contract number DE-SC0014664. M. R. R. acknowledges the DOE Office of Science (Basic Energy Sciences) for additional research funding and the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility operated under Contract No. DE-AC02-05CH11231 for access to supercomputing resources. H.-C. Z. acknowledges the Robert A. Welch Foundation for a Welch Endowed Chair (A-0030). The research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. The authors also acknowledge the Texas A&M Microscopy and Imaging Center and Materials Characterization Facility.References
- B. Chen, Q. Ma, C. Tan, T.-T. Lim, L. Huang and H. Zhang, Carbon-Based Sorbents with Three-Dimensional Architectures for Water Remediation, Small, 2015, 11(27), 3319–3336 CrossRef CAS PubMed.
- S. Sircar, T. C. Golden and M. B. Rao, Activated carbon for gas separation and storage, Carbon, 1996, 34(1), 1–12 CrossRef CAS.
- F. Rodríguez-reinoso, The role of carbon materials in heterogeneous catalysis, Carbon, 1998, 36(3), 159–175 CrossRef.
- M. A. Yahya, Z. Al-Qodah and C. W. Z. Ngah, Agricultural bio-waste materials as potential sustainable precursors used for activated carbon production: a review, Renewable Sustainable Energy Rev., 2015, 46, 218–235 CrossRef CAS.
- N. Hernandez, J. Iniesta, V. M. Leguey, R. Armstrong, S. H. Taylor, E. Madrid, Y. Rong, R. Castaing, R. Malpass-Evans, M. Carta, N. B. McKeown and F. Marken, Carbonization of polymers of intrinsic microporosity to microporous heterocarbon: capacitive pH measurements, Appl. Mater. Today, 2017, 9, 136–144 CrossRef.
- H. Teng, Y.-J. Chang and C.-T. Hsieh, Performance of electric double-layer capacitors using carbons prepared from phenol–formaldehyde resins by KOH etching, Carbon, 2001, 39(13), 1981–1987 CrossRef CAS.
- W. Zhong, H. Liu, C. Bai, S. Liao and Y. Li, Base-Free Oxidation of Alcohols to Esters at Room Temperature and Atmospheric Conditions using Nanoscale Co-Based Catalysts, ACS Catal., 2015, 5(3), 1850–1856 CrossRef CAS.
- V. P. Santos, T. A. Wezendonk, J. J. D. Jaén, A. I. Dugulan, M. A. Nasalevich, H.-U. Islam, A. Chojecki, S. Sartipi, X. Sun, A. A. Hakeem, A. C. J. Koeken, M. Ruitenbeek, T. Davidian, G. R. Meima, G. Sankar, F. Kapteijn, M. Makkee and J. Gascon, Metal organic framework-mediated synthesis of highly active and stable Fischer-Tropsch catalysts, Nat. Commun., 2015, 6, 6451 CrossRef CAS PubMed.
- W. Chaikittisilp, N. L. Torad, C. Li, M. Imura, N. Suzuki, S. Ishihara, K. Ariga and Y. Yamauchi, Synthesis of Nanoporous Carbon–Cobalt-Oxide Hybrid Electrocatalysts by Thermal Conversion of Metal–Organic Frameworks, Chem.–Eur. J., 2014, 20(15), 4217–4221 CrossRef CAS PubMed.
- P. Veerakumar, V. Veeramani, S.-M. Chen, R. Madhu and S.-B. Liu, Palladium Nanoparticle Incorporated Porous Activated Carbon: Electrochemical Detection of Toxic Metal Ions, ACS Appl. Mater. Interfaces, 2016, 8(2), 1319–1326 CrossRef CAS PubMed.
- E. Pérez-Mayoral, I. Matos, M. Bernardo and M. I. Fonseca, New and Advanced Porous Carbon Materials in Fine Chemical Synthesis. Emerging Precursors of Porous Carbons, Catalysts, 2019, 9(2), 133 CrossRef.
- H.-C. Zhou, J. R. Long and O. M. Yaghi, Introduction to Metal–Organic Frameworks, Chem. Rev., 2012, 112(2), 673–674 CrossRef CAS PubMed.
- M. R. Ryder and J. C. Tan, Nanoporous metal organic framework materials for smart applications, Mater. Sci. Technol., 2014, 30(13), 1598–1612 CrossRef CAS.
- H. Li, K. Wang, Y. Sun, C. T. Lollar, J. Li and H.-C. Zhou, Recent advances in gas storage and separation using metal–organic frameworks, Mater. Today, 2018, 21(2), 108–121 CrossRef CAS.
- J. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. T. Nguyen and J. T. Hupp, Metal–organic framework materials as catalysts, Chem. Soc. Rev., 2009, 38(5), 1450–1459 RSC.
- K. Shen, X. Chen, J. Chen and Y. Li, Development of MOF-Derived Carbon-Based Nanomaterials for Efficient Catalysis, ACS Catal., 2016, 6(9), 5887–5903 CrossRef CAS.
- N. L. Torad, M. Hu, S. Ishihara, H. Sukegawa, A. A. Belik, M. Imura, K. Ariga, Y. Sakka and Y. Yamauchi, Direct Synthesis of MOF-Derived Nanoporous Carbon with Magnetic Co Nanoparticles toward Efficient Water Treatment, Small, 2014, 10(10), 2096–2107 CrossRef CAS PubMed.
- A. Banerjee, R. Gokhale, S. Bhatnagar, J. Jog, M. Bhardwaj, B. Lefez, B. Hannoyer and S. Ogale, MOF derived porous carbon–Fe3O4 nanocomposite as a high performance, recyclable environmental superadsorbent, J. Mater. Chem., 2012, 22(37), 19694–19699 RSC.
- J. Long, K. Shen, L. Chen and Y. Li, Multimetal-MOF-derived transition metal alloy NPs embedded in an N-doped carbon matrix: highly active catalysts for hydrogenation reactions, J. Mater. Chem. A, 2016, 4(26), 10254–10262 RSC.
- P. Khare, N. Talreja, D. Deva, A. Sharma and N. Verma, Carbon nanofibers containing metal-doped porous carbon beads for environmental remediation applications, Chem. Eng. J., 2013, 229, 72–81 CrossRef CAS.
- S. Chinthakindi, A. Purohit, V. Singh, V. Tak, D. R. Goud, D. K. Dubey and D. Pardasani, Iron oxide functionalized graphene nano-composite for dispersive solid phase extraction of chemical warfare agents from aqueous samples, J. Chromatogr. A, 2015, 1394, 9–17 CrossRef CAS PubMed.
- S. Bhattacharyya, B. Konkena, K. Jayaramulu, W. Schuhmann and T. K. Maji, Synthesis of nano-porous carbon and nitrogen doped carbon dots from an anionic MOF: a trace cobalt metal residue in carbon dots promotes electrocatalytic ORR activity, J. Mater. Chem. A, 2017, 5(26), 13573–13580 RSC.
- L. Oar-Arteta, T. Wezendonk, X. Sun, F. Kapteijn and J. Gascon, Metal organic frameworks as precursors for the manufacture of advanced catalytic materials, Mater. Chem. Front., 2017, 1(9), 1709–1745 RSC.
- J. Alcañiz-Monge, D. Lozano-Castelló, D. Cazorla-Amorós and A. Linares-Solano, Fundamentals of methane adsorption in microporous carbons, Microporous Mesoporous Mater., 2009, 124(1), 110–116 CrossRef.
- K. Konstas, T. Osl, Y. Yang, M. Batten, N. Burke, A. J. Hill and M. R. Hill, Methane storage in metal organic frameworks, J. Mater. Chem., 2012, 22(33), 16698–16708 RSC.
- H. S. Kim, M. S. Kang and W. C. Yoo, Highly Enhanced Gas Sorption Capacities of N-Doped Porous Carbon Spheres by Hot NH3 and CO2 Treatments, J. Phys. Chem. C, 2015, 119(51), 28512–28522 CrossRef CAS.
- S. Bhattacharyya, C. Das and T. K. Maji, MOF derived carbon based nanocomposite materials as efficient electrocatalysts for oxygen reduction and oxygen and hydrogen evolution reactions, RSC Adv., 2018, 8(47), 26728–26754 RSC.
- D. Feng, K. Wang, Z. Wei, Y.-P. Chen, C. M. Simon, R. K. Arvapally, R. L. Martin, M. Bosch, T.-F. Liu, S. Fordham, D. Yuan, M. A. Omary, M. Haranczyk, B. Smit and H.-C. Zhou, Kinetically tuned dimensional augmentation as a versatile synthetic route towards robust metal–organic frameworks, Nat. Commun., 2014, 5, 5723 CrossRef CAS PubMed.
- A. Dhakshinamoorthy, M. Alvaro, H. Chevreau, P. Horcajada, T. Devic, C. Serre and H. Garcia, Iron(iii) metal–organic frameworks as solid Lewis acids for the isomerization of α-pinene oxide, Catal. Sci. Technol., 2012, 2(2), 324–330 RSC.
- J.-J. Tang and B. Liu, Reactivity of the Fe2O3(0001) Surface for Methane Oxidation: A GGA + U Study, J. Phys. Chem. C, 2016, 120(12), 6642–6650 CrossRef CAS.
- M. Munoz, Z. M. de Pedro, J. A. Casas and J. J. Rodriguez, Preparation of magnetite-based catalysts and their application in heterogeneous Fenton oxidation – a review, Appl. Catal., B, 2015, 176–177, 249–265 CrossRef CAS.
- Y. Fang, S. Banerjee, E. A. Joseph, G. S. Day, M. Bosch, J. Li, Q. Wang, H. Drake, O. K. Ozdemir, J. M. Ornstein, Y. Wang, T.-B. Lu and H.-C. Zhou, Incorporating Heavy Alkanes in Metal–Organic Frameworks for Optimizing Adsorbed Natural Gas Capacity, Chem.–Eur. J., 2018, 24(64), 16977–16982 CrossRef CAS PubMed.
- D. Barton, M. Hodgett, P. Skirving, M. Whelton, K. Winter and C. Vardy, The thermal decomposition of azobenzene, Can. J. Chem., 1983, 61(8), 1712–1718 CrossRef CAS.
- B. H. Toby and R. B. Von Dreele, GSAS-II: the genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46(2), 544–549 CrossRef CAS.
- H. Okudera, Single crystal X-ray studies of cation-deficient magnetite, Z. Kristallogr. - Cryst. Mater., 1997, 212, 458 CAS.
- J. Neuefeind, M. Feygenson, J. Carruth, R. Hoffmann and K. K. Chipley, The Nanoscale Ordered MAterials Diffractometer NOMAD at the Spallation Neutron Source SNS, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 287, 68–75 CrossRef CAS.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals, J. Phys.: Condens. Matter, 2007, 19(33), 335219 CrossRef CAS PubMed.
- B. A. Frandsen, X. Yang and S. J. L. Billinge, Magnetic pair distribution function analysis of local magnetic correlations, Acta Crystallogr., Sect. A: Found. Adv., 2014, 70(1), 3–11 CrossRef CAS PubMed.
- B. A. Frandsen and S. J. L. Billinge, Magnetic structure determination from the magnetic pair distribution function (mPDF): ground state of MnO, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71(3), 325–334 CrossRef CAS PubMed.
- P. Juhas, C. L. Farrow, X. Yang, K. R. Knox and S. J. L. Billinge, Complex modeling: a strategy and software program for combining multiple information sources to solve ill posed structure and nanostructure inverse problems, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71(6), 562–568 CrossRef PubMed.
- A. H. Hill, F. Jiao, P. G. Bruce, A. Harrison, W. Kockelmann and C. Ritter, Neutron Diffraction Study of Mesoporous and Bulk Hematite, α-Fe2O3, Chem. Mater., 2008, 20(15), 4891–4899 CrossRef CAS.
- S. K. Banerjee and B. M. Moskowitz, Ferrimagnetic Properties of Magnetite, in Magnetite Biomineralization and Magnetoreception in Organisms: A New Biomagnetism, ed. J. L. Kirschvink, D. S. Jones and B. J. MacFadden, Springer US, Boston, MA, 1985, pp. 17–41 Search PubMed.
- L. Yang, G. Xu, J. Ban, L. Zhang, G. Xu, Y. Lv and D. Jia, Metal-organic framework-derived metal-free highly graphitized nitrogen-doped porous carbon with a hierarchical porous structure as an efficient and stable electrocatalyst for oxygen reduction reaction, J. Colloid Interface Sci., 2019, 535, 415–424 CrossRef CAS PubMed.
- V. Petkov, Y. Ren, S. Kabekkodu and D. Murphy, Atomic pair distribution functions analysis of disordered low-Z materials, Phys. Chem. Chem. Phys., 2013, 15(22), 8544–8554 RSC.
- K. Kodama, S. Iikubo, T. Taguchi and S.-i. Shamoto, Finite size effects of nanoparticles on the atomic pair distribution functions, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62(6), 444–453 CrossRef PubMed.
- P. Trucano and R. Chen, Structure of graphite by neutron diffraction, Nature, 1975, 258(5531), 136–137 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Materials and methods, experimental details, elemental analysis data, thermogravimetric analysis of PCN-250, pore size distributions for MOF-derived carbons, SEM and TEM images of MOF-derived carbons, Rietveld refinement of neutron diffraction data, N2 adsorption and PXRD data for air-free calcined MOFs. See DOI: 10.1039/c9na00720b |
| This journal is © The Royal Society of Chemistry 2020 |