Open Access Article
Open Access ArticleTemperature mediated ‘photonic hook’ nanoparticle manipulator with pulsed illumination†
Marat
Spector‡
 a,
Angeleene S.
Ang‡
a,
Angeleene S.
Ang‡
 a,
Oleg V.
Minin
bc,
Igor V.
Minin
a,
Oleg V.
Minin
bc,
Igor V.
Minin
 bc and
Alina
Karabchevsky
bc and
Alina
Karabchevsky
 *a
*a
aSchool of Electrical and Computer Engineering, Ben-Gurion University of the Negev, Beer-Sheva 8410501, Israel. E-mail: alinak@bgu.ac.il; maratspector@gmail.com
bNational Research Tomsk State University, Tomsk, 634050, Russia
cTomsk Polytechnic University, Tomsk, 634050, Russia
First published on 27th April 2020
Abstract
Optical forces applied on an object or cell in a non-destructive manner have revolutionised scientific instruments. Optical tweezers and atomic traps are just two representative examples. Curved forces such as photonic hooks are of particular interest for non-destructive manipulation; however, they are extremely weak in low-contrast media. Here, for the first time, we report the amplification of optical forces generated by a photonic hook via pulsed illumination mediated by temperature effects. We show that the optical force generated by the photonic hook subjected to illumination by an incident Gaussian pulse is significantly larger than the optical force generated by the photonic hook subjected to a continuous wave. We notice that under the applied photonic hook generated by a Gaussian beam, a spherical gold nanoparticle experiences a variation in its lattice temperature of ΔTl ∼ 2–4 K, leading to high index resolution. We envision that heat-associated effects can be further mitigated to achieve temperature assisted photonic hook manipulation of nanoparticles in a controllable manner by taking into account the thermo-optical properties of metals. Our findings are particularly important for tracing objects in low-contrast environments, such as optomechanically controlled drug delivery with nanoparticles in intercellular and intracellular media or cellular differentiation, to list a few examples.
1 Introduction
Shortly after the laser was invented, Ashkin proposed and demonstrated1 that the incident laser beam can be implemented to trap and manipulate dielectric particles. Moreover, while the traditional microscope-based trap has found applications in a wide variety of disciplines, such as biophysical research,2 this free-space optical approach is diffraction limited. Thus, achieving manipulation on the nanoscale requires auxiliary structures that generate tightly confined electric fields. Field localization has been successfully demonstrated in plasmonics research.3–7 An alternative route to sub-diffraction trapping and manipulation8–13 has been explored using high-intensity narrow light beams generated by dielectric structures, referred to as photonic nanojets.14Photonic nanojets (PNJs) are usually generated using spherical structures subjected to illumination by a plane continuous wave (CW). When a PNJ is applied to a metallic nanoparticle, the optical forces acting on the nanoparticle result from momentum exchange.12 In addition, PNJs can also be generated using other symmetric structures.15 By breaking this symmetry, the generated structured light beams become curved. This effect is known as a photonic hook (PH)15,16 and has unique properties. Specifically, a PH experiences both lateral size and a radius of curvature as a fraction of the incident wavelength.17 PH configurations have been optimized,18 investigated for optomechanically moving nanoparticles around obstacles,16 and experimentally demonstrated.19 Previously, we explored PH-based optical manipulation under CW illumination and concluded that the generated force has a small magnitude for realistic applications.16,20 In the context of optical manipulation, CW field-based illumination causes heating of the system, which can be potentially destructive if a very large input amplitude is required.
One way to mitigate the destructive effect of CW illumination21 is by utilizing a pulsed input field.22 This largely overlooked method of increasing optical force performance has been studied numerically23 and demonstrated experimentally for femtosecond input sources for trapping latex nanoparticles.24 Pulsed illumination has also been studied for structure-based optical manipulation.25 Some applications that have been explored include the use of a pulsed laser to overcome the adhesive interaction of a particle stuck on a surface26 and as a high-speed microfluidic switch.27
Absolute trapping forces depend on the details of the beam structure and the type of illuminated wave: CW or pulsed. Here we study the photonic hook effect generated by a Gaussian pulse and its influence on the temporal dynamics of electronic and lattice temperature. Fig. 1 illustrates the studied system in which a pulsed beam, linearly polarized along the y-axis, illuminates a dielectric cuboid with broken symmetry (called a cuboid below for simplicity) with an index of n = 1.4 embedded in air. This refractive index corresponds to that of fused silica, chosen to create the optimal conditions – i.e., there needs to be a sufficient refractive index contrast between the cuboid material and the surrounding medium – for creating the photonic hook.15
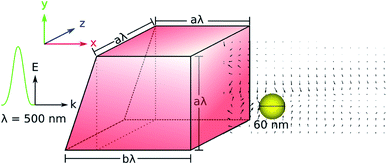 | ||
| Fig. 1 The dielectric cuboid, with refractive index n = 1.4, is embedded in air and irradiated by a pulsed Gaussian input field. The a/b ratio used for the cuboid is 3/4, as in ref. 16. The incident field wavelength is λ = 500 nm. | ||
The photonic hook is generated at the output of the cuboid and is applied on a metallic probe. We utilize a gold nanoparticle (GNP) as a probe due to its biocompatibility for in vivo micro-manipulation.28 In addition, GNPs can be modified to carry cargo. To study the influence of applied pulsed illumination, we calculate the complex polarizability, α, of GNP under illumination by a Gaussian pulse as a function of temperature and search for the wavelength at which the optical force is maximal. According to ref. 29, the optical force is directly related to the imaginary part of GNP’s polarizability, α, which is shown in Fig. 2. We noticed that the imaginary part of α reaches its maximum at λ = 500 nm. This signifies the largest possible force that can be obtained with the studied particle.
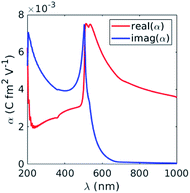 | ||
| Fig. 2 Real and imaginary parts of the polarizability, α (eqn (5)), of GNP subjected to a CW electric field as a function of the incident wavelength. | ||
Since the polarizability, α, is directly linked to the particle’s scattering cross-section, σsca, by measuring the latter at different time intervals, σsca can be related to the particle displacement. In the case of temporal dynamics, the polarizability becomes time-dependent with α = α(t), and the relation to σsca(t) is
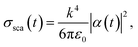 | (1) |
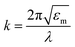 is the wavevector, εm is the dielectric function of the surrounding medium, and ε0 and λ are the dielectric constant and the wavelength in free space, respectively. Thus, assuming that the initial position of the GNP is known, one can measure the scattering cross-section at different time intervals and relate it to GNP displacement. This technique can be implemented in future experiments for thermo-optomechanical manipulation and tracking metallic nanoparticles.
is the wavevector, εm is the dielectric function of the surrounding medium, and ε0 and λ are the dielectric constant and the wavelength in free space, respectively. Thus, assuming that the initial position of the GNP is known, one can measure the scattering cross-section at different time intervals and relate it to GNP displacement. This technique can be implemented in future experiments for thermo-optomechanical manipulation and tracking metallic nanoparticles.
2 Results and discussion
The optical force acting on an arbitrary object is obtained by integrating the Maxwell stress tensor over a closed surface over the object.30 However, this method is computationally ineffective due to the cumbersome modelling of the object at all points where the force is obtained. To simplify the calculations, we assume that the radius of GNP, R, is much smaller than the incident wavelength, λ, i.e. R ≪ λ, so that the particle can be approximated as an electric dipole. In this case, the force becomes| F = (p·∇)E + ṗ × B, | (2) |
Taking the time average of eqn (2), we obtain
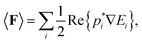 | (3) |
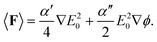 | (4) |
The polarizability of GNP reads as α = α′ + iα′′, and ϕ reads as the phase. The first term of eqn (4) is known as the gradient force, Fgrad, responsible for trapping (or repelling) the probe particle at locations where the field intensity gradient is high. The second term is the scattering force, Fsca, which moves in parallel to the k-vector, and is responsible for unrestricted particle motion.
Eqn (4) shows that the scattering force is directly proportional to the imaginary part of the polarizability, α′′. Assuming that the probe particle is spherical, the polarizability in the Rayleigh approximation can be written as the Clausius–Mossotti relation9,31
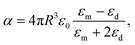 | (5) |
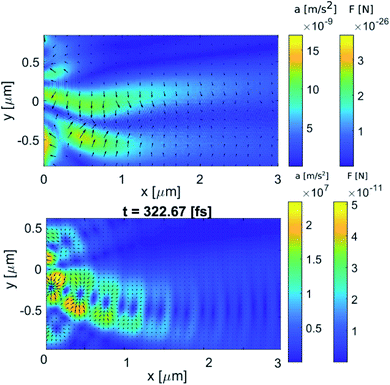 | ||
| Fig. 3 Calculated acceleration, a, of GNP according to eqn (6a), and forces acting on a spherical GNP with a radius of 30 nm due to (top) CW illumination and (bottom) pulsed illumination (shown here at t = 322 fs) with a wavelength of 500 nm. The optical force dynamics are shown in ESI Video 2.† The arrows indicate the direction of the optical force. | ||
Fig. 3 shows that, contrary to CW illumination, the structure of the optical forces for pulsed radiation in the region of the photonic hook resembles a typical picture of standing waves—the presence of a chain of anti-nodes and nodes,33 located along a curved line. Specifically, the acceleration and the force for CW illumination are 15 orders of magnitude less as than for pulsed illumination. Physically, this is related to significantly larger absorbed power density by GNP, pabs,34 for the case of pulsed illumination; see eqn (8) below.
Given the acceleration in Fig. 3, we can use simple kinematics to estimate the distance traveled by the GNP during a single cycle of the electric field,
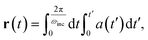 | (6a) |
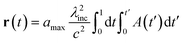 | (6b) |
The pulsed beam used in this work is defined by the pulsed input pre-defined in the finite difference time domain (FDTD) algorithm of Lumerical (see Methods). To better illustrate the pulse as it propagates through time and space, we set the pulse duration to 100 fs, and the time delay is arbitrarily set to 300 fs. Using the pulsed beam, we tune the incident field amplitude from 1 V m−1 to 15 MV m−1. In this case, inevitable heat effects related to the non-elastic electron–electron e–e and electron–phonon e–ph scattering must be taken into account.
To account for the interaction of the incident laser light with the metallic NP, we employ the extended Two Temperature Model (eTTM) (eqn (7)–(10)). This model describes the spatio-temporal dynamics of the non-thermal electron energy UNT, as well as of the electron and phonon (lattice) temperatures, Te and Tl, respectively. It is customary to describe the energy density evolution of NT electrons as
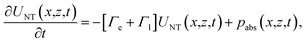 | (7) |
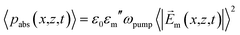 | (8) |
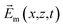 is the electric field absorbed by the GNP.
is the electric field absorbed by the GNP.
For the Gaussian temporal profile of the incoming pulse, the solution of eqn (7) is
| UNT(x,z,t) = uabs(x,z,t)Z[ΓNT,τp,t], | (9a) |
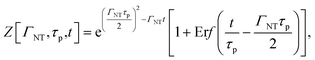 | (9b) |
| ΓNT ≡ Γe + Γl, | (9c) |
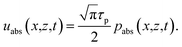 | (9d) |
The equations for the electron (Te) and lattice (Tl) temperatures are given as
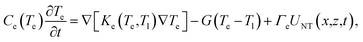 | (10a) |
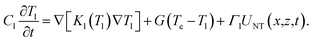 | (10b) |
We now solve eqn (7)–(10) numerically with the parameters suitable for Au specified in Table 1.
Assuming that the variation of the electron (Te) and the lattice (Tl) temperatures is small with respect to their initial value (Te = Tl = Tin = 300 K), we compare the numerical solution of eqn (7)–(10) to the analytical one given by
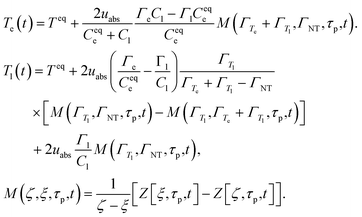 | (11) |
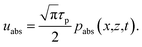 | (12) |
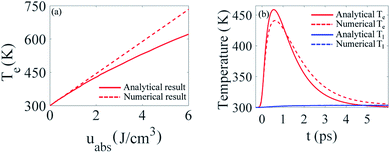
The calculated electronic (Te) and lattice (Tl) temperature dynamics are shown in Fig. 4. We note that Fig. 4 shows the calculated results for Te and Tl when the GNP is subject to uniform Gaussian pulse excitation. The duration of the pulse is τp = 0.1 ps, the wavelength of excitation is λ = 500 nm, and the absorbed electric field is Em = 15 MV m−1.
We see that both the analytical and the numerical results for the maximum values of Te show a linear dependence on uabs for low energy densities. In this case, the deviation between the analytical and the numerical result is less than 5%. However, further increasing uabs leads to higher values of Te, which in turn limits the validity of our assumption, namely, that the variation of the electron temperature, Te, is small with respect to its initial value (Te = Tin = 300 K). This in turn leads to a deviation of 25% between the analytical and the numerical results.
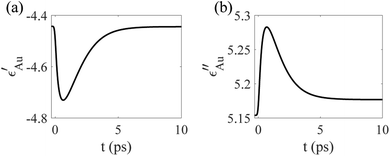
To account for the temporal dynamics of the dielectric function of GNP, εm(Te,Tl), we use the temperature-dependent permittivity model described in detail in ref. 38. Specifically, the GNP is excited at λ = 500 nm, which is in the vicinity of the interband transition of Au.39 Thus, we take into account the interband (εinter(Te,Tl)) and intraband (εintra(Te,Tl)) contributions to the dielectric function of Au as a function of time, which is represented in Fig. 5.
Furthermore, by taking into account the temporal dynamics of the interband and intraband dielectric functions, the temporal dependence of the particle polarizability, α, is easily obtained from eqn (5), and is shown in Fig. 6. According to eqn (4), the optical force depends on the polarizability of the GNP, which becomes diminishingly small after 10 ps. Thus, in the temporal range of interest, the thermal dissipation effect of the metallic particle need not be considered, since the relaxation of the lattice temperature occurs on a much slower time scale.
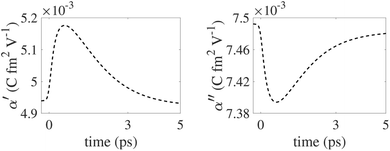 | ||
| Fig. 6 Dynamics of α′ (left) and α′′ (right) as a result of uniform excitation at λ = 500 nm (eqn (5)). The duration of the pump pulse is τp = 0.1 ps and the absorbed electric field is Em = 15 MV m−1. | ||
As it interacts with the dielectric cuboid, the pulsed field generating the photonic hook is shown in ESI Video 1.† From the electric and magnetic fields generated by the simulation, we then use eqn (2) to calculate the force, along with the time-dependent polarizability shown in Fig. 6. The optical force acting on the probe GNP is shown in ESI Video 2.† Integrating the acceleration with respect to time, the velocity of the GNP after the pulsed field excitation dissipates at t ≈ 500 fs is shown in Fig. 7.
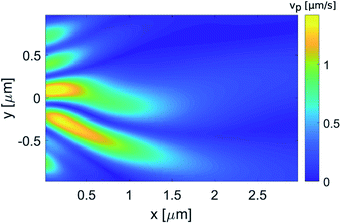 | ||
| Fig. 7 Calculated velocity, vpar, of GNP subject to the pulsed illumination. The incident wavelength is λ = 500 nm and the radius of the GNP is R = 30 nm. | ||
3 Purcell factor calculation
The ability to track particles in inter- and intracellular media is of the highest importance for revealing molecular transport, studying fundamental biological mechanisms and drug delivery, to list a few examples. However, the main limitation of cellular medium is its optical low contrast. To track the GNP studied here in low-contrast medium, we propose first encapsulating it with a photoluminescent emitter.40,41 Once encapsulated with an emitter, a possible implementation can be accomplished by measuring the dynamically varying Purcell factor. The Purcell factor, Fp,42 can be defined as the ratio between the density of surface plasmon modes, ρSP, and the density of modes in free space, ρfree,43 namely,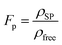 | (13) |
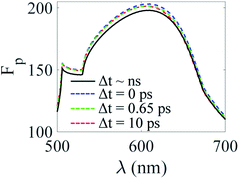
The Purcell factor depends on the dielectric function of the GNP, εm (which in our case is time-dependent), and of the surrounding media, εd. By taking into account the temporal dynamics of the dielectric function of Au and utilizing the approach of Sun et al.,43 we calculate the wavelength dependence of the Purcell factor, Fp, at different time periods Δt after excitation by a pulsed laser beam (Fig. 8). We found that the spectral location of the maximum value of the Purcell factor is shifted by 6 nm due to the heating effect of the ‘hot’ GNP as compared to the ‘cold’ one. This important observation can be utilized for tracking the GNP when it is in intercellular medium (n = 1.33) and when it passes the cellular phospholipid membrane (n = 1.34).
4 Methods
The electric and magnetic fields generated by the plane wave incident on the cuboid are simulated using Lumerical FDTD. We used the scattered field formalism with the source offset by an arbitrarily selected amount (300 fs) in order to input the full Gaussian signal into the system. The simulation is bounded by perfectly matched layers on all sides. We used a mesh size of 5 nm along both x and y in the shadow region (the mesh along z was left as default) and a monitor with a time sampling rate of 5728.89 THz (corresponding to a minimum sampling rate per cycle of 10), in order to obtain a reasonably-sized dataset of electric and magnetic field data. The resulting dataset was then input in Matlab, where the field derivatives were obtained using the central difference method.5 Conclusion
To conclude, we reported on an amplification of optical forces generated by a photonic hook applied on a spherical nanoparticle via pulsed illumination mediated by temperature effects. We analyzed the influence of a Gaussian pulse applied on a spherical GNP. Importantly, the magnitude of the optical force acting on the gold nanoparticle and the velocity achieved by the GNP subject to the pulsed illumination are greater than the force and velocity of the same GNP under CW illumination. We proposed a novel tracking concept for particle movement in low-contrast media. We noticed that the effective scattering cross-section of the heated particle depends on the intensity of the input laser beam; therefore the scattering cross-section of the particle can be tuned for its tracking. In addition, as a possible implementation of tracking a nanoparticle in low index contrast medium, we analyzed the wavelength dependence of the Purcell factor, Fp, at different time intervals after excitation by a Gaussian pulse. We found that by illuminating the GNP with a Gaussian pulse at 500 nm and increasing the refractive index of the GNP surrounding media by 0.75%, the Purcell factor (Fp) peak experiences a spectral shift of 6 nm. An experimental analogue of the Purcell factor, Fp, is the measurement of the recombination rate enhancement, which is defined as the ratio between the total recombination rate of the photoluminescent emitter encapsulated GNP and the total recombination rate of the bare photoluminescent emitter.44 The reported photonic hook can easily be extended to other types of localized structure beams.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was partially funded by the Israel Innovation Authority KAMIN program grant number 69073. The work was partially carried out within the framework of the Tomsk Polytechnic University Competitiveness Enhancement Program, Russia, and was partially supported by the RFBR Grant No. 20-57-S52001.Notes and references
- A. Ashkin, Phys. Rev. Lett., 1970, 24, 156–159 CrossRef CAS.
- J. E. Baker, R. P. Badman and M. D. Wang, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2018, 10, e1477 Search PubMed.
- T. Shoji and Y. Tsuboi, J. Phys. Chem. Lett., 2014, 5, 2957–2967 CrossRef CAS PubMed.
- W. Zhang, L. Huang, C. Santschi and O. J. F. Martin, Nano Lett., 2010, 10, 1006–1011 CrossRef CAS PubMed.
- V. Pacheco-Peña, I. V. Minin, O. V. Minin and M. Beruete, Ann. Phys., 2016, 528, 684–692 CrossRef.
- A. Ivinskaya, M. I. Petrov, A. A. Bogdanov, I. Shishkin, P. Ginzburg and A. S. Shalin, Light: Sci. Appl., 2017, 6, e16258 CrossRef CAS PubMed.
- I. V. Minin, O. V. Minin, D. S. Ponomarev and I. A. Glinskiy, Ann. Phys., 2018, 530, 1800359 CrossRef.
- A. Kovrov, A. Novitsky, A. Karabchevsky and A. S. Shalin, Ann. Phys., 2018, 530, 1800129 CrossRef.
- I. V. Minin, O. V. Minin, Y. Cao, Z. Liu, Y. E. Geints and A. Karabchevsky, Sci. Rep., 2019, 9, 12748 CrossRef PubMed.
- Y.-C. Li, H.-B. Xin, H.-X. Lei, L.-L. Liu, Y.-Z. Li, Y. Zhang and B.-J. Li, Light: Sci. Appl., 2016, 5, e16176 CrossRef CAS PubMed.
- H. Wang, X. Wu and D. Shen, Opt. Lett., 2016, 41, 1652–1655 CrossRef PubMed.
- X. Cui, D. Erni and C. Hafner, Opt. Express, 2008, 16, 13560–13568 CrossRef CAS PubMed.
- M. Dienerowitz, M. Mazilu and K. Dholakia, J. Nanophotonics, 2008, 2, 021875 CrossRef.
- B. S. Luk’yanchuk, R. Paniagua-Domínguez, I. V. Minin, O. V. Minin and Z. Wang, Opt. Mater. Express, 2017, 7, 1820 CrossRef.
- I. V. Minin and O. V. Minin, Diffractive Optics and Nanophotonics, Springer International Publishing, Cham, 2016 Search PubMed.
- A. S. Ang, A. Karabchevsky, I. V. Minin, O. V. Minin, S. V. Sukhov and A. S. Shalin, Sci. Rep., 2018, 8, 2029 CrossRef PubMed.
- K. Dhloakia and G. D. Bruce, Nat. Photonics, 2019, 13, 229–230 CrossRef.
- L. Yue, O. V. Minin, Z. Wang, J. N. Monks, A. S. Shalin and I. V. Minin, Opt. Lett., 2018, 43, 771–774 CrossRef PubMed.
- I. V. Minin, O. V. Minin, G. M. Katyba, N. V. Chernomyrdin, V. N. Kurlov, K. I. Zaytsev, L. Yue, Z. Wang and D. N. Christodoulides, Appl. Phys. Lett., 2019, 114, 031105 CrossRef.
- A. S. Ang, I. V. Minin, O. V. Minin, S. V. Sukhov, A. S. Shalin and A. Karabchevsky, Proc. of the 9th Int. conf. on Metamaterials, Photonic crystals and Plasmonics, 2018 Search PubMed.
- K. Setoura, Y. Okada and S. S. Hashimoto, Phys. Chem. Chem. Phys., 2014, 16, 26938–26945 RSC.
- C. Schaffer, A. Brodeur and E. Mazur, Meas. Sci. Technol., 2001, 12, 1784–1794 CrossRef CAS.
- N. du Preez-Wilkinson, A. B. Stilgoe, T. Alzaidi, H. Rubinsztein-Dunlop and T. A. Nieminen, Opt. Express, 2015, 23, 7190–7208 CrossRef CAS PubMed.
- A. K. De, D. Roy, A. Dutta and D. Goswami, Appl. Opt., 2009, 48, G33–G37 CrossRef PubMed.
- B. J. Roxworthy and K. C. J. Toussaint, Sci. Rep., 2012, 2, 660 CrossRef PubMed.
- J.-l. Deng, Q. Wei, Y.-z. Wang and Y.-q. Li, Opt. Express, 2005, 13, 3673–3680 CrossRef PubMed.
- T.-H. Wu, L. Gao, Y. Chen, K. Wei and P.-Y. Chiou, Appl. Phys. Lett., 2008, 93, 144102 CrossRef.
- F. Hajizadeh and S. Reihani, Opt. Express, 2010, 18, 551–559 CrossRef CAS PubMed.
- K. Svoboda and S. M. Block, Annu. Rev. Biophys. Biomol. Struct., 1994, 23, 247–285 CrossRef CAS PubMed.
- L. Novotny and B. Hecht, Principles Of Nano Optics, 2006 Search PubMed.
- K. Svoboda and S. M. Block, Opt. Lett., 1994, 19, 930–934 CrossRef CAS PubMed.
- J. Steehler, J. Chem. Educ., 1997, 74, 378 CrossRef.
- I. Minin, O. Minin, V. Pacheco-Peña and M. Beruete, Quantum Electron., 2016, 46, 555–557 CrossRef CAS.
- J. D. Jackson, Classical electrodynamics, Wiley & Sons, 3rd edn, 1998 Search PubMed.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Saunders College, Philadelphia, 1976 Search PubMed.
- P. Allen, Phys. Rev. Lett., 1987, 59, 1460–1463 CrossRef CAS PubMed.
- C. Sun, F. Vallee, L. Acioli, E. Ippen and J. G. Fujimoto, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 12365–12368 CrossRef CAS PubMed.
- T. Stoll, P. Maioli, A. Crutt, G. Wurtz and A. Zayatz, Nano Lett., 2012, 12, 1561–1565 CrossRef PubMed.
- M. Guerrisi, R. Rosei and P. Winsemius, Phys. Rev. B: Solid State, 1975, 12, 557–563 CrossRef CAS.
- A. Karabchevsky, S. Karabchevsky and I. Abdulhalim II, J. Nanophotonics, 2011, 5, 051813 CrossRef.
- I. Abdulhalim, A. Karabchevsky, C. Patzig, B. Rauschenbach, B. Fuhrmann, E. E. Eltzov, R. Marks, J. J. Xu, F. Zhang and A. Lakhtakia, Appl. Phys. Lett., 2009, 94, 063106 CrossRef.
- E. M. Purcell, in Spontaneous Emission Probabilities at Radio Frequencies, Springer US, Boston, MA, 1995, pp. 839–839 Search PubMed.
- G. Sun, J. B. Khurgin and R. A. Soref, J. Opt. Soc. Am. B, 2008, 25, 1748–1755 CrossRef CAS.
- I. Gontijo, M. Boroditsky, E. Yablonovitch, S. Keller, U. K. Mishra and S. P. DenBaars, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11564 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: (1) acceleration.avi and (2) force.avi. See DOI: 10.1039/c9na00759h |
| ‡ These authors contributed equally to the work. |
| This journal is © The Royal Society of Chemistry 2020 |