Open Access Article
Open Access ArticleStructural rigidity accelerates quantum decoherence and extends carrier lifetime in porphyrin nanoballs: a time domain atomistic simulation†
Ritabrata
Sarkar
 a,
Md
Habib
a,
Md
Habib
 a,
Moumita
Kar
b,
Anup
Pramanik
a,
Moumita
Kar
b,
Anup
Pramanik
 b,
Sougata
Pal
*a and
Pranab
Sarkar
b,
Sougata
Pal
*a and
Pranab
Sarkar
 *b
*b
aDepartment of Chemistry, University of Gour Banga, Malda – 732103, India. E-mail: sougatapal_1979@yahoo.co.in
bDepartment of Chemistry, Visva-Bharati University, Santiniketan – 731235, India. E-mail: pranab.sarkar@visva-bharati.ac.in
First published on 18th February 2020
Abstract
Nonradiative electron–hole (e–h) recombination is the primary source of energy loss in photovoltaic cells and inevitably, it competes with the charge transfer process, leading to poor device performance. Therefore, much attention has to be paid for delaying such processes; increasing the excitonic lifetime may be a solution for this. Using the real-time, density functional tight-binding theory (DFTB) combined with nonadiabatic molecular dynamics (NAMD) simulations, we demonstrate the exciton relaxation phenomena of different metal-centered porphyrin nanoballs, which are supposed to be very important for the light-harvesting process. It has been revealed that the carrier recombination rate gradually decreases with the increase in the molecular stiffness by introducing metal-coordinating templating agents into the nanoball. Our simulation demonstrates that the lower atomic fluctuations lead to poorer electron–phonon nonadiabatic coupling in association with weak phonon modes and these as a whole are responsible for shorter quantum coherence and hence delayed recombination events. Our analysis is in good agreement with the recent experimental observation. By replacing the Zn metal center with a heavier Cd atom, a similar trend is observed; however, the rate slows down abruptly. The present simulation study provides the fundamental mechanism in detail behind the undesired energy loss during exciton recombination and suggests a rational design of impressive nanosystems for future device fabrication.
1. Introduction
The recombination of charge carriers is one of the major obstacles for achieving high photon-to-electrical energy conversion efficiency.1–4 It always occurs as a backward competing process along with charge separation and transfer.5 The charge carriers, as an outcome of excitonic dissociation, may eventually relax to the corresponding ground states by following primary paths.6–8 These mainly include two processes: (a) the nonradiative process converts excess energy of the carriers into heat via multiphonon emission, and (b) the radiative process converts the excess energy by photon emission. If, however, a suitable scavenger or surface defect state is available to trap the electron or hole, recombination can be prevented and the subsequent transfer of charge or redox reactions may occur.9 In the absence of such scavengers, the stored energy is dissipated in an ultrafast time scale, which severely affects the efficiency of the solar cell device.10–12 Therefore, a deep-level physical understanding of the resulting relaxation dynamics of the photocarrier is crucial for the application of these materials in light-harvesting devices.13–18 Carrier lifetime is the key factor here, which is defined as the average time spent by a carrier as a free entity between the processes of its generation and capture.Researchers have been actively engaged in increasing the charge carrier lifetime to delay the recombination processes. For example, the carrier lifetime is shown to be very sensitive to the size and shape of nanocrystals.19 Additionally, the presence of impurities and vacancies is a determining factor of the charge recombination dynamics. Defects are very common in the condensed matter systems and also have immense effects on the dynamics of carrier relaxation.20 Not only a rigorous change in the system but also the surroundings like pressure,21 temperature,22,23 electric field,24 photon recycling,25 pH,26 and the presence of oxygen27 can affect the charge carrier recombination dynamics. Recently, Prezhdo's group has shown that the lattice stiffness and/or contraction can suppress the rate of nonradiative charge carrier recombination.28
Conjugated arrays of porphyrin, where porphyrin rings are either directly fused or bridged by planar aromatic subsystems, have been demonstrated as promising materials in the nano world owing to their exceptionally large delocalization of π-electrons. These are found to show long-range charge transport and promisingly high electrical conductivity.29–33 Such systems are also attractive candidates in the area of materials science: logic gates,31 switches,34 very robust molecular memories,35 and light-emitting diodes.36 The arrays of porphyrins have often been utilized in artificial photosynthesis to imitate the natural photosynthesis.37 In a recent experiment, Cremers et al.38 have demonstrated that rapid (less than 5 ps) migration of charge takes place in porphyrin nanoballs, making the material a suitable candidate for solar radiation harvest. Although various opto-electronic properties of such materials have been studied, in-depth investigation studies of photocarrier relaxation dynamics are still scarce. It is, therefore, essential to understand the recombination mechanism by assessing the dynamical behavior of carriers based on nonradiative processes to give a positive feedback to the fabrication of photonic devices.
An ab initio time-domain study of nonradiative electron–hole (e–h) recombination in metal-centered (Zn/Cd) porphyrin nanoballs is presented herein. Our simulation shows that nanoballs become stiffer when bound to templates, which subsequently suppress the recombination rate. The structural rigidity reduces the fluctuation that weakens the nonadiabatic (NA) coupling between the HOMO and LUMO states. In addition, fewer optical phonon modes with lower frequency are shown to participate in the systems bound to the template. Slower atomic motion is responsible for shortening the lifetime of the quantum coherence in the templated system. As a result, we infer that nonadiabatic e–h recombination would be suppressed, and consequently, the lifetime of the excited state would be prolonged. Furthermore, replacement of Zn with Cd results in a more rigid system, which further delays the relaxation dynamics by several orders of magnitude.
2. Methods of computation
The photoinduced charge recombination dynamics of porphyrin nanoballs has been studied using the recently developed methodology,39 combining NA molecular dynamics (MD) with the self-consistent-charge density functional tight-binding (SCC-DFTB) theory. The electronic degrees of freedom are treated quantum mechanically, whereas the nuclear degrees of freedom are treated semi-classically. The nonadiabatic e–h recombination is modeled using decoherence-induced surface hopping (DISH),40 which includes quantum coherence correction into the quantum-classical approximation, developing on the idea that decoherence provides the physical mechanism for surface hops. Decoherence time is computed as pure dephasing time from optical response theory.41 DISH has been used effectively for studying the charge recombination phenomena in various systems.42–44 A detailed theoretical approach can be found elsewhere.42,45–49 All quantum-mechanical calculations including geometry optimization and electronic structure are carried out by the SCC-DFTB method as implemented in the DFTB+ code.50,51 The SCC-DFTB parameter set (Slater–Koster files) used in the present calculations has been tested widely for a broad range of systems as reported earlier.52–54 After optimizations, the systems have been heated to 300 K using velocity rescaling. Then, 5 ps microcanonical trajectories have been generated using the Verlet algorithm with the 1 fs time step. At each time step, the energy of the Kohn–Sham molecular orbitals and the NA coupling matrix elements have been calculated, and as-obtained time-dependent information has been used to carry out the NAMD simulation using the DISH methods, as implemented within the Python eXtension for the Ab Initio Dynamics (PYXAID) program.45,46 Note that the present theoretical methodologies have been successfully used for studying the quantum coherence phenomena in 2D CdSe nanostructures,49 multi-particle auger recombination in CNT,48 hole trapping dynamics in core–shell CdSe/CdS systems47 as well as charge transfer and recombination dynamics at different nano interfaces.42,43 Moreover, note that the current simulation uses the conventional classical path approximation (CPA), which greatly reduces the computational cost but describes the dynamics efficiently. We have tested the applicability of CPA for the present systems of interest; a more detail would be discussed later.3. Results and discussion
3.1 Structural rigidity and nonadiabatic electron–phonon coupling
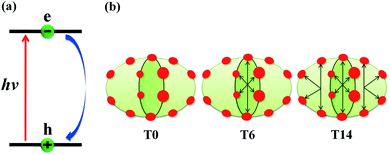
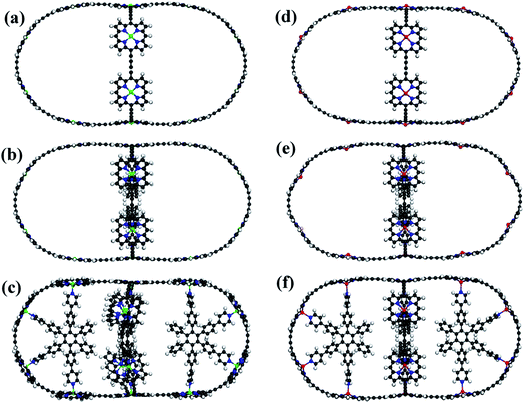
The schematics of energy levels involved in the photoinduced e–h recombination dynamics in the porphyrin nanoball is displayed in Fig. 1 (left most panel). After photoinduced generation of excitons (bound e–h pair), they relax to the ground states. Now, looking back to the geometry, the porphyrin nanoball has a prolate-ellipsoidal structure with 14 porphyrin units shared by two perpendicular rings, typically represented in Fig. 1 (marked as T0, having no template). The large ring along the major axis contains 10 units of porphyrin, while 6 units of porphyrin form the small ring along the minor axis. Individual porphyrin units are linked by acetylenic linkages, so that the π-electron can delocalize over the entire nanosystem. Two types of templates were considered in the current study to coordinate the metal centers of the porphyrins. Six porphyrin units of the nanoball's small ring are coordinated by one hexadentate template (T6) as denoted by both headed arrow. Additionally, two tetradentate templates are used to bind the remaining porphyrin units along the main axis in order to fully template (T14) the ball. Herein, we seek to focus on the excited state decay dynamics of total six nanosystems containing Zn and Cd as metal centers. Ground-state optimized geometries of all the nanoballs are represented in Fig. 2. The calculated dimensions of the Zn-T0 nanoball are 53.55 (major axis), 27.41, and 24.51 Å (two minor axes, respectively), which corroborate the earlier finding.38 Upon inclusion of templates, the shortening of length along both major and minor axes is noticed, implying that the system becomes more compact. To gain a deeper insight regarding the structural rigidity of the porphyrin nanoball, the fluctuation of the distance along the major and minor axes of the ellipsoidal ball over 5 ps MD trajectory was accounted. Fluctuations of distances were computed from the standard deviation,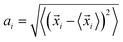 , where
, where ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i is the exact distance of the two points along the axis at a particular time and 〈
i is the exact distance of the two points along the axis at a particular time and 〈![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i〉 is the time average distance between those two points in the MD trajectory. Calculations were performed at 300 K and we summarized the results in Table 1. Note that fluctuations are the determining factors of NA coupling because electron–phonon coupling depends on the nuclear velocity. Typically, a lower value of ai reflects smaller fluctuation or slower dynamics and, therefore, weaker NA electron–phonon coupling.28 However, a large fluctuation or fast nuclear motion gives rise to a dynamic disorder, which modulates the electronic states. By implementing templates to the nanoball, fluctuation gradually decreases along both the major and minor axes. For example, Zn-T6 nanoballs experience smaller fluctuations along both the axes and they are reduced significantly for the Zn-T14 system (please see Table 1). That the inclusion of templates makes the system more rigid is in good agreement with the experimental observation.38 We further extend our investigation by replacing Zn with Cd as the metal center of porphyrin. It has been revealed that the effects of both metal substitution and template addition increase the rigidity of the nanoball as manifested from the fluctuation data (Table 1). Besides, we inspected the atomic fluctuations of Zn and Cd metal centers, which also decrease in the following sequence T0 > T6 > T14, for both the systems (see Table S1 in ESI†). As already stated, the rigid conformation enforced by the template weakens the NA electron–phonon coupling, the consequences of which would be discussed later.
i〉 is the time average distance between those two points in the MD trajectory. Calculations were performed at 300 K and we summarized the results in Table 1. Note that fluctuations are the determining factors of NA coupling because electron–phonon coupling depends on the nuclear velocity. Typically, a lower value of ai reflects smaller fluctuation or slower dynamics and, therefore, weaker NA electron–phonon coupling.28 However, a large fluctuation or fast nuclear motion gives rise to a dynamic disorder, which modulates the electronic states. By implementing templates to the nanoball, fluctuation gradually decreases along both the major and minor axes. For example, Zn-T6 nanoballs experience smaller fluctuations along both the axes and they are reduced significantly for the Zn-T14 system (please see Table 1). That the inclusion of templates makes the system more rigid is in good agreement with the experimental observation.38 We further extend our investigation by replacing Zn with Cd as the metal center of porphyrin. It has been revealed that the effects of both metal substitution and template addition increase the rigidity of the nanoball as manifested from the fluctuation data (Table 1). Besides, we inspected the atomic fluctuations of Zn and Cd metal centers, which also decrease in the following sequence T0 > T6 > T14, for both the systems (see Table S1 in ESI†). As already stated, the rigid conformation enforced by the template weakens the NA electron–phonon coupling, the consequences of which would be discussed later.
| Systems | Fluctuation of distance (in Å) along axes | ||
|---|---|---|---|
| Major axis | Minor axis | ||
| Zn | T0 | 0.924 | 0.939 |
| T6 | 0.386 | 0.229 | |
| T14 | 0.182 | 0.142 | |
| Cd | T0 | 0.428 | 0.419 |
| T6 | 0.326 | 0.236 | |
| T14 | 0.152 | 0.137 | |
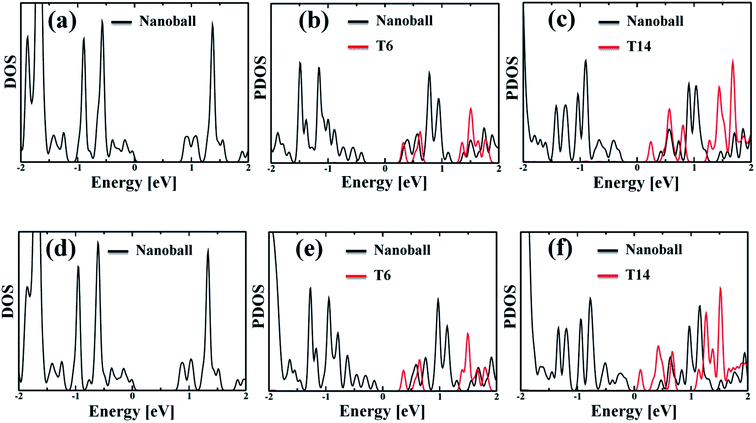
The partial density of state (PDOS) values of the systems projected over the nanoballs and the templates are shown in Fig. 3. The calculated band gaps of the systems are given in Table 2, which demonstrates that all the nanoballs are of low band gap systems and the band gap gradually decreases with the increase in the degree of templation. Noteworthy, the group of Anderson has recently studied the nanoballs experimentally.38 The authors have also performed some theoretical calculations. The reported band gap of the Zn-T0 system is 1.43 eV, based on the DFT computation with moderate basis sets. Our simulated band gap of Zn-T0 (0.87 eV), within SCC-DFTB computation, is quite comparable with the reported value. Moreover, the decreasing trend of band gap is found with the increase in molecular weight of the system. This finding is in line with the observed red shifting of the absorption spectra. Hence, our methodology is quite reliable and efficient enough to deal with such large systems.
| Systems | Band gap (eV) | Reorganization energy (eV) | NA coupling (meV) | Dephasing time (fs) | Recombination time (ps) | |
|---|---|---|---|---|---|---|
| Zn | T0 | 0.87 | 0.020 | 7.11 | 53 | 13 |
| T6 | 0.65 | 0.026 | 3.04 | 25 | 57 | |
| T14 | 0.54 | 0.028 | 1.99 | 13 | 154 | |
| Cd | T0 | 0.79 | 0.022 | 6.83 | 58 | 17 |
| T6 | 0.53 | 0.032 | 2.19 | 16 | 100 | |
| T14 | 0.29 | 0.063 | 1.09 | 11 | 326 | |
Although the band gap of a system is one of the guiding factors that can alter the NA coupling, other important factors such as nature of wave function and nuclear velocity of the atoms of a particular system also have large effects on the NA coupling. In fact, there are many instances where it is not the band gap, rather the nature of wave function and nuclear velocity are the main guiding factors for NA coupling.44 Noteworthy, the nonradiative e–h relaxation process is fundamentally governed by the interaction between the electron (LUMO) and hole (HOMO) wave function, as they constitute the initial and final states, respectively. It can be observed from Fig. 3 and 4 (charge density distribution plots) that the HOMOs are mainly distributed over the nanoball, comprising the porphyrin units, while the templates contribute to the LUMOs. The situation is more prominent for the T14 templated nanoballs for both Zn and Cd as metal centers. Since there is a significant contribution of the templating agent at the band edge state, one can assume that it can directly influence the NA electron–phonon coupling and hence the charge recombination process. In fact, the NA coupling depends on the extent of spatial overlap between the initial and final states of a system for e–h recombination; the poorer overlap between the states involved generates weaker NA coupling. Likewise, when this overlap is considerably reduced by spatially separating photogenerated e–h pair, a significantly large recombination time is achieved as could be found in Table 2. Our calculations show that the NA coupling of Zn-T0 (7.11 meV) is two orders of magnitude larger than Zn-T6 and 3.5 times larger than Zn-T14. This can be rationalized by the larger fluctuations along the axes (Table 1) as well as the considerable wave function overlap of Zn-T0 (Fig. 4(a)). Similar is the situation for Cd–porphyrin systems. Here, it should be pointed out that the present systems do not undergo so much structural distortion upon photoexcitation. To demonstrate the fact, we have presented the ground and excited state geometries (Fig. S1†) as well as some structural parameters (Table S2†) for the Zn-T0 system as a prototypical example. Furthermore, we have also calculated the reorganization energy of each system, following the standard protocol55–58 and the values are given in Table 2. Noteworthy, the reorganization energies of the systems are fairly low and are well matched with the porphyrin systems reported earlier.59,60 Such low reorganization energy values of the systems further support the validity of using CPA for simulating the carrier transfer dynamics of those systems.
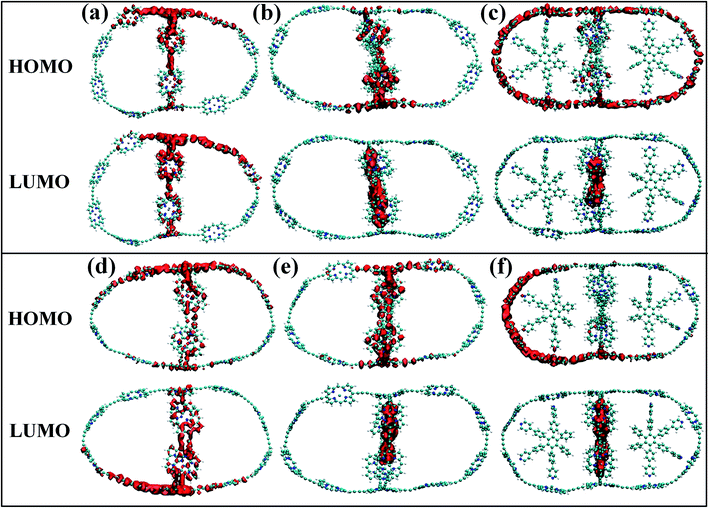 | ||
| Fig. 4 (a–c) The isosurface plots for Zn systems having templates T0, T6 and T14, respectively, at 300 K. (d–f) The same plots for Cd systems. For without template (T0) nanoballs, both HOMO and LUMO densities are delocalized uniformly over the porphyrin unit of the nanoball. The LUMO density appeared at the template T6 for Cd. On the contrary, such states are delocalized in between the porphyrin unit and T6 in the minor ring of Zn, clearly observable in Fig. 3b and e. However, in case of T14 templated nanoballs, charge densities of HOMO arise from the whole nanoring and LUMO densities are localized on the T14 moieties of the nanoballs. | ||
3.2 Participation of phonon modes in carrier recombination
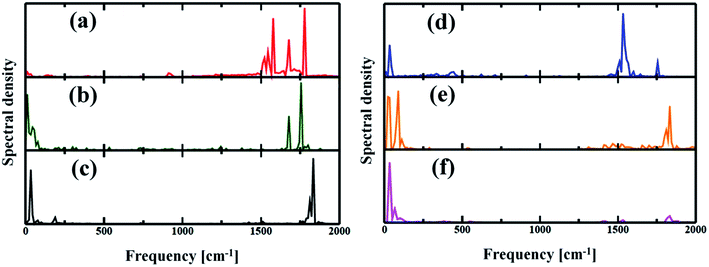
The electron–phonon interaction is supposed to be the most efficient pathways for nonradiative e–h relaxation in the nanostructures. The dynamics of nonradiative e–h recombination is governed by both elastic and inelastic scattering. The latter one, especially, contributes to the NA electron–phonon coupling by accommodating the loss of electronic energy during the population transition from LUMO to HOMO. Elastic scattering, however, typically destroys the coherence formed between the states during the carrier recombination process. Fig. 5 presents the Fourier transformations (FTs) of the phonon-induced fluctuations of the energy gaps during exciton relaxation, commonly known as influence spectrum, the frequency and amplitude of which characterize the phonon modes involved in the nonradiative e–h recombination.61 Note that the phonon modes in the region 1500–1800 cm−1 are due to the in-plane skeletal modes, while the modes in lower frequency region (within 250 cm−1) can be assigned to be out-of-plane skeletal modes of porphyrin in the nanoball.62 It can be observed from Fig. 5(a) that a wide range of phonon modes (1500–1800 cm−1) couple with the electronic degrees of freedom for Zn-T0. The participation of a wide range of phonon modes into nonradiative relaxations provides additional channels for NA coupling that would accelerate the carrier recombination. The contribution of multiple higher frequency phonon modes and faster atomic motion can rationalize the largest value of NA coupling possessed for Zn-T0. As a result, it is expected that Zn-T0 nanoballs would dissipate energy more quickly through vibrational modes. In contrast, for the Zn-T6 system, a new mode appears in the low-frequency region and, at the same time, a few high-frequency phonon modes disappear (Fig. 5(b)). The intensity of the low-frequency component becomes more prominent and a single phonon mode at 1800 cm−1 is observed for the fully templated system (Zn-T14). Therefore, going from T0 to T14, a gradual lowering of NA electron–phonon coupling is observed as can also be found in Table 2. For the Cd–porphyrin nanoball, the spectra again display both low- and high-frequency phonon modes (Fig. 5(d)); however, the number of high-frequency phonon modes is quite less than that of the analogous Zn–porphyrin nanoball. Upon further templation with T6 and T14, the intensity of the high-frequency modes decreases and becomes almost insignificant for the fully templated system (Cd-T14). As could be found from Fig. 5(f), for the Cd-T14 system, the carrier recombination can be described by a solitary phonon mode at ∼100 cm−1. The creation of rigid nanoballs pushes the vibrational modes towards a lower frequency, reasoned as a decrease in atomic motion. Only low-frequency vibrations are available for energy dissipation in case of fully templated nanoballs, which results in the least NA coupling between the final and initial states. Hence, on the basis of phonon mode analysis, we can speculate that the energy dissipation and hence the rate of carrier relaxation would be much slower for the Cd-T14 system.3.3 Decoherence-induced carrier relaxation
In quantum dynamics, the role of coherence has been paid considerable attention in recent times.63–65 Herein, we show the effect of quantum coherence on the charge carrier relaxation dynamics within the studied systems. As already stated, pure dephasing characterizes the elastic electron–phonon scattering. During the carrier recombination, strong coherence between the initial and final states results in quick loss of the exciton formed. The decoherence time or pure dephasing time is computed based on the optical response theory with second-order cumulant approximation.41 The pure dephasing time (τ) is obtained by the Gaussian fitting, y = −0.5(t/τ)2 of pure dephasing function. Fig. 6 illustrates decoherence between the HOMO–LUMO states for the nanoball. The decoherence curve actually bears information about how long the two states are in the same phase. The computed quantum coherence loss for an electronic transition from the LUMO to HOMO is considerably shorter than the e–h recombination. Consequently, decoherence correction is applied in our computation to describe the elastic e–h scattering.66–68 In case of Zn-T0, the system sustains over a longer time of 53 fs in the phase but when it is ligated with T6 template, the pure dephasing time is reduced to half. Interestingly, the pure dephasing time decreases abruptly for the Zn-T14 system. Therefore, it can be argued that atomic mobility decreases on going from T0 to T14, which shortens the time of quantum coherence. In other words, a more rigid system randomizes between the concerned phases very quickly. The insets of Fig. 6(a) and (b) show the auto-correlation functions (ACFs) for the transition between the LUMO and HOMO states of the nanoballs. The ACF decays more rapidly for the template-free (T0) nanoball than that for the template nanoballs, T6 or T14. Specifically, for Zn-T0, the ACF decays rapidly to zero at a time less than 10 fs (red line, inset of Fig. 6(a)). Such rapid decay is a consequence of coupling of the electronic subsystem with multiple phonon vibrations (Fig. 5(a)). Cd-T0 exhibits a pure dephasing time of 58 fs (Fig. 6(b)). Partially templating the ball with T6 accelerates the quantum decoherence and results in 4-fold shortening of the dephasing time. Most notably, the dephasing time for Cd-T14 is suppressed almost by 6 times compared with that of Cd-T0. Such a low value of dephasing time (10 fs), for Cd-T14, may be ascribed as the complete localization of the HOMO and LUMO states at two different moieties of Cd-T14, as shown in Fig. 4(c). Templations in the nanoball enhance the structural rigidity, which inhibits atomic dynamics, resulting in smaller quantum coherence. A decrease in the dephasing time is verified using the simulated fluctuations, as shown in Tables 1 and 2. We, therefore, speculate that template-bound nanoballs would show slower carrier recombination.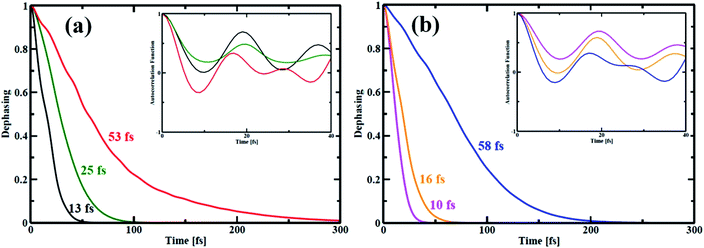 | ||
| Fig. 6 Pure-dephasing functions for the HOMO–LUMO transition of all the porphyrin nanoball structures. The decay curves represent the elastic electron–phonon scattering time. The time scales obtained by Gaussian fits are summarized in Table 2. (a) shows dephasing curves of Zn-nanoball; red, green, black with T0, T6 and T14 templates respectively. (b) shows the same as above for Cd-nanoball. Here blue, orange and magenta lines represents dephasing curves for T0, T6 and T14 templates accordingly. | ||
3.4 Electron–hole recombination
Now, e–h recombination is one of the primary events where the first excitation is diminished in between the optical-gap. The nonradiative decay of the lowest excited state leads to the recovery of the ground-state population with the compensation of energy loss. Fig. 7 presents the time-evolution of the excited-state populations, and the corresponding data are reported in Table 2. The stimulated e–h recombination time scales are obtained by exponential fitting, y = exp(−t/τ) ≈ 1 − t/τ of the decay curves, considering 5 ps MD trajectory. The computed time scales for e–h recombination of the studied systems are in picosecond (ps) regime that agrees well with the experiment.69,70 The Zn-T0 system shows faster charge carrier relaxation with a time scale of 13 ps (see Fig. 7(a) and Table 2). Of note, the charge carrier relaxation can be shown to slow down by a factor of 5 when locking the nanoball with T6. At fully locked state in T14, the exciton recombines in 154 ps, i.e., it becomes 12 times longer lived than T0. The introduction of the templating agent into the nanoball dramatically reduces the recombination rate, resulting in a longer period of free carrier lifetime. According to the Fermi golden rule, the rate of population transfer depends on the square of the NA coupling.68 In addition, a quantum transition is fast if the quantum coherence is longer lived. Alternatively, one can state that shorter coherence slows down the recombination dynamics. Likewise, the dynamics of charge recombination virtually stops when the coherence is infinitely small, known as the quantum Zeno effect.71,72 Lastly, the rate of e–h recombination is also governed by the extent of phonon mode participation. Zn-T0 shows the largest value of NA coupling (Table 2), and higher phonon modes are involved for releasing the excited energy (Fig. 5(a)). Moreover, it sustains over a longer period in phases (Fig. 6(a), Table 2) and thus, the e–h recombination rate is the highest in comparison to its analogous systems, T6 and T14. It is therefore argued that structural rigidity assists to weaken the NA electron–phonon coupling, shorten the quantum coherence and, thus, suppress the dynamics of e–h recombination. The present results nicely obey the kinetics of the Fermi golden rule. Nanoball, when fully template, remarkably slows down the e–h recombination and thereby extends the excited-state lifetime. Now, by replacing Zn with Cd, the atomic motions become more restricted, NA coupling becomes weaker and a dominant slow vibrational mode is involved in the energy transfer process, as already stated. Consequently, the coherence time involving the carrier states decreases and thus, the recombination times of the corresponding nanoballs gradually increase, as shown in Table 2. The higher excitonic lifetime for Cd-nanoballs may further be rationalized in terms of their higher molecular weights as compared to that of Zn-nanoballs, and this is in accordance with the previous findings.73,74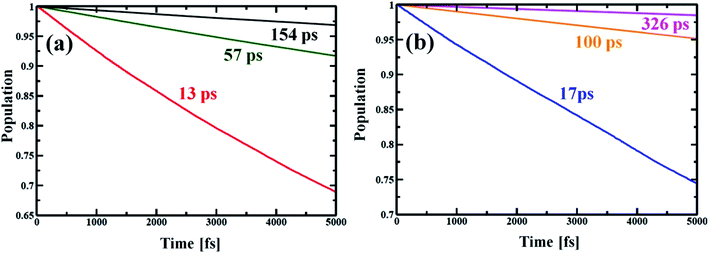 | ||
| Fig. 7 Electron–hole recombination dynamics for different porphyrin nanoball structures at 300 K. (a) shows population decay of Zn-nanoball; red, green, black with T0, T6 and T14 templates, respectively. (b) shows the same as above for Cd-nanoball. Here blue, orange and magenta lines represent population decay for T0, T6 and T14 templates, respectively. The rate of exciton diminishing to ground state is very fast for the T0 template. High NA coupling values between the band edge, long coherence and high frequency phonon mode involved in energy dissipation made the relaxation process very rapid for porphyrin nanoballs without templates. As the ball is coordinated with templates the rate becomes slower with manifold magnitude (Table 2). The carrier lifetime for Cd nanoballs is longer than the ball with the lighter atom Zn. | ||
4. Conclusion
In this work, nonradiative e–h recombination dynamics in metal–porphyrin nanoballs have been studied using recently developed SCC-DFTB-based NAMD techniques. As evident, such nanosystems hold great promise to be future light-harvesting materials. The present simulation demonstrates that the rate of nonradiative exciton relaxation can be suppressed up to 12 orders of magnitude with the incorporation of templates into the Zn–porphyrin nanoball. Templates coordinate to the metal centers of the porphyrin units, thereby making the nanostructures more rigid. The suppressed atomic fluctuation significantly weakens the NA electron–phonon coupling. Moreover, the presence of templates pushes the involving phonon modes toward the lower energy region and significantly reduces the time of quantum coherence, involving the carrier states. As a result, the charge carrier recombination time increases enormously. The replacement of Zn with a heavier Cd atom shows a similar trend, but strikingly the fully template Cd-nanoball experiences a huge recombination time of 326 ps, which is almost double that of the corresponding Zn-nanoball. In the present study, we demonstrate the fundamental photophysics behind the energy loss during the carrier relaxation process. Our simulation provides valuable guidelines to prevent the undesired energy dissipation during the e–h recombination for porphyrin-based nanosystem by controlling the structural rigidity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors sincerely acknowledge the financial support from DST Nano-Mission Project (SR/NM/NS-1005/2016(G)). SP acknowledges the financial support from CSIR, Govt. of India through project Ref. No. 01(2956)/18/EMR-II. RS and MK thank CSIR for proving them with Senior Research Fellowship (SRF).References
- Y. Liu, T. Wu, Y. Liu, T. Song and B. Sun, APL Mater., 2019, 7, 021102 CrossRef.
- K. Zhao, Z. Pan, I. Mora-Seró, E. Cánovas, H. Wang, Y. Song, X. Gong, J. Wang, M. Bonn, J. Bisquert and X. Zhong, J. Am. Chem. Soc., 2015, 137, 5602–5609 CrossRef CAS PubMed.
- Q. Wu, J. Hou, H. Zhao, Z. Liu, X. Yue, S. Peng and H. Cao, Dalton Trans., 2018, 47, 2214–2221 RSC.
- K. Zhao, Z. Pan and X. Zhong, J. Phys. Chem. Lett., 2016, 7, 406–417 CrossRef CAS PubMed.
- C. S. Ponseca Jr, T. J. Savenije, M. Abdellah, K. Zheng, A. Yartsev, T. r. Pascher, T. Harlang, P. Chabera, T. Pullerits and A. Stepanov, J. Am. Chem. Soc., 2014, 136, 5189–5192 CrossRef PubMed.
- K. E. Knowles, E. A. McArthur and E. A. Weiss, ACS Nano, 2011, 5, 2026–2035 CrossRef CAS PubMed.
- V. I. Klimov, Annu. Rev. Condens. Matter Phys., 2014, 5, 285–316 CrossRef CAS.
- V. I. Klimov, J. Phys. Chem. B, 2000, 104, 6112–6123 CrossRef CAS.
- G. J. Wetzelaer, M. Scheepers, A. M. Sempere, C. Momblona, J. Avila and H. J. Bolink, Adv. Mater., 2015, 27, 1837–1841 CrossRef CAS PubMed.
- W. Zhou, Y. Zhao, C. Shi, H. Huang, J. Wei, R. Fu, K. Liu, D. Yu and Q. Zhao, J. Phys. Chem. C, 2016, 120, 4759–4765 CrossRef CAS.
- G. Nan, X. Zhang, M. Abdi-Jalebi, Z. Andaji-Garmaroudi, S. D. Stranks, G. Lu and D. Beljonne, Adv. Energy Mater., 2018, 8, 1702754 CrossRef.
- D.-Y. Son, J.-W. Lee, Y. J. Choi, I.-H. Jang, S. Lee, P. J. Yoo, H. Shin, N. Ahn, M. Choi, D. Kim and N.-G. Park, Nat. Energy, 2016, 1, 16081 CrossRef CAS.
- A. V. Akimov and O. V. Prezhdo, J. Am. Chem. Soc., 2014, 136, 1599–1608 CrossRef CAS PubMed.
- S. V. Kilina, D. S. Kilin and O. V. Prezhdo, ACS Nano, 2009, 3, 93–99 CrossRef CAS PubMed.
- X. He, K. A. Velizhanin, G. Bullard, Y. Bai, J. H. Olivier, N. F. Hartmann, B. J. Gifford, S. Kilina, S. Tretiak, H. Htoon, M. J. Therien and S. K. Doorn, ACS Nano, 2018, 12, 8060–8070 CrossRef CAS PubMed.
- V. Chikan and D. F. Kelley, Nano Lett., 2002, 2, 1015–1020 CrossRef CAS.
- P. Peng, D. J. Milliron, S. M. Hughes, J. C. Johnson, A. P. Alivisatos and R. J. Saykally, Nano Lett., 2005, 5, 1809–1813 CrossRef CAS PubMed.
- O. A. Dyatlova, C. Kohler, E. Malic, J. Gomis-Bresco, J. Maultzsch, A. Tsagan-Mandzhiev, T. Watermann, A. Knorr and U. Woggon, Nano Lett., 2012, 12, 2249–2253 CrossRef CAS PubMed.
- Y. Nam, L. Li, J. Y. Lee and O. V. Prezhdo, J. Phys. Chem. C, 2018, 122, 5201–5208 CrossRef CAS.
- Y. Yamada, M. Hoyano, R. Akashi, K. Oto and Y. Kanemitsu, J. Phys. Chem. Lett., 2017, 8, 5798–5803 CrossRef CAS PubMed.
- X. Zhou, L. Li, D. D. Dlott and O. V. Prezhdo, J. Phys. Chem. C, 2018, 122, 13600–13607 CrossRef CAS.
- W. Li, J. Tang, D. Casanova and O. V. Prezhdo, ACS Energy Lett., 2018, 3, 2713–2720 CrossRef CAS.
- X. Zhou, L. Li, H. Dong, A. Giri, P. E. Hopkins and O. V. Prezhdo, J. Phys. Chem. C, 2017, 121, 17488–17497 CrossRef CAS.
- D.-H. Lien, S. Z. Uddin, M. Yeh, M. Amani, H. Kim, J. W. Ager, E. Yablonovitch and A. Javey, Science, 2019, 364, 468–471 CrossRef CAS PubMed.
- T. W. Crothers, R. L. Milot, J. B. Patel, E. S. Parrott, J. Schlipf, P. Muller-Buschbaum, M. B. Johnston and L. M. Herz, Nano Lett., 2017, 17, 5782–5789 CrossRef CAS PubMed.
- Y. Yang, M. Forster, Y. Ling, G. Wang, T. Zhai, Y. Tong, A. J. Cowan and Y. Li, Angew. Chem., Int. Ed., 2016, 55, 3403–3407 CrossRef CAS PubMed.
- M. Lorenzon, L. Sortino, Q. Akkerman, S. Accornero, J. Pedrini, M. Prato, V. Pinchetti, F. Meinardi, L. Manna and S. Brovelli, Nano Lett., 2017, 17, 3844–3853 CrossRef CAS PubMed.
- J. He, W.-H. Fang, R. Long and O. V. Prezhdo, ACS Energy Lett., 2018, 3, 2070–2076 CrossRef CAS.
- G. Sedghi, V. M. García-Suárez, L. J. Esdaile, H. L. Anderson, C. J. Lambert, S. Martín, D. Bethell, S. J. Higgins, M. Elliott and N. Bennett, Nat. Nanotechnol., 2011, 6, 517 CrossRef CAS PubMed.
- Z. Li, T.-H. Park, J. Rawson, M. J. Therien and E. Borguet, Nano Lett., 2012, 12, 2722–2727 CrossRef CAS PubMed.
- G. Kuang, S. Z. Chen, L. Yan, K. Q. Chen, X. Shang, P. N. Liu and N. Lin, J. Am. Chem. Soc., 2018, 140, 570–573 CrossRef CAS PubMed.
- A. Pramanik and H. S. Kang, J. Chem. Phys., 2011, 134, 094702 CrossRef PubMed.
- M. Kar, R. Sarkar, S. Pal and P. Sarkar, J. Phys. Chem. C, 2019, 123, 5303–5311 CrossRef CAS.
- P. A. Liddell, G. Kodis, A. L. Moore, T. A. Moore and D. Gust, J. Am. Chem. Soc., 2002, 124, 7668–7669 CrossRef CAS PubMed.
- D. T. Gryko, C. Clausen, K. M. Roth, N. Dontha, D. F. Bocian, W. G. Kuhr and J. S. Lindsey, J. Org. Chem., 2000, 65, 7345–7355 CrossRef CAS PubMed.
- O. Fenwick, J. K. Sprafke, J. Binas, D. V. Kondratuk, F. Di Stasio, H. L. Anderson and F. Cacialli, Nano Lett., 2011, 11, 2451–2456 CrossRef CAS PubMed.
- M. S. Choi, T. Yamazaki, I. Yamazaki and T. Aida, Angew. Chem., Int. Ed., 2004, 43, 150–158 CrossRef CAS PubMed.
- J. Cremers, R. Haver, M. Rickhaus, J. Q. Gong, L. Favereau, M. D. Peeks, T. D. Claridge, L. M. Herz and H. L. Anderson, J. Am. Chem. Soc., 2018, 140, 5352–5355 CrossRef CAS PubMed.
- S. Pal, D. J. Trivedi, A. V. Akimov, B. l. Aradi, T. Frauenheim and O. V. Prezhdo, J. Chem. Theory Comput., 2016, 12, 1436–1448 CrossRef CAS PubMed.
- H. M. Jaeger, S. Fischer and O. V. Prezhdo, J. Chem. Phys., 2012, 137, 22A545 CrossRef PubMed.
- S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford university press, New York, 1995 Search PubMed.
- R. Sarkar, M. Habib, S. Pal and O. V. Prezhdo, Nanoscale, 2018, 10, 12683–12694 RSC.
- M. Habib, M. Kar, S. Pal and P. Sarkar, Chem. Mater., 2019, 31, 4042–4050 CrossRef CAS.
- C.-J. Tong, L. Li, L.-M. Liu and O. V. Prezhdo, ACS Energy Lett., 2018, 3, 1868–1874 CrossRef CAS.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2013, 9, 4959–4972 CrossRef CAS PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2014, 10, 789–804 CrossRef CAS PubMed.
- S. Dong, S. Pal, J. Lian, Y. Chan, O. V. Prezhdo and Z.-H. Loh, ACS Nano, 2016, 10, 9370–9378 CrossRef CAS PubMed.
- S. Pal, D. Casanova and O. V. Prezhdo, Nano Lett., 2017, 18, 58–63 CrossRef PubMed.
- S. Pal, P. Nijjar, T. Frauenheim and O. V. Prezhdo, Nano Lett., 2017, 17, 2389–2396 CrossRef CAS PubMed.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684 CrossRef CAS PubMed.
- T. Frauenheim, G. Seifert, M. Elstner, T. Niehaus, C. Köhler, M. Amkreutz, M. Sternberg, Z. Hajnal, A. Di Carlo and S. Suhai, J. Phys.: Condens. Matter, 2002, 14, 3015 CrossRef CAS.
- R. Sarkar, S. Sarkar, A. Pramanik, P. Sarkar and S. Pal, RSC Adv., 2016, 6, 86494–86501 RSC.
- S. Sarkar, S. Pal, P. Sarkar, A. Rosa and T. Frauenheim, J. Chem. Theory Comput., 2011, 7, 2262–2276 CrossRef CAS PubMed.
- B. Rajbanshi and P. Sarkar, J. Phys. Chem. C, 2016, 120, 17878–17886 CrossRef CAS.
- T. B. Tai, V. T. T. Huong and M. T. Nguyen, J. Phys. Chem. C, 2013, 117, 14999–15008 CrossRef CAS.
- S. Biswas, A. Pramanik and P. Sarkar, J. Phys. Chem. C, 2018, 122, 14296–14303 CrossRef CAS.
- S. Biswas, A. Pramanik, S. Pal and P. Sarkar, J. Phys. Chem. C, 2017, 121, 2574–2587 CrossRef CAS.
- S. Biswas, A. Pramanik and P. Sarkar, Comput. Theor. Chem., 2017, 1103, 38–47 CrossRef CAS.
- X. Amashukeli, N. E. Gruhn, D. L. Lichtenberger, J. R. Winkler and H. B. Gray, J. Am. Chem. Soc., 2004, 126, 15566–15571 CrossRef CAS PubMed.
- E. Sigfridsson, M. H. Olsson and U. Ryde, J. Phys. Chem. B, 2001, 105, 5546–5552 CrossRef CAS.
- J. Liu, S. V. Kilina, S. Tretiak and O. V. Prezhdo, ACS Nano, 2015, 9, 9106–9116 CrossRef CAS PubMed.
- T. S. Rush, P. M. Kozlowski, C. A. Piffat, R. Kumble, M. Z. Zgierski and T. G. Spiro, J. Phys. Chem. B, 2000, 104, 5020–5034 CrossRef CAS.
- L. B. Ioffe, V. B. Geshkenbein, M. V. Feigel'Man, A. L. Fauchere and G. Blatter, Nature, 1999, 398, 679 CrossRef.
- I. Chiorescu, Y. Nakamura, C. M. Harmans and J. Mooij, Science, 2003, 299, 1869–1871 CrossRef CAS PubMed.
- R. Schoelkopf and S. Girvin, Nature, 2008, 451, 664 CrossRef CAS PubMed.
- B. F. Habenicht and O. V. Prezhdo, Phys. Rev. Lett., 2008, 100, 197402 CrossRef PubMed.
- O. V. Prezhdo, J. Chem. Phys., 1999, 111, 8366–8377 CrossRef CAS.
- O. V. Prezhdo and P. J. Rossky, J. Chem. Phys., 1997, 107, 5863–5878 CrossRef CAS.
- J. Li, A. Ambroise, S. I. Yang, J. R. Diers, J. Seth, C. R. Wack, D. F. Bocian, D. Holten and J. S. Lindsey, J. Am. Chem. Soc., 1999, 121, 8927–8940 CrossRef CAS.
- R. W. Wagner, J. Seth, S. I. Yang, D. Kim, D. F. Bocian, D. Holten and J. S. Lindsey, J. Org. Chem., 1998, 63, 5042–5049 CrossRef CAS.
- O. V. Prezhdo, Phys. Rev. Lett., 2000, 85, 4413 CrossRef CAS PubMed.
- S. V. Kilina, A. J. Neukirch, B. F. Habenicht, D. S. Kilin and O. V. Prezhdo, Phys. Rev. Lett., 2013, 110, 180404 CrossRef PubMed.
- B. Philippa, M. Stolterfoht, R. D. White, M. Velusamy, P. L. Burn, P. Meredith and A. Pivrikas, J. Chem. Phys., 2014, 141, 054903 CrossRef PubMed.
- A. G. Dixon, R. Visvanathan, N. A. Clark, N. Stingelin, N. Kopidakis and S. E. Shaheen, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 31–35 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00001a |
| This journal is © The Royal Society of Chemistry 2020 |