Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the shape-dependent propulsion of nano- and microparticles by traveling ultrasound waves
Johannes
Voß
and
Raphael
Wittkowski
 *
*
Institut für Theoretische Physik, Center for Soft Nanoscience, Westfälische Wilhelms-Universität Münster, D-48149 Münster, Germany. E-mail: raphael.wittkowski@uni-muenster.de
First published on 21st July 2020
Abstract
We address the propulsion mechanism of ultrasound-propelled nano- and microparticles that are exposed to a traveling ultrasound wave. Based on direct computational fluid dynamics simulations, we study the effect of two important aspects of the particle shape on the propulsion: rounded vs. pointed and filled vs. hollow shapes. We also study the flow field generated around such particles. Our results reveal that pointedness leads to an increase of the propulsion speed, whereas it is not significantly affected by hollowness. Furthermore, we show that the flow field near to ultrasound-propelled particles can look similar to the flow field generated by pusher squirmers.
I. Introduction
With the experimental discovery of fuel-less ultrasound-propelled colloidal particles in 2012,1 important potential applications of motile nano- and microparticles (also called “active particles”)2 have become within reach.3 One of their most attractive potential applications is the usage as propelled nano- or microdevices in medicine4–6 that allows for targeted drug delivery,7–12 enhanced biodetoxification,13,14 nanosurgery,15,16 enhanced diagnostics,4,17–19 and many more fascinating applications.16,20–27 In contrast to different propulsion mechanisms like chemical propulsion,20,28,29 other fuel-based propulsion,30 light-propulsion,31 and X-ray propulsion,32 the acoustic propulsion1,5–9,13,18,33–44 has important advantages: it is fuel-free, biocompatible, and allows to supply the particles continuously with energy. Similar to chemically powered particles, ultrasound-propelled particles are supplied only with energy but not with directional information so that their direction of motion is determined only by their instantaneous orientations. Ultrasound-propelled particles can be rigid1,7,9,33–38,41,42,44–47 or have moveable components.30,42,48,49 The latter ones include bubble-propelled particles,30,49 which can reach rather high propulsion speeds, but since the former ones are easier to produce, they are more likely to be applied in the near future. There exist also hybrid particles combining acoustic propulsion with a different propulsion mechanism.37,40,44,50,51Ultrasound-propelled nano- and microparticles have been intensively investigated in recent years.1,33–35,38,39,41,42,44–47,52–54 While the most studies are based on experiments,1,33–35,38,39,41,42,44,47 there are only two theory-based studies so far.45,46 Despite the large number of existing studies on acoustically propelled particles, we are still at the beginning of exploring and understanding their features. Even the details of their propulsion mechanism are still unclear. For example, it is not yet known how the propulsion speed depends on the properties of the particles and their environment, what the maximal speed of the particles for a given ultrasound intensity is, and which structure the flow field generated around the particles has. One of the most basic properties of the particles is their shape. Nevertheless, only very few particle shapes have been considered so far. The main reason for this is that the particle shape cannot easily be varied in experimental studies and that the existing theoretical studies focus on the particle shapes used in the experiments. The particle shapes studied so far are mostly cylinders with a concave and a convex end.1,34–36,47 As a limiting case, also cup-shaped particles were studied.38,44 Apart from that, there exist only a study that addresses gear-shaped particles41 and studies on particles with movable components30,42,48,49 and thus a nonconstant shape.
For a cylindrical shape with spherical concave and convex ends, the direction of movement was found in experiments to point towards the concave end,39 but the newest theoretical study suggests that this depends on the shape of the caps.46 The direction of propulsion seems to depend also on the length of the cylinder, since cup-shaped particles were found to move towards their convex end.38 Hence, we can conclude that the propulsion speed depends sensitively on the particles' shape, but we have not yet a deeper understanding of this dependence.
A better understanding of the shape-dependence of the propulsion would be helpful for future studies, since it would provide a good opportunity for optimizing the particle speed and thus the efficiency of the particles' propulsion. Large propulsion speeds are crucial for medical applications, where the maximal ultrasound intensity is limited by the requirement of biocompatibility and the particles must be fast enough to withstand the blood flow that tends to carry the particles away. The fastest ultrasound-propelled fuel-free particles observed so far reached a speed of about 250 μm s−1.33 This is faster than the blood flow in the vascular capillaries with a typical speed of about 100 μm s−1,16 but the transducer voltage of 10 V applied in the corresponding experiments indicates that the acoustic energy density was about 10–100 J m−3 (ref. 55) and thus too high for usage in the human body, where the energy density should be below 4.9 J m−3 to avoid damage to the tissue.56
A further limitation related to the experiments is the usage of a standing ultrasound wave in all but one42 experimental studies. To facilitate observation of the particles with a microscope, they are enclosed by a thin chamber with two parallel horizontal walls, of which at least the upper one is transparent, and a standing wave field that levitates the particles in a nodal plane between the horizontal walls of the chamber. However, in many important potential applications, such as medical ones, the sound waves would be traveling.
In this article, we advance the knowledge about the acoustic propulsion of homogeneous rigid nano- and microparticles that are exposed to traveling ultrasound waves. Using direct computational fluid dynamics simulations based on numerically solving the compressible Navier–Stokes equations, we determine the sound-induced forces acting on these particles together with their resulting propulsion velocity as well as the flow field generated around the particles. To address the shape-dependence of these quantities, we consider some particle shapes that differ with respect to two aspects not studied previously: we compare rounded with pointed shapes and filled with hollow ones.
II. Methods
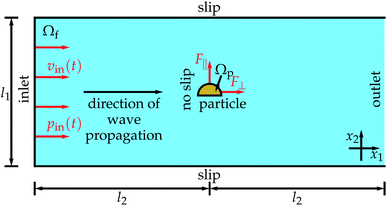
The setup for our study is shown in Fig. 1. A traveling ultrasound wave with frequency f = 1 MHz enters a rectangular domain Ωf of an initially quiescent fluid, which we assume to be water, at an inlet of width l1 = 200σ, where σ = 1 μm is the particle diameter. At the inlet, the ultrasound wave is prescribed by a time-dependent inflow velocity vin(t) = (Δp/(ρ0cf))sin(2πft) perpendicular to the inlet and a time-dependent inflow pressure pin(t) = Δp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πft) with the pressure amplitude Δp = 10 kPa, the density of the quiescent fluid ρ0 = 998 kg m−3, and the sound velocity in the fluid cf = 1484 m s−1. The pressure amplitude corresponds to an acoustic energy density E = Δp2/(2ρ0cf2) = 22.7 mJ m−3. Starting at the inlet, the ultrasound wave propagates through the fluid domain parallel to its lateral boundaries, where we prescribe slip boundary conditions. After a distance l2 = λ/4 with the wavelength of the ultrasound λ = 1.484 mm, the wave arrives the fixed rigid particle, which is oriented perpendicular to the propagation direction of the wave. In the simulations, we describe the particle by a particle domain Ωp and prescribe no-slip conditions at the particle's boundary ∂Ωp. Through the ultrasound, a time-averaged propulsion force with a component F∥ parallel to and a component F⊥ perpendicular to the particle's orientation is exerted on the particle. The wave then propagates a further distance l2 until it reaches an outlet at the end of the domain Ωf.
sin(2πft) with the pressure amplitude Δp = 10 kPa, the density of the quiescent fluid ρ0 = 998 kg m−3, and the sound velocity in the fluid cf = 1484 m s−1. The pressure amplitude corresponds to an acoustic energy density E = Δp2/(2ρ0cf2) = 22.7 mJ m−3. Starting at the inlet, the ultrasound wave propagates through the fluid domain parallel to its lateral boundaries, where we prescribe slip boundary conditions. After a distance l2 = λ/4 with the wavelength of the ultrasound λ = 1.484 mm, the wave arrives the fixed rigid particle, which is oriented perpendicular to the propagation direction of the wave. In the simulations, we describe the particle by a particle domain Ωp and prescribe no-slip conditions at the particle's boundary ∂Ωp. Through the ultrasound, a time-averaged propulsion force with a component F∥ parallel to and a component F⊥ perpendicular to the particle's orientation is exerted on the particle. The wave then propagates a further distance l2 until it reaches an outlet at the end of the domain Ωf.
To avoid approximations like perturbation expansions that are involved in all previous studies using analytical45,46 or numerical41,42,44 methods to determine the propulsion velocity of acoustically propelled particles, we base our work on direct fluid dynamics simulations. Our simulations are carried out by numerically solving the compressible Navier–Stokes equations together with the continuity equation for the mass-density field ρ(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) of the fluid and a constitutive equation for the fluid's pressure field p(
,t) of the fluid and a constitutive equation for the fluid's pressure field p(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) in the two-dimensional fluid domain Ωf. Here,
,t) in the two-dimensional fluid domain Ωf. Here, ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) = (x1,x2)T is the position vector and t denotes time.
= (x1,x2)T is the position vector and t denotes time.
When ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (
(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) with
,t) with ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) = (v1,v2)T is the velocity field of the fluid and we use the short notation ∂i = ∂/∂xi with i ∈ {1, 2} for the spatial derivatives, the continuity equation that describes mass conservation is given by57
= (v1,v2)T is the velocity field of the fluid and we use the short notation ∂i = ∂/∂xi with i ∈ {1, 2} for the spatial derivatives, the continuity equation that describes mass conservation is given by57
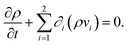 | (1) |
Momentum conservation of the fluid is then described by the Navier–Stokes equations57
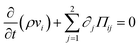 | (2) |
| Πij = ρvivj − Σij | (3) |
| Σij = Σij(p) + Σij(v) | (4) |
| Σij(p) = −pδij | (5) |
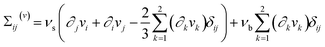 | (6) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t). When the sound intensity is sufficiently small, so that the fluid is acoustically nondispersive and heating of the fluid by the sound wave can be neglected, the local pressure p(
,t). When the sound intensity is sufficiently small, so that the fluid is acoustically nondispersive and heating of the fluid by the sound wave can be neglected, the local pressure p(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) is given by the constitutive equation
,t) is given by the constitutive equation| p(ρ) = p0 + cf2(ρ − ρ0) | (7) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t). Here, p0 = p(ρ0) is the constant mean pressure of the fluid. To solve eqn (1)–(7) numerically, we used the software package OpenFOAM,58 which applies the finite volume method.
,t). Here, p0 = p(ρ0) is the constant mean pressure of the fluid. To solve eqn (1)–(7) numerically, we used the software package OpenFOAM,58 which applies the finite volume method.
The time-dependent force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (t) with
(t) with ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) = (F1,F2)T and the time-dependent torque T(t) acting on the particle are calculated in the laboratory frame. Since the particle, which is described by the particle domain Ωp, has no-slip boundary conditions and is fixed in space in our simulations, the fluid velocity
= (F1,F2)T and the time-dependent torque T(t) acting on the particle are calculated in the laboratory frame. Since the particle, which is described by the particle domain Ωp, has no-slip boundary conditions and is fixed in space in our simulations, the fluid velocity ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) (
(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) is zero at the fluid–particle interface ∂Ωp. So the total force and torque exerted on the particle are given by
,t) is zero at the fluid–particle interface ∂Ωp. So the total force and torque exerted on the particle are given by ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) =
= ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p) +
(p) + ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (v) and T = T(p) + T(v) with the components57
(v) and T = T(p) + T(v) with the components57
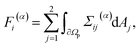 | (8) |
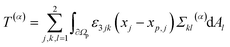 | (9) |
![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0041_20d1.gif) (
(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) with d
) with d![[A with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0041_20d1.gif) = (dA1,dA2)T is the normal and outwards oriented surface element of ∂Ωp at position
= (dA1,dA2)T is the normal and outwards oriented surface element of ∂Ωp at position ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) = (x1,x2)T when
= (x1,x2)T when ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ∈ ∂Ωp, εijk the Levi-Civita symbol, and
∈ ∂Ωp, εijk the Levi-Civita symbol, and ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) p = (xp,1,xp,2)T the center-of-mass position of the particle. Since the position of the particle is fixed in our simulations, the results for the propulsion force correspond to a particle that is held in place. For a freely moving particle, the results correspond to a particle material with infinite mass density and can thus be seen as an upper bound for the propulsion force of a particle made of gold or another material with a large mass density.
p = (xp,1,xp,2)T the center-of-mass position of the particle. Since the position of the particle is fixed in our simulations, the results for the propulsion force correspond to a particle that is held in place. For a freely moving particle, the results correspond to a particle material with infinite mass density and can thus be seen as an upper bound for the propulsion force of a particle made of gold or another material with a large mass density.
By time-averaging ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p)(t),
(p)(t), ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (v)(t), T(p)(t), and T(v)(t) locally over one period τ of the ultrasound wave in the stationary state (i.e., for large t), we obtain the time-averaged stationary forces 〈
(v)(t), T(p)(t), and T(v)(t) locally over one period τ of the ultrasound wave in the stationary state (i.e., for large t), we obtain the time-averaged stationary forces 〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p)〉, 〈
(p)〉, 〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (v)〉, and 〈
(v)〉, and 〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) 〉 = 〈
〉 = 〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p)〉 + 〈
(p)〉 + 〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (v)〉 and the time-averaged stationary torques 〈T(p)〉, 〈T(v)〉, and 〈T〉 = 〈T(p)〉 + 〈T(v)〉, where 〈·〉 denotes the time average. Using 〈
(v)〉 and the time-averaged stationary torques 〈T(p)〉, 〈T(v)〉, and 〈T〉 = 〈T(p)〉 + 〈T(v)〉, where 〈·〉 denotes the time average. Using 〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) 〉, we then calculate the time-averaged stationary propulsion velocity59,60
〉, we then calculate the time-averaged stationary propulsion velocity59,60
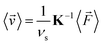 | (10) |
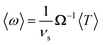 | (11) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 〉 and 〈ω〉 thus involves three approximations. First, we use the flow field around the particle, which we have determined only for two instead of three spatial dimensions, to calculate the propulsion force and torque. Second, we use the time-averaged propulsion force and torque acting on the particle with fixed position and orientation to determine the time-averaged propulsion velocity and angular velocity such a particle would have if it could move freely. Third, we neglect hydrodynamic translational–rotational coupling associated with the particle shape.
〉 and 〈ω〉 thus involves three approximations. First, we use the flow field around the particle, which we have determined only for two instead of three spatial dimensions, to calculate the propulsion force and torque. Second, we use the time-averaged propulsion force and torque acting on the particle with fixed position and orientation to determine the time-averaged propulsion velocity and angular velocity such a particle would have if it could move freely. Third, we neglect hydrodynamic translational–rotational coupling associated with the particle shape.
From 〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) 〉 and 〈
〉 and 〈![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 〉, we directly obtain the propulsion-force components F∥ = (〈
〉, we directly obtain the propulsion-force components F∥ = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) 〉)2 = F∥,p + F∥,v and F⊥ = (〈
〉)2 = F∥,p + F∥,v and F⊥ = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) 〉)1 = F⊥,p + F⊥,v, their pressure components F∥,p = (〈
〉)1 = F⊥,p + F⊥,v, their pressure components F∥,p = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p)〉)2 and F⊥,p = (〈
(p)〉)2 and F⊥,p = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (p)〉)1 and viscous components F∥,v = (〈
(p)〉)1 and viscous components F∥,v = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (v)〉)2 and F⊥,v = (〈
(v)〉)2 and F⊥,v = (〈![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (v)〉)1, as well as the propulsion-velocity components v∥ = (〈
(v)〉)1, as well as the propulsion-velocity components v∥ = (〈![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 〉)2 and v⊥ = (〈
〉)2 and v⊥ = (〈![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 〉)1 as the force- and velocity contributions parallel and perpendicular to the particle's orientation, i.e., parallel and perpendicular to the x2 axis.
〉)1 as the force- and velocity contributions parallel and perpendicular to the particle's orientation, i.e., parallel and perpendicular to the x2 axis.
Nondimensionalization of the equations introduced above leads to the Helmholtz number He, a Reynolds number corresponding to the shear viscosity Res, another Reynolds number corresponding to the bulk viscosity Reb, and the product Ma2Eu, with the Mach number Ma and Euler number Eu, corresponding to the pressure amplitude Δp of the ultrasound wave that enters the simulated system. Table 1 shows the names, symbols, and assigned values of the parameters that are relevant for our simulations. The parameters related to the fluid are based on assuming that the fluid is water at normal temperature T0 = 293.15 K and normal pressure p0 = 101325 Pa. With the parameter values from Table 1, our simulations correspond to the following values of the dimensionless numbers:
| He = 2πfσ/cf ≈ 4.234 × 10−3, | (12) |
| Res = ρ0cfσ/νs ≈ 1478, | (13) |
| Reb = ρ0cfσ/νb ≈ 516, | (14) |
| Ma2Eu = Δp/(ρ0cf2) ≈ 4.550 × 10−6. | (15) |
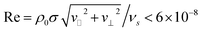 characterizing the particle motion through the fluid is much less than one, when using the results for the propulsion velocity described in section III, and thus ensures that eqn (10) and (11) are applicable.
characterizing the particle motion through the fluid is much less than one, when using the results for the propulsion velocity described in section III, and thus ensures that eqn (10) and (11) are applicable.
| Name | Symbol | Value |
|---|---|---|
| Particle diameter | σ | 1 μm |
| Sound frequency | f | 1 MHz |
| Speed of sound | c f | 1484 m s−1 |
| Time period of sound | τ = 1/f | 1 μs |
| Wavelength of sound | λ = cf/f | 1.484 mm |
| Mean mass density of fluid | ρ 0 | 998 kg m−3 |
| Mean pressure of fluid | p 0 | 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 Pa 325 Pa |
| Initial velocity of fluid |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 0
0
|
![[0 with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/char_0030_20d1.gif) m s−1 m s−1 |
| Sound pressure amplitude | Δp | 10 kPa |
| Acoustic energy density | E = Δp2/(2ρ0cf2) | 22.7 mJ m−3 |
| Shear/dynamic viscosity of fluid | ν s | 1.002 mPa s |
| Bulk/volume viscosity of fluid | ν b | 2.87 mPa s |
| Domain width | l 1 | 200σ |
| Inlet-particle or particle-outlet distance | l 2 | λ/4 |
| Mesh-cell size | Δx | 15 nm to 1 μm |
| Time-step size | Δt | 1–10 ps |
| Simulation duration | t max | 500τ |
We discretized the fluid domain Ωf using a structured mixed rectangular-triangular mesh with about 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cells. The typical cell size Δx varied from about 15 nm near the particle to about 1 μm far away from the particle. For the time integration, we used an adaptive time-step method with a maximum time-step size ensuring that the Courant–Friedrichs–Lewy number
000 cells. The typical cell size Δx varied from about 15 nm near the particle to about 1 μm far away from the particle. For the time integration, we used an adaptive time-step method with a maximum time-step size ensuring that the Courant–Friedrichs–Lewy number
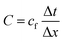 | (16) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CPU core hours.
000 CPU core hours.
Since the simulations would require even more time to fully converge, we determined the stationary forces F∥,p, F∥,v, F⊥,p, and F⊥,v and the stationary torque 〈T〉 by extrapolation. For this purpose, we used the fit function
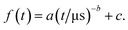 | (17) |
An example for the extrapolation, corresponding to a hollow-half-ball particle and considering the forces F∥,p and F∥,v, is shown in Fig. 2. The fit curves for the other forces, torques, and particle shapes look similar. In the inset of this figure, the experimental data38 available for the addressed particle shape are indicated by a yellow band. The values of the fit parameters for all considered particle shapes are listed in Table 2.
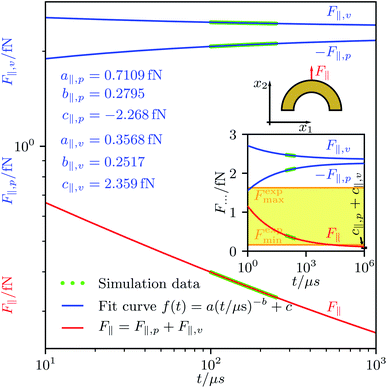 | ||
| Fig. 2 Simulation data for the time-dependent forces F∥,p(t) and F∥,v(t) acting on a particle with the shape of a hollow half ball as well as an extrapolation of the forces with the fit function f(t). The extrapolation of the total propulsion force parallel to the particle orientation F∥(t) = F∥,p(t) + F∥,v(t) converges against c∥,p + c∥,v, where c∥,p and c∥,v are the offset fit coefficients in f(t) for F∥,p(t) and F∥,v(t), respectively. Its limiting value is consistent with corresponding experimental data from Soto et al.38 that can be tied to the interval [Fexpmin, Fexpmax] = [0.163 fN, 1.63 fN]. | ||
| Fit parameter | Half ball | Cone | Hollow half ball | Hollow cone |
|---|---|---|---|---|
| a ∥,p | 0.5188 fN | 0.7301 fN | 0.7109 fN | 0.9332 fN |
| b ∥,p | 0.2825 | 0.2919 | 0.2795 | 0.2808 |
| c ∥,p | −2.995 fN | −6.455 fN | −2.268 fN | −6.007 fN |
| a ∥,v | 0.2506 fN | 0.2033 fN | 0.3568 fN | 0.2686 fN |
| b ∥,v | 0.2447 | 0.2180 | 0.2517 | 0.2104 |
| c ∥,v | 3.073 fN | 6.943 fN | 2.359 fN | 6.529 fN |
| a ⊥,p | −0.4885 pN | −0.4563 pN | −0.5982 pN | −0.5250 pN |
| b ⊥,p | 1.240 | 1.234 | 1.240 | 1.233 |
| c ⊥,p | 0.07838 fN | 0.08258 fN | 0.1011 fN | 0.09072 fN |
| a ⊥,v | −0.7505 pN | −0.6662 pN | −0.6360 pN | −0.5802 pN |
| b ⊥,v | 1.240 | 1.234 | 1.240 | 1.233 |
| c ⊥,v | 0.1253 fN | 0.1050 fN | 0.1026 fN | 0.09062 fN |
III. Results and discussion
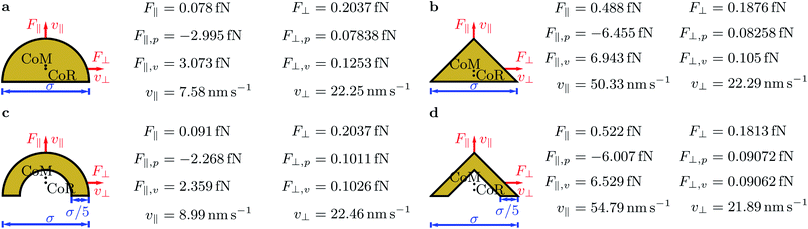
Since we are interested in studying the effect of pointedness and hollowness on the particle propulsion, we consider four different particle shapes: a half ball, a cone, and hollowed-out versions of both shapes (see Fig. 3).All considered particles have diameter σ and the hollow ones have wall width σ/5. Both the particles' center of mass (CoM) and center of resistance (CoR) are on the symmetry axes of the particles. These particle shapes are chosen, since they are relatively simple with an axis of rotational symmetry, have a head-tail asymmetry that is necessary for acoustic propulsion, and differ with respect to pointedness and hollowness. The half ball is neither pointed nor hollow, the cone is pointed but not hollow, the hollow half ball is not pointed but hollow, and the hollow cone is both pointed and hollow. Due to the huge computational expense of the simulations, we did not consider additional particle shapes. A further motivation for choosing the mentioned particle shapes is the fact that there exist experimental data from a previous study that considered cup-shaped particles that are similar to our hollow half ball.38
Fig. 3 shows also the results for the propulsion force parallel to the particles' symmetry axis F∥ = F∥,p + F∥,v, the propulsion force perpendicular to this axis F⊥ = F⊥,p + F⊥,v, their pressure components F∥,p and F⊥,p and viscous components F∥,v and F⊥,v, and the corresponding propulsion-velocity components v∥ and v⊥. For all particle shapes, F∥ and v∥ are positive. The components F∥,p and F∥,v are always negative and positive, respectively, where the latter component is dominating. Remarkably, both cone-shaped particles are associated with propulsion speeds v∥ ≈ 50 nm s−1 that are one order of magnitude larger than those for the half-ball shapes. This suggests that pointed shapes allow much faster acoustic propulsion parallel to the symmetry axis than rounded ones. Comparing the corresponding filled and hollowed-out particle shapes reveals that the hollow particles reach slightly (less than 20 percent) larger propulsion speeds parallel to the symmetry axis than their filled counterparts. This suggests that cavities in the particles have no significant effect on their propulsion speed. Among the considered particles, that with a hollow-cone shape reaches the largest propulsion force F∥ = 0.522 fN and the largest propulsion speed v∥ = 54.79 nm s−1.
Our result for v∥ for the hollow-half-ball particle can be compared to results from experiments described in ref. 38, where particles with a similar shape and size were found to propel with speed v∥ = 82.4(54) μm s−1. However, the comparison is complicated by the fact that this reference mentions not the acoustic energy density the particles were exposed to, but instead, as it is usual in experimental studies on acoustically propelled particles, only the amplitude of the alternating voltage applied to the piezoelectric transducer. To estimate the energy density that is related to the known voltage amplitude, we use the typical energy-density values for some voltage ranges given in ref. 55. According to this reference, a voltage amplitude lower than 10 V, as is used in the experiments described in ref. 38, is typically associated with an acoustic energy density of 10–100 J m−3. In our simulations, the energy density was 22.7 mJ m−3 and thus much smaller than in the experiments. Calculating the propulsion force F∥ that corresponds to the propulsion speed v∥ reported in the experiments and assuming that this force scales linearly with the acoustic energy density, we find a range of force values [Fexpmin, Fexpmax] with Fexpmin = 0.163 fN and Fexpmax = 1.63 fN that could have been observed in the experiments when using the same energy density as in our simulations. This is consistent with our finding for F∥. To be precise, our value for F∥ is slightly below Fexpmin, but given that Fexpmin and Fexpmax have been determined by a rough estimate, that we simulated traveling ultrasound waves whereas the experiments involved standing waves, that the frequency of the ultrasound was different in the simulations and experiments, and that we applied additional approximations as described in section II, the agreement of the force interval estimated from the experimental data with our result is very good.
The force components F⊥, F⊥,p, and F⊥,v are all positive. This is not trivial, since these force components are a result of two opposing physical effects: the acoustic radiation force, which originates from the scattering of the ultrasound wave by the particles, and the acoustic streaming force, which originates from acoustic streaming caused by viscous damping of the ultrasound in the fluid and the associated drag on the particles. While the acoustic radiation force points in the direction of propagation of the ultrasound, the acoustic streaming velocity near the particles points in the opposite direction. For the particles and parameter values considered in this work, the acoustic radiation force is always dominant, but this can change for other particle sizes and shapes. When considering a sphere in a standing sound wave with frequency 1 MHz, the critical radius at which the acoustic radiation force and the acoustic streaming force balance each other is about 1 μm.55 For nonspherical particles and traveling waves, the critical radius is different. The force components F⊥, F⊥,p, and F⊥,v and the velocity component v⊥ are rather similar for all considered particle shapes. In all cases, we found F⊥ ≈ 0.2 fN and v⊥ ≈ 22 nm s−1. For the half-sphere-shaped particles, F⊥ is 2–3 times larger than F∥. In contrast, for cone-shaped particles, F⊥ is 2–3 times smaller than F∥, which makes these particles more relevant as active colloidal particles.
We found no significant torques acting on the particles. This suggests that the particle orientation considered in this study is stable.
Next, we study the flow field around the particles. Fig. 4 shows the time-averaged mass-current density 〈ρ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 〉 and reduced pressure 〈p − p0〉 for all considered particles. In each case, the far field of the flow shows two large counter-rotating vortices with diameters of about 100σ, which are in front of and behind the particle, respectively. Such a flow field is typical for acoustic streaming around a particle exposed to ultrasound even for simple shapes like a sphere.63 The flow from the far field seems to move the particle in the direction antiparallel to the propagation of the ultrasound, but in fact there acts also the acoustic radiation force on the particle, which is oriented parallel to the propagation direction and here dominates the acoustic streaming force that is exerted by this flow. Also the near field of the flow is similar for all considered particle shapes. The structure of the near field, however, is qualitatively different from that of the far field. There are now four vortices to the left and right in front of and behind the particles. The diameter of these vortices is about 2σ. There is an inflow towards the particles from their left and right and an outflow away from the particles at their front and back. For the reduced pressure, negative values are observed in front of and behind the particles, whereas positive values are observed to their left and right. The near field looks rather symmetric, but this does not prevent propulsion of the particles. Since the head-tail symmetry of the particles is broken, even a fully symmetric near field could lead to propulsion.
〉 and reduced pressure 〈p − p0〉 for all considered particles. In each case, the far field of the flow shows two large counter-rotating vortices with diameters of about 100σ, which are in front of and behind the particle, respectively. Such a flow field is typical for acoustic streaming around a particle exposed to ultrasound even for simple shapes like a sphere.63 The flow from the far field seems to move the particle in the direction antiparallel to the propagation of the ultrasound, but in fact there acts also the acoustic radiation force on the particle, which is oriented parallel to the propagation direction and here dominates the acoustic streaming force that is exerted by this flow. Also the near field of the flow is similar for all considered particle shapes. The structure of the near field, however, is qualitatively different from that of the far field. There are now four vortices to the left and right in front of and behind the particles. The diameter of these vortices is about 2σ. There is an inflow towards the particles from their left and right and an outflow away from the particles at their front and back. For the reduced pressure, negative values are observed in front of and behind the particles, whereas positive values are observed to their left and right. The near field looks rather symmetric, but this does not prevent propulsion of the particles. Since the head-tail symmetry of the particles is broken, even a fully symmetric near field could lead to propulsion.
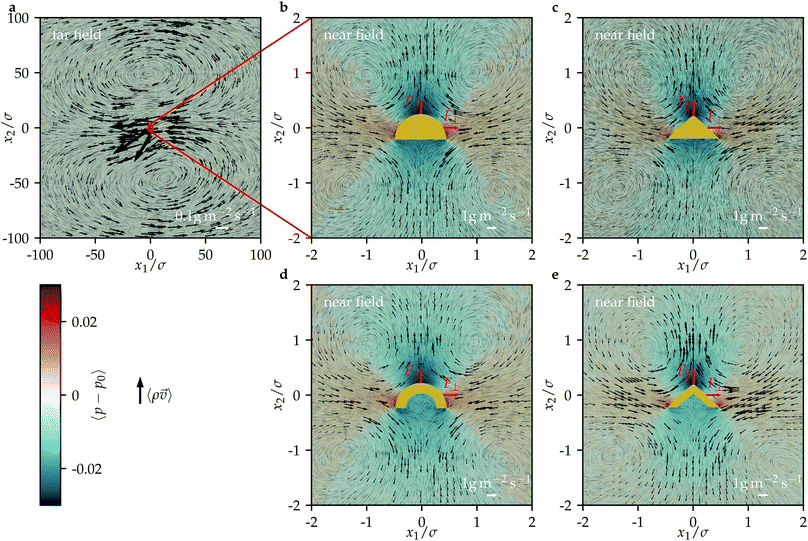 | ||
Fig. 4 The time-averaged mass-current density 〈ρ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 〉 and reduced pressure 〈p − p0〉 for all considered particle shapes (see Fig. 3). (a) The far field is shown for a half-ball particle and looks similar for the other particle shapes; (b)–(e) the near field is shown for each particle shape. 〉 and reduced pressure 〈p − p0〉 for all considered particle shapes (see Fig. 3). (a) The far field is shown for a half-ball particle and looks similar for the other particle shapes; (b)–(e) the near field is shown for each particle shape. | ||
The structure of the near fields is similar to that of the flow fields generated by pusher squirmers.64,65 Identifying the particles as pushers would be an important result, since it would allow us to translate the known properties and modeling techniques for pushers to the so far much less investigated acoustically propelled particles. However, based on the present simulations with flow fields in two spatial dimensions and the consideration only of particles that are oriented perpendicular to the propagation direction of the ultrasound, it cannot be assessed whether the flow fields around ultrasound-propelled particles and pushers are in fact similar. Our results for the flow fields suggest that they are caused by local acoustic streaming close to the particles, as predicted in the theoretical work 45.
IV. Conclusions
Based on direct numerical simulations, we have studied the acoustic propulsion of nonspherical nano- and microparticles by traveling ultrasound. For particle shapes that were either rounded or pointed and either filled or hollow, we have calculated the propulsion force acting on the particle, the resulting propulsion velocity, as well as the flow field around the particle. This allowed us to obtain important new insights into the propulsion of such particles. Our results, which are consistent with experiments from Soto et al.38 for cup-shaped particles, confirmed that the particles' propulsion parallel to their symmetry axis is very sensitive to the particle shape.46 The results revealed that a particle with a pointed shape can show a much more efficient propulsion than one with a rounded shape and that a cavity in the particle shape has no significant effect on the propulsion efficiency. For the propulsion perpendicular to the particles' symmetry axis, no significant dependence on the shape was found. Considering the small number of different particle shapes that have been addressed in previous studies, these findings suggest to use conical particles in future studies further investigating or applying acoustically propelled colloidal particles to reach higher propulsion speeds than for cup-shaped particles38 and the commonly used bullet-shaped particles.1,33,34,39 Since we found only a negligible effect of a cavity in the particle shape on its propulsion efficiency, the conical particle can have or have not a cavity, depending on which particle shape is easier to synthesize. Knowing that the propulsion efficiency of the particles can significantly be enhanced by choosing a more suitable particle shape is an important insight with respect to potential applications of this type of active particles, e.g., in nanomedicine, where the particles need a large propulsion speed to withstand blood flow while the ultrasound intensity is limited to physiologically harmless values.16,66,67 When the particles shall be used for drug delivery in nanomedicine, a filled particle is advantageous, as its larger volume is associated with a larger capacity for transporting drugs.The obtained time-averaged flow fields support the understanding of the particles' propulsion mechanism as originating basically from local acoustic streaming, as predicted by Nadal and Lauga.45 Remarkably, the flow's near field was observed to be similar to that of a pusher squirmer. A future study determining the full flow field in three spatial dimensions and for different particle orientations will have to clarify whether this agreement applies only to the particular situation studied here or these particles in fact constitute pushers. Identifying the particles as pushers would allow us to transfer the large existing knowledge about the motion of pushers and, e.g., their interactions with obstacles and other particles to ultrasound-propelled particles, for which most of these issues have not yet been addressed. We expect that this would strongly boost the future theoretical investigation of ultrasound-propelled colloidal particles. For example, one could then use modified squirmer models to describe the motion of the particles on much larger time scales, which are no longer set by the high frequency of the ultrasound but instead by the rather small time-averaged flow velocities near the particles. This would reduce the computational effort to simulate the motion of the particles by several orders of magnitude and enable studies that were well-nigh impossible up to now. In addition, such modeling would even allow for the application of new analytical approaches, such as field theories derived via, e.g., symmetry-based modeling,68,69 classical dynamical density functional theory,70,71 or the interaction-expansion method72 for describing the collective dynamics of many interacting particles on mesoscopic or macroscopic scales. Furthermore, the identification of the ultrasound-propelled particles as pushers would have intriguing consequences for future materials science. Since it is known from suspensions of bacteria that pushers can strongly reduce the viscosity of a liquid, one could then expect that it is possible to use suspensions of ultrasound-propelled particles to realize novel active materials with a viscosity that can be tuned via the ultrasound intensity from the normal positive viscosity of the suspension in the absence of ultrasound through to suprafluidity up to even negative viscosities.73,74
If such a future study shows instead that the particles are not squirmers, it still needs to be clarified whether they can be seen as nano- or microswimmers or constitute actuated particles. For swimmers, the particles' direction of motion has to rotate with the particles and needs to be independent of the direction of propagation of the ultrasound wave, whereas for actuated particles the energy source transmits also directional information to the particles. Apart from that, the basic understanding of the details of the particles' propulsion mechanism should further be extended by additional computational fluid dynamics simulations. As a task for the future, e.g., the dependence of the propulsion efficiency on the aspect ratio of conical particles should be studied in detail. Examples for other parameters, whose influence on the particles' propulsion still needs to be studied, are their orientation relative to the direction of sound propagation, the viscosity of the fluid, and the frequency of the ultrasound. Furthermore, the simulations should be extended towards three spatial dimensions and freely movable particles.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We thank Patrick Kurzeja for helpful discussions. R.W. is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – WI 4170/3-1. The simulations for this work were performed on the computer cluster PALMA II of the University of Münster.References
- W. Wang, L. Castro, M. Hoyos and T. E. Mallouk, Autonomous motion of metallic microrods propelled by ultrasound, ACS Nano, 2012, 6, 6122–6132 CrossRef CAS.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Active particles in complex and crowded environments, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- T. Xu, L. Xu and X. Zhang, Ultrasound propulsion of micro-/nanomotors, Appl. Mater. Today, 2017, 9, 493–503 CrossRef.
- K. Kim, J. Guo, Z. Liang and D. Fan, Artificial micro/nanomachines for bioapplications: biochemical delivery and diagnostic sensing, Adv. Funct. Mater., 2018, 28, 1705867 CrossRef.
- Z. Wu, et al., Turning erythrocytes into functional micromotors, ACS Nano, 2014, 8, 12041–12048 CrossRef CAS.
- Z. Wu, B. Esteban-Fernández de Ávila, A. Martín, C. Christianson, W. Gao, S. K. Thamphiwatana, A. Escarpa, Q. He, L. Zhang and J. Wang, RBC micromotors carrying multiple cargos towards potential theranostic applications, Nanoscale, 2015, 7, 13680–13686 RSC.
- V. Garcia-Gradilla, S. Sattayasamitsathit, F. Soto, F. Kuralay, C. Yardımcı, D. Wiitala, M. Galarnyk and J. Wang, Ultrasound-propelled nanoporous gold wire for efficient drug loading and release, Small, 2014, 10, 4154–4159 CAS.
- B. Esteban-Fernández de Ávila, D. E. Ramírez-Herrera, S. Campuzano, P. Angsantikul, L. Zhang and J. Wang, Nanomotor-enabled pH-responsive intracellular delivery of caspase-3: toward rapid cell apoptosis, ACS Nano, 2017, 11, 5367–5374 CrossRef.
- M. Uygun, B. Jurado-Sánchez, D. A. Uygun, V. V. Singh, L. Zhang and J. Wang, Ultrasound-propelled nanowire motors enhance asparaginase enzymatic activity against cancer, Nanoscale, 2017, 9, 18423–18429 RSC.
- M. Luo, Y. Feng, T. Wang and J. Guan, Micro-/nanorobots at work in active drug delivery, Adv. Funct. Mater., 2018, 28, 1706100 CrossRef.
- W. Wang, S. Li, L. Mair, S. Ahmed, T. J. Huang and T. E. Mallouk, Acoustic propulsion of nanorod motors inside living cells, Angew. Chem., Int. Ed., 2014, 53, 3201–3204 CrossRef CAS.
- B. Esteban-Fernández de Ávila, C. Angell, F. Soto, M. A. Lopez-Ramirez, D. F. Báez, S. Xie, J. Wang and Y. Chen, Acoustically propelled nanomotors for intracellular siRNA delivery, ACS Nano, 2016, 10, 4997–5005 CrossRef.
- Z. Wu, T. Li, W. Gao, W. Xu, B. Jurado-Sánchez, J. Li, W. Gao, Q. He, L. Zhang and J. Wang, Cell-membrane-coated synthetic nanomotors for effective biodetoxification, Adv. Funct. Mater., 2015, 25, 3881–3887 CrossRef CAS.
- B. Esteban-Fernández de Ávila, P. Angsantikul, D. E. Ramírez-Herrera, F. Soto, H. Teymourian, D. Dehaini, Y. Chen, L. Zhang and J. Wang, “Hybrid biomembrane–functionalized nanorobots for concurrent removal of pathogenic bacteria and toxins, Science Robotics, 2018, 3, eaat0485 CrossRef.
- J. Li, B. Esteban-Fernández de Ávila, W. Gao, L. Zhang and J. Wang, Micro/nanorobots for biomedicine: delivery, surgery, sensing, and detoxification, Science Robotics, 2017, 2, eaam6431 CrossRef.
- P. Erkoc, I. C. Yasa, H. Ceylan, O. Yasa, Y. Alapan and M. Sitti, Mobile microrobots for active therapeutic delivery, Adv. Ther., 2019, 2, 1800064 CrossRef.
- A. Chalupniak, E. Morales-Narváez and A. Merkoci, Micro and nanomotors in diagnostics, Adv. Drug Delivery Rev., 2015, 3, 104–116 CrossRef.
- J. R. Qualliotine, G. Bolat, M. Beltrán-Gastélum, B. Esteban-Fernández de Ávila, J. Wang and J. A. Califano, Acoustic nanomotors for detection of human papillomavirus-associated head and neck cancer, Otolaryngol.--Head Neck Surg., 2019, 161, 814–822 CrossRef.
- B. Esteban-Fernández de Ávila, A. Martín, F. Soto, M. A. Lopez-Ramirez, S. Campuzano, G. M. Vásquez-Machado, W. Gao, L. Zhang and J. Wang, Single cell real-time miRNAs sensing based on nanomotors, ACS Nano, 2015, 9, 6756–6764 CrossRef.
- F. Peng, Y. Tu and D. A. Wilson, Micro/nanomotors towards in vivo application: cell, tissue and biofluid, Chem. Soc. Rev., 2017, 46, 5289–5310 RSC.
- F. Soto and R. Chrostowski, Frontiers of medical micro/manorobotics: in vivo applications and commercialization perspectives toward clinical uses, Front. Bioeng. Biotech., 2018, 6, 170 CrossRef.
- W. He, J. Frueh, N. Hu, L. Liu, M. Gai and Q. He, Guidable thermophoretic Janus micromotors containing gold nanocolorifiers for infrared laser assisted tissue welding, Adv. Sci., 2016, 3, 1600206 CrossRef.
- S. Balasubramanian, et al., Micromachine-enabled capture and isolation of cancer cells in complex media, Angew. Chem., Int. Ed., 2011, 50, 4161–4164 CrossRef CAS.
- W. Gao, B. Esteban-Fernández de Ávila, L. Zhang and J. Wang, Targeting and isolation of cancer cells using micro/nanomotors, Adv. Drug Delivery Rev., 2018, 125, 94–101 CrossRef CAS.
- J. Hu, S. Huang, L. Zhu, W. Huang, Y. Zhao, K. Jin and Q. ZhuGe, Tissue plasminogen activator-porous magnetic microrods for targeted thrombolytic therapy after ischemic stroke, ACS Appl. Mater. Interfaces, 2018, 10, 32988–32997 CrossRef CAS.
- T. Xu, W. Gao, L.-P. Xu, X. Zhang and S. Wang, Fuel-free synthetic micro-/nanomachines, Adv. Mater., 2017, 29, 1603250 CrossRef.
- D. Wang, C. Gao, W. Wang, M. Sun, B. Guo, H. Xie and Q. He, Shape-transformable, fusible rodlike swimming liquid metal nanomachine, ACS Nano, 2018, 12, 10212–10220 CrossRef CAS.
- B. Esteban-Fernández de Ávila, P. Angsantikul, J. Li, W. Gao, L. Zhang and J. Wang, Micromotors go in vivo: from test tubes to live animals, Adv. Funct. Mater., 2018, 28, 1705640 CrossRef.
- M. Safdar, S. U. Khan and J. Jänis, Progress toward catalytic micro- and nanomotors for biomedical and environmental applications, Adv. Mater., 2018, 30, 1703660 CrossRef.
- D. Kagan, M. J. Benchimol, J. C. Claussen, E. Chuluun-Erdene, S. Esener and J. Wang, Acoustic droplet vaporization and propulsion of perfluorocarbon-loaded microbullets for targeted tissue penetration and deformation, Angew. Chem., Int. Ed., 2012, 51, 7519–7522 CrossRef CAS.
- M. Xuan, J. Shao, C. Gao, W. Wang, L. Dai and Q. He, Self-propelled nanomotors for thermomechanically percolating cell membranes, Angew. Chem., Int. Ed., 2018, 57, 12463–12467 CrossRef CAS.
- Z. Xu, M. Chen, H. Lee, S.-P. Feng, J. Y. Park, S. Lee and J. T. Kim, X-ray-powered micromotors, ACS Appl. Mater. Interfaces, 2019, 11, 15727–15732 CrossRef CAS.
- V. Garcia-Gradilla, J. Orozco, S. Sattayasamitsathit, F. Soto, F. Kuralay, A. Pourazary, A. Katzenberg, W. Gao, Y. Shen and J. Wang, Functionalized ultrasound-propelled magnetically guided nanomotors: toward practical biomedical applications, ACS Nano, 2013, 7, 9232–9240 CrossRef CAS.
- S. Ahmed, W. Wang, L. O. Mair, R. D. Fraleigh, S. Li, L. A. Castro, M. Hoyos, T. J. Huang and T. E. Mallouk, Steering acoustically propelled nanowire motors toward cells in a biologically compatible environment using magnetic fields, Langmuir, 2013, 29, 16113–16118 CrossRef CAS.
- A. L. Balk, L. O. Mair, P. P. Mathai, P. N. Patrone, W. Wang, S. Ahmed, T. E. Mallouk, J. A. Liddle and S. M. Stavis, Kilohertz rotation of nanorods propelled by ultrasound, traced by microvortex advection of nanoparticles, ACS Nano, 2014, 8, 8300–8309 CrossRef CAS.
- S. Ahmed, D. T. Gentekos, C. A. Fink and T. E. Mallouk, Self-assembly of nanorod motors into geometrically regular multimers and their propulsion by ultrasound, ACS Nano, 2014, 8, 11053–11060 CrossRef CAS.
- W. Wang, W. Duan, Z. Zhang, M. Sun, A. Sen and T. E. Mallouk, A tale of two forces: simultaneous chemical and acoustic propulsion of bimetallic micromotors, Chem. Commun., 2015, 51, 1020–1023 RSC.
- F. Soto, G. L. Wagner, V. Garcia-Gradilla, K. T. Gillespie, D. R. Lakshmipathy, E. Karshalev, C. Angell, Y. Chen and J. Wang, Acoustically propelled nanoshells, Nanoscale, 2016, 8, 17788–17793 RSC.
- S. Ahmed, W. Wang, L. Bai, D. T. Gentekos, M. Hoyos and T. E. Mallouk, Density and shape effects in the acoustic propulsion of bimetallic nanorod motors, ACS Nano, 2016, 10, 4763–4769 CrossRef CAS.
- L. Ren, D. Zhou, Z. Mao, P. Xu, T. J. Huang and T. E. Mallouk, Rheotaxis of bimetallic micromotors driven by chemical-acoustic hybrid power, ACS Nano, 2017, 11, 10591–10598 CrossRef CAS.
- S. Sabrina, M. Tasinkevych, S. Ahmed, A. M. Brooks, M. Olvera de la Cruz, T. E. Mallouk and K. J. M. Bishop, Shape-directed microspinners powered by ultrasound, ACS Nano, 2018, 12, 2939–2947 CrossRef CAS.
- D. Ahmed, T. Baasch, B. Jang, S. Pane, J. Dual and B. J. Nelson, Artificial swimmers propelled by acoustically activated flagella, Nano Lett., 2016, 16, 4968–4974 CrossRef CAS.
- X. Lu, H. Shen, Z. Wang, K. Zhao, H. Peng and W. Liu, Micro/Nano machines driven by ultrasound power sources, Chem.–Asian J., 2019, 14, 2406–2416 CrossRef CAS.
- S. Tang, et al., Structure-dependent optical modulation of propulsion and collective behavior of acoustic/light-driven hybrid microbowls, Adv. Funct. Mater., 2019, 29, 1809003 CrossRef.
- F. Nadal and E. Lauga, Asymmetric steady streaming as a mechanism for acoustic propulsion of rigid bodies, Phys. Fluids, 2014, 26, 082001 CrossRef.
- J. F. Collis, D. Chakraborty and J. E. Sader, Autonomous propulsion of nanorods trapped in an acoustic field, J. Fluid Mech., 2017, 825, 29–48 CrossRef CAS.
- C. Zhou, L. Zhao, M. Wei and W. Wang, Twists and turns of orbiting and spinning metallic microparticles powered by megahertz ultrasound, ACS Nano, 2017, 11, 12668–12676 CrossRef CAS.
- D. Ahmed, M. Lu, A. Nourhani, P. E. Lammert, Z. Stratton, H. S. Muddana, V. H. Crespi and T. J. Huang, Selectively manipulable acoustic-powered microswimmers, Sci. Rep., 2015, 5, 9744 CrossRef.
- L. Ren, N. Nama, J. M. McNeill, F. Soto, Z. Yan, W. Liu, W. Wang, J. Wang and T. E. Mallouk, 3D steerable, acoustically powered microswimmers for single-particle manipulation, Sci. Adv., 2019, 5, eaax3084 CrossRef CAS.
- J. Li, T. Li, T. Xu, M. Kiristi, W. Liu, Z. Wu and J. Wang, Magneto-acoustic hybrid nanomotor, Nano Lett., 2015, 15, 4814–4821 CrossRef CAS.
- L. Ren, W. Wang and T. E. Mallouk, Two forces are better than one: combining chemical and acoustic propulsion for enhanced micromotor functionality, Acc. Chem. Res., 2018, 51, 1948–1956 CrossRef CAS.
- K. J. Rao, F. Li, L. Meng, H. Zheng, F. Cai and W. Wang, A force to be reckoned with: a review of synthetic microswimmers powered by ultrasound, Small, 2015, 11, 2836–2846 CrossRef CAS.
- K. Kim, J. Guo, Z. Liang, F. Zhu and D. Fan, Man-made rotary nanomotors: a review of recent developments, Nanoscale, 2016, 8, 10471–10490 RSC.
- X.-Z. Chen, B. Jang, D. Ahmed, C. Hu, C. De Marco, M. Hoop, F. Mushtaq, B. J. Nelson and S. Pané, Small-scale machines driven by external power sources, Adv. Mater., 2018, 30, 1705061 CrossRef.
- H. Bruus, Acoustofluidics 7: The acoustic radiation force on small particles, Lab Chip, 2012, 12, 1014–1021 RSC.
- S. B. Barnett, G. R. Ter Haar, M. C. Ziskin, H. D. Rott, F. A. Duck and K. Maeda, International recommendations and guidelines for the safe use of diagnostic ultrasound in medicine, Ultrasound Med. Biol., 2000, 26, 355–366 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Fluid Mechanics, Landau and Lifshitz: Course of Theoretical Physics, Butterworth-Heinemann, Oxford, 2nd edn, 1987, vol. 6 Search PubMed.
- H. G. Weller, G. Tabor, H. Jasak and C. Fureby, A tensorial approach to computational continuum mechanics using object-oriented techniques, Comput. Phys., 1998, 12, 620–631 CrossRef.
- J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, Mechanics of Fluids and Transport Processes, Kluwer Academic Publishers, Dordrecht, 2nd edn, 1991, vol. 1 Search PubMed.
- J. Voß and R. Wittkowski, Hydrodynamic resistance matrices of colloidal particles with various shapes, preprint, arXiv:1811.01269, 2018.
- J. Voß, J. Jeggle and R. Wittkowski, HydResMat – FEM-based code for calculating the hydrodynamic resistance matrix of an arbitrarily-shaped colloidal particle, Zenodo, 2019 DOI:10.5281/zenodo.3541588.
- M. J. Holmes, N. G. Parker and M. J. W. Povey, Temperature dependence of bulk viscosity in water using acoustic spectroscopy, J. Phys.: Conf. Ser., 2011, 269, 012011 CrossRef.
- Y. Xie, N. Nama, P. Li, Z. Mao, P.-H. Huang, C. Zhao, F. Costanzo and T. Huang, Probing cell deformability via acoustically actuated bubbles, Small, 2015, 12, 902–910 CrossRef.
- E. Lauga and T. R. Powers, The hydrodynamics of swimming microorganisms, Rep. Prog. Phys., 2009, 9, 096601 CrossRef.
- Z. Shen, A. Würger and J. S. Lintuvuori, Hydrodynamic interaction of a self-propelling particle with a wall, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 39 CrossRef.
- T. Nitschke and R. Wittkowski, Collective guiding of acoustically propelled nano- and microparticles for medical applications, in preparation, 2020.
- H. Ceylan, I. C. Yasa, U. Kilic, W. Hu and M. Sitti, Translational prospects of untethered medical microrobots, Prog. Biomed. Eng., 2019, 1, 012002 CrossRef.
- D. Marenduzzo, E. Orlandini and J. M. Yeomans, Hydrodynamics and rheology of active liquid crystals: a numerical investigation, Phys. Rev. Lett., 2007, 98, 118102 CrossRef CAS.
- A. Tiribocchi, R. Wittkowski, D. Marenduzzo and M. E. Cates, Active Model H: scalar active matter in a momentum-conserving fluid, Phys. Rev. Lett., 2015, 115, 188302 CrossRef.
- H. H. Wensink and H. Löwen, Aggregation of self-propelled colloidal rods near confining walls, Phys. Rev. E, 2008, 78, 031409 CrossRef CAS.
- R. Wittkowski and H. Löwen, Dynamical density functional theory for colloidal particles with arbitrary shape, Mol. Phys., 2011, 109, 2935–2943 CrossRef CAS.
- J. Bickmann and R. Wittkowski, Predictive local field theory for interacting active Brownian spheres in two spatial dimensions, J. Phys.: Condens. Matter, 2019, 32, 214001 CrossRef.
- D. Saintillan, Rheology of active fluids, Annu. Rev. Fluid Mech., 2018, 50, 563–592 CrossRef.
- H. M. López, J. Gachelin, C. Douarche, H. Auradou and E. Clément, Turning bacteria suspensions into superfluids, Phys. Rev. Lett., 2015, 115, 028301 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |