Open Access Article
Open Access ArticleChemical affinity and dispersibility of boron nitride nanotubes†
C. S.
Torres Castillo
 ,
C.
Bruel
,
C.
Bruel
 and
J. R.
Tavares
and
J. R.
Tavares
 *
*
CREPEC, Chemical Engineering Department, Polytechnique Montréal, 2900 Edouard Montpetit Blvd, Montréal, Québec QC H3T 1J4, Canada. E-mail: jason.tavares@polymtl.ca
First published on 5th May 2020
Abstract
Boron nitride nanotubes (BNNTs) are electrically insulating nanoparticles that display highly competitive elastic modulus and thermal conductivity. Long presented as potential fillers for nanocomposite applications, their poor dispersibility in most commodity polymers has, however, limited their spread. In this work, the chemical affinity of purified BNNTs, measured in terms of Hansen solubility parameters (HSP), were obtained through sedimentation tests in a wide set of organic solvents, taking into account relative sedimentation time. The parameters obtained were {δd; δp; δh} = {16.8; 10.7; 14.7} ± {0.3; 0.9; 0.3} MPa1/2, with a Hildebrand parameter, δt = 24.7 MPa1/2 and a sphere radius of 5.4 MPa1/2. The solubility parameters were determined considering complete dispersion of the purified nanomaterial, as well as the viscosity and density of the host solvent. These factors, combined with the high purity of the BNNTs, are crucial to minimize the uncertainty of the HSP characterization. Such refined values provide necessary insights both to optimize the solvent casting of unmodified BNNTs, and to orient the surface modification efforts that would be needed to integrate these nanomaterials into a wider range of host matrices.
Introduction
Boron nitride nanotubes are counterparts to carbon nanotubes (CNTs) in which C atoms are replaced by alternating B and N atoms in a honeycomb network (Fig. 1).1–4 First synthesized in 1995,3 these nanomaterials have properties that may outmatch those of CNTs for high temperature or electrical insulation related applications. Compared with CNTs, BNNTs display a competitive Young modulus (∼1.18 TPa) and thermal conductivity (up to ∼350 W m K−1). Contrary to CNTs, they have a high thermal stability (up to 1100 °C in air)4 and are electrical insulators, with a constant band gap of ∼5.5 eV. CNTs degrade from ∼500 °C in air and are conductive or semi-conductive materials.1,3 The two nanotube types also differ in their physical appearance: pure BNNTs present a white color while CNTs are black.3The partially ionic B–N bonds in BNNTs bring about their unique properties.3,4 A difference in electronegativity between B and N atoms leads to the formation of local dipole moments, providing BNNTs with a polar behavior.3
BNNTs find potential applications as a reinforcing agents in polymeric and ceramic materials4 and, due to their high surface area, are good candidates for hydrogen storage devices.3,5 In addition, because of their unique combination of thermal conductivity and electrical insulation, BNNTs can be used for heat dissipation in electronics and computers.6–8 However, in spite of these attractive properties, their incorporation into composites has been hindered mainly by production limitations: few methods exist to produce large quantities and high-quality material (high crystallinity, small diameter and few walls).2,3 In 2013, the National Research Council of Canada patented an industrially-scalable approach for the increased production (20 g h−1) of few-walled and small diameter (∼5 nm) BNNTs.9–11 In brief, hexagonal boron nitride (h-BN), N2 and H2 are used as precursors in a thermal plasma reactor. These are dissociated into individual atoms (B, N and H) and recombine as BNNTs. Hydrogen acts as a catalyst and is crucial in reaching a high production rate for BNNTs. It enables the formation of nitrogen reactive species and impedes the formation of N2 as a side product.9 While high production rates have therefore become possible, there remains little available knowledge to reliably disperse BNNTs in solvents and polymers.
As a starting point to predict dispersion behaviour, Mutz et al.12 determined the Hildebrand solubility parameter of BNNTs, on the basis of the Hildebrand–Scatchard solution theory. Using this parameter, they proposed a list of potential good solvents for dispersing these nanotubes. However, predicting chemical affinity by considering only the Hildebrand solubility parameter (δt) is not reliable, unless the chemical in question displays a purely non-polar behavior, such as saturated aliphatic hydrocarbons.13 Otherwise, dispersive, polar, and hydrogen bonding interactions should be considered.
In another work, Tiano et al.14 determined the Hansen solubility parameters (HSP) of few-walled BNNTs (up to three walls) through sedimentation tests. They used as-synthesized material without any further purification, containing boron nanoparticles as impurities. These impurities not only have different surface chemistry than the nanotubes but also different density (∼2.3 vs. 1.4 g mL−1), which significantly modifies the sedimentation rate. In addition, some discrepancies are found in their work regarding the determination of good solvents.
Solubility parameters of purified BNNTs are necessary to orient surface modification efforts. Indeed, according to the literature, several covalent15–17 and non-covalent18–22 functionalization methods have been carried out on BNNTs in attempts to properly disperse them in a specific medium. However, in most cases, the methodology applied is not specifically tailored or targeted, relying instead on general assumptions to promote dispersion. Given that surface modification approaches can be complicated and time consuming, that they employ costly molecules such as surfactant/modifier agents and that, in the case of covalent functionalization, the intrinsic properties of BNNTs are often modified (initial sp2 structure altered), these efforts must be guided by a strong initial knowledge of the BNNTs dispersion to target the most appropriate surface treatment.
In order to have a proper characterization of the dispersibility of purified BNNTs, here, we apply the Hansen solubility theory, taking into account differences in density and viscosity of the solvents, to characterize the surface properties of BNNTs through sedimentation tests. Having defined their HSP, three scenarios may be addressed. First, surface modification may be performed depending on the chemical affinity (or lack of it) between the BNNTs and the polymeric matrix. Second, if the functionalization method is solvent-based, then, knowing the proper solvents to disperse BNNTs will allows us to select the best media in which to conduct surface modification. Third, when using solvents casting techniques, the selection of an appropriate solvent will improve nanocomposite fabrication.
Theory
Solubility parameters rely on the principle that “like seeks like”, which states that liquids with similar parameters will form homogeneous mixtures.13 Transposed to particles, this principle means that solvents will better disperse particles with similar surface chemistry. The Hansen solubility method has been successfully used to characterize solid surfaces such as pigments,23 fibers, nanoparticles14,24–31 and fillers.Solubility parameters, also known as cohesion parameters, can be related to the amount of energy necessary to evaporate a liquid.13 This is a measure of the total energy required to keep the molecules of a liquid together, expressed as the cohesive energy density (E/V) (eqn (1)):
| δt = (E/V)1/2 | (1) |
The Hildebrand solubility parameter can be divided in three components related to dispersion (δd), polar (δp) and hydrogen bonding (δh) interactions.13 These are known as Hansen solubility parameters (HSP) (eqn (2)) and provide a measure of the strength of the interactions that a chemical may form in a specific solvent.13
| δt2 = δd2 + δp2 + δh2 | (2) |
Dispersion forces (δd), produced by atomic interactions, accounts for non-polar London interactions.13 Polar forces (δp) are present when permanent dipole-permanent dipole interactions are formed. These interactions occur at the molecular level and the dipole moment is used to determine this type of attractions.13 Like in polar forces, hydrogen bonding interactions (δh) take place at a molecular level. δh has been generally used to describe the capability of electron exchange determined by Lewis' acid and base theory.23δh has been divided into sub-parameters such as acid–base, dispersion, induction, orientation, as well as proton-donors and proton-acceptors. However, the use of a single parameter to describe hydrogen bonding interactions has been proven to give satisfactory results.13
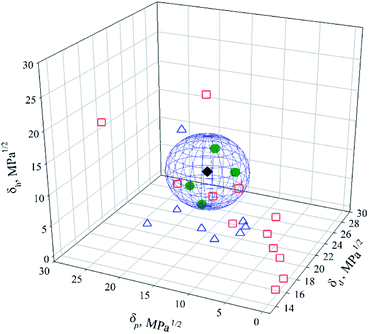
Based on Hansen solubility theory, it is possible to plot the particle of interest and solvents in a three-dimensional (3D) space (Hansen space) with their corresponding HSP {δd; δp; δh} as coordinates. The center of the solubility sphere is determined by the particle coordinates with an experimental radius, Ro. The solvents with coordinates located inside the sphere will disperse the particle, with higher dispersibility for the solvents that are closer to the center of the sphere.13 The distance between the solvent and the particle, Ra, in the Hansen space can be determined applying eqn (3):
| Ra2 = 4(δd1 − δd2)2 + (δp1 − δp2)2 + (δh1 − δh2)2 | (3) |
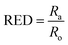 | (4) |
The ratio between Ra and Ro (eqn (4)), known as the relative energy difference (RED), estimates the position of the solvent in the solubility sphere.13 RED < 1 indicates that the solvent will disperse the particle. For RED = 1, partial dispersion is expected and for RED > 1, the particle will not disperse in the solvent. HSP can also be used for binary mixtures of solvents (co-solvents).
When determining the HSP of nanoparticles, several factors should be considered, owing to different interactions that may occur. For instance, Bergin et al.24 demonstrated that increasing the diameter of the nanotubes decreases δt by reducing the surface to volume ratio: this structural link between δt and morphology is also expected for BNNTs (eqn (5)).
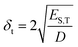 | (5) |
Empirically, HSP may be determined by depositing small quantities of particles in test tubes containing a fixed volume of liquid and subsequently agitating.13 Stability is assessed based on the presence of agglomerates in suspension, assessed visually or through spectroscopic means. If the particle size of the solid is large (>5 μm), surface effects are less significant compared to particles with smaller sizes (<0.01 μm). Nonetheless, viscosity and buoyancy effects can impede proper analysis of a solid suspension. To compensate for differences in density and viscosity, a relative sedimentation time (RST) can be used instead of absolute sedimentation time, tsed, (eqn (6)).13
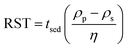 | (6) |
Experimental part
Materials and methods
Purified BNNTs were provided by Tekna Plasma Systems, Inc. (Sherbrooke, Qc, Canada) in the form of buckypapers (2 cm × 2 cm). They were obtained from the previously described induction thermal plasma process.9,33 The as-obtained BNNTs possessed a beige color, attributed to the presence of amorphous boron.9,34 These impurities were removed through the purification method described by Cho et al.34 Briefly, the as-obtained BNNTs were dried for 3 h at 150 °C. They were then pre-heated in a quartz tube at 105 °C in an Ar atmosphere, keeping the temperature constant for 20 min. The quartz tube was then filled with Cl2. The temperature was raised to 750 °C, under a flow of 1 standard liter per min of Cl2. The exposure time was set at 1 min per gram of as-obtained BNNTs. These selective chlorine etching conditions were used to remove boron allotropes, including BxNyHz derivatives.34 The system was then purged with N2 and allowed to cool under a steady flow of N2. The purified material was subsequently bath sonicated in methanol. Despite the purification process, SEM images suggest that some BN hollow cages are, however, still present in the material.9,34 These structures are also visible on our TEM images (Fig. 2C and D).Organic solvents were obtained by chemical suppliers and were used without any further purification. Most of them were of high purity (≥99%) with exception of D-limonene (96%) and ethanol (95%). The list of solvents employed, as well as their physical properties (density, viscosity and molar volume) and HSP, are available in Tables 1 and S1.† Solvent selection considered the list of solvents proposed by Hansen for sedimentation tests, for which solubility parameters have been validated experimentally,13 and expanded with a few additional solvents: ethyl benzoate, D-limonene and heptane, whose HSP values were determined through modelling.
| Solvent | δ d (MPa1/2) | δ p (MPa1/2) | δ h (MPa1/2) | Sedimentation time (h) | R a | RED |
|---|---|---|---|---|---|---|
| a Reaching a good dispersion state required a stronger sonication. b Additional test solvent but not considered for the HSP analysis. | ||||||
| Good dispersion state | ||||||
| N,N′-Dimethylacetamide | 16.8 | 11.5 | 10.2 | 48.0 | 5.36 | 1.00 |
| N,N′-Dimethylformamide | 17.4 | 13.7 | 11.3 | 42.6 | 4.69 | 0.88 |
| Ethanol | 15.8 | 8.8 | 19.4 | 51.3 | 5.45 | 1.00 |
| 2-Propanol | 15.8 | 6.1 | 16.4 | 78.5 | 5.30 | 0.97 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Intermediate dispersion state | ||||||
| Acetone | 15.5 | 10.4 | 7.0 | 14.1 | 8.13 | 1.51 |
| Acetonitrile | 15.3 | 18.0 | 6.1 | 14.0 | 11.7 | 2.16 |
| Ethyl acetate | 15.8 | 5.3 | 7.2 | 20.6 | 9.46 | 1.75 |
| Ethyl benzoate | 17.9 | 6.2 | 6.0 | 114 | 10.0 | 1.87 |
| Methanol | 15.1 | 12.3 | 22.3 | 23.8 | 8.83 | 1.62 |
| Methyl ethyl ketone | 16.0 | 9.0 | 5.1 | 15.8 | 9.88 | 1.83 |
| Propylene carbonate | 20.0 | 18.0 | 4.1 | 267 | 14.4 | 2.67 |
| Tetrahydrofuran | 16.8 | 5.7 | 8.0 | 25.8 | 8.36 | 1.55 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Poor dispersion state | ||||||
| Acetic acid | 14.5 | 8.0 | 13.5 | 65.8 | 5.47 | 1.00 |
| tert-Butanol | 15.2 | 5.1 | 14.7 | 139 | 6.45 | 1.19 |
| Chloroform | 17.8 | 3.1 | 5.7 | 529 | 12.0 | 2.22 |
| Cyclohexane | 16.8 | 0 | 0.2 | 39.7 | 18.0 | 3.34 |
| Dichloromethane | 17.0 | 7.3 | 7.1 | 72.3 | 8.34 | 1.55 |
| Dimethyl sulfoxide | 18.4 | 16.4 | 10.2 | 142 | 7.94 | 1.48 |
| 1,4-Dioxane | 17.5 | 1.8 | 9.0 | 81.4 | 10.7 | 1.98 |
| Ethylene glycola | 17.0 | 11.0 | 26.0 | 1573 | 11.3 | 2.09 |
| Formamide | 17.2 | 26.2 | 19.0 | 255 | 16.1 | 2.98 |
| Heptane | 15.3 | 0 | 0 | 13.7 | 18.4 | 3.42 |
| D-Limonene | 17.2 | 1.8 | 4.3 | 38.9 | 13.7 | 2.54 |
| Toluene | 18.0 | 1.4 | 2.0 | 26.8 | 15.9 | 2.96 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Additional solvents | ||||||
| Benzyl alcohola,b | 18.4 | 6.3 | 13.7 | 342 | 5.53 | 1.02 |
| Waterb | 15.1 | 20.4 | 16.5 | 50.6 | 10.4 | 1.93 |
Microscopy
TEM analysis was performed in BNNT dispersions using ethanol as a solvent. In brief, 1 mg of BNNTs was added to 10 mL of anhydrous ethanol and the resulting mixture was sonicated with a probe sonicator supplying 500 J of energy. A drop of the solution was deposited on a copper TEM grid and dried overnight. The analyses were performed using a Jeol JEM 2100F transmission electron microscope in bright field imaging mode, operating at 200 kV.Sedimentation tests
10 mL of solvent were added to 1 mg of BNNTs in a glass vial of diameter 2.5 cm. This concentration was chosen as an intermediate value to form stable BNNTs dispersions in different solvents, according to previous works.12,14To disperse the nanoparticles, a Cole–Parmer probe sonicator was employed with an operation frequency of 20 kHz using a cylindrical probe (type 410–08). The treatment consisted of pulsations operating with 5 s ON/2 s OFF cycles set at 30% of amplitude and a power in the range of 20–30 W. A total energy of 500 J mgBNNTs−1 was used, which is high compared to typical standards for nanomaterial dispersion (e.g. 10 J mg−1 required to disperse cellulose nanocrystals in water),35 attributable to the BNNTs high aspect ratio. To prevent any overheating, the vials were kept in an ice bath during sonication. The resulting suspensions were kept in a quiescent state at room temperature to allow the nanoparticles to sediment. The density of BNNTs was obtained from the literature12,36 and an average of 1.5 g cm−3 was used. A relative sedimentation time (RST) of 1.03 × 1011 s2 m−2 was considered, corresponding to an absolute sedimentation time (tsed) of 48 h in N,N′-dimethylacetamide (DMAc). This solvent was chosen as a reference because it remained in a good dispersion state even after two days. The calculated absolute sedimentation time for each solvent is shown in Table 1.
Results and discussion
Ultrasonication and dispersion
According to TEM images (Fig. 2), the BNNTs used in the dispersions are doubled-walled (Fig. 2A and B) with a diameter of ∼5 nm and a length of a few micrometers (Fig. 2C and D). These dimensions agree with the results reported by Kim et al.9 where nanotubes with 2, 4 or 5 walls were obtained. The most common damages induced by ultrasonication treatments to BNNTs are peeling, shortening, and formation of Y-junctions or nanoribbons. All these phenomena are detectable through TEM,37–40 namely for dispersion in ethanol, the solvent that was used in the preparation of the TEM grids, which has been reported to induce peeling under some circumstances.37 However, based on our own images and on a comparison with those prior to sonication,9 we have no reasons to believe that our ultrasonication conditions may cause significant damages to the BNNTs. The effect of a more severe ultrasonication, as performed in benzyl alcohol and ethylene glycol, was not investigated and we cannot rule out that some morphological damages occurred under these harsher conditions. That being said, the main driver for morphological changes, cavitation, is notoriously less efficient in viscous media.41Pictures of the dispersions were taken immediately after sonication (Fig. S1†) and after their respective sedimentation time (Fig. S4†). According to Fig. S1,† nine solvents were able to form good BNNT dispersions. These solvents were: ethanol (EtOH), propylene carbonate, 2-propanol (IPA), dimethyl acetamide (DMAc), dimethyl formamide (DMF), ethyl benzoate, dimethyl sulfoxide (DMSO), formamide and tetrahydrofuran (THF). All are Lewis bases, and are hence susceptible to interact with B atoms in the BN structure by sharing a pair of electrons. Over time, however, BNNTs progressively lost part or all their stability in propylene carbonate, ethyl benzoate, DMSO, formamide, and THF. This suggests that other phenomena may be at play besides Lewis acid–base interactions. Results presented in Table 1 report the dispersion observed at the end of the sedimentation time. At this point, only four solvents remain good: DMAc, DMF, EtOH, and IPA.
Dispersions in methanol (MeOH), methyl ethyl ketone (MEK), acetonitrile, acetone and ethyl acetate showed some dispersed particles at the top of the vial, while some sedimented at the bottom. On the other hand, when using ethylene glycol (EG), agglomerates of BNNTs were observed. The formation of these agglomerates most probably happened because the energy provided during sonication was not sufficient in such a highly viscous solvent (20.9 mPa s). In order to properly disperse the nanotubes, the dispersion was repeated, applying higher energy during sonication. An energy of 1800 J mgBNNTs−1 was used. This new system is shown in Fig. S2† and, given its good dispersion behaviour after applying higher energy, EG has been added to the list of good media (thus bringing the total to 10 solvents).
In toluene, cyclohexane and heptane, BNNTs lost their stability and stuck to the glass right after sonication (Fig. S1†). These solvents are the three least polar and, in this case, our results align with those of Tiano et al.14 for hexane. The instability of BNNTs can be attributed to a large difference in polarity between the nanotubes and the solvent. Due to a difference in electronegativity between B and N atoms, BN structures possess a dipolar moment.
This finding concurs with previous works on hexagonal boron nitride (h-BN) films, showing these are hydrophilic, with water contact angles of 50–55°.42,43 However, there is controversy concerning the hydrophilicity of BNNTs films. Some studies have determined that BNNTs films are superhydrophobic, with contact angles in the range of 145–167°.43–45 However, morphological characteristics in the films such as the packing density, length and alignment of the nanotubes43 as well as the roughness and surface chemical heterogeneities46 have an impact on the wettability of BNNTs films. In addition, theoretical studies have demonstrated that the spreading of a liquid over a highly curved surface is different from that on a flat surface,42 with high surface curvature being associated with more hydrophobic behavior.43
Time-dependent dispersion state
In order to evaluate the evolution of the dispersions, three solvents were studied over a period of 150 h: propylene carbonate, ethyl benzoate and DMSO. These were chosen because, while their dispersion state was good immediately after sonication (Fig. S1†), it worsened over time (Fig. S3†). This emphasizes the need to determine a normalized sedimentation time in order to make objective evaluations of the dispersions.The interval of time after which observation is performed varies due to differences in viscosity and density for each solvent. In order to compensate for these variations, a corrected relative sedimentation time (RST) (eqn (6)) is employed.13 The calculated absolute sedimentation times, tsed, for ethyl benzoate, DMSO and propylene carbonate were 114, 142 and 267 h, respectively. At 114 h, the dispersion state in ethyl benzoate showed a cloudy region at the top of the vial (around 20% of the volume) and the rest (80% of the volume) are swollen particles (Fig. S3B, S4A and B†). For DMSO, at 142 h after sonication, phase separation can be observed. In the case of propylene carbonate, the dispersion state observed at 267 h (Fig. S4A and B†) is similar to that observed at 150 h (Fig. S3A†). Given these observations at tsed, these 3 solvents can no longer be considered “good” as they were for t = 0 observations in the previous section. It is worth noting that the cloudy agglomerates formed by BNNTs over time may be easily be redispersed by simply hand mixing the vials.
Dispersion end state
The quality of the dispersions was evaluated after their respective sedimentation time, tsed (Table 1). The dispersions were classified as good, intermediate or poor (Fig. 3). Good solvents were able to form dispersions that were cloudy, but uniformly throughout the whole vial (Fig. 3A). Intermediate solvents presented dispersed material at the top of the vial while having sedimented BNNTs at the bottom (Fig. 3B). Poor solvents led to the formation of phase separation, with transparent regions at the top of the vial (Fig. 3C).24 organic solvents were used for these sedimentation tests (Table 1). Dispersion in water was also conducted, but this solvent was not considered for the analysis because it has a strong tendency to structure itself in clusters, which may alter its HSP.13 Four solvents were able to form cloudy and uniform dispersions of BNNTs (Fig. S4†): DMAc, DMF, ethanol and 2-propanol. These solvents contain amide or hydroxyl groups on their structure, which may lead to hydrogen bonding interactions with the nanotubes. In fact, these four are Lewis bases, characterized by the ability to donate a pair of electrons. On the other hand, B atoms on BN nanostructures present an electron deficiency, and thus, make them vulnerable to interactions with Lewis bases such as amines.21,47 These interactions have in fact been specifically exploited by researchers aiming to non-covalently surface modify BNNTs. Xie et al.20 used diamine-terminated polyethylene glycol (PEG) to functionalize the surface of BNNTs in order to disperse them in water. Similarly, Pal et al.21 used trioctylamine and tributylamine to modify the BNNTs, while Maguer et al.48 employed quinuclidine for modification, and Iannitto et al.49 exploited similar chemistry in an ammonia plasma system.
As can be seen in Table 1, the calculated RED (eqn (4)) for these four good solvents was in the range of 0.88–1.0, which indicates that the solvents will be located inside or in the borders of the sphere. N,N′-Dimethylformamide and 2-propanol were found inside the sphere while N,N′-dimethylacetamide and ethanol were in the border.
Intermediate solvents were acetone, methanol, THF, ethyl acetate, acetonitrile, ethyl benzoate, MEK and propylene carbonate, with calculated RED values (eqn (4)) in the range of 1.51–2.67. These solvents possess δd and δp similar to the solvents classified as “good”, but a significantly lower δh (Table 1). Low values of this parameter would prevent hydrogen bonding interactions required to obtain total dispersion of BNNTs. The exception to this was methanol, with an extremely high δh. For acid–base Lewis interactions to happen, a certain compatibility between the donor and acceptor is necessary. When the donor is much stronger than the acceptor, the former may prefer to interact with itself. In the case of methanol (the donor), it is likely that its molecules might have been able to self-associate, hiding most of their OH groups within itself and leaving the CH3 groups exposed at the surface of the clusters.32 The HSP of “clustered” methanol have been reported as {δd; δp; δh}Cluster = {14.7; 5; 10} MPa1/2,32 where δd and δh are significantly lower compared to the standard HSP of methanol {δd; δp; δh}MeOH = {15.1; 12.3; 22.3} MPa1/2. Therefore, these CH3 groups should not been able to interact with the BNNTs.
It is worth noting that different types of interparticle forces are expected during the assembly of nanoparticles. These include van der Waals forces, magnetic and electrostatic forces, repulsive steric, confining or jamming forces, solvation, structural and depletion forces, capillary forces, convective forces and friction and lubrication forces.50 Their study would require a more detailed analysis, beyond the scope of the present work.
Dispersions with phase separation (i.e. “poor”) at tsed were observed in chloroform, acetic acid, DMSO, toluene, cyclohexane, heptane, D-limonene, formamide, 1,4-dioxane, ethylene glycol, tert-butanol and dichloromethane (DCM). The highest RED values (RED > 3) were obtained when non-polar solvents were used, reaching values of 3.34 and 3.42 for cyclohexane and heptane, respectively.
HSP analysis
Having probed the dispersibility of BNNTs in a large set of solvents, it becomes possible to determine their HSP using the HSPiP software. Solvents are classified as good (score = 1) or bad (score = 0) and their respective score (“0” or “1”) is inputted into the HSPiP software. Calculations are performed based on the maximisation of a desirability function, FIT, that relies on the HSP distance, Ra.32 FIT reaches a maximum of 1.0 when a sphere of center {δd; δp; δh} and of radius R0 may be fitted to simultaneously include all the good solvents while excluding all the bad ones. When this is impossible, FIT is decreased by a factor that considers the various HSP distances. In circumstances where several combinations yield the same FIT, the software calculates an uncertainty on the true position of the sphere's center. Details and equations are provided in ESI and in Table S2.†Since we witnessed three categories of behavior for the dispersions (good, intermediate, and poor), various combinations may be considered for the fitting. In the following paragraph, we will first attribute the grade 1 to good solvents only (DMF, DMAc, ethanol and 2-propanol), and grade 0 for intermediate and poor ones. Then, the grade 1 to good and intermediate solvents alike and grade 0 for poor solvents only. Two sets of HSP coordinates will thus be determined, corresponding to a main and to an extended chemical affinity, respectively.
Attributing the grade 1 to good solvents (green circles) only, the Hansen space for the BNNTs has them distributed inside the sphere, while the intermediate (blue triangles – grade 0) and poor solvents (red squares – grade 0) are located outside (Fig. 4). 2D plots (Fig. 5) help to visualize the data presented in Fig. 4. These provide upper and lower bounds for the various HSP. From Fig. 5A and B it can be concluded that the dispersive component (δd) of the BNNTs is in the range of 15.8–17.4 MPa1/2. From Fig. 5A and C, the polar component (δp) should be in the interval of 6.1–13.7 MPa1/2.
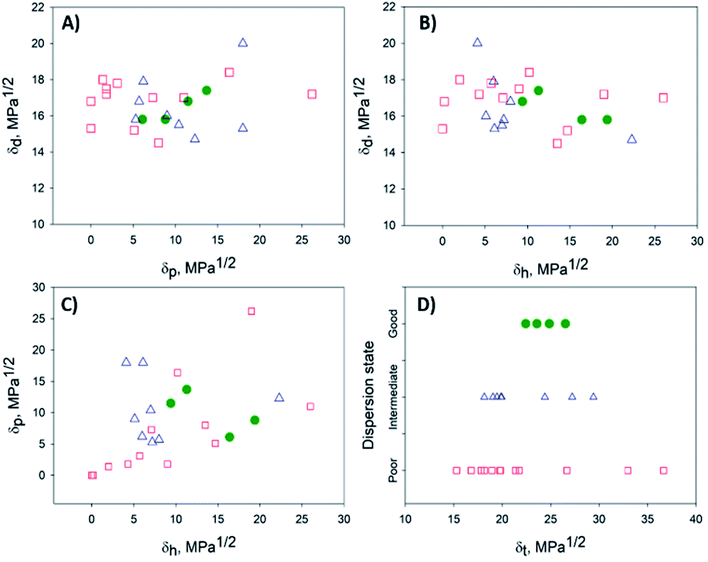 | ||
| Fig. 5 2D projections to help with the visualization of the data presented in Fig. 4. (A) δdvs. δp, (B) δdvs. δh, (C) δpvs. δh and (D) dispersion state vs. δt. Good, intermediate and bad solvents are represented by green, blue and red circles, respectively. | ||
The hydrogen-bonding component (δh) can be determined from Fig. 5B and C, in the range of 10.2–19.4 MPa1/2. The dispersion state versus the Hildebrand parameter (δt) is plotted in Fig. 5D. Good solvents for the dispersion of BNNTs will be those with a δt in the range of 22.4–26.5 MPa1/2, that also respect conditions for Ra (eqn (3)) and RED (eqn (4)) such that RED < 1. However, as mentioned before, the selection of potential solvents should be done based on the HSP distance (eqn (3)) considering the three HSP: dispersive, polar and hydrogen bonding interactions, not just the Hildebrand parameter.
The first set of calculated HSP for BNNTs is: {δd; δp; δh}main = {16.8; 10.7; 14.7} ± {0.3; 0.9; 0.3} MPa1/2. The radius of the sphere is R0 = 5.4 MPa1/2 and the δt = 24.7 MPa1/2. A FIT = 1.0 was obtained, meaning that all the grade 1-solvents were located inside the sphere and all the grade 0-solvents outside. The HSP of BNNTs obtained in this work differ from those obtained by Tiano et al.14 In their work, the center of the sphere was determined by {δd; δp; δh}Tiano = {16.8; 10.7; 9.0} MPa1/2 with a δt = 21.8 MPa1/2 and R0 = 4.3 MPa1/2. They used as-synthesized material containing boron nanoparticles as impurities, affecting not only the surface chemistry of the nanotubes but also their density. They determined 4 good solvents: DMAc, DMF, acetone and N-methyl-2-pyrrolidone (NMP). However, based on their vial pictures, the dispersion in acetone should not be qualified as “good”, as a large fraction of nanotubes are sedimented after settling for 1 week. This behaviour is corroborated in our experiments, where just after sonication some nanotubes sedimented while other fractions were suspended (Fig. S1†). In addition, when comparing the HSP of acetone {δd; δp; δh}ACE = {15.5; 10.4; 7} MPa1/2 with the intervals proposed in the present work to estimate good solvents for BNNTs, only the δd value is within its corresponding interval and a RED = 1.51 (eqn (4)) was obtained. This indicates that acetone is not a good solvent to disperse the BNNTs. Regarding NMP, with {δd; δp; δh}NMP = {18; 12.3; 7.2} MPa1/2, similar to acetone, only δp is within the interval proposed, while δd and δh are outside the range provided. The calculated RED = 1.49 (eqn (4)) indicates that NMP is situated outside the sphere, and thus considered as a poor solvent. In both cases, a low value of δh prevents some hydrogen bonding interactions from happening, impeding complete dispersion of BNNTs.
An explanation for the deviations between Tiano's results14 and those presented in this work could be the concentration (0.25 mg mL−1, compared with 0.1 mg mL−1 in this work). This could have caused some dispersions to oversaturate and thus, favored a sedimentation of the BNNTs. Another factor arises from the sedimentation time: their analysis considered an absolute sedimentation time of 1 week for all the dispersions. As discussed earlier, the use of a normalized sedimentation time, tsed, is preferred. Variations in chemical composition, as well as in length and diameter of the nanotubes could also affect the HSP determination.14,24 Tiano et al.14 concluded that their HSP correlate well with the BNNTs used. However, they stated that dispersions should be repeated if different methods of synthesis and/or purification processes are used, this being the main limitation of their work.
In the present study, we minimized the uncertainty in the HSP values by using purified material and compensating for differences in density and viscosity of the solvents. Nonetheless, the uncertainty of ±{0.3; 0.9; 0.3} MPa1/2 with which the HSP of BNNTs were determined means that the border of the sphere is a soft one. With an HSP radius of R0 = 5.4 MPa1/2, it translates in an uncertainty of roughly ±0.2 on RED values: any predictions made on solvents whose RED is comprised between 0.8 and 1.2 must be considered with caution. This may be highlighted by investigating the behaviour of BNNTs in a solvent like benzyl alcohol. With HSP of {δd; δp; δh}BA = {18.4; 6.3; 13.7} MPa1/2, benzyl alcohol has a RED value (eqn (4)) of ∼1.02, meaning that it is located right at the outer edge of the border of the BNNTs' Hansen sphere. With a RED strictly above 1, it should thus be a poor solvent. However, it is right in the middle of the uncertain area for RED values. Experimentally, it was found to be a good solvent (Fig. S4†). This proves the soft nature of the border between good and poor solvents when RED values are close to 1. Calculating the RED according to Tiano's results yields a value of 1.33, which suggests that their range of uncertainty regarding RED values was probably even larger than ours. It is worth noting that, because of its high viscosity (5.47 mPa s), a higher energy (1600 J mgBNNTs−1) was applied during sonication to properly disperse the BNNTs in benzyl alcohol. Our analysis is performed based on the assumption that the BNNTs were not damaged by this more intense ultrasonication step.
To make a graphical comparison between the Hansen space obtained by Tiano et al.14 and the one obtained in this work, a 3D graph containing both spheres was plotted (Fig. 6). The blue sphere corresponds to the results obtained in this work, {δd; δp; δh}main = {16.8; 10.7; 14.7} MPa1/2, while the black one to Tiano's, {δd; δp; δh}Tiano = {16.8; 10.7; 9.0} MPa1/2. Even though δd and δp are the same in both cases, the differences in δh and R0 cause the spheres to locate in different regions. A partial overlap is observed in the space limited by δd = 15.8–17.8 MPa1/2, δp = 7.3–13.7 MPa1/2 and δh = 9.4–14.7 MPa1/2. These HSP values are within the intervals proposed in this work for the prediction of good solvents for BNNTs. The center of the intersection region was found at {δd; δp; δh}intersection = {16.8; 10.6; 11.5} MPa1/2. Only two solvents were found in that space: DMF, located within the overlapped region, and DMAc, located in the border. On the other hand, 2-propanol was found inside the blue sphere, centered at {δd; δp; δh}main, while ethanol and benzyl alcohol were on the border. DCM and acetone were located inside the black sphere, with center at {δd; δp; δh}Tiano. Three of the four expected solvents (DMF, DMAc and acetone) were located inside this sphere. The fourth one, NMP, with coordinates {δd; δp; δh}NMP = {18; 12.3; 7.2} MPa1/2, was not used as a test solvent in the present work. Instead, DCM, with {δd; δp; δh}DCM = {17; 7.3; 7.1} MPa1/2, was found to be inside the black sphere. Although δd and δh possess similar values, a difference of 5 MPa1/2 is observed in the polar component, δp. According to Tiano's results, the dispersion in DCM was not good and a phase separation was observed 30 min after sonication, with swollen particles at the bottom of the vial. These results are in agreement with the ones obtained in the present work.
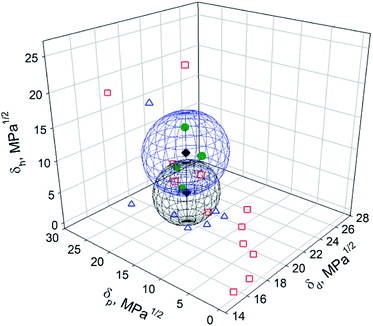 | ||
| Fig. 6 Hansen space of BNNTs obtained in this work (blue sphere) and the results obtained by Tiano et al.14 (black sphere). The green circles, blue triangles and red squares correspond to good, intermediate and poor solvents determined in this work. | ||
To visualize the influence of partial dispersibility in the Hansen space, a second analysis was performed, expanding the list of good solvents with the intermediate ones (Table 1). These solvents were acetone, methanol, THF, ethyl acetate, acetonitrile, ethyl benzoate, MEK and propylene carbonate. They were scored as “1” and added to the list of good solvents previously defined (DMAc, DMF, EtOH and IPA). The “poor” solvents were kept scored “0”. The resulting Hansen sphere (gray sphere) is shown in Fig. 7. The Hansen space determined previously, considering total dispersibility of BNNTs (blue sphere) and the one obtained by Tiano et al.14 (black sphere) are also plotted. As can be seen in Fig. 7, the blue and black spheres are located inside the gray one. This trend was expected because good solvents should remain suitable when good and intermediate solvents are considered.13 However, the addition of more solvents to the list of “good” ones will modify the coordinates and radius of the Hansen sphere. In this case, the solvents added to the list of good ones possess a wide range of HSP, covering different spaces in the Hansen space but leaving some uncovered regions.
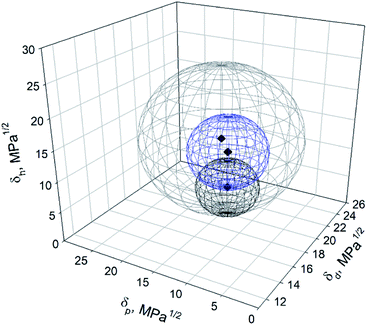 | ||
| Fig. 7 Hansen space of BNNTs obtained in this work considering total dispersibility (blue sphere), partial dispersibility (gray sphere) and Tiano's results (black sphere). | ||
The Hansen solubility parameters of the gray sphere were {18.8; 13.9; 14.4}extended ± {0.2; 0.4; 0.3} MPa1/2, with a radius R0 = 11.4 MPa1/2. A FIT = 0.434 was obtained, meaning that some good solvents were located outside the sphere while some poor ones are inside (see ESI†). DCM, acetic acid, DMSO and tert-butanol, considered as bad solvents (Table 1), were located inside this gray Hansen sphere while methanol, MEK, acetonitrile, ethyl benzoate and ethyl acetate (good solvents) are located outside. This relocation of the solvents by the HSPiP software could have happened due to the large differences in their HSP, making difficult to get a good FIT. Low values in the desirability function FIT will provide less reliable values of the HSP of the particle in question.
As mentioned earlier, Mutz et al.12 determined the total solubility parameter, δt = 18.53 MPa1/2, using static light scattering and the Flory and Hildebrand–Scatchard solution theories. The BNNTs used had a diameter in the range of 30–100 nm, in comparison with the 5 nm diameter nanotubes used in our work. Based on the expression developed by Bergin et al.24 for CNTs (eqn (5)), larger nanotubes have lower δt values. We suggest it may be the reason why our δt is higher than the one reported by Mutz et al.12 Based on that, Mutz et al. proposed a list of potential good solvents: ethyl acetate, isophorone, diamyl phthalate, vinyltoluene and cis-1,2-dichloroethyelene. However, as mentioned before, the prediction of solvents considering only the Hildebrand solubility parameter (δt) is not reliable for particles presenting polar and hydrogen interactions.13 In addition, it is pertinent to note that one of the good solvents predicted was ethyl acetate, which is indeed able to partially disperse the BNNTs, as demonstrated in this work (intermediate score).
Conclusions
In this work, the Hansen solubility parameters of purified BNNTs were determined for the first time through sedimentation tests accounting for relative sedimentation time. The HSP obtained were {δd; δp; δh} = {16.8; 10.7; 14.7} ± {0.3; 0.9; 0.3} MPa1/2. The radius of the sphere was R0 = 5.4 MPa1/2 and the Hildebrand parameter δt = 24.7 MPa1/2. Evaluation of the dispersion state in different organic solvents was done after an appropriate relative sedimentation time, taking into account differences in density and viscosity of the solvents. However, the method of synthesis used, the presence of impurities and the diameter of the nanotubes play an important role when determining their HSP. Four solvents were able to form uniform dispersions of BNNTs. These were DMF, DMAc, ethanol and 2-propanol. It is thought that the hydrogen bonding interactions between the solvents and the nanotubes are crucial for good dispersion. Having defined the HSP of BNNTs more precisely, this data can now be used to guide dispersion into host matrices, as well as methodologies for surface treatment.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the Natural Sciences and Engineering Research Council of Canada (NSERC), Prima Québec, the Mexican National Council for Science and Technology (CONACyT), Tekna Plasma Systems, Michelin Canada and Polytechnique Montréal. The Fonds de Recherche du Québec - Nature et Technologies (FRQNT) provided C. Bruel with a scholarship (number 208324). Mr Paul-Henri Verger and Ms Alekhya V. Veerubhotla are also thanked for their valuable contributions to the early versions of this work.Notes and references
- C. Zhi, Y. Bando, C. C. Tang, Q. Huang and D. Golberg, J. Mater. Chem., 2008, 18, 3900 RSC.
- M. Terrones, J. M. Romo-Herrera, E. Cruz-Silva, F. López-Urías, E. Muñoz-Sandoval, J. J. Velázquez-Salazar, H. Terrones, Y. Bando and D. Golberg, Mater. Today, 2007, 10, 30 CrossRef CAS.
- C. Zhi, Y. Bando, C. Tang and D. Golberg, Mater. Sci. Eng., R, 2010, 70, 92 CrossRef.
- J. Wang, C. H. Lee and Y. K. Yap, Nanoscale, 2010, 2, 2028 RSC.
- T. Terao, Y. Bando, M. Mitome, K. Kurashim, C. Y. Zhi, C. C. Tang and D. Golberg, Phys. E, 2007, 40, 2551 CrossRef.
- J. Su, Y. Xiao and M. Ren, Phys. Status Solidi A, 2013, 12, 2699 CrossRef.
- C. Zhi, Y. Bando, T. Terao, C. Tang, H. Kuwahara and D. Golberg, Adv. Funct. Mater., 2009, 19, 1857 CrossRef CAS.
- X. Huang, C. Zhi, P. Jiang, D. Golberg, Y. Bando and T. Tanaka, Adv. Funct. Mater., 2013, 23, 1824 CrossRef CAS.
- K. Kim, C. T. Kingston, A. Hrdina, M. B. Jakubinek, J. Guan, M. Plunkett and B. Simard, ACS Nano, 2014, 8, 6211 CrossRef CAS PubMed.
- K. Kim, M. B. Jakubinek, Y. Martinez-Rubi, B. Ashrafi, J. Guan, K. O'Neill, M. Plunkett, A. Hrdina, S. Lin, S. Denommee, C. Kingston and B. Simard, RSC Adv., 2015, 5, 41186 RSC.
- K. S. Kim, C. Kingston and B. Simard, Patent app. no. US61/813324, 2013.
- M. Mutz, E. Eastwood and M. Dadmun, J. Phys. Chem. C, 2013, 117, 13230 CrossRef CAS.
- C. M. Hansen, Hansen solubility parameters: A user's handbook, Taylor & Francis, 2nd edn, 2007 Search PubMed.
- A. L. Tiano, L. Gibbons, M. Tsui, S. I. Applin, R. Silva, C. Park and C. C. Fay, Nanoscale, 2016, 8, 4348 RSC.
- C. Zhi, Y. Bando, C. Tang, S. Honda, K. Sato, H. Kuwahara and D. Golberg, Angew. Chem., 2005, 44, 7932 CrossRef CAS PubMed.
- C. Zhi, Y. Bando, T. Terao, C. C. Tang, H. Kuwahara and D. Golberg, Chem.–Asian J., 2009, 4, 1536 CrossRef CAS PubMed.
- S. Zhou, C. Y. Ma, Y. Y. Meng, H. F. Su, Z. Zhu, S. L. Deng and S. Y. Xie, Nanotechnology, 2012, 23, 055708 CrossRef PubMed.
- J. Yu, Y. Chen and B. M. Cheng, Solid State Commun., 2009, 149, 763 CrossRef CAS.
- C. Lee, D. Zhang and Y. K. Yap, J. Phys. Chem. C, 2011, 116, 1798 CrossRef.
- S. Xie, W. Wang, K. A. Shiral Fernando, X. Wang, Y. Lin and Y. P. Sun, Chem. Commun., 2005, 3670 RSC.
- S. Pal, S. R. C. Vivekchand, A. Govindaraj and N. R. Rao, J. Mater. Chem., 2007, 17, 450 RSC.
- Z. Gao, C. Zhi, Y. Bando, D. Golberg and T. Serizawa, Appl. Mater. Interfaces, 2011, 3, 627 CrossRef CAS PubMed.
- S. Süβ, T. Sobisch, W. Peukert, D. Lerche and D. Segets, Adv. Powder Technol., 2018, 29, 1550 CrossRef.
- S. D. Bergin, Z. Sun, D. Rickard, P. V. Streich, J. P. Hamilton and J. N. Coleman, ACS Nano, 2009, 3, 2340 CrossRef CAS PubMed.
- H. T. Ham, Y. S. Choi and I. J. Chung, J. Colloid Interface Sci., 2005, 286, 216 CrossRef CAS PubMed.
- S. Detriche, G. Zorzini, J. F. Colomer, A. Fonseca and J. B. Nagy, J. Nanosci. Nanotechnol., 2008, 8, 6082 CrossRef CAS PubMed.
- S. Detriche, J. B. Nagy, Z. Mekhalif and J. Delhalle, J. Nanosci. Nanotechnol., 2009, 9, 6015 CrossRef CAS PubMed.
- Y. Hernandez, M. Lotya, D. Rickard, S. D. Bergin and J. N. Coleman, Langmuir, 2010, 26, 3208 CrossRef CAS PubMed.
- S. Gårdebjer, M. Andersson, J. Engström, P. Restorp, M. Persson and A. Larsson, Polym. Chem., 2016, 7, 1756 RSC.
- C. Bruel, J. Tavares, P. Carreau and M. Heuzey, Carbohydr. Polym., 2019, 205, 184 CrossRef CAS PubMed.
- C. Bruel, T. S. Davies, P. J. Carreau, J. R. Tavares and M.-C. Heuzey, J. Colloid Interface Sci., 2020, 574, 399 CrossRef CAS PubMed.
- S. Abbott, C. M. Hansen and H. Yamamoto, Hansen solubility parameters in practice, 2008 Search PubMed.
- K. Kim, M. Couillard, H. Shin, M. Plunkett, D. Ruth, C. Kingston and B. Simard, ACS Nano, 2018, 12, 884 CrossRef CAS PubMed.
- H. Cho, S. Walker, M. Plunkett, D. Ruth, R. Iannitto, Y. Martinez-Rubi, K. S. Kim, C. M. Homenick, A. Brinkmann, M. Couillard, S. Dénommée, J. Guan, M. B. Jakubinek, Z. J. Jakubek, C. T. Kingston and B. Simard, Chem. Mater., 2020 DOI:10.1021/acs.chemmater.0c00144.
- Q. Beuguel, J. Tavares, P. Carreau and M. C. Heuzey, J. Colloid Interface Sci., 2018, 516, 23 CrossRef CAS PubMed.
- C. Zhi, Y. Bando, C. Tang and D. Golberg, Solid State Commun., 2011, 151, 183 CrossRef CAS.
- D. Kim, S. Nakajima, T. Sawada, M. Iwasaki, S. Kawauchi, C. Zhi, Y. Bando, D. Golberg and T. Serizawa, Chem. Commun., 2015, 51, 7104 RSC.
- Y. Lin, T. V. Williams, T.-B. Xu, W. Cao, H. E. Elsayed-Ali and J. W. Connell, J. Phys. Chem. C, 2011, 115, 2679 CrossRef CAS.
- C. Zhi, Y. Bando, C. Tang, H. Kuwahara and D. Golberg, Adv. Mater., 2009, 21, 2889 CrossRef CAS.
- Q. Huang, Y. Bando, C. Zhi, D. Golberg, K. Kurashima, F. Xu and L. Gao, Angew. Chem., 2006, 45, 2044 CrossRef CAS PubMed.
- J. A. Gallego-Juarez, and K. F. Graff, Power Ultrasonics Applications of High-intensity Ultrasound, Woodhead Publishing, Cambridge, U.K., 2014 Search PubMed.
- C. Lee, J. Drelich and Y. K. Yap, Langmuir, 2009, 25, 4853 CrossRef CAS PubMed.
- L. Boinovich, A. M. Emelyanenko, A. S. Pashinin, C. H. Lee, J. Drelich and Y. K. Yap, Langmuir, 2012, 28, 1206 CrossRef CAS PubMed.
- L. Li, H. L. Li, S. Ramakrishnan, X. J. Dai, K. Nicholas, Y. Chen, Z. Chen and X. Liu, J. Phys. Chem. C, 2012, 116, 18334 CrossRef CAS.
- C. Lee, Boron Nitride Nanotubes: Synthesis, Characterization, Ph.D. dissertation, Functionalization and Potential Applications, 2010.
- C. Bruel, S. Queffeulou, T. Darlow, N. Virgilio and J. R. Tavares, Can. J. Chem. Eng., 2019, 97, 832 CrossRef CAS.
- Y. Liao, Z. Chen, J. W. Connell, C. C. Fay, C. Park, J. W. Kim and Y. Lin, Adv. Funct. Mater., 2014, 24, 4497 CrossRef CAS.
- A. Maguer, E. Leroy, L. Bresson, E. Doris, A. Loiseau and C. Mioskowski, J. Mater. Chem., 2009, 19, 1271 RSC.
- R. Iannitto, H. Shin, Y. Martinez-Rubi, B. Simard and S. Coulombe, ACS Appl. Nano Mater., 2020, 3(1), 294–302 CrossRef CAS.
- Y. Min, M. Akbulut, K. Kristiansen, Y. Golan and J. Israelachvili, Nat. Mater., 2008, 7, 527 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00136h |
| This journal is © The Royal Society of Chemistry 2020 |