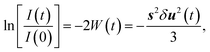Open Access Article
Open Access ArticleUltrafast lattice and electronic dynamics in single-walled carbon nanotubes†
Dingguo
Zheng‡
 ab,
Chunhui
Zhu‡
a,
Zian
Li
a,
Zhongwen
Li
ab,
Chunhui
Zhu‡
a,
Zian
Li
a,
Zhongwen
Li
 a,
Jun
Li
a,
Shuaishuai
Sun
a,
Jun
Li
a,
Shuaishuai
Sun
 a,
Yongzhao
Zhang
ab,
Fengqiu
Wang
a,
Yongzhao
Zhang
ab,
Fengqiu
Wang
 e,
Huanfang
Tian
a,
Huaixin
Yang
e,
Huanfang
Tian
a,
Huaixin
Yang
 abcd and
Jianqi
Li
*abc
abcd and
Jianqi
Li
*abc
aBeijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: ljq@aphy.iphy.ac.cn
bSchool of Physical Sciences, University of Chinese Academy of Science, Beijing, 100190, China
cYangtze River Delta Physics Research Center Co., Ltd., Liyang, Jiangsu 213300, China
dSongshan Lake Materials Laboratory, Dongguan, Guangdong 523808, China
eSchool of Electronic Science and Engineering, Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing 210093, China
First published on 22nd May 2020
Abstract
Understanding the photoinduced ultrafast structural transitions and electronic dynamics in single-walled carbon nanotubes (SWCNTs) is important for the development of SWCNT-based optoelectronic devices. In this study, we conducted femtosecond-resolved electron diffraction and electron energy-loss spectroscopy (EELS) measurements on SWCNTs using ultrafast transmission electron microscopy. The experimental results demonstrated that dominant time constants of the dynamic processes were ∼1.4 ps for electron-driven lattice expansion, ∼17.4 ps for thermal phonon-driven lattice expansion associated with electron–phonon coupling. The time-resolved EELS measurements clearly revealed a notable red shift of plasmon peaks by ∼100 meV upon femtosecond laser excitation. Different features of charge carrier excitation and relaxation were carefully discussed in correlation with the lattice dynamics and photoinduced absorption signals of SWCNTs. Our results provide a comprehensive understanding of the ultrafast dynamics in SWCNTs and powerful techniques to characterize the dynamics of low-dimensional structures.
Introduction
Single-walled carbon nanotubes (SWCNTs) have been studied extensively as important low-dimensional materials. SWCNTs exhibit a rich variety of physical properties that are attractive for many optoelectronic and photonics applications, such as light harvesting, high-speed photodetection, and ultrafast all-optical modulation.1–5 Certain optical properties of SWCNTs have been explained by a combination of exciton effects and the red tail of π-plasmon resonance.6–9 However, the physical mechanisms behind the ultrafast optical responses of SWCNTs are still not fully understood.Transient absorption (TA) spectroscopy is a useful tool for studying ultrafast optical processes.10 Numerous TA spectroscopy experiments on SWCNTs have provided information about their electronic dynamic features; e.g., biexciton and exciton annihilation.11–16 However, the plasmonic and lattice dynamics of SWCNTs cannot be directly revealed by TA spectroscopy with probe wavelengths in the visible to infrared range. Several independent investigations have demonstrated that ultrafast behaviors of plasmons and the lattice may strongly affect the ultrafast features of SWCNTs.11,13,17 Electron energy-loss spectroscopy (EELS) has been used to study the plasmonic properties of SWCNTs and revealed certain prominent features of tubular structures.8,9 Unfortunately, few time-resolved EELS experiments on photoinduced plasmonic dynamics in SWCNTs and dynamic changes of lattice structures have been performed to date. The structural dynamics of nanotubes is still an important issue that is under investigation.18,19 For example, time-resolved Raman spectroscopy of SWCNTs showed the notable evolution of phonon population and the lattice dynamics of multi-walled carbon nanotubes (MWCNTs) have been extensively investigated using ultrafast X-ray diffraction and ultrafast electron diffraction (UED).18,20–22 In particularly, the correlation between the structure dynamics and electronic dynamics has been never directly revealed.
Herein, we using ultrafast transmission electron microscope (UTEM) perform time-resolved EELS and UED measurements on SWCNTs. Both electronic and lattice structures of the SWCNTs show notable dynamic changes after femtosecond laser excitation. The general signatures in TA spectra of SWCNTs are also investigated. It is demonstrated that the photoinduced absorption (PA) signals could be correlated with the red shift of π plasmons and other contributions.
Results and discussion
Lattice dynamics
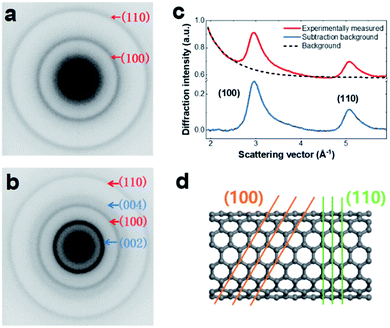
Sample preparation and experimental measurement details are presented in the Experimental section (ESI†). The SWCNT samples were a mixture of metallic and semiconducting types with diameters of 1.2–1.7 nm. For UTEM observation, the SWCNTs were dispersed on 2000-mesh copper (Cu) grids by solution processing. As shown in Fig. S1,† the SWCNTs existed as bunched structures with random tube orientation. A typical EELS profile of a SWCNT sample is shown in Fig. S2,† illustrating the characteristic peaks of the SWCNTs. The UED measurements were performed using our custom-built UTEM developed based on a JEOL-2000EX microscope. The dynamic processes were initiated by a 520 nm pump laser with a fluence of ∼47 mJ cm−2, repetition rate of ∼100 kHz, and duration of ∼300 fs.As shown in Fig. 1, the microstructure of the SWCNT sample was characterized. Fig. 1a shows a typical 2D diffraction pattern of SWCNTs. The two Debye–Scherrer rings were attributed to the (100) and (110) lattice planes. For comparison, we also show an electron diffraction pattern of MWCNTs in Fig. 1b, which contains a strong (002) reflection ring. To facilitate data analysis, the SWCNT diffraction pattern was transformed into a 1D profile by azimuthal integration and subsequent background subtraction (Fig. 1c). An atomic model of an armchair tube is shown in Fig. 1d, in which the (100) and (110) crystal planes are indicated.
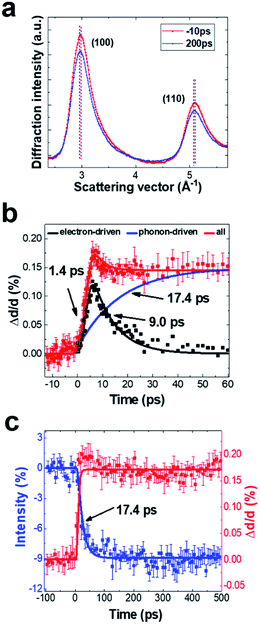
A series of UED patterns at different time delays were obtained to reveal the lattice dynamics of SWCNTs. In Fig. 2a, we show two typical diffraction profiles obtained before (−10 ps) and after time zero (200 ps). After femtosecond-laser excitation, the lattice spacings of the (100) and (110) planes increase, whereas diffraction intensity shows a visible decrease. The peak position of the (100) plane as functions of short and long-time delays is shown in Fig. 2b and c, respectively. The (100) lattice spacing reaches a maximum value at a time delay of ∼5 ps. In addition, we also observed a fast decay signal (<30 ps) and long-lived signal (>500 ps) accompanied with clear lattice expansion. The long-lived signal shows similar features to the thermal phonon-driven process in MWCNTs,18,20–22 which can be well described by a single exponential process, as demonstrated by the two-temperature mode.23 During this process, energy transforms from the hot electrons to the lattice by strongly coupled optical phonons,24,25 resulting in a quick increase of lattice temperature and a decrease of the diffraction intensity according to the Debye–Waller factor. Fig. 2c shows the diffraction intensity as a function of time delay, illustrating the intensity decrease with a time constant of ∼17.4 ps after laser excitation. We consider that the lattice plane expands by about 0.15%, so C–C bond length is estimated to increase by 0.21 pm (C–C bond length is ∼1.421 Å). The lattice temperature rise was estimated to be ∼800 K using an axial thermal expansion coefficient of 2 × 10−6 K−1.26
The fast components on the picosecond time scale are electron-driven lattice expansion processes, which are caused by the depopulation of electrons in the π- and σ-bonds upon femtosecond laser excitation.18–22 To isolate these non-thermal components, we subtracted the phonon-driven process (Fig. 2c), as shown in Fig. 2b. Careful analysis on the electron-driven transient state revealed that this fast process can be well characterized by an exponential increase with a time constant of ∼1.4 ps and then the relaxation time was about ∼9.0 ps. We also extracted information about the (110) plane dynamics from the time-resolved electron diffraction data, as displayed in Fig. S3.† The fundamental changes of the (110) plane showed similar features to those obtained for the (100) plane, although the lattice expansion along the [110] direction was slightly slower than that along the [100] direction. In addition, the intensity of the (100) diffraction peak decreased more than that of the (110) diffraction peak. This phenomenon can be well explained by the Debye–Waller factor (W(t)):27
Electronic dynamics
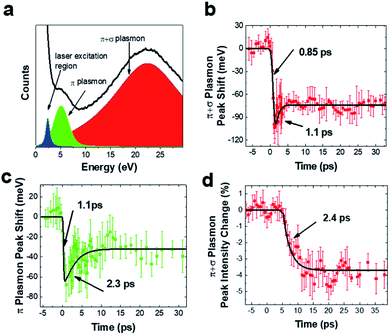
Fig. 3 presents the time-resolved EELS results obtained under similar experimental conditions to those used for the UED measurements. The low-loss EELS profile of the SWCNTs is shown in Fig. 3a. The plasmonic peaks observed at ∼5.0 and 22.4 eV can be attributed to the π and π + σ plasmons of SWCNTs, respectively.8,30,31Fig. 3b and c show shifts of the π and π + σ plasmonic peaks as functions of time delay. The maximum peak shifts were observed at a time delay of about 1 ps. Careful measurements showed that these electronic dynamic transitions firstly recovered by a fast process with a time constant of ∼2.0 ps, and then followed by a long-lived red-shifted signal. It is also known that photon-induced near-field electron microscopy (PINEM) signals of SWCNTs appear in the femtosecond time domain after femtosecond laser pumping. Therefore, the rising time of the curves in Fig. 3 could contain certain error. However, the PINEM signals disappeared after ∼0.6 ps, so they had no visible influence on the main process of the plasmon peaks.According to a theoretical study of 1D systems, the plasmon resonance energy Ep in SWCNTs is correlated with the resonance frequency ωp and density of valence electrons N as follows,32
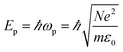 | (1) |
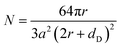 | (2) |
The lattice expansion may bring in another factor that affects the plasmon resonance. The maximum lattice expansion, as shown in Fig. 2b, was only ∼1.5‰ and a plasmon red shift of ∼37 meV was calculated from eqn (1) and (2) using the parameters of r = 0.7 nm, a = 0.246 nm, and dD = 0.34 nm (both r and a increase 1.5‰). This suggests that lattice expansion partially responsible for the long-lived red shift of plasmons with a typical value of several tens of millielectronvolts. Our UTEM sample contained bundles of nanotubes, so dD may also play the other role in the plasmonic dynamics after femtosecond laser excitation, as reported in studies of MWCNTs, in which the interlayer space of carbon sheets is noticeably enlarged following laser excitation because of the weak van der Waals bonding.18,20–22 We estimated the red shift of the plasmon peak using eqn (1) and (2) and obtained a change of the resonance frequency of ∼73 meV upon increasing dD by 1%, r and a by 1.5‰ (the radial expansion observed in MWCNTs is ∼2.5% at fluence of 44 mJ cm−2).18,21,22 This result is in agreement with the experimental data discussed above. It should be pointed out that the long-lived trapped photocarriers, which are often located at defect sites and interfaces, could also contribute to the electronic process in the present system, as discussed elsewhere.10 Moreover, our careful analysis also revealed that the intensity of π + σ plasmons decreased (∼3.5%) with a time constant of ∼2.4 ps, as illustrated in Fig. 3d. This alteration is likely correlated with the increase of lattice temperature induced via electron–phonon coupling, which occurs on the time scale of a few picoseconds.
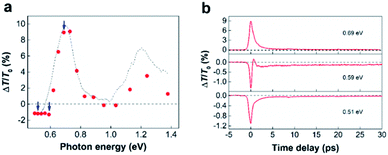
The red shift of π plasmons can impact the ultrafast photoresponse of SWCNTs.33,34 To illustrate this point, we reproduced the absorbance of SWCNTs by four Gaussian using the data in literature.35 As shown in Fig. S4,† a 10 meV shift of π-plasmon resonance can already rise a few percent absorbance change for SWCNTs in visible to IR wavelength. In particularly, it is found that the enhance of absorbance in nonresonant range is much larger than that in resonant range. We performed broadband TA spectroscopy measurements on SWCNT samples with 1.55 eV pumping and 0.5–1.3 eV probing. The sample was dispersed on a quartz substrate and the pump fluence was fixed at ∼3 mJ cm−2 (Fig. 4) and 0.1 mJ cm−2 (Fig. S5†). Similar to previous reported results,12,13,33,36,37 two PA bands in the nonresonant range and two PB (photon bleaching) in the resonant range are observed in the TA spectroscopy (Fig. 4a). As demonstrated in the previous works, we attribute the PB signal to the state filling effects.10–13 The optical transition with ∼1.6 eV excitation occurs at energy level higher than the second excitonic transitions (S22). In this case, photocarrier would transfer to the S22 and first excitonic transition (S11) very fast by intratube relaxation, which fill the states of S11 and S22, thus leading to two PB bands. In addition, intertube energy transfer usually occurs in SWCNT bundles,38 and this process also contributes to the exciton population redistribution. Although the redshift of the π-plasmon resonance can be attribute to the PA signals, we believe that there are multiple physical mechanisms behind these PA signals. This can be confirmed by a clear delay time-dependent PA–PB–PA transition observed at a probing energy of ∼0.59 eV in Fig. 4b. Besides the redshift of the π-plasmon resonance, PA signals have been described by different mechanisms including, intersubband transitions,39 multiple-exciton formation,13,37,40,41 dark-bright exciton transitions,42 charge induced Stark effect43 and carrier-hot phonon coupling17etc. Based on the results in Fig. 4, it hard to completely certain which one is responsible to the two PA bands. However, considering the pump fluence is very high, multiple-exciton coupling (biexciton, triexciton, and exciton annihilation) may be occurred.13,37,40,41 No blue-shifted PA signal may exclude the dark-bright exciton transitions,42 but we cannot rule out any charge induced Stark effect and carrier-hot phonon coupling effects.17,43 Furthermore, the intertube energy relaxation can result a large exciton population in the SWCNTs with low energy exciton resonant states, thus leading to a more significant PA signal at red side of S11. Notably, the ultrafast dynamics in SWCNTs is strong pump fluence dependent,44,45 resulting in that TR-EELS results and TA spectroscopy cannot directly compare. Nonetheless, a solid experimental evidence for the redshift of π plasmons still helpful to understand the ultrafast optical response in SWCNTs.
Finally, we briefly discuss the dynamic processes and transient states in photoexcited SWCNTs based on the measured lattice structural evolution and photophysical properties. For ultrafast investigations, the nonequilibrium states are initialized with an ultrashort laser pulse typically in the visible to infrared region. Considering the large bandgap of the σ band in SWCNTs, the laser pulse will promote electrons from the π band to the π* band. In other words, optical excitation leads to electron depopulation of the valence band and an increase of the electron population in the conduction band. Such an electron population change can directly result in Pauli blocking effects, which account for PB signals in TA spectroscopy. Other electronic effects, e.g., the red shift of plasmons and photoinduced multiple-exciton formation, also occur during or immediately after laser excitation. Then, the photocarriers will relax to the ground state with a lifetime of about 1–2 ps, which contributes to the fast decay at short time delay in both ultrafast optical spectroscopy and time-resolved EELS. It should be noted that during these electronic processes, electron-driven lattice expansion is also activated by electron depopulation of the π band. Electron-driven expansion exhibits a build-up time of ∼1–2 ps and a decay time of several picoseconds (∼9.0 ps in this paper). Thermal phonon-driven lattice expansion is established with a characteristic time ∼17 ps, then leave a quasi-equilibrium state lasts more than 500 ps.
Experiment
Sample preparation
High-purity SWCNTs (>99%) dissolved in aqueous surfactant solution were purchased from Nanjing XFNANO Materials Technology Corporation Limited, Nanjing, China. The SWCNTs were a mixture of metallic and semiconducting types with diameters of 1.2–1.7 nm and lengths of 300 nm to 4 μm. To prepare UTEM samples, SWCNTs were diluted in distilled water and then sonicated for 10 min. The solution was added dropwise onto a 2000-mesh Cu grid and then dried by annealing at 90 °C for 30 min. A 400-mesh Cu grid was placed on top of the 2000-mesh Cu grid to form a sandwich structure to enhance mechanical stability and heat conduction for UTEM experiments.UED experiment
The UED experiments were performed in the UTEM developed based on a JEOL-2000EX (JEOL Inc.) microscope.21,22,46 The original laser beam (λ = 1040 nm, full width at half-maximum = 300 fs) was split into two paths; one was frequency-quadrupled and focused to the LaB6 cathode to obtained pulsed electrons and the other was frequency-doubled and focused on the sample with a beam diameter ∼50 μm to excite dynamic processes. The pulsed electrons were accelerated to 160 keV and then focused to a beam diameter of ∼20 μm on the sample. Considering the heat dispersion of the UTEM sample and the signal-to-noise ratio, a laser repetition frequency of 100 kHz was used in our measurements. The diffraction patterns were recorded by a charge coupled device with an exposure time of ∼5 s. The temporal resolution of the ultrafast UED experiments is ∼800 fs. No distinct optical damage and heat accumulation effects were observed in these experimental conditions.Time-resolved EELS experiment
The time-resolved EELS measurement was performed using another UTEM that was developed based on a JEOL-2100F (JEOL Inc.) microscope with a field-emission gun.47 In this setup, the original laser beam had a pulse width of ∼190 fs and a central wavelength of ∼1030 nm. The diameter of the laser beam on the sample was ∼38 μm with a fluence of ∼44 mJ cm−2. A laser repetition frequency of 200 kHz was used in the time-resolved EELS measurement. No object aperture was inserted into the electron optical system; the collection angle was estimated to be more than 100 mrad. A Gatan spectrometer (GIF 965) was used to record the EELS and an exposure time of 50 s was used in the time-resolved measurement. The zero-loss peak center and plasmon peak center were determined by gravity arithmetic. The temporal resolution of the ultrafast TR-EELS experiments is ∼500 fs.TA spectroscopy
An 800 nm (∼1.55 eV) 1 kHz Ti:sapphire amplifier (Libra, Coherent Inc.) was used as a laser source. Infrared (0.5–1.3 eV) pulses were generated by a feeding 800 nm pulses into an optical parametric amplifier system (OPA-SOLO, Coherent Inc.). The pump-induced differential transmission changes were recorded by a photodetector and lock-in amplifier referenced to a 334 Hz chopped pump.Conclusions
Ultrafast dynamics in SWCNTs were investigated by combining measurements of time-resolved EELS, UED, and TA spectroscopy. Importantly, a red shift of plasmons approaching 100 meV and clear lattice expansion of the SWCNTs were observed upon femtosecond laser excitation. The non-thermal transient and thermal-phonon driving changes in the SWCNTs were addressed based on measurements of electronic and lattice temporal changes. Considering general signatures in TA spectroscopy, we carefully discussed the relevant transient states on time scales of femtoseconds to hundreds of picoseconds. Our study firstly discusses the correlation between the structural transients and electronic dynamics. Emerging UTEM techniques have the potential to markedly improve our understanding of the dynamics of low-dimensional materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Program of China (Grant No. 2016YFA0300303, 2017YFA0504703, 2017YFA0302904, and 2017YFA0303000), the National Basic Research Program of China (Grant No. 2015CB921304), the National Natural Science Foundation of China (Grant No. 11774391, 11774403, and 11804381), the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (Grant No. XDB25000000 and XDB33000000), the Scientific Instrument Developing Project of the Chinese Academy of Sciences (Grant No. ZDKYYQ20170002), and the China Postdoctoral Science Foundation funded project (Grant No. BX20180351). We thank Natasha Lundin, PhD, from Liwen Bianji, Edanz Editing China (http://www.liwenbianji.cn/ac), for editing the English text of a draft of this manuscript.References
- P. Avouris, M. Freitag and V. Perebeinos, Nat. Photonics, 2008, 2, 341–350 CrossRef CAS.
- M. F. L. De Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539 CrossRef CAS PubMed.
- T. Hasan, Z. Sun, F. Wang, F. Bonaccorso, P. H. Tan, A. G. Rozhin and A. C. Ferrari, Adv. Mater., 2009, 21, 3874–3899 CrossRef CAS.
- A. Martinez and Z. Sun, Nat. Photonics, 2013, 7, 842–845 CrossRef CAS.
- L.-M. Peng, Z. Zhang and C. Qiu, Nat. Electron., 2019, 2, 499–505 CrossRef CAS.
- M. J. O'Connell, S. M. Bachilo, C. B. Huffman, V. C. Moore, M. S. Strano, E. H. Haroz, K. L. Rialon, P. J. Boul, W. H. Noon, C. Kittrell, J. Ma, R. H. Hauge, R. B. Weisman and R. E. Smalley, Science, 2002, 297, 593–596 CrossRef PubMed.
- F. Wang, G. Dukovic, L. E. Brus and T. F. Heinz, Science, 2005, 308, 838–841 CrossRef CAS PubMed.
- R. Kuzuo, M. Terauchi and M. Tanaka, Jpn. J. Appl. Phys., 1992, 31, L1484–L1487 CrossRef CAS.
- M. F. Lin and K. W. Shung, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17744–17747 CrossRef CAS PubMed.
- G. Soavi, F. Scotognella, G. Lanzani and G. Cerullo, Adv. Opt. Mater., 2016, 4, 1670–1688 CrossRef CAS.
- Y.-Z. Ma, J. Stenger, J. Zimmermann, S. M. Bachilo, R. E. Smalley, R. B. Weisman and G. R. Fleming, J. Chem. Phys., 2004, 120, 3368–3373 CrossRef CAS PubMed.
- O. J. Korovyanko, C.-X. Sheng, Z. V. Vardeny, A. B. Dalton and R. H. Baughman, Phys. Rev. Lett., 2004, 92, 017403 CrossRef CAS PubMed.
- G. N. Ostojic, S. Zaric, J. Kono, V. C. Moore, R. H. Hauge and R. E. Smalley, Phys. Rev. Lett., 2005, 94, 097401 CrossRef CAS PubMed.
- L. Lüer, S. Hoseinkhani, D. Polli, J. Crochet, T. Hertel and G. Lanzani, Nat. Phys., 2008, 5, 54–58 Search PubMed.
- D. Stich, F. Späth, H. Kraus, A. Sperlich, V. Dyakonov and T. Hertel, Nat. Photonics, 2013, 8, 139–144 CrossRef.
- S. Xu, F. Wang, C. Zhu, Y. Meng, Y. Liu, W. Liu, J. Tang, K. Liu, G. Hu, R. C. Howe, T. Hasan, R. Zhang, Y. Shi and Y. Xu, Nanoscale, 2016, 8, 9304–9309 RSC.
- C. Zhu, Y. Liu, J. Xu, Z. Nie, Y. Li, Y. Xu, R. Zhang and F. Wang, Sci. Rep., 2017, 7, 11221 CrossRef PubMed.
- G. M. Vanacore, R. M. van der Veen and A. H. Zewail, ACS Nano, 2015, 9, 1721–1729 CrossRef CAS PubMed.
- T. Jiang, H. Hong, C. Liu, W. T. Liu, K. Liu and S. Wu, Nano Lett., 2018, 18, 2590–2594 CrossRef CAS PubMed.
- S. T. Park, D. J. Flannigan and A. H. Zewail, J. Am. Chem. Soc., 2012, 134, 9146–9149 CrossRef CAS PubMed.
- G. Cao, S. Sun, Z. Li, H. Tian, H. Yang and J. Li, Sci. Rep., 2015, 5, 8404 CrossRef CAS PubMed.
- S. Sun, Z. Li, Z. A. Li, R. Xiao, M. Zhang, H. Tian, H. Yang and J. Li, Nanoscale, 2018, 10, 7465–7471 RSC.
- J. Hohlfeld, S.-S. Wellershoff, J. Güdde, U. Conrad, V. Jähnke and E. Matthias, Chem. Phys., 2000, 251, 237–258 CrossRef CAS.
- T. Kampfrath, L. Perfetti, F. Schapper, C. Frischkorn and M. Wolf, Phys. Rev. Lett., 2005, 95, 187403 CrossRef PubMed.
- O. A. Dyatlova, C. Köhler, E. Malic, J. Gomis-Bresco, J. Maultzsch, A. Tsagan-Mandzhiev, T. Watermann, A. Knorr and U. Woggon, Nano Lett., 2012, 12, 2249–2253 CrossRef CAS PubMed.
- H. Jiang, B. Liu, Y. Huang and K. C. Hwang, J. Eng. Mater. Technol., 2004, 126, 265–270 CrossRef CAS.
- F. Carbone, D. S. Yang, E. Giannini and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20161–20166 CrossRef CAS PubMed.
- A. Gambetta, C. Manzoni, E. Menna, M. Meneghtti, G. Cerullo, G. Lanzani, S. Tretiak, A. Piryatinski, A. Saxena, R. L. Martin and A. R. Bishop, Nat. Phys., 2006, 21, 515–520 Search PubMed.
- L. Lüer, C. Gadermaier, J. Crochet, T. Hertel, D. Brida and G. Lanzani, Phys. Rev. Lett., 2009, 102, 127401 CrossRef PubMed.
- F. S. Hage, T. P. Hardcastle, A. J. Scott, R. Brydson and Q. M. Ramasse, Phys. Rev. B, 2017, 95, 195411 CrossRef.
- M. Knupfer, T. Pichler, M. S. Golden, J. Fink, A. Rinzler and R. E. Smalley, Carbon, 1999, 37, 733–738 CrossRef CAS.
- R. Kuzuo, M. Terauchi, M. Tanaka and Y. Saito, Jpn. J. Appl. Phys., 1994, 33, L1316–L1319 CrossRef CAS.
- J. S. Lauret, C. Voisin, G. Cassabois, C. Delalande, P. Roussignol, O. Jost and L. Capes, Phys. Rev. Lett., 2003, 90, 057404 CrossRef PubMed.
- Y. Long, L. Song, C. Li, C. Zhang, G. P. Wang, S. Xie, L. Wang, P. Fu and Z. Zhang, Chem. Phys. Lett., 2005, 405, 300–303 CrossRef CAS.
- M. E. Itkis, D. E. Perea, R. Jung, S. Niyogi and R. C. Haddon, J. Am. Chem. Soc., 2005, 127, 3439–3448 CrossRef CAS PubMed.
- L. Lüer, G. Lanzani, J. Crochet, T. Hertel, J. Holt and Z. V. Vardeny, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205411 CrossRef.
- D. J. Styers-Barnett, S. P. Ellison, B. P. Mehl, B. C. Westlake, R. L. House, C. Park, K. E. Wise and J. M. Papanikolas, J. Phys. Chem. C, 2008, 112, 4507–4516 CrossRef CAS.
- L. Lüer, J. Crochet, T. Hertel, G. Cerullo and G. Lanzani, ACS Nano, 2010, 4, 4265–4273 CrossRef PubMed.
- C. Manzoni, A. Gambetta, E. Menna, M. Meneghetti, G. Lanzani and G. Cerullo, Phys. Rev. Lett., 2005, 94, 207401 CrossRef CAS.
- Y. Ma, L. Valkunas, S. L. Dexheimer, S. M. Bachilo and R. Fleming, Phys. Rev. Lett., 2005, 94, 157402 CrossRef PubMed.
- S. M. Santos, B. Yuma, S. Berciaud, J. Shaver, M. Gallart, P. Gilliot, L. Cognet and B. Lounis, Phys. Rev. Lett., 2011, 107, 187401 CrossRef PubMed.
- Z. Zhu, J. Crochet, M. S. Arnold, M. C. Hersam, H. Ulbricht, D. Resasco and T. Hertel, J. Phys. Chem. C, 2007, 111, 3831–3835 CrossRef CAS.
- G. Soavi, F. Scotognella, D. Brida, T. Hefner, F. Späth, M. R. Antognazza, T. Hertel, G. Lanzani and G. Cerullo, J. Phys. Chem. C, 2013, 117, 10849–10855 CrossRef CAS.
- J. Park, P. Deria, J. Olivier and M. J. Therien, Nano Lett., 2014, 14, 504–511 CrossRef CAS PubMed.
- L. Huang and T. D. Krauss, Phys. Rev. Lett., 2006, 96, 057407 CrossRef PubMed.
- Z. Li, R. J. Xiao, P. Xu, C. Zhu, S. Sun, D. Zheng, H. Wang, M. Zhang, H. Tian, H. X. Yang and J. Q. Li, ACS Nano, 2019, 13, 11623–11631 CrossRef CAS.
- C. Zhu, D. Zheng, H. Wang, M. Zhang, Z. Li, S. Sun, P. Xu, H. Tian, Z. Li, H. Yang and J. Li, Ultramicroscopy, 2020, 209, 112887 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00269k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |