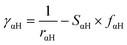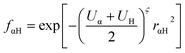TETT-functionalized TiO₂ nanoparticles for DOX loading: a quantum mechanical study at the atomic scale

Abstract

In this work, we present a quantum mechanical investigation, based on the self-consistent charge density functional tight-binding (SCC-DFTB) method, of the functionalization with silane-type ligands (TETT) of a spherical TiO₂ nanoparticle of realistic size (2.2 nm containing 700 atoms) to create an efficient nanosystem for simultaneous photodynamic therapy and drug transport. We determine the mechanism of the TETT ligand anchoring and its stability under thermal treatment, through molecular dynamics simulations at 300 K. Then, we build a medium and a full coverage model (22 and 40 TETTs, respectively) and analyze the interaction among TETT ligands and between the ligands and the surface. Finally, on the fully covered nanoparticle, we succeed in localizing two minimum energy structures for an attached doxorubicin anticancer molecule (DOX) and provide the atomistic details for both the covalent and the non-covalent (electrostatic) types of interaction. A future development of this work will be the investigation of the loading capacity of this drug delivery system and of the pH effect of the surrounding aqueous environment.

---

1. Introduction

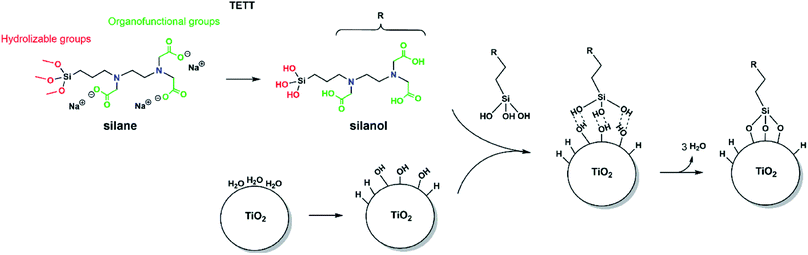
TiO₂ nanoconjugates have gained increasing attention during the last few years as interesting nanosystems for simultaneous photodynamic therapy (PDT) and drug delivery (DD). Curved TiO₂ are the most effective nanostructures for functionalization since they present a large number of low-coordinated Ti sites. Through an ad hoc surface functionalization, it is possible to make TiO₂ nanoparticles hydrophilic and biocompatible, to reduce their aggregation and toxicity, to transform them into good carriers.

Metal oxide surface are rich in surface hydroxyls and therefore, can be efficiently functionalized through alkoxy silanes. Organofunctional silanes have a chemical structure that allows them to link either with organic and inorganic matrices. The general formula is Y–R–Si–X₃, where X is a hydrolysable leaving group (e.g. methoxy, ethoxy, etc.) which provides a site for attaching Si to the surface, while Y is a functional group (e.g. carboxyl group, amine, etc.) and R is an alkyl chain. The silane reacts with water to form a silanol group (Si–OH) and, by condensation of surface hydroxyls on the nanoparticle surface with these Si–OH bonds, a silane-surface bond is formed. The use of multidentate anchoring groups and the strength of the covalent bonds formed (D_e(Si–O) = 466 kJ mol⁻¹) ensure the stability of the resulting nanoconjugate. The functional group Y at the end of the alkyl chain R can be used to improve the nanoconjugate hydrophilicity or to tether polymers or bioactive molecules.

Several reports exist that describe protocols for the conjugation of biomolecules onto TiO₂ surfaces and these have been partially reviewed by Beutner et al. in ref. 1. For example, TiO₂ nanoparticles have been functionalized with 3-amino-propyl-triethoxysilane (APTES).² The external amino group can tether biotin molecules, which are usually conjugated to an enzyme or antibody or target protein to form a selective complex for many metabolic processes.^3–5

Regarding other metal oxide-based nanosystems, we can mention that water-dispersible Gd₂O₃ nanoparticles were obtained by oleate ligands exchange with carboxylic silanes, namely N-(trimethoxysilylpropyl) ethylene diamine triacetic acid trisodium salt (TETT).⁶ The large number of carboxylic groups from the anchored TETT moieties allowed the coupling with polyethylene glycol polymer (PEG) to form PEG-coated Gd₂O₃ nanoparticles. The biocompatible PEG layer further stabilizes Gd₂O₃ nanoparticles, thus enhancing their blood circulation time and improving their dispersibility in water. As a result, the PEG-coated Gd₂O₃ nanoparticles have been successfully exploited as glioma-target contrast agents.⁶

Similarly, MnO nanoparticles have also been functionalized by TETT ligands for further conjugation with folic acid (FA),⁷ since the latter was found to be an effective target towards glioma cells, which contain an overexpressed folate receptor. The MnO–TETT–FA conjugate was also proven to be biocompatible and therefore it can be used as a magnetic resonance imaging contrast agent for the early diagnosis of brain gliomas.⁷

TETT functionalized nanoparticles are also suitable for drug delivery. Ying et al.⁸ have succeeded in loading doxorubicin (DOX) on TETT-functionalized TiO₂ nanoparticles. The drug biological and pharmaceutical activity was found not to be affected. This type of ligand can anchor firmly the metal oxide NPs surface, induce their water dispersibility and allow for an easy and effective drug loading.

Modelling functionalized metal oxide nanoparticles at an atomistic level is not a simple task. Few computational studies exist in the literature where classical molecular dynamics (MD) simulations of large organic molecules ranging from aminoacids⁹ to peptides^10,11 or dipeptides,¹² up to full proteins¹³ on flat or curved TiO₂ surfaces have been performed by means of force-field methods. However, these approaches present several intrinsic limits, which do not allow the description of the electronic properties of the system and, more importantly, of the chemical processes at the interface since they involve bond breaking and bond formation.

There are several crucial questions that would require computational studies at a quantum mechanical level of theory to be answered. It is relevant for example to understand how the ligands anchor the surface, the type of binding (for TETT it could be mono-, bi- or tridentate binding mode), the extent of ligand surface coverage (which could be limited by the number of available surface sites or by the steric hindrance of the ligands), the type of interaction with the drug (which may range from a weak complexation to a strong covalent conjugation), just to mention a few.

In this work, we present a quantum mechanical investigation, based on the self-consistent charge density functional tight-binding (SCC-DFTB) method,¹⁴ where we unravel the details of functionalization with TETT ligands for a spherical TiO₂ nanoparticle of realistic size (2.2 nm containing 700 atoms).^15,16 These curved nanoparticles are similar to those used in many experimental studies of NP + ligand complexation.^17–23 We analyzed the mechanism of the ligand anchoring, the effect of the surface curvature, the effect of temperature and of ligand coverage. For a fully covered NP–TETT system, we also present the atomistic details of the non covalent (electrostatic) and of the covalent interaction with DOX.

2. Computational details

In the present study, we used the self-consistent charge density functional tight-binding (SCC-DFTB) approach for geometry optimization and molecular dynamics simulations. This method has already been applied successfully to investigate adsorbed molecules on titanium oxides.^24–26 The details about the DFTB method and its derivation can be found in ref. 14, 27 and 28.

For all the SCC-DFTB calculations we used the DFTB+ 18.2 open-source package.²⁹ We employed the MATORG³⁰ parameterization set for the Ti–O pairwise interaction in the TiO₂ model, and C, N, O, and H of the adsorbed molecules. In addition, we incorporated the Si–Ti, Ti–Ti, and Si–Si pairwise interactions in the MATORG set.³¹

In our calculations we included the D3 dispersion corrections to consider long-range van der Waals interactions.³² The description of the hydrogen bonding^33,34 has been further improved with the inclusion of the empirical hydrogen bonding damping (HBD) function γ_αH, only for the interaction between an atom α and a hydrogen atom

where U_α and U_H are the atomic Hubbard parameters, which are linked to the chemical hardness of atom α and the corresponding hydrogen, respectively. The parameter ζ = 4 is generally determined by fitting to hydrogen-bonding energies from high level ab initio calculations. As a result, γ_αH becomes more positive in the short range, leading to stronger polarization for the atoms forming H-bonds, thus increasing the accuracy of describing hydrogen bonds.

The anatase TiO₂ spherical nanoparticle model used throughout this work has been designed in previous work by our group.¹⁵ The stoichiometry of the model is (TiO₂)₂₂₃·10H₂O, and the NP has an equivalent diameter of 2.2 nm. The nanoparticle has been treated as a large isolated molecule in vacuum without any periodic boundary condition.

For geometry relaxations, the threshold for the convergence of the self-consistent charge (SCC) procedure was set to 10⁻⁶ au. The atomic positions of all structures in this work were fully relaxed using the conjugate-gradient algorithm until the root mean square of the residual force was below 10⁻⁴ au.

The total adsorption energy per TETT linker on the spherical nanoparticle has been defined as:

ΔE^mol_ads = (E_NP+nmol − [E_NP + n_molE_mol])/n_mol

where E_(NP+nmol) is the total energy of the whole system, E_NP is the energy of the NP, E_mol is the energy of the molecule in the gas phase, and n_mol is the number of the molecules adsorbed on the NP.

The DFTB results has been validated by DFT(B3LYP-D*) calculations. The obtained DFTB geometries are in agreement with the DFT equilibrium ones for the mono-, bi- and tri-dentate TETT on the tri-site C (compare Fig. S1†). However, the binding energies are largely overestimated by DFTB, as shown in Table S1.† We defined a scaling factor of 0.69 to be applied to all tridentate models by calculating the ratio between DFT/DFTB adsorption energies for the tridentate TETT on tri-site C. Correspondingly, for the mono- and bi-dentate models the scaling factors are 0.88 and 0.73, respectively.

All the DFT calculations have been carried out with the CRYSTAL14 (ref. 35) simulation code where the Kohn–Sham orbitals are expanded in Gaussian-type orbitals. The all-electron basis sets are Ti 86-4111(d41), O 8-4111(d1) for the titanium and oxygen atoms of TiO₂; Si 86-311 (d1), H 5-111(p1), C 6-31111 (d1), O 8-41111 (d1), and N 6-311(d1) have been employed for silicon, hydrogen, oxygen, and nitrogen atoms of the adsorbed TETT molecule, respectively. We used the B3LYP functional,^36,37 corrected by Grimme's D* to include dispersion forces.^38,39 The cut off limits in the evaluation of Coulomb and exchange series/sums appearing in the SCF equation were set to 10⁻⁷ for Coulomb overlap tolerance, 10⁻⁷ for Coulomb penetration tolerance, 10⁻⁷ for exchange overlap tolerance, 10⁻⁷ for exchange pseudo-overlap in the direct space and 10⁻¹⁴ for exchange pseudo-overlap in the reciprocal space. The condition for the SCF convergence was set to 10⁻⁶ au on the total energy difference between two subsequent cycles. The equilibrium structure is determined by using a quasi-Newton algorithm with a BFGS Hessian updating scheme.⁴⁰

Geometry optimization was performed without any symmetry constraint; forces were relaxed to be less than 4.5 × 10⁻⁴ au, and displacements to be less than 1.8 × 10⁻³ au.

Fig. 1 The structure of the silane molecule TETT [N-(trimethoxysilylpropyl) ethylene diamine triacetic acid, trisodium salt], with the hydrolyzable groups in red and the carboxylic groups in green. Starting from the left, the hydrolysis of TETT to trisilanol and the synthesis of TiO₂ NP in an aqueous environment, then the hydrogen bonded trisilanol on the TiO₂ NP and finally the formation of Si–O–Ti covalent bonds.

Born–Oppenheimer molecular dynamics (MD) simulations were performed within the canonical ensemble (NVT). The Newton equations of motion were integrated with the velocity Verlet algorithm, and a relatively small time step of 0.5 fs was used. During the molecular dynamics simulation, the temperature has been kept constant to 300 K by using the Nosé–Hoover thermostat (time constant of 0.04 ps) and the system has been evolved for 20 ps. For the medium (1689 atoms) and high coverage (2499 atoms) the time step was set to 1 fs, and the system has been let evolve for 15 ps, due to the large number of atoms.

For each run of the MD simulations the initial velocity was randomly generated with the Boltzmann distribution at 300 K.

3. Results and discussion

3.1 Mechanism of TETT anchoring to the TiO₂ nanoparticle surface

In order to observe the N-(trimethoxysilylpropyl) ethylene diamine triacetic acid, trisodium salt (TETT) anchoring to a metal oxide surface, the following classical reaction steps must take place (as sketched in Fig. 1): the trialkoxysilane must first undergo hydrolysis to be converted into the corresponding trisilanol (Fig. S2†) that is then reactive towards surface hydroxyls forming Ti–O–Si bridges through a condensation reaction. Finally, TETT results to be firmly anchored to the surface by strong Si–O–Ti covalent bonds.

3.2 TiO₂ nanoparticle model and potential adsorption sites

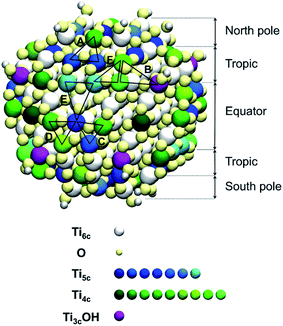
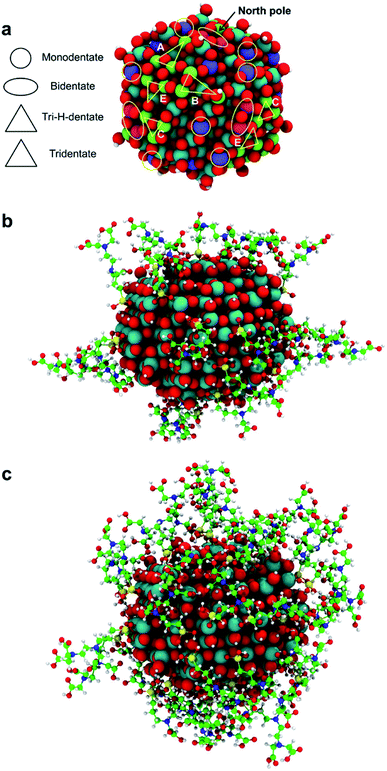
Since the trisilanol derived from TETT hydrolysis contains three hydroxyl groups, up to three SiO–Ti bonds can be formed for each TETT unit anchored to the surface. However, a triple anchoring process is not trivial since it requires the presence on the nanoparticle surface of three undercoordinated Ti atoms in close proximity one of the other and all three Ti ions must be hydroxylated to trigger the condensation reaction with the Si–(OH)₃ groups. It should be noted that this is not possible on a flat (101) anatase TiO₂ surface where there are not three Ti sites in the proper spatial disposition.

In the following, first we have investigated and mapped the surface of the spherical nanoparticle model prepared in previous works by our group in order to define how many Ti tri-sites, i.e. three undercoordinated Ti sites in close proximity, can be identified where TETT could anchor in a tridentate fashion (Table 1). We found six Ti tri-sites (triads) sketched as triangles with the vertexes at the low-coordinated Ti sites (labeled A–F in Fig. 2 and in Table 1). They are located in different positions of the nanoparticle, defined as equator, tropics and poles, and they involve either five-fold or four-fold Ti ions (see color coding of Ti spheres in Fig. 2).

Table 1 Calculated binding energies (ΔE, in eV) as obtained by DFTB-D3 for the tridentate adsorption mode of the TETT molecule on the NP model, with the corresponding localization, label of the Ti tri-sites (see Fig. 2) and occurrence in the model. The tri-H-dentate adsorption mode was considered if the tridentate adsorption was not successful

Localization	Triad	Sites	Occurrence	ΔE (eV)	ΔE (eV)
				Tri-	Tri-H
North pole	A	Ti4c Ti5c Ti5c	4	−3.81
Tropic	B	Ti4c Ti4c Ti3cOH	4	−3.93
Equator	C	Ti4c Ti5c Ti5c	4	−2.58
Equator	D	Ti4c Ti4c Ti5c	4	−2.44
Tropic	E	Ti5c Ti5c Ti5c	4	—	−2.53
Tropic	F	Ti4c Ti4c Ti5c	4	—	−2.66

---

Fig. 2 Map of the Ti atoms of the spherical anatase TiO₂ nanoparticle with different coordination environments, visually shown by the colour coding. The black triangles identify the potential Ti tri-sites in the model. Different areas of the sphere are defined: poles, tropics, and equator.

As a further step, we have investigated whether those tri-sites are reactive sites towards water dissociation, leading to the formation of three Ti–OH species for the condensation reaction with TETT. Indeed, we observe that water dissociation on all the Ti sites of the six triads is an exothermic process (see Fig. S3† where the associated energy release is reported).

Based on the results above, we conclude that anchoring of TETT on the curved TiO₂ nanoparticle in tridentate fashion is viable. In the next paragraph, we present the resulting structures that we have succeeded to localize of the optimized adsorbed TETT on the available tri-sites on the surface.

3.3 TETT binding modes and binding energy

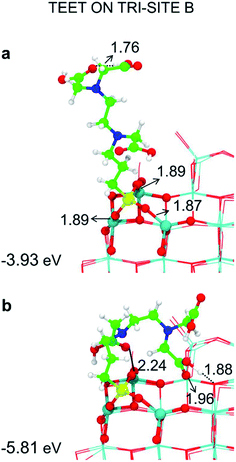
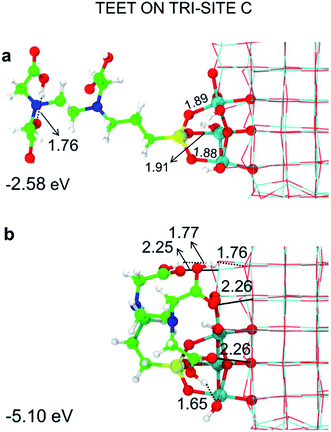
Among the potential tri-sites on the spherical nanoparticle considered in this study, only four of them (A, B, C and D) are found to establish three stable bonds for a tridentate adsorption of a TETT molecule with binding energy of −3.81, −3.93, −2.58, −2.44 eV, respectively (see Table 1). The TETT molecules have been optimized on the surface starting from a straight conformation of the C chain, where only the silanol functionality interacts directly with the surface.

Tri-site A is located close to the north pole of the nanoparticles and involves two five-fold and one four-fold coordinated Ti atoms. Tri-site B is located at the north tropic of the nanoparticle and involves three fourfold coordinated Ti atoms. Tri-sites C and D are located at the equator of the nanoparticles and involve five-fold and four-fold coordinated Ti atoms.

We can rationalize the lower binding energy for a tridentate binding mode of TETT on tri-site C as due to the presence of a disturbing bridging oxygen in the center of the three Ti atoms of the tri-site, as it can be clearly observed in Fig. S4.† Upon TETT adsorption, these O atoms must be pushed back inside the nanoparticle by 1.3 Å because of the repulsion towards the incoming Si atom in TETT (as shown in Fig. S4†). Similarly, in tri-site D we can observe two disturbing bridging O atoms in Fig. S5† that largely reduce the binding energy. Even if tri-site A and tri-site B are based on Ti with different coordination, they present similar (and large) binding energy for the tridentate binding mode of TETT. This is because the tri-site B, which would be expected as much more favorable given the lower degree of coordination of the Ti sites, is characterized by unfavorable distances between those Ti atoms (5.57, 5.21 and 2.68 Å before TETT binding for the tri-site B, as shown in Fig. S6,†vs. 5.14, 5.01 and 3.40 Å before TETT binding for the tri-site A, as shown in Fig. S7†), which are less compatible with the distances among the three O atoms in the TETT that are going to make the surface bond.

On the tri-sites E and F, only two SiO–H bonds of the TETT molecule dissociate whereas the third one does not dissociate but establishes a H-(bridge)-bond with a surface O atom. The overall binding energy for E and F are −2.53 and −2.66 eV. We name this as a tri-H-dentate adsorption mode (shown in Fig. S8†).

We have tried to evaluate the binding energy for mono- vs. bi- and tri-dentate for the tri-sites A and C in order to establish whether there is a proportional gain in binding energy or whether increasing the number of bonds per TETT molecule causes a large structural strain that reduces the benefit of an additional SiO–Ti bond. However, this is not a simple task. For the tri-site A, we could not succeed in localizing a purely monodentate (Fig. 3a) and a purely bidentate (Fig. 3b) model because, in both cases, we could not avoid the establishment of other additional interactions, such as OH coordination to surface Ti atoms or H-bonding. Therefore, the resulting binding energies for Fig. 3a and for Fig. 3b are larger then what expected for a monodentate and a bidentate TETT on the TiO₂ surface. The binding in the case of Fig. 3b is very close to the one for the true tridentate model in Fig. 3c, which are both about 1 eV larger than for the case in Fig. 3a.

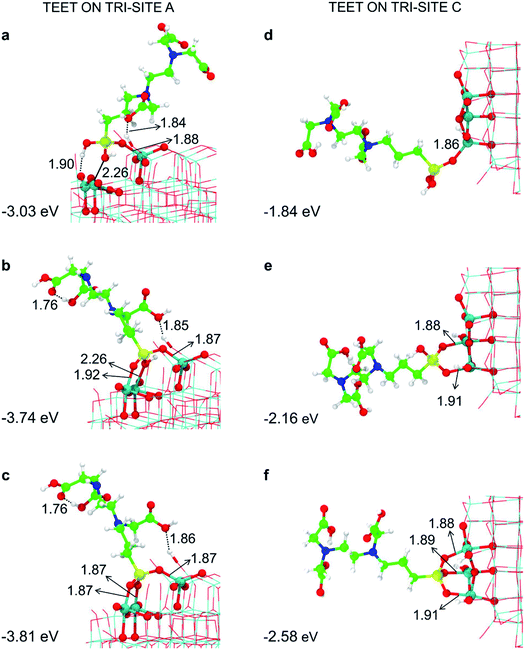Fig. 3 Monodentate (a and d), bidentate (b and e) and tridentate (c and f) adsorption modes (side views) and adsorption energy per TETT molecule (in eV) on the tri-site A and C of the spherical NP (in Fig. 2), as obtained by the DFTB-D3, respectively. Ti atoms are shown in cyan, O atoms in red, H atoms in white, Si atoms in yellow, C atoms in green and N atoms in blue. Relevant H-bonds and coordinative bonds (in Å) are represented by dashed lines and solid lines, respectively.

For the tri-site C, which is less reactive, we could localize the true mono-, bi- and tridentate models (Fig. 3d–f). The ratio between the mono- and bi-dentate binding energy is 0.85, whereas that between bi- and tri-dentate is 0.84. These results indicate that the second and third SiO–Ti bond lead to a lower energy gain, probably due to a large structural distortion and to a large steric hindrance. Similar ratios in binding energies for models in Fig. 3d–f have been computed at the DFT/B3LYP-D* level of theory, as shown in Fig. S1 and reported in Table S1.†

3.4 Effect of temperature on the multibinding and the conformation of a TETT unit

In the previous section, we have investigated and analyzed the adsorption modes of TETT on the TiO₂ nanoparticle surface at 0 K. In this section, we study the effect of temperature by sampling the configurational space through molecular dynamics (MD) at 300 K. The kinetic energy introduced in the simulation through temperature allows the system to overcome the barriers in the order of k_BT and to reach the global minimum. Through MD, we have verified the stability of the investigated adsorption modes and of their evolution with time. For few selected adsorption sites (A–C), we have obtained some statistical sampling to present a conformational analysis of this flexible linker.

To perform the conformational analysis, we have monitored several structural parameters related to atomic distances (SiO–Ti), bond angles (Si–O–Ti) and TETT orientation. The evolution of the TETT orientation was investigated in terms of the absolute value of the θ angle, which is defined in Fig. S9† and is the angle between the plane containing the three Ti atoms of the tri-site under study and the straight line passing through the Si atom and the farthest N atom contained in the TETT molecule.

3.4.1 Tri-site A – MD simulations. For the TETT linker bound to the tri-site A, we have performed four different simulation runs at 300 K to have a sufficiently large statistics on the conformational evolution of the linker. At the end of each simulation run, we performed the full atomic relaxation and we have obtained the four structures shown in Fig. S10.† In three of the cases (except for Fig. S10† after md3) the TETT molecules rotate and bend towards the curved surface, establishing some interaction between the TETT O atoms and surface Ti atoms. The most stable optimized structure after MD is also shown in Fig. 4b and compared to the starting geometry from the previous section in Fig. 4a, where only the silanol groups interact with the surface.

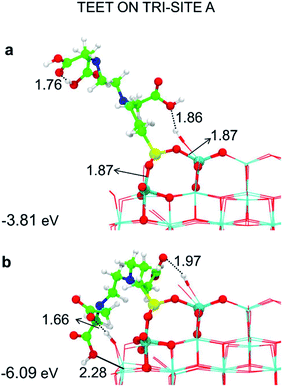Fig. 4 Tridentate adsorption mode (side views) and adsorption energy per TETT molecule (in eV) on the tri-site A of the spherical NP (in Fig. 2), as obtained by the DFTB-D3: (a) optimized starting geometry at 0 K; (b) optimized structure from the last snapshot of the MD run. Ti atoms are shown in cyan, O atoms in red, H atoms in white, Si atoms in yellow, C atoms in green and N atoms in blue. Relevant H-bonds and coordinative bonds (in Å) are represented by dashed lines and solid lines, respectively.

We observe an increase in binding energy of 2.3 eV after MD reorganization. We observe that the OH of a COOH group forms a coordinative bond with a surface Ti atom and a surface OH makes a H-bond with another COOH. Additionally, larger van der Waals interactions will be established once the TETT molecule bends towards the surface. If we look at the evolution in time of the structural parameters (Fig. 5a), we observe that the SiO–Ti distances are always between 1.85–1.90 Å. Also the Si–O–Ti angles are maintained around 135° and the θ angle (defined in Fig. S9†), starting from a large value around 60–70°, slowly decreases to reach an equilibrium value around 15–20°, which is a clear indication that the spontaneous tendency of the molecule to bend towards the curved surface.

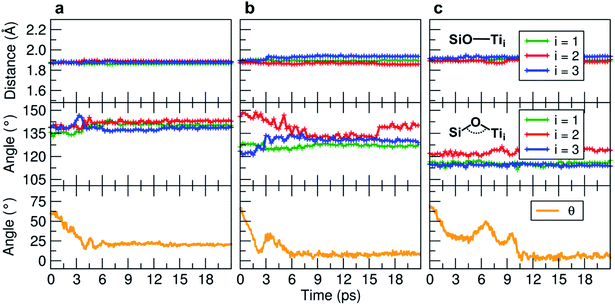Fig. 5 Evolution of the MD indicators: in the upper graphs the SiO–Ti distances (in Å), in the middle graphs the corresponding Si–O–Ti angles (in °), and in the lower graphs the evolution of the θ angle (in °). The θ angle is defined in Fig. S9.† Three MD runs are reported: (a) evolution of the TETT molecule on the tri-site A (Fig. 4), (b) evolution of the TETT molecule on the tri-site B (Fig. 6), and (c) evolution of the TETT molecule on the tri-site C (Fig. 7).

3.4.2 Tri-site B – MD simulations. Similarly to the previous case, for the TETT linker bound to the tri-site B, we have performed four different simulation runs at 300 K, followed by full atomic relaxation. We have obtained the four model structures shown in Fig. S11,† which are characterized by different types of interaction with the surface: CO–Ti or HOCO–Ti or H-bonds with TETT both as donor or acceptor. The most stable optimized structure after MD is also shown in Fig. 6b and compared to the starting geometry from the previous section in Fig. 6a, where only the silanol groups interact with the surface. The SiO–Ti bonds are ∼1.88 in both structures. One can clearly observe that the TETT folds and gets close to the curved surface forming coordinative interactions with the surface Ti atoms with two O atoms of two different COOH groups and forming donor H-bonds through the OH of one COOH group. The binding energy largely increases (by 1.9 eV) upon molecular folding, also because of the closer contact between the molecule and the surface atoms that enhances the van der Waals interactions. In Fig. 5b, we can analyze the time evolution of the structural parameters of SiO–Ti distances, Si–O–Ti angles and of the θ angle. The variations are analogous to those discussed for the TETT on tri-site A (Fig. 5a), except that there are some more oscillations, that the SiO–Ti bonds are not all exactly the same, the Si–O–Ti angles are more distorted and the θ angle (defined in Fig. S9†) gets quite soon close to zero indicating a strong interaction of the extreme tail of TETT with the surface (see Fig. S11†).

Fig. 6 Tridentate adsorption mode (side views) and adsorption energy per TETT molecule (in eV) on the tri-site B of the spherical NP (in Fig. 2), as obtained by the DFTB-D3: (a) optimized starting geometry at 0 K; (b) optimized structure from the last snapshot of the MD run. Ti atoms are shown in cyan, O atoms in red, H atoms in white, Si atoms in yellow, C atoms in green and N atoms in blue. Relevant H-bonds and coordinative bonds (in Å) are represented by dashed lines and solid lines, respectively.

3.4.3 Tri-site C – MD simulations. For the TETT linker bound to the tri-site C, we have performed six different simulation runs at 300 K, followed by full atomic relaxation that lead to the structures in Fig. S12.† In Fig. 7 we report the starting optimized structure where the TETT is interacting with the TiO₂ nanoparticle only through the SiO–Ti anchoring bonds (Fig. 7a) and the most stable configuration obtained after MD simulation (Fig. 7b). In analogy with what observed for the previous tri-sites A and B considered above, the TETT molecule tends to fold during the MD simulation to maximize the van der Waals interactions and to establish three OHCO–Ti coordinative bonds and several H-bonds as donor species. The TETT binding energy, for the two optimized structures before and after MD is found to increase by more than 2.5 eV.

Fig. 7 Tridentate adsorption mode (side views) and adsorption energy per TETT molecule (in eV) on the tri-site B of the spherical NP (in Fig. 2), as obtained by the DFTB-D3: (a) optimized starting geometry at 0 K; (b) optimized structure from the last snapshot of the MD run. Ti atoms are shown in cyan, O atoms in red, H atoms in white, Si atoms in yellow, C atoms in green and N atoms in blue. Relevant H-bonds and coordinative bonds (in Å) are represented by dashed lines and solid lines, respectively.

During the MD run, the structural parameters show a similar evolution as observed for TETT on other tri-sites (compare Fig. 5c with Fig. 5a and b). The SiO–Ti are kept rather constant, the Si–O–Ti angles are slightly asymmetric and finally the θ angle, after some oscillations, approaches zero due to the close interaction of the furthest portion of the TETT molecule with the surface.

3.5 Higher TETT coverage on the curved surface

In the previous sections, we have shown that the tri-dentate binding modes provide the largest binding energy and are stable throughout the MD simulations for different surface tri-sites. We have also seen that the molecule tends to fold and establish as many interactions as possible with the oxide surface, even at the expenses of some intramolecular H-bonds. The next step of investigation concerns the increasing coverage of TETT molecules on the nanoparticle. We have considered two different regimes, i.e. a medium and a full coverage.

3.5.1 Medium coverage. At medium coverage, 22 TETT molecules anchor the TiO₂ spherical nanoparticles through SiO–Ti bonds (total number of atoms of the system is 1689). The highest number of TETT units has been bound to the surface through a tridentate adsorption mode on tri-sites A, B and C and their equivalents for symmetry, which are four for each site (see Fig. 8a). In this way we could host twelve tridentate TETT units (4 × A, 4 × B and 4 × C). Then, we added other four TETT units in the tri-H-dentate fashion (described in the Section 3.3) on the tri-site E and its symmetry equivalents (4 × E). Two more TETT units are bound in a bidentate mode to a surface bi-site at the north pole and at the south pole of the nanoparticle. Finally, four TETT molecules are bound in a bidentate fashion to the site D. The total number of SiO–Ti bonds is 56. The average binding energy per SiO–Ti bond is −1.53 eV, whereas that per TETT molecule is −2.69 eV.

Fig. 8 In (a) the map of the sites on the spherical TiO₂ NP that bind TETT in the monodentate, bidentate, tri-H-dentate and tridentate adsorption modes. The tri-H-dentate and tridentate symmetrical equivalents sites are shown in light green and sketched by triangles; bi-sites are shown in pink and sketched by ellipsis; mono-sites are shown in violet and sketched by circles. In (b) the 3D structure of the medium coverage model with 22 TETT molecules, and in (c) the high coverage model with 40 TETT molecules. Ti atoms are shown in cyan, O atoms in red, H atoms in white, Si atoms in yellow, C atoms in green and N atoms in blue.

For this medium coverage, we have performed a short MD simulation at 300 K (15 ps), which has been followed by full atomic relaxation. In Fig. 9a, we report the evolution of the θ angle of the 22 anchoring TETT molecules, grouped together according to the type of anchoring mode (tri-, tri-H- and bi-dentate). We observe that, in the case of the tridentate mode, on the tri-site A and B the θ angle soon converge between 20°–70°, whereas on tri-site C some molecules are stable at a null value of the θ angle (defined in Fig. S9†), which means that there is the possibility for these TETT units to bend toward the surface atoms. For the tridentate-H species, the θ angle spans a range between 25°–75°. In the case of the bidentate mode, the θ angles are larger, between 50°–100°, except on the north and south poles of the NP where they are between 25°–50°.

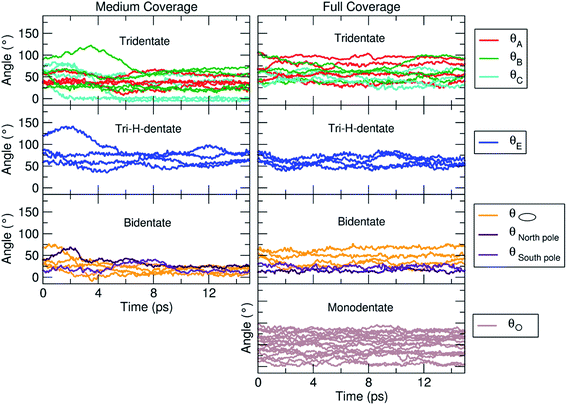Fig. 9 Evolution of the θ angle (in °), defined in Fig. S9,† for each TETT molecule in the medium (Fig. 8b) and full (Fig. 8c) coverage models. The molecules are grouped according to the type of anchoring mode (tri-, tri-H-, bi- and mono-dentate), as defined in Fig. 8a.

At the end of the simulation, after atomic relaxation, we observe that the molecules tend to approach each other or the surface to establish the highest number of H-bond or coordinative bonds, as detailed in Table 2.

Table 2 Overview of the interactions in the medium and full coverage models of TETT on the spherical TiO₂ NP, shown in the Fig. 8b and c, respectively. The established H-bonds are classified in terms of H-bonds with the surface, intermolecular and intramolecular. The number of coordinative bonds in the medium and full coverage is also given

	Medium coverage	High coverage
H-bonds
TETT with the NP surface	38 (13 donors, 25 acceptors)	65 (29 donors, 36 acceptors)
Intermolecular H-donor⋯H-acceptor	26	83
Intermolecular (COOH)⋯(COOH) mono	13	33
Intermolecular (COOH)⋯(COOH) dimer	4	14
Intermolecular (COOH)⋯(SiO3)	2	3
Intermolecular (SiO3H)⋯(COOH)	7	26
Intermolecular (SiO3H)⋯(SiO3H)	—	7
Intramolecular	18	32
Total	82	180
Coordinative bonds
C=O⋯Ti	4	6
HO⋯Ti	2	3

---

First, we observe H-bonds between TETT molecules and the nanoparticle surface. This type of H-bonds sums up to a total of 38, where 13 TETT molecules are H-donors, whereas 25 TETT are H-acceptors. Then, we may distinguish between intermolecular and intramolecular H-bonds. Different types of intermolecular H-bonds are established. They may involve two COOH units on different molecules, either to form one H-bond (where one molecule is donor and the other acceptor, mono in Table 2) or two specular H-bond whether both molecule act as donor and as acceptor (dimer in Table 2). Other intermolecular H-bonds are established between a COOH group of one molecule and the SiO₃ group of another. The intramolecular are within a COOH fragment or they involve the interaction between a COOH group and a SiO₃H fragment. The total number of H-bonds at the medium TETT coverage is 82. We also observe several coordinative interactions between TETT and the NP surface: four between C=O and a surface Ti atom and two between the O atom of an OH and a surface Ti atom.

3.5.2 Full coverage. To reach the full coverage of TETT on the TiO₂ nanoparticle, we added further 18 TETT molecules (total of 40), which could be anchored only through a monodentate mode on the remaining surface undercoordinated Ti sites (see Fig. 8). During the MD simulation, we observe that all the TETT molecules are kept anchored to the surface. Only one SiO–Ti bond of a tridentate TETT molecule is converted back into a SiOH, with the O atom still coordinated to the surface Ti one. The total number of SiO–Ti bonds is 73. The average binding energy per SiO–Ti bond is −2.13 eV, whereas that per TETT molecule is −2.68 eV.

As for the medium coverage, we have performed a short MD simulation at 300 K (15 ps), which has been followed by full atomic relaxation. In Fig. 9b, we report the evolution of the θ angle (defined in Fig. S9†) of the 40 anchoring TETT molecules, grouped together according to the type of anchoring mode (tri-, tri-H-, bi- and mono-dentate). We observe that, in contrast with the medium coverage, here θ angles do not get close to zero as we have observed in the case of the medium coverage. The steric hindrance of the large number of TETT molecules prevents them to bend towards the surface and, therefore, the values of the θ angles are kept rather the same along the entire MD run, i.e. the curves appear flat.

In Table 2 we report the number of H-bond or coordinative bonds established at the end of the MD simulation, after full atomic relaxation. We observe a total number of H-bonds between TETT molecules and the nanoparticle surface of 65, where 29 TETT molecules are H-donors, whereas 36 TETT are H-acceptors. Then, we observe a large increase for both intermolecular and intramolecular H-bonds with respect to what registered for the medium coverage. One additional intermolecular H-bond between a COOH group (donor) of one molecule and the SiO₃ group (acceptor) of another molecule is observed. The intramolecular H-bonds increases from 18 to 32. The total number of H-bonds at the full TETT coverage is 180. We observe few coordinative interactions between TETT and the NP surface, three more than what observed for the medium TETT coverage.

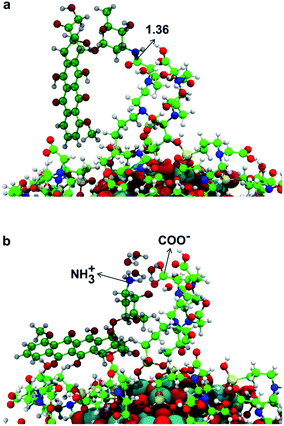
3.6 DOX loading on the fully covered TiO₂–TETT nanosystem

In this section, we present some preliminary results on the tethering of one DOX (doxorubicin) molecule by the fully covered TiO₂–TETT nanosystem. We have considered a covalent and an electrostatic (non covalent) binding mode and succeeded in providing atomistic models for both (as shown in Fig. 10a and b, respectively).

Fig. 10 3D model structures of DOX on the TiO₂ nanoparticle functionalized with 40 TETT molecules as obtained by the DFTB-D3. In (a) DOX is covalently conjugated to the TiO₂–TETT model through the formation of an amide bond between the carboxyl group of TETT and the amino group of DOX, whose distance is indicated by a black arrow. In (b) DOX is non-covalently conjugated through the electrostatic attraction between the deprotonated form of one –COOH group in a TETT molecule (–COO⁻) and the protonated form of –NH₂ group in DOX (–NH₃⁺). Ti atoms are shown in cyan, O atoms in red, H atoms in white, Si atoms in yellow, C atoms of the TETT in green, C atoms of the DOX in dark green and N atoms in blue.

We could localize the two minimum energy structures on the potential energy surface. For the covalent interaction to be established (Fig. 10a), an amide bond must be formed between a primary amino group of DOX with an ending carboxylic group of a TETT residue, producing one water molecule. The non covalent interaction is observed when a proton from the carboxylic group of a TETT residue is transferred to a primary amino group of the DOX molecule, leading to a –COO⁻⋯⁺H₃N– electrostatic interaction. This proton transfer is only stabilized by the presence of some water molecules (in our model we added four water molecules). This latter binding mode, although rather strong, is clearly more easily reversible since it only depends on the DOX protonation/deprotonation process, which can be controlled by pH conditions. For this reason, it can be more effective for the drug transport and release.

4. Conclusions

In this work, we have presented a quantum mechanical investigation, based on the self-consistent charge density functional tight-binding (SCC-DFTB) method, where we provide the details of the functionalization with TETT ligands for a spherical TiO₂ nanoparticle of realistic size (2.2 nm containing 700 atoms). We have determined the mechanism of the ligand anchoring on the various surface sites of a curved surface and established the stability of the tridentate adsorption mode, even during MD simulations at 300 K. As a next step, we have built a medium coverage model (22 TETT) and analyzed the effect of temperature on the interaction between TETT ligands and between TETT ligands and the NP surface, monitoring the degree of folding of the ligands induced by these interactions. Finally, we performed the same type of analysis on a fully covered TiO₂–TETT nanosystem that has been created by adsorbing 40 TETT molecules on the surface. This latter model is a realistic system for tethering DOX molecules for drug transport and release. Thus, we have also localized two minimum energy structures for the covalent and non covalent (electrostatic) type of binding of DOX with a TETT ligand anchored to the TiO₂ nanoparticle.

This computational study unravels fundamental aspects of the TiO₂ nanoparticles functionalization with silane-type ligands (TETT) for drug binding for transport and release. A future development of this work will be the investigation of the drug loading capacity of this drug delivery system and of the pH effect of the surrounding aqueous environment. However, due to the increasing size, we will have to resort to lower level theories. The model structures obtained in the present work will be a good starting point for future studies. A comprehensive understanding of these systems is crucial to develop new experimental protocols for a more efficient drug transport and release in combination with photodynamic therapy, which is allowed by the use of TiO₂ nanoparticles that are excellent photosensitizers and photochemical ROS (reactive oxygen species) producers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful to Dr Igor Baburin for his technical help and for fruitful discussions. The project has received funding from the European Research Council (ERC) under the European Union's HORIZON2020 research and innovation programme (ERC Grant Agreement No. [647020]).

References

1. R. Beutner, J. Michael, B. Schwenzer and D. Scharnweber, J. R. Soc., Interface, 2010, 8, S93–S105.
2. L. Ye, R. Pelton and M. A. Brook, Langmuir, 2007, 23, 5630–5637.
3. S. P. Pujari, L. Scheres, A. T. M. Marcelis and H. Zuilhof, Angew. Chem., Int. Ed., 2014, 53, 6322–6356.
4. E. P. Plueddemann, Silane Coupling Agents, Plenum Press, New York, 2nd edn, 1991.
5. A. Ahmed, C. Bonner and A. D. Desai, Biomed. Microdevices, 2001, 3, 89–96.
6. W. Gu, G. Song, S. Li, C. Shao, C. Yana and L. Ye, RSC Adv., 2014, 4, 50254–50260.
7. N. Chen, C. Shao, Y. Qu, S. Li, W. Gu, T. Zheng, L. Ye and C. Yu, ACS Appl. Mater. Interfaces, 2014, 6, 19850–19857.
8. Y. Qin, L. Sun, X. Li, Q. Cao, H. Wang, X. Tang and L. Ye, J. Mater. Chem., 2011, 21, 18003–18010.
9. S. Liu, X. Y. Meng, J. M. Perez-Aguilar and R. Zhou, Sci. Rep., 2016, 6, 37761.
10. V. Carravetta and S. Monti, J. Phys. Chem. B, 2006, 110, 6160–6169.
11. S. Monti, J. Phys. Chem. C, 2007, 111, 6086–6094.
12. S. Monti, V. Carravetta, C. Battocchioa, G. Iucci and G. Polzonetti, Langmuir, 2008, 24, 3205–3214.
13. B. Luan, T. Huynh and R. Zhou, J. Chem. Phys., 2015, 142, 234102.
14. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268.
15. G. Fazio, L. Ferrighi and C. Di Valentin, J. Phys. Chem. C, 2015, 119, 20735–20746.
16. D. Selli, G. Fazio and C. Di Valentin, J. Chem. Phys., 2017, 147, 164701.
17. E. A. Rozhkova, I. Ulasov, B. Lai, N. M. Dimitrijevic, M. S. Lesniak and T. Rajh, Nano Lett., 2009, 9, 3337–3342.
18. E. A. Rozhkova, I. Ulasov, D.-H. Kim, N. M. Dimitrijevic, V. Novosad, S. Bader, M. S. Lesniak and T. Rajh, Int. J. Nanosci., 2011, 10, 899–908.
19. T. Rajh, L. Chen, K. Lukas, T. Liu, M. Thurnauer and D. Tiede, J. Phys. Chem. B, 2002, 106, 10543–10552.
20. J. Liu, L. de la Garza, L. Zhang, N. M. Dimitrijevic, X. Zuo, D. M. Tiede and T. Rajh, Chem. Phys., 2007, 339, 154–163.
21. M. B. Radoičić, I. A. Janković, V. N. Despotović, D. V. Šojić, T. D. Savić, Z. V. Šaponjić and B. F. Abramović, Appl. Catal., B, 2013, 138, 122–127.
22. L. D. L. Garza, Z. V. Saponjic, N. M. Dimitrijevic, M. C. Thurnauer and T. Rajh, J. Phys. Chem. B, 2006, 110, 680–686.
23. M. Niederberger, G. Garnweitner, F. Krumeich, R. Nesper, H. Cölfen and M. Antonietti, Chem. Mater., 2004, 16, 1202–1208.
24. C. Ronchi, M. Datteo, M. Kaviani, D. Selli and C. Di Valentin, J. Phys. Chem. C, 2019, 123, 10130–10144.
25. C. Ronchi, D. Selli, W. Pipornpong and C. Di Valentin, J. Phys. Chem. C, 2019, 123, 7682–7695.
26. R. Luschtinetz, J. Frenzel, T. Milek and G. Seifert, J. Phys. Chem. C, 2009, 113, 5730–5740.
27. M. Elstner and G. Seifert, Philos. Trans. R. Soc., A, 2014, 372, 1–12.
28. G. Seifert and J.-O. Joswig, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 456–465.
29. B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684.
30. D. Selli, G. Fazio, G. Seifert and C. Di Valentin, J. Chem. Theory Comput., 2017, 13, 3862–3873.
31. A. N. Enyashin and S. Gemming, Phys. Status Solidi B, 2007, 10, 3593–3600.
32. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
33. H. Hu, Z. Lu, M. Elstner, J. Hermans and W. Yang, J. Phys. Chem. A, 2007, 111, 5685–5691.
34. M. Elstner, Theor. Chem. Acc., 2006, 116, 316–325.
35. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. D. L. Pierre, P. D'Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317.
36. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
37. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
38. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
39. B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, CrystEngComm, 2008, 10, 405–410.
40. B. Civalleri, P. D'Arco, R. Orlando, V. R. Saunders and R. Dovesi, Chem. Phys. Lett., 2001, 348, 131–138.

---

Footnote

† Electronic supplementary information (ESI) available: Comparison between DFT and DFTB structures and energetics per one TETT molecule; comparison between DFT and DFTB adsorption energy per one TETT molecule; optimized free TETT molecule after performing MD; DFT energy for three undissociated and three dissociate water molecules on the identified tri-sites in the spherical NP; displacement of the O_2c oxygen in the NP due the TETT adsorption; DFTB adsorption mode and adsorption energy per one TETT molecule on tri site D of the spherical NP; DFTB adsorption modes and adsorption energy per one TETT molecule on the tri-sites B of the spherical NP; DFTB adsorption modes and adsorption energy per one TETT molecule on the tri-sites A of the spherical NP; DFTB adsorption modes and adsorption energy per one TETT molecule on the tri-H-bidentate E and tri-H-bidentate F sites of the spherical NP; definition of the angle θ; DFTB optimized structures for one TETT molecule on the tri-site A of the spherical NP after performing MD; DFTB optimized structures for one TETT molecule on the tri-site B of the spherical NP after performing MD; DFTB optimized structures for one TETT molecule on the tri-site C of the spherical NP after performing MD. See DOI: 10.1039/d0na00275e

---