Tailored viscoelasticity of a polymer cellular structure through nanoscale entanglement of carbon nanotubes

Abstract

A three-dimensional carbon nanotube (CNT) cellular structure presents a unique revelation of microstructure dependent mechanical and viscoelastic properties. Tailored CNT–CNT entanglement demonstrated a direct impact on both the strength and viscosity of the structure. Unlike traditional foams, an increase in the CNT–CNT entanglement progressively increases both the strength and the viscosity. The study reveals that an effective load is directly transferred within the structure through the short-range entanglements (nodes) resulting in an enhanced mechanical strength, whereas the long-range entanglements (bundles) regulate the energy absorption capacity. A three-dimensional structure of entangled CNT–CNT shows ∼15 and ∼26 times enhancement in the storage and loss moduli, respectively. The higher peak stress and energy loss are increased by ∼9.2 fold and ∼8.8 fold, respectively, compared to those of the cellular structures without entanglement. The study also revealed that the viscoelastic properties i.e. the Young's modulus, stress relaxation, strain rate sensitivity and fatigue properties can be modulated by tailoring the CNT–CNT entanglements within the cellular structure. A qualitative analysis is performed using finite element simulation to show the impact of CNT–CNT entanglements on the viscoelastic properties. The finding paves a way for designing a new class of meta-cellular materials which are viscous yet strong for shock absorbing or mechanical damping applications.

---

Introduction

Viscoelastic materials have both elastic (reversible deformation) and viscous (energy dissipation) properties suitable for an extensive range of industrial applications in biomedicals, aerospace, mechanical appliances, etc.^1–3 In polymer based materials, mechanical behavior is dominated by viscoelastic characteristics, which mainly depend on macromolecular distribution, long-range and short-range inter-molecular interactions, configurational rearrangements, etc.⁴ Furthermore, incorporation of filler particles within the polymer matrix contributes to changes in both rheological and viscoelastic properties by significantly changing the morphology of the structure. Introduction of filler particles within the polymer chains induces interactive forces between the filler particles and the polymer chains at the microscopic level, which restricts the movement of polymer chains, and hence there is an increase in both rheological and viscoelastic properties.⁵ Moreover, polymer composites with a nanofiller show a higher degree of viscosity than those with a coarse filler due to the large specific surface area of nanoparticles.^5,6 Among various types of nanofillers, carbon nanotubes (CNTs) are highly preferable for viscoelastic materials due to their outstanding combination of mechanical strength⁷ along with high thermal conductivity (∼9.5 W cm⁻¹ K⁻¹)⁸ and electrical conductivity (within 10² to 10³ S m⁻¹).^9,10 For example, Suhr et al. reported 15-fold enhancement in the damping factor of an engineered CNT–polymer composite structure (damping factor of 0.3) compared to the pristine polymer (damping factor of 0.02).¹¹ A low-density CNT sponge is reported with high viscoelasticity (damping factor of 0.3) and superior compressibility.³ Different types of CNT–polymer composite structures in the form of bulk,¹² foams,^13,14 films,^15,16 an aerogel,¹⁷ a hydrogel,¹⁸ composites,¹¹etc. have shown a high degree of viscoelasticity along with large recovery, fatigue resistance, super compressibility and energy dissipation capacity. In terms of viscous properties, cellular structures have always been the better choice than solid structures due to their high energy absorption capacity¹⁹ and they are also gaining rapid popularity due to their light weight, porosity, high damping factor, mechanical strength and high compressibility.^20–23 During the deformation of open cell foams, viscous friction between the polymer chains, air friction inside the cells and buckling of the cellular walls mainly contribute to the energy absorption within the cellular structure.^20,24,25 In addition, a wide range of viscoelasticity is achieved by tailoring the porosity or structural properties such as crystallinity or phase.^2,26–28 So far, there have been numerous studies reporting the effect of variation in cell size, cell density,^29,30 CNT content,^31–33etc. within CNT polymer foams for controlling the viscosity of the structure. Moreover, a noticeable change in viscoelastic properties can be achieved with the optimum amount of CNT density.³⁴ Besides, modification of the surface chemistry or surface roughness of CNTs can also promote modulation of the viscoelastic properties of a foam.^35,36

It has also been reported that the CNT–CNT entanglement due to van der Waals interaction plays a key role in controlling the deformation behavior such as wrinkling (wavelike distortion) or buckling in CNT based structures.^21,37,38 Using molecular dynamics simulation, Li et al. have shown that inter-tube entanglements within the flexible CNT network act as a key factor in controlling viscoelastic properties such as stress–strain behavior, storage modulus, loss modulus, energy dissipation, etc.³⁹ It is shown in twisted CNT yarn that different properties such as elastic modulus, tensile strength, failure strain, toughness, etc. significantly depend on the CNT–CNT entanglements, which govern the frictional motion between the CNTs during deformation.⁴⁰ However, to date, the role of CNT–CNT entanglements in regulating the viscoelastic properties of CNT polymer cellular structures has not been reported in detail. The designing of cellular structures is crucial to evaluate the role of CNT entanglements in tuning viscoelasticity. We propose a novel and facile approach to develop an open cell meta-foam for controlling CNT entanglements.

In this work, the viscoelastic properties of a CNT/PDMS (polydimethylsiloxane) based cellular structure are tuned by controlling the CNT–CNT entanglements. The control of CNT–CNT entanglements is achieved by varying the mass percentage of CNTs (1 to 5%) within the open cell polymer foams, which also undergo a net change in density (ρ). The mechanical response of the open cell foams is normalized with respect to the corresponding foam density to highlight the microstructural contributions arising from CNT–CNT entanglements only. Both dynamic and quasi-static studies revealed that the viscoelastic properties of the CNT/PDMS open cell foam are a strong function of CNT–CNT entanglements. Unlike conventional foams, the viscosity of these open cell foams enhances without sacrificing the elasticity. It has been observed that in the CNT/PDMS open cell foams, load transfer within the structure occurs through the nodes (short span of two overlapped CNTs), whereas the frictional force within CNT bundles (large span of multiple overlapped CNTs) governs the energy dissipation. These structures sustain large mechanical strain up to 70% with exceptional recoverability (up to 1000 cycles) and high mechanical strength. An increase in the CNT–CNT entanglements causes an enhancement in the storage modulus, loss modulus, tan delta, strain rate sensitivity, stress relaxation time and fatigue, resulting in more viscoelasticity along with high stiffness. Finite element analysis presents a qualitative analysis to observe the key role of CNT–CNT interactions in the modulation of the viscoelasticity of CNT/PDMS open cell foams.

Results and discussion

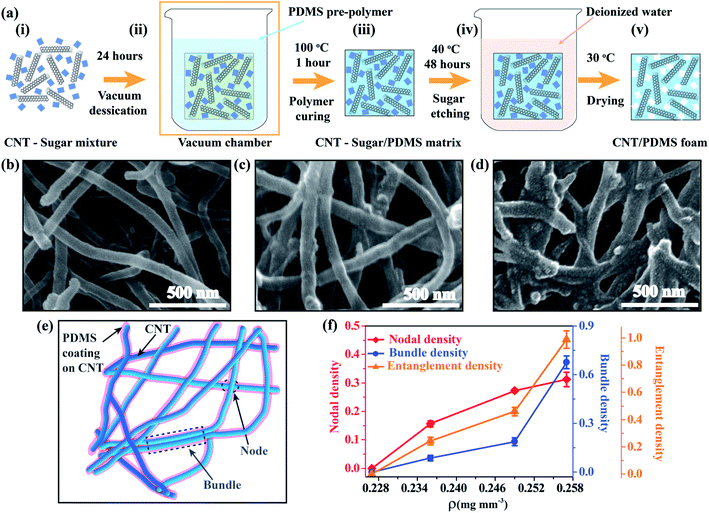
Multiwalled CNTs with diameter 20–50 nm and length 2–3 μm were synthesized using a chemical vapor deposition (CVD) method using toluene as the precursor and ferrocene as the catalyst inside a three-zone furnace at 825 °C. The details of the growth process can be found in ref. 41 and the sample fabrication process is depicted in Fig. 1(a). Commercially available sugar powder was mixed with CNT powder in a 1 : 1 ratio and ball milled with 40 g of steel balls for 20 minutes to avoid CNT agglomeration in PDMS. This process was followed to minimize non-uniform CNT dispersion. The mixture was kept within a cylindrical mold under 5000 pound force for half an hour to obtain cylindrical shaped samples. Thereafter, the CNT–sugar cylinder was dipped into PDMS (Slygard 184, Dow Corning Silicones Malaysia Sdn Bhd), which was prepared by mixing the monomer with the linker in a 10 : 1 weight ratio and kept for 24 hours in a vacuum chamber. PDMS enters the CNT–sugar cylinder through capillary forces.⁴² Then, the sample was cured at 100 °C for 1 hour to fabricate the CNT/PDMS open cell foam. A similar procedure was followed with a sugar–PDMS cylinder to obtain an open cell PDMS foam. Thereafter, all the samples were kept at 50 °C in deionized water for 48 hours to remove sugar from the three-dimensional structures. The resulting samples were dried in an oven at 120 °C overnight to obtain the final structure of interconnected CNT/PDMS and PDMS open cell foams. Three different microstructures of the CNT/PDMS open cell foam were obtained with ρ ∼ 0.236, 0.249 and 0.257 mg mm⁻³ (which is calculated by dividing the mass by the corresponding sample volume) by varying the CNT fraction within the PDMS foam to modulate the viscoelasticity of the open cell foams.

Fig. 1 (a) Schematic of step-by-step fabrication of open cell CNT/PDMS foams. Microstructures of the open cell CNT/PDMS foams with density, ρ, (b) 0.236, (c) 0.249 and (d) 0.257 mg mm⁻³, respectively. (e) Schematic illustration of node and bundle formation within the CNT/PDMS porous structure. (f) Nodal density, bundle density and entanglement density plots with sample density, ρ, of all three CNT/PDMS open cell foams along with those of the pristine PDMS foam.

The microstructures of all three open-cell CNT/PDMS foams as shown in Fig. 1(b)–(d) were analyzed using a Zeiss ultra 55 SEM with 30 kV biasing voltage at 9.5 mm working distance. CNT bundles in all porous structures are coated with the PDMS polymer and connected to each other through adhesive van der Waals force.^43–45 The microstructures reveal that the open cell CNT/PDMS foams exhibit both the nodes and bundles together (Fig. 1(e)). It can be observed from the scanning electron microscopy (SEM) images that as ρ increases, the number of nodes and bundles also increases due to the higher CNT–CNT entanglement. Hence, the inter-nodal distance becomes shorter due to the convergence of multiple CNTs. The degree of entanglement between CNTs was quantified using three parameters, such as nodal density, bundle density and total entanglement density. The calculation was inspired from ref. 3, where the total CNT nodal density was calculated by multiplying the CNT density by the node density per CNT. In this work, the nodal density is indicated by the average areal fraction of CNTs, contributing to node formation, which was calculated through dividing the total area of nodes connected to a single CNT by the total area of a single CNT (details can be found in ESI Fig. S1†). Bundle density was calculated following a similar method (total area of bundles connected to a single CNT/area of a single CNT), whereas the entanglement density is defined as the summation of nodal and bundle densities, describing the total degree of entanglement between the CNTs. Here, areal fractions were estimated from the SEM images of the samples. The analysis for each foam was performed for more than three different images, and for each SEM image, several random spots were selected for the nodes or bundles. The error bars given in Fig. 1(f) indicate the standard deviation of the analysis. Variations in nodal, bundle and entanglement frequencies are plotted as a function of ρ in Fig. 1(f). All three plots show an increasing trend with increasing ρ; however, as ρ increases from 0.249 to 0.257 mg mm⁻³, the bundle density increases by ∼240%, whereas the nodal density increases progressively (∼11%). This signifies that after a certain value of ρ, CNTs show a higher degree of entanglement where most of the nodes converged to form a bundle.

All the density values for the PDMS foam are set to zero as there is no CNT–CNT entanglement (Fig. 1(f)). The open cell PDMS foam with ρ ∼ 0.227 mg mm⁻³ and CNT/PDMS foams with ρ ∼ 0.236, 0.249 and 0.257 mg mm⁻³ are labelled F_0.00, F_0.24, F_0.46 and F_0.98, respectively, based on their corresponding entanglement densities.

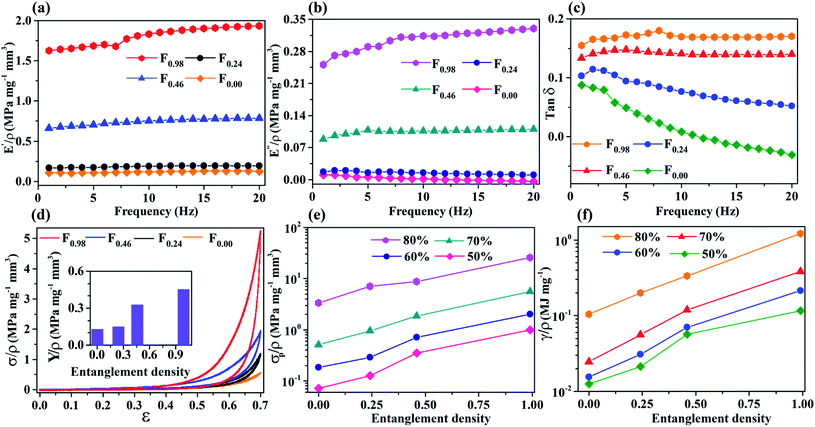
Viscoelastic properties of the open cell foams are quantified by studying the mechanical behavior in both dynamic and quasi-static modes. In the dynamic study, the storage modulus (E′) is associated with elasticity and stiffness of the material, whereas the loss modulus (E′′) describes the energy dissipation ability, and the ratio of loss modulus over storage modulus (known as tan delta (or tan δ) or damping factor) defines the degree of viscosity over elasticity. The mechanical behavior of all the samples under dynamic mode is studied at room temperature (30 °C) using dynamic mechanical analysis (DMA) with an oscillation amplitude of 50 μm over the frequency range from 1 to 20 Hz (Fig. 2(a)–(c)). All the responses have been normalized with the corresponding density of the foams. The results show that the storage modulus in the F_0.98 foam was almost 1472% higher and the loss modulus was 26 times greater than those of the F_0.00 foam (Fig. 2(a) and (b)) at 1 Hz. Similarly, tan delta (or damping ratio) in the F_0.98 foam is ∼0.16 while the F_0.00 foam has a tan delta of ∼0.087 (Fig. 2(c)). For the foams F_0.46 and F_0.24, the magnitude of storage modulus, loss modulus and tan delta lie between the respective values of F_0.98 and F_0.00 foams (Fig. 2(a)–(c)). The overall dynamic studies show that the increasing entanglement density increases the storage and loss moduli and tan delta chronologically and the highest value was obtained for the F_0.98 foam. This indicates that engineering the CNT–CNT entanglements allows tailoring of viscous properties of the CNT/PDMS open cell foams without sacrificing the elastic properties of the structure. This behavior is completely different from that of the existing conventional foams where an increase in stiffness (storage modulus) results in the reduction of the damping factor (tan delta).² In conventional foams, as stiffness increases, the mobility of individual segments decreases resulting in a lowering of the damping factor. In contrast, CNTs in CNT/PDMS foams are attached through the entanglements and can easily slide on each other during compression, thus inducing higher frictional force for the increased damping factor.^2,27

Fig. 2 Normalized (a) storage modulus, (b) loss modulus and (c) tan delta of the open cell foams are plotted as a function of frequency at room temperature. (d) Stress–strain response of the open cell foams for various entanglement densities at a strain rate of 10⁻² s⁻¹, and the inset shows the variation of the normalized Young's modulus with entanglement density. (e) Variation of the normalized peak stress and (f) the normalized energy loss in a full cycle at different compressive strains with entanglement density at a compression rate of 10⁻² s⁻¹.

Quasi-static compression tests are performed to study the effect of entanglement density on the viscoelastic properties of the CNT/PDMS open cell foams (Fig. 2(d)–(f)). The normalized stress (σ/ρ) vs. strain (ε) curves of all four samples, F_0.00, F_0.24, F_0.46 and F_0.98, are plotted at 70% compressive strain (Fig. 2(d)). Loading and unloading trajectories follow different paths and display a finite hysteresis loop. The area bounded by these two trajectories quantifies the amount of energy loss (γ) during the deformation because of the viscoelastic nature of the foams.^46,47 The overall stress–strain plot can be subdivided into three distinct regions: (i) an elastic region at low strains (<40%) where the response is linear, (ii) a plateau region in between 40% and 60% strain, where the slope of the response curve increases gradually, and (iii) a densified state beyond 60% strain, where nonlinearity dominates with a steep rise in the amplitude of stress over small applied strain. The energy loss in a full cycle was measured by calculating the area of the stress–strain curve, which arises because of the frictional force between CNT bundles, arising due to the sliding during the compression.

The CNT/PDMS open cell foam with the highest entanglement density (F_0.98) shows 790% and 840% improvement in the normalized peak stress (σ_p/ρ) and energy loss (γ/ρ), respectively, compared to the only PDMS foam (F_0.00). It was also observed for CNT/PDMS open cell foams that the increase in the inter-tube entanglement density from 0.24 (F_0.24) to 0.98 (F_0.98) induces a substantial enhancement in the normalized peak stress and energy loss by 346% and 190%, respectively. The Young's modulus (Y) of these open cell foams also increases with the progressive increase in entanglement density (inset of Fig. 2(d)) and shows 41%, 213% and 246% enhancement in the normalized Young's modulus (Y/ρ) of the F_0.98 foam compared to the F_0.46, F_0.24 and F_0.00 foams, respectively.

Further to highlight the effect of entanglement density on the foam properties, i.e. strength and viscosity, both the normalized peak stress and energy loss are plotted against entanglement density up to a strain of 80% (Fig. 2(e) and (f)). The graphs show that both the viscosity and mechanical strength increase with increasing entanglement density, which is different from the case of traditional foams, where mechanical strength increases and viscosity decreases.^2,27 Therefore, CNT/PDMS open cell foams are highly applicable for practical usage where viscous but strong materials are needed. It is clear from the results that the entanglement density plays a crucial role in tailoring both the peak stress and the energy loss together with the overall viscoelastic properties of these open cell foams. The nodes present in the foam structure control the strength, whereas the bundles govern the energy dissipation part.² As the nodal density increases, due to a higher degree of inter-connectivity, the effective load easily transfers from one node to another and hence the mechanical strength is improved.^48–50 Also, shorter internodal distance provides high stiffness by enhancing the nodal strength with the higher nodal density. During the loading and unloading process, CNTs present at nodes and bundles reversibly attach and detach from each other through the zipping and unzipping process.^2,3,51 This process is required to overcome the inter-tube frictional force that causes energy loss during unloading which is the origin of viscosity in the foam.^2,11 In the bundles, a larger number of CNTs remain attached with each other over a long span of contact area through van der Waals force, and thus, the energy loss at the bundles is higher than at the nodes. Therefore, bundles are expected to govern the viscous properties (i.e. energy loss) of the foams, and with the increase in entanglement density, bundle density also becomes higher and contributes to a large energy dissipation (Fig. 2(f)).

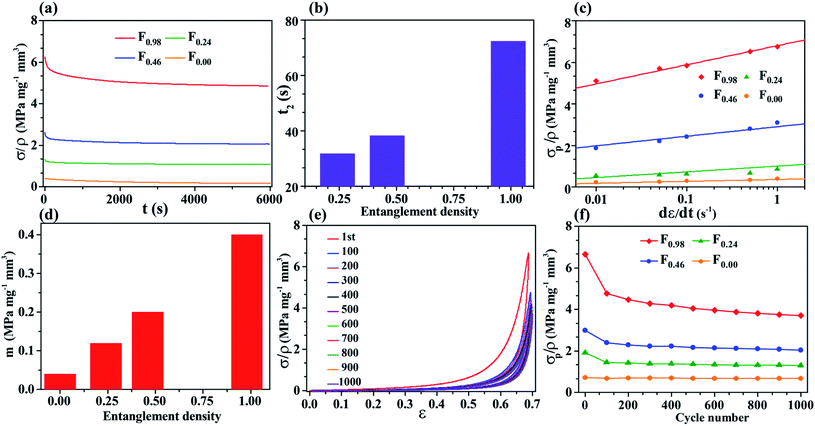
Materials with inherent viscoelasticity always exhibit time dependent mechanical behavior. Stress relaxation measurement is one of the most efficient ways to study the viscoelastic properties of a material by monitoring the variation in stress with time at a constant strain. A compressive strain of 70% was applied for the stress relaxation study on all the foams at a strain rate of 1 s⁻¹ and then the decreasing stress was measured over a period of 6000 s (Fig. 3(a)). The results show that the normalized stress decays over time (t) from the initial value. The resulting response can be fitted using Maxwell's model in an exponential relation given by σ/ρ = ∑σ_i exp^−x/t_i where σ_i is a parameter related to the distributed normalized stress and t_i is the corresponding average relaxation time.^1,52 It is observed from the curve fitting that the PDMS foam i.e. F_0.00 follows single exponential fitting with the relaxation time t₁ ∼ 1500 s, whereas all the CNT/PDMS open cell foams follow double exponential fitting. All the CNT/PDMS open cell foams showed relaxation time t₁ ∼ 1500 s and t₂ in the range of 100 s (Fig. 3(b)). The result confirms that the presence of CNTs within the PDMS foam induces additional relaxation time (t₂), which increases with the increasing entanglement density indicating a higher degree of viscosity.

Fig. 3 (a) Stress relaxation at 70% strain and (b) the variation of stress relaxation time of CNT/PDMS open cell foams with entanglement density. (c) Variation of normalized peak stress with different strain rates at 70% strain and (d) the plot of strain rate sensitivity coefficient vs. entanglement density. (e) Cyclic compression for 1000 cycles of F_0.98 and (f) the variation of normalized peak stress for all the samples at 70% strain with cycle number.

Viscoelastic materials exhibit high strain rate sensitive deformation and with the increase in strain rate, stress increases due to the faster loading and unloading rate.⁴⁷ In this study, all four open cell foams were compressed at 70% strain with the strain rate varying from 0.01 to 1 s⁻¹ (Fig. 3(c)). The density normalized peak stress increases logarithmically with the strain rate and follows the relation σ_p/ρ = σ₀ + mln(dε/dt), where σ₀, dε/dt and m are stress constant, strain rate and strain rate sensitivity coefficient, respectively, which describe the effect of strain rate on the mechanical properties of the structures.⁵³ In Fig. 3(d), m is plotted against entanglement density, where the value of m is nominal for the F_0.00 foam and with the increase in entanglement density, the value of m enhances progressively. The F_0.98 foam shows ∼101%, 236% and 1038% increment in the m value compared to F_0.46, F_0.24 and F_0.00 foams, respectively. Besides m, with the increasing entanglement density, the strength of the material i.e. σ₀ values are 6.8, 2.9, 1 and 0.36 MPa mg⁻¹ mm³ for F_0.98, F_0.46, F_0.24 and F_0.00 foams, respectively, showing higher mechanical strength of the foam structures accordingly. It is also observed that the peak stress enhances with the increase in strain rate (Fig. 3(c)). At a lower strain rate, the deformation is higher, which results in a lower peak stress (Fig. 3(c)) and higher energy loss (ESI Fig. S2(a)†). At a slower strain rate, generally with the application of compressive strain, individual nodes rearrange at the high entropy state by rotation, twisting, bending, etc. During compression, the nodes come closer to each other forming new CNT–CNT contacts because of van der Waals force and the multiple nodes merge together to form a densified structure. Due to the higher adhesion at a lower strain rate, deformation remains within the structure during unloading and shows high energy loss (ESI Fig. S2(a)†). In contrast, at a higher strain rate, nodes come in close proximity to each other for a short span of time, and both inter-tube contact and adhesive force reduce and show higher stress with lower hysteresis loss.⁴⁷ In this case, as the entanglement density increases, both the nodes and bundles suffer a higher order of rearrangement due to the larger numbers of nodes and bundles that result in a larger m value, hence higher viscosity. The F_0.98 foam shows the largest value of m indicating the highest degree of viscoelasticity.

A cyclic compression test was performed at a constant strain of 70% as a function of compression cycle for 1000 cycles at a strain rate of 1 s⁻¹ to study the mechanical recoverability of the open cell foams (Fig. 3(e)). It can be observed that the first cycle shows a distinct stress–strain response from the rest of the cycles and both the peak stress and hysteresis loss are quite higher than those of the later cycles (Fig. 3(f) and ESI Fig. S2(b)†). In subsequent cycles, stress decreases gradually, then it becomes stationary and reaches a constant value, which is due to the cyclic softening of stress within the foams as observed in soft tissues.^46,54 Cyclic softening generally occurs due to the CNT–CNT interaction, relocation and rearrangement within the structures. During the cyclic compression, long range inter-tube van der Waals interaction breaks in the initial cycles and after a few cycles it gradually settles down.⁵⁴ The viscosity of any structure can directly be related to cyclic softening and a highly viscous structure takes a longer time to achieve a constant response. The fatigue curve for the F_0.98 foam (Fig. 3(f)) stabilized approximately after 200 cycles, whereas it became constant after 50 cycles for the other open cell foams, which is attributed to the higher viscosity of the F_0.98 foam, where van der Waals force is highly dominant due to the higher entanglement density.

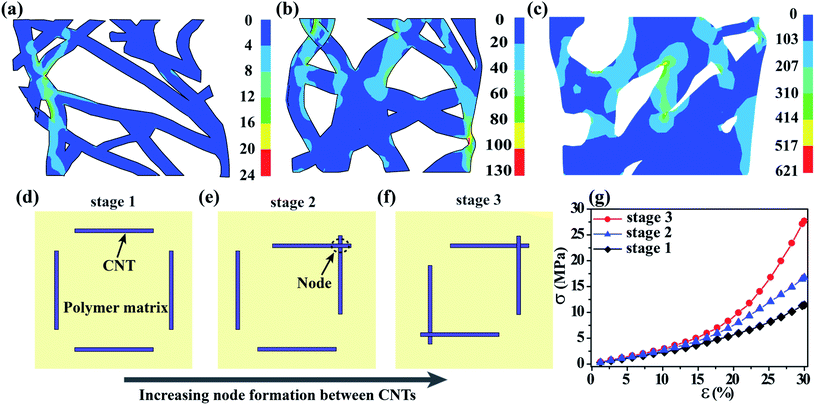
Finite element simulation is performed to evaluate the qualitative analysis of the stress distribution within different microstructures of foams during the compression. For the simulation, an area of 1 × 1 μm² was taken from the SEM image in Fig. 1(b)–(d) and modeled using Ansys software. The analysis was performed by incorporating viscous properties of the PDMS matrix, which contributes to the viscosity of the structure. The simulation does not include the interaction between node–polymer connections i.e. the frictional force between nodes and the polymer. However, for the quantitative measurements, it is expected that the inclusion of frictional force between nodes, nodes and polymer would increase the viscoelasticity of the structure.

Using the hyper-elastic model (Ogden 1^st order), the structures were simulated with the experimental data for a 10% strain. In the Ogden model, the strain energy density (W) is expressed as W = (μ/α) × λ^α, where λ is the stretch (1 + strain) of the hyperelastic material, and μ and α are known as the Ogden modulus and Ogden exponent, respectively.⁵⁵ The variables of the Ogden 1^st order equation, μ and α, were obtained, 5.45 kPa mg mm⁻³, 7.78 for the F_0.24 foam, 28.291 kPa mg mm⁻³, 5.65 for F_0.46 and 153.74 kPa mg mm⁻³, 4.75 for F_0.98 foams, respectively, from the experimental curve fitting. The simulated foam structures are shown in Fig. 4(a)–(c). As the entanglement density increases in F_0.24, F_0.46 and F_0.98 foams, the net stress also enhances; however, within any structure, stress is found to be lower at the nodes and distributed into the entire structure through the nodes. The net stress in the F_0.98 foam was measured to be ∼10 and ∼50 times higher than that of F_0.46 and F_0.24 foams, respectively. A preliminary simulation was performed with four CNTs embedded in a solid PDMS matrix (Fig. 4(d)–(f)) to highlight the function of nodes in predominantly transferring a load within a structure, where (i) in stage-1 four CNTs are randomly distributed in the PDMS polymer without any node formation (Fig. 4(d)), (ii) in stage-2 CNTs form one node (Fig. 4(e)), and (iii) in stage-3 CNTs form two nodes (Fig. 4(f)). For all three stages, the sizes of the PDMS block and CNT were kept the same and the structures were compressed up to 30% strain. For simulation, PDMS was assumed to follow the hyperelastic Ogden model with μ and α being 1.3 MPa and 9.22, respectively (ESI Fig. S3†), and CNTs were assumed to be highly elastic where the Young's modulus and Poisson's ratio were assumed to be 1.28 TPa (ref. 56) and 0.16,⁷ respectively. The stress versus strain graph (Fig. 4(g)) shows that as the node number increases the stress also enhances, which clearly signifies that the nodes are the main bridging factor to transfer load from one CNT to another which results in high stiffness. The most interesting outcome of this simulation is the non-linear stress–strain curve indicating the viscosity of the materials. The non-linearity arises in stage-1 and stage-2 structures at around 20% and 15% strain, whereas the stage-3 structure shows non-linearity from 10% strain signifying the highest degree of viscosity in stage-3 compared to other structures. Qualitatively, the result confirms that without altering the CNT number (or wt%) within the PDMS matrix and only changing the structural distribution i.e. by moderating CNT–CNT interaction, both the stress and viscosity can be modulated, thus opening avenues to design a new structure with improved strength and enhanced viscosity.

Fig. 4 Distribution of von Mises stress at 10% compressive strain in (a) F_0.24, (b) F_0.46 and (c) F_0.98 foams. A schematic illustration is presented for four CNTs embedded in the PDMS matrix with (d) zero nodes in stage 1, (e) one node in stage 2 and (f) two nodes in stage 3. The variation in compressive stress is plotted with the increasing strain for all three stages (g).

The present study is focused on compressive behavior; however, it should be noted that the role of CNT–CNT interaction may differ in the case of tension or shear force. It has been observed for the polymer foams alone that the compressive and the tensile performances are not much different, but there may be a variation in shear performance. Walter et al. carried out both tensile and compressive tests on Divinycell® (cross linked PVC) foam sheets.⁵⁷ The reported values of compressive and tensile moduli did not differ much (typical magnitude difference 50% to 180%). In another study by Sparks and Arvidson, compression, tension and shear tests were performed on a polyurethane foam.⁵⁸ No significant differences in the compression modulus (range 8–50 MPa) and tensile modulus (range 13–28 MPa) were observed, but the shear modulus was very low (range 0.2–0.85 MPa). Thus, an important correlation can be established while studying the CNT/PDMS foam in tension and shear as well.

Conclusion

In summary, a series of open cell CNT/PDMS foams are fabricated with varying microstructures by modulating inter-tube entanglement density. The mechanical behavior revealed a high strength along with an increased degree of viscoelasticity compared to pristine open cell PDMS foams without any CNT–CNT entanglement. The results further show that the incorporation of CNTs within the PDMS foam changes its mechanical behavior. The foam with an entanglement density of 0.98 (F_0.98) shows 1472% and 26 times improvement in storage and loss moduli along with 790% and 840% enhancement in peak stress and energy loss, respectively, compared to the foam with zero entanglement density, F_0.00. The results also confirm that unlike traditional foams both the mechanical strength and viscosity enhance simultaneously with higher entanglement density, which will help in designing a new class of open cell foam structures which are viscous as well as strong. The elasticity and viscosity mainly depend on the nodes and bundles present in the structures. The finite element simulation shows a qualitative analysis revealing that CNT–CNT entanglement plays a key role in modulating both the strength and viscosity of the structure. These open cell foams have potential application in building synthetic biomaterial nanostructures, electromechanical devices, nanocomposites, and nanostructures for the purpose of cushioning, mechanical damping, packaging, shock absorbing, energy dissipation, etc..

Characterization methods

For the dynamic study, a DMA Q800 instrument was used with a compression clamp. The quasi-static compression tests were performed using a Bose electro force (3510 model). Both the height and diameter of the cylindrical samples were kept at 10 mm. Finite element analysis was performed using Ansys mechanical APDL 18.2 student version.

Conflicts of interest

There are no conflicts to declare.

References

1. R. Lakes, Viscoelastic Materials, Cambridge University Press, 2009.
2. M. Xu, D. N. Futaba, M. Yumura and K. Hata, Tailoring Temperature Invariant Viscoelasticity of Carbon Nanotube Material, Nano Lett., 2011, 11, 3279–3284.
3. M. Xu, D. N. Futaba, T. Yamada, M. Yumura and K. Hata, Carbon Nanotubes with Temperature-Invariant Viscoelasticity from −196 °C to 1000 °C, Science, 2010, 330(6009), 1364–1368.
4. J. D. Ferry, Viscoelastic Properties of Polymers, John Wiley and Sons, New York, 3rd edn, 1980.
5. M. Joshi, B. S. Butola, G. Simon and N. Kukaleva, Rheological and Viscoelastic Behavior of HDPE/Octamethyl-POSS Nanocomposites, Macromolecules, 2006, 39, 1839–1849.
6. T. Hanemann and D. V. Szabó, Polymer-Nanoparticle Composites: From Synthesis to Modern Applications, Materials, 2010, 3(6), 3468–3517.
7. S. Gupta, K. Dharamvir and V. K. Jindal, Elastic Moduli of Single-Walled Carbon Nanotubes and Their Ropes, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(16), 165428.
8. J. Che, T. A. Cagın and W. Goddard III, Thermal Conductivity of Carbon Nanotubes, Nanotechnology, 2000, 11, 65–69.
9. P. R. Bandaru, Electrical Properties and Applications of Carbon Nanotube Structures, J. Nanosci. Nanotechnol., 2007, 7, 1–29.
10. B. Marinho, M. Ghislandi, E. Tkalya, C. E. Koning and G. de With, Electrical Conductivity of Compacts of Graphene, Multi-Wall Carbon Nanotubes, Carbon Black, and Graphite Powder, Powder Technol., 2012, 221, 351–358.
11. J. Suhr, N. Koratkar, P. Keblinski and P. Ajayan, Viscoelasticity in Carbon Nanotube Composites, Nat. Mater., 2005, 4(2), 134–137.
12. A. Misra, J. R. Greer and C. Daraio, Strain Rate Effects in the Mechanical Response of Polymer-Anchored Carbon Nanotube Foams, Adv. Mater., 2009, 21, 334–338.
13. R. Verdejo, R. Stämpfli, M. Alvarez-Lainez, S. Mourad, M. A. Rodriguez-Perez, P. A. Brühwiler and M. Shaffer, Enhanced Acoustic Damping in Flexible Polyurethane Foams Filled with Carbon Nanotubes, Compos. Sci. Technol., 2009, 69, 1564–1569.
14. X.-B. Xu, Z.-M. Li, L. Shi, X.-C. Bian and Z.-D. Xiang, Ultralight Conductive Carbon-Nanotube–Polymer Composite, Small, 2007, 3, 408–411.
15. F. X. Wang, W. Y. Liang, Z. Q. Wang, B. Yang, L. He and K. Zhang, Preparation and Property Investigation of Multi-Walled Carbon Nanotube (MWCNT)/Epoxy Composite Films as High-Performance Electric Heating (Resistive Heating) Element, eXPRESS Polym. Lett., 2018, 12, 285–295.
16. A. Badawi and N. Al Hosiny, Dynamic Mechanical Analysis of Single Walled Carbon Nanotubes/Polymethyl Methacrylate Nanocomposite Films, Chin. Phys. B, 2015, 24(10), 105101.
17. J. Zou, J. Liu, A. S. Karakoti, A. Kumar, D. Joung, Q. Li, S. I. Khondaker, S. Seal and L. Zhai, Ultralight Multiwalled Carbon Nanotube Aerogel, ACS Nano, 2010, 4(12), 7293–7302.
18. S. R. Shin, S. M. Jung, M. Zalabany, K. Kim, P. Zorlutuna, S. Kim, M. Nikkhah, M. Khabiry, M. Azize and J. Kong, et al. Carbon-Nanotube-Embedded Hydrogel Sheets for Engineering Cardiac Constructs and Bioactuators, ACS Nano, 2013, 7, 2369–2380.
19. C.-J. Yu, H. H. Eifert, J. Banhart and J. Baumeister, Metal Foaming by a Powder Metallurgy Method: Production, Properties and Applications, Mater. Res. Innovations, 1998, 2, 181–188.
20. L. J. Gibson and M. F. Ashby, Cellular Solids: Structure and Properties, Cambridge University Press, Cambridge, UK, 2nd edn, 1999.
21. A. Cao, P. L. Dickrell, W. G. Sawyer, M. N. Ghasemi-Nejhad and P. M. Ajayan, Super-Compressible Foamlike Carbon Nanotube Films, Science, 2005, 310, 1307–1310.
22. X. Gui, J. Wei, K. Wang, A. Cao, H. Zhu, Y. Jia, Q. Shu and D. Wu, Carbon Nanotube Sponges, Adv. Mater., 2010, 22, 617–621.
23. Z. Dai, L. Liu, X. Qi, J. Kuang, Y. Wei, H. Zhu and Z. Zhang, Three-Dimensional Sponges with Super Mechanical Stability: Harnessing True Elasticity of Individual Carbon Nanotubes in Macroscopic Architectures, Sci. Rep., 2016, 6(January), 1–9.
24. K. Sudhakar, N. N. Reddy, T. Jayaramudu, J. Jayaramudu, A. B. Reddy, B. Manjula and E. R. Sadiku, Aerogels and Foamed Nanostructured Polymer Blends, in Design and Applications of Nanostructured Polymer Blends and Nanocomposite Systems, Elsevier, 2016, pp. 75–99.
25. S. K. Maiti, L. J. Gibson and M. F. Ashby, Deformation and Energy Absorption Diagrams for Cellular Solids, Acta Metall., 1984, 32, 1963–1975.
26. A. Barbetta, M. Dentini, E. M. Zannoni and M. E. De Stefano, Tailoring the Porosity and Morphology of Gelatin-Methacrylate PolyHIPE Scaffolds for Tissue Engineering Applications, Langmuir, 2005, 21(26), 12333–12341.
27. P. Liu, Q. Tan, L. Wu and G. He, Compressive and Pseudo-Elastic Hysteresis Behavior of Entangled Titanium Wire Materials, Mater. Sci. Eng., A, 2010, 527(15), 3301–3309.
28. J. Song, C. Chen, S. Zhu, M. Zhu, J. Dai, U. Ray, Y. Li, Y. Kuang, Y. Li and N. Quispe, et al. Processing Bulk Natural Wood into a High-Performance Structural Material, Nature, 2018, 554(7691), 224–228.
29. S. Pilla, A. Kramschuster, S. Gong, A. Chandra and L.-S. Turng, Solid and Microcellular Polylactide-Carbon Nanotube Nanocomposites, Int. Polym. Process. XXII, 2007, 22, 418–428.
30. M. M. Bernal, M. Martin-Gallego, I. Molenberg, I. Huynen, M. A. López Manchado and R. Verdejo, Influence of Carbon Nanoparticles on the Polymerization and EMI Shielding Properties of PU Nanocomposite Foams, RSC Adv., 2014, 4, 7911.
31. R. Rizvi, O. Khan and H. E. Naguib, Development and Characterization of Solid and Porous Polylactide-Multiwall Carbon Nanotube Composites, Polym. Eng. Sci., 2011, 51, 43–53.
32. J. Thomassin, C. Pagnoulle, L. Bednarz, I. Huynen, R. Jérômea, C. Detrembleura and ACenter, Foams of Polycaprolactone/MWNT Nanocomposites for Efficient EMI Reduction, J. Mater. Chem., 2008, 18, 792–796.
33. E. Ciecierska, M. Jurczyk-Kowalska, P. Bazarnik, M. Gloc, M. Kulesza, M. Kowalski, S. Krauze and M. Lewandowska, Flammability, Mechanical Properties and Structure of Rigid Polyurethane Foams with Different Types of Carbon Reinforcing Materials, Compos. Struct., 2016, 140, 67–76.
34. R. Iglio, S. Mariani, V. Robbiano, L. Strambini and G. Barillaro, Flexible Polydimethylsiloxane Foams Decorated with Multiwalled Carbon Nanotubes Enable Unprecedented Detection of Ultralow Strain and Pressure Coupled with a Large Working Range, ACS Appl. Mater. Interfaces, 2018, 10(16), 13877–13885.
35. C. Zeng, N. Hossieny, C. Zhang, B. Wang and S. M. Walsh, Morphology and Tensile Properties of PMMA Carbon Nanotubes Nanocomposites and Nanocomposites Foams, Compos. Sci. Technol., 2013, 82, 29–37.
36. P. D. Bradford, X. Wang, H. Zhao and Y. T. Zhu, Tuning the Compressive Mechanical Properties of Carbon Nanotube Foam, Carbon, 2011, 49(8), 2834–2841.
37. S. P. Timoshenko and J. M. Gere, Theory of Elastic Stability, McGraw Hill, New York, 1936.
38. A. Pantano, M. C. Boyce and D. M. Parks, Nonlinear Structural Mechanics Based Modeling of Carbon Nanotube Deformation, Phys. Rev. Lett., 2003, 91, 1–4.
39. Y. Li and M. Kröger, Viscoelasticity of Carbon Nanotube Buckypaper: Zipping–Unzipping Mechanism and Entanglement Effects, Soft Matter, 2012, 8, 7822.
40. J. C. Anikea, K. Belayb and J. L. Abot, Effect of Twist on the Electromechanical Properties of Carbon Nanotube Yarns, Carbon, 2019, 142, 491–503.
41. S. K. Reddy, A. Suri and A. Misra, Influence of Magnetic Field on the Compressive Behavior of Carbon Nanotube with Magnetic Nanoparticles, Appl. Phys. Lett., 2013, 102(24), 241919.
42. S. J. Choi, T. H. Kwon, H. Im, D. Il Moon, D. J. Baek, M. L. Seol, J. P. Duarte and Y. K. Choi, A Polydimethylsiloxane (PDMS) Sponge for the Selective Absorption of Oil from Water, ACS Appl. Mater. Interfaces, 2011, 3(12), 4552–4556.
43. Y. Hu, O. Shenderova, Z. Hu, C. W. Padgett and D. W. Brenner, Carbon Nanostructures for Advanced Composites, Rep. Prog. Phys., 2006, 69(6), 1847–1895.
44. M. Wong, M. Paramsothy, X. J. Xu, Y. Ren, S. Li and K. Liao, Physical Interactions at Carbon Nanotube-Polymer Interface, Polymer, 2003, 44, 7757–7764.
45. K. Liao, S. Li, K. Liao and S. Li, Interfacial Characteristics of a Carbon Nanotube–Polystyrene Composite System, Appl. Phys. Lett., 2001, 79, 4225–4227.
46. R. Ghosh, S. K. Reddy, S. Sridhar and A. Misra, Temperature Dependent Compressive Behavior of Graphene Mediated Three-Dimensional Cellular Assembly, Carbon, 2016, 96, 439–447.
47. S. Pathak, E. J. Lim, P. Pour Shahid Saeed Abadi, S. Graham, B. A. Cola and J. R. Greer, Higher Recovery and Better Energy Dissipation at Faster Strain Rates in Carbon Nanotube Bundles: An in-Situ Study, ACS Nano, 2012, 6(3), 2189–2197.
48. R. Andrews, D. Jacques, D. L. Qian and T. Rantell, Multiwall Carbon Nanotubes: Synthesis and Application, Acc. Chem. Res., 2002, 35(12), 1008–1017.
49. L. S. Schadler, S. C. Giannaris and P. M. Ajayan, Load Transfer in Carbon Nanotube Epoxy Composites, Appl. Phys. Lett., 1998, 73(26), 3842–3844.
50. M. Zhang, K. R. Atkinson and R. H. Baughman, Multifunctional Carbon Nanotube Yarns by Downsizing an Ancient Technology, Science, 2004, 306(5700), 1358–1361.
51. Y. Won, Y. Gao, M. A. Panzer, R. Xiang, S. Maruyama, T. W. Kenny, W. Cai and K. E. Goodson, Zipping, Entanglement, and the Elastic Modulus of Aligned Single-Walled Carbon Nanotube Films, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20426–20430.
52. J. Sheng, H. Chen, L. Liu, J. Zhang, Y. Wang and S. Jia, Dynamic Electromechanical Performance of Viscoelastic Dielectric Elastomers, J. Appl. Phys., 2013, 114(13), 134101.
53. S. Oberoi, D. Sonawane and P. Kumar, Effect of Strain Rate and Filler Size on Mechanical Behavior of a Cu Filled Elastomer Based Composite, Compos. Sci. Technol., 2016, 127, 185–192.
54. J. Suhr, P. Victor, L. Ci, S. Sreekala, X. Zhang, O. Nalamasu and P. M. Ajayan, Fatigue Resistance of Aligned Carbon Nanotube Arrays under Cyclic Compression, Nat. Nanotechnol., 2007, 2, 417–421.
55. R. W. Ogden, G. Saccomandi and I. Sgura, Fitting Hyperelastic Models to Experimental Data, Comput. Mech., 2004, 34(6), 484–502.
56. E. W. Wong, P. E. Sheehan and C. M. Lieber, Nanobeam Mechanics: Elasticity, Strength, and Toughness of Nanorods and Nanotubes, Science, 1997, 277(5334), 1971–1975.
57. T. R. Walter, A. W. Richards and G. Subhash, A Unified Phenomenological Model for Tensile and Compressive Response of Polymeric Foams, J. Eng. Mater. Technol., 2009, 131, 011009-1–011009-6.
58. L. L. Sparks and J. M. Arvidson, Thermal and Mechanical Properties of Polyurethane Foams and a Survey of Insulating Concretes at Cryogenic Temperatures, National Bureau of Standards, Boulder, CO, 1984, Report NTIS PB85-100949.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0na00333f

---