Open Access Article
Open Access ArticleZero-mode waveguides can be made better: fluorescence enhancement with rectangular aluminum nanoapertures from the visible to the deep ultraviolet†
Mikhail
Baibakov
,
Aleksandr
Barulin
,
Prithu
Roy
 ,
Jean-Benoît
Claude
,
Satyajit
Patra
,
Jean-Benoît
Claude
,
Satyajit
Patra
 and
Jérôme
Wenger
and
Jérôme
Wenger
 *
*
Aix Marseille Univ, CNRS, Centrale Marseille, Institut Fresnel, 13013 Marseille, France. E-mail: jerome.wenger@fresnel.fr
First published on 23rd July 2020
Abstract
Nanoapertures milled in metallic films called zero-mode waveguides (ZMWs) overcome the limitations of classical confocal microscopes by enabling single molecule analysis at micromolar concentrations with improved fluorescence brightness. While the ZMWs have found many applications in single molecule fluorescence studies, their shape has been mainly limited to be circular. Owing to the large parameter space to explore and the lack of guidelines, earlier attempts using more elaborate shapes have led to unclear conclusions whether or not the performance was improved as compared to a circular ZMW. Here, we comparatively analyze the performance of rectangular-shaped nanoapertures milled in aluminum to enhance the fluorescence emission rate of single molecules from the near infrared to the deep ultraviolet. Our new design is based on rational principles taking maximum advantage of the laser linear polarization. While the long edge of the nanorectangle is set to meet the cut-off size for the propagation of light into the nanoaperture, the short edge is reduced to 30 nm to accelerate the photodynamics while maintaining bright fluorescence rates. Our results show that both in the red and in the ultraviolet, the nanorectangles provide 50% brighter photon count rates as compared to the best performing circular ZMWs and achieve fluorescence lifetimes shorter than 300 ps. These findings can be readily used to improve the performance of ZMWs, especially for fast biomolecular dynamics, bright single-photon sources, and ultraviolet plasmonics.
Introduction
The limited spatial resolution of classical confocal microscopes in the hundreds of nanometers restricts the detection of single fluorescent molecules for two main reasons.1–3 First, the total fluorescence signal collected from a single molecule is bound by the diffraction phenomenon in a homogeneous environment. This is a problem when fast sub-millisecond events need to be probed, requiring high photon count rates.4,5 Second, the molecules have to be diluted to sub-nanomolar concentrations in order to isolate only a single molecule in the diffraction-limited laser spot. The requirement of low concentrations cannot handle enzymatic reactions, protein–protein or protein–DNA interactions which typically occur at much higher micromolar concentrations in physiological conditions.1To overcome these challenges and improve the detection of single fluorescent molecules at high micromolar concentrations, nanoapertures milled in opaque metallic films with diameters from 50 to 200 nm have been introduced to confine the light at the nanometer scale, and have been termed zero-mode waveguides (ZMWs).6,7 The metal nanostructure increases the local excitation intensity thanks to the plasmonic enhancement.8 It also modifies the fluorescence photokinetics decay rates,9 improving the net detected photon count rate per molecule.10–20 Moreover, as the aperture diameter is largely below half the optical wavelength, the light exponentially decays inside the nanoaperture,8 leading to an effective detection volume in the attoliter (10−18 L) range, one thousand fold smaller than with a diffraction-limited confocal microscope.1,6 These improvements have enabled a wide range of applications, including DNA sequencing,21–23 enzymatic reactions,13,24,25 protein–protein interactions,26–30 nanopore detection,31–36 and biomembrane studies.37–41
So far, most studies on zero-mode waveguide nanoapertures consider only circular shapes, as this is an intuitive form which appears also simple to fabricate.42–44 Few reports have considered non-circular aperture shapes such as rectangles,45–50 triangles,51,52 bowties,53,54 C- or H-apertures.55,56 While these more advanced shapes offer more parameters to tune the nanoaperture response, in the absence of clear guidelines the parameter space to explore becomes also larger, and the performance gain as compared to a circular nanoaperture is often unclear or marginal. Achieving the brightest emission rate together with short fluorescence lifetimes is important for applications on fast biomolecular dynamics,4,5 single-photon sources,14 and also for the newly-developing field of ultraviolet plasmonics.57–62
Here we rationally explore the use of rectangular-shaped nanoapertures milled in aluminum to enhance the fluorescence emission rate of single molecules from the near infrared (excitation 635 nm, detection 655 to 755 nm) down to the deep ultraviolet (excitation 266 nm, detection 310 to 410 nm). We use aluminum layers with optimized deposition parameters,63,64 as the response for gold films falls below 600 nm and hence gold films cannot be used efficiently for dyes with emission from the green to the ultraviolet.65 The rationale behind our aluminum nanorectangle design is based on the fact that for a linearly polarized incoming light, the propagation constant inside the nanoaperture is mainly set by the aperture dimension in the direction perpendicular to the laser polarization.8 As for a circular ZMW, the aperture dimension along this direction has to be around the cut-off size to maximize the local intensity gain and the quantum yield enhancement. The aperture dimension along the other direction (parallel to the laser polarization) can be made as short as 30 nm to take maximum advantage of the plasmonic enhancement and accelerate the emission photodynamics. Quite strangely, despite the large interest for zero-mode waveguide nanoapertures, this simple configuration was never tested before.45–49 Here, we go one step further by exploring the design parameter space, quantitatively assessing the performance as compared to circular nanoapertures of optimized dimensions and maximizing the fluorescence enhancement for UV plasmonics.
Results
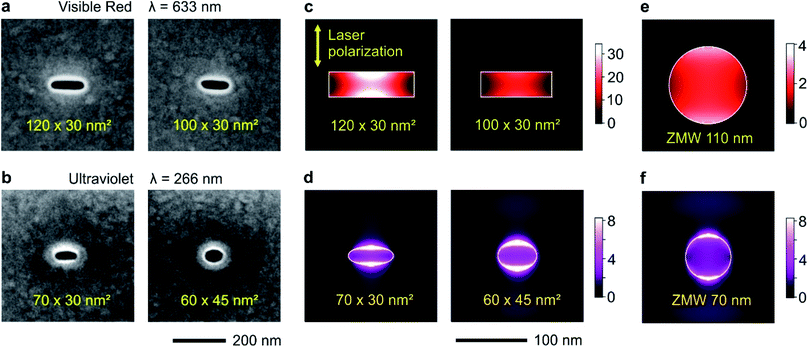
Circular and rectangular nanoapertures are milled using focused ion beam (FIB) on the same aluminum layers deposited microscope coverslips (Fig. 1a and b). The design is guided as the long edge of the nanorectangle (NR) should correspond to the cut-off size for the propagation of the fundamental mode inside the aperture. For rectangular apertures milled in a perfect electrical conductor, the theoretical cut-off size is 0.5 λ/n where n is the refractive index of the medium filling the aperture (for a circular aperture, the cut-off diameter is 0.59 λ/n).8 For real metals, the cut-off dimension is slightly shorter as some part of the electromagnetic field penetrates into the metal.47 From experiments on circular nanoapertures milled in aluminum, we know that the optimum size for experiments in the visible spectral range is about 110 nm,20 while it amounts to 60–70 nm for the UV.60 The other dimension is then made as small as 30 nm to maximize the plasmonic coupling between the two long edges of the NR aperture.45 Please note that the milling depths in the substrate is optimized as well following earlier works,19,27 see Fig. S1 in the ESI.†The numerical simulations indicate that for a 120 × 30 nm2 NR, the local intensity enhancement can be higher than 30× (Fig. 1c), about 8 times higher than for a circular ZMW of optimized diameter (Fig. 1e). Slight deviations from the optimum size tend to decrease the intensity enhancement: for a 100 × 30 nm2 NR, the enhancement is about twice lower at 15×, but still higher than the circular ZMW. The same conclusions still hold in the UV (Fig. 1d and f): while the average intensity enhancement for a circular ZMW is about 3.5×, it increases to 5.6× for a 60 × 45 nm2 NR and 6.0× for a 70 × 30 nm NR. Due to the short UV wavelength, achieving even higher local intensity enhancement values would require NR widths of about 10 nm, which are presently challenging to achieve using FIB.
To verify experimentally these predictions and quantify the performance of nanorectangles to enhance the fluorescence of single molecules, we start by performing experiments in the red spectral range. The fluorescent dyes are Alexa Fluor 647, which do not adsorb on the aluminum surface and enable accurate quantification of the aperture influence.66 The excitation is 635 nm and the collection is performed in the 655–755 nm window (Fig. 2a). Single NR and ZMWs are covered with the solution at 2.8 μM concentration of Alexa Fluor 647. Fluorescence correlation spectroscopy (FCS) and fluorescence lifetime data are then recorded for individual apertures while the fluorescent molecules are constantly diffusing across the aperture volume. Fig. 2b shows the raw and the normalized FCS correlation functions inside a 120 × 30 nm2 NR and a 110 nm diameter circular ZMW.
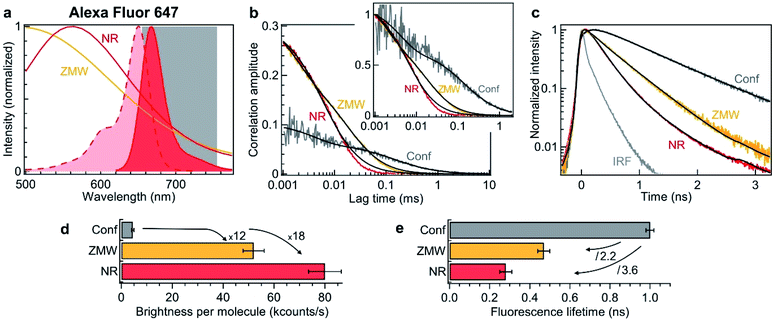 | ||
| Fig. 2 Nanorectangle (NR) performance comparison with a circular zero-mode waveguide (ZMW) nanoaperture for the red fluorescent dye Alexa Fluor 647. Here the NR size is 120 × 30 nm2 and the ZMW diameter is 110 nm. Both are milled in the same 100 nm thick aluminum layer deposited on a borosilicate glass substrate. (a) Absorption and emission spectra of Alexa Fluor 647 (shaded curves). The curves for the ZMW and NR are the computed intensity transmission spectra (normalized at by the peak transmission). The 655–755 nm region used for fluorescence collection is indicated. (b) FCS correlation traces for the NR and ZMW taken at 2.8 μM Alexa concentration. The confocal reference data is recorded at 15 nM. The insert shows the amplitude-normalized correlations, indicating a clear shortening of the diffusion time in the NR. Black lines are numerical fits; the results are summarized in Table 1. (c) Fluorescence lifetime decay traces for the different cases, together with the instrument response function (IRF). Again, the black lines are numerical fits; the results are summarized in Table 2. (d) Average brightness per molecule measured by dividing the average fluorescence intensity by the number of molecules monitored by FCS in (b). (e) Fluorescence lifetime extracted from the data fits in (c). For the ZMW and the NR, a biexponential fit is used and the intensity-averaged lifetime is shown. | ||
The FCS analysis quantifies various parameters: the average number of molecules, their diffusion time across the aperture and their fluorescence brightness (see Methods section). All the fit results for Fig. 2b are summarized in Table 2. Comparing the NR to the ZMW, we observe a lower number of molecules indicating a smaller detection volume. This feature is confirmed independently by the shorter diffusion time of 8 μs in the NR as compared to 25 μs in the ZMW. Moreover, the fluorescence count rate per molecule (CRM) is 1.5× brighter in the NR as compared to the ZMW, leading to a 18× fluorescence enhancement inside the NR as compared to the confocal reference (Fig. 2d).
| N | τ d (μs) | T ds | τ ds (μs) | F (kHz) | CRM (kHz) | |
|---|---|---|---|---|---|---|
| Confocal | 16 | 140 | 0.41 | 4 | 72 | 4.5 |
| ZWM 110 nm | 4.2 | 25 | 0.36 | 1.7 | 219 | 52 |
| NR 120 × 30 nm2 | 3.0 | 8.3 | 0.06 | 2 | 239 | 80 |
| τ 1 (ns) | τ 2 (ns) | I 1 | I 2 | τ avg (ns) | |
|---|---|---|---|---|---|
| Confocal | 1.0 | — | 1 | — | 1.0 |
| ZWM 110 nm | 0.12 | 0.55 | 0.2 | 0.8 | 0.47 |
| NR 120 × 30 nm2 | 0.15 | 0.6 | 0.7 | 0.3 | 0.28 |
To complement the fluorescence brightness enhancement, another important figure of merit is the fluorescence lifetime reduction. For a circular ZMW, 3× shorter lifetimes can be achieved for diameters below 80 nm, but this comes at the expense of higher quenching losses and lower fluorescence count rates, nearly losing the fluorescence enhancement. While preserving the maximum fluorescence brightness on ZMWs, the lifetime reduction is typically about 2×. On the contrary, NRs allow to achieve faster photoemission dynamics (Fig. 2c) and 3.6× reduction in the fluorescence lifetime without compromising on the fluorescence brightness (Fig. 2e and Table 2). Importantly, Fig. 2 shows that for red fluorescent dyes, the NR apertures outperform the circular ZMWs by providing brighter emission rates and faster fluorescence lifetimes. We have also checked these features for green fluorescent dyes Alexa Fluor 546 excited at 557 nm and confirmed the results obtained in the red spectral range. While all these results have been obtained on diffusing molecules and FCS analysis, we confirm the validity of our conclusions by recording fluorescence time traces on immobilized single molecules (ESI Section S2†). Both FCS and single molecule approaches converge towards similar values for the fluorescence brightness enhancement and lifetime reduction. Lastly, the excitation power dependence is reported in the ESI Fig. S6.†
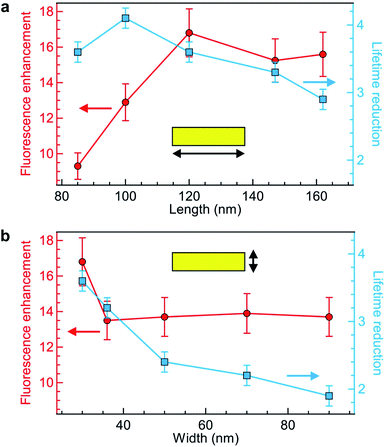
Keeping the fluorescence brightness enhancement and the lifetime reduction as two important figures of merit, we explore the influence of the NR length and width (Fig. 3a and b). The experimental conditions are identical to those of Fig. 2 with Alexa Fluor 647 excited at 635 nm. As indicated by the numerical simulations (Fig. 1c), the NR length plays a key role in setting the fluorescence brightness enhancement, with an optimum value at 120 nm for 635 nm wavelength which corresponds to the cut-off size for the propagation of 635 nm light into the NR. The fluorescence lifetime also depends on the NR length, but more moderately as the lifetime reduction stays in the 3–4× range while the NR length is varied from 85 to 160 nm (Fig. 3a). On the contrary, changing the NR width only affects the fluorescence enhancement for the smallest 30 nm value (Fig. 3b) while for all other widths the brightness is nearly constant. The fluorescence lifetime shows a more pronounced dependence with the NR width as this controls the proximity from the fluorescent dye to the metal: the lifetime is significantly reduced for smaller widths. Altogether from the parameter space exploration in Fig. 3 (and other ESI† not shown), we confirm the rationale behind the NR design: the NR length determines mainly the fluorescence enhancement and should be set close to the cut-off condition, while the NR width sets the fluorescence lifetime reduction which should be as small as possible in the 20 to 30 nm range. Due to nanofabrication difficulties, we could not explore NR widths smaller than 30 nm. However, an optimum must exist for this parameter also as if for instance we consider a 10 nm width, the fluorescent dye is always at less than 5 nm from the metal and then strong fluorescence quenching is expected.67
Comparing our results in Fig. 3 with earlier works on rectangular nanoapertures, fluorescence enhancement factors in the range from 10 to 25 were found for gold films featuring an additional aluminum layer on top,49 or 3 to 10 for gold films featuring an additional silicon layer on at the bottom.50 Previously studied aluminum layers only provided only a moderate 1.3× fluorescence increase,49 but the comparison is difficult as the aluminum deposition parameters critically influence on the material plasmonic response.63 In all cases, the fluorescence lifetime reduction remained below 2.5×, while we achieve now higher values up to 4-fold without compromising on the fluorescence brightness.
Using the information obtained in the red region of the spectrum, we now turn to explore the NR performance in the UV range, using deep UV 266 nm excitation and 310–410 nm fluorescence collection. The fluorescent dye used here is p-terphenyl, which has a quantum yield of 93% in cyclohexane,68 with absorption and emission spectra matching the UV range (Fig. 4a). As compared to Alexa Fluor 647 which has an extinction coefficient of 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 M−1 at 635 nm, the extinction coefficient of p-terphenyl at 266 nm is 5.6× less with 30
000 cm−1 M−1 at 635 nm, the extinction coefficient of p-terphenyl at 266 nm is 5.6× less with 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 M−1. Due to the limited availability of aberration-corrected microscope objectives in the UV, the numerical aperture (NA) used with p-terphenyl is only 0.6 while a 1.2 NA was used in the visible. The transmission of UV objectives is also lower with typically 30% transmission while microscope objectives in the visible range achieve transmission higher than 70%. Altogether, and taking into account the higher 200 μW power used in the UV, the brightness expected per p-terphenyl molecule in the UV is about 20× lower than for Alexa Fluor 647 (comparing the confocal results in Fig. 2, 4, Tables 1 and 3, we retrieve this attenuation value). This calculation shows that despite the best currently available optical components are used in the UV, the brightness per molecule will be low. This highlights the major interest brought by UV plasmonics to enhance this low fluorescence brightness.
400 cm−1 M−1. Due to the limited availability of aberration-corrected microscope objectives in the UV, the numerical aperture (NA) used with p-terphenyl is only 0.6 while a 1.2 NA was used in the visible. The transmission of UV objectives is also lower with typically 30% transmission while microscope objectives in the visible range achieve transmission higher than 70%. Altogether, and taking into account the higher 200 μW power used in the UV, the brightness expected per p-terphenyl molecule in the UV is about 20× lower than for Alexa Fluor 647 (comparing the confocal results in Fig. 2, 4, Tables 1 and 3, we retrieve this attenuation value). This calculation shows that despite the best currently available optical components are used in the UV, the brightness per molecule will be low. This highlights the major interest brought by UV plasmonics to enhance this low fluorescence brightness.
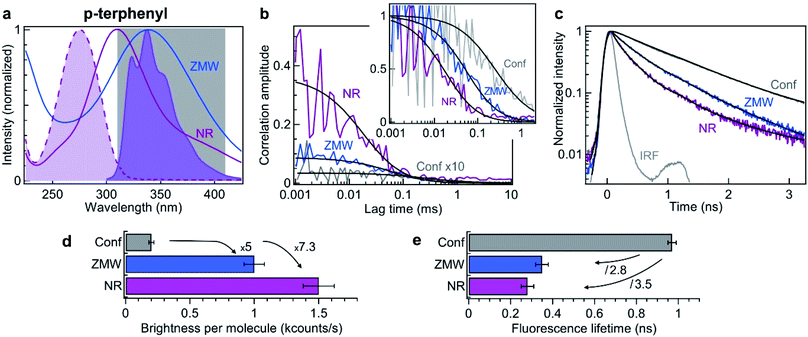 | ||
| Fig. 4 Nanorectangle (NR) performance comparison with a circular zero-mode waveguide (ZMW) nanoaperture for the UV fluorescent dye p-terphenyl. Here the NR size is 60 × 45 nm2 and the ZMW diameter is 70 nm. Both are milled in the same 50 nm thick aluminum layer deposited on quartz substrate. (a) Absorption and emission spectra of p-terphenyl (shaded curves). The curves for the ZMW and NR indicate their computed transmission spectra (normalized at by the peak transmission). The 310–410 nm region used for fluorescence collection is indicated. (b) FCS correlation traces for the NR and ZMW taken at 10 μM concentration in ethanol solution with 40% glycerol. The confocal reference data is recorded at 290 nM and multiplied by 10 for clarity. The insert shows the amplitude-normalized correlations, indicating a clear shortening of the diffusion time in the NR. Black lines are numerical fits; the results are summarized in Table 3. (c) Fluorescence lifetime decay traces for the different cases, together with the instrument response function (IRF). Again, the black lines are numerical fits; the results are summarized in Table 4. (d) Average brightness per molecule measured by dividing the average fluorescence intensity by the number of molecules monitored by FCS in (b). (e) Fluorescence lifetime extracted from the data fits in (c). For the ZMW and the NR, the lifetime of the second component is shown as it is the one representative of the nanostructure influence. | ||
| N | τ d (μs) | F (kHz) | B (kHz) | CRM (kHz) | |
|---|---|---|---|---|---|
| Confocal | 290 | 250 | 56.2 | 0.4 | 0.2 |
| ZWM 70 nm | 8.7 | 86 | 10.3 | 1.5 | 1.0 |
| NR 60 × 45 nm2 | 0.9 | 27 | 2.3 | 1.0 | 1.5 |
Similar experiments to those displayed on Fig. 2 are conducted in the UV using 10 μM solution of p-terphenyl diluted in ethanol with 40% glycerol to slow down the diffusion. Fig. 4b shows the raw and the normalized FCS correlation functions inside a 60 × 45 nm2 NR and a 70 nm diameter circular ZMW. Despite our best attempts, we could not record useful data on the NRs with smaller widths, we suspect some UV-induced photopolymerization occurring preferentially in the narrow width NRs which would disturb our FCS measurements. However, the numerical simulations (Fig. 1d) already indicate that 60 × 45 nm2 NR provides a better performance than a circular ZMW. The FCS analysis reveals a higher amplitude for the NR as compared to the ZMW, indicating a lower number of molecules and a smaller detection volume. All the fit results for Fig. 4b are summarized in Table 3. As for Alexa 647 dyes, this feature is confirmed independently by the shorter diffusion time of 27 ± 5 μs for p-terphenyl in the NR as compared to 86 ± 10 μs in the ZMW (Table 3). Importantly, the fluorescence count rate per molecule (CRM) is 1.5× brighter in the NR as compared to the ZMW, leading to the highest 7.3× fluorescence enhancement inside the NR as compared to the confocal reference (Fig. 4d).
In addition to the FCS data, we investigate the fluorescence lifetime decays (Fig. 4c). Both Alexa Fluor 647 and p-terphenyl have a fluorescence lifetime of about 1 ns in homogeneous medium making the comparison between them quite straightforward. As for Alexa 647, we find that the emission dynamics of p-terphenyl are further accelerated inside the NR as compared to the ZMW (Fig. 4c) with 3.5× reduction in the fluorescence lifetime inside the NR without compromising on the fluorescence brightness (Fig. 4e). All lifetime fit results in the UV are summarized in Table 4.
| τ 1 (ns) | τ 2 (ns) | τ 3 (ns) | I 1 | I 2 | I 3 | τ avg (ns) | |
|---|---|---|---|---|---|---|---|
| Confocal | 0.01 | 0.97 | — | 0.06 | 0.94 | — | 0.91 |
| ZWM 70 nm | 0.01 | 0.35 | 0.91 | 0.14 | 0.28 | 0.57 | 0.62 |
| NR 60 × 45 nm2 | 0.01 | 0.28 | 0.91 | 0.26 | 0.38 | 0.36 | 0.43 |
Altogether, the data in Fig. 4 confirms in the UV the superior performance of rectangular nanoapertures as compared to their circular counterparts. The design concepts derived from the visible experiments remain valid even down to 266 nm. The results are fully scalable and in line with the observations in the red spectral range demonstrating an extended optical characterization from the deep UV to the near infrared.
Conclusions
As compared to conventional circular ZMWs, nanorectangle apertures open new possibilities to achieve brighter fluorescence emission, faster lifetime and smaller detection volume. What previously required a compromise with circular ZMWs (reducing the diameter to achieve small volumes and short lifetimes but at the expense of low photon count rates) can now be obtained simultaneously with an even improved fashion with nanorectangles. We have shown that in the red and in the ultraviolet, NRs provide about 50% brighter photon count rates together with lifetimes shorter than 300 ps. The design principle based on aluminum film holds from the near infrared down to the deep UV, taking maximum advantage of the laser linear polarization. The long edge of the NR (perpendicular to the laser polarization) has to be around the cut-off size to maximize the local intensity gain. The short edge of the NR (parallel to the laser polarization) can be reduced to 30 nm to accelerate the emission photodynamics while maintaining bright emission. These results find application in improving the performance of ZMWs for single molecule analysis at high concentrations, and are especially relevant for monitoring fast biomolecular dynamics,4,5 realizing ultrafast single-photon sources,14 and for interrogating molecules with ultraviolet plasmonics.57–62Methods
Nanorectangle apertures fabrication
An opaque layer of aluminum is deposited by electron-beam evaporation (Bühler Syrus Pro 710) at a 10 nm s−1 rate and a chamber pressure of 5 ×10−7 mbar. For the visible experiments, we use 100 nm thickness on borosilicate glass microscope coverslip, while for UV experiments we use 50 nm aluminum thickness on quartz microscope coverslips. The nanorectangle apertures are then milled using a gallium-based focused ion beam (FEI dual beam DB 235 Strata) with 30 kV voltage and 10 pA current.Visible microscope
The experiments performed on Alexa Fluor 647 dyes in the visible spectral range use a custom build confocal microscope described in ref. 20. A LDH series laser diode (PicoQuant, pulse duration ∼50 ps, 40 MHz repetition rate) is used to excite the molecules at 635 nm with a laser power below 20 μW measured at the microscope entrance port. The laser light is focused by a Zeiss C-Apochromat 63×, 1.2 NA water immersion objective, and the fluorescence is collected by the same objective. A 3-axis piezoelectric stage (Physik Instrumente P-517.3CD) is used to place single nanoapertures on the laser focus spot. A dichroic mirror (ZT 405/488/561/640rpc, Chroma) and an emission filter (ZET405/488/565/640mv2, Chroma) filter the fluorescence light. The detection is performed after a 50 μm pinhole conjugated to the object plane. We use an avalanche photodiodes in single photon counting mode (MPD-5CTC with <50 ps timing jitter, Picoquant). The photodiode output is recorded with a time correlated single photon counting module (HydraHarp 400, Picoquant) featuring 110 ps overall temporal resolution.Ultraviolet microscope
The experiments performed on p-terphenyl dyes in the ultraviolet use a custom build confocal microscope described in ref. 60. A 266 nm picosecond laser (Picoquant LDH-P-FA-266, 70 ps pulse duration, 80 MHz repetition rate) is used with a laser power up to 200 μW at the microscope entrance port. The laser light is focused by a Zeiss Ultrafluar 40×, 0.6 NA glycerin immersion objective, and the fluorescence is collected by the same objective. A dichroic mirror (Semrock FF310-Di01-25-D) and two emission filters (Semrock FF01-300/LP-25 and Semrock FF01-375/110-25) filter the fluorescence light. The detection is performed by a single photon counting photomultiplier tube (Picoquant PMA 175) after a 50 μm pinhole conjugated to the object plane. The photomultiplier tube output is recorded with a time correlated single photon counting module (Picoharp 300, Picoquant) featuring 150 ps overall temporal resolution.FCS analysis
All fluorescence traces are analyzed using Symphotime 64 software (Picoquant). As in our previous works,12,20,60 we fit the FCS correlation functions with a standard Brownian diffusion model taking into account the background fluorescence level and the photoblinking:69,70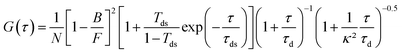 | (1) |
Fluorescence lifetime analysis
The fluorescence decay histograms are fitted using Picoquant SymPhoTime 64 sofware with an iterative reconvolution fit considering the instrument response function (IRF). The fits always consider more that 95% of the total collected photons in the region of interest. All the fit parameters are summarized in Tables 2 and 4. For Alexa Fluor 647, the data for the confocal reference is fitted with a single exponential decay, while for the nanoapertures a biexponential function provides a better fit. While the signal to background is excellent in the visible, for the UV experiments we decide to include a supplementary component with fixed 10 ps lifetime to account for the laser scattering and the metal photoluminescence. For UV experiments, we also observe that the long decay tail has a 0.91 ns lifetime similar to the lifetime of p-terphenyl in the confocal homogeneous environment. This contribution is likely to stem from a residual emission from molecules lying away from the aperture which do not experience the near-field enhancement from the plasmonic nanostructure. Therefore, in the analysis of Fig. 4e, we decide to focus on the central component which represents essentially the nanoaperture contribution.Numerical simulations
The intensity distributions displayed on Fig. 1c–f are computed using finite-difference time-domain (FDTD) method with RSoft Fullwave software. The simulated geometry accounts for the fabricated nanorectangles dimensions (Fig. 1a and b). The simulations are run with 0.5 nm mesh size for the UV (1 nm for the visible) and are checked for convergence after more than ten optical periods. The real and imaginary parts of aluminum permittivity are taken from ref. 64, the other refractive indexes are taken from ref. 71.Funding sources
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement 723241) and from the Agence Nationale de la Recherche (ANR) under grant agreement ANR-17-CE09-0026-01.Conflicts of interest
The authors declare no competing financial interest.References
- P. Holzmeister, G. P. Acuna, D. Grohmann and P. Tinnefeld, Chem. Soc. Rev., 2014, 43, 1014–1028 RSC.
- D. Punj, P. Ghenuche, S. B. Moparthi, J. de Torres, V. Grigoriev, H. Rigneault and J. Wenger, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2014, 6, 268–282 CAS.
- E. D. Fabrizio, S. Schlücker, J. Wenger, R. Regmi, H. Rigneault, G. Calafiore, M. West, S. Cabrini, M. Fleischer, N. F. van Hulst, M. F. Garcia-Parajo, A. Pucci, D. Cojoc, C. A. E. Hauser and M. Ni, J. Opt., 2016, 18, 063003 CrossRef.
- B. Schuler and H. Hofmann, Curr. Opin. Struct. Biol., 2013, 23, 36–47 CrossRef CAS.
- A. Soranno, B. Buchli, D. Nettels, R. R. Cheng, S. Müller-Späth, S. H. Pfeil, A. Hoffmann, E. A. Lipman, D. E. Makarov and B. Schuler, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17800–17806 CrossRef CAS.
- M. J. Levene, J. Korlach, S. W. Turner, M. Foquet, H. G. Craighead and W. W. Webb, Science, 2003, 299, 682–686 CrossRef CAS.
- P. Zhu and H. G. Craighead, Annu. Rev. Biophys., 2012, 41, 269–293 CrossRef CAS.
- F. J. Garcia-Vidal, L. Martin-Moreno, T. W. Ebbesen and L. Kuipers, Rev. Mod. Phys., 2010, 82, 729–787 CrossRef.
- V. V. Klimov, Phys. Rev. Appl., 2019, 12, 014049 CrossRef CAS.
- Y. Liu and S. Blair, Opt. Lett., 2003, 28, 507–509 CrossRef CAS.
- H. Rigneault, J. Capoulade, J. Dintinger, J. Wenger, N. Bonod, E. Popov, T. W. Ebbesen and P.-F. Lenne, Phys. Rev. Lett., 2005, 95, 117401 CrossRef.
- J. Wenger, D. Gérard, J. Dintinger, O. Mahboub, N. Bonod, E. Popov, T. W. Ebbesen and H. Rigneault, Opt. Express, 2008, 16, 3008–3020 CrossRef CAS.
- J. Wenger, D. Gérard, H. Aouani, H. Rigneault, B. Lowder, S. Blair, E. Devaux and T. W. Ebbesen, Anal. Chem., 2009, 81, 834–839 CrossRef CAS.
- J. T. Choy, B. J. M. Hausmann, T. M. Babinec, I. Bulu, M. Khan, P. Maletinsky, A. Yacoby and M. Lončar, Nat. Photonics, 2011, 5, 738–743 CrossRef CAS.
- X. Jiao, E. M. Peterson, J. M. Harris and S. Blair, ACS Photonics, 2014, 1, 1270–1277 CrossRef CAS.
- E. Pibiri, P. Holzmeister, B. Lalkens, G. P. Acuna and P. Tinnefeld, Nano Lett., 2014, 14, 3499–3503 CrossRef CAS.
- M. S. Alam, F. Karim and C. Zhao, Nanoscale, 2016, 8, 9480–9487 RSC.
- W. E. Martin, B. R. Srijanto, C. P. Collier, T. Vosch and C. I. Richards, J. Phys. Chem. A, 2016, 120, 6719–6727 CrossRef CAS.
- M. Wu, W. Liu, J. Hu, Z. Zhong, T. Rujiralai, L. Zhou, X. Cai and J. Ma, Opt. Express, 2019, 27, 19002–19018 CrossRef CAS.
- M. Baibakov, S. Patra, J.-B. Claude, A. Moreau, J. Lumeau and J. Wenger, ACS Nano, 2019, 13, 8469–8480 CrossRef CAS.
- J. Eid, A. Fehr, J. Gray, K. Luong, J. Lyle, G. Otto, P. Peluso, D. Rank, P. Baybayan, B. Bettman, A. Bibillo, K. Bjornson, B. Chaudhuri, F. Christians, R. Cicero, S. Clark, R. Dalal, A. deWinter, J. Dixon, M. Foquet, A. Gaertner, P. Hardenbol, C. Heiner, K. Hester, D. Holden, G. Kearns, X. Kong, R. Kuse, Y. Lacroix, S. Lin, P. Lundquist, C. Ma, P. Marks, M. Maxham, D. Murphy, I. Park, T. Pham, M. Phillips, J. Roy, R. Sebra, G. Shen, J. Sorenson, A. Tomaney, K. Travers, M. Trulson, J. Vieceli, J. Wegener, D. Wu, A. Yang, D. Zaccarin, P. Zhao, F. Zhong, J. Korlach and S. Turner, Science, 2009, 323, 133–138 CrossRef CAS.
- S. Uemura, C. E. Aitken, J. Korlach, B. A. Flusberg, S. W. Turner and J. D. Puglisi, Nature, 2010, 464, 1012–1017 CrossRef CAS.
- J. Larkin, R. Y. Henley, V. Jadhav, J. Korlach and M. Wanunu, Nat. Nanotechnol., 2017, 12, 1169–1175 CrossRef CAS.
- Y. Zhao, D. Chen, H. Yue, M. M. Spiering, C. Zhao, S. J. Benkovic and T. J. Huang, Nano Lett., 2014, 14, 1952–1960 CrossRef CAS.
- M. P. Goldschen-Ohm, D. S. White, V. A. Klenchin, B. Chanda and R. H. Goldsmith, Angew. Chem., 2017, 129, 2439–2442 CrossRef.
- K. T. Samiee, M. Foquet, L. Guo, E. C. Cox and H. G. Craighead, Biophys. J., 2005, 88, 2145–2153 CrossRef CAS.
- T. Miyake, T. Tanii, H. Sonobe, R. Akahori, N. Shimamoto, T. Ueno, T. Funatsu and I. Ohdomari, Anal. Chem., 2008, 80, 6018–6022 CrossRef CAS.
- T. Sandén, R. Wyss, C. Santschi, G. Hassaïne, C. Deluz, O. J. F. Martin, S. Wennmalm and H. Vogel, Nano Lett., 2012, 12, 370–375 CrossRef.
- J. Chen, R. V. Dalal, A. N. Petrov, A. Tsai, S. E. O'Leary, K. Chapin, J. Cheng, M. Ewan, P.-L. Hsiung, P. Lundquist, S. W. Turner, D. R. Hsu and J. D. Puglisi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 664–669 CrossRef CAS.
- A. Barik, L. M. Otto, D. Yoo, J. Jose, T. W. Johnson and S.-H. Oh, Nano Lett., 2014, 14, 2006–2012 CrossRef CAS.
- D. Garoli, H. Yamazaki, N. Maccaferri and M. Wanunu, Nano Lett., 2019, 19, 7553–7562 CrossRef CAS.
- A. B. Dahlin, Analyst, 2015, 140, 4748–4759 RSC.
- T. Auger, J. Mathé, V. Viasnoff, G. Charron, J.-M. Di Meglio, L. Auvray and F. Montel, Phys. Rev. Lett., 2014, 113, 028302 CrossRef.
- O. N. Assad, T. Gilboa, J. Spitzberg, M. Juhasz, E. Weinhold and A. Meller, Adv. Mater., 2017, 29, 1605442 CrossRef.
- V. Jadhav, D. P. Hoogerheide, J. Korlach and M. Wanunu, Nano Lett., 2019, 19, 921–929 CrossRef.
- D. V. Verschueren, S. Pud, X. Shi, L. De Angelis, L. Kuipers and C. Dekker, ACS Nano, 2019, 13, 61–70 CrossRef CAS.
- K. T. Samiee, J. M. Moran-Mirabal, Y. K. Cheung and H. G. Craighead, Biophys. J., 2006, 90, 3288–3299 CrossRef CAS.
- J. Wenger, F. Conchonaud, J. Dintinger, L. Wawrezinieck, T. W. Ebbesen, H. Rigneault, D. Marguet and P.-F. Lenne, Biophys. J., 2007, 92, 913–919 CrossRef CAS.
- C. V. Kelly, B. A. Baird and H. G. Craighead, Biophys. J., 2011, 100, L34–L36 CrossRef CAS.
- C. V. Kelly, D. L. Wakefield, D. A. Holowka, H. G. Craighead and B. A. Baird, ACS Nano, 2014, 8, 7392–7404 CrossRef CAS.
- C. I. Richards, K. Luong, R. Srinivasan, S. W. Turner, D. A. Dougherty, J. Korlach and H. A. Lester, Nano Lett., 2012, 12, 3690–3694 CrossRef CAS.
- M. Foquet, K. T. Samiee, X. Kong, B. P. Chauduri, P. M. Lundquist, S. W. Turner, J. Freudenthal and D. B. Roitman, J. Appl. Phys., 2008, 103, 034301 CrossRef.
- C.-H. Teng, T. A. Lionberger, J. Zhang, E. Meyhöfer and P.-C. Ku, Nanotechnology, 2012, 23, 455301 CrossRef.
- R. M. Jamiolkowski, K. Y. Chen, S. A. Fiorenza, A. M. Tate, S. H. Pfeil and Y. E. Goldman, PLoS One, 2019, 14, e0222964 CrossRef CAS.
- A. Degiron, H. J. Lezec, N. Yamamoto and T. W. Ebbesen, Opt. Commun., 2004, 239, 61–66 CrossRef CAS.
- J. Wenger, P.-F. Lenne, E. Popov, H. Rigneault, J. Dintinger and T. W. Ebbesen, Opt. Express, 2005, 13, 7035–7044 CrossRef CAS.
- F. J. García-Vidal, L. Martín-Moreno, E. Moreno, L. K. S. Kumar and R. Gordon, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 153411 CrossRef.
- C. Zhao, Y. Liu, J. Yang and J. Zhang, Nanoscale, 2014, 6, 9103–9109 RSC.
- P. Ponzellini, X. Zambrana-Puyalto, N. Maccaferri, L. Lanzanò, F. D. Angelis and D. Garoli, Nanoscale, 2018, 10, 17362–17369 RSC.
- X. Zambrana-Puyalto, P. Ponzellini, N. Maccaferri, E. Tessarolo, M. G. Pelizzo, W. Zhang, G. Barbillon, G. Lu and D. Garoli, Chem. Commun., 2019, 55, 9725–9728 RSC.
- D. Molenda, G. C. des Francs, U. C. Fischer, N. Rau and A. Naber, Opt. Express, 2005, 13, 10688–10696 CrossRef CAS.
- P. Schön, N. Bonod, E. Devaux, J. Wenger, H. Rigneault, T. W. Ebbesen and S. Brasselet, Opt. Lett., 2010, 35, 4063–4065 CrossRef.
- G. Lu, W. Li, T. Zhang, S. Yue, J. Liu, L. Hou, Z. Li and Q. Gong, ACS Nano, 2012, 6, 1438–1448 CrossRef CAS.
- M. Mivelle, T. S. van Zanten, L. Neumann, N. F. van Hulst and M. F. Garcia-Parajo, Nano Lett., 2012, 12, 5972–5978 CrossRef CAS.
- E. X. Jin and X. Xu, Appl. Phys. Lett., 2005, 86, 111106 CrossRef.
- S. Fore, Y. Yuen, L. Hesselink and T. Huser, Nano Lett., 2007, 7, 1749–1756 CrossRef CAS.
- X. Jiao, E. M. Peterson, J. M. Harris and S. Blair, ACS Photonics, 2014, 1, 1270–1277 CrossRef CAS.
- X. Jiao, Y. Wang and S. Blair, J. Phys. D: Appl. Phys., 2015, 48, 184007 CrossRef.
- Y. Wang, E. M. Peterson, J. M. Harris, K. Appusamy, S. Guruswamy and S. Blair, J. Phys. Chem. C, 2017, 121, 11650–11657 CrossRef CAS.
- A. Barulin, J.-B. Claude, S. Patra, N. Bonod and J. Wenger, Nano Lett., 2019, 19, 7434–7442 CrossRef CAS.
- D. Gérard and S. K. Gray, J. Phys. D: Appl. Phys., 2014, 48, 184001 CrossRef.
- Y. Kumamoto, A. Taguchi and S. Kawata, Adv. Opt. Mater., 2019, 7, 1801099 CrossRef.
- M. W. Knight, N. S. King, L. Liu, H. O. Everitt, P. Nordlander and N. J. Halas, ACS Nano, 2014, 8, 834–840 CrossRef CAS.
- K. M. McPeak, S. V. Jayanti, S. J. P. Kress, S. Meyer, S. Iotti, A. Rossinelli and D. J. Norris, ACS Photonics, 2015, 2, 326–333 CrossRef CAS.
- J. de Torres, P. Ghenuche, S. B. Moparthi, V. Grigoriev and J. Wenger, ChemPhysChem, 2015, 16, 782–788 CrossRef CAS.
- S. Patra, M. Baibakov, J.-B. Claude and J. Wenger, Sci. Rep., 2020, 10, 5235 CrossRef CAS.
- S. Kühn, G. Mori, M. Agio and V. Sandoghdar, Mol. Phys., 2008, 106, 893–908 CrossRef.
- I. Berlman, Handbook of florescence spectra of Aromatic Molecules, Academic press, 2nd edn, 1971 Search PubMed.
- T. Kohl and P. Schwille, in Microscopy Techniques, ed. J. Rietdorf, Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 107–142 Search PubMed.
- J. Widengren and Ü. Mets, in Single Molecule Detection in Solution, John Wiley & Sons, Ltd, 2003, pp. 69–120 Search PubMed.
- M. N. Polyanskiy, Refractive index database, https://refractiveindex.info, accessed July 19, 2019 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Influence of the milling depth, single molecule fluorescence time traces in circular ZMWs. See DOI: 10.1039/d0na00366b |
| This journal is © The Royal Society of Chemistry 2020 |