Open Access Article
Open Access ArticleStrong suppression of emission quenching in core quantum dots coupled to monolayer MoS2†
H. L.
Pradeepa
 ,
Aveek
Bid
,
Aveek
Bid
 and
Jaydeep K.
Basu
and
Jaydeep K.
Basu
 *
*
Department of Physics, Indian Institute of Science, Bangalore 560012, India. E-mail: basu@iisc.ac.in
First published on 6th July 2020
Abstract
Non-radiative processes like energy and charge transfer in 0D–2D semiconductor quantum dot (QD)-transition metal dichalcogenides (TMDs) and other two-dimensional layered materials, like graphene and analogs, leading to strong quenching of the photoluminescence (PL) of the usually highly emissive QDs, have been widely studied. Here we report control of the emission efficiency of core QDs placed in close proximity to the monolayers of MoS2. The QDs are transferred in the form of a high-density compact monolayer with the dot–dot separation, δ as well as the MoS2–QD separation, d, being controlled through chemical methods. While at larger separations we observe some quenching due to non-radiative processes, at smaller separations we observe enhanced emission from QDs on MoS2 as compared to the reference despite the presence of significant non-radiative charge transfer. Interestingly, at small separations δ, we see evidence of strong dot–dot interactions and a significant red shift of QD PL which enhances spectral overlap with the B exciton of MoS2. However, we observe significant reduction of PL quenching of QDs relative to longer δ and d cases, despite increased probability of non-radiative resonant energy transfer to MoS2, due to the enhanced spectral overlap, as well as charge transfer. Significantly we observe that simultaneously the intensity of the B exciton of MoS2 increases significantly suggesting the possibility of coherent and resonant radiative energy exchange between the 0D excitons in QDs and the 2D B exciton in MoS2. Our study reveals interesting nanoscale light–matter interaction effects which can suppress quenching of QDs leading to potential applications of these nanoscale materials in light emitting and photonic devices.
1 Introduction
Hybrid devices consisting of monolayers of two-dimensional (2D) layered transition metal dichalcogenides (TMDs) like MoS2 and zero-dimensional (0D) semiconductor quantum dots (QDs) have attracted increasing interest over the last decade.1–5 From the fundamental perspective, interest has been focused on the novel aspects of light–matter interactions that can occur between the two nanoscale materials in the form of energy and charge transfer processes between photo excited excitons which can be generated in one or both the layers, while under certain conditions, formation of interlayer or hybrid excitons can also take place.6–8 Thus these materials act as a playground for rich excitonic physics due to the interaction of 0D and 2D excitons with the 0D excitons being size tunable, while the 2D exciton being electrically and chemically tunable.2,9,10 Apart from interest in the fundamental science of these systems, there has been tremendous interest in their potential applications in photo-detectors, photovoltaic devices, photocatalysts and sensors.11–13 Most of the applications rely on the broad band gap tunability and highly efficient light harvesting properties of the QDs and the electrical properties, especially the high carrier mobility, of the TMDs which has led to development of various ultra-thin nanoscale opto-electronic devices13–15 based on this hybrid architecture. A key aspect in such device applications is the ability to tune the rate of energy or charge transfer after photo-excitation of the QDs to the TMDs by spectral tuning of the QDs or through electrical or chemical control of carrier density and mobility of the TMDs. In all cases, the device application relies on fast energy or charge transfer from 0D excitons in the photo-excited QDs to the TMDs leading to strong quenching of the dots. As a result, these materials are not very useful as light emitting or photonic devices and it is not possible to utilize the ability to tune the brightness of these emitters (QDs) through electrical control of the TMD based field effect transistor (FET) devices.Here we report control of the emission efficiency of core QDs placed in close proximity to the monolayers of MoS2. The QDs are transferred in the form of a high-density compact monolayer with the dot–dot separation, δ as well as the MoS2–QD separation, d, being controlled through chemical methods. At larger separations δ and d, we observe some quenching of QD emission on MoS2 relative to emission intensity on a silicon substrate, due to non-radiative processes. Surprisingly, at smaller separations we observe reduced quenching of QD emission on MoS2, despite the presence of significant non-radiative charge transfer. Interestingly, at small separations δ, we see evidence of strong dot–dot interactions and a significant red shift of QD PL spectral maxima which enhances spectral overlap with the absorption of B excitons of MoS2. However, instead of increased probability of non-radiative resonant energy transfer to MoS2 from QDs and strong quenching of QD photoluminescence (PL), due to the enhanced spectral overlap, we find considerable reduction in the quenching of the PL of QDs compared to that expected from standard non-radiative processes. Significantly we observe that simultaneously the intensity of the B exciton of MoS2 increases significantly suggesting the possibility of coherent and resonant radiative energy exchange between the 0D excitons in QDs and the 2D B exciton in MoS2. Our study reveals interesting nanoscale light–matter interaction effects which can suppress the conventional quenching of QDs leading to potential applications of these nanoscale devices in light emitting and photonic devices.
2 Experimental details
MoS2 monolayers were exfoliated on polydimethylsiloxane (PDMS) sheets and then transferred onto 300 nm SiO2 substrates. Monolayers were confirmed through optical and Raman spectroscopy. QDs were synthesized following methods described earlier.16,17 The monolayer of QDs was transferred onto MoS2 using the Langmuir–Blodgett (LB) technique.18,19 QDs in chloroform were spread on a deionized (DI) water-filled LB trough(Kibron Microtrough G2, Finland) to get a monolayer and the monolayer was slowly transferred onto the substrate at constant surface pressure. The ligand exchange was done by slightly modifying an earlier20 report (ESI†). In a typical ligand exchange, the vapor of K2S in formamide solution was exposed to the QD–MoS2 sample overnight and the excess ligand was washed with toluene and formamide solution, and using this method we exchanged the TOPO (long) ligand with the sulfur (short) ligand.Atomic force microscopy was performed using a Park system (NX model) in non-contact mode. PL spectra were collected using a Horiba (LabRam model) instrument, using a 532 nm continues wave (CW) laser. A laser power of ∼ 1 μW was used to avoid the bleaching of QDs. Signals were collected using a charge coupled device (CCD). A 300 g mm−1 grating and 1800 g mm−1 grating were used to collect the PL and the Raman spectra respectively. Time resolved PL (TRPL) data were collected using a PicoQuant MicroTime 200 system, with a temporal resolution of 25 ps. A 507 nm laser with 40 MHz repetition rate was used to excite the sample keeping the power at ∼ 1 μW. A band pass filter was used to collect QD TRPL spectra. A 50× (Olympus NA-0.45) objective was used to collect both PL and TRPL data.
3 Results and discussion
Fig. 1 shows the schematic of how the ligand exchange affects the separation (coupling) between the QD–MoS2 hetero-structure. The ligand exchange not only decreases the separation d between the QDs and MoS2 but also decreases the separation between the QDs δ themselves. When the long TOPO capped ligand is attached to QDs the d is ∼2 nm, and the δ is ∼4 nm. After ligand exchange these separations decrease to ∼0.3 nm and ∼0.6 nm respectively.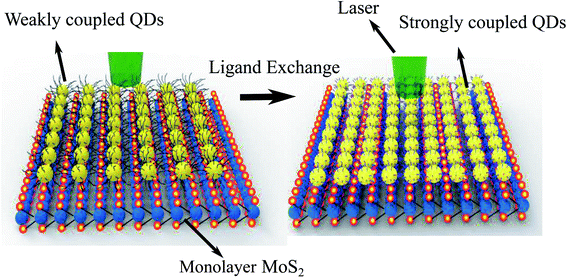 | ||
| Fig. 1 The schematic of how the ligand exchange treatment affects the separation between the QD–MoS2 hetero-structure; this treatment also modifies the dot–dot separation. | ||
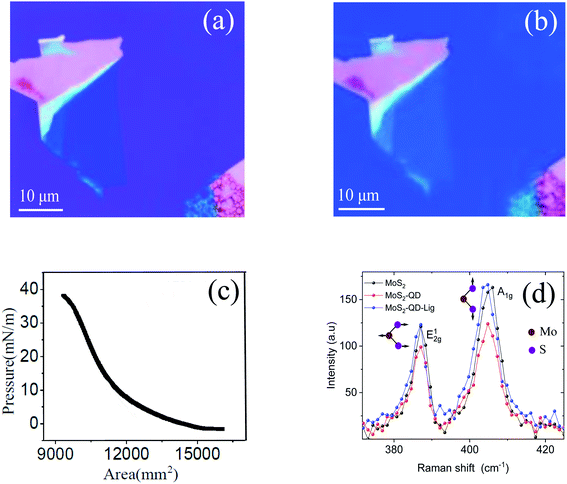
Fig. 2(a) shows the optical image of MoS2 before the transfer of monolayer QDs. Fig. 2(b) shows the optical images of the MoS2–QD hetero-structure after transferring the monolayer of the QD film using the LB technique. The QD monolayer is transferred uniformly onto the MoS2 layer. Fig. 2(c) shows the isotherm (surface pressure vs. area plot) of LB transfer; the QD monolayer was transferred at a surface pressure of 35 mN m−1. The 0D–2D hetero-structures were further characterized using atomic force microscopy (AFM). Fig. 2(d) shows the Raman spectra of MoS2 and the MoS2–QD hetero-structure before and after ligand exchange. The A1g mode is slightly affected after transferring the QD layer.
Fig. 3 shows the PL spectra of the QD–MoS2 hetero-structure. The energy of QDs was at 2.168 eV. The MoS2 PL spectra consist of two excitonic peaks at ∼1.85 eV and ∼2 eV, related to spin–orbit splitting in the valence band.21,22 The emission spectra of the chosen QD overlap with the absorption spectra of the higher energy exciton peak of MoS2. Both the PL intensities of QDs and MoS2 decrease in the hetero-structure compared to the PL intensity of the individuals on SiO2, consistent with previous reports.1,2 To quantify the quenching we introduce the quenching factor Q defined as Q = ISiO2/IMoS2, where ISiO2 is the intensity of QDs on SiO2, and IMoS2 is the intensity of QDs on MoS2. When d is ∼2 nm, the value of Q is ∼2.12 ± 0.05. Further the QD energy is blue shifted from 2.168 eV to 2.182 eV which is due to the coupling in the hetero-structure.4 After ligand exchange, the distance between MoS2 and QD reduces to ∼0.3 nm, and the value of Q becomes 1.42 ± 0.01. It can be noted that the PL maxima significantly red shift to 2.091 eV and 2.069 eV on SiO2 and MoS2, respectively (Table 1). The full width at half maximum (FWHM) of the QD monolayer on SiO2 is increased from 203 meV to 263 meV after ligand exchange; this broadening and red shift indicate that the coupling between QDs in the highly compact itself has increased due to reduction in δ.23–25 The details are shown in Table 1. Thus the analysis of PL spectra already reveals significant reduction in expected QD PL quenching. However, we do not have complete information about the energy or charge transfer processes from these PL spectra which are known to occur between these 0D–2D hybrid materials. For this we next discuss the TRPL data collected on the same systems as discussed above.
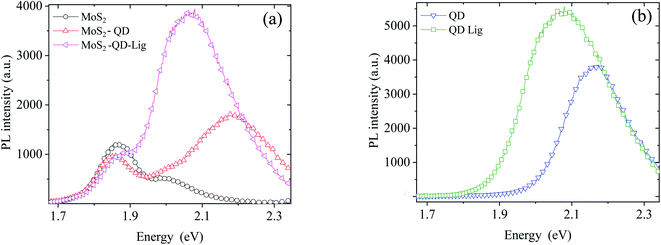 | ||
| Fig. 3 PL data of (a) the QD–MoS2 monolayer hetero-structure before and after ligand exchange while (b) shows the same on SiO2 before and after ligand exchange. | ||
| System | Centre (eV) | FWHM (meV) | Intensity (a.u) |
|---|---|---|---|
| QD | 2.168 ± 0.002 | 203 ± 6 | 3766 ± 17 |
| QD-Lig | 2.091 ± 0.004 | 263 ± 9 | 5501 ± 12 |
| MoS2–QD | 2.182 ± 0.001 | 210 ± 4 | 1770 ± 36 |
| MoS2–QD-Lig | 2.069 ± 0.004 | 218 ± 2 | 3847 ± 27 |
Fig. 4 shows the TRPL data of the QD in the QD–MoS2 monolayer hetero-structure. All data can be fitted with bi-exponential functions. For the QD monolayer before ligand exchange on SiO2 the longer lifetime (amplitude) τ1 is 5.8 ns (30%), while the shorter lifetime (amplitude) τ2 is 0.9 ns (70%) with the total weighted average lifetime τ of 4.5 ns. On MoS2 these values become τ1 = 4.4 ns (17%), τ2 = 0.7 ns (83%), and τ = 2.8 ns, respectively. This decrease in lifetime along with the decrease in PL intensity of QD PL on MoS2 indicates nonradiative energy transfer from the QD monolayer to MoS2. After ligand exchange and a consequent reduction of δ and d, τ on SiO2 itself decreases to 1.4 ns with τ1 = 3.0 ns (10%), and τ2 = 0.5 ns (90%). This indicates that the coupling between QDs has significant influence on the lifetime. The lifetime further decreases on MoS2 after ligand exchange to 0.9 ns with τ1 = 2.6 ns (5%), and τ2 = 0.3 ns (95%). This decrease indicates the enhanced nonradiative decay rate of the QD monolayer in the hetero-structure after the ligand exchange. Table 2 shows the lifetime details of QDs in the hetero-structure. The longer lifetime is usually associated with the intrinsic decay of the QDs while the shorter lifetime can be associated with the interaction between QDs or with the surrounding environment.26–28 So the shorter lifetime and its amplitude will be very sensitive to the changes in the environment.
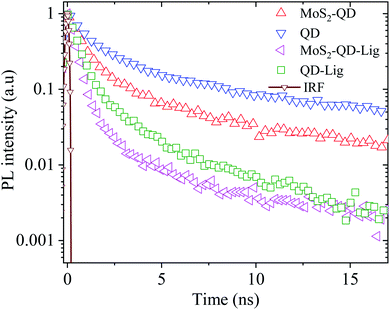 | ||
| Fig. 4 TRPL data of the QD–MoS2 monolayer hetero-structure along with the instrument response function (IRF). All data were fitted with bi-exponential functions as discussed in the ESI.† | ||
| System | Longer lifetime τ1 (ns) | Shorter lifetime τ2 (ns) | τ (ns) |
|---|---|---|---|
| QD | 5.8 ± 0.04 (30 ± 2.0%) | 0.9 ± 0.04 (70 ± 3.0%) | 4.56 ± 0.05 |
| QD-Lig | 3.0 ± 0.04 (10 ± 1.0%) | 0.5 ± 0.03 (90 ± 1.5%) | 1.48 ± 0.01 |
| MoS2–QD | 4.4 ± 0.05 (17 ± 1.6%) | 0.7 ± 0.03 (83 ± 2.0%) | 2.76 ± 0.07 |
| MoS2–QD-Lig | 2.6 ± 0.05 (5 ± 0.5%) | 0.3 ± 0.03 (95 ± 1.9%) | 0.94 ± 0.11 |
Two major non-radiative processes have been suggested to occur in such 0D–2D hybrids29 – Förster resonance energy transfer (FRET) and charge transfer (CT). The nonradiative energy transfer rate, ΓFRET, for emitters on 2D materials like graphene and MoS2, is related to the distance, d, as follows,2,29
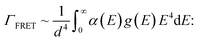 | (1) |
While there are several methods to estimate ΓFRET we have utilized a method which combines information from both the PL and TRPL measurements following2
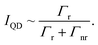 | (2) |
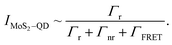 | (3) |
From the above expressions and using 1/(Γr + Γnr) = τQD we get
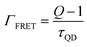 | (4) |
For the TOPO capped QD monolayers, using the value Q = 2.12 ± 0.05 for longer capped QDs, from the above equation we get ΓFRET = (2.4 ± 0.08) × 108 s−1. Similarly after ligand exchange, using the value Q = 1.43 ± 0.01 we get ΓFRET = (2.8 ± 0.04) × 108 s−1.
This slight increase in ΓFRET is due to the decrease in d and the increase in the spectral overlap after ligand exchange. But, as discussed in eqn (1), ΓFRET varies, as 1/d4 according to eqn (1). The center to center distance is calculated from the AFM data (see ESI Fig. S7†) of the QD film by taking the radius of QDs which is ∼ 3.5 nm before ligand exchange and ∼2 nm after ligand exchange with half the MoS2 thickness (0.3 nm) being added to these values. The ratio of 1/d4 after and before ligand exchange is ∼7.4. Also the increase in the spectral overlap should further increase the FRET rate in the system. However the ratio of ΓFRET after and before ligand exchange is only ∼1.1, which suggests that FRET is not the dominant energy transfer process in our hetero-structures. This is surprising given the spectral overlap.
It is well known that there are several conditions which need to be satisfied for FRET to take place between emitters and 2D semiconductors. Two of the main factors are spectral overlap (absorption of MoS2 and emission of QDs) and small separation. However, another key factor is related to the kinetics of energy transfer. This involves comparison of the lifetime, τ, of the QD and (ΓFRET)−1. Basically, τ > (ΓFRET)−1 for FRET to be dominant. It is to be noted that τ, for our case, has two components, τ1 and τ2 (Table 2). As mentioned earlier, the longer lifetime, τ1, is the intrinsic excitonic decay while the shorter one, τ2, is due to the QD–QD interaction which is dominant in our compact QD monolayer films. In fact, even for pristine QD films the weight factor for τ2 is ∼70% and this becomes even more dominant upon adding additional decay channels due to interactions with MoS2 or even upon ligand exchange on SiO2 leading to much shorter QD–QD lateral separation and hence even stronger interactions. Clearly, in our compact QD monolayer films τ (τ2) < (ΓFRET)−1. While this relationship might also hold for τ1 it is definitely valid for τ2, which, in any case, is the dominant lifetime component. This suggests that there are alternative processes which lead to enhancement of decay rate.
However, since our QDs are core only it is possible that other non-radiative processes can exist, especially charge transfer (CT), as has been also suggested to occur in these systems.11,30,31 Some indication of the presence of CT is also revealed from analysis of the PL data of MoS2. For example, if we consider the ratio Itrion/Iexciton for MoS2 with the TOPO capped QD monolayer on top we find it to be 1.18. We observe an increase in this ratio from 1.18 to 2.08 after ligand exchange treatment of QDs on MoS2 suggesting an increase in CT. However, we did not observe a significant change in the MoS2 PL intensity suggesting that other, possibly, radiative processes might be in operation in the hetero-structures. Nevertheless, if we consider that the CT is present, the CT rate can be estimated using the expression:11
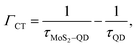 | (5) |
We now consider the effect of resonant radiative energy transfer from the QD to MoS2 due to the spectral overlap between the QD and B exciton. In order to understand this possible mechanism better we carefully fitted the PL spectra with the combination of Lorentzian and Gaussian peak functions. It is to be noted that (ESI Fig. S2†) pure MoS2 PL spectra can be well modeled with 3 Lorentzians corresponding to the A exciton and trion and B exciton. On the other hand the QD PL on SiO2 which shows extrinsic broadening due to size dispersity and thermal effects can be well fitted with a single Gaussian peak fitting function (ESI Fig. S3†). Fig. 5(a) shows the cumulative fit of the full PL spectrum including that of MoS2 and QDs and also displays the individual fits to the A trion, exciton and B exciton components as well as that due to the QD peak for the TOPO capped QDs on MoS2, using 3 Lorentzians (MoS2)and 1 Gaussian (QD). It can be seen clearly that the intensity of the trion component is higher than that of A and B exciton components. Fig. 5(b) on the other hand shows the same fitted components, as in Fig. 5(a), corresponding to the system after ligand exchange. However, we could only fit the MoS2–QD spectra satisfactorily with two Lorentzians (A exciton and trion) and two Gaussians (B exciton and QD). It is clearly observed that the B exciton intensity has increased compared to the other components on the A exciton as well as the QDs. The IA exciton/IB exciton is decreased from 3.23 to 1.24 after transferring QDs onto MoS2. This suggests that there is energy transfer between the QD and B exciton although we do not observe a similar decrease in QD PL intensity. In fact the QD component of the PL spectrum cannot be well fitted with a single Gaussian (ESI Fig. S4†) as well indicating a strong overlap between the B exciton (2D) and the QD exciton (0D). Thus coupled with the observation that after ligand exchange the PL spectra can be fitted better with 2 Lorentzians (MoS2 A) and 2 Gaussians (QD + B), it is suggested that a hybrid state (0D–2D) in this resonantly coupled system is, possibly, formed with the B exciton and coupled QDs exchanging energy coherently such that simultaneous enhancement of B exciton intensity and strong suppression of QD PL quenching take place.
4 Conclusions
In summary, we control the emission efficiency of core QDs in the monolayers of the MoS2–QD hetero-structure using ligand exchange treatment. At larger separations we observe quenching of QD PL due to non-radiative processes, at smaller separations we observe enhanced emission from QDs on MoS2 as compared to the larger d despite the presence of significant non-radiative charge transfer. Interestingly, at small separations, we see evidence of strong dot–dot interactions and a significant red shift of QD PL maxima which enhances spectral overlap with the absorption of B excitons of MoS2. Despite the increased probability of non-radiative resonant energy transfer to MoS2 from QDs due to increased spectral overlap as well as that due to enhanced CT we find that the quenching of the PL of QDs is significantly reduced as compared to longer separations as well as to what would be expected from the non-radiative processes. Concurrent with this reduced QD PL quenching, the intensity of the B exciton of MoS2 increases significantly suggesting the possibility of coherent and resonant radiative energy exchange between the 0D excitons in QDs and the 2D B exciton in MoS2. We observe that the ligand exchange is an effective technique to tune the nonradiative decay channels in the 0D–2D hetero-structure. Our study reveals interesting nanoscale light–matter interaction effects which can suppress the conventional quenching of QDs leading to potential applications of these nanoscale devices in photonics.Conflicts of interest
There are no conflicts to declare.Acknowledgements
HLP thanks CSIR-UGC for financial support. The authors thank DST nanomission for funding. The authors thank SERB, India for funding. HLP thanks Mangesh and Puspender for help in using Igor software.Notes and references
- A. Raja, A. Montoya-Castillo, J. Zultak, X.-X. Zhang, Z. Ye, C. Roquelet, D. A. Chenet, A. M. Van Der Zande, P. Huang, S. Jockusch and T. F. Heinz, Nano Lett., 2016, 16, 2328–2333 CrossRef CAS PubMed
.
- D. Prasai, A. R. Klots, A. Newaz, J. S. Niezgoda, N. J. Orfield, C. A. Escobar, A. Wynn, A. Efimov, G. K. Jennings and S. J. Rosenthal, Nano Lett., 2015, 15, 4374–4380 CrossRef CAS PubMed
.
- H. Zang, P. K. Routh, Y. Huang, J.-S. Chen, E. Sutter, P. Sutter and M. Cotlet, ACS Nano, 2016, 10, 4790–4796 CrossRef CAS PubMed
.
- K. M. Goodfellow, C. Chakraborty, K. Sowers, P. Waduge, M. Wanunu, T. Krauss, K. Driscoll and A. N. Vamivakas, Appl. Phys. Lett., 2016, 108, 021101 CrossRef
.
- S. Sampat, T. Guo, K. Zhang, J. A. Robinson, Y. Ghosh, K. P. Acharya, H. Htoon, J. A. Hollingsworth, Y. N. Gartstein and A. V. Malko, ACS Photonics, 2016, 3, 708–715 CrossRef CAS
.
- A. Boulesbaa, K. Wang, M. Mahjouri-Samani, M. Tian, A. A. Puretzky, I. Ivanov, C. M. Rouleau, K. Xiao, B. G. Sumpter and D. B. Geohegan, J. Am. Chem. Soc., 2016, 138, 14713–14719 CrossRef CAS PubMed
.
- P. Rivera, J. R. Schaibley, A. M. Jones, J. S. Ross, S. Wu, G. Aivazian, P. Klement, K. Seyler, G. Clark and N. J. Ghimire, Nat. Commun., 2015, 6, 1–6 Search PubMed
.
- M. Okada, A. Kutana, Y. Kureishi, Y. Kobayashi, Y. Saito, T. Saito, K. Watanabe, T. Taniguchi, S. Gupta and Y. Miyata, ACS Nano, 2018, 12, 2498–2505 CrossRef CAS PubMed
.
- H. L. Pradeepa, P. Mondal, A. Bid and J. K. Basu, ACS Appl. Nano Mater., 2020, 3, 641–647 CrossRef
.
- J. S. Ross, S. Wu, H. Yu, N. J. Ghimire, A. M. Jones, G. Aivazian, J. Yan, D. G. Mandrus, D. Xiao and W. Yao, Nat. Commun., 2013, 4, 1474 CrossRef PubMed
.
- J.-S. Chen, M. Li, Q. Wu, E. Fron, X. Tong and M. Cotlet, ACS Nano, 2019, 13, 8461–8468 CrossRef CAS PubMed
.
- S. Zhang, X. Wang, Y. Chen, G. Wu, Y. Tang, L. Zhu, H. Wang, W. Jiang, L. Sun and T. Lin, ACS Appl. Mater. Interfaces, 2019, 11(26), 23667–23672 CrossRef CAS PubMed
.
- M. Li, J.-S. Chen, P. K. Routh, P. Zahl, C.-Y. Nam and M. Cotlet, Adv. Funct. Mater., 2018, 28, 1707558 CrossRef
.
- D. Kufer, I. Nikitskiy, T. Lasanta, G. Navickaite, F. H. Koppens and G. Konstantatos, Adv. Mater., 2015, 27, 176–180 CrossRef CAS PubMed
.
- H. Chen, H. Liu, Z. Zhang, K. Hu and X. Fang, Adv. Mater., 2016, 28, 403–433 CrossRef CAS PubMed
.
- L. Qu and X. Peng, J. Am. Chem. Soc., 2002, 124, 2049–2055 CrossRef CAS PubMed
.
- C. de Mello Donega, S. G. Hickey, S. F. Wuister, D. Vanmaekelbergh and A. Meijerink, J. Phys. Chem. B, 2003, 107, 489–496 CrossRef CAS
.
- J. R. Heath, C. M. Knobler and D. V. Leff, J. Phys. Chem. B, 1997, 101, 189–197 CrossRef CAS
.
- M. Haridas, J. K. Basu, A. Tiwari and M. Venkatapathi, J. Appl. Phys., 2013, 114, 064305 CrossRef
.
- H. J. Yun, T. Paik, M. E. Edley, J. B. Baxter and C. B. Murray, ACS Appl. Mater. Interfaces, 2014, 6, 3721–3728 CrossRef CAS PubMed
.
- A. Kormányos, G. Burkard, M. Gmitra, J. Fabian, V. Zólyomi, N. D. Drummond and V. Fal'ko, 2D Mater., 2015, 2, 022001 CrossRef
.
- K. F. Mak, K. He, C. Lee, G. H. Lee, J. Hone, T. F. Heinz and J. Shan, Nat. Mater., 2013, 12, 207 CrossRef CAS PubMed
.
- J.-H. Choi, A. T. Fafarman, S. J. Oh, D.-K. Ko, D. K. Kim, B. T. Diroll, S. Muramoto, J. G. Gillen, C. B. Murray and C. R. Kagan, Nano Lett., 2012, 12, 2631–2638 CrossRef CAS PubMed
.
- C. R. Kagan and C. B. Murray, Nat. Nanotechnol., 2015, 10, 1013 CrossRef CAS PubMed
.
- J.-S. Lee, M. V. Kovalenko, J. Huang, D. S. Chung and D. V. Talapin, Nat. Nanotechnol., 2011, 6, 348 CrossRef CAS PubMed
.
- W.-S. Chae, T. D. T. Ung and Q. L. Nguyen, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2013, 4, 045009 Search PubMed
.
- M. Praveena, T. Phanindra Sai, R. Dutta, A. Ghosh and J. K. Basu, ACS Photonics, 2017, 4, 1967–1973 CrossRef CAS
.
- R. Dutta, K. Jain, M. Venkatapathi and J. K. Basu, Phys. Rev. B, 2019, 100, 155413 CrossRef CAS
.
- B. Guzelturk and H. V. Demir, Adv. Funct. Mater., 2016, 26, 8158–8177 CrossRef CAS
.
- H. Wu, Z. Kang, Z. Zhang, Z. Zhang, H. Si, Q. Liao, S. Zhang, J. Wu, X. Zhang and Y. Zhang, Adv. Funct. Mater., 2018, 28, 1802015 CrossRef
.
- A. J. Goodman, N. S. Dahod and W. A. Tisdale, J. Phys. Chem. Lett., 2018, 9, 4227–4232 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: S1: CdSe QD synthesis; S2: MoS2 PL fitting details, etc. See DOI: 10.1039/d0na00384k |
| This journal is © The Royal Society of Chemistry 2020 |