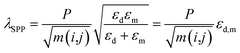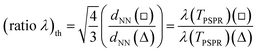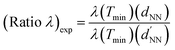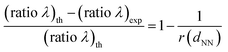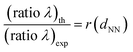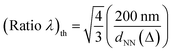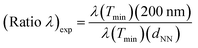Short-range ordered 2D nanoholes: lattice-model and novel insight into the impact of coordination geometry and packing on their propagating-mode transmittance features

Abstract

Optically thin perforated gold films, fabricated using template colloidal masks self-assembled by following an elsewhere described simplified colloidal lithography protocol, are presented and discussed with the aim to develop a theory of short-range ordered nanoholes without straightforwardly extending concepts strictly related to periodic nanoholes. By Scanning Electron Microscopy (SEM) analysis of the evolution of nanohole short-range ordering and spatial coordination geometry under increasing interhole average spacing (d_NN), unprecedented differences in the spectroscopic response are pointed out with respect to periodic systems. First, the dependence of the wavelength of a propagating plasmon mode on d_NN is demonstrated to deviate from the linear relationship predicted by the grating-coupling picture developed for periodic arrays. Second, d_NN cannot be straightforwardly interpreted as the counterpart of the lattice constant of periodic nanoholes, which demands to introduce a conceptually more rigorous periodicity-like length-scale. Once the impact of these findings on setting the operating parameters of a nanohole distribution is demonstrated, they are related, experimentally and by using a theoretical model developed by the authors, to the changes of the local coordination geometry (from quasi-hexagonal to quasi-square packing through mixed hexagonal–square coordination) induced by varying d_NN over a wide interval. Autocorrelation analysis of SEM images is exploited to estimate a short-range periodicity-like length-scale, as a conceptual advance for laying the foundation of the concept of short-range ordered nanohole lattices and for deeper insight into the spectral response. As discussion is based on realistic, rather than simulated, evolution of colloidal arrangements, the formulated interpretative model accounts for realistic effects impacting transmission resonances.

---

1. Introduction

Resonantly enhanced light transmission, leading to extraordinary optical transmission (EOT) phenomena, is a fascinating property exhibited by periodic arrays of sub-wavelength holes, periodically milled in an optically thick (>100 nm) metal film.^1,2 Since the seminal report on EOT,¹ metal nanohole (NH) distributions have attracted worldwide interest for several applications: for instance, plasmonic solar cells and photodetectors,³ plasmonic color-filter devices,^4,5 surface enhanced Raman scattering,⁶ surface enhanced fluorescence spectroscopy,^7,8 monitoring of surface-binding events in chemical and biochemical sensing,^9–11 preferably by microfluidic-chip based detection due to the benefits of a simple optical set-up, dense integration of sensors, multiplexing for parallel and selective analyte sampling in miniaturized and high throughput sensors.^12,13

From the fundamental standpoint, resonant transmission phenomena were first ascribed to coupling between free-space photons and Bloch-wave surface plasmon polaritons mediated by diffractive hole grating (grating-coupling model).^14,15 In this picture, quasi-momentum and energy matching conditions determine the spectral position of transmission peaks depending on structural parameters (lattice geometry and periodicity), the choice of metal and dielectric environment, Bragg integer diffraction orders, the incidence angle and polarization of the excitation radiation.^14,16 Further theoretical and experimental studies pointed out that the theoretical relationship predicting the spectral position of transmission resonances in the grating-coupling picture was not fulfilled in that, (i) transmission peaks are red-shifted with respect to the theoretical prediction due to hole-related scattering mechanisms,^14,16–18 and (ii) transmission minima rather than maxima may be associated with propagating plasmon modes in optically thin films (<50 nm).^19–21 Optically thin semi-transparent perforated metal films differ from their optically thick (>100 nm) opaque counterparts in that the propagating plasmon modes generated on both sides of the film are strongly coupled^22,23 as well as transmission peaks or dips form depending on the interference between the direct reflection and transmission through the holes (incoherent path) and the radiation coupled to propagating surface plasmon polariton-modes.^24,25

Interestingly, transmission peaks and dips were also found to occur in the absence of translational symmetry in quasi-periodic^26,27 and short range-ordered^21,28 hole arrays and to be absent in completely disordered NH distributions.²⁹ Therefore, even if periodicity is not a crucial requirement, metal NH array distributions with positional correlation between nearest neighbors are in principle demanding to observe resonantly enhanced light transmission associated with propagating surface plasmon resonance (PSPR) modes excited along the surface of a perforated metal film and localized surface plasmon resonance (LSPR) modes with field enhancement at the edges and along the depth of the hole. In practice, nanofabrication approaches leading to short-range ordered NH arrangements are becoming an attractive low cost alternative to conventional lithography.^9,30–32 Indeed, while mainly electron-beam lithography (EBL)³³ and focused-ion beam (FIB) lithography³⁴ enable manufacturing of periodic metal NH arrays with repeatability and controlled size, shape and relative positioning, they present important practical disadvantages. For instance, specialized equipment, costly procedures, and multi-step and time-consuming processing greatly limit their application for large-area (larger than a few μm²) patterning and mass production of NH lattices. Differently, short-range ordered NH distributions self-assembled by colloidal lithography are not as sensitive as periodic arrays to fabrication imperfections and can be produced massively over a large area. Also, the working principle of colloidal lithography is very simple: it relies on electrostatically driven adsorption and self-assembly of likely charged polymer colloids onto a counter-charged collector surface.³⁵

From the fundamental standpoint, the practical convenience in fabricating short-range ordered metal NH distributions has raised questions about eventual analogies with periodic distributions in regard to spectral properties^{26,28,36–38} as well as the mechanisms leading to resonant transmission in the absence of long-range order.^21,28,39 These studies assumed, straightforwardly and in principle, the average center-to-center distance of nearest neighbor short-range ordered NHs as the counterpart of the periodicity parameter (i.e., the lattice constant) of NH lattices.^21,39 Under this assumption, since in the canonical grating-coupling picture a transmittance feature associated with a PSPR mode linearly blue-shifts for increasing lattice constant,⁹ the same behaviour should be expected in the case of a short-range ordered metal NH distribution versus changes of the NH-to-NH spacing. Comparative studies between ordered and short-range ordered NH systems pointed out deviations in the prediction of the resonances in the presence of short-range ordering²¹ and evidenced a not completely linear trend in line with the theoretical expectations of periodic NH systems.³⁹

Recent studies on short-range ordered NH distributions⁴⁰ demonstrated a general linear dependence of the spectral position of a PSPR mode on the center-to-center distance of nearest neighbour NHs, here termed d_NN, varied over the 110–178 nm range. Notably, the occurrence of a slight deviation of a few data with respect to the linear trend was observed.

The aim of this paper is to extend this early study in order to clarify/unravel this point and more deeply investigate the impact of short-range ordering on the transmittance response of NH systems. Herein, short-range ordered gold NH systems, fabricated by following a simplified colloidal lithography protocol described in detail elsewhere⁴⁰ and termed hereafter MNL-CL (where MNL and CL stand for monolayer and colloidal lithography, respectively), are presented. Based on these systems, the evolution of the spectral position of the transmission feature associated with a PSPR mode versus d_NN ranging over a wider interval (i.e., from 110 to 203 nm) than the previously investigated one is discussed. Since transition from short-time to long-time colloid adsorption was exploited to increase the fractional coverage, the developed analysis allows a correlation between the optical response of the metal NH array and the temporal evolution of the colloid arrangement, dictated by the interplay between the active interactions, which characterizes the degree of ordering. Hence, a realistic physical insight into the mechanisms (interplay between electrostatic interparticle, colloid–collector surface interactions and capillary forces) which impact the level of positional correlated ordering during colloid self-assembly is provided.

Noteworthily, it is demonstrated that, while the spectral position of a PSPR mode doesn't vary linearly versus d_NN over the entire sampled range, the linear trend is recovered over narrower contiguous ranges of d_NN which correspond to distributions with different local coordination numbers of the NHs (transition of the order from locally quasi-hexagonal to locally quasi-square packing). In this respect, a conceptual interpretative model is also developed and discussed which is able to relate the observed dependence of the wavelength of a PSPR mode on d_NN to the local geometry (transition from quasi-hexagonal to quasi-cubic) of NH arrangements.

The presented discussion enables to introduce the concept of a short-range ordered NH lattice, to characterize it and to rigorously assess differences with respect to periodic systems without straightforward application of the knowledge available for periodic NH arrays. For instance, we demonstrate that the interparticle distance evaluated by statistical analysis is not the counterpart of the lattice constant of periodic NH arrays.

To the best of our knowledge, results and discussion presented in this manuscript are not reported in the literature.

2. Experimental

2.1 Fabrication methods and conditions

The colloidal lithography technique was implemented for fabricating short range ordered NH distributions onto glass substrates according to the experimental procedure detailed elsewhere⁴⁰ and sketched in Fig. 1. Following cleaning of microscope glass slides by ultra-sonication in acetone (Sigma Aldrich) at 60 °C for 20 minutes and isopropylic alcohol (Sigma Aldrich) at 60 °C for 20 minutes, the substrates were carefully dried by N₂-blowing and their surface was made negatively charged by an oxygen-plasma treatment (100 sccm, 50 Watt, 250 mTorr, and 1 min process time). 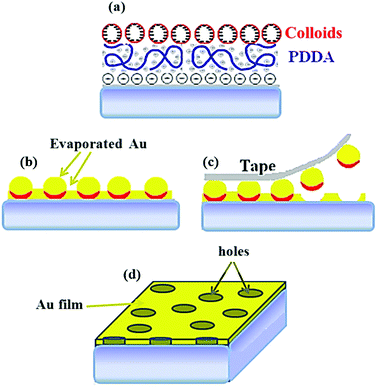Then, a positively charged monolayer of polydiallyldimethylammonium (PDDA) (MW 200 000–350 000, Sigma Aldrich) polyelectrolyte was adsorbed onto the oxidized substrate from an aqueous solution (0.2 wt% in Milli-Q water) for an adsorption time Δt_PDDA ranging from 40 s to 2 min. Careful rinsing of the PDDA surface under a deionized water flow and N₂ blow-drying were applied before depositing the colloidal distribution. In this respect, negatively charged commercial polystyrene nanospheres (Thermo Fisher Scientific), with diameter D_PS = (80 ± 4) nm, were adsorbed onto the PDDA counter-charged layer from a salt-free aqueous solution (0.1% wt) for an adsorption time Δt_PS lasting from 25 s to 10 min. The obtained colloidal distributions were immersed for 1 minute in distilled water, previously heated up to 100 °C, and subsequently carefully N₂ blow-dried.³⁵ The colloidal distributions resulting from the above protocol (Fig. 1(a)) were covered by a thermally evaporated (20 ± 2) nm thick gold (Au) film (Fig. 1(b)). Then, the removal of the Au-capped colloids by tape stripping (Fig. 1(c)) resulted in a perforated optically thin Au film onto a glass substrate (Fig. 1(d)). Since tape stripping leaves NHs in the same positions as the polystyrene beads, the NH arrangement is dictated by the associated precursor colloidal mask. Based on several experiments devoted to exploiting the interplay between the chosen adsorption times Δt_PDDA and Δt_PS, d_NN was varied from 110 to 203 nm.

Fig. 1 Schematics of the experimental protocol (MNL-CL protocol) applied to fabricate Au NHs onto glass substrates. (a) Colloidal mask self-assembled onto a PDDA polyelectrolyte monolayer anchored onto the oxygen plasma treated surface of a glass substrate. (b) Thermal evaporation of a Au film over the colloidal mask. (c) Removal of the Au-capped colloids by tape stripping and (d) resulting perforated Au film.

2.2 Morphological and ordering characterization

Scanning electron microscopy (SEM) was applied to image and characterize the fabricated distributions of Au-capped polystyrene nanospheres, which consequently provide information about the arrangement of the associated NH distributions. A Zeiss NVISION 40 dual beam Focused Ion Beam (FIB) system, equipped with a high resolution SEM Gemini column and an Oxford 350 x-act Energy Dispersive X-ray Spectrometer (EDS), was used for acquiring SEM images that were processed by using Digital Micrograph software.⁴¹ Based on statistical analysis of the SEM images, the quantity d_NN (i.e., the average center-to-center distance between nearest neighbor polystyrene nanospheres) and the corresponding fractional coverage were evaluated. The latter quantity was quoted with an uncertainty amounting to nearly 6%. Statistical histograms of the nearest neighbor distance were obtained for each nanosphere arrangement (area 5.4 μm²) under study, hence giving information about the distribution of the shortest nanosphere-to-nanosphere distance and, in particular, about the impact of capillary-induced agglomeration and nanosphere coordination on d_NN. Furthermore, autocorrelation (Autocor) and Fast Fourier Transform (FFT) image processing tools were applied to analyze SEM images according to the purposes and guidelines applied by the authors for the first time to SEM images of short-range ordered colloidal distributions in a recent study.⁴⁰

2.3 Spectral characterization analysis

The zero-order transmission spectra of the fabricated NH samples were recorded by using a Cary 500 UV-VIS-NIR Spectrometer (Varian, USA) in air at room temperature under white light incident perpendicularly on the surface of the Au NH films. All transmission spectra were acquired in the spectral range from 400 to 1000 nm with a spectral resolution Δλ = 1 nm and normalized to the transmission spectrum of a bare cleaned glass substrate.

3. Results and discussion

3.1 Preliminary remarks: motivation and aim of the study

Detailed discussion about the applicability, repeatability and peculiarity of the MNL-CL protocol developed by the authors is reported elsewhere.⁴⁰ To briefly summarize the main points of the experimental protocol under consideration, it is worth remarking that:

(i) It uses a polyelectrolyte monolayer rather than the uppermost surface of a polyelectrolyte multi-layer, as commonly reported in the literature, to electrostatically bind colloids,

(ii) The chosen concentration of the salt-free PDDA solution guarantees flat configuration of the adsorbed chains,

(iii) d_NN is varied by the interplay between the adsorption time of PDDA (Δt_PDDA), which affects the adsorption efficiency of the PDDA surface, and the adsorption time of polystyrene colloids (Δt_PS), which is tuned from short- to long-time adsorption,⁴⁰

(iv) Salt-free colloidal suspensions are considered to limit detrimental effects such as clustering stemming from weakened inter-particle Coulomb repulsion and lateral capillary forces.⁴⁰

Prior to presenting and discussing the results of interest for the present paper, a summary of the main conclusions concerning the spectral response of the short-range ordered NH distributions fabricated by following the MNL-CL protocol to put forward the raised fundamental questions that motivate an extended study is demanded.

(i) Unshielded rather than shielded inter-colloidal electrostatic repulsion was demonstrated to be effective to obtain short-range-ordered and well-separated NHs with controllable and tunable coverage for d_NN varying from 110 to 178 nm, meaning, unlike saturated coverage commonly reported in the literature, by exploiting unsaturated adsorption conditions too.⁴⁰ While resonant transmission features were observed over the whole investigated coverage range as a signature of short-range ordering, an eventual impact of correlated disorder in terms of geometry of the spatial correlation at intermediate coverage, before saturation, was not investigated and is still missing information in the literature.

(ii) Angle-resolved transmission spectra demonstrated the occurrence of a transmission peak unaffected by the incidence angle and an angle-dependent transmission dip, blue-shifting when going from normal incidence to 50°. Such a transmittance peak and dip were consequently assigned to a localized and propagating plasmon mode, respectively.⁴⁰ On the basis of this assignment, the relationship between the wavelength of the propagating plasmon mode (PSPR) and d_NN was discussed,⁴⁰ in analogy with a periodic NH array for which a linear dependence of the PSPR wavelength on the lattice constant is theoretically predicted. In our study, a linear trend was generally confirmed, but slight deviations of a few data were observed.⁴⁰

(iii) In regard to the observed deviations from a clearly linear trend of the dependence of the wavelength of the PSPR mode on d_NN, agglomeration effects on the occurrence of two linear trends of unclear origin over contiguous intervals of values of d_NN were hypothesized. This point would contrast with the common assumption that d_NN is a universal length-scale of both periodic and short-range ordered NH systems^21,39 and deserves further physical insight.

Going forward, in this paper we focus on the following main aims. First, a systematic investigation of SEM micrographs of the deposited colloidal distributions is performed to individuate any relationship between the geometry of the local coordination and ordering under changes of the fractional coverage, dictated by inter-particle interactions. While going from low to saturated coverage, the distribution of the adsorbed polystyrene nanospheres deposited by colloidal lithography is expected to change from weakly correlated arrangements of colloids, with empty spaces in between them, to electrostatically stabilized configurations with a better defined short-range geometric arrangement (e.g. triangular lattice or hexagonal coordination) and less dispersed neighboring particle distance.⁴²

According to this picture, detailed analysis of the evolution of the colloidal arrangements under conditions of progressively increasing coverage may allow mapping their ordering formation process and individuate eventual lattice-like short-range ordered patterns. In this perspective, we studied the ordering/disordering properties of real colloidal masks rather than artificially generating disorder by random displacement of colloids. This approach allows us to realistically picture the ordering formation process depending on the active interactions and, importantly, by including the impact of lateral capillary forces on the colloidal distribution while increasing its coverage.

Second, in this study a deeper investigation of the slight deviation from the linearity of the wavelength of a PSPR mode versus d_NN envisaged in a previous study is presented.⁴⁰

According to the above purposes, short-range ordered NH arrangements were fabricated based on a previously experimentally validated MNL-CL protocol,⁴⁰ by extending the range of values of d_NN from 110–178 nm (ref. 40) to 110–203 nm. Throughout the paper the fabricated distributions of Au-capped polystyrene nanospheres will be named PS(d_NN), and the associated NH sample will be straightforwardly referred to as NH(d_NN).

Gold thin films are considered for two main reasons. First, deviations from the proposed theories were reported in the case of optically thin films due to not-vanishing direct transmission.^24,25 Second, more localized field distribution of the bonding plasmon mode^22,43 is expected to provide a spectral response less affected by loss mechanisms (absorption from the metal and scattering by the hole apertures) impacting the propagation length of propagating plasmon modes. Hence, thin films are a favourable condition to yield more general discussion of the inherent correlation between the arrangement and spectral properties of short-range ordered NH systems. From the applicative standpoint, optically thin perforated metal slabs exhibit appealing sensing behaviour of LSPR modes²¹ and more homogeneous and strong field enhancement inside the NH region for NH diameters around 50–70 nm.⁴⁴ All of this motivated the choice of colloids with a diameter of 80 nm, leading to a smaller NH diameter of about 60 nm, due to shadow effects during Au evaporation.

3.2 Ordering and coordination analysis

Fig. 2–4 show typical SEM micrographs (left column panels) of colloidal distributions with gradually decreasing coverage, as demonstrated by the relevant values of d_NN, ranging from 110 to 203 nm, derived from the statistical analyses of SEM micrographs. The distributions of the nearest inter-particle spacing are reported in the histogram of the right column panels. As overviewed in the experimental and method sections, coverage was varied by means of the interplay between the adsorption times Δt_PDDA and Δt_PS according to the principle that increasing coverage is favored by improved binding efficiency of the PDDA collector surface (i.e., Δt_PDDA > 40 s) and Δt_PS approaching the saturated adsorption.⁴⁰ In practice, for a given Δt_PDDA, the simplest way to tune d_NN is to interrupt the adsorption process at progressively increasing values of Δt_PS before achieving the saturation coverage.

Fig. 2(a)–(c) show the arrangement of colloidal masks with d_NN given as (110 ± 22) nm, (128 ± 21) nm and (141 ± 31) nm. The associated values of fractional coverage were estimated to be (26 ± 2)% for PS(110 nm), (22 ± 1)% for PS(128 nm) and (18 ± 1)% for PS(141 nm). The sparse agglomeration occurring in the case of PS(110 nm) can be ascribed to the impact of lateral capillary forces during drying favored by the high coverage of the sample under consideration. Consistently, for increasing d_NN, more homogeneous arrangement with better separated units and smaller clusters was obtained.

Fig. 2 (a–c) SEM micrographs of the samples PS(110 nm), PS(128 nm) and PS(141 nm) and (d–f) associated histogram distributions of the nearest inter-particle spacing.

The histograms in Fig. 2(d)–(f) clearly indicate the presence in this first group of colloidal distributions of agglomerated units (nearest neighbor distance < 100 nm). At the shortest d_NN (i.e., PS(110 nm)), a bimodal distribution is evident, with a family of colloids, whose nearest neighbor distance varies between 50 nm (overlapped colloids) and 100 nm (nearly touching colloids), representing about 28% of the entire distribution. For increasing d_NN (i.e., PS(128 nm)), the distribution proceeds through a three-modal distribution, where the family with the shortest nearest neighbor distance is emptying, whereas two families form with larger nearest neighbor distances, peaked at about 117 nm and 146 nm, respectively. Finally, in the case of PS(141 nm), a bimodal distribution is recovered, with the shortest nearest neighbor distance family representing about 20% of the entire distribution and the largest family peaked at about 153 nm.

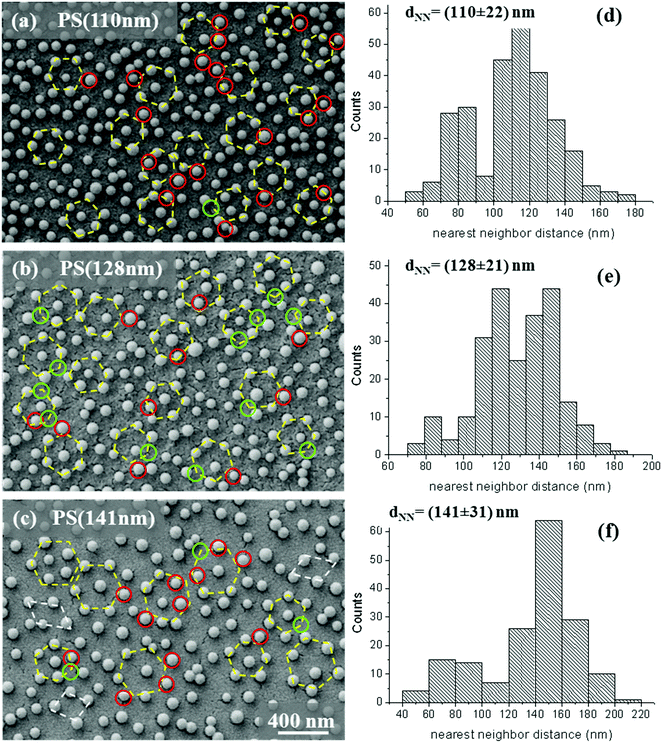
Fig. 3(a)–(c) show colloidal masks with d_NN values of (156 ± 32) nm, (161 ± 32) nm, and (178 ± 30) nm. The associated values of fractional coverage were estimated to be (15.3 ± 0.9)% for PS(156 nm), (13.7 ± 0.8)% for PS(161 nm), and (10.6 ± 0.6)% for PS(178 nm). In this case, a few agglomerates are evident in the left tail of the histogram distributions (Fig. 3(d)–(f)), with overlapping phenomena disappearing for d_NN larger than 161 nm.

Fig. 3 (a–c) SEM micrographs of the samples PS(156 nm), PS(161 nm) and PS(178 nm) and (d–f) associated histogram distributions of the nearest inter-particle spacing.

Well isolated polystyrene nanospheres are observable starting from d_NN ∼ 178 nm, with few units of nearly touching but not overlapping colloids.

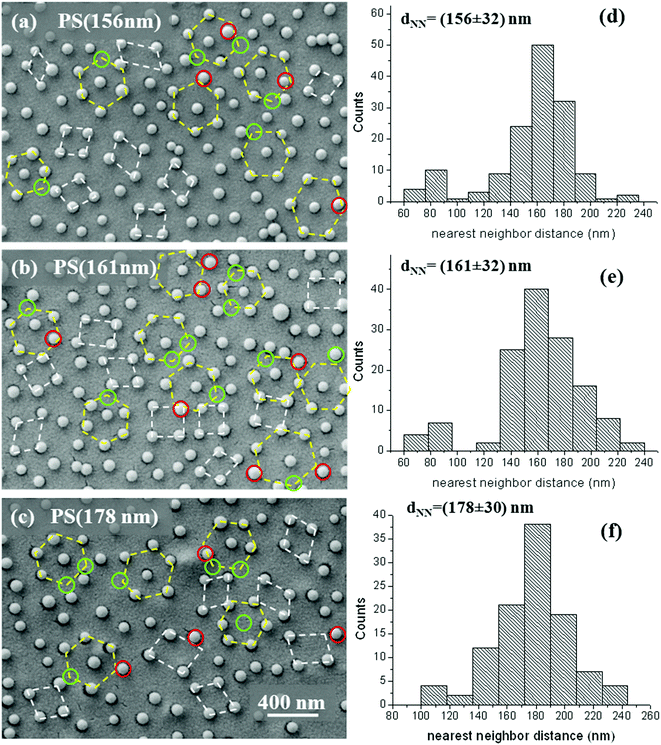
Fig. 4(a)–(d) show colloidal distributions with values of d_NN given as (187 ± 31) nm, (192 ± 31) nm, (200 ± 31) nm and (203 ± 31) nm, associated with the fractional coverage values of (10.8 ± 0.6)% for PS(187 nm), (9.1 ± 0.5)% for PS(192 nm), (10.2 ± 0.6)% for PS(200 nm) and (8.2 ± 0.5)% for PS(203 nm). In these cases the distributions are monomodal (Fig. 4(e)–(h)), with a long right tail, extending up to 280–300 nm, related to the formation of voids. For increasing inter-particle spacing, the formation of void zones in between colloids is expected in not electrostatically stabilized colloidal arrangements due to short-time adsorption conditions.

Fig. 4 (a–d) SEM micrographs of the samples PS(187 nm). PS(192 nm), PS(200 nm) and PS(203 nm) and (e–h) associated histogram distributions of the nearest inter-particle spacing.

Definitively, well-separated polystyrene nanospheres with correlated positional disorder and minimal influence of capillarity induced clustering as well as controllable and tunable coverage even at relatively closely spaced NHs (coverage up to ∼27%) have been demonstrated.

A careful analysis of SEM micrographs also allowed inspecting any change of the local-order coordination and degree of positional correlated disorder at increasing d_NN. In particular, the eventual occurrence of six-nearest-neighbor coordination (triangular-like lattice) and/or four-nearest-neighbor coordination (square-like lattice) was closely inspected and it was possible to distinguish colloids organized according to a hexagonal geometry (as indicated by the dashed yellow hexagons drawn in the SEM images) and colloids which tend to be placed at the vertices of a four edge polygon (as indicated by the dashed white irregular parallelograms drawn in the SEM images). Of course, defects can be observed, such as displaced colloids (highlighted by red circles) and missing colloids (highlighted by green circles).

It is worth noticing that the samples with the shortest d_NN (i.e., PS(110 nm) and PS(128 nm) in Fig. 2(a) and (b), respectively) mainly present short-range ordering with six nearest-neighbor coordination (hexagonal arrangements). In the sample PS(141 nm) (Fig. 2(c)), sparse square coordination appears, mixed with the predominant six nearest-neighbor coordination. For increasing d_NN (Fig. 3(a)–(c) and 4(a)–(c)), the presence of local hexagonal arrangements progressively decreases, being replaced by local square-like coordination, which gradually becomes predominant. For the largest d_NN (i.e., PS(203 nm) in Fig. 4(d)), the colloids are almost totally square-coordinated. Therefore, despite the presence of large voids and largely spaced colloids, indicative of increased disorder, the observed recurring four-nearest-neighbor coordination demonstrates local ordering even under conditions of not electrostatically stabilized arrangements.

A further remark is worth mentioning in regard to the quality of the evaporated Au film, which degrades at high coverage, exhibiting the presence of nanocracks (Fig. 2). Indeed, the high density of colloids represents a surface discontinuity in terms of topography and chemistry which affects the surface migration of the Au species during the evaporation of the Au film. With respect to using the colloidal masks as a template for the fabrication of NH arrays (Fig. 1), since the nanocracks of the Au films are much smaller than the NHs, they may have a poor scattering impact for the wavelength range sampled in the transmittance spectra of our samples (400–1000 nm). Instead, scattering effects affecting the PSPR mode may stem from NH clusters.

In order to assess more quantitatively the occurrence of short-range ordering even under the conditions of minimum coverage, Fast Fourier Transform (FFT) and autocorrelation processing of SEM images of PS(203 nm) were performed, according to the procedure established and applied for the first time by the authors to SEM images of short-range ordered colloidal distributions in a recent study.⁴⁰ Notably, since the intercolloid center-to-center distance exactly corresponds to the interhole center-to-center distance (i.e., a NH distribution exactly corresponds to the arrangement of the precursor colloidal mask, according to the fabrication protocol), statistical image processing of SEM analysis may be performed on colloidal masks as well as on NH distributions without any loss of information and restrictions.

Fig. 5(a) shows the SEM micrograph of the colloidal distribution under consideration, along with the area (pointed out by a red square) considered for calculating the autocorrelation image (briefly termed “Autocor” and reported in Fig. 5(b)) and the FFT of the autocorrelation image (briefly termed “FFT(Autocor)” and reported in Fig. 5(c)).

Fig. 5 (a) SEM micrograph of PS(203 nm) along with the area (pointed out by a red square) considered for calculating (b) the autocorrelation image (Autocor) and (c) the FFT of the autocorrelation image (FFT(Autocor)).

The autocorrelation pattern presents a bright peak of correlation in the middle (corresponding to no shift of the image) and a background without evident periodicities, which suggests the absence of long range-ordering. Nevertheless, FFT(Autocor) evidences two intensity maxima, represented by two small arcs symmetrically placed around the center (highlighted by two arrows), which demonstrates short-range periodicity, associated with a spatial frequency of about (190 ± 5) nm, which is consistent with d_NN = (203 ± 31) nm within the experimental uncertainty.

Definitively, the observed trend of disordering with decreasing coverage is indicative of and consistent with deviations from the electrostatically stabilized configurations. Despite the decreasing degree of short-range ordering, short-range spatial correlation was demonstrated for different coverage conditions resulting from the net interparticle interaction (including electrostatic and lateral capillary forces). Noteworthily, situations with d_NN > 203 nm were not considered in experiments because the evidence that PS(200 nm) and PS(203 nm) exhibit equivalent distributions indicates that d_NN > 203 nm would correspond to colloid adsorption and arrangement mainly dictated by attractive colloid–collector surface interaction rather than by interparticle repulsion. In this situation, decreasing the fractional coverage couldn't be a strategy to induce a specific coordination and/or tune the degree of ordering. Therefore, the range of values of d_NN sampled in our experiments (from 110 nm to 203 nm) is the effective one to comprehensively study the impact of the correlated disorder on the spectral response of short-range ordered NH arrangements when an NH diameter is 60 nm.

3.3 Spectral characterization

On the basis of the working principle of colloidal lithography, it is known that the relative positioning of colloids evolves towards a hexagonal electrostatically stabilized coordination when going from low to high coverage.⁴²

However, in the absence of visual characterization of the colloidal distribution (allowed by SEM analysis, for instance), it is not possible to argue how the geometrical coordination evolves as a function of d_NN. All of this impacts the knowledge of the relationship between the short-range ordering and spectral response of short-range ordered NH distributions.

Noteworthily, although the occurrence of locally hexagonal and locally square lattice geometry was reported while modeling the electrostatically driven formation mechanism of colloidal distributions,⁴² to the best of our knowledge, the impact of geometry transition and mixed-geometry on the spectral response of metal NHs has not been yet investigated. This issue is the focus of the following discussion. It is worth noting that, in comparison with the preliminary results reported in our recent publication,⁴⁰ herein the spectral analyses were carried out on a wider wavelength range (going from 400 nm to 1000 nm instead of 400 nm to 800 nm) and over an extended set of d_NN values, representing the comparison parameter between the spectra.

Following the SEM characterization of the fabricated colloidal masks, we turn to the discussion of the zero-order transmittance spectra of the associated gold NH samples reported in Fig. 6, which presents an extended set of data with respect to our recent publication.⁴⁰ Over the acquisition wavelength range the following can be observed in all cases: (i) a transmission peak narrower and shifted with respect to the transmission maximum at 532 nm of the reference 20 nm thick continuous Au film,⁴⁰ (ii) a transmission dip between 600 and 700 nm, depending on the NH sample, (iii) a further wide band transmission peak at wavelengths larger than 800 nm, and (iv) maximum transmittance intensity ranging from 45 to 65%, which is slightly lower than the 65% transmittance of the reference bare Au film because of multiple incoherent scattering from the short-range ordered NHs and metal losses.

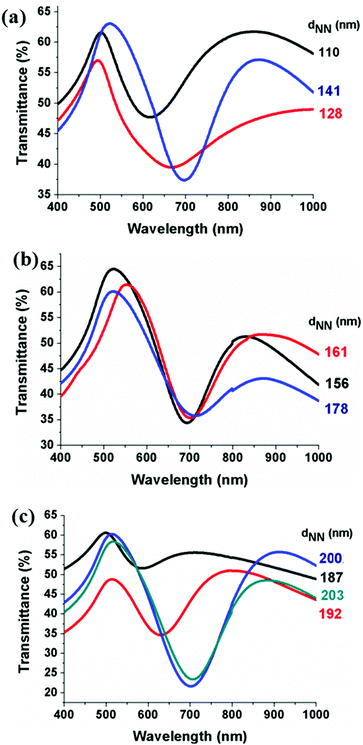Fig. 6 Transmittance spectra of: (a) PS(110 nm), PS(128 nm) and PS(141 nm); (b) PS(156 nm), PS(161 nm) and PS(178 nm); (c) PS(187 nm), PS(192 nm), PS(200 nm) and PS(203 nm).

A less pronounced spectral dip together with a slight blue shift occurs for d_NN decreasing down to 110 nm. This finding is consistent with a reduction of the contribution of the PSPR mode due to an increased density of NHs.³⁸

Definitively, the fabricated NH samples present the transmission maxima and minima characteristics of NH arrays without any loss of spectral features over the whole sampled coverage range (from ∼8 to ∼27%), which is consistent with the presence of short-range ordering pointed out by SEM analysis.

According to previous reports on angle-dependent transmission spectra,⁴⁰ the transmittance minimum between 600 and 700 nm can be associated with a PSPR wave. Based on this assignment and the general picture of free photon-hole grating coupling, we investigated how our NH samples compare with long-range ordered NH arrays.

Turning back to the possible impact of the quality of the Au film on the spectral response of our NH distributions, the rough surface and grain boundaries of the metal film⁴⁵ are reported to have a negative impact on the propagation distance of PSPR modes, resulting in a reduced transmission peak and increased linewidth by light scattering and losses. In the case of short-range ordered NH distributions, the quality of the metal film is not expected to be as critical as in periodic systems because enhanced and suppressed transmission are phenomena localized to a limited number of holes rather than originating from photon-lattice coupling.²⁸ In accordance with this discussion, Fig. 6(a) shows that the transmittance spectra of PS(110 nm), PS(128 nm) and PS(141 nm) present no particularly reduced intensity and increased linewidth compared to the other samples with a better quality of the Au film.

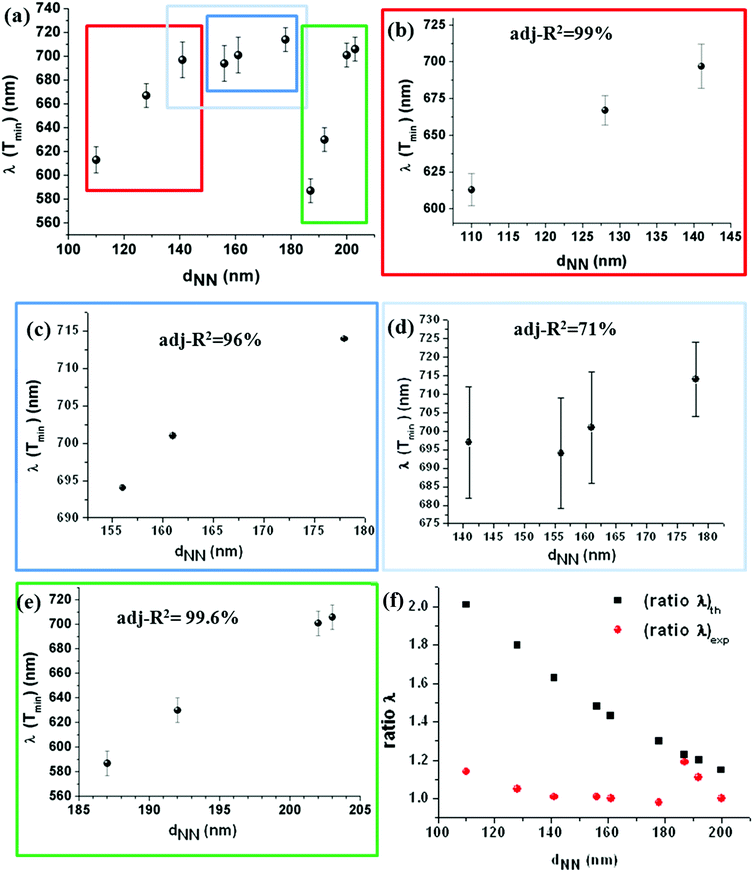
The plot showing the dependence of the wavelength of the transmittance minimum between 600 and 700 nm (referred to as λ(T_min)) on d_NN is reported in Fig. 7(a), which presents an extended set of data with respect to our recent publication.⁴⁰ Interestingly, two main remarks are worth mentioning. First, λ(T_min) varies linearly versus d_NN over contiguous ranges of values of d_NN without showing a general linear trend over the full d_NN range from 110 to 203 nm. In contrast, it is possible to notice that there are three subsets of d_NN values, highlighted by rectangles with different colors. A perfect linear dependence with adjusted-R² = 99% for d_NN in the range 110 to 141 nm (Fig. 7(b)), adjusted-R² = 96% for d_NN ranging from 156 to 178 nm (Fig. 7(c)), and adjusted-R² = 99.6% for d_NN increased from 187 to 203 nm (Fig. 7(e)) can be observed. Noteworthily, d_NN ∼ 141 nm could be indicative of a transition in the distribution because the light-blue rectangle in Fig. 7(d) indicates that a linear dependence with adjusted-R² = 71% also occurs if d_NN ∼ 141 nm is added to the d_NN range in Fig. 7(c). This clearly indicates that the interparticle spacing 141 nm is a border point better associated with hexagonal local coordination.

Fig. 7 Dependence of λ(T_min) on d_NN over different ranges of values of d_NN. Rectangles with different colors in panel (a) let us identify the subset of experimental data plotted in panels from (b) to (e). (f) Comparison between (ratio λ)_th and (ratio λ)_exp plotted versus d_NN ranging over the whole range sampled experimentally (from 110 to 200 nm).

Definitively, spectral analyses indicate that the linear relationship between the spectral position of a PSPR mode and the lattice constant is not fully satisfied in the case of short-range ordering, where d_NN is assumed to play the role of the periodicity length of ordered distribution. Since the spectral response of NH systems is related to geometrical arrangement and ordering properties, it is reasonable to envisage a connection between the observed unconventional (with respect to the behavior of periodic NH patterns) dependence of λ(T_min) on d_NN and the evolution of local geometric arrangements pointed out by SEM analysis of the colloidal masks presented in this study.

Notably, the above discussion points out how a lattice-like model can be developed for short-range ordered NH arrays that is not a straightforward extension of the knowledge on periodic systems. From the practical standpoint, to characterize and predict the spectral properties of short range ordered NH arrays in terms of the dependence of λ(T_min) on d_NN, the coordination geometry has to be accounted for. This point is an unprecedented result of our lattice-like analysis considering a periodicity parameter related to the occurrence of correlated disorder with degree depending on coverage and associated coordination geometry.

4. Interpretative model of the experimental results

4.1 Interpretative model: preliminary remarks and definitions

In order to gain physical insight into the nature of the observed dependence of λ(T_min) on d_NN, here we present an interpretative model relating the spectral behaviour of a PSPR mode to the geometric arrangement of NHs based on the following guidelines.

A linear relationship between the transmittance resonance of a PSPR mode and the characteristic length-scale of periodically arranged NHs is expected on the basis of the momentum matching condition, that is k_SPP = k_∥ ± mG_x ± nG_y, where k_SPP is the wave-vector of the surface plasmon polariton mode depending on the incident wavelength and direction, m and n are integers (Bragg integer diffraction orders), G_x and G_y are the reciprocal lattice vectors of the bidimensional hole lattice along x- and y-directions and k_∥is the in-plane component of the incident photon's wave-vector (k_∥ = 0 for normal incidence). As a consequence of the momentum conservation constraint, the wavelength of a PSPR mode supported by a hole lattice, under normal incidence conditions, is given by^14,20

where P is the periodicity of the hole array, the integers i and j are related to the scattering order of the grating, m(i,j) = i² + j² for a square lattice and m(i,j) = (4/3)(i² + j² + 2ij) for a triangular lattice, ε_d is the relative permittivity of the dielectric environment in contact with the metal surface and ε_m is the dielectric constant of the metal. Notably, a systematic red shift of the theoretically predicted wavelength occurs experimentally, due to scattering effects introduced by the density and finite size of the metal NH lattice. Under the assumption that the fundamental (i,j) = (1,0) PSPR mode was excited at the metal–dielectric interface (which is the case of optically thin gold perforated films), the wavelength of this mode can be expressed as λ(1,0)(□) = P(□)ε_d,m for a square lattice (□) with periodicity P(□) and λ(1,0)(Δ) = (√3/4)P(Δ) ε_d,m for a triangular lattice (Δ) with periodicity P(Δ). Hence, the ratio λ(1,0)(□)/λ(1,0)(Δ) depends on the periodicity length-scales and Bragg indexes of the square and triangular lattices by means of the formula λ(1,0)(□)/λ(1,0)(Δ) = (√4/3)P(□)/P(Δ), where the prefactor √4/3 has to be replaced by unity when two lattices with the same geometry are considered.

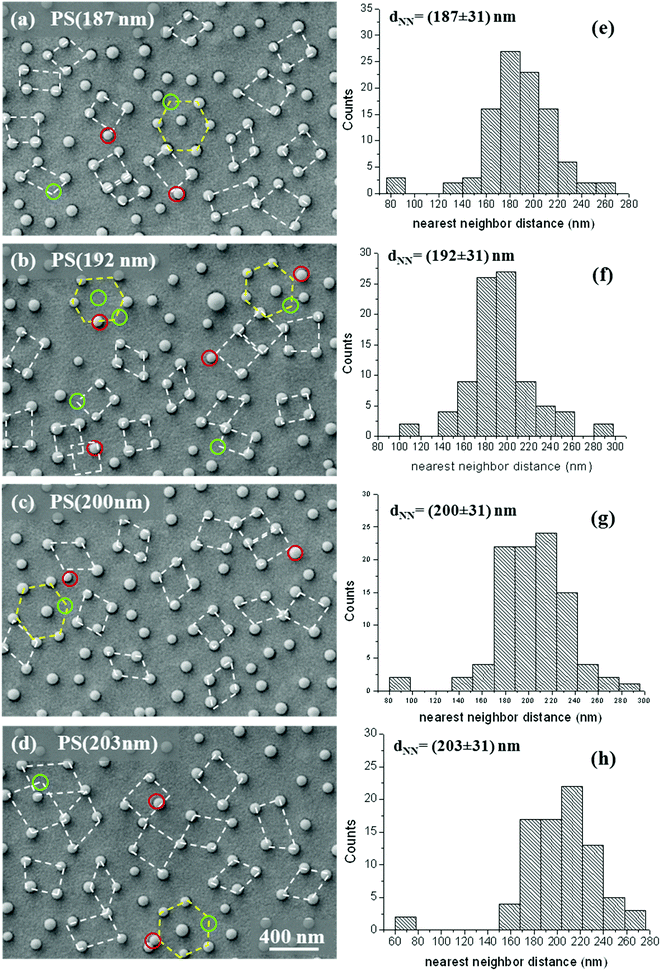
In order to gain insight into the occurrence of deviations from a general linear relationship λ(T_min) versus d_NN, we can compare the theoretical prediction of the grating-coupling model with a properly defined quantity accounting for the characteristics (short-range ordering and geometry of the local coordination) of our colloidal masks. According to this purpose, we estimate the ratio λ(□)/λ(Δ) by means of two independent procedures, as detailed here.

(i) First, we define the quantity

where d_NN(□) and d_NN(Δ) refer to the periodicity length-scale of a NH distribution with square and triangular lattice geometry, respectively. Alternatively, (ratio λ)_th can also be expressed by the wavelength of the transmission PSPR mode supported by a square lattice, λ(T_PSPR)(□), and triangular lattice, λ(T_PSPR)(Δ). The subscript “th” indicates that (ratio λ)_th is defined by considering the theoretical grating-coupling model as described above. Since our SEM analyses demonstrate the occurrence of hexagonal-like or square-like or mixed coordination, (ratio λ)_th can be consistently calculated for our NH distributions.

To implement the calculation of (ratio λ)_th in the case of our experiments, we assume the statistically estimated d_NN as the periodicity parameter, consistently with the general assumption adopted in the literature.²¹ Hence, each value of d_NN is associated with a square or triangular lattice depending on the occurrence of square or hexagonal local coordination of the short-range ordered NH system.

(ii) Second, in analogy with the expression of (ratio λ)_th in terms of the ratio between transmission spectral positions, we define the experimental ratio

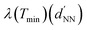where λ(T_min)(d_NN) and refer to the wavelength position of the transmittance minimum of our samples with average interparticle spacing d_NN and 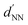, respectively. The subscript “exp” indicates that only experimental values are considered in its evaluation. Although no geometry and/or coordination of the NH distributions were mentioned, this information is inherently accounted for (ratio λ)_exp by means of the measured transmittance response. In practice, SEM analyses demonstrated that any value of d_NN corresponds to a local coordination geometry (square-like or hexagonal-like or mixed).

Additionally, in order to rationalize and gain physical insight into the difference between (ratio λ)_th and (ratio λ)_exp, based on simple mathematics we relate the relative variation between (ratio λ)_th and (ratio λ)_exp to their ratio, termed r(d_NN), by means of the following formula

where

4.2 Interpretative model: physical insight into the role played by the geometry coordination and realistic effects

In order to implement consistently our interpretative model, while calculating (ratio λ)_th and (ratio λ)_exp for d_NN increasing from 110 nm to 200 nm, we consider PS(200 nm) (that exhibits square-like local coordination and has the same ordering characteristics and d_NN as PS(200)) as a reference square lattice. Therefore we calculate
and

Since increasing d_NN is associated with the changes of local coordination geometry, this procedure provides the evolution of (ratio λ)_th and (ratio λ)_expversus the packing geometry of the short-range ordered NH lattice.

Noteworthy, for 187 nm < d_NN < 203 nm, (ratio λ)_th was calculated by retaining the prefactor √4/3 rather than unity (corresponding to both square lattices) because residual random localized hexagonal coordination is still present (Fig. 4(a)–(d)). In principle, this occurrence indicates that a triangular lattice associated with large d_NN is possible. As the definition of (ratio λ)_th means to include inherently the presence of the two geometries observed in the real distributions, replacing the prefactor √4/3 by unit for large d_NN would be, in principle and conceptually, inconsistent with the reasoning leading to the definition of (ratio λ)_th that considers the wavelength positions of the same mode (i.e., (1,0,0) in our case) supported by lattices with different geometries and periodicity lengths. On the other hand, the evaluation of a prefactor weighting the contribution from simultaneously occurring different geometries is not straightforward and, in practice, is not the key point in the present discussion. In this respect, it is worth observing that the deviation between (ratio λ)_th and (ratio λ)_exp is more relevant over the range of values of d_NN, where the prefactor √4/3 is rightly used (i.e., high and intermediate coverage regimes) than at low coverage. This observation is consistent and further supports the fact that (ratio λ)_th is not able to describe realistically the distributions, including the role played by the lattice geometry. Differently, (ratio λ)_exp is expected to be a more appropriate quantity that includes no a priori information about the lattice geometry and is determined by the transmittance response of the real distributions with mixed or dominant geometry.

In Fig. 7(f) the calculated (ratio λ)_th and (ratio λ)_exp are compared: it is possible to observe that (ratio λ)_th deviates from (ratio λ)_exp with a deviation that increases for decreasing d_NN. The reason for such a deviation must be searched in the peculiarities of the real short-range ordered colloidal distribution and their relevant effects on (ratio λ)_th and (ratio λ)_exp as well as different effects accounted for (ratio λ)_th and (ratio λ)_exp.

As a general consideration, we can state that in the framework of short-range ordered NH arrangements, a square lattice is inherently less ordered and forms at lower coverage than an electrostatically stabilized triangular lattice.⁴²

Hence, in principle, assuming d_NN as the equivalent of the periodicity of ordered colloidal arrangements implies that it includes information about the coordination geometry through the transition of the lattice when going from low to high coverage. Since d_NN decreases while adsorption drives the distribution towards the saturated configuration, unlike periodic NH arrays it is improbable that pure triangular and pure square short range lattices can occur associated with comparable d_NN in the case of short-range ordered NHs.

Nevertheless, according to its meaning and statistical calculation, d_NN is not always strictly representative of the geometry of the relative NH-to-NH positioning. This is the case of mixed square–hexagonal coordination where the same value of d_NN represents two different types of coordination geometry; here, the assumption that d_NN is the counterpart of the periodicity of ordered colloidal arrangements would be, in principle, not completely consistent.

It is therefore important to understand, on the basis of our model and by comparing (ratio λ)_th and (ratio λ)_exp, if and to which extent d_NN can be really regarded as the periodicity length of short-range ordered colloidal systems.

From Fig. 7(f), it is evident that (ratio λ)_th increases for increasing coverage. Noteworthily, different coverage is expected to affect the transmittance properties by other phenomena which are not taken into account by (ratio λ)_th due to its derivation based on a hole grating-coupling model. Indeed, (ratio λ)_th does not take into account any red-shift due to the finite size of NHs as well as scattering effects stemming from the correlated disorder and different degrees of ordering of square and hexagonal coordination occurring in the case of short-range ordered NH systems.⁴² In contrast, (ratio λ)_exp exhibits a linear dependence over contiguous intervals of values of d_NN consistent with the behaviour reported while studying λ(T_min) versus d_NN.

Turning to r(d_NN), it was found that r(d_NN) is a constant depending on the range of values of d_NN, that is r(d_NN) = 1.69 ± 0.08 (adjusted-R² of 84%) for 110 nm < d_NN < 141 nm, r(d_NN) = 1.40 ± 0.07 (adjusted-R² of 99.8%) for 156 nm < d_NN < 178 nm and r(d_NN) = 1.09 ± 0.06 (adjusted-R² of 99.8%) for 187 nm < d_NN < 203 nm.

The evidence that r(d_NN) takes similar values for intervals of d_NN associated with the same kind of local NH coordination (SEM analyses in Fig. 3–5) indicates that (ratio λ)_exp is sensitive to the geometry of the NH arrangement. In contrast, in the case of (ratio λ)_th any information about lattice geometry is assumed by d_NN(□) and d_NN(Δ) associated with a square and a triangular lattice, respectively.

Therefore, in regard to the relative variation between (ratio λ)_th and (ratio λ)_exp, two main conclusions can be remarked. First, it depends on the changes of the local coordination of our short-range ordered distributions consistently with the intervals of values of d_NN individuated by SEM analysis. Second, it progressively decreases being related to the observed transition of the geometrical coordination number from hexagonal at high coverage to square at low coverage through hexagonal–square mixed coordination at intermediate coverage.

From the physical standpoint, the difference between (ratio λ)_th and (ratio λ)_exp that plays a role in the above discussion and conclusions is that, unlike (ratio λ)_exp, (ratio λ)_th doesn't account for the realistic characteristics of the NH distributions related to deviations from the periodic ordering (such as coverage-related ordering/disordering and changes of the local coordination) impacting the experimental transmission response. On this basis, the difference between (ratio λ)_th and (ratio λ)_exp is expected to quantitatively increase in situations where scattering effects are enhanced (such as for an increased density of NHs and capillary-induced clustering).

As a concluding remark, the developed model and the presented discussion are independent on the diameter of metal NHs. Once such a geometrical parameter if given, our conceptual model is well stated over the range of values of d_NN corresponding to the evolution of the distribution from saturated adsorption to low coverage still sensitive to interparticle repulsion (i.e., d_NN up to 203 nm under our experimental conditions). Indeed, under very low coverage conditions, colloid adsorption is dominated by colloid–collector attraction and interparticle repulsion poorly drives colloid self-assembly. Hence, decreasing coverage is associated with a progressively decreasing degree of correlated disorder which impacts the possibility of observing transmission resonances.

Definitively, several unprecedented results and comprehensive, both fundamental and applicative, discussion presented in this paper may lay the foundation for a fundamental description, in terms of a lattice-like model, of short-range ordered nanoholes that does not exploit straightforwardly and qualitatively concepts strictly related to periodic systems.

5. Conclusions

In this paper, the short-range order and spatial coordination geometry of NH distributions obtained by following a simplified colloidal lithography protocol in optically thin gold films have been studied based on an accurate qualitative and quantitative analysis of SEM micrographs.

For each distribution, a characteristic NH-to-NH average nearest neighbor spacing d_NN was derived from statistical analyses and treated, according to the common assumption, as the equivalent of the periodicity parameter of long-range ordered nanohole lattices. A transition of the order from locally quasi-hexagonal, at short d_NN, to locally quasi-square, at large d_NN, was observed and carefully related to the changes of the spectral response of the NH distributions as a function of fractional coverage and colloidal coordination. First, our study points out that, unlike long-range periodic distributions, the linear dependence of the wavelength of a propagating plasmon mode on the periodicity, here represented by d_NN, is not demonstrated for the entire range of d_NN values. An interpretative model has been developed demonstrating that, for short range ordered arrangements, d_NN can be considered as the counterpart of the periodicity to a certain extent, depending on the degree of correlated disorder. Based on our model we discuss how short-range ordering, changes in the geometry of the local coordination and ordering/disordering-related scattering effects are responsible for the deviations of the spectral response of short-range ordered metal NH real distributions from ideal periodic systems.

Their effects, not accounted for in the statistical average d_NN, have been found to have more impact at increasing coverage where capillary effects also impact the colloid arrangement.

To summarize the main conceptual results of our study: (i) the impact of mixed (hexagonal–square) coordination-geometry on the spectral response of short-range ordered NHs has been investigated, (ii) unlike the straightforward assumption, it has been demonstrated that d_NN cannot be interpreted as the counterpart of the periodicity pitch of periodic NH arrays, and (iii) the conceptually rigorous periodicity-like length-scale has been recovered based on autocorrelation analysis of SEM images.

Therefore, unprecedented experimental results have been presented, which point out important differences between short-range and long-range ordered NHs and indicate a conceptual advance that may open the way to new directions for a deeper physical understanding of the mechanisms leading to resonant transmission features in short-range ordered metal NHs.

Noteworthily, the presented discussion points out how a lattice-like model can be developed for short-range ordered NH arrays and this model differs from the straightforwardly extended model used to describe periodic systems.

From the practical standpoint, whenever a short range ordered NH array is considered, any prediction of the trend of the dependence of λ(T_min) on d_NN has to account for the local coordination geometry as dictated by coverage.

Funding sources

This work was supported by a grant from the Ministry of Education, University and Research (MIUR) for the Scientific Program SIR2014 Scientific Independence of young Researcher (RBSI1455LK).

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors acknowledge Antonio Pinna for technical support during SEM experiments, Enrico Melissano (IMM-CNR, Lecce) for the thermal deposition of gold films as well as Adriana Campa (IMM-CNR, Lecce) and Maria Concetta Martucci (IMM-CNR, Lecce) for oxygen plasma treatments.

References

1. T. W. Ebbesen, H. J. Lezec, H. F. Ghaemi, T. Thio and P. A. Wolff, Nature, 1998, 391, 667–669.
2. C. Genet and T. W. Ebbesen, Nature, 2007, 445, 39–46.
3. H. A. Atwater and A. Polman, Nat. Mater., 2010, 9, 205–213.
4. F. F. Mahani, A. Mokhtari and M. Mehran, Nanotechnology, 2017, 28, 385203.
5. S. Yokogawa, S. P. Burgos and H. A. Atwater, Nano Lett., 2012, 12, 4349–4354.
6. A. G. Brolo, E. Arctander, R. Gordon, B. Leathem and K. L. Kavanagh, Nano Lett., 2004, 4, 2015–2018.
7. A. G. Brolo, S. C. Kwok, M. G. Moffitt, R. Gordon, J. Riordon and K. L. Kavanagh, J. Am. Chem. Soc., 2005, 127, 14936–14941.
8. M. Bauch, K. Toma, M. Toma, Q. Zhang and J. Dostalek, Plasmonics, 2014, 9, 781–789.
9. A. Prasad, J. Choi, Z. Jia, S. Park and M. R. Gartia, Biosens. Bioelectron., 2019, 130, 185–203.
10. A. De Leebeeck, L. K. S. Kumar, V. de Lange, D. Sinton, R. Gordon and A. G. Brolo, Anal. Chem., 2007, 79, 4094–4100.
11. M. P. Jonsson, A. B. Dahlin, L. Feuz, S. Petronis and F. Höök, Anal. Chem., 2010, 82, 2087–2094.
12. C. Escobedo, Lab Chip, 2013, 13, 2445–2463.
13. A. B. Dahlin, Analyst, 2015, 140, 4748–4759.
14. F. J. Garcia-Vidal, L. Martin-Moreno, T. W. Ebbesen and L. Kuipers, Rev. Mod. Phys., 2010, 82, 729–787.
15. J. Bravo-Abad, A. Degiron, F. Przybilla, C. Genet, F. J. García-Vidal, L. Martín-Moreno and T. W. Ebbesen, Nat. Phys., 2006, 2, 120–123.
16. H. F. Ghaemi, T. Thio, D. E. Grupp, T. W. Ebbesen and H. J. Lezec, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 6779–6782.
17. M. Sarrazin, J.-P. Vigneron and J.-M. Vigoureux, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 085415.
18. C. Genet, M. P. van Exter and J. P. Woerdman, Opt. Commun., 2003, 225, 331–336.
19. E. S. H. Kang, H. Ekinge and M. P. Jonsson, Opt. Mater. Express, 2019, 9, 1404–1415.
20. F. J. García de Abajo, Rev. Mod. Phys., 2007, 79, 1267–1290.
21. T. Sannomiya, O. Scholder, K. Jefimovs, C. Hafner and A. B. Dahlin, Small, 2011, 7, 1653–1663.
22. J. J. Burke, G. I. Stegeman and T. Tamir, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 5186–5201.
23. F. Yang, J. R. Sambles and G. W. Bradberry, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 5855–5872.
24. W. A. Murray, S. Astilean and W. L. Barnes, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 165407.
25. I. S. Spevak, A. Y. Nikitin, E. V. Bezuglyi, A. Levchenko and A. V. Kats, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 161406.
26. T. Matsui, A. Agrawal, A. Nahata and Z. V. Vardeny, Nature, 2007, 446, 517.
27. F. Przybilla, C. Genet and T. W. Ebbesen, Appl. Phys. Lett., 2006, 89, 121115.
28. D. Pacifici, H. J. Lezec, L. A. Sweatlock, R. J. Walters and H. A. Atwater, Opt. Express, 2008, 16, 9222–9238.
29. A. Agrawal, T. Matsui, Z. V. Vardeny and A. Nahata, Opt. Express, 2008, 16, 6267–6273.
30. C. Valsecchi, E. L. Gomez Armas and J. Weber de Menezes, Sensors, 2019, 19, 2182.
31. S.-D. Liu, P. Yue, S. Zhang, M. Wang, H. Dai, Y. Chen, Z.-Q. Nie, Y. Cui, J.-B. Han and H. Duan, Adv. Opt. Mater., 2020, 8, 1901109.
32. Q. Liu, Y. Song, P. Zeng, C. Zhang, Y. Chen, H. Wang, Y. Luo and H. Duan, Appl. Surf. Sci., 2020, 526, 146690.
33. C. Vieu, F. Carcenac, A. Pépin, Y. Chen, M. Mejias, A. Lebib, L. Manin-Ferlazzo, L. Couraud and H. Launois, Appl. Surf. Sci., 2000, 164, 111–117.
34. S. Matsui and Y. Ochiai, Nanotechnology, 1996, 7, 247–258.
35. P. Hanarp, D. S. Sutherland, J. Gold and B. Kasemo, Colloids Surf., A, 2003, 214, 23–36.
36. J. Prikulis, P. Hanarp, L. Olofsson, D. Sutherland and M. Käll, Nano Lett., 2004, 4, 1003–1007.
37. M. Q. Liu, C. Y. Zhao, B. X. Wang and X. Fang, J. Opt. Soc. Am. B, 2018, 35, 504–513.
38. F. Przybilla, C. Genet and T. W. Ebbesen, Opt. Express, 2012, 20, 4697–4709.
39. T. H. Reilly, R. C. Tenent, T. M. Barnes, K. L. Rowlen and J. van de Lagemaat, ACS Nano, 2010, 4, 615–624.
40. M. Cesaria, A. Taurino, M. G. Manera, M. Minunni, S. Scarano and R. Rella, Nanoscale, 2019, 11, 8416–8432.
41. Digital Micrograph software (DM Vers. 3.21.1374.0), https://www.myendnoteweb.com/EndNoteWeb.html?func=downloadInstallers%26cat=download%26.
42. S. Watanabe, M. Miyahara and K. Higashitani, J. Chem. Phys., 2005, 122, 104704.
43. B. Brian, B. Sepúlveda, Y. Alaverdyan, L. M. Lechuga and M. Käll, Opt. Express, 2009, 17, 2015–2023.
44. K. Xiong, G. Emilsson and A. B. Dahlin, Analyst, 2016, 141, 3803–3810.
45. J. Zhang, M. Irannejad, M. Yavuz and B. Cui, Nanoscale Res. Lett., 2015, 10, 238.

---

Footnote

† Present address: Department of Mathematics and Physics “Ennio De Giorgi”, University of Salento, prov. le Arnesano, 73100, Lecce, Italy.

---