Open Access Article
Open Access ArticleGrowth mechanistic insights into perovskite nanocrystals: dimensional growth†
Prasenjit
Mandal
 ac,
Angira
Roy
ac,
Angira
Roy
 b,
Subhashri
Mannar
b and
Ranjani
Viswanatha
b,
Subhashri
Mannar
b and
Ranjani
Viswanatha
 *abc
*abc
aNew Chemistry Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore, 560064, India
bInternational Centre for Materials Science, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore, 560064, India
cSchool of Advanced Materials, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore, 560064, India. E-mail: rv@jncasr.ac.in
First published on 17th September 2020
Abstract
The optical and electronic properties of lead halide perovskite nanocrystals have been explored extensively due to their increasing demand in photovoltaic and optoelectronic applications. But little is known about the growth kinetics of these nanocrystals. In this work, we demonstrate an interesting new mechanism using the method of arrested growth and precipitation to isolate the intermediates. We find that growth is driven by oriented attachment competing with the surface energetics. Hence, we observe a rare example of self-assembly driven dimensional growth characterized by suitable surface passivation that competes with the exposed surface facets through dimensional growth. This provides an explanation for not only the lack of size and shape tunability but also the emergence of a cubic shape rather than commonly observed spherical shapes in nanocrystals. Additionally, we find that this also corresponds to the observed phase transitions as well as correlating with pathways of decay of the photoluminescence spectra.
Introduction
Lead halide perovskite nanocrystals (LHP NCs) with their remarkable properties including a wide range of bandgap tunability, negligible electron-phonon coupling,1 large absorption cross-section2 and narrow emission linewidth in addition to their solution processability, low-cost synthesis and compatibility with other existing device components3,4 are promising materials for potential optoelectronic applications, such as light-emitting displays, lasers, and nanocrystal inks for large area printable light harvesting devices.5–10 However, in spite of their high quantum yield (QY) and surface insensitivity, the first light emitting diodes (LEDs) based on solution processed perovskites showed an external quantum efficiency of less than 0.2%.11 Sustained efforts to understand the electron hole recombination pathways and selective improvisation of the radiative pathways have been necessary to improve the performance to about 15%.12 This has been largely achieved by addressing issues like the increasing confinement of the highly mobile charges, ligand exchange and ligand density control, surface defect passivation, doping and suppression of Auger non-radiative recombination.13–17 However, an understanding of the physical origin of poor efficiencies, particularly arising from the crystal packing, is lacking. Specifically, with the current emphasis shifting from a mesoscopic cell architecture to planar devices, the ability to fabricate continuous, conformal layers is key. In this scenario, the formation of continuous layers depends on the correlation of the film and crystal morphology, and hence the first step towards optimization of the perovskite thin films would be to control their packing.18 Thus, the crystal morphology and dimensionality are the key parameters to modulate the performance of these devices.However, modulating the morphology and size of LHP NCs has proven to be particularly difficult. Despite significant efforts, including size modulation, stabilization of other crystal facets beyond the facets of the cube have largely been unsuccessful.19,20 In fact, the most energy efficient path of nanocrystal formation is through the formation of spherical dots. This has clearly been observed in several II–VI and other metallic NCs. In most cases, formation of irregularly shaped crystals occurs only during instantaneous formation due to the entropic issues. In fact, early literature on II–VI NCs have extensively shown this large size distribution due to the non-uniform quick growth, with slowing down of the growth being one of the main paths forward to increasing homogeneity. In contrast, in the case of perovskites, we observe that even though the growth of NCs is instantaneous at that temperature, we observe the uniform growth of nano cubes rather than the irregular crystals. This suggests that it is not a one-step random growth but rather a structured, energy minimization driven fast process. In spite of extensive research being carried out by several groups21–28 on post-synthetic phase transition by heat treatment, the time dependent nucleation mechanism, step growth in a single reaction, formation of a heterostructure, the mechanism of cation and anion exchange, ligand contribution and the doping effect, morphology modulation of LHP NCs has not been reported. This relative inability to modulate the size suggests the presence of a fundamentally different growth mechanism. The growth kinetics and hence its mechanism in CsPbX3 materials have remained elusive largely due to their fast formation and ice cooled harvesting procedure. Only recently, a couple of reports shed light on the differential crystal facet energetics leading to partial directional growth, that is, growing arms in the preferential direction of the cube.29,30 In this work, we use the method of arrested precipitation by heating to lower synthesis temperature to isolate the transient intermediates specifically to understand the thermodynamics and kinetics of the growth mechanism. These intermediates are characterized based on their crystal structure using X-ray diffraction (XRD), their shape using transmission electron microscopy (TEM) and their optical properties. Based on these properties, the mechanism of growth has been extrapolated suggesting the first example of self-assembly driven dimensional growth in this class of compounds within this work.
Results
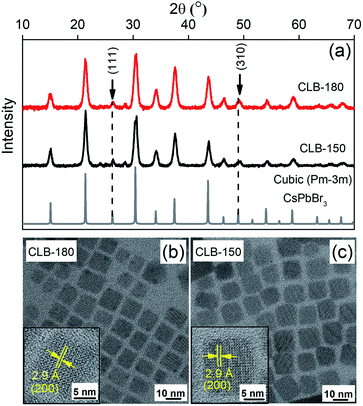
Different intermediates of nanocrystals (NCs) were synthesized by following a modified procedure described by Protesescu et al.5 Details of the synthesis procedure are mentioned in the Experimental section. LHP NCs are usually synthesized by ice cooling the crystals immediately after the injection of the Cs-precursor. With this method, they are well known to retain their size and morphology for differing ligands, precursor concentrations as well as any other change in synthesis conditions. Hence isolation of intermediates has proven to be tricky. It was noted that the only parameter that gave rise to higher bandgap, possibly due to quantum confinement, was the temperature of the synthesis. Here we isolate these intermediates by heating to various temperatures to study their crystal structure, shape and optical properties to shed light on the elusive growth mechanism of perovskite halides. The details of the respective samples along with their codes at varying temperatures are shown in Table TS1 of the ESI.† The absorption and the photoluminescence (PL) shown in Fig. S1† show a gradual shift of the band gap from about 430 nm (2.88 eV) to about 510 nm (2.43 eV). This dramatic increase in band gap has been attributed to a strong quantum confinement. Extensive studies beyond the high band gap of the material and their correlation of various properties are not available in the literature as their potential in applications is limited due to their low QY. However, such a correlation could provide important insights into the growth mechanism of these halide systems.Fig. 1(a) depicts the XRD patterns of the CsPbBr3 NCs synthesized at 180 °C (CLB-180) and at 150 °C (CLB-150) along with the bulk structure obtained from the ICSD demonstrating a clear cubic structure as expected. Broadening of the XRD planes is known to occur due to their smaller size and we fit each of the planes with the Scherrer formula and the results are tabulated in Table TS2, ESI.† Here we make specific note of characteristic cubic reflections, namely, the (111) and (310) planes. Additionally, the morphological features demonstrated by a majority of cubes of these NCs are obtained by TEM for both CLB-180 and CLB-150 as shown in Fig. 1(b) and (c), respectively. The average size of these cubic NCs in both cases was found to be about 10.5 ± 1.0 nm (histogram for size analysis is shown in Fig. S2(a) and (b), ESI†). The high-resolution TEM (HRTEM) images shown in the corresponding insets reveal a lattice spacing of 2.9 Å corresponding to the formation of the (200) plane of cubic CsPbBr3 NCs.
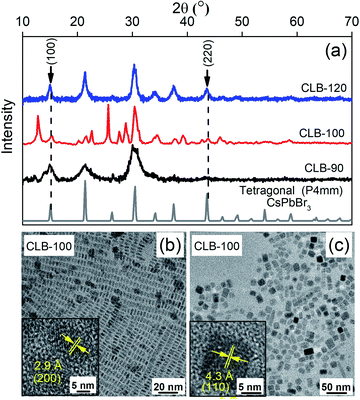
Bulk CsPbBr3 is known to crystallize in three different phases, namely, the orthorhombic space group (Pnma) at temperatures below 88 °C followed by the tetragonal space group (P4/mbm) up to 130 °C eventually leading to the cubic space group (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) at higher temperature.21 It is important to note that these phase transitions occur largely due to the orientation of the {PbBr6}4− octahedra with respect to the orthogonal geometry and are hence extremely facile and can also be largely motivated by the surface of the NCs. However, while these phase transitions are reported under thermodynamic conditions of sample heating, so far, the kinetic nature of these phases as obtained by ice-cooling the samples has been unclear. Hence in this work, we arrest the samples in their kinetically stabilized phase and study the origin and consequences of the various phases on its properties. Hence, we reduce the sample synthesis temperature to 120 °C and 100 °C, below the prescribed 130 °C phase transition temperature from the cubic to the tetragonal phase. Given the very low energy required to tilt the {PbBr6}4− octahedra, the kinetically stable tetragonal phase is stabilized as shown by the characteristic (100) and (220) planes of the tetragonal phase in the XRD pattern as shown in Fig. 2(a). The XRD patterns of CLB-90 and CLB-120 perfectly match the tetragonal phase of bulk CsPbBr3 suggesting phase purity of these NCs. However, the presence of additional peaks around 12° and 25° for CLB-100 can be accounted for the Cs4PbBr6 impurity phase. We do observe the high energy band gap corresponding to the Cs4PbBr6 phase in the unwashed sample. However, upon washing this is not observable. The transition between these two phases is extremely facile for this phase, particularly for the sample synthesized at 100 °C. Wen et al.31 showed a phase evolution occurring within a short period of 2 hours. Further repeated measurements of this sample show varying intensity ratios for the two phases suggesting the role of the environment in an extremely long measurement timescale (∼4 hours). The phases obtained above and below this temperature show an extremely pure phase suggesting this to be a kinetic equilibrium point for the two phases. However, surprisingly, the TEM image for the sample maintained in a glove box and under vacuum conditions shows the presence of two distinct sizes, namely, 6.8 ± 0.8 nm and 3.8 nm ± 0.4 nm, as shown in Fig. 2(b) and (c), respectively, and the histogram is shown in Fig. S3, ESI.† Though the presence of two sizes is surprising at first, observation of HRTEM images shown in the insets of Fig. 2(b) and (c) show different lattice spacings of 2.9 Å and 4.3 Å. These planes are known to correspond to the (200) and the (110) planes of the tetragonal phase suggesting that we are indeed observing the particles from two different projections (edge-on and face-on) rather than two different size distributions. The projective nature of the TEM technique does not allow the differentiation between a two- (platelet) or three-dimensional (dot) confinement. Similar results with the demonstration of the tetragonal (110) plane with a lattice spacing of 4.1 Å and an average size of 9.9 ± 0.8 nm are observed for the sample quenched at 120 °C as observed from the TEM image in Fig. S4, ESI.†
m) at higher temperature.21 It is important to note that these phase transitions occur largely due to the orientation of the {PbBr6}4− octahedra with respect to the orthogonal geometry and are hence extremely facile and can also be largely motivated by the surface of the NCs. However, while these phase transitions are reported under thermodynamic conditions of sample heating, so far, the kinetic nature of these phases as obtained by ice-cooling the samples has been unclear. Hence in this work, we arrest the samples in their kinetically stabilized phase and study the origin and consequences of the various phases on its properties. Hence, we reduce the sample synthesis temperature to 120 °C and 100 °C, below the prescribed 130 °C phase transition temperature from the cubic to the tetragonal phase. Given the very low energy required to tilt the {PbBr6}4− octahedra, the kinetically stable tetragonal phase is stabilized as shown by the characteristic (100) and (220) planes of the tetragonal phase in the XRD pattern as shown in Fig. 2(a). The XRD patterns of CLB-90 and CLB-120 perfectly match the tetragonal phase of bulk CsPbBr3 suggesting phase purity of these NCs. However, the presence of additional peaks around 12° and 25° for CLB-100 can be accounted for the Cs4PbBr6 impurity phase. We do observe the high energy band gap corresponding to the Cs4PbBr6 phase in the unwashed sample. However, upon washing this is not observable. The transition between these two phases is extremely facile for this phase, particularly for the sample synthesized at 100 °C. Wen et al.31 showed a phase evolution occurring within a short period of 2 hours. Further repeated measurements of this sample show varying intensity ratios for the two phases suggesting the role of the environment in an extremely long measurement timescale (∼4 hours). The phases obtained above and below this temperature show an extremely pure phase suggesting this to be a kinetic equilibrium point for the two phases. However, surprisingly, the TEM image for the sample maintained in a glove box and under vacuum conditions shows the presence of two distinct sizes, namely, 6.8 ± 0.8 nm and 3.8 nm ± 0.4 nm, as shown in Fig. 2(b) and (c), respectively, and the histogram is shown in Fig. S3, ESI.† Though the presence of two sizes is surprising at first, observation of HRTEM images shown in the insets of Fig. 2(b) and (c) show different lattice spacings of 2.9 Å and 4.3 Å. These planes are known to correspond to the (200) and the (110) planes of the tetragonal phase suggesting that we are indeed observing the particles from two different projections (edge-on and face-on) rather than two different size distributions. The projective nature of the TEM technique does not allow the differentiation between a two- (platelet) or three-dimensional (dot) confinement. Similar results with the demonstration of the tetragonal (110) plane with a lattice spacing of 4.1 Å and an average size of 9.9 ± 0.8 nm are observed for the sample quenched at 120 °C as observed from the TEM image in Fig. S4, ESI.†
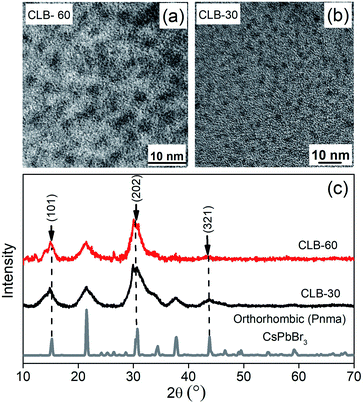
These data suggest the formation of a platelet-like structure in the tetragonal phase rather than the three-dimensional cube observed at higher temperature. Further we go down in temperature to 90 °C which is near the transition temperature of the orthorhombic to the tetragonal phase. From the TEM image shown in Fig. S5, ESI,† we observe small zero-dimensional dots aligning in the form of a one-dimensional array of lines. This indicates the growth of the NCs in one direction which upon a further increase in temperature to 100 °C aligns to form nanoplatelets as discussed earlier. Further decrease of the temperature to 60 °C and 30 °C shows the presence of small dots with sizes of 3.3 ± 0.4 nm and 2.6 ± 0.3 nm as shown in Fig. 3(a) and (b), respectively, while the histogram is shown in Fig. S6, ESI.† Additionally, the XRD patterns in Fig. 3(c) show the formation of orthorhombic space groups at this temperature of synthesis. All the major reflections from the orthorhombic phase of CsPbBr3 are absent from the tetragonal and cubic phases, including (101), (202) and (321) planes. So effectively the orthorhombic phase is aligning in a preferred orientation forming a rod from spherical dots at 90 °C.
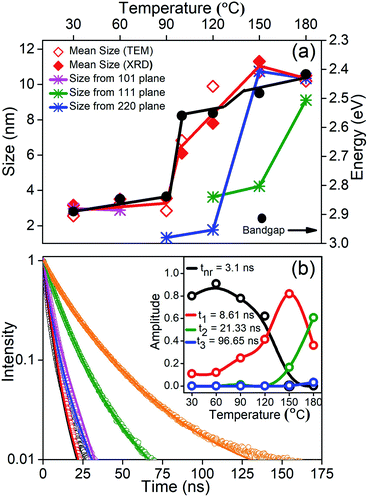
Finally, in order to understand the nature of these phase transitions and their relation to the morphology, we use an ensemble averaged measurement like the band gap of the material. It is well known in the literature that the optical properties are controlled largely by the direction of weakest confinement especially when the sizes are below the Bohr radius of the material and one does not expect any band crossing during this shape transformation.32 In this work, in the absence of any theoretical studies regarding the change of the band structure as we change the shape of the NCs, we assume that there exists no band crossing. Hence in all cases, the band gap is controlled by the direction of weakest confinement and hence is reflective of the growth in that direction. We plot the band gap as well as the size obtained from TEM and specific XRD planes as a function of temperature in Fig. 4(a). It is important to note that in the size regime where the band gap is highly sensitive to size, we observe a jump in the band gap (∼278 meV) during the phase transition between rods to platelets at 90 °C to 100 °C as shown by the black line in Fig. 4(a). However, with an excitonic radius of about 7 nm, the shift in band gap during the phase transition from platelets to cubes at ∼130 °C is within the error bar.33 It is important to note that the morphology changes and the change of dimensionality observed through TEM images is further confirmed by this jump. To understand the role of various growth facets, least squares error fitting to the Scherrer formula was carried out on the phase characteristic XRD peaks and the results are shown in Fig. 4(a). CLB-30 and CLB-60 indicate growth along the (101) direction (magenta line) while reflections along the tetragonal and cubic phases are absent. Similarly, (220) planes (olive line) start to grow in the tetragonal phase (CLB-90, CLB-100, and CLB-120) and this is continued in the cubic phase (CLB-150 and CLB-180). But (111) planes (blue line) are absent in CLB-90 and they start to grow in CLB-120 and the growth continues to the cubic phase. Though (111) planes are a sharp feature for the cubic phase, they are also present in the tetragonal phase, possibly due to the small difference in the lattice parameter in between the tetragonal (P4mm) (a = b = 5.859 Å, c = 5.895 Å) and cubic (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) (a = b = c = 5.874 Å) phase.
m) (a = b = c = 5.874 Å) phase.
Further, it is well known that the perovskites are known to have a high QY. We obtain 93% QY for CLB-180 NCs similar to the literature reports. However, even though we measured the absolute QY, we obtained >100% QY for some samples. Upon in-depth analysis of this issue, it was observed that most of the data in the literature was an artifact arising from the absence of the excitation correction arising due to the inhomogeneous nature of the xenon lamp. Upon performing this correction, the QY for CLB-180 NCs decreased to 43% and accordingly we measured the relative QY for other samples. It was observed that the photoluminescence QY of CsPbBr3 NCs drops dramatically from 43% for the sample synthesized at the highest temperature to 2.1% for the sample synthesized at the lowest temperature (shown in Fig. S7, ESI†). This suggests that the decay lifetimes could shed some light on the possible kinetic and thermodynamic factors. Fig. 4(b) shows the lifetime of all the samples synthesized at different growth temperatures and the solid lines are fits to the curves. Fitting was performed using global analysis for all the lifetimes using three probable lifetimes to accommodate rod, platelet and cubic growth, along with a fast non-radiative component. The inset of Fig. 4(b) depicts the relative intensities of the various decay pathways. From the figure, consistent with high QY for samples synthesized at high temperature, it is evident that the non-radiative path with an average lifetime of about 3.1 ns decreases in intensity, eventually going down to zero in samples synthesized at high temperature. Additionally, we observe that the phase transitions as obtained from the intensities of the relevant decay lifetimes match with the phase transitions observed by XRD and TEM. For example, the samples prepared at 30 °C and 60 °C do not show more than one lifetime (t1 = 8.61 ns). Similarly, the second lifetime (t2 = 21.33 ns) starts to appear from 90 °C onwards with increasing intensity, while the third lifetime (t3 = 96.65 ns) appears from 150 °C onwards. It is well known that the lifetime of trapped excitons is normally much longer than that of free excitons.34 Various factors affecting the lifetime include composition variation and changes due to size and morphology. An extensive survey of the literature has shown that large changes in lifetime by an order of magnitude are usually related to the shape or morphology change rather than the change of size. Secondly, absorption spectra do not show the presence of any new phases, such as Cs4PbBr6, and this phase is normally known to be largely non-fluorescent or weakly fluorescent suggesting that the observed lifetime changes are unlikely to be due to compositional differences. However, it is interesting to note that the optical properties of the NCs are in sync with the additional energy barrier arising due to exposure of different growth facets during the growth of these NCs. This suggests that the optical properties are highly correlated with the dimensionality of the NCs. This is not surprising as the presence of surface states in perovskites is known to be energetically expensive.
Discussion
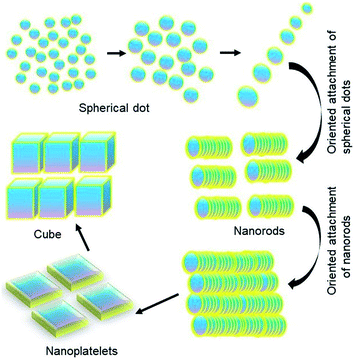
Based on all these factors observed so far, we propose a self-assembly driven dimensional growth mechanism as shown in Scheme 1. In other words, we observe that small nucleated particles align in a preferred direction to form a rod, which upon reaching a certain length becomes energetically unviable due to the highly expensive surface states. These energetics are balanced by the rods aligning to form platelets, simultaneously going through a phase transition, and finally the platelets align to form a highly symmetric cube through the coordinated asymmetric oriented attachment growth mechanism followed by internal competition between the different crystal facets as observed from TEM, XRD and optical properties. It is important to note that even though none of the properties individually show that platelets come together to form cubes, this mechanism can successfully explain all the properties arising from these multiple characterization studies.Kinetically controlled oriented attachment growth of NCs is a well-studied mechanism for the preparation of anisotropic samples. However, knowing that the surface state energetics of perovskites is quite high, and the literature has shown the competition driven dimensional growth across many size specific assemblies in thermodynamically stable phases like metal organic frameworks, supramolecular assemblies or inorganic materials,21,35–38 we believe that this could be one of the possibilities. In fact, some of the work39,40 in the literature in the context of forming bigger shape specific LHP NCs has shown that directional oriented attachment is indeed probable. Hence, we believe that as a first step towards understanding this growth mechanism of the perovskites, oriented dimensional growth is a highly probable possibility. However, this is the first instance wherein transient intermediates demonstrating these phenomena have been isolated. The underlying growth mechanism, specifically competitive energetics limited oriented attachment, is yet to be fully understood even in the thermodynamically stable phases. The most rational understanding for this dimensional growth has been demonstrated in substrate adhered 2-dimensional to 3-dimensional NCs41 as well as nanoscale metal–organic framework materials. In both the cases, competitive interactions have been recognized to be the core propellent in the changing dimensionality of the NCs. While the strain between the substrate and the NC interface has been singled out in the first case, in the case of framework materials, introduction of similar functional groups between the linkers and modulators has successfully introduced competitive interactions. This leads to alteration of the coordination equilibrium at the interface and hence modulation on specific crystallographic planes leading to anisotropic crystal growth.19 Similarly, in the present case, the presence of energetically expensive surface states as well as the small amount of energy required to rotate the octahedra leading to the phase transition drives the growth of perovskite halides into cubic shapes. This study opens up a new horizon for the dimensionality-based exploration of anisotropic growth via asymmetrically coordinated oriented attachment in perovskite halide-based NCs which helps in large scale synthesis of NCs and understanding the thermodynamics and kinetics of the growth mechanism.
Experimental
Chemicals
Lead(II) bromide (PbBr2) (98%) was purchased from Alfa-Aesar. Cesium carbonate (Cs2CO3) (99.9%), oleyl amine (OA) (technical grade 70%), oleic acid (OAc) (technical grade 90%), 1-octadecene (ODE) (technical grade 90%) and methyl acetate anhydrous (MeOAc) (99.5%) were purchased from Sigma Aldrich. Hexane (AR grade) was purchased from Thermo Fisher Scientific India Pvt. Ltd. All the chemicals were used without any purification.Methods
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the DST Nanomission, SERB and JNCASR for funding. PM thanks the CSIR for the research fellowship and AR and SM thank the SERB for the research fellowship.Notes and references
- A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Pérez-Osorio, H. J. Snaith, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2016, 7, 11755 CrossRef.
- J. Puthenpurayil, O. H.-C. Cheng, T. Qiao, D. Rossi and D. H. Son, J. Chem. Phys., 2019, 151, 154706 CrossRef.
- R. J. Sutton, G. E. Eperon, L. Miranda, E. S. Parrott, B. A. Kamino, J. B. Patel, M. T. Hörantner, M. B. Johnston, A. A. Haghighirad, D. T. Moore and H. J. Snaith, Adv. Energy Mater., 2016, 6, 1502458 CrossRef.
- B. Ai, C. Liu, Z. Deng, J. Wang, J. Han and X. Zhao, Phys. Chem. Chem. Phys., 2017, 19, 17349–17355 RSC.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nano Lett., 2015, 15, 3692–3696 CrossRef CAS.
- X. Li, Y. Wu, S. Zhang, B. Cai, Y. Gu, J. Song and H. Zeng, Adv. Funct. Mater., 2016, 26, 2435–2445 CrossRef CAS.
- A. Swarnkar, V. K. Ravi and A. Nag, ACS Energy Lett., 2017, 2, 1089–1098 CrossRef CAS.
- L.-J. Chen, J.-H. Dai, J.-D. Lin, T.-S. Mo, H.-P. Lin, H.-C. Yeh, Y.-C. Chuang, S.-A. Jiang and C.-R. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 33307–33315 CrossRef CAS.
- Q. A. Akkerman, M. Gandini, F. Di Stasio, P. Rastogi, F. Palazon, G. Bertoni, J. M. Ball, M. Prato, A. Petrozza and L. Manna, Nat. Energy, 2016, 2, 16194 CrossRef.
- R. Sorrentino, M. Gandini, J. M. Figueroa Tapia and A. Petrozza, Sustainable Energy Fuels, 2020, 4, 171–176 RSC.
- J. Song, J. Li, X. Li, L. Xu, Y. Dong and H. Zeng, Adv. Mater., 2015, 27, 7162–7167 CrossRef CAS.
- T. Chiba, Y. Hayashi, H. Ebe, K. Hoshi, J. Sato, S. Sato, Y.-J. Pu, S. Ohisa and J. Kido, Nat. Photonics, 2018, 12, 681–687 CrossRef CAS.
- M. A. Becker, R. Vaxenburg, G. Nedelcu, P. C. Sercel, A. Shabaev, M. J. Mehl, J. G. Michopoulos, S. G. Lambrakos, N. Bernstein, J. L. Lyons, T. Stöferle, R. F. Mahrt, M. V. Kovalenko, D. J. Norris, G. Rainò and A. L. Efros, Nature, 2018, 553, 189–193 CrossRef CAS.
- J. Li, L. Xu, T. Wang, J. Song, J. Chen, J. Xue, Y. Dong, B. Cai, Q. Shan, B. Han and H. Zeng, Adv. Mater., 2017, 29, 1603885 CrossRef.
- H. Wang, X. Zhang, Q. Wu, F. Cao, D. Yang, Y. Shang, Z. Ning, W. Zhang, W. Zheng, Y. Yan, S. V. Kershaw, L. Zhang, A. L. Rogach and X. Yang, Nat. Commun., 2019, 10, 665 CrossRef CAS.
- M. Lu, X. Zhang, X. Bai, H. Wu, X. Shen, Y. Zhang, W. Zhang, W. Zheng, H. Song, W. W. Yu and A. L. Rogach, ACS Energy Lett., 2018, 3, 1571–1577 CrossRef CAS.
- F. Yan, J. Xing, G. Xing, L. Quan, S. T. Tan, J. Zhao, R. Su, L. Zhang, S. Chen, Y. Zhao, A. Huan, E. H. Sargent, Q. Xiong and H. V. Demir, Nano Lett., 2018, 18, 3157–3164 CrossRef CAS.
- P. Zhu, S. Gu, X. Shen, N. Xu, Y. Tan, S. Zhuang, Y. Deng, Z. Lu, Z. Wang and J. Zhu, Nano Lett., 2016, 16, 871–876 CrossRef CAS.
- Y. Dong, T. Qiao, D. Kim, D. Parobek, D. Rossi and D. H. Son, Nano Lett., 2018, 18, 3716–3722 CrossRef CAS.
- A. Dutta, S. K. Dutta, S. Das Adhikari and N. Pradhan, ACS Energy Lett., 2018, 3, 329–334 CrossRef CAS.
- C. C. Stoumpos, C. D. Malliakas, J. A. Peters, Z. Liu, M. Sebastian, J. Im, T. C. Chasapis, A. C. Wibowo, D. Y. Chung, A. J. Freeman, B. W. Wessels and M. G. Kanatzidis, Cryst. Growth Des., 2013, 13, 2722–2727 CrossRef CAS.
- J. Zhang, L. Fan, J. Li, X. Liu, R. Wang, L. Wang and G. Tu, Nano Res., 2019, 12, 121–127 CrossRef CAS.
- L. Peng, A. Dutta, R. Xie, W. Yang and N. Pradhan, ACS Energy Lett., 2018, 3, 2014–2020 CrossRef CAS.
- Z. Shi, Y. Li, Y. Zhang, Y. Chen, X. Li, D. Wu, T. Xu, C. Shan and G. Du, Nano Lett., 2017, 17, 313–321 CrossRef CAS.
- G. Nedelcu, L. Protesescu, S. Yakunin, M. I. Bodnarchuk, M. J. Grotevent and M. V. Kovalenko, Nano Lett., 2015, 15, 5635–5640 CrossRef CAS.
- S. Sun, D. Yuan, Y. Xu, A. Wang and Z. Deng, ACS Nano, 2016, 10, 3648–3657 CrossRef CAS.
- S. Zou, Y. Liu, J. Li, C. Liu, R. Feng, F. Jiang, Y. Li, J. Song, H. Zeng, M. Hong and X. Chen, J. Am. Chem. Soc., 2017, 139, 11443–11450 CrossRef CAS.
- S. Jeon, M.-C. Jung, J. Ahn, H. K. Woo, J. Bang, D. Kim, S. Y. Lee, H. Y. Woo, J. Jeon, M. J. Han, T. Paik and S. J. Oh, Nanoscale Horiz., 2020, 5, 960–970 RSC.
- L. Peng, S. K. Dutta, D. Mondal, B. Hudait, S. Shyamal, R. Xie, P. Mahadevan and N. Pradhan, J. Am. Chem. Soc., 2019, 141, 16160–16168 CrossRef CAS.
- B. Hudait, S. K. Dutta and N. Pradhan, ACS Energy Lett., 2020, 5, 650–656 CrossRef CAS.
- J.-R. Wen, B. J. Roman, F. A. Rodriguez Ortiz, N. Mireles Villegas, N. Porcellino and M. Sheldon, Chem. Mater., 2019, 31, 8551–8557 CrossRef CAS.
- L.-s. Li, J. Hu, W. Yang and A. P. Alivisatos, Nano Lett., 2001, 1, 349–351 CrossRef CAS.
- D. Zhang, Y. Yu, Y. Bekenstein, A. B. Wong, A. P. Alivisatos and P. Yang, J. Am. Chem. Soc., 2016, 138, 13155–13158 CrossRef CAS.
- Z. Gan, F. Zheng, W. Mao, C. Zhou, W. Chen, U. Bach, P. Tapping, T. W. Kee, J. A. Davis, B. Jia and X. Wen, Nanoscale, 2019, 11, 14676–14683 RSC.
- G. Ghosh, B. Jana, S. Sain, A. Ghosh and A. Patra, Phys. Chem. Chem. Phys., 2019, 21, 19318–19326 RSC.
- G. Almeida, L. Goldoni, Q. Akkerman, Z. Dang, A. H. Khan, S. Marras, I. Moreels and L. Manna, ACS Nano, 2018, 12, 1704–1711 CrossRef CAS.
- N. Sikdar, M. Bhogra, U. V. Waghmare and T. K. Maji, J. Mater. Chem. A, 2017, 5, 20959–20968 RSC.
- X. Zhang, X. Bai, H. Wu, X. Zhang, C. Sun, Y. Zhang, W. Zhang, W. Zheng, W. W. Yu and A. L. Rogach, Angew. Chem., Int. Ed., 2018, 57, 3337–3342 CrossRef CAS.
- R. Grisorio, E. Fanizza, I. Allegretta, D. Altamura, M. Striccoli, R. Terzano, C. Giannini, V. Vergaro, G. Ciccarella, N. Margiotta and G. P. Suranna, Nanoscale, 2020, 12, 623–637 RSC.
- Z. Dang, B. Dhanabalan, A. Castelli, R. Dhall, K. C. Bustillo, D. Marchelli, D. Spirito, U. Petralanda, J. Shamsi, L. Manna, R. Krahne and M. P. Arciniegas, Nano Lett., 2020, 20, 1808–1818 CrossRef CAS.
- X. Li, Y. Cao and G. Yang, Phys. Chem. Chem. Phys., 2010, 12, 4768–4772 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Quantum yield, TEM images and size analysis. See DOI: 10.1039/d0na00732c |
| This journal is © The Royal Society of Chemistry 2020 |