Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Strong size selectivity in the self-assembly of rounded nanocubes into 3D mesocrystals†
Elisabeth
Josten‡§
 *a,
Manuel
Angst§
*a,
Manuel
Angst§
 a,
Artur
Glavic
b,
Paul
Zakalek
a,
Ulrich
Rücker
a,
Artur
Glavic
b,
Paul
Zakalek
a,
Ulrich
Rücker
 a,
Oliver H.
Seeck
c,
András
Kovács
d,
Erik
Wetterskog
e,
Emmanuel
Kentzinger
a,
Oliver H.
Seeck
c,
András
Kovács
d,
Erik
Wetterskog
e,
Emmanuel
Kentzinger
 a,
Rafal E.
Dunin-Borkowski
a,
Rafal E.
Dunin-Borkowski
 d,
Lennart
Bergström
f and
Thomas
Brückel
d,
Lennart
Bergström
f and
Thomas
Brückel
 a
a
aJülich Centre for Neutron Science (JCNS) and Peter Grünberg Institute (PGI), JARA-FIT, Forschungszentrum Jülich GmbH, 52425 Jülich, Germany. E-mail: e.josten@fz-juelich.de
bLaboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, 5232 Villigen PSI, Switzerland
cDeutsches Elektronen-Synchrotron DESY, Notkestraße 85, 22607 Hamburg, Germany
dErnst Ruska-Centre for Microscopy and Spectroscopy with Electrons (ER-C) and Peter Grünberg Institute (PGI), Forschungszentrum Jülich, 52425 Jülich, Germany
eDepartment of Engineering Sciences, Angström Laboratory, Uppsala University, 75121 Uppsala, Sweden
fDepartment of Materials and Environmental Chemistry, Stockholm University, 10691 Stockholm, Sweden
First published on 15th June 2020
Abstract
The self-assembly of nanoparticles into highly ordered crystals is largely influenced by variations in the size and shape of the constituent particles, with crystallization generally not observed if their polydispersity is too large. Here, we report on size selectivity in the self-assembly of rounded cubic maghemite nanoparticles into three-dimensional mesocrystals. Different X-ray scattering techniques are used to study and compare a nanoparticle dispersion that is used later for self-assembly, an ensemble of mesocrystals grown on a substrate, as well as an individual mesocrystal. The individual μm-sized mesocrystal is isolated using a focused-ion-beam-based technique and investigated by the diffraction of a micro-focused X-ray beam. Structural analysis reveals that individual mesocrystals have a drastically smaller size dispersity of nanoparticles than that in the initial dispersion, implying very strong size selectivity during self-assembly. The small size dispersity of the nanoparticles within individual mesocrystals is accompanied by a very narrow lattice parameter distribution. In contrast, the lattice parameter distribution within all mesocrystals of an ensemble is about four times wider than that of individual mesocrystals, indicating significant size fractionalization between mesocrystals during self-assembly. The small size dispersity within each mesocrystal has important implications for their physical properties.
New conceptsThe self-assembly of nanoparticles potentially enables the creation of devices with various functionalities. Size polydispersity of the nanoparticles within the self-assembled mesocrystals (3D lattices of nanoparticles) is a key parameter for device performance and its elucidation is therefore of great importance. Previous determinations of this key parameter were hampered either by access to only a subset of the involved nanoparticles (SEM sees only those at the surface) or by ensemble statistics hiding the size dispersities of the individual mesocrystals (GISAXS can see only the statistics of all nanoparticles in an ensemble of mesocrystals). We have overcome this limitation by a special extraction procedure separating an individual mesocrystal, which we then comprehensively investigated using X-ray diffraction and structural analysis. The analysis yields a nanoparticle size dispersity within an individual mesocrystal that is more drastically reduced from that within the initial dispersion than expected. Comparison with results on a mesocrystal ensemble furthermore indicates a size fractionalization leading to smaller dispersity within each mesocrystal than across different mesocrystals. These results call for further theoretical investigations of the self-assembly process, and the single mesocrystal diffraction method developed opens the door to studying further properties of individual mesocrystals, unimpeded by an ensemble average. |
Introduction
Self-assembled,1 ordered configurations of nanoparticles are of great interest for applications in information technology, plasmonics and photonics, biological and chemical sensing, as well as many further areas.2–5 Their importance has led to an increase in reports dealing with their preparation, characterization and functionalization.4–9 Just as for crystals that are built of atoms, there is a large structural diversity for “mesocrystals” that are built of nanoparticles and whose properties and functionalities are related to their structure.10 The variety of structures into which nanoparticles self-assemble is further enhanced by the anisotropic interactions that are present for non-spherical nanoparticles.5,7,11,12 For example, cube-like nanoparticles have been observed to form simple cubic, body-centered tetragonal, or rhombohedral lattices, depending on their corner truncation and on the solvent employed.13–15 The structures that are formed are determined by an interplay between competing interactions, which depend on the shapes and sizes of the nanoparticles and on their associated surfactant corona.5,16The analogy between crystals of nanoparticles and atoms is not perfect.17 In particular, the former invariably have some variations in their size and shape. If these variations are too large, then the nanoparticles cannot assemble into ordered lattices. Indeed, it was already observed more than 30 years ago that, for spherical nanoparticles with a size dispersity larger than about 10%, crystallization is suppressed.18 It was also observed that crystalline quality is improved upon lowering the size dispersity.19 The effects of size dispersity on crystallization have also been investigated in various theoretical studies, although mostly focusing on spherical nanoparticles. Intriguingly, the results indicate that the dispersity can be lowered by the crystallization itself, with the possibility of fractionalization, i.e., the emergence of several crystalline phases with different average sizes of the participating nanoparticles.20 Such size selectivity during the self-assembly process has also been indicated by the statistical analysis of scanning electron microscope (SEM) images of crystallized octahedral nanoparticles and of those nanoparticles left over in the dispersion, with the former having an approximately three times narrower size distribution.21 However, SEM is sensitive only to the surface, which may not be representative of all of the nanoparticles involved.
Here, we use scattering methods that are sensitive to all of the nanoparticles involved to demonstrate the presence of strong size selectivity in the self-assembly of cube-like maghemite nanoparticles. The experiments include the use of a focused ion beam to isolate an individual μm-sized mesocrystal, followed by its investigation by diffraction using a micro-focused X-ray beam, thereby pushing the limits of X-ray crystallography for the study of very small objects. The analysis of the diffraction data is indicative of a much narrower size distribution of the nanoparticles than in dispersion prior to assembly. The size distribution of all of the nanoparticles in any of the mesocrystals in an ensemble deposited on the substrate, obtained by grazing-incidence small-angle X-ray scattering (GISAXS) from the existing Bragg peaks, is significantly larger than the corresponding width within an individual mesocrystal. These results indicate very stringent size selectivity in a single mesocrystal, as well as size fractionalization between different mesocrystals in an ensemble. The small size dispersity in each mesocrystal has important implications for their physical properties and functionalities, especially for dipolar magnetic interactions, which have a strong distance dependence.22
Experimental, results and discussion
Oleic-acid-capped maghemite nanoparticles, which have previously been demonstrated to form high-quality mesocrystals,14,23–25 were prepared by the thermal decomposition of iron oleate.26 Small-angle X-ray scattering (SAXS) was performed on dilute nanoparticle dispersions in toluene, employing a Bruker AXS Nanostar SAXS instrument. The resulting data (Fig. 1a) can be well fitted by a model of cubes, whose corners are rounded off (sketched in Fig. 1c), with the corresponding parameters given in Fig. 1a and Table 1. The shape of the “nanocubes” was confirmed in real space using an FEI Titan transmission electron microscope (TEM). The particles were drop-casted onto a thin C layer supported by a TEM grid. The inset to Fig. 1a shows an image of the rounded cubic-shaped crystals. Further details about their characterization using SAXS and about the rounded cubical form factor model are given in the ESI,† (Section S1).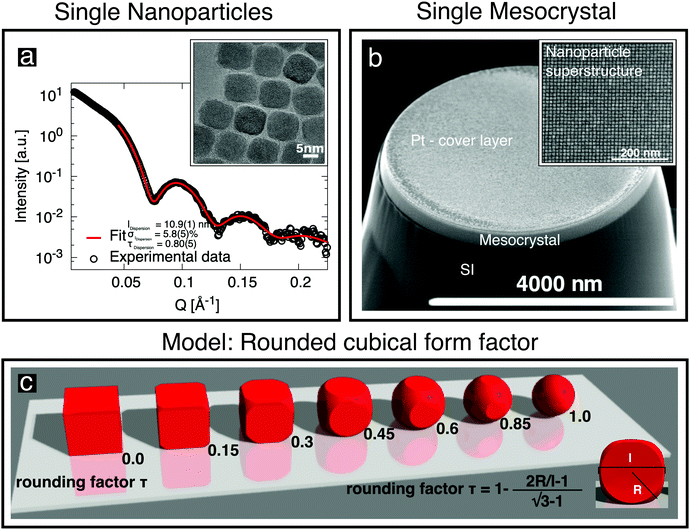 | ||
| Fig. 1 (a) SAXS data obtained from cubic nanoparticles in dilute dispersion (○) are fitted (red line) using the depicted rounded cube model (c), which is described in the ESI.† The characterization of individual cubic nanoparticles provides information about the cube size l, the particle size distribution σl and the truncation factor τ. The inset shows a TEM image of a deposited monolayer of nanoparticles. (b) SEM image of a single mesocrystal of the nanoparticles grown on a Si substrate, with a Pt cover layer, after being cut free using a focused ion beam. The inset shows the regular arrangement of the nanoparticles recorded before Pt deposition. | ||
| Parameter | Dispersion | Ensemble | Single mesocrystal |
|---|---|---|---|
| a Incorporates all finite size effects (see Section S3 in the ESI). b Fixed to the value obtained by SAXS. | |||
| Cube size l [nm] | 10.9(1) | 10.4(1) | |
| Lattice constant a [nm] | 14.75(3) | 13.47(3) | |
| Lattice constant c [nm] | 21.57(4) | 15.08(7) | |
| Particle size distribution σl [%] | 5.8(5) | 0.0(26) | |
| Lattice constant distribution σlattice [%] | 2.03(7) | 0.42(2) | |
| Tilt distribution σtilt [°] | 1.09(4) | 0.09(2) | |
| In-plane GISAXS correlation lengthaεab [nm] | 1145(40) | ||
| Out-of-plane GISAXS correlation lengthaεc [nm] | 256(9) | ||
| Mesocrystal height NLaue·c [nm] | 196.0(9) | ||
| Rounding factor τ [ ] (cf.Fig. 2c) | 0.80(5) | 0.8b | |
| Average displacement aDW [nm] | 0.6(2) | ||

|
|||
Mesocrystals, i.e., three-dimensional (3D) periodic arrangements of nanoparticles, were obtained by self-assembly of the rounded cubic maghemite particles. First, the nanoparticle dispersion in toluene was dripped onto a Si(001) substrate. The particles were then induced to self-assemble into μm-sized mesocrystals by evaporating the toluene under controlled conditions, as described elsewhere.23,24 The ensemble (or collection) of mesocrystals on the substrate (see Fig. S5 in the ESI,† for a SEM top view) is partially oriented: all of the mesocrystals have their c-axes (001 direction; see Fig. 2d) aligned perpendicular to the substrate, but each mesocrystal has a random in-plane orientation. The ensemble was characterized using GISAXS in the in-house high-brilliance instrument GALAXI27 (λ = 1.34 Å) at an incident angle of 0.4°. The partial orientation is sufficient to give rise to Bragg peaks, as also observed in previous GISAXS studies.14,25 Analysis of their shape was used to determine model parameters, including in particular the lattice parameter distribution, as given in Table 1. Further details about the characterization of the ensemble by GISAXS and the extraction of model parameters are given in the ESI,† (Section S3).
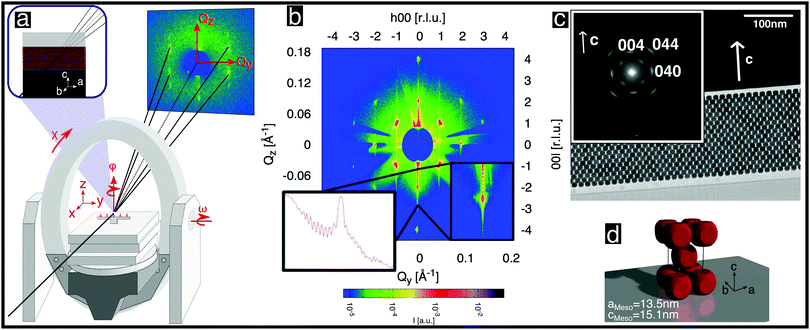 | ||
| Fig. 2 Structural analysis of a single mesocrystal of rounded cubic nanoparticles. (a) Schematic diagram of the experimental setup and scattering geometry used. The area detector is stationary. The axes of sample rotation are indicated. (b) Scattered intensity shown on a logarithmic color scale for the (h0l) reciprocal space plane obtained from angle-scans, as described in the ESI,† (Section S5.2). The inset shows the (00l) line once as a zoom-in and once as a cross-section. (c) Cross-sectional TEM image of a thinned mesocrystal layer deposited on a Si single crystal viewed from the [100] direction. The inset shows a selected area electron diffraction pattern recorded from the layer. The spots correspond to Bragg peaks of the atomic inverse spinel structure of the nanoparticles. (d) Depiction of the unit cell of the nanoparticle mesocrystal. | ||
Individual mesocrystals were extracted from the ensemble using a focused ion beam (FIB) system in a dual-beam FEI Helios NanoLab 400S. A specific sample preparation process was used to isolate sensitive samples with high precision to obtain only a few μm-sized well-shaped mesocrystals. For this purpose, the sample was covered with a Pt layer for protection during the cutting process and transferred to a standard Cu Omniprobe grid. The setup is described in the ESI,† (Fig. S6a). More details about the extraction process are given in the ESI,† (Section S4). Each resulting isolated single mesocrystal (Fig. 1b) was then ready for structural characterization.
X-ray diffraction was performed on single mesocrystals at beamline P08 of PETRAIII, DESY28 using a general setup similar to that used in ref. 29. We used photons of energy 12.4 keV, a Kohzu NZD-3 high-precision diffractometer with Eulerian geometry and a Roper Scientific area detector (see Fig. 2a). In order to maximize the flux on the small samples (Fig. 1b) and to minimize the background, the incoming X-ray beam was focused by a set of compound refractive lenses,30 achieving a spot size of 5 μm vertically × 10 μm horizontally. The background was further reduced by installing an evacuated pipe between the sample and the CCD detector.
The small focused beam was required to hit an even smaller mesocrystal with a height of a few tenths of μm and a diameter of a few μm, making this a challenging experiment with stringent requirements for the precision of the alignment. Moreover, quantitative analysis of the intensities and shapes of the Bragg peaks, as is necessary to extract the size distribution of the nanoparticles in a single mesocrystal, had to take into account the precision of the center of rotation of the different diffractometer circles, which is of the same order of magnitude (the “sphere of confusion” has a diameter of about 15 μm28), requiring readjustments of the alignment for each peak. The alignment procedures and further experimental details are given in the ESI,† (Section S5.1).
With the mesocrystal aligned as in Fig. 2a, reciprocal space planes at various ϕ positions were mapped by rocking both ω and ϕ angles, as described in the ESI,† (Section S5.20). One such plane is shown in Fig. 2b and additional examples in Fig. S8 in the ESI.† The mapped planes exhibit clear and sharp Bragg reflections (note the logarithmic intensity scale) of the mesocrystal structure. Planes related by a rotation of ϕ by 90° exhibit the same pattern, indicating tetragonal symmetry. Furthermore, the reflection condition h + k + l = 2n is always observed. All of the observed reflections of the mesocrystal structure can be indexed within the tetragonal space group I4/mmm (#139), in accordance with previous GISAXS investigations.14,25
The orientation of the rounded cubes within the mesocrystal lattice was determined as follows: Fig. 2c shows a TEM image of a cut through a mesocrystal, corresponding to a projection onto the bc plane. The inset shows a selected area electron diffraction (SAED) pattern of the layer, corresponding to the crystalline orientation of all of the particles within the field of view. Reflections originating from the atomic structures of single nanoparticles, which are consistent with the inverse spinel atomic structure (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, # 227), are visible. The (004) reflection of the atomic lattice is parallel to the c-axis of the mesocrystal structure visible in the TEM image. This observation is consistent with additional X-ray reflectivity measurements, which are described in the ESI,† (Section S2). The presence of only two reflections of the atomic structures of all of the individual nanoparticles confirmed that the atomic lattice c direction coincides with the mesocrystal c direction, indicating a strict orientation of the atomic structures of the rounded nanocubes with respect to the cube faces. The principal axes of the spinel structure within each rounded cube nanoparticle are therefore parallel to the edges of that cube. Moreover, the (040) reflection, which is visible in the inset, is parallel to the b-axis of the TEM image. No additional reflections corresponding to reciprocal space planes of rotated cubes inside the mesocrystal structure are visible, precluding a systematic rotation of all or some of the nanocubes inside the mesocrystal, e.g. by 45°, as shown in Fig. 4b in ref. 25: Apart from possible small random rotations, the edges of the rounded cubes in the mesocrystal are parallel to the edges of the mesocrystal cell, as sketched in Fig. 2d, in agreement with I4/mmm symmetry.
m, # 227), are visible. The (004) reflection of the atomic lattice is parallel to the c-axis of the mesocrystal structure visible in the TEM image. This observation is consistent with additional X-ray reflectivity measurements, which are described in the ESI,† (Section S2). The presence of only two reflections of the atomic structures of all of the individual nanoparticles confirmed that the atomic lattice c direction coincides with the mesocrystal c direction, indicating a strict orientation of the atomic structures of the rounded nanocubes with respect to the cube faces. The principal axes of the spinel structure within each rounded cube nanoparticle are therefore parallel to the edges of that cube. Moreover, the (040) reflection, which is visible in the inset, is parallel to the b-axis of the TEM image. No additional reflections corresponding to reciprocal space planes of rotated cubes inside the mesocrystal structure are visible, precluding a systematic rotation of all or some of the nanocubes inside the mesocrystal, e.g. by 45°, as shown in Fig. 4b in ref. 25: Apart from possible small random rotations, the edges of the rounded cubes in the mesocrystal are parallel to the edges of the mesocrystal cell, as sketched in Fig. 2d, in agreement with I4/mmm symmetry.
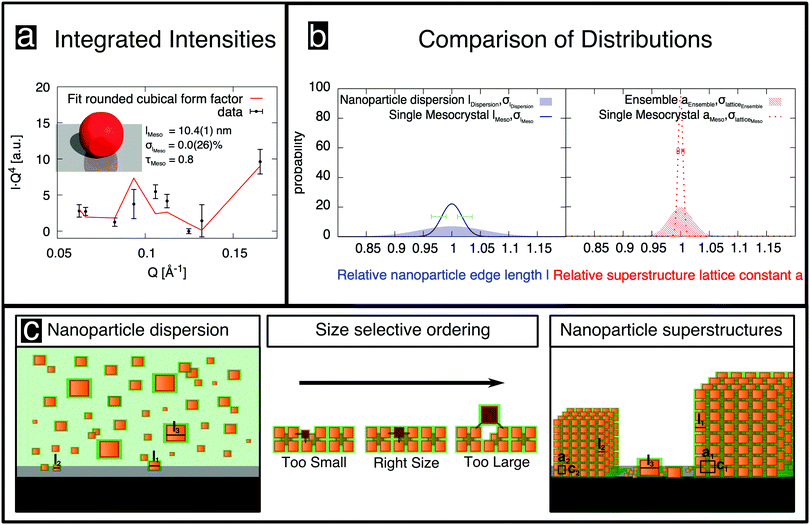
The observed sharp mesocrystal structural reflections (Fig. 2b) were analyzed in depth to obtain the size distribution width and other structural parameters. The structure of atomic crystals is commonly determined by modeling the integrated intensity of reflections, merged into symmetry-unique reflections.31,32 We applied the same method and obtained the integrated intensities of 74 observations of reflections from rocking scans, as detailed in the ESI,† (Section S5.3). By merging these reflections in the indicated mesocrystal space group I4/mmm, 9 symmetry-unique reflections were obtained. The corresponding internal R value, Rint = 0.26, which is a measure of the variability of the observations,32 is rather high when compared to typical values obtained in small-molecule crystallography. We attribute this variability to the very small sample size, combined with the very small and non-uniform beam focus, both of which are smaller than the diffractometer sphere of confusion.28 The merged integrated intensities are shown in Fig. 3a (unmerged intensities are shown in Fig. S10 in the ESI†) as a function of Q, multiplied by Q4 for better visibility of high-index reflections. The minima around 0.06 and 0.13 Å−1 arise from the form factor, akin to form factor minima observed in SAXS (cf.Fig. 1a), but we emphasize that in contrast to SAXS there is no directional averaging, i.e. the form factor also depends on the direction of the Q-vector.
The nanoparticle position in the cell is fixed and the calculated intensities therefore depend only on a direction-dependent form factor (possibly incorporating variations in the size and shape of the nanoparticles) and a Debye–Waller factor describing random displacements of the nanoparticles from the ideal lattice position. When modeling the data, we assumed an isotropic Debye–Waller factor and the rounded cube model already used for SAXS analysis, including a rounding factor τ (defined in Fig. 2c), a log-normal size distribution of the nanoparticles and taking into account the fact that the particles are oriented as indicated in Fig. 2d. In the modeling, we observed that the intensities did not depend sensitively on the rounding parameter τ, which was therefore set to the value of 0.8 that had been obtained from SAXS. A detailed assessment of the influence of nanoparticle shape on the size-selective assembly of nanocubes is beyond the scope of the present study.
The best fit of this model (Fig. 3a; for further information about the analysis of the merged integrated intensities see Section S7 in the ESI†) corresponds to a residual32R1 = 0.23, which is higher than usual in small molecule crystallography, but reasonable in comparison with the data quality, as indicated by Rint. This result indicates that the simple rounded cube model, incorporating a size distribution but no distribution of shapes, provides a reasonable description of the nanoparticle mesocrystal. The optimal parameters (Table 1) suggest that displacements of the nanoparticles from their ideal positions are small, and are otherwise consistent with those deduced from SAXS, with the exception of the size distribution, which is fitted as σl = 0%, albeit with a large error bar of 2.6%. Nevertheless, the size distribution of the single mesocrystal is well below that of the nanoparticles in the dispersion, σl = 5.8(5)%. Given that the size distribution cannot be negative, the expectation value for the mesocrystal size distribution is 1.8%, with asymmetric error bars, as indicated by the dark blue line and horizontal error bars in Fig. 3b, with the size distribution of the nanoparticles in the dispersion also shown for comparison (blue shaded area).
Further structural information can be obtained from an analysis of the Bragg peak shapes. The widths of the reflections of individual (meso)crystals are determined by a combination of finite size effects (finite sample size and finite correlations), the distribution of lattice parameters, as well as the distribution of tilts, which is also referred to as mosaicity in the individual crystal case (see also the sketches in Table 1), together with instrumental broadening. We analyzed the reflection widths in terms of a uniform contribution to all of the reflections and reflection-dependent contributions (see Section S6 in the ESI,† for details of the analysis). From the former parameters, we observe an in-plane broadening that is fully accounted for by the instrumental resolution, with no discernible finite size effects (cf. Section S6.5 in the ESI†). Out-of-plane, instrumental broadening accounts for only a minor part of the overall uniform broadening. Here, the dominant contribution originates from the small thickness of the mesocrystal (13 unit cells according to SEM) and reflects the Laue function for small lattices. Close inspection of Fig. 2b between the peaks in the vertical direction (magnified in the inset, with a second inset showing the profile) reveals the Laue oscillations that are expected for very small crystals. To the best of our knowledge, Laue oscillations only previously been observed in artificial structures such as heteroepitaxial thin films (e.g.ref. 33 and 34). From the distance of the oscillations, the number of unit cells can be obtained as 13, in agreement with SEM. The sharp minima in the Laue oscillations show that the mesocrystal is very flat. The mosaic spread (tilt distribution) σtilt obtained from the analysis is approximately 0.1°, which is less than the mosaic spread observed in some atomic (small molecule) crystals (e.g.ref. 35). The smallness of the misorientations is remarkable, given the much weaker bonding interactions between neighboring nanoparticles, as well as the variability in their shape and size.
Finally, the width analysis yields distributions of the lattice parameters of σlatticeMeso = 0.42(2)%, as sketched in Fig. 3b (dotted red line). Given the relatively close packing (Fig. 2d), variations of the lattice parameters can be expected to follow variations of the sizes of the nanoparticles,24 although the capping ligands might to some extent compensate the polydispersity of the cores, leading to a smaller width of the lattice parameter distribution compared to the particle size distribution. The analysis of peak widths suggests a lattice parameter distribution of approximately 0.4%, which is considerably smaller than the expectation value of 1.8% for the width of the size distribution obtained from the intensity analysis, but well within the large error bar of the latter value. Overall, the very small lattice parameter distribution width is consistent with the conclusion of the intensity analysis: the variation of the sizes of nanoparticles within a single mesocrystal is much smaller than the size polydispersity within the initial dispersion (blue shaded area in Fig. 3b).
Given the strong difference in size distributions obtained between all of the nanoparticles in the initial dispersion and those within a single mesocrystal, it is of interest to estimate the size distribution of all of the nanoparticles incorporated into any of the mesocrystals in the ensemble deposited on the substrate. For this purpose, we used the fairly standard technique of GISAXS. Whereas a structural analysis of the intensities observed in GISAXS is considerably less straightforward than for an isolated mesocrystal, obtaining lattice constant distributions from an analysis of the peak widths is possible23 and proceeds analogously to the situation for the single mesocrystal. The analysis is described in detail in Section S3 in the ESI,† while the results are given in Table 1. The lattice parameter distribution is also plotted in Fig. 3b (red patterned area). Its width of 2% is considerably larger than the corresponding distribution for the single mesocrystal (dotted red line). Its width is also much smaller than the width of the size distribution of the nanoparticles in the dispersion (blue shaded area), although the already mentioned caveat of a partial compensation by capping ligands applies, rendering this last conclusion tentative. On the other hand, any potential effect of the capping ligands in reducing widths of lattice parameter distributions compared to nanoparticle size distributions would affect all mesocrystals in the same way. Therefore, the more than four times smaller width in the lattice parameter distribution within a single mesocrystal compared to the ensemble one also implies a much lower size distribution width of the nanoparticles in one mesocrystal than in all mesocrystals of the ensemble.
In contrast to previous investigations (e.g. by SEM), our results are representative of the statistics of all nanoparticles in a single mesocrystal, in all mesocrystals of an ensemble, as well as in the initial dispersion. They imply that the crystallization process, which is sketched in Fig. 3c, acts as a filter that selects, from a dispersion of nanoparticles of various size, those having approximately the same size, as indicated in various theoretical studies.20,36–40 It is intuitively clear that nanoparticles that are too large cannot be incorporated into a crystal lattice because they will not fit or cause a large strain in the mesocrystal. Conversely, too small nanoparticles would fit, but they would not realize the bonding energy that ultimately stabilizes the crystalline arrangement.5,16,41,42 Van der Waals interactions between particles are not only smaller for smaller particles but also decrease rapidly with increasing separation.16 This size selection mechanism raises the question of how sufficiently matching nanoparticles reach (and insufficiently matching nanoparticles leave) the nucleation region of each mesocrystal, in order to allow the rapid formation of highly-ordered 3D superlattices. Agthe et al.43 showed that mesocrystal self-assembly can be described by a diffusion-driven two-dimensional growth model proposed by Bigioni et al.44 It has been shown that the onset of mesocrystal formation can be related to a critical nanoparticle concentration and the formation of a drying front, i.e. the interface between the saturated dispersion and partially-dry regions, which suggests that pushing oleate-capped nanocubes, similar to the systems studied here, sufficiently close by a concentration increase or capillary forces can promote the transition from a disordered cluster to a highly ordered mesocrystal.23,45 The diffusion length of nanoparticles that are in the vicinity of the drying front44 (over 100 μm according to ref. 46) permits exchange of particles that can be included at energetically-favorable positions in the growing mesocrystals and expulsion of unsuitable particles. However, the very small size dispersity of the nanoparticles in an individual mesocrystal indicates size selectivity during self-assembly that is more dramatic than expected.
The intermediate size dispersivity found by GISAXS can be explained in a straightforward way. Upon dispersion of the nanoparticles on a substrate, mesocrystals of like-sized nanoparticles self-assemble. As a result, a collection of mesocrystals is obtained with a small variation of sizes within each mesocrystal, but with significant variations in nanoparticle size between different mesocrystals, as sketched in the right panel in Fig. 3c. This size fractionalization is in qualitative agreement with theoretical predictions.20 The ensemble average, as measured by GISAXS, corresponds to the overall variation of sizes in all of the mesocrystals. For very small and very large nanoparticles, at the tail ends of the size distribution, there are too few like-sized nanoparticles in the dispersion. Therefore, these outliers do not crystallize and are instead deposited individually on the substrate, as also indicated in the right panel in Fig. 3c. This observation explains the reduction in the distribution width of the mesocrystal ensemble, as compared to that of the nanoparticles in the dispersion. Furthermore, it also explains the observation that mesocrystals can grow only from a dispersion of nanoparticles that has a sufficiently narrow size distribution.18,26 If the distribution is too wide, then there are insufficient numbers of like-sized nanoparticles present within each others' proximity to form mesocrystals of nanoparticles of any size. If the distribution is sufficiently narrow for mesocrystals to self-assemble, then the individual mesocrystals consist of nanoparticles of very similar size, with good crystalline quality.
Conclusions
In summary, we have demonstrated a stringent size-selectivity in the self-assembly of nanoparticles into mesocrystals. By applying primarily X-ray diffraction to isolated single mesocrystals of rounded cubic-shaped maghemite nanoparticles, we observed that they have very good crystallinity, with very sharp Bragg reflections. A detailed analysis of the integrated intensities of the Bragg peaks for an isolated mesocrystal directly indicates that the size distribution of the nanoparticles that make up this mesocrystal is much smaller than that of the nanoparticles in the dispersion from which the mesocrystal was grown. Furthermore, a comparison of the lattice parameter distribution widths from the Bragg peak shapes between the single mesocrystal and the ensemble of mesocrystals indicates that the size distribution width of all the nanoparticles in an ensemble of mesocrystals is significantly larger than the corresponding width for the nanoparticles within a single mesocrystal, implying size fractionalization. These results show that, from the many nanoparticles that are present in the initial dispersion, only those that have an extremely similar size can crystallize into a given mesocrystal. The availability of isolated and structurally well-characterized single mesocrystals also opens the door to the determination, e.g. by magnetic resonance techniques, of structure–property relationships that may be hidden in ensemble averages.Author contributions
E. W. synthesized the iron oxide nanocubes and was supervised by L. B. E. J. produced the ensemble of mesocrystals by controlled self-assembly. E. J. and U. R. planned the sample holder for the diffraction experiment. E. J., M. A., A. G., P. Z. and O. H. S. performed the single mesocrystal X-ray diffraction experiments. E. J. and E. K. performed the GISAXS experiments. E. J. preformed the SAXS analysis. A. K. performed the electron microscopy experiments and was supervised by R. E. D. B. E. J., M. A. and A. G. analyzed the data. T. B. supervised the work. E. J. and M. A. wrote the manuscript with support from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge Doris Meertens for FIB preparation and Mathias Meyer for his assistance with the SAXS measurements. We thank Raphael Herrmann for fruitful discussions and Michael Smik for helping with the merging script at GALAXI. We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association (HGF), for the provision of experimental facilities. Parts of this research were carried out at P08, PETRA III. L. B. and E. W. acknowledge the Swedish Research Council for funding. E. W. acknowledges partial funding from the FP-7 Nanomag project (FP7-NMP-604448).References
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- S. Sun, Science, 2000, 287, 1989–1992 CrossRef CAS PubMed.
- Q. Dai, D. Berman, K. Virwani, J. Frommer, P.-O. Jubert, M. Lam, T. Topuria, W. Imaino and A. Nelson, Nano Lett., 2010, 10, 3216–3221 CrossRef CAS PubMed.
- Z. Nie, A. Petukhova and E. Kumacheva, Nat. Nanotechnol., 2009, 5, 15–25 CrossRef PubMed.
- X. Bouju, É. Duguet, F. Gauffre, C. R. Henry, M. L. Kahn, P. Mélinon and S. Ravaine, Adv. Mater., 2018, 30, 1706558 CrossRef PubMed.
- C. B. Murray, C. R. Kagan and M. G. Bawendi, Annu. Rev. Mater. Sci., 2000, 30, 545–610 CrossRef CAS.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed.
- V. N. Manoharan, Science, 2015, 349, 1253751 CrossRef PubMed.
- M. A. Boles, M. Engel and D. V. Talapin, Chem. Rev., 2016, 116, 11220–11289 CrossRef CAS PubMed.
- E. V. Shevchenko, D. V. Talapin, N. A. Kotov, S. O'Brien and C. B. Murray, Nature, 2006, 439, 55–59 CrossRef CAS PubMed.
- N. R. Jana, Angew. Chem., Int. Ed., 2004, 43, 1536–1540 CrossRef CAS PubMed.
- G. van Anders, N. K. Ahmed, R. Smith, M. Engel and S. C. Glotzer, ACS Nano, 2013, 8, 931–940 CrossRef PubMed.
- Z. Quan, H. Xu, C. Wang, X. Wen, Y. Wang, J. Zhu, R. Li, C. J. Sheehan, Z. Wang, D.-M. Smilgies, Z. Luo and J. Fang, J. Am. Chem. Soc., 2014, 136, 1352–1359 CrossRef CAS PubMed.
- S. Disch, E. Wetterskog, R. P. Hermann, D. Korolkov, P. Busch, P. Boesecke, O. Lyon, U. Vainio, G. Salazar-Alvarez, L. Bergström and T. Brückel, Nanoscale, 2013, 5, 3969–3975 RSC.
- X. Huang, J. Zhu, B. Ge, K. Deng, X. Wu, T. Xiao, T. Jiang, Z. Quan, Y. C. Cao and Z. Wang, J. Am. Chem. Soc., 2019, 141, 3198–3206 CrossRef CAS PubMed.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Small, 2009, 5, 1600–1630 CrossRef CAS PubMed.
- B. Li, D. Zhou and Y. Han, Nat. Rev. Mater., 2016, 1, 15011 CrossRef CAS.
- P. Pusey, J. Phys., 1987, 48, 709–712 CrossRef CAS.
- M. C. Weidman, Q. Nguyen, D.-M. Smilgies and W. A. Tisdale, Chem. Mater., 2018, 30, 807–816 CrossRef CAS.
- M. Fasolo and P. Sollich, Phys. Rev. Lett., 2003, 91, 068301 CrossRef PubMed.
- S. Xie, X. Zhou, X. Han, Q. Kuang, M. Jin, Y. Jiang, Z. Xie and L. Zheng, J. Phys. Chem. C, 2009, 113, 19107–19111 CrossRef CAS.
- E. Wetterskog, C. Jonasson, D.-M. Smilgies, V. Schaller, C. Johansson and P. Svedlindh, ACS Nano, 2018, 12, 1403–1412 CrossRef CAS PubMed.
- E. Josten, E. Wetterskog, A. Glavic, P. Boesecke, A. Feoktystov, E. Brauweiler-Reuters, U. Rücker, G. Salazar-Alvarez, T. Brückel and L. Bergström, Sci. Rep., 2017, 7, 2802 CrossRef PubMed.
- E. Wetterskog, A. Klapper, S. Disch, E. Josten, R. P. Hermann, U. Rücker, T. Brückel, L. Bergström and G. Salazar-Alvarez, Nanoscale, 2016, 8, 15571–15580 RSC.
- S. Disch, E. Wetterskog, R. P. Hermann, G. Salazar-Alvarez, P. Busch, T. Brückel, L. Bergström and S. Kamali, Nano Lett., 2011, 11, 1651–1656 CrossRef CAS PubMed.
- E. Wetterskog, M. Agthe, A. Mayence, J. Grins, D. Wang, S. Rana, A. Ahniyaz, G. Salazar-Alvarez and L. Bergström, Sci. Technol. Adv. Mater., 2014, 15, 055010 CrossRef PubMed.
- Jülich Centre for Neutron Science, GALAXI: Gallium anode low-angle X-ray instrument, Journal of Large-Scale Research Facilities, 2016, 2, A61, DOI:10.17815/jlsrf-2-109.
- O. H. Seeck, C. Deiter, K. Pflaum, F. Bertam, A. Beerlink, H. Franz, J. Horbach, H. Schulte-Schrepping, B. M. Murphy, M. Greve and O. Magnussen, J. Synchrotron Radiat., 2012, 19, 30–38 CrossRef CAS PubMed.
- R. Li, J. Zhang, R. Tan, F. Gerdes, Z. Luo, H. Xu, J. A. Hollingsworth, C. Klinke, O. Chen and Z. Wang, Nano Lett., 2016, 16, 2792–2799 CrossRef CAS PubMed.
- B. Lengeler, C. G. Schroer, B. Benner, A. Gerhardus, T. F. Günzler, M. Kuhlmann, J. Meyer and C. Zimprich, J. Synchrotron Radiat., 2002, 9, 119 CrossRef CAS PubMed.
- A. J. Blake, J. M. Cole, J. S. O. Evans, P. Main, S. Parsons and D. J. Watkin, Crystal Structure Analysis, OUP, Oxford, 2009 Search PubMed.
- M. Ladd and R. Palmer, Structure Determination by X-ray Crystallography, Springer, 2014 Search PubMed.
- M. Izumi, Y. Murakami, Y. Konishi, T. Manako, M. Kawasaki and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 1211–1215 CrossRef CAS.
- A. Glavic, J. Voigt, J. Persson, Y. X. Su, J. Schubert, J. de Groot, W. Zande and T. Bruckel, J. Alloys Compd., 2011, 509, 5061–5063 CrossRef CAS.
- M. Angst, R. P. Hermann, W. Schweika, J.-W. Kim, P. Khalifah, H. J. Xiang, M.-H. Whangbo, D.-H. Kim, B. C. Sales and D. Mandrus, Phys. Rev. Lett., 2007, 99, 256402 CrossRef CAS PubMed.
- M. A. Bates and D. Frenkel, J. Chem. Phys., 1998, 109, 6193–6199 CrossRef CAS.
- P. Bartlett, Progress in Colloid and Polymer Science, Springer, Berlin Heidelberg, 2000, pp. 137–140 Search PubMed.
- H. J. Schöpe, G. Bryant and W. van Megen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 060401 CrossRef PubMed.
- M. Hermes and M. Dijkstra, Europhys. Lett., 2010, 89, 38005 CrossRef.
- H. Tong, P. Tan and N. Xu, Sci. Rep., 2015, 5, 15378 CrossRef CAS PubMed.
- Y. Min, M. Akbulut, K. Kristiansen, Y. Golan and J. Israelachvili, Nat. Mater., 2008, 7, 527–538 CrossRef CAS PubMed.
- J. Lee, E. Nakouzi, M. Song, B. Wang, J. Chun and D. Li, ACS Nano, 2018, 12, 12778–12787 CrossRef CAS PubMed.
- M. Agthe, E. Wetterskog and L. Bergström, Langmuir, 2017, 33, 303–310 CrossRef CAS PubMed.
- T. P. Bigioni, X.-M. Lin, T. T. Nguyen, E. I. Corwin, T. A. Witten and H. M. Jaeger, Nat. Mater., 2006, 5, 265–270 CrossRef CAS PubMed.
- A. F. Routh, Rep. Prog. Phys., 2013, 76, 046603 CrossRef PubMed.
- M. Agthe, T. S. Plivelic, A. Labrador, L. Bergström and G. Salazar-Alvarez, Nano Lett., 2016, 16, 6838–6843 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional experimental details on SAXS and definition of rounded cube form factor, supplementary X-ray reflectometry measurements, additional experimental details and analysis on GISAXS, isolation of the mesocrystal, alignment procedures, details of mapping reciprocal space planes and of collection of integrated intensities of single mesocrystal diffraction, additional details on the analysis of Bragg peak shapes, and additional details on structural analysis of intensities. See DOI: 10.1039/d0nh00117a |
| ‡ Present address: Ernst Ruska-Centre for Microscopy and Spectroscopy with Electrons (ER-C) and Peter Grünberg Institute (PGI), Forschungszentrum Jülich, 52425 Jülich, Germany. |
| § These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |