Integration of graphene and two-dimensional ferroelectrics: properties and related functional devices

Abstract

Ferroelectric (FE) thin films have been investigated for many years due to their broad applications in electronic devices. It was recently demonstrated that FE functionality persists in ultrathin films, possibly even in monolayers of two-dimensional (2D) FEs. However, the feasibility of 2D-based FE functional devices remains an open challenge. Here, we employ density-functional-theory calculations to propose and document the possible integration of graphene with 2D FE materials on metal substrates in the form of functional FE devices. We show that monolayers of proposed M₂O₃ (M = Al, Y) in the quintuple layer (QL) In₂Se₃ struCture are stable 2D FE materials and that QL-M₂O₃ is a functional tunnel barrier in a graphene/QL-M₂O₃/Ru heterostructure. The QL-M₂O₃ barrier width can be modulated by its polarization direction, whereby the heterostructure can function as a prototype ferroelectric tunnel junction. Moreover, alternating the polarization of QL-M₂O₃ modulates the doping type of graphene, enabling the fabrication of graphene p–n junctions. By design, the proposed heterostructures can in principle be fabricated by intercalation, which is known to produce high-quality, large-scale 2D-based heterostructures.

---

New concepts

Ferroelectric (FE) devices based on vertical monolayer heterostructures have been hampered by difficulties in fabricating known layered FE materials in monolayer (ML) form. Here, motivated by recent demonstrations of the fabrication of high-quality graphene-ML heterostructures on metal substrates by first growing epitaxial graphene and subsequently growing MLs or multilayers by intercalation, we employ density-functional theory calculations and predict new, stable, ML FE materials, QL-M₂O₃, where M = Al or Y, in the QL-In₂Se₃ structure, and that metal/QL-M₂O₃/graphene structures can function as prototype monolayer-based FE tunnel junctions or potentially graphene p–n junctions. These findings provide new perspectives on the integration of graphene and monolayer FEs, as well as related functional devices.

Introduction

Ferroelectric (FE) materials, which possess an electrically switchable spontaneous polarization, generate broad interest because of potential applications in nonvolatile memory, field-effect transistors, and photovoltaics.^1–4 Motivated by the miniaturization of electronic devices, extensive research has been pursued on the fabrication of ferroelectric films that are only a few nanometers thick or even a monolayer. Recently, several two-dimensional (2D) FE materials were discovered.^5–10 For example, SnTe, which is not a layered material, was discovered to maintain stable in-plane polarization when its thickness is reduced to one unit cell (0.63 nm).⁶ On the other hand, for FE materials with out-of-plane polarization, thickness reduction is generally limited by the depolarization field.^11–13 Nevertheless, BiFeO₃ has been demonstrated to possess an out-of-plane polarization when its thickness is reduced to ∼1 nm (two unit cells),¹⁰ while the layered materials CuInP₂S₆ and In₂Se₃ have been shown to maintain an out-of-plane polarization when their thickness is 4 nm (∼5 layers) and 2–6 nm (∼2 to 6 layers) respectively.^5,8,9,14 Moreover, it has been theoretically predicted that robust ferroelectricity persists in monolayer In₂Se₃, which is usually referred to as In₂Se₃ quintuple layer (QL-In₂Se₃) because each In₂Se₃ layer contains five planes of atoms.⁷ This robust ferroelectricity has been explained in terms of dipole locking that is enabled by the unique atomic arrangements of QL-In₂Se₃.⁹

Integration of 2D materials, such as graphene, with nanoscale-thickness or bulk FE materials has been shown to enable fabrication of functional devices. For example, a Au/In₂Se₃/graphene heterostructure with 6 nm of In₂Se₃ (∼6 QLs) has been fabricated.¹⁴ In this structure, Au and graphene serve as top and bottom electrodes, respectively, while the 6 nm In₂Se₃ works as a tunnel barrier. The heterostructure shows resistive switching behavior driven by polarization reversal, by which the heterostructure can work as a ferroresistive memory device. Until now, there are no theoretical investigations about this heterostructure. Another case is the integration of graphene with FE bulk LiNbO₃.¹⁵ Graphene was transferred onto bulk single-domain LiNbO₃ that is poled periodically, i.e., it possesses stripes of opposite polarization vectors, by which the doping level of graphene on top of each stripe is modulated. This integration provides a method to fabricate a graphene p–n junction, which is the core part of graphene-based photodetectors.^16,17

Despite the above successes, so far there have not been any investigations of functional FE devices based on monolayer FEs with out-of-plane polarization, integrated with other monolayers such as graphene into vertical heterostructures. Such increased miniaturization is always desirable as it improves performance.¹ The main difficulty has been the inability so far to fabricate monolayer FEs starting with known layered FEs in bulk or thin-film form or grow them directly by chemical vapor deposition or other methods. The main motivation for the present paper is the existence of an experimental technique that, not only produces large-scale, high-quality monolayers, but does it by naturally integrating them into high-quality heterostructures with graphene monolayers on a metal substrate. It has been demonstrated that large-scale, high-quality graphene can be grown epitaxially on transition-metal substrates such as Ru(0001)^18,19 and, subsequently, monolayers or multilayers of other materials can be grown by intercalation in the graphene–metal interface.^20–24 This process eliminates the need for a transfer process that can induce defects and contamination. Recently, bilayer SiO₂ with similar thickness as QL-In₂Se₃ was fabricated in this fashion and proved to be crystalline and weakly bonded to the Ru metal substrate.^20,25,26 QL-In₂Se₃ has not been grown in this fashion yet, but there may be other possibilities as well. Considering that O and Se are same-group elements and the robust ferroelectricity of QL-In₂Se₃ is enabled by its unique atomic arrangements,⁹ oxides that adopt the structure of QL-In₂Se₃ might also be stable monolayer FEs, providing new perspective about the possible integration of graphene and monolayer FEs, as well as related functional devices.

In this paper, we employ density-functional-theory (DFT) calculations and explore theoretically if a single QL of In₂Se₃ or other 2D materials that may also exhibit out-of-plane ferroelectricity can be integrated with graphene on a metal substrate, e.g., Ru (0001), which would enable the fabrication of functional FE devices. We find that QL-In₂Se₃ bonds strongly to the Ru substrate, which destroys its FE properties. We predict, however, that two 2D oxides of the form M₂O₃ (M = Al, Y) in the QL-In₂Se₃ structure, fulfill all the necessary requirements. More specifically, these materials indeed form In₂Se₃-like, energetically stable, QL structures. We then investigate the properties of graphene/QL-M₂O₃/Ru(0001) heterostructures. We find that the QL-M₂O₃ layer works as a ferroelectric tunnel barrier. The barrier width can be modulated by reversing the polarization of the QL-M₂O₃, which leads to a resistance switching behavior, whereby the graphene/QL-M₂O₃/Ru(0001) heterostructure can work as a prototype ferroelectric tunnel junction (FTJ). Moreover, we show that the doping type of graphene (n- or p-type doping) can also be modulated in principle by alternating the polarization of the QL-M₂O₃, which provides a method to fabricate a graphene p–n junction.¹⁵ These results show the possibility of achieving 2D-materials-based non-volatile memory devices and graphene-based optoelectronics through the integration of graphene and monolayer ferroelectrics.

Computational methods

We performed DFT calculations using the Vienna ab initio simulation package (VASP)^27–29 with the projected augmented wave (PAW)³⁰ method. The generalized gradient approximation of Perdew–Burke–Ernzerhof (PBE)³¹ was used to describe the exchange–correlation potential of electrons. The plane-wave cutoff was set at 500 eV for all calculations and Γ-centered (24 × 24 × 1) and (18 × 18 × 1) k-meshes were used for freestanding Al₂O₃ and Y₂O₃ quintuple layers, respectively. The supercell sizes were 7 × 7 and 5 × 5, respectively. The phonon dispersion calculations for freestanding Al₂O₃ and Y₂O₃ quintuple layers were done by the finite-displacement method as implemented in the PHONOPY package.^32–34

To decrease the lattice mismatch of graphene and the intercalated M₂O₃ (M = Al, Y), two kinds of supercells, 6 × 6 graphene/5 × 5 Al₂O₃/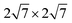 Ru(0001) and 3 × 3 graphene/2 × 2 Y₂O₃/ 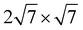Ru(0001) were constructed. For both supercells, the graphene was compressed by 3.6% while the lattice constant of Ru(0001) was set to the experimentally measured value (2.696 Å). The intercalated Al₂O₃ and Y₂O₃ quintuple layers in the corresponding supercells were compressed by 3.0% and 1.1% respectively. We also performed calculations to illustrate that these artificial strains do not have a significant effect on the properties of the heterostructure, as shown in Fig. S8 (ESI†). Vacuum layers more than 15 Å were introduced in both supercells to decrease the interaction between periodic images. Γ-Centered (3 × 3 × 1) and (9 × 9 × 1) k-meshes were applied to supercells containing Al₂O₃ and Y₂O₃ respectively. The atoms in all supercells were fully relaxed by a conjugate gradient method until the interaction force between atoms was less than 0.01 eV Å⁻¹, while the bottom two layers of Ru(0001) substrate were fixed to describe the interaction with bulk Ru. The DFT-D3 approach³⁵ was employed to include van der Waals interactions.

Results and discussion

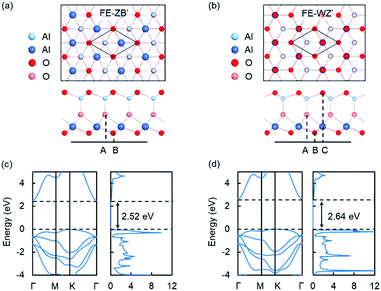
The theoretical results obtained by DFT calculations for graphene/QL-In₂Se₃/Ru(0001) heterostructures are displayed in Fig. S1 (ESI†), showing that the QL-In₂Se₃ bonds strongly to the Ru substrate and loses its FE properties. Clearly, the Ru substrate is not suitable for QL-In₂Se₃, unlike a Au substrate, which has been demonstrated experimentally to preserve the FE properties of 6QL-In₂Se₃.¹⁴ We performed calculations for a QL-In₂Se₃/Au(111) and indeed found weak bonding, which is a necessary condition for the preservation of FE properties (Fig. S2, ESI†). The result is expected to hold for 6QL-In₂Se₃/Au(111), in accord with observations. Nevertheless, we pursued investigations of QL-M₂O₃/Ru(111) expecting that, like bilayer SiO₂,^25,26 they also bond weakly to Ru(0001). Turning to 2D QL-M₂O₃ (M = Al, Y), we first investigated the atomic configurations and properties of freestanding QL's. As mentioned above, starting from QL-In₂Se₃, we replace the Se atoms by O atoms, anticipating that oxides in a QL-In₂Se₃ structure may be stable monolayer ferroelectrics. The In atoms are replaced by M (M = Al, Y) atoms as both Al₂O₃ and Y₂O₃ layers are expected to be insulating, which can work as a tunnel barrier. Here, we show the results of QL-Al₂O₃, while the results of QL-Y₂O₃, which are quite similar, are shown in ESI.†

The predicted atomic configurations of freestanding QL-Al₂O₃ are shown in Fig. 1. QL-Al₂O₃ possesses two phases that are nearly energetically degenerate. The two side views reveal that each phase is noncentrosymmetric with a nonzero polarization. Given that the polarization of QL-In₂Se₃ has been shown to be reversible by a lateral shift of the middle Se layer,⁷ the reversal of the polarization of QL-Al₂O₃ should also be achievable by lateral displacement of the middle O layer, resulting in an identical structure with reverse polarization, i.e., like QL-In₂Se₃, the two QL-Al₂O₃ phases are 2D ferroelectrics with out-of-plane polarization. We adopt a terminology introduced for In₂Se₃ structures⁷ and label the two phases as FE-ZB′ and FE-WZ′. The lattice constants of both FE-ZB′ and FE-WZ′ QL-Al₂O₃ are 2.94 Å. In FE-ZB′ and FE-WZ′ QL-Al₂O₃, the O atoms are stacked in A–B and A–B–C sequences respectively, as shown in Fig. 1(a) and (b). For Al atoms in QL-Al₂O₃, there are two different types of coordination, tetrahedral and octahedral, which is common in several bulk Al₂O₃ polymorphs.³⁷

Fig. 1 Atomic configurations and electronic structures of freestanding QL-Al₂O₃. (a) and (b) Top and side views of two phases of freestanding QL-Al₂O₃. Oxygen atoms are stacked in A–B and A–B–C sequence in FE-ZB′ and FE-WZ′, respectively. (c) and (d) Band structure and DOS of freestanding FE-ZB′ and FE-WZ′ Al₂O₃ QL.

We then calculated the phonon dispersions of freestanding QL-Al₂O₃ and QL-Y₂O₃ to check their stability, and the results are shown in Fig. S5 (ESI†). The absence of imaginary-frequency modes indicates that both QL-Al₂O₃ and QL-Y₂O₃ are dynamically stable. To demonstrate the likely feasibility of synthesizing QL-Al₂O₃, we compare the energy of α-Al₂O₃ with that of layered bulk Al₂O₃ comprising a stack of Al₂O₃ QLs, as well as the energy of freestanding Al₂O₃ layer in different configurations. Other bulk-alumina polymorphs, e.g., γ-Al₂O₃, are not considered in the calculations since α-Al₂O₃ is the most stable bulk alumina polymorph and can be truncated into a 2D form with the 2 : 3 stoichiometry. The calculated energies are shown in Table 1, while the configurations employed in calculations are shown in Fig. S3 (ESI†). We note that the energy of layered bulk Al₂O₃ is only slightly higher (91 meV per f.u.) than that of α-Al₂O₃. However, in 2D form, the QL-Al₂O₃ is energetically favored over α-Al₂O₃ (0001) layer or Al₂O₃ ML. These results indicate that it may be possible to fabricate stable 2D M₂O₃ in the prototype structure of QL-In₂Se₃. We note in particular that the bilayer SiO₂ that has been fabricated by intercalation in a graphene-on-Ru(0001) structure also is not known to correspond to a bulk SiO₂ polymorph.

Table 1 Relative energies of different bulk Al₂O₃ polymorphs and different freestanding Al₂O₃ layer configurations. The unit of the relative energies are eV per formula unit (eV per f.u.). The data of monolayer (ML) Al₂O₃ were obtained by performing calculations based on the reported configurations.³⁶ For bulk Al₂O₃ and freestanding Al₂O₃ layer, the energy of α-Al₂O₃ and FE-ZB′ QL-Al₂O₃ are set as zero respectively. All the configurations employed in the calculations are shown in Fig. S3 (ESI)

	Bulk			Freestanding layer
	α-Al2O3	α-2H Al2O3	α-3R Al2O3	α-Al2O3 (0001)	ML Al2O3	FE-ZB′ QL-Al2O3	FE-WZ′ QL-Al2O3
Relative energy (eV per f.u.)	0	0.091	0.114	0.153	2.326	0	0.007

---

We further investigated the electronic properties of QL-Al₂O₃ and QL-Y₂O₃ and show the results of QL-Al₂O₃ in Fig. 1(c) and (d). The PBE-calculated band structure and DOS show that the two phases of QL-Al₂O₃ possess indirect band gaps of 2.52 eV and 2.64 eV, respectively. Similar results for QL-Y₂O₃ are shown in Fig. S4 (ESI†). PBE-based calculations are known to underestimate band gaps by about a factor 2, whereby the gaps of these materials are substantially larger, perhaps of order 5 eV, which would be very practical for tunnel barriers. All the results so far indicate that the fabrication of QL-M₂O₃ (M = Al, Y) is possible and that the two materials could serve as a tunnel barrier in graphene/QL-M₂O₃/metal heterostructures.

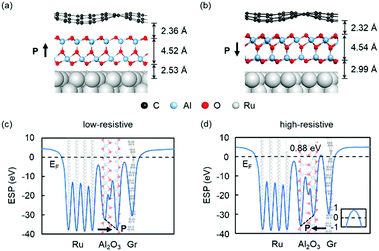
We now examine the properties of graphene/QL-M₂O₃/Ru heterostructures (M = Al, Y). Here, we report results for graphene/QL-Al₂O₃/Ru(0001), while the results for QL-Y₂O₃ are shown in ESI.† We used the FE-ZB′ phase of QL-Al₂O₃ to construct the heterostructure because it is energetically favored, as shown in Table 1. As QL-Al₂O₃ possesses out-of-plane polarization, there are two possible configurations for graphene/QL-Al₂O₃/Ru(0001) heterostructures, in which the polarization points towards or away from graphene [see Fig. 2(a) and (b)]. After relaxation, graphene in the heterostructure becomes corrugated, which is likely to result from the small compressive strain in graphene in the heterostructure,³⁸ which we imposed to enable practical computations. As shown in Fig. 2(a) and (b), the vertical distance between the bottom surface of the QL-Al₂O₃ and Ru(0001), 2.53 and 2.99 Å for up and down polarization, respectively, is much larger than the typical Ru–O bond length, 1.94–1.98 Å,³⁹ which indicates that QL-Al₂O₃ and Ru(0001) are bonded through van der Waals interactions. Graphene and QL-Al₂O₃ are also bonded through van der Waals interactions.

Fig. 2 Configurations and plane-averaged electrostatic potential of graphene/QL-Al₂O₃/Ru(0001) heterostructure. (a) and (b) Relaxed configurations of graphene/QL-Al₂O₃/Ru(0001) heterostructure with opposite polarizations. The black, light blue, red and gray balls represent C, Al, O and Ru atoms, respectively. (c) and (d) Plane-averaged electrostatic potential of (a) and (b), respectively. The horizontal and sloped dashed lines represent the Fermi energy (EF) and potential drop across QL-Al₂O₃, respectively. The inset in (d) shows a zoom-in of the potential barrier.

We further calculated the plane-averaged electrostatic potential (ESP) for the two heterostructures. The results are shown in Fig. 2(c) and (d). An electrostatic potential drop is present across the QL-Al₂O₃ in the polarization direction, shown as a sloped dashed line, which indicates that the out-of-plane polarization of the QL-Al₂O₃ is preserved in Gr/QL-Al₂O₃/Ru heterostructures. When the polarization points to graphene, as shown in Fig. 2(c), there are no potential barriers above the Fermi energy. However, when the polarization is reversed, as shown in Fig. 2(d), a barrier of 0.88 eV above the Fermi energy is present. These results indicate the emergence of two different states in Gr/QL-Al₂O₃/Ru heterostructure with the reversal of the polarization.

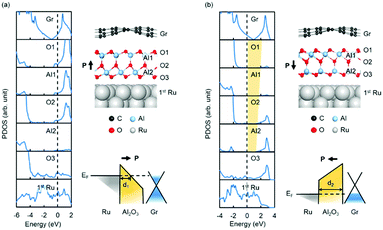
The influence of the polarization direction of QL-Al₂O₃ is further investigated by calculating the electronic structure of a graphene/QL-Al₂O₃/Ru(0001) heterostructure. The layer-resolved PDOS in Fig. 3(a) shows that, when the polarization points towards graphene, a metallic region near the graphene/QL-Al₂O₃ interface forms, whereby the whole system is conductive. The mechanism for this feature is shown schematically in the band diagram: the polarization-induced potential drop causes the barrier's CBM near the graphene/QL-Al₂O₃ interface drop below the Fermi level, which reduces the barrier width dramatically. However, when the polarization is reversed, as shown in Fig. 3(b), a tunnel barrier between graphene and Ru(0001) forms, which is shown by the yellow region in the layer-resolved PDOS. When a bias voltage is applied between graphene and Ru, the heterostructure shown in Fig. 3a exhibits a relatively low-resistive state comparing with that in Fig. 3b. This “reversible barrier metallization” mechanism, which was first reported in SrRuO₃/BaTiO₃/n-SrTiO₃⁴⁰ and Co/PbTiO₃/La_0.7Sr_0.3MnO₃ heterostructures⁴¹ FTJs, induces a large tunnelling electroresistance (TER) effect. Thus, we expect that the graphene/QL-Al₂O₃/Ru(0001) heterostructure can work as a prototype FTJ.

Fig. 3 The layer resolved PDOS of graphene/QL-Al₂O₃/Ru(0001) heterostructure. (a) and (b) The layer-resolved PDOS of graphene/QL-Al₂O₃/Ru(0001) heterostructure when the polarization points toward and away from graphene respectively. The Fermi level is represented by black dashed line and the tunnel barrier is represented by the yellow region. The band schematics are deduced from the PDOS.

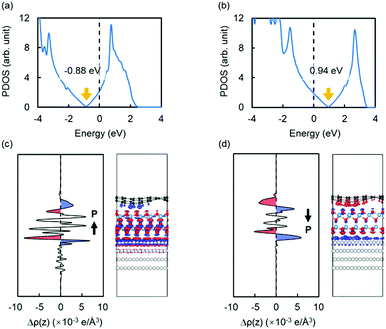
We also found that the doping type of graphene changes by reversing the polarization of the QL-Al₂O₃. As shown in Fig. 4(a) and 4(b), graphene is doped n- or p-type when the polarization points towards or away from graphene, respectively. For n- and p-type doped graphene, the Fermi level locates 0.88 eV above and 0.94 eV below the Dirac point of graphene, respectively. The doping of graphene can be understood by calculating the plane-averaged electron-density difference. The results, calculated using the formula Δρ = ρ(graphene/QL − Al₂O₃/Ru(0001)) − ρ(graphene) − ρ(QL-Al₂O₃) − ρ(Ru(0001)), are shown in Fig. 4(c) and (d). It is clear that the doping of graphene originates from the effect of polarization charge. For example, in Fig. 4(d), when the polarization points away from graphene, negative polarization charge accumulates at the top surface of QL-Al₂O₃, which induces positive charge in graphene, making graphene to be p-doped.

Fig. 4 The doping of graphene in graphene/QL-Al₂O₃/Ru(0001) heterostructure. (a) and (b) The PDOS of graphene in graphene/QL-Al₂O₃/Ru(0001) heterostructure. (c) and (d) The plane averaged charge density difference of the heterostructure. The blue and red region represent electron accumulation and depletion respectively. The isosurface value is set as 0.01 e Å⁻³.

On the basis of the properties we presented above, we propose two kinds of model devices based on graphene/QL-Al₂O₃/Ru(0001) heterostructures. First, a ferroelectric tunnel junction (FTJ), a kind of non-volatile memory device. As shown in Fig. 5(a), we demonstrated that the graphene/QL-Al₂O₃/Ru(0001) heterostructure is in low-resistive or high-resistive state when polarization points towards or away from graphene, corresponding to the ON and OFF state of the FTJ. The polarization of QL-Al₂O₃ can be reversed by applying an electric field between graphene and Ru. Second, a graphene p–n junction, which is the core component of a graphene-based photodetector. As we presented above, the doping type of graphene can be modulated by reversing the polarization of QL-Al₂O₃. If an experimental way can be found to pole adjacent regions of the FE layer in opposite directions, a graphene p–n junction and even a graphene p–n junction array can in principle be fabricated, as shown in Fig. 5(b). Here we note that a clean graphene-FE interface is crucial for the modulation of graphene's doping by ferroelectric polarization.¹⁵ Thus, it is useful to consider how such structures might be fabricated and how a clean interface can be assured in the fabrication process.

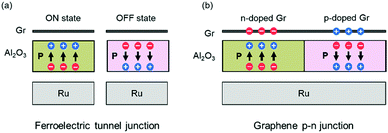Fig. 5 Schematic of devices based on graphene/QL-Al₂O₃/Ru(0001) heterostructures. (a) Ferroelectric tunnel junction. (b) Graphene p–n junction.

Motivated by the fact that Gr/SiO₂/Ru and Gr/Al₂O₃/Ni₃Al heterostructures have been achieved experimentally by the intercalation method,^20,24 intercalation of the QL-FEs under monolayer graphene grown epitaxially on Ru(0001) appears most promising for the following reasons: (i) graphene epitaxially grown on Ru(0001) substrates has been demonstrated to be large-scale, single-crystal and high-quality,^18,19 which is necessary for high-quality graphene/monolayer-ferroelectrics heterostructures. (ii) By using the intercalation method, a clean graphene-ferroelectric interface can be assured^22,23 and the degradation of monolayer ferroelectrics, which may be induced during the electrode evaporation process,⁴² can be avoided. (iii) It has been demonstrated that graphene/silicene/Ru(0001) heterostructures fabricated by intercalation method show good air stability for up to two weeks,²² the heterostructures proposed here should exhibit the same robustness in air, i.e., we do not expect O₂ and water contaminants to passivate the ferroelectric surface charge⁴³ or oxidize the Ru substrate. Long-term protection can be achieved by proper encapsulation of the device.

Conclusions

In this work, we investigated the effects of intercalating 2D ferroelectric materials into a graphene/metal-substrate interface. We demonstrated that freestanding monolayer M₂O₃ (M = Al, Y) are in principle stable in the prototype structure of QL-In₂Se₃. We found that graphene/QL-M₂O₃/Ru(0001) heterostructures exhibit reversible resistive/non-resistive switching behavior by reversing the polarization of intercalated QL-M₂O₃, whereby such heterostructures work as prototype ferroelectric tunnel junctions. Moreover, we found that the doping type of graphene can be changed by reversing the polarization of the intercalated QL-M₂O₃, potentially providing a way to fabricate graphene-based p–n junctions for photovoltaic applications. Finally we propose that intercalation is likely to be an effective method to achieve the integration of graphene and 2D FE materials, as well as corresponding device fabrication.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Work in China is supported by the National Natural Science Foundation of China (Grants No. 51922011 and 61888102), the National Key Research & Development Projects Program of China (No. 2016YFA0202300, 2018YFA0305800, and 2019YFA0308500), K. C. Wong Education Foundation, the Strategic Priority Research Program of Chinese Academy of Sciences (No. XDB30000000). A portion of the research was performed in CAS Key Laboratory of Vacuum Physics. Work at Vanderbilt was supported in part by the McMinn Endowment.

References

1. V. Garcia and M. Bibes, Nat. Commun., 2014, 5, 4289.
2. S. Yuan, Z. Yang, C. Xie, F. Yan, J. Dai, S. P. Lau, H. L. W. Chan and J. Hao, Adv. Mater., 2016, 28, 10048–10054.
3. M. Si, P.-Y. Liao, G. Qiu, Y. Duan and P. D. Ye, ACS Nano, 2018, 12, 6700–6705.
4. C. Paillard, X. Bai, I. C. Infante, M. Guennou, G. Geneste, M. Alexe, J. Kreisel and B. Dkhil, Adv. Mater., 2016, 28, 5153–5168.
5. F. Liu, L. You, K. L. Seyler, X. Li, P. Yu, J. Lin, X. Wang, J. Zhou, H. Wang, H. He, S. T. Pantelides, W. Zhou, P. Sharma, X. Xu, P. M. Ajayan, J. Wang and Z. Liu, Nat. Commun., 2016, 7, 12357.
6. K. Chang, J. Liu, H. Lin, N. Wang, K. Zhao, A. Zhang, F. Jin, Y. Zhong, X. Hu, W. Duan, Q. Zhang, L. Fu, Q.-K. Xue, X. Chen and S.-H. Ji, Science, 2016, 353, 274–278.
7. W. Ding, J. Zhu, Z. Wang, Y. Gao, D. Xiao, Y. Gu, Z. Zhang and W. Zhu, Nat. Commun., 2017, 8, 14956.
8. C. Cui, W.-J. Hu, X. Yan, C. Addiego, W. Gao, Y. Wang, Z. Wang, L. Li, Y. Cheng, P. Li, X. Zhang, H. N. Alshareef, T. Wu, W. Zhu, X. Pan and L.-J. Li, Nano Lett., 2018, 18, 1253–1258.
9. J. Xiao, H. Zhu, Y. Wang, W. Feng, Y. Hu, A. Dasgupta, Y. Han, Y. Wang, D. A. Muller, L. W. Martin, P. Hu and X. Zhang, Phys. Rev. Lett., 2018, 120, 227601.
10. D. Ji, S. Cai, T. R. Paudel, H. Sun, C. Zhang, L. Han, Y. Wei, Y. Zang, M. Gu, Y. Zhang, W. Gao, H. Huyan, W. Guo, D. Wu, Z. Gu, E. Y. Tsymbal, P. Wang, Y. Nie and X. Pan, Nature, 2019, 570, 87–90.
11. R. R. Mehta, B. D. Silverman and J. T. Jacobs, J. Appl. Phys., 1973, 44, 3379–3385.
12. J. Junquera and P. Ghosez, Nature, 2003, 422, 506–509.
13. C. H. Ahn, K. M. Rabe and J.-M. Triscone, Science, 2004, 303, 488–491.
14. S. M. Poh, S. J. R. Tan, H. Wang, P. Song, I. H. Abidi, X. Zhao, J. Dan, J. Chen, Z. Luo, S. J. Pennycook, A. H. Castro Neto and K. P. Loh, Nano Lett., 2018, 18, 6340–6346.
15. C. Baeumer, D. Saldana-Greco, J. M. P. Martirez, A. M. Rappe, M. Shim and L. W. Martin, Nat. Commun., 2015, 6, 6136.
16. F. H. L. Koppens, T. Mueller, P. Avouris, A. C. Ferrari, M. S. Vitiello and M. Polini, Nat. Nanotechnol., 2014, 9, 780.
17. G. Wang, M. Zhang, D. Chen, Q. Guo, X. Feng, T. Niu, X. Liu, A. Li, J. Lai, D. Sun, Z. Liao, Y. Wang, P. K. Chu, G. Ding, X. Xie, Z. Di and X. Wang, Nat. Commun., 2018, 9, 5168.
18. Y. Pan, H. Zhang, D. Shi, J. Sun, S. Du, F. Liu and H.-J. Gao, Adv. Mater., 2009, 21, 2777–2780.
19. H. Guo, X. Wang, H. Lu, L. Bao, H. Peng, K. Qian, J. Ma, G. Li, L. Huang, X. Lin, Y.-Y. Zhang, S. Du, S. T. Pantelides and H.-J. Gao, 2D Mater., 2019, 6, 045044.
20. S. Lizzit, R. Larciprete, P. Lacovig, M. Dalmiglio, F. Orlando, A. Baraldi, L. Gammelgaard, L. Barreto, M. Bianchi, E. Perkins and P. Hofmann, Nano Lett., 2012, 12, 4503–4507.
21. Z. Y. Al Balushi, K. Wang, R. K. Ghosh, R. A. Vilá, S. M. Eichfeld, J. D. Caldwell, X. Qin, Y.-C. Lin, P. A. DeSario, G. Stone, S. Subramanian, D. F. Paul, R. M. Wallace, S. Datta, J. M. Redwing and J. A. Robinson, Nat. Mater., 2016, 15, 1166.
22. G. Li, L. Zhang, W. Xu, J. Pan, S. Song, Y. Zhang, H. Zhou, Y. Wang, L. Bao, Y.-Y. Zhang, S. Du, M. Ouyang, S. T. Pantelides and H.-J. Gao, Adv. Mater., 2018, 30, 1804650.
23. J. Mao, L. Huang, Y. Pan, M. Gao, J. He, H. Zhou, H. Guo, Y. Tian, Q. Zou, L. Zhang, H. Zhang, Y. Wang, S. Du, X. Zhou, A. H. C. Neto and H.-J. Gao, Appl. Phys. Lett., 2012, 100, 093101.
24. L. Omiciuolo, E. R. Hernández, E. Miniussi, F. Orlando, P. Lacovig, S. Lizzit, T. O. Menteş, A. Locatelli, R. Larciprete, M. Bianchi, S. Ulstrup, P. Hofmann, D. Alfè and A. Baraldi, Nat. Commun., 2014, 5, 5062.
25. B. Yang, W. E. Kaden, X. Yu, J. A. Boscoboinik, Y. Martynova, L. Lichtenstein, M. Heyde, M. Sterrer, R. Włodarczyk, M. Sierka, J. Sauer, S. Shaikhutdinov and H.-J. Freund, Phys. Chem. Chem. Phys., 2012, 14, 11344–11351.
26. D. Löffler, J. J. Uhlrich, M. Baron, B. Yang, X. Yu, L. Lichtenstein, L. Heinke, C. Büchner, M. Heyde, S. Shaikhutdinov, H. J. Freund, R. Włodarczyk, M. Sierka and J. Sauer, Phys. Rev. Lett., 2010, 105, 146104.
27. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
28. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
29. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
30. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066.
33. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
34. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
35. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
36. T. T. Song, M. Yang, J. W. Chai, M. Callsen, J. Zhou, T. Yang, Z. Zhang, J. S. Pan, D. Z. Chi, Y. P. Feng and S. J. Wang, Sci. Rep., 2016, 6, 29221.
37. K. Sohlberg, S. J. Pennycook and S. T. Pantelides, J. Am. Chem. Soc., 1999, 121, 7493–7499.
38. Y. Zhang and F. Liu, Appl. Phys. Lett., 2011, 99, 241908.
39. A. A. Bolzan, C. Fong, B. J. Kennedy and C. J. Howard, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 373–380.
40. X. Liu, J. D. Burton and E. Y. Tsymbal, Phys. Rev. Lett., 2016, 116, 197602.
41. A. Quindeau, V. Borisov, I. Fina, S. Ostanin, E. Pippel, I. Mertig, D. Hesse and M. Alexe, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035130.
42. Y. Liu, J. Guo, E. Zhu, L. Liao, S.-J. Lee, M. Ding, I. Shakir, V. Gambin, Y. Huang and X. Duan, Nature, 2018, 557, 696–700.
43. A. Kakekhani and S. Ismail-Beigi, J. Mater. Chem. A, 2016, 4, 5235–5246.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nh00255k

---