Fullerene rotational dynamics generate disordered configurations that suppress thermal conductivity in superatomic crystals

Abstract

The thermal conductivity of fullerene-based superatomic crystals (SACs) is investigated using molecular dynamics simulations. The temperature-dependent predictions agree with the trends of previous measurements. The thermal conductivity behavior emerges as a result of the C₆₀ molecule rotational dynamics and orientation, which are quantified using the root mean square displacements of the carbon atoms and the relative orientations of the C₆₀s. At low temperatures, the C₆₀s exhibit small rotations around equilibrium positions (i.e., librations). When the librating C₆₀s are orientationally-ordered, as in the [C₆₀] and [Co₆Se₈(PEt₃)₆][C₆₀]₂ SACs, thermal conductivity decreases with increasing temperature, as is typical for a crystal. When the librating C₆₀s are orientationally-disordered, however, as in the [Co₆Te₈(PEt₃)₆][C₆₀]₂ SAC, thermal conductivity is lower and temperature independent, as is typical for an amorphous solid. At higher temperatures, where the C₆₀s in all three SACs freely-rotate and are thus dynamically disordered, thermal conductivity is temperature independent. The abrupt changes driven by the C₆₀ dynamics suggest that fullerene-based SACs can be designed to be thermal conductivity switches based on a variety of external stimuli.

---

New concepts

Superatoms are atomically-precise nanometer-sized clusters that can self-assemble to form superatomic crystals (SACs). SACs have emergent and unexpected electrical, optical, and magnetic properties. Very little is understood about thermal transport in SACs. We perform the first-ever molecular dynamics simulations of SACs to identify the atomic mechanisms that dictate thermal transport. The SACs are built from C₆₀ and chalcogen-based superatoms. We discover that the temperature dependence of thermal conductivity can be explained by the rotational dynamics and orientational ordering of the C₆₀s, mechanisms that had only been hinted at by previous experimental studies. Our key insight is that SACs only have a crystal-like thermal conductivity (i.e., decreasing with increasing temperature) when the C₆₀s are locked in place in an ordered manner. If the C₆₀s are disordered, in either a locked-in-place configuration or freely rotating, then the thermal conductivity is lower and amorphous-like (i.e., temperature independent). This new link between fullerene rotational dynamics, orientational order, and thermal transport suggest a new paradigm for designing SACs whose thermal conductivities can be switched by external mechanical, electrical, and optical fields. Such thermal conductivity switches could have profound impacts on managing and controlling heat flow in electronics and energy conversion devices.

Superatoms are atomically-precise and chemically-stable clusters that can emulate atoms, but at the nanometer scale.^1–9 Examples include C₆₀, Co₆Se₈(PEt₃)₆, and Ni₁₂Te₁₂(PEt₃)₈. Superatoms can interact through electrostatic,² covalent,⁵ and/or van der Waals⁴ interactions, leading to the formation of amorphous and ordered solids. The latter are called superatomic crystals (SACs), which can behave like traditional rare earth elements,¹ semiconductors,⁶ and superconductors.⁷ For example, the n-doped SAC [Re₆Se₈Cl₂] is a superconductor with a critical temperature of ∼8 K.⁷

The tunability of superatom composition and the ability to mix different superatoms result in an immense design space for SACs beyond that for atomic crystals, which can lead to beneficial properties. For example, the surface of a two-dimensional SAC can be functionalized without affecting the intralayer bonding.¹⁰

Our interest here is thermal transport in SACs that are built from C₆₀, Co₆Se₈(PEt₃)₆, and Co₆Te₈(PEt₃)₆ superatoms. These large unit cell crystals exhibit more complex thermal transport behaviors than those found in simple, small unit cell crystals. Experimental measurements of the C₆₀ molecular crystal, [C₆₀], show a switch from a crystal-like thermal conductivity (i.e., one that decreases with increasing temperature) to an amorphous-like thermal conductivity (i.e., one that is temperature independent) across a phase transition at a temperature of 260 K, where the lattice constant abruptly increases and the C₆₀s begin to freely rotate.^11,12 The high-temperature phase has dynamic disorder, in that the centers of mass of the C₆₀s sit on a lattice, but their orientations are random and time-dependent.

Molecular dynamics (MD) simulations have also been conducted on [C₆₀] to study its thermal behavior from an atomic perspective.^13–16 Giri et al. found that the librational modes are suppressed with increasing pressure, leading to a rapidly increasing thermal conductivity.¹⁵ Kumar et al. predicted thermal conductivity across the phase transition in [C₆₀].¹⁶ They found that while the free rotations do not carry significant heat, they increase the scattering of the phonons associated with C₆₀ center of mass vibrations, leading to the temperature-independent thermal conductivity.

Ong et al. experimentally measured the thermal conductivity of the isostructural binary SACs [Co₆Se₈(PEt₃)₆][C₆₀]₂ and [Co₆Te₈(PEt₃)₆][C₆₀]₂,³ which we will refer to as [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂. They found that the thermal conductivity of [CoSe][C₆₀]₂ has a similar temperature dependence as that of pure [C₆₀] (i.e., crystal-like at temperatures below 190 K and amorphous-like at higher temperatures). This result suggests a transition from librating to freely-rotating C₆₀s (i.e., the emergence of dynamic disorder) that was supported by an increase in the lattice constant at the same temperature where the thermal conductivity trend changed. [CoTe][C₆₀]₂ showed an amorphous-like thermal conductivity at all temperatures considered (150–350 K), suggesting free rotations of the C₆₀s due to the larger size of the Te ion compared to the Se ion. O'Brien et al. measured the thermal conductivity of [Co₆Te₈(PEt₃)₆][C₇₀]₂, which contains larger and non-spherical C₇₀ molecules.¹⁷ They found that dynamic disorder emerges above a temperature of 240 K.

How C₆₀ rotational dynamics affect the thermal conductivity of [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂ has only been qualitatively inferred from structural and thermal measurements.³ We herein apply MD simulations to [C₆₀], [CoSe][C₆₀]₂, and [CoTe][C₆₀]₂ to directly observe the rotational dynamics and to determine the impact on thermal conductivity. In addition to observing the emergence of dynamic disorder, we distinguish between static low-temperature phases that are rotationally-ordered and rotationally-disordered and formulate criteria for the observation of a crystal-like thermal conductivity in fullerene-based SACs.

Above a temperature of 260 K, [C₆₀] has a face-centered cubic structure with a one-molecule basis. Due to the free rotations, there is no order in the molecular orientations. Below this temperature, the lattice constant contracts by 0.3% and the molecules develop orientational order, such that the crystal structure becomes simple cubic with a four-molecule basis [Fig. S1 in the ESI†].^12,16,18

Both [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂ have one Co₆(Se or Te)₈(PEt₃)₆ and two C₆₀s in each unit cell. [CoSe][C₆₀]₂ takes on the P3̄ phase at temperatures below 190 K and the higher symmetry P3̄m1 phase at higher temperatures. [CoTe][C₆₀]₂ is observed to be in the P3̄m1 phase at all studied temperatures (150–350 K).³ Further details are provided in Section S1 (ESI†).

The MD simulations were performed using LAMMPS¹⁹ between temperature of 25 and 300 K with a time step of 1 fs and periodic boundary conditions in all directions. Due to the accessible system sizes and time scales, it is generally not possible to capture experimentally-observed phase transitions in standard MD simulations. To do so, enhanced sampling methods are needed.^20,21 Furthermore, due to limitations in the interatomic potentials, phase transition temperatures are difficult to accurately predict. As such, for completeness, we modeled both the P3̄ and P3̄m1 phases at all temperatures for both [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂. The ESI† also contains simulation results for the unary SACs characterized by Ong et al.³ The atomic interactions were modeled using the universal force field (UFF),²² which includes bonded, angular, dihedral, and non-bonded interactions (van der Waals and electrostatic). The partial charges for the electrostatic interactions were obtained by the extended charge equilibration method.²³ All potential parameters are provided in the ESI.† Molecular dynamics simulations are classical, such that quantum effects on phonon populations and heat capacity are not included.²⁴ Our goal is thus to study general questions of the nature of thermal transport in fullerene-based SACs.

Simulation boxes of size 2 × 2 × 2 unit cells were built using experimentally-measured lattice parameters and atomic positions.³ The system was then evolved in the NPT ensemble (i.e., constant number of atoms N, pressure P, and temperature T) at zero pressure and the desired temperature for 3 × 10⁷ time steps. The [C₆₀] simulation cell was constrained to be cubic, while the three side lengths of the [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂ simulation cells were controlled independently. The angles for the [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂ simulation cells were fixed at the experimental values. The side lengths were recorded every ten time steps over the last 10⁷ time steps, averaged, and then used to obtain the lattice constants, with additional averaging based on known symmetries. Details for the unary SACs and on bulk modulus predictions are provided in Sections S1 and S2 (ESI†).

The thermal conductivity was predicted using the Green–Kubo method.²⁵ The expression for the heat current provided by Boone et al. was used to properly include the three- and four-body terms in the UFF.²⁶ A 3 × 3 × 3 unit cell simulation box (required to eliminate size effects, see Section S3, ESI†) was built using the zero-pressure lattice constants and thermalized in the NVT (i.e., constant number of atoms, volume V, and temperature) ensemble with a Nose–Hoover thermostat for 2 × 10⁶ time steps and then equilibrated in the NVE ensemble (i.e., constant number of atoms, volume, and total energy E) for 10⁵ time steps. The heat current vector was then collected every five time steps in the NVE ensemble for 3 × 10⁶ time steps for [C₆₀] and 5 × 10⁶ time steps for [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂. The heat current autocorrelation functions (HCACF) were obtained for ten independent simulations with random initial velocities and then averaged. The thermal conductivity was then specified by averaging the averaged HCACF between correlation times of 50 and 200 ps. For [C₆₀], the isotropic thermal conductivity was obtained by averaging the three directions. For the SACs, the full anisotropic thermal conductivity tensor was calculated, with subsequent averaging based on known symmetries. The uncertainty was estimated by calculating the standard deviation of ten thermal conductivities, each obtained by averaging the HCACF over nine of the ten independent simulations.

We quantified the C₆₀ rotational dynamics using the root mean square displacement (RMSD) of the carbon atoms and the angle between neighboring C₆₀s. The RMSD of a carbon atom was calculated every ten time steps in an NVT simulation for 10⁶ time steps, using the time-averaged position as the reference. The reported RMSD is an average over all carbon atoms in all C₆₀s. The orientation of a C₆₀ was quantified by building vectors from its center to the center of each of its twelve pentagonal faces. The relative angle θ between two C₆₀s is the minimum of the 144 angles formed between them by the two sets of twelve vectors. By recording θ for every pair of C₆₀s every 100 time steps in an NVT simulation and averaging them over 10⁶ time steps, the average relative angle [small theta, Greek, macron] was obtained.

The predicted zero-pressure lattice constants of [C₆₀] are plotted in Fig. 1(a) along with experimental data¹¹ and the predictions of Kumar et al.¹⁶ The UFF lattice constants are ∼0.2 Å lower than the experimental values, while those from Kumar et al., who used the polymer consistent force field (PCFF), are ∼0.3 Å higher. All three data sets show a change in the lattice constant at the point where the C₆₀ molecules begin to freely rotate: 100 K for PCFF (clearly seen in the rotational diffusion coefficient data in ref. 16, 212 K for UFF, and 260 K in the experiments). The experimental lattice constant data show a larger jump than the MD predictions at the phase transition. Spirk et al. developed a force field for a rigid-body model of [C₆₀] that raised the transition temperature closer to the experimental value and generated a larger jump in the lattice constant at the transition.²⁷ We did not use the Spirk et al. force field because the chalcogen atoms in the SACs limited our choices. For this reason, we used the UFF, which, as shown, performs better than the PCFF. These results point to the sensitivity in the behavior of [C₆₀] based on the chosen force field, which is also evident when analyzing other MD studies.¹⁴

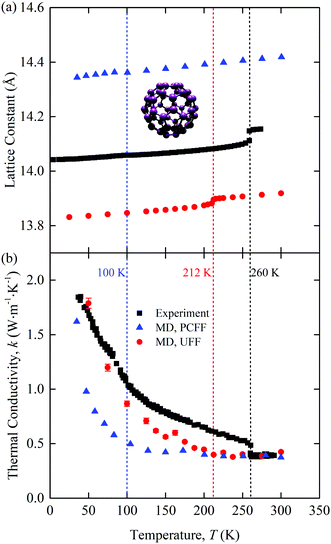Fig. 1 Temperature-dependent (a) lattice constant and (b) thermal conductivity of [C₆₀]. The atomic structure of one molecule is provided in the inset of (a). C = purple. Experimental data^11,12 and PCFF-predicted data¹⁶ are included for comparison. The phase transition temperatures are 100 K for PCFF (clearly seen in the rotational diffusion coefficient data in ref. 16), 212 K for UFF, and 260 K in the experiments.

The thermal conductivity of [C₆₀] is plotted in Fig. 1(b) as a function of temperature. Included are predictions from our UFF calculations, the PCFF,¹⁶ and experiments.¹² All three data sets show the same qualitative behavior. There is a crystal-like thermal conductivity at low temperatures and an amorphous-like thermal conductivity at high temperatures. The transition occurs at the same temperature as the transition in the lattice constant observed in Fig. 1(a), shown with dashed vertical lines. The MD-predicted thermal conductivities are continuous with temperature, which is in contrast to the experimental data, where there is a jump at the transition. We hypothesize that the lack of a jump in the MD thermal conductivity data is a result of the classical nature of MD simulations, such that all vibrational modes are activated at all temperatures. Support for this assertion can be found in the work of Kumar et al.,¹⁶ who applied MD simulations and the PCFF to predict the thermal conductivity of [C₆₀] using three approaches: a full degree of freedom model (as we have done here), a rigid body model, and a point mass model. Their full degree of freedom thermal conductivity, which is plotted in Fig. 1(b), shows a continuous thermal conductivity trend with temperature, as we found with the UFF. Their rigid body model, however, has a jump in thermal conductivity at the phase transition. A rigid body model is potentially a better representation of the experimental system, where the majority of the intramolecular degrees of freedom are not activated at room temperature and below. The activated intramolecular degrees of freedom in the MD simulations both carry heat and scatter with the intermolecular degrees of freedom, leading to the continuous thermal conductivity behavior. We also note that the rigid body thermal conductivity at a given temperature is always lower than the corresponding full degree of freedom value. This behavior suggests that the use of classical statistics leads to an overestimation of the MD-predicted thermal conductivity of [C₆₀] and thus that of the binary SACs.

The predicted zero-pressure lattice constants of [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂ between temperatures of 25 and 300 K are provided in Tables S2–S5 (ESI†). The results are all within 0.29 Å of the corresponding experimental values (measured between temperatures of 100 and 300 K), with a relative error of at most 1.8%.

The predicted thermal conductivities of [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂ and the measurements of Ong et al. are plotted in Fig. 2(a)–(d). Our results are consistent with the measurements in terms of trend and magnitude. For [CoSe][C₆₀]₂, the low-temperature P3̄ phase shows the same decrease in thermal conductivity with increasing temperature as the experiments, albeit with the transition happening at a lower temperature, which is consistent with the [C₆₀] predictions. The high-temperature P3̄m1 phase has a temperature-independent thermal conductivity, also consistent with the measurements. For [CoTe][C₆₀]₂ in the P3̄m1 phase, which is observed at all experimental temperatures, the predicted thermal conductivity is temperature-independent, again consistent with the experiments.

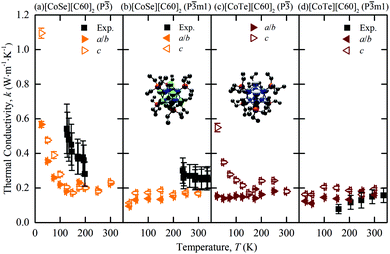Fig. 2 Temperature-dependent MD-predicted and experimental³ thermal conductivities of [CoSe][C₆₀]₂ [(a), (b)] and [CoTe][C₆₀]₂ [(c), (d)] in the P3̄ [(a), (c)] and P3̄m1 [(b), (d)] phases. The atomic structures of the CoSe and CoTe superatoms are provided in the insets of (b) and (c). Co = blue; Se = green; Te = white; P = red, C = black. Hydrogen atoms are removed to clarify the view. The experimental data are plotted corresponding to the observed phase.

The c direction thermal conductivity is generally larger than that along the a and b directions. This anisotropy was not resolved in the measurements. At a temperature of 300 K, the direction-averaged predicted thermal conductivities for the P3̄m1 phases are 0.171 ± 0.007 for [CoSe][C₆₀]₂ and 0.178 ± 0.006 W m K⁻¹ for [CoTe][C₆₀]₂, which are comparable with the measured values of 0.25 ± 0.06 W m K⁻¹ and 0.16 ± 0.04 W m K⁻¹.

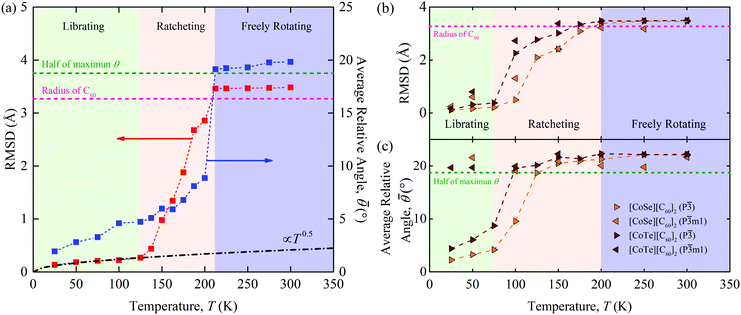
As shown in Fig. 3(a), three distinct regimes are evident in both the RMSD and [small theta, Greek, macron] data for [C₆₀].

Fig. 3 RMSD and [small theta, Greek, macron] for (a) [C₆₀] and (b), (c) [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂ as a function of temperature. The black dot dash line in (a) represents RMSD ∝ T^0.5. The pink dash line represents the radius of the C₆₀ molecule. The green dash line represents half of the maximum possible angle θ (37.5°) between two C₆₀ molecules. Three distinct regimes are evident in both the RMSD and [small theta, Greek, macron] for [C₆₀] and the P3̄ phases of the binary SACs.

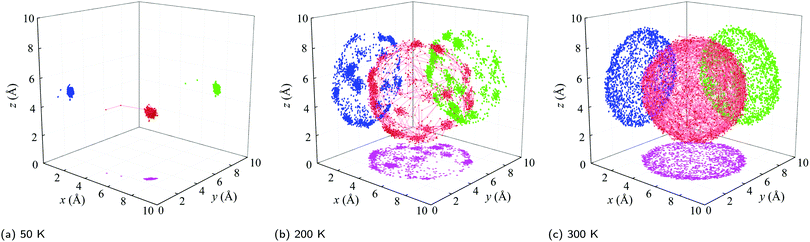
(i) Below a temperature of 125 K, the RMSD scales as T^1/2, consistent with the harmonic crystal approximation.²⁸ From the distribution plotted in Fig. S16 (ESI†), the relative angle θ between two cages is less than 10°. The resulting [small theta, Greek, macron] is below 5° and increases slowly with increasing temperature. These results indicate that the C₆₀s in [C₆₀] in this temperature range are librating around an equilibrium position and are orientationally ordered. This behavior is confirmed by the atomic trajectory of a single carbon at a temperature of 50 K plotted in Fig. 4. The single cluster of points on the x–y (pink), x–z (blue), and y–z (green) planes and overall (red) indicate that the carbon atom is vibrating around a single equilibrium position.

Fig. 4 Trajectories of a carbon atom in [C₆₀] at various temperatures. The trajectory (red) and its projections onto the x–y (pink), x–z (blue), and y–z (green) planes are shown. (a) At a temperature of 50 K, there is a single cluster, indicating that the C₆₀ molecule is librating around a single equilibrium position. (b) At a temperature of 200 K, there are multiple discrete clusters, indicating that the C₆₀ molecule ratchets between multiple equilibrium positions. (c) At a temperature of 300 K, the points are uniformly distributed on a sphere, indicating that the C₆₀ molecule is freely rotating.

(ii) Between temperatures of 125 and 212 K, the RMSD increases rapidly with increasing temperature. The θ distribution (Fig. S16, ESI†) broadens and its peak shifts to larger values, giving rise to the [small theta, Greek, macron] increase from 5° to 10°. The atomic trajectory at a temperature of 200 K plotted in Fig. 4(b) shows multiple discrete clusters, indicating that there are many equilibrium positions. In this temperature range, we conclude that the C₆₀s librate around an equilibrium position and periodically ratchet to a new equilibrium position. With increasing temperature, the ratcheting frequency increases.

(iii) Above a temperature of 212 K, the RMSD value is constant with a value close to the radius of the C₆₀ molecule. The small deviation results from the collective movement of the atoms with respect to the molecule's center. The relative angle θ is nearly evenly distributed and shows no temperature dependence (Fig. S16, ESI†). Thus, [small theta, Greek, macron] is temperature independent with a value of 20°, which is about half of the maximum possible angle (37.5°) between two C₆₀ molecules. These results indicate that the C₆₀ molecules are freely rotating and are thus dynamically disordered, which is confirmed by the atomic trajectory at a temperature of 300 K plotted in Fig. 4(c).

We note that the transition temperature from (ii) to (iii) matches that seen in the lattice constant and thermal conductivity data, plotted in Fig. 1(a) and (b). This transition was also observed by Kumar et al.,¹⁶ who found that the free rotations lead to the temperature-independent thermal conductivity. Kumar et al. quantified the nature of the C₆₀ rotation using the rotational diffusion coefficient and did not observe the transition from (i) to (ii).

We now apply this analysis framework to understand how C₆₀ rotational dynamics impact the thermal conductivity of [CoSe][C₆₀]₂ and [CoTe][C₆₀]₂. The RMSD and [small theta, Greek, macron] for both materials in the P3̄ and P3̄m1 phases are plotted in Fig. 3(b) and (c). The θ distributions are plotted in Fig. S17(a)–(d) (ESI†).

Similar to [C₆₀], the results for both materials in the P3̄ phase can be divided into three regimes. Below a temperature of 75 K, the RMSD scales as T^1/2 and [small theta, Greek, macron] is below 5° and increases slightly with increasing temperature. The atomic trajectory of a carbon atom at a temperature of 50 K, plotted in Fig. S12(a) (ESI†) for [CoSe][C₆₀]₂ and in Fig. S14(a) (ESI†) for [CoTe][C₆₀]₂, generates one cluster. Thus, the C₆₀s in the P3̄ phases are librating and orientational ordered at low temperatures, consistent with their crystal-like thermal conductivity. As temperature increases, the RMSD, [small theta, Greek, macron], and atomic trajectories in the P3̄ phases mirror those found for [C₆₀]. Between temperatures of 75 K and 200 K, the C₆₀s ratchet, as shown in Fig. S12(b) and S14(b) (ESI†). Above a temperature of 200 K, they are freely rotating, as shown in Fig. S12(c) and S14(c) (ESI†).

For the P3̄m1 phases, the RMSD is similar to that for the P3̄ phases over the entire temperature range, although the maximum temperature at which the C₆₀s only librate is lower. A striking difference, however, is seen in the [small theta, Greek, macron] data, which remain above 20° at all temperatures. This result indicates that the C₆₀s are orientationally-disordered over the entire temperature range, even when they are librating. It is this disorder that prevents the crystal-like thermal conductivity at low temperatures seen in the P3̄ phases, which have C₆₀s that are orientationally ordered. The amorphous-like thermal conductivity behavior in fullerene-based SACs is thus a result of orientational disorder, either static or dynamic, in the C₆₀s that can exist at any temperature.

We now turn to the question of why the P3̄ phases are orientationally ordered at low temperatures while the P3̄m1 phases are orientationally disordered. To do so, we calculated the superatom centroid-to-centroid spacings, which show a weak temperature dependence. The values at a temperature of 300 K are provided in Table 1. The CoSe–C₆₀ and CoTe–C₆₀ separations are within 0.1 Å between corresponding P3̄ and P3̄m1 phases. The C₆₀–C₆₀ separations, however, are more than 1 Å larger for the P3̄m1 phases than those for the P3̄ phases and for [C₆₀]. As two C₆₀s get closer together, they interact more strongly and the energy barriers for rotation increase (Fig. S19, ESI†). As temperature decreases, the kinetic energy of each C₆₀ decreases such that it may not be able to overcome the rotational energy barriers. Because the rotational energy barriers for the P3̄ phases are large (>1 eV), we hypothesize that the C₆₀ relative orientations lock in place at the rotational energy minima as temperature is decreased, leading to the observed static orientational order. In contrast, the rotational energy barriers of the P3̄m1 phases are too small (∼0.04 eV) to enforce orientational order as temperature is decreased. Instead, the C₆₀s take on a statically disordered state that is mediated by their interactions with the other superatom types.

Table 1 Superatom (SA) centroid-to-centroid distances in [C₆₀], [CoSe][C₆₀]₂, and [CoTe][C₆₀]₂ at a temperature of 300 K

	Distance (Å)
	SA–C60	C60–C60
[C60]	—	9.8420
[CoSe][C60]2 (P3̄)	10.0858	9.9495
[CoSe][C60]2 (P3̄m1)	10.1524	11.2408
[CoTe][C60]2 (P3̄)	10.1855	10.1835
[CoTe][C60]2 (P3̄m1)	10.1715	11.3267

---

The thermal conductivity of [CoTe][C₆₀]₂ in the P3̄ phase, a phase that is not observed experimentally, is plotted in Fig. 2(c). The rotational dynamics of this phase are captured in Fig. 3(b) and (c). Based on the [small theta, Greek, macron] data, the c-direction thermal conductivity shows the expected low-temperature behavior of a decreasing thermal conductivity with increasing temperature. The a/b-direction thermal conductivity, however, is temperature-independent at all temperatures considered, a result that we cannot yet explain.

In summary, we conducted MD simulations to study thermal transport in the fullerene-based SACs [C₆₀], [CoSe][C₆₀]₂, and [CoTe][C₆₀]₂. The C₆₀ molecule rotational dynamics were quantified by the carbon atom RMSD and the angle between neighboring C₆₀ molecules. Three distinct regimes are evident for all three SACs as temperature increases that correspond to librating, ratcheting, and freely-rotating C₆₀ molecules. We determined that a crystal-like thermal conductivity occurs when there is orientational order, which can only happen when the C₆₀ molecules are librating. An amorphous-like thermal conductivity occurs when there is orientational disorder, which can be either static (librating) or dynamic (ratcheting or freely-rotating). Our results clearly demonstrate that the thermal conductivity of fullerene-based SACs can be manipulated by controlling the rotational dynamics of C₆₀ molecules. Beyond temperature, SACs could be designed where stress, electric fields, and light could realize this control to create a thermal conductivity switch.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Paul Boone and Chris Wilmer for useful discussions. This work was supported by Army Research Office Grant W911NF-17-1-0397 and the Major Program of the National Natural Science Foundation of China (Grant No. 51590902). Q. L. acknowledges the financial support from a program of the China Scholarship Council (Award No. 201806280084).

References

1. F. Shimojo, S. Ohmura, R. K. Kalia, A. Nakano and P. Vashishta, Phys. Rev. Lett., 2010, 104, 126102.
2. X. Roy, C.-H. Lee, A. C. Crowther, C. L. Schenck, T. Besara, R. A. Lalancette, T. Siegrist, P. W. Stephens, L. E. Brus, P. Kim, M. L. Steigerwald and C. Nuckolls, Science, 2013, 341, 157–160.
3. W.-L. Ong, E. S. O'Brien, P. S. M. Dougherty, D. Paley, C. F. Higgs, A. J. H. McGaughey, J. A. Malen and X. Roy, Nat. Mater., 2017, 16, 83–88.
4. B. Choi, J. Yu, D. W. Paley, M. T. Trinh, M. V. Paley, J. M. Karch, A. C. Crowther, C.-H. Lee, R. A. Lalancette, X. Zhu, P. Kim, M. L. Steigerwald, C. Nuckolls and X. Roy, Nano Lett., 2016, 16, 1445–1449.
5. A. M. Champsaur, J. Yu, X. Roy, D. W. Paley, M. L. Steigerwald, C. Nuckolls and C. M. Bejger, ACS Cent. Sci., 2017, 3, 1050–1055.
6. X. Zhong, K. Lee, B. Choi, D. Meggiolaro, F. Liu, C. Nuckolls, A. Pasupathy, F. De Angelis, P. Batail, X. Roy and X. Zhu, Nano Lett., 2018, 18, 1483–1488.
7. E. J. Telford, J. C. Russell, J. R. Swann, B. Fowler, X. Wang, K. Lee, A. Zangiabadi, K. Watanabe, T. Taniguchi, C. Nuckolls, P. Batail, X. Zhu, J. A. Malen, C. R. Dean and X. Roy, Nano Lett., 2020, 20, 1718–1724.
8. J. Yang, B. Zhang, A. D. Christodoulides, Q. Xu, A. Zangiabadi, S. R. Peurifoy, C. K. McGinn, L. Dai, E. Meirzadeh, X. Roy, M. L. Steigerwald, I. Kymissis, J. A. Malen and C. Nuckolls, J. Am. Chem. Soc., 2019, 141, 10967–10971.
9. E. A. Doud, A. Voevodin, T. J. Hochuli, A. M. Champsaur, C. Nuckolls and X. Roy, Nat. Rev. Mater., 2020, 5, 371–387.
10. B. Choi, K. Lee, A. Voevodin, J. Wang, M. L. Steigerwald, P. Batail, X. Zhu and X. Roy, J. Am. Chem. Soc., 2018, 140, 9369–9373.
11. W. I. F. David, R. M. Ibberson and T. Matsuo, Proc. R. Soc. London, Ser. A, 1993, 442, 129–146.
12. R. C. Yu, N. Tea, M. B. Salamon, D. Lorents and R. Malhotra, Phys. Rev. Lett., 1992, 68, 2050–2053.
13. L. Chen, X. Wang and S. Kumar, Sci. Rep., 2015, 5, 2045–2322.
14. A. Giri and P. E. Hopkins, J. Phys. Chem. Lett., 2017, 8, 2153–2157.
15. A. Giri and P. E. Hopkins, Phys. Rev. B, 2017, 96, 220303.
16. S. Kumar, C. Shao, S. Lu and A. J. H. McGaughey, Phys. Rev. B, 2018, 97, 104303.
17. E. S. O'Brien, J. C. Russell, M. Bartnof, A. D. Christodoulides, K. Lee, J. A. DeGayner, D. W. Paley, A. J. H. McGaughey, W.-L. Ong, J. A. Malen, X.-Y. Zhu and X. Roy, J. Am. Chem. Soc., 2018, 140, 15601–15605.
18. N. H. Tea, R. C. Yu, M. B. Salamon, D. C. Lorents, R. Malhotra and R. Ruoff, Appl. Phys. A: Mater. Sci. Process., 1993, 56, 219–225.
19. S. Plimpton, J. Comp. Phys., 1995, 117, 1–19.
20. R. Martoňák, A. Laio and M. Parrinello, Phys. Rev. Lett., 2003, 90, 075503.
21. J. Debnath, M. Invernizzi and M. Parrinello, J. Chem. Theory Comput., 2019, 15, 2454–2459.
22. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
23. C. E. Wilmer, K. C. Kim and R. Q. Snurr, J. Phys. Chem. Lett., 2012, 3, 2506–2511.
24. J. E. Turney, A. J. H. McGaughey and C. H. Amon, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 224305.
25. A. J. H. McGaughey and M. Kaviany, Adv. Heat Transfer, 2006, 39, 169–255.
26. P. Boone, H. Babaei and C. E. Wilmer, J. Chem. Theory Comput., 2019, 15, 5579–5587.
27. M. Sprik, A. Cheng and M. L. Klein, J. Phys. Chem., 1992, 96, 2027–2029.
28. M. T. Dove, Introduction to Lattice Dynamics, Cambridge University Press, 1993.

---

Footnotes

† Electronic supplementary information (ESI) available: The crystal structures and unit cell parameters, input and potential generating files for our implementation of the UFF for SACs in LAMMPS, bulk modulus predictions for the unary and binary SACs, thermal conductivity predictions for the unary SACs, carbon atom trajectories in the binary SACs, relative angle distributions, and rotational potential energy barriers. See DOI: 10.1039/d0nh00358a

‡ These authors contributed equally to this work.

---