Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Demonstration of k-vector selective microscopy for nanoscale mapping of higher order spin wave modes
Nick
Träger
 *a,
Paweł
Gruszecki
bc,
Filip
Lisiecki
c,
Felix
Groß
a,
Johannes
Förster
a,
Markus
Weigand
ad,
Hubert
Głowiński
c,
Piotr
Kuświk
c,
Janusz
Dubowik
c,
Maciej
Krawczyk
*a,
Paweł
Gruszecki
bc,
Filip
Lisiecki
c,
Felix
Groß
a,
Johannes
Förster
a,
Markus
Weigand
ad,
Hubert
Głowiński
c,
Piotr
Kuświk
c,
Janusz
Dubowik
c,
Maciej
Krawczyk
 b and
Joachim
Gräfe
b and
Joachim
Gräfe
 *a
*a
aMax Planck Institute for Intelligent Systems, Stuttgart, Germany. E-mail: traeger@is.mpg.de; graefe@is.mpg.de
bFaculty of Physics, Adam Mickiewicz University, Poznań, Poland
cInstitute of Molecular Physics, Polish Academy of Sciences, Poznań, Poland
dHelmholtz-Zentrum Berlin, Germany
First published on 8th June 2020
Abstract
As a potential route towards beyond CMOS computing magnonic waveguides show outstanding properties regarding fundamental wave physics and data transmission. Here, we use time resolved scanning transmission X-ray microscopy to directly observe spin waves in magnonic permalloy waveguides with nanoscale resolution. Additionally, we demonstrate an approach for k-vector selective imaging to deconvolute overlapping modes in real space measurements. Thereby, we observe efficient excitation of symmetric and antisymmetric modes. The profiles of higher order modes that arise from sub-micron confinement are precisely mapped out and compared to analytical models. Thus, we lay a basis for the design of multimode spin wave transmission systems and demonstrate a general technique for k-specific microscopy that can also be used beyond the field of magnonics.
I. Introduction
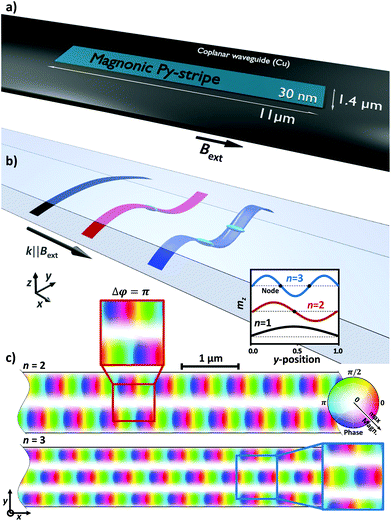
Magnons, which describe the quanta of spin waves, have been recently investigated in terms of new fundamental physics at the nanoscale and their potential for future data communication applications.1–8 Due to a bottleneck of CMOS transistor miniaturization, magnonics are increasingly discussed as a complementary technology.3,4,8 Futhermore, there are many interesting analogies to photonics, like guiding of propagating waves or evanescent wave phenomena.9–13 Especially, magnonic waveguides were discussed in literature revealing outstanding fundamental characteristics and useful properties regarding data transmission.4,10,14The equivalent to magnonic waveguides in photonics is the concept of single- and multimode propagation in fiber optics.15 Multimode propagation allows scalable transmission rates reached by various multiplexing techniques, e.g. amplitude, phase or wavelength multiplexing.16–18 However, in comparison to these photonic waveguides, the magnonic dispersion is highly anisotropic.19 Thus, the generation of a steady system and the manipulation of bands become more complicated. In literature, micromagnetic simulations and experiments have shown multiple applications of magnonic waveguides as majority gates, couplers or frequency filters.8,20–22 Furthermore, a spin wave spectrum analyzer that could be used for demultiplexing has been proposed.23
However, downscaling magnonic waveguides to the nanometer regime introduces different physics than in larger structures,24e.g. interference of lateral standing spin waves by spatial confinement leading to higher order modes has been predicted theoretically.25 Furthermore, Guslienko et al. already showed calculations of effective dipolar boundary conditions in a magnetic stripe geometry.26
Brächer et al. considered this fact by extending the classical spin wave dispersion relation to
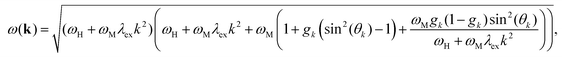 | (1) |
Assuming a fixed wavevector component k⊥ = n·π/weff along the width of the waveguide in eqn (1), a change in the component k‖ along the length of the waveguide results in a continuous variation of the angle θk. The effective width weff = w[p/(p − 2)] can be calculated by considering the pinning parameter p and the geometrical width w of the waveguide.26 With this approximation one can calculate the dispersion relation in Damon–Eshbach (DE, k⊥Bext) or backward-volume (BV, k‖Bext) geometry, where θDEk(k‖) = arctan(k‖/k⊥) and θBVk(k‖) = arctan(k⊥/k‖), respectively.25Bext represents the applied external field.
For higher modes, e.g. n = 2, a node in the middle of the waveguide with mz = 0 appears, as visualized in Fig. 1(b). This is also observed in micromagnetic simulations, shown in Fig. 1(c). Additionally, n = 3 is depicted revealing two nodes. These simulations predict that the lateral standing spin waves interfere with propagating magnons along the x-direction. Accordingly, excitation of symmetric and antisymmetric modes with a phase shift of Δφ = π should be observable which is visualized in the zoomed areas of the simulation in Fig. 1(c).
The experimental investigation of these simultaneous excited spin wave modes by one single driving frequency poses a problem to conventional measuring techniques like Kerr microscopy or Brillouin light scattering. The needed spatial and temporal resolution with the additional information of phase and amplitude is not accessible with these methods. Here, we report the direct spatially and temporally resolved observation of both symmetric and antisymmetric mode excitation in a magnonic permalloy (Py, Fe20Ni80) waveguide via global sinusoidal excitation. To deconvolve the excited higher order modes, we introduce an evaluation technique, which permits mode selective imaging with both amplitude and relative phase information. This direct imaging is achieved by time resolved scanning transmission X-ray microscopy (STXM) with magnetic X-ray circular dichroism (XMCD) contrast, that features the necessary spatial (<20 nm) and temporal (<40 ps) resolution.5,28–32 The evaluation technique paves the way not only for mode selective imaging in magnonic waveguides, but also for any kind of overlapping modes.
II. Results and discussion
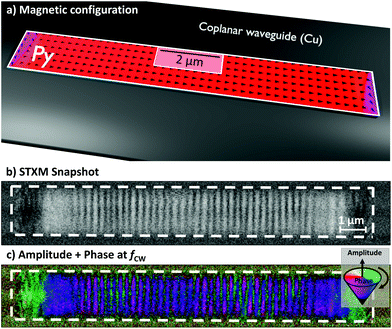
The magnonic waveguide consists of a simple slab of Py below a coplanar waveguide which is much larger than the stripe itself as illustrated in Fig. 1(a). An external field Bext is applied along the long axis of the waveguide, i.e. spin wave excitation in backward-volume geometry.For spin wave excitation, a global continuous wave (CW) radio frequency (RF) field BCW is applied. Inhomogeneities of the magnetization on the short edges caused by the demagnetizing field and the physical confinement lead to local reduction of the resonance frequency.33 The simulated magnetic configuration in Fig. 2(a) demonstrates this variation of the magnetization at the edges. By using a homogeneous RF field at fCW, spin waves can be excited at these regions resulting in directed emission within the waveguide. Interference from the left and right end leads to the formation of a standing spin wave pattern.
Fig. 2(b) shows the mz component measured by STXM during excitation with fCW = 4.2 GHz and Bext = 8 mT. After applying a temporal FFT algorithm, relative spin wave phase and amplitude information become accessible, which are encoded into color and brightness respectively (cf.Fig. 2(c)).34
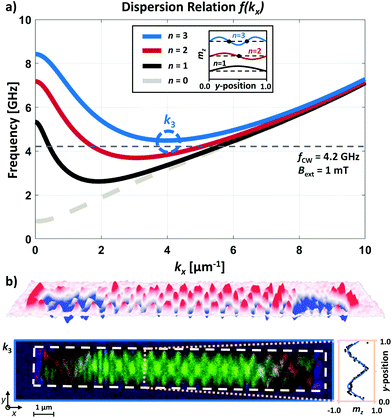
Subsequent application of a spatial FFT algorithm transforms the measurement into k-space shown in Fig. 3(b). Three peaks next to the DC-peak are clearly visible at k1a = 0.4 μm−1, k2 = 2.5 μm−1 and k1b = 5 μm−1. This indicates the efficient emission of three different waveguide modes. Fig. 3(a) shows the corresponding dispersion relation in x-direction, calculated using eqn (1) and θBVk(k‖). For comparison, the mode n = 0 represents the dispersion for an infinite thin film without lateral confinement. The following three modes n = 1, 2, 3 are depicted for the used waveguide geometry. The comparison between the measured k-space and the calculated dispersion relation shows perfect agreement. While the frequency fCW (dashed gray line) intersects with k1a and k1b, i.e. with the mode n = 1, k2 is located on the mode branch n = 2.
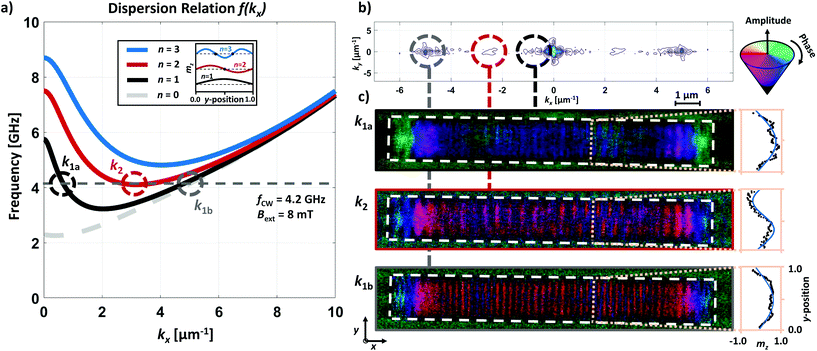 | ||
| Fig. 3 (a) Dispersion relation f(kx) of the magnonic waveguide. The mode n = 0 for an infinite thin film (dashed gray line) and the first three modes n = 1, 2, 3 (solid lines) of the waveguide are depicted. The continuous wave excitation at fCW = 4.2 GHz is indicated by the gray dashed line. The legend illustrates the theoretical standing spin waves with mz in lateral dimension. Three different modes are indicated by the dashed circles. (b) Resulting k-space of the two dimensional FFT of the image in Fig. 2(b). Three different modes become visible. (c) By emphasizing each peak separately, the corresponding mode profiles are accessible selectively. The plots next to the mode profiles show the mz cross sections indicated by the dashed line across the waveguide. The measured data (black dots) and the corresponding fits (blue line) are presented. | ||
To gain insights into the different mode profiles of the overlapping modes in Fig. 2(c), we emphasize each k-vector separately to highlight the related mode profile. Fig. 3(c) shows the resulting mode profiles of k1a, k1b and k2. The three insets next to the profiles reveal the lateral cross sections at the dashed line within the mode profiles, revealing very good agreement of the theoretical predicted mz profile (blue line) and the measured data (black dots).
In literature, RF antennas are usually being used for multiple mode excitation in waveguides which is crucial for the fundamental understanding of excitation and propagation characteristics for prospective applications.35,36 Due to a homogeneous RF field across the width of a waveguide, direct excitation of symmetric modes, i.e. n = 1, 3, 5, with respect to the central axis of the waveguide is permitted. Apart from that, antisymmetric modes cannot be directly excited by an oscillating RF field with a homogeneous RF field distribution. However, a translation symmetry break or a curved waveguide can convert symmetric into antisymmetric modes during wave propagation.35–37 Here, the width of the signal line is much larger compared to the waveguide width, thus, the distribution of the RF field BCW can be assumed homogeneous across the lateral dimension. Nevertheless, the mode profile of k2 reveals direct excitation of the antisymmetric mode n = 2 with a phase shift of Δφ = π. k1a and k1b show the expected symmetric mode profiles.
We assume that the excitation of antisymmetric modes, i.e. n = 2, 4, 6 in Fig. 3(c), can be attributed to the non-reciprocity of DE modes, that are mixed with BV modes to generate the higher-order modes discussed here.25 Unlike conventional RF antennas, where spin wave excitation is limited to a specific area, we use an antenna structure that is much larger than the magnonic waveguide itself. Thus, a quasi-homogeneous global RF field BCW is applied. This field not only excites BV spin waves from the short edges, but also DE spin waves from the long edges of the waveguide. While BV spin waves are volume waves and have reciprocal emission properties, DE waves are surface spin waves that show a significant difference in amplitude depending on their propagation direction.38 This non-reciprocity effect was described by Schneider et al. as non-trivial intermixing of excitation field components, the dynamic magnetization, and the RF susceptibility tensor in this geometry.38
To excite different modes selectively, the dispersion relation can be shifted to higher or lower frequencies by varying the external field Bext. Thus, the next higher order mode n = 3 (two nodes) becomes accessible at fCW = 4.2 GHz by decreasing the field to Bext = 1 mT. Fig. 4(a) shows the corresponding dispersion relation that features the n = 3 mode at k3 = 4 μm−1. The small mismatch between the calculated mode branch and the observation frequency is related to an experimental misalignment of the external field. Nevertheless, the mode profile in Fig. 4(b) shows two nodes across the width of the waveguide. Additionally, the lateral cross section fits the expected mz profile for n = 3 (cf.Fig. 4(a)). The three dimensional representation of the mz component above the mode profile nicely illustrates the two nodes and the related phase shifts of Δφ = π. In principle, the excitation of mode branch n = 3 can also be achieved by the variation of the excitation frequency fCW while a constant field Bext is applied.
In optical data communication, multimode fibres are the backbone of present data and network technology.15 Towards a possible application, the waveguide discussed here can be seen as the magnonic analogue of such a multimode fibre that transmits multiple data streams simultaneously which is crucial for achieving enhanced data rates. Additionally, well-known multiplexing techniques, e.g. phase and amplitude multiplexing,16,17 will play a major role for future data transmission via magnonic waveguides. The same principle also applies to the design of waveguides in magnonic transceivers or logic structures at the nanoscale. Thus, k-selective imaging will be vital to characterize multimode propagation and localization patterns within these structures.
Besides the utilization of mode selective imaging in waveguide scenarios, we want to emphasize the versatility of this evaluation method regarding further nanotechnological fields. The only requirement is a spatially resolved map of phase and amplitude which can be transformed into k-space. In consideration of that fact, multimode spin wave excitation, e.g. in vortex discs as magnonic emitter or magnonic whispering gallery modes (WGM) would be a possible application for mode selective.5,39 In addition, the photonic equivalent of WGMs as microresonators could also be a potential candidate to deconvolve overlapping mode numbers. WGMs are highly discussed, due to their extreme sensitivity regarding biosensing.40,41
III. Conclusion
We have shown direct real space observation of higher order spin wave modes in Py waveguides. Utilizing the ultimate resolution of STXM allowed us to image the nanoscale fine structure of these modes that arises from micron and sub-micron confinement. Thereby, we experimentally revealed the mode profiles up to the third order and the amplitude distribution with a resolution better than 100 nm.The experimental imaging of the spin wave modes was complemented by micromagnetic simulations and perfect agreement both with the simulation as well as the analytical theory was found. This agreement was not only found for the frequency response of the systems, but also extends to the microscopic mode profiles. Thus, we were able to validate the nanoscale accuracy of the present models and can confirm their applicability for design of minituarized magnonic systems.
Furthermore, we have demonstrated an efficient way to excite symmetric and antisymmetric spin wave modes at the same time. This is achieved by inducing non-reciprocal DE type modes from a pseudo-global RF field that form a standing wave on top of the propagating BV type modes. Thus, the structure shown here can be used as a simple implementation for inducing multi mode signals into a magnonic waveguide. This simultaneous excitation of higher order modes could pave the way for data multiplexing in magnonic systems. Especially as it is shown to be robust and easily tunable with field and frequency.
Finally, we demonstrated a general approach to deconvolute multiple overlapping modes. This type of k-vector selection allows for mode selective imaging with any real space technique. Thus, extending the capabilities of microscopy into an area that is otherwise only accessible by scattering techniques which often lack spatial information. We envision this approach to be useful beyond magnonics and magnetism, e.g. for investigation of plasmonic and photonics excitations.
IV. Methods
As a first step of e-beam lithography, the magnonic Py waveguide (l = 11 μm, w = 1.4 μm, d = 30 nm) was deposited on a silicon nitride membrane. Subsequently, the coplanar waveguide (copper) was fabricated. In doing so, the signal line was placed right on top of the Py waveguide (cf.Fig. 1(a)).Time resolved STXM measurement were performed at the MAXYMUS end station at the UE46-PGM2 beam line at the BESSY II synchrotron radiation facility. An internal magnetic in-plane field of up to 240 mT was applied using a set of four rotatable permanent magnets.42 The sample was illuminated by normal incident circular polarized X-rays at the L3-edge to maximize XMCD contrast.
After the original STXM measurement, the resulting movie consists of multiple frames in time. Thus, a three dimensional stack of images originates. To gain insights into the frequency domain, a FFT algorithm was used to transform each pixel of the image stack. The result is a second stack of images with the information of relative phase and amplitude for the corresponding frequency (cf.Fig. 2(c)). The map of phase and amplitude at fCW was transformed by a two dimensional FFT to reveal the k-space. Further description of the evaluation steps can be found elsewhere.34
For the calculation of the dispersion relation with eqn (1), the saturation magnetization Ms = 660 kA m−1, the exchange constant Aex = 13 pJ m−1, the external fields Bext = 8 and 1 mT, and the gyromagnetic ratio γ = 176 rad ns−1 T−1. Micromagnetic simulations were performed using MuMax3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43 with the same parameter set.
43 with the same parameter set.
Author contributions
J.G., M.K., J.D. and P.K. conceived the study. F.L., H.G. and P.K. prepared the samples. N.T., F.G., J.F., M.W. and J.G. performed the measurements. N.T., F.G. and J.G. analyzed the data. P.G. and M.K. performed and analyzed the simulations. N.T. and J.G. wrote the manuscript. All authors commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Michael Bechtel for support during beam times. We thank HZB for the allocation of synchrotron radiation beamtime. N. T., F. G., M. W. and J. G. acknowledge the financial support by the Federal Ministry of Education and Research of Germany in the framework of DynaMAX (project number 05K18EYA). Open Access funding provided by the Max Planck Society.References
- B. Lenk, H. Ulrichs, F. Garbs and M. Münzenberg, The building blocks of magnonics, Phys. Rep., 2011, 507(4–5), 107–136 CrossRef.
- S. Neusser and D. Grundler, Magnonics: Spin Waves on the Nanoscale, Adv. Mater., 2009, 21(28), 2927–2932 CrossRef CAS.
- A. V. Chumak, A. A. Serga and B. Hillebrands, Magnon transistor for all-magnon data processing, Nat. Commun., 2014, 5, 4700 CrossRef CAS PubMed.
- A. V. Chumak, V. I. Vasyuchka, A. A. Serga and B. Hillebrands, Magnon spintronics, Nat. Phys., 2015, 11(6), 453–461 Search PubMed.
- S. Wintz, V. Tiberkevich, M. Weigand, J. Raabe, J. Lindner, A. Erbe, A. Slavin and J. Fassbender, Magnetic vortex cores as tunable spin-wave emitters, Nat. Nanotechnol., 2016, 11(11), 948–953 CrossRef CAS PubMed.
- F. Ma, Y. Zhou, H. B. Braun and W. S. Lew, Skyrmion-Based Dynamic Magnonic Crystal, Nano Lett., 2015, 15(6), 4029–4036 CrossRef CAS PubMed.
- A. V. Chumak, A. A. Serga and B. Hillebrands, Magnonic crystals for data processing, J. Phys. D: Appl. Phys., 2017, 50(24), 244001 CrossRef.
- A. Khitun, M. Bao and K. L. Wang, Magnonic logic circuits, J. Phys. D: Appl. Phys., 2010, 43(26), 264005 CrossRef.
- V. E. Demidov, J. Jersch, S. O. Demokritov, K. Rott, P. Krzysteczko and G. Reiss, Transformation of propagating spin-wave modes in microscopic waveguides with variable width, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(5), 054417 CrossRef.
- A. V. Sadovnikov, C. S. Davies, V. V. Kruglyak, D. V. Romanenko, S. V. Grishin, E. N. Beginin, Y. P. Sharaevskii and S. A. Nikitov, Spin wave propagation in a uniformly biased curved magnonic waveguide, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 96(6), 060401 CrossRef.
- M. Collet, O. Gladii, M. Evelt, V. Bessonov, L. Soumah, P. Bortolotti, S. O. Demokritov, Y. Henry, V. Cros, M. Bailleul, V. E. Demidov and A. Anane, Spin-wave propagation in ultra-thin YIG based waveguides, Appl. Phys. Lett., 2017, 110(9), 092408 CrossRef.
- V. E. Demidov, M. P. Kostylev, K. Rott, J. Münchenberger, G. Reiss and S. O. Demokritov, Excitation of short-wavelength spin waves in magnonic waveguides, Appl. Phys. Lett., 2011, 99(8), 082507 CrossRef.
- P. Pirro, T. Brächer, A. V. Chumak, B. Lägel, C. Dubs, O. Surzhenko, P. Görnert, B. Leven and B. Hillebrands, Spin-wave excitation and propagation in microstructured waveguides of yttrium iron garnet/Pt bilayers, Appl. Phys. Lett., 2014, 104(1), 012402 CrossRef.
- V. E. Demidov, S. O. Demokritov, K. Rott, P. Krzysteczko and G. Reiss, Mode interference and periodic self-focusing of spin waves in permalloy microstripes, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(6), 064406 CrossRef.
- E. Hecht, Optics, Addison-Wesley, 2002 Search PubMed.
- M. L. F. Abbade, E. A. M. Fagotto, R. S. Braga, I. E. Fonseca, E. Moschim and F. R. Barbosa, Optical amplitude multiplexing through four-wave mixing in optical fibers, IEEE Photonics Technol. Lett., 2005, 17(1), 151–153 Search PubMed.
- L. Guo-Wei, K. S. Abedin and T. Miyazaki, All-Optical RZ-DPSK WDM to RZ-DQPSK Phase Multiplexing Using Four-Wave Mixing in Highly Nonlinear Fiber, IEEE Photonics Technol. Lett., 2007, 19(21), 1699–1701 Search PubMed.
- M. Koshiba, Wavelength division multiplexing and demultiplexing with photonic crystal waveguide couplers, J. Lightwave Technol., 2001, 19(12), 1970 CrossRef.
- B. A. Kalinikos and A. N. Slavin, Theory of dipole-exchange spin wave spectrum for ferromagnetic films with mixed exchange boundary conditions, J. Phys. C: Solid State Phys., 1986, 19(35), 7013–7033 CrossRef.
- S. Klingler, P. Pirro, T. Brächer, B. Leven, B. Hillebrands and A. V. Chumak, Design of a spin-wave majority gate employing mode selection, Appl. Phys. Lett., 2014, 105(15), 152410 CrossRef.
- Q. Wang, P. Pirro, R. Verba, A. Slavin, B. Hillebrands and A. V. Chumak, Reconfigurable nanoscale spin-wave directional coupler, Sci. Adv., 2018, 4(1), e1701517 CrossRef PubMed.
- A. V. Sadovnikov, S. A. Odintsov, E. N. Beginin, S. E. Sheshukova, Y. P. Sharaevskii and S. A. Nikitov, Spin-Wave Switching in the Side-Coupled Magnonic Stripes, IEEE Trans. Magn., 2017, 53(11), 1–4 Search PubMed.
- A. Papp, W. Porod, A. I. Csurgay and G. Csaba, Nanoscale spectrum analyzer based on spin-wave interference, Sci. Rep., 2017, 7(1), 9245 CrossRef PubMed.
- Q. Wang, B. Heinz, R. Verba, M. Kewenig, P. Pirro, M. Schneider, T. Meyer, B. Lägel, C. Dubs, T. Brächer and A. V. Chumak, Spin Pinning and Spin-Wave Dispersion in Nanoscopic Ferromagnetic Waveguides, Phys. Rev. Lett., 2019, 122(24), 247202 CrossRef CAS PubMed.
- T. Brächer, P. Pirro and B. Hillebrands, Parallel pumping for magnon spintronics: Amplification and manipulation of magnon spin currents on the micron-scale, Phys. Rep., 2017, 699(Supplement C), 1–34 CrossRef.
- K. Y. Guslienko, S. O. Demokritov, B. Hillebrands and A. N. Slavin, Effective dipolar boundary conditions for dynamic magnetization in thin magnetic stripes, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(13), 132402 CrossRef.
- P. Krivosik and C. E. Patton, Hamiltonian formulation of nonlinear spin-wave dynamics: Theory and applications, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(18), 184428 CrossRef.
- M. Weigand, Realization of a new magnetic scanning X-ray microscope and investigation of Landau structures under pulsed field excitation, Cuvillier Verlag, 2015 Search PubMed.
- J. Gräfe, F. Haering, T. Tietze, P. Audehm, M. Weigand, U. Wiedwald, P. Ziemann, P. Gawronski, G. Schutz and E. J. Goering, Perpendicular magnetisation from in-plane fields in nano-scaled antidot lattices, Nanotechnology, 2015, 26(22), 225203 CrossRef PubMed.
- S. Woo, K. Litzius, B. Krüger, M.-Y. Im, L. Caretta, K. Richter, M. Mann, A. Krone, R. M. Reeve and M. Weigand, Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets, Nat. Mater., 2016, 15(5), 501 CrossRef CAS PubMed.
- M. Kammerer, M. Weigand, M. Curcic, M. Noske, M. Sproll, A. Vansteenkiste, B. Van Waeyenberge, H. Stoll, G. Woltersdorf, C. H. Back and G. Schuetz, Magnetic vortex core reversal by excitation of spin waves, Nat. Commun., 2011, 2, 279 CrossRef PubMed.
- K. Litzius, I. Lemesh, B. Krüger, P. Bassirian, L. Caretta, K. Richter, F. Büttner, K. Sato, O. A. Tretiakov, J. Förster, R. M. Reeve, M. Weigand, I. Bykova, H. Stoll, G. Schütz, G. S. D. Beach and M. Kläui, Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy, Nat. Phys., 2016, 13, 170 Search PubMed.
- F. B. Mushenok, R. Dost, C. S. Davies, D. A. Allwood, B. J. Inkson, G. Hrkac and V. V. Kruglyak, Broadband conversion of microwaves into propagating spin waves in patterned magnetic structures, Appl. Phys. Lett., 2017, 111(4), 042404 CrossRef.
- F. Groß, N. Träger, J. Förster, M. Weigand, G. Schütz and J. Gräfe, Nanoscale detection of spin wave deflection angles in permalloy, Appl. Phys. Lett., 2019, 114(1), 012406 CrossRef.
- P. Clausen, K. Vogt, H. Schultheiss, S. Schäfer, B. Obry, G. Wolf, P. Pirro, B. Leven and B. Hillebrands, Mode conversion by symmetry breaking of propagating spin waves, Appl. Phys. Lett., 2011, 99(16), 162505 CrossRef.
- X. Xing, W. Yin and Z. Wang, Excitation of antisymmetric modes and modulated propagation of spin waves in bent magnonic waveguides, J. Phys. D: Appl. Phys., 2015, 48(21), 215004 CrossRef.
- S. Mieszczak, O. Busel, P. Gruszecki, A. N. Kuchko, J. W. Kłos and M. Krawczyk, An anomalous refraction of spin waves as a way to guide signals in curved magnonic multimode waveguides, 2020, arXiv preprint arXiv:2001.11356.
- T. Schneider, A. A. Serga, T. Neumann, B. Hillebrands and M. P. Kostylev, Phase reciprocity of spin-wave excitation by a microstrip antenna, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(21), 214411 CrossRef.
- K. Schultheiss, R. Verba, F. Wehrmann, K. Wagner, L. Körber, T. Hula, T. Hache, A. Kákay, A. A. Awad, V. Tiberkevich, A. N. Slavin, J. Fassbender and H. Schultheiss, Excitation of Whispering Gallery Magnons in a Magnetic Vortex, Phys. Rev. Lett., 2019, 122(9), 097202 CrossRef CAS PubMed.
- F. Vollmer and S. Arnold, Whispering-gallery-mode biosensing: label-free detection down to single molecules, Nat. Methods, 2008, 5, 591 CrossRef CAS PubMed.
- J. Zhu, S. K. Özdemir, H. Yilmaz, B. Peng, M. Dong, M. Tomes, T. Carmon and L. Yang, Interfacing whispering-gallery microresonators and free space light with cavity enhanced Rayleigh scattering, Sci. Rep., 2014, 4, 6396 CrossRef CAS PubMed.
- D. Nolle, M. Weigand, P. Audehm, E. Goering, U. Wiesemann, C. Wolter, E. Nolle and G. Schutz, Note: unique characterization possibilities in the ultra high vacuum scanning transmission X-ray microscope (UHV-STXM) “MAXYMUS” using a rotatable permanent magnetic field up to 0.22 T, Rev. Sci. Instrum., 2012, 83(4), 046112 CrossRef CAS PubMed.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. V. Waeyenberge, The design and verification of MuMax3, AIP Adv., 2014, 4(10), 107133 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |