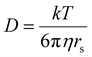A [Pd₂L₄]⁴⁺ cage complex for n-octyl-β-D-glycoside recognition

Abstract

The cage complex [Pd₂9₄]⁴⁺ (3′) binds n-octyl glycosides in DCM/DMSO (9 : 1) solution with K_a ≈ 51 M⁻¹ for n-Oct-β-D-Glc and K_a ≈ 29 M⁻¹ for n-Oct-β-D-Gal.

---

Carbohydrates are Nature's most abundant and versatile molecules.¹ Several diseases have been linked to processes involving carbohydrates (e.g. diabetes, infection, and cancer metastasis).² Many other regular processes are also mediated by carbohydrate molecules, including fertilization,³ neuronal development,⁴ hormonal activities,⁵ immune surveillance⁶ and inflammatory responses.⁷ Understanding and intervening in these processes are therefore exploited in medicinal therapies, glycobiology, and biomedical research in general.⁸ Such research efforts require strategies to selectively bind carbohydrates. In Nature carbohydrates are bound by using lectins, which generally have relatively low affinities for their target monosaccharides (K_a ∼ 10²–10³ M⁻¹)⁹ and are often rather non-selective. An inspirational exception is the affinity of E. coli galactose chemoreceptor protein for glucose (K_a = 10⁶–10⁷ M⁻¹).¹⁰ The structure of the binding site of this complex is shown in Fig. 1a (2GBP)¹¹ and reveals a high degree of interaction complementarity. Two aromatic residues (Trp and Phe) sandwich the flat glucose molecule with hydrophobic CH⋯π interactions¹² and an array of polar residues complement the hydroxyl exterior of glucose by hydrogen bonding. This interaction complementarity has been mimicked by artificial carbohydrate binding molecules.¹³ One example is the macrocyle 1 shown in Fig. 1b, which comprises pyrenyl surfaces for CH⋯π interactions and polar isophthalamide spacers for hydrogen bonding.^13a One drawback of such covalent constructs, however, is that their synthetic routes culminate in one (or more) macrocyclization step(s) that rarely exceed ∼20%.^13a,c,14 This drawback can in principle be remedied if the cyclization is accomplished by use of dynamic bonds, such as coordination bonds between a ligand (L) and a transition metal (M). Interestingly, [M₂L₄]⁴⁺ complexes in which M is a square planar d⁸ metal (e.g. Pd²⁺ or Pt²⁺) and L is a dipyridyl ligand have been known for more than 20 years and generally have a fairly small cavity.¹⁵ While such [M₂L₄]⁴⁺ complexes are typically filled with counter anions,¹⁶ complex 2 shown in Fig. 1c was recently reported to bind D-sucrose using CH⋯π interactions.¹⁷

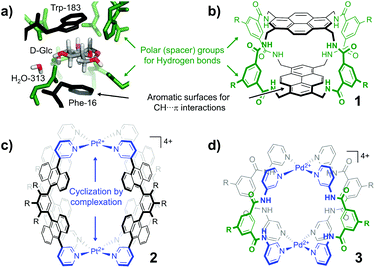Fig. 1 Cage design for binding carbohydrates: (a) Galactose lectin (2GBP) with D-glucose.¹¹ (b) Covalent macrocycle 1.^13a (c) Coordination cage 2 with aromatic (hydrophobic) spacers.¹⁷ (d) Coordination cage 3 with polar spacers (also used in this work). R = a group that can be used to control solubility.

We envisioned that the polar isophthalamide spacers employed in 1 could be combined with the easy synthesis of [M₂L₄]⁴⁺ type complexes such as 2. Indeed, structures like 3 shown in Fig. 1d have been reported, although they were mainly studied in the solid state and are reportedly only sparingly soluble in solvents such as N,N-dimethylformamide (DMF) and dimethyl sulfoxide (DMSO).¹⁸ Herein, we report a version of cage 3 (cage 3′) that is soluble in apolar media and show that the cavity of 3′ binds to n-octyl glycosides. This facile solubilisation was realized by installation of an aliphatic dendritic side group (R′), as is shown in Scheme 1.

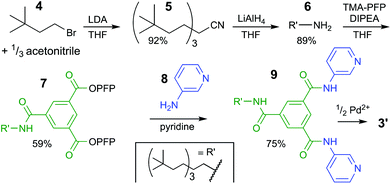Scheme 1 Synthetic pathway to bis-pyridyl ligand 9. See ESI† for experimental details and full charachterizations. LDA = lithium diisopropylamide, THF = tetrahydrofuran, TMA-PFP = the pentafluoro-phenyl(PFP) ester of trimesic acid, DIPEA = N,N-diisopropylethylamine.

The synthesis of the solubilizing group started with triple alkylation of acetonitrile with 3,3-dimethyl-1-bromobutane (4), which was obtained by bromination of the commercial available alcohol. The resulting nitrile 5 was reduced to amine 6, which was used to displaced one pentafluorophenyl (PFP) on 1,3,5-benzenetricarboxylic acid tris-PFP ester to form intermediate 7. The resulting compound was treated with a six-fold excess of 3-aminopyridine (8) forming the desired ligand 9 in 75% isolated yield (see section S2† for full details).

The intended [Pd₂9₄]²⁺ caging complex was readily prepared in DMSO-d₆ as is detailed on pages 22–30 of the ESI.†‡ To study this cage and its binding properties in a less competitive matrix, we probed if complex synthesis was also possible in a CD₂Cl₂/DMSO-d₆ (9 : 1) solvent mixture.

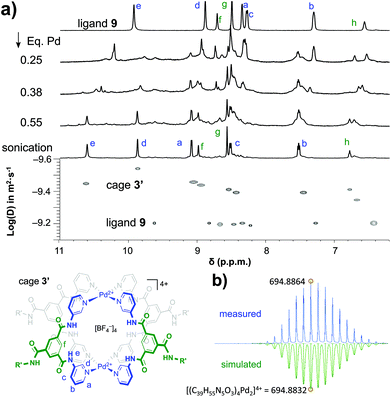
As is shown in Fig. 2a, the stepwise addition of [Pd(MeCN)₄](BF₄)₂ to ligand 9 in this mixture resulted in significant downfield shifts and signal broadening of the ¹H-NMR signals in the aromatic region of 9 (∼7–10 ppm). No more changes were observed after addition of 0.55 equivalents of Pd. Sonication of this sample resulted in a well-defined spectrum of a major species in which all protons originating from 9 can be identified and are consistent with cage structure[Pd₂9₄]⁴⁺ (i.e.3′). The large downfield shifts of protons such as a (8.35 → 9.09 ppm) and d (8.89 → 9.87 ppm) are highly indicative of pyridyl-Pd coordination.^18a,c The DOSY NMR of this sample is shown in the bottom of Fig. 2a, and reveals that the diffusion constant (D) of the major species is substantially smaller than that of ligand 9 alone (log(D) = −9.42 vs. −9.21 for 9). Applying the Stokes–Einstein equation§ to the measured log(D) of −9.42 predicts a radius of about 13.9 Å. This radius is in line with an estimated mean radius of 17.5 Å of a model 3′, assuming the complex has an overall oblate spheroid shape (see Fig. S65†). Moreover, as is depicted in Fig. 2b, the isotope distribution and highest intensity isotopic mass of the major species measured in the final solution is in agreement with a 2 : 4 Pd : 9 ratio expected for [Pd₂9₄]⁴⁺ (m/z = 694.8864, highlighted in yellow).

Fig. 2 Formation and characterization of 3′. (a) Top: NMR data of formation of 3′ from ligand 9 by stepwise addition of [Pd₂(MeCN)₄](BF₄)₂; bottom: comparison of DOSY NMR of 3′and 9. (b) CSI HRMS isotope distribution of 3′ (4 + species) with indicated highest isotopic mass (measured, top and simulated, bottom).

The binding of cage 3′ for n-oct-β-D-Glc (10) and n-oct-β-D-Gal (11) was investigated by ¹H-NMR titration experiments in CD₂Cl₂/DMSO-d₆ (9 : 1). Selected spectra of such a titration with 10 are shown in the left-hand side of Fig. 3 (see Fig. S51 and S59† for complete spectra of titrations with 10 and 11). With increasing concentration of glucoside 10, all resonances of 3′ in the aromatic region (∼7–11 ppm) broadened and shifted. The resonances for the inwards oriented H-atoms labelled d (9.9), e (10.7) and f (9.0) broaden to an extend that they could barely be detected at 115 mM concentration of 10. In contrast, the signals of H-atoms a (9.1) and g (8.6) remain much sharper throughout the titration and these data can be fitted to a 1 : 1 model of 3′ : 10. As is shown in the right-hand side of Fig. 3, both fits are consistent with an association constant (K_a) of 51.1 ± 1.8 M⁻¹.

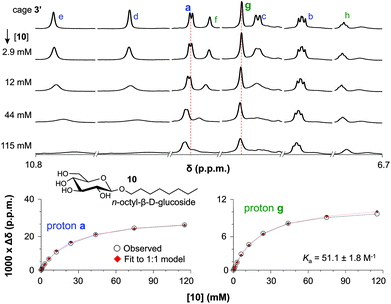Fig. 3 (a) Titration with OctGlc. (b) Plot experimental vs. calculated data for 1 : 1 binding for proton a. (c) Plot experimental vs. calculated data for 1 : 1 binding for proton g.

A similar titration with n-oct-β-D-Gal (11) gave comparable observations, leading to a K_a of 29.1 ± 4.8 M⁻¹ (Fig. S59 and S61†). This lower binding affinity of 3′ for 11 can be rationalized by the axial hydroxyl group in the galactoside, presumably leading to a worse fit of 11 inside 3′.

To probe if, as these data suggest, a simple 1 : 1 [3′⊂10]⁴⁺ complex had formed, this sample was investigated further. The DOSY-NMR spectrum of the sample (see Fig. S56†) gave a similar diffusion constant as pure cage 3′ (Fig. 2a), indicating that the cage is still intact. Moreover, as can be seen in Fig. 4a, a cold spray ionisation high resolution mass spectroscopic analysis (CRS-HRMS) revealed a species with a mass and isotope distribution consistent with the anticipated 1 : 1 molar ratio of [3′⊂10]⁴⁺ (m/z = 767.9344). Shown in Fig. 4b is the full ¹H-NMR spectrum of the sample (top), together with several of 1D nuclear Overhauser effect (nOe) spectra. As can be seen in this figure, irradiation of the outwards pointing CH b did not result in an nOe signal in the carbohydrate region (grey background), while irradiation of the inwards pointing CH d clearly did. Irradiation of the amidic NH e gave a much smaller nOe with 10, presumably because H's e are further away from the CH protons of 10. Interestingly, the {¹H–¹⁹F}-HOESY spectrum of pure 3′(BF₄⁻)₄ shows clear nOes between BF₄⁻ and the inwards pointing e, d and f (see Fig. S66a†). These {¹H–¹⁹F}-HOESY signals could not be observed in the solution after addition of 10 (see Fig. S66b†).

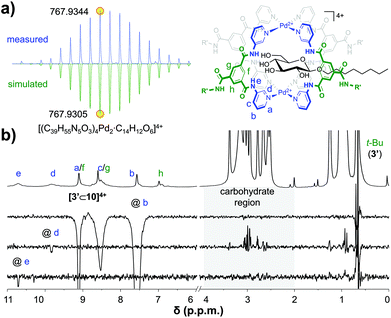Fig. 4 CSI HRMS isotope distribution of [3′⊂10]⁴⁺with indicated monoisotopic mass (measured, top and simulated, bottom) (a) and 1D selective nOes of [3′⊂10]⁴⁺ with t_m = 500 ms (b). See Fig. S60† for full mass spectrum, Fig. S58† for more nOe spectra, and see Fig. S59† for a plot with linear fit of peak intensity vs. t_m in the region 50–700 ms.

All the above data indicate the formation of a 1 : 1 [3′⊂10]⁴⁺ complex where glucoside 10 resides within the cavity of 3′ after replacing the BF₄⁻ counter anions. The binding motif of [3′⊂10]⁴⁺ was modelled starting from a crystal structures of 3 ^18a,b and our nOe data that show that the CH protons of 10 are closest to the inwards pointing pyridyl protons d.¶

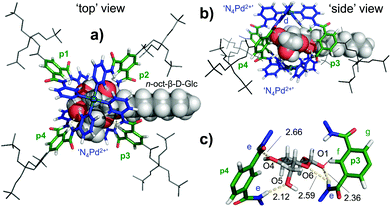Fig. 5 Molecular model of [3′⊂10]⁴⁺obtained by a combined conformational search (MMFF) and DFT geometry optimization of the core structure with (ωB97X-D/6-31G*) as seen from the ‘top’ (a) or the ‘side’ (b) of the complex (see note || in text). In (c) a zoom-in of the hydrogen bonding pattern is presented. The average of the eight shortest d-CH⋯HC(10) distances is 2.59 Å, while this is 3.65 Å for the eight shortest e-NH⋯HC(10) distances. See Table S3† for atomic coordinates.

As can be seen in the ‘top’ and ‘side’ views of the model depicted in Fig. 5, 10 is positioned between the two N₄Pd²⁺ centres (blue) and is surrounded by the four polar spacer groups of 3′ (p1–p4, green). From these views, it is also clear that the CH protons of 10 are closest to the pyridyl protons d, which is consistent with the strongest nOes observed with d (Fig. 4b).

Indeed, the average of the eight shortest d-CH⋯HC(10) distances is 2.59 Å, while this is 3.65 Å for the eight shortest e-NH⋯HC(10) distances (only very weak nOe observes, see Fig. 4b). As can be seen from Fig. 5c, glucoside 10 establishes a total of four hydrogen bonds in this model, but only involving two out of four polar spacers; p3 (e⋯O1 and e⋯O6) and p4 (e⋯O4 and e⋯O5). The model thus suggests that the cavity in 3′ is somewhat too large to fully encapsulate a glucoside such as 10 by hydrogen bonding. This in turn might rationalize the moderate binding affinity of 3′ for glucoside 10 (K_a ≈ 51 M⁻¹). There are also several weaker interactions between the inwards pointing pyridyl hydrogens d, and some hydroxyl O-atom which likely further stabilize the complex (shortest is 2.46 Å with O4). Such interactions have been observed as the major binding interaction in similar M₂L₄ complexes that do not have the much more acidic amide NH protons present in 3′.¹⁹

In conclusion, a new building block (9) is reported that forms a self-assembled molecular cage (3′) in the presence of Pd²⁺. The cage has the proper size and functional groups to bind n-oct-β-D-Glc (10) with a K_a of 51 M⁻¹ or n-oct-β-D-Gal (11) with 29 M⁻¹. We consider these relatively low affinities as a promising first step in establishing the principle that M₂L₄-like cages with a H-bonding interior such as 3′ can bind carbohydrates in very competitive media. As such, one can actually consider these affinities as significant in the CD₂Cl₂/DMSO-d₆ (9 : 1) solvent used. It is known that DMSO is one of the most competitive solvents for carbohydrate recognition⁹ and the first reported covalently-assembled cage for carbohydrate binding in a competitive medium (a biphenyl analogue of 1) has an affinity (K_a) of merely 4.6 M⁻¹ for D-glucose in water.²⁰ The ease with which carbohydrate binders such as 3′ can be prepared bodes well for their further development. We thus anticipate that future studies will unveil structures with improved affinities and selectivity.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was financially supported by the Netherlands Organisation for Scientific Research (NWO) with VIDI grant number 723.015.006.

Notes and references

1. D. Voet and J. G. Voet, Biochemistry, John Wiley and Sons, New York, 4th edn, 2011.
2. (a) H. J. Gabius, H. C. Siebert, S. Andre, J. Jimenez-Barbero and H. Rudiger, Chem. Biochem., 2004, 5, 740–764; (b) C. A. Aarnoudse, J. J. G. Vallejo, E. Saeland and Y. van Kooyk, Curr. Opin. Immunol, 2006, 18, 105–111; (c) C. R. Bertozzi and L. L. Kiessling, Science, 2001, 291, 2357–2364; (d) B. Wang and G. J. Boons, Carbohydrate Recognition: Biological Problems, Methods, and Applications, John Wiley & Sons Ltd., New Jersey, 2011; (e) H. J. Gabius, The Sugar Code: Fundamentals of Glycosciences, Wiley-VCH, Weinheim, 2009; (f) K. S. Lau and J. W. Dennis, Glycobiology, 2008, 18, 750–760; (g) D. Solis, N. V. Bovin, A. P. Davis, J. Jimenez-Barbero, A. Romero, R. Roy, K. Smetana and H. J. Gabius, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 186–235.
3. (a) D. J. Miller, M. B. Macek and B. D. Shur, Nature, 1992, 357, 589–593; (b) W. J. Snell and J. M. White, Cell, 1996, 85, 629–637.
4. H. E. Murrey and L. C. Hsieh-Wilson, Chem. Rev., 2008, 108, 1708–1731.
5. G. Caltabiano, M. Campillo, A. De Leener, G. Smits, G. Vassart, S. Costagliola and L. Pardo, Cell. Mol. Life Sci., 2008, 65, 2484–2492.
6. E. I. Buzas, B. Gyorgy, M. Pasztoi, I. Jelinek, A. Falus and H.-J. Gabius, Autoimmunity, 2006, 39, 691–704.
7. D. A. Calarese, C. N. Scanlan, M. B. Zwick, S. Deechongkit, Y. Mimura, R. Kunert, P. Zhu, M. R. Wormald, R. L. Stanfield, K. H. Roux, J. W. Kelly, P. M. Rudd, R. A. Dwek, H. Katinger, D. R. Burton and I. A. Wilson, Science, 2003, 300, 2065–2071.
8. (a) R. D. Astronomo and D. R. Burton, Nat. Rev. Drug Discovery, 2010, 9, 308–324; (b) S. Jin, Y. Cheng, S. Reid, M. Li and B. Wang, Med. Res. Rev., 2010, 30, 171–257; (c) J. Balzarini, Nat. Rev. Microbiol., 2007, 5, 583–597; (d) Y. Nakagawa, T. Doi, T. Taketani, K. Takegoshi, Y. Igarashi and Y. Ito, Chem. – Eur. J., 2013, 19, 10516–10525; (e) B. Ernst and J. L. Magnani, Nat. Rev. Drug Discovery, 2009, 8, 661–677; (f) T. J. Boltje, T. Buskas and G.-J. Boons, Nat. Chem., 2009, 1, 611–622; (g) P. H. Seeberger and D. B. Werz, Nat. Rev. Drug Discovery, 2005, 4, 751–763.
9. E. J. Toone, Curr. Opin. Struct. Biol., 1994, 4, 719–728.
10. (a) N. K. Vyas, M. N. Vyas and F. A. Quiocho, Science, 1988, 242, 1290–1295; (b) F. A. Quiocho, Pure Appl. Chem., 1989, 61, 1293–1306.
11. A. R. Kolatkar and W. I. Weis, J. Biol. Chem., 1996, 271, 6679–6685.
12. K. L. Hudson, G. J. Bartlett, R. C. Diehl, J. Agirre, T. Gallagher, L. L. Kiessling and D. N. Woolfson, J. Am. Chem. Soc., 2015, 137, 15152–15160.
13. (a) P. Rios, T. S. Carter, T. J. Mooibroek, M. P. Crump, M. Lisbjerg, M. Pittelkow, N. T. Supekar, G.-J. Boons and A. P. Davis, Angew. Chem., Int. Ed., 2016, 55, 3387–3392; (b) P. Stewart, C. M. Renney, T. J. Mooibroek, S. Ferheen and A. P. Davis, Chem. Commun., 2018, 54, 8649–8652; (c) R. A. Tromans, T. S. Carter, L. Chabanne, M. P. Crump, H. Y. Li, J. V. Matlock, M. G. Orchard and A. P. Davis, Nat. Chem., 2019, 11, 52–56; (d) N. Chandramouli, Y. Ferrand, G. Lautrette, B. Kauffmann, C. D. Mackereth, M. Laguerre, D. Dubreuil and I. Huc, Nat. Chem., 2015, 7, 334–341; (e) P. Mateus, B. Wicher, Y. Ferrand and I. Huc, Chem. Commun., 2018, 54, 5078–5081; (f) O. Francesconi, F. Cicero, C. Nativi and S. Roelens, ChemPhysChem, 2020, 21, 257–262; (g) O. Francesconi, M. Martinucci, L. Badii, C. Nativi and S. Roelens, Chem. – Eur. J., 2018, 24, 6828–6836.
14. (a) A. P. Davis and R. S. Wareham, Angew. Chem., Int. Ed., 1998, 37, 2270–2273; (b) T. J. Mooibroek, J. M. Casas-Solvas, R. L. Harniman, C. M. Renney, T. S. Carter, M. P. Crump and A. P. Davis, Nat. Chem., 2015, 8, 69–74; (c) C. Ke, H. Destecroix, M. P. Crump and A. P. Davis, Nat. Chem., 2012, 4, 718–723.
15. (a) D. A. McMorran and P. J. Steel, Angew. Chem., Int. Ed., 1998, 37, 3295–3297; (b) M. Han, D. M. Engelhard and G. H. Clever, Chem. Soc. Rev., 2014, 43, 1848–1860.
16. (a) S. Freye, J. Hey, A. Torras-Galan, D. Stalke, R. Herbst-Irmer, M. John and G. H. Clever, Angew. Chem., Int. Ed., 2012, 51, 2191–2194; (b) A. V. Zhukhovitskiy, M. Z. Zhong, E. G. Keeler, V. K. Michaelis, J. E. P. Sun, M. J. A. Hore, D. J. Pochan, R. G. Griffin, A. P. Willard and J. A. Johnson, Nat. Chem., 2016, 8, 33–41.
17. M. Yamashina, M. Akita, T. Hasegawa, S. Hayashi and M. Yoshizawa, Sci. Adv., 2017, 3, 6.
18. (a) N. L. S. Yue, D. J. Eisler, M. C. Jennings and R. J. Puddephatt, Inorg. Chem., 2004, 43, 7671–7681; (b) N. Yue, Z. Q. Qin, M. C. Jennings, D. J. Eisler and R. J. Puddephatt, Inorg. Chem. Commun., 2003, 6, 1269–1271; (c) N. L. S. Yue, M. C. Jennings and R. J. Puddephatt, Inorg. Chim. Acta, 2016, 445, 37–45.
19. (a) T. A. Young, V. Marti-Centelles, J. Z. Wang, P. J. Lusby and F. Duarte, J. Am. Chem. Soc., 2020, 142, 1300–1310; (b) D. Preston, K. F. White, J. E. M. Lewis, R. A. S. Vasdev, B. F. Abrahams and J. D. Crowley, Chem. – Eur. J., 2017, 23, 10559–10567; (c) D. P. August, G. S. Nichol and P. J. Lusby, Angew. Chem., Int. Ed., 2016, 55, 15022–15026; (d) L. S. Lisboa, J. A. Findlay, L. J. Wright, C. G. Hartinger and J. D. Crowley, Angew. Chem., Int. Ed., 2020, 59, 2–9.
20. E. Klein, M. P. Crump and A. P. Davis, Angew. Chem., Int. Ed., 2005, 44, 298–302.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthetic procedures, details of NMR and mass measurements, spectra and binding analysis curves. See DOI: 10.1039/d0ob01081b

‡ Complex formation in DMSO-d₆ also led to a major species, although many other smaller peaks were also clearly visible (Fig. S27†). These peaks reversibly disappeared when the sample was heated to 80 °C (see Fig. S29† for a VT study), indicating that the additional peaks originate from conformational flexibility in 3′.

§ Stokes –Einstein equation:
wherein D is the molar diffusion coefficient (assuming a spherical size of the molecule), k is the Boltzman constant, T is the temperature in Kelvin, μ the viscosity of the liquid and r_s the hydrodynamic radius of the molecule. See section S1 of ESI for further details

¶ An initial model of [3′⊂10]⁴⁺ was subjected to a conformational search with the Merck Molecular Force Field MMFF (including the dendrimers), leading to one major binding conformer. The binding pocket of this structure was optimized with DFT/ωB97X-D/6-31G* leading to the core structure depicted in Fig. 5 (i.e., as depicted in Fig. 2 with R′ = CH₃). All the atoms in this structure were frozen, the dendrimers were drawn again and the geometry of the resulting [3′⊂10]⁴⁺ structure was allowed optimize with MMFF to yield the final model used (while keeping the DFT optimized core-structure frozen). Calculations were done with Spartan 2016.

|| An initial model of [3′⊂10]⁴⁺ was subjected to a conformational search with the Merck Molecular Force Field MMFF (including the dendrimers), leading to one major binding conformer. The binding pocket of this structure was optimized with DFT/ωB97X-D/6-31G* leading to the core structure depicted in Fig. 5 (i.e., as depicted in Fig. 2 with R′ = CH₃). All the atoms in this structure were frozen, the dendrimers were drawn again and the geometry of the resulting [3′⊂10]⁴⁺ structure was allowed optimize with MMFF to yield the final model used (while keeping the DFT optimized core-structure frozen). Calculations were done with Spartan 2016.

---