Open Access Article
Open Access ArticleKinetic modeling study of the group-transfer polymerization of alkyl crotonates using a silicon Lewis acid catalyst†
Motosuke
Imada
 abc,
Yasumasa
Takenaka
abc,
Yasumasa
Takenaka
 *a,
Takeharu
Tsuge
*a,
Takeharu
Tsuge
 b and
Hideki
Abe
ab
b and
Hideki
Abe
ab
aBioplastic Research Team, RIKEN Center for Sustainable Resource Science, 2-1 Hirosawa, Wako, Saitama 351-0198, Japan. E-mail: yasumasa.takenaka@riken.jp
bDepartment of Materials Science and Engineering, Tokyo Institute of Technology, 4259 Nagatsuta, Midori-ku, Yokohama 226-8502, Japan
cResearch Center, Innovation and Business Development Division, Nippon Shokubai Co., Ltd, 5-8 Nishi Otabi-cho, Suita, Osaka 564-0034, Japan
First published on 14th September 2020
Abstract
Kinetic modeling is effective in the development of efficient and manageable polymerization systems. Herein, a kinetic model of the group-transfer polymerization (GTP) of an alkyl crotonate using a silicon Lewis acid catalyst having a trialkylsilyl (trimethylsilyl, triethylsilyl, tert-butyldimethylsilyl, or triisopropylsilyl) moiety and various silyl ketene acetals with a corresponding trialkylsilyl moiety as an initiator is developed to understand the polymerization mechanism. The kinetic model quantitatively verifies proposed elementary reactions. When using a trimethylsilyl moiety, the activation energy of the cyclization reaction (a well-known termination reaction in GTP; Ec = 37.8 kJ mol−1) exceeds that of the propagation reaction (Ep = 28.6 kJ mol−1). This reveals that termination reactions are accelerated more than propagation reactions at high temperatures. In addition, comparison of various trialkylsilyl moieties confirmed that the greater bulkiness of the alkyl substituent on the silyl group increases the ratio of the activation energies of the cyclization and propagation reactions.
Introduction
Crotonic acid (CA) and its derivatives, such as crotonates, are structural isomers of methacrylic acid and its derivatives. A methyl group exists at the β-position of these α,β-unsaturated carboxylic compounds.1,2 Because of β-substituent steric hindrance and/or an electronic factor, there are well-known difficulties in using these compounds as monomers to produce homopolymers with high molecular weights via conventional radical polymerization methods based on 2,2′-azobisisobutyronitrile or benzoyl peroxide and via typical anionic polymerization methods based on alkyl lithium or Grignard reagents.3–7Recently, we reported the group-transfer polymerization (GTP) method for the homopolymerization of various alkyl crotonates using only an organic acid catalyst, such as N-(trimethylsilyl)bis(trifluoromethanesulfonyl)imide (Tf2NSiMe3), which is a silicon Lewis acid (LA), and 1-trimethylsiloxyl-1-methoxy-2-methyl-1-propene (MTS) as the initiator.8,9 In general, organocatalysis without metal compounds is beneficial for industrial applications because of the well-known advantages of metal-free polymeric products and processes.10,11
However, the alkyl crotonate GTP mentioned above is usually performed at low temperatures (preferably −40 °C or below) because high reaction temperatures, even ambient temperatures, accelerate termination reactions such as cyclization and/or isomerization of propagating chain-end groups.12–15 Briefly, despite the living-polymerization characteristics of GTP, the propagation reaction declines, with the unreacted monomer remaining after the reaction ceases. Consequently, a polymeric material with a molecular weight that is sufficiently large to realize high-performance applications cannot be produced. Furthermore, the requirement of such low temperatures severely limits the application of GTP to industrial processes.16,17
The construction of a kinetic model is an effective approach toward the development of efficient and manageable polymerization systems that operate at high temperatures. The kinetic model quantitatively demonstrates the elementary reactions and provides useful knowledge related to the polymerization mechanism and design of optimum polymerization systems.
Herein, we develop a kinetic model of the GTP of alkyl crotonates using silicon LA catalysts having a trialkylsilyl moiety (Tf2NSiR1R2R3) and various silyl ketene acetals (R1R2R3SKAs) as the initiator. The kinetic model includes monomer activation steps, propagation reactions of living species, and termination reactions of living species. Furthermore, various trialkylsilyl moieties are compared and analyzed to investigate steric hindrance effects.
Experimental
Materials
Methyl crotonate (MC), ethyl crotonate (EC), 1-trimethylsiloxyl-1-methoxy-2-methyl-1-propene (MTS), methyl isobutyrate, chlorotriethylsilane, tert-butyldimethylchlorosilane, chlorotriisopropylsilane, N,N’-dimethylpropyleneurea, lithium(diisopropylamide) (1.5 M in THF), N-(trimethylsilyl)bis(trifluoromethanesulfonyl)imide (Tf2NSiMe3), and bis(trifluoromethanesulfonyl)imide (Tf2NH) were obtained from Tokyo Chemical Industry Co., Ltd (TCI). Distillation using CaH2 was performed for MC, EC, and MTS before they were stored in a glovebox. CH2Cl2, THF, and 1,2-dichloroethane (Kanto Chemical Co., super dehydrated grade) were purified using an SPS 800 system (MBraun). Argon and nitrogen were used after purification by passing them through a dry clean column (4A molecular sieves) and a gas clean CC-XR column (Nikka Seiko).Synthesis of silyl ketene acetal (SKA)
1-Methoxy-1-(triethylsiloxy)-2-methyl-1-propene (Et3SKA) was synthesized via the reaction of methyl isobutyrate and chlorotriethylsilane, in accordance with a method reported in the literature.18 Methyl isobutyrate (14.0 g, 137 mmol) in THF solution (200 mL) was charged into a flask filled with dry nitrogen gas, following which 1.5 M lithium(diisopropylamide) (100 mL, 150 mmol) in THF was added dropwise with vigorous stirring at −78 °C for 30 min. Subsequently, N,N’-dimethylpropyleneurea (200 mmol) and chlorotriethylsilane (22.6 g, 150 mmol) in THF solution (50 mL) were added, and the reagents were stirred at −78 °C for 60 min, following which they were warmed to room temperature. The reagents were then stirred for 24 h at room temperature, following which they were concentrated. The resulting mixture was taken in 500 mL of hexane and washed with 100 mL of water thrice. Next, the mixture was washed with 100 mL of saturated aq. NaHCO3 and 100 mL of brine and subsequently dried over MgSO4. After filtration, the organic layer was concentrated. Distillation under vacuum resulted in a 90% yield of Et3SKA as a clear colorless liquid with purity >97%, as measured using 1H nuclear magnetic resonance (NMR). 1-Methoxy-1-(tert-butyldimethylsiloxy)-2-methyl-1-propene (tBuMe2SKA) (54% yield as a clear colorless liquid with purity >99%) and 1-methoxy-1-(triisopropylsiloxy)-2-methyl-1-propene (iPr3SKA) (70% yield as a clear colorless liquid with purity >97%) were synthesized in a similar manner.Measurements
All molecular weight data of polymer samples were obtained through size exclusion chromatography (SEC) at 40 °C using a Shimadzu GPC system equipped with a RID-10A refractive index detector, a Shodex GPC K-802 column, and a Shodex GPC K-806M column. CHCl3 was used as an eluent at a flow rate of 0.8 mL min−1. Polystyrene standards with low polydispersity values were used to draw the calibration curve.Matrix-assisted laser desorption/ionization time-of-flight mass spectroscopy (MALDI-TOF-MS) was conducted using an ultrafleXtreme MALDI-TOF spectrophotometer (Bruker Daltonics, Billerica, MA) operated in reflection mode at an accelerating voltage of 20 kV. The samples that underwent MALDI-TOF-MS were combinations of the reaction mixture (2 μL), the matrix (1,8-dihydroxy-9(10H)-anthracenone (dithranol), 10 mg mL−1, 8 μL), and the ionizing agent (sodium trifluoroacetate, 10 mg mL−1, 2 μL) in THF. These samples were deposited on an MTP 384 ground steel target plate TF in a glovebox. External calibration was conducted prior to data acquisition. The detected mass list was extracted using FlexAnalysis software (Bruker Daltonics).
1H and 13C NMR measurements were performed with a Varian NMR system. The samples were dissolved in CDCl3, and 500 MHz 1H NMR and 125 MHz 13C NMR spectra were recorded at room temperature. The data were calibrated against tetramethylsilane (TMS, δ 0.00) and analyzed using the Mnova NMR software.
Group-transfer polymerization
All manipulations were performed under a dry and oxygen-free argon atmosphere using standard high-vacuum Schlenk techniques or a glovebox. A typical polymerization procedure (entry 1, Table 1) is as follows: EC (2.85 g, 25 mmol), MTS (10.9 mg, 0.0625 mmol), and CH2Cl2 (6 mL) were charged into a Schlenk tube in a glovebox. A CH2Cl2 solution (3.4 mL) of Tf2NSiMe3 (22.1 mg, 0.0625 mmol) was added to initiate the polymerization reaction at −40 °C. After 8 h, methanol (10 mL) was added to the reaction mixture, following which the solvents were removed by evaporation under reduced pressure. The residue was dissolved in CHCl3, and the solution was poured into a large volume of hexane. The precipitated polymer was collected as the hexane-insoluble part by filtration, washed several times with hexane, and dried under vacuum for 24 h. The hexane-soluble part was obtained by the evaporation of the filtrate, followed by drying under vacuum for 24 h. The monomer conversion was calculated from the sum of the weights of the hexane-insoluble and hexane-soluble parts.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a
a
| Entry | [EC]0 (M) | [MTS]0 (M) | [Tf2NSiMe3]0 (M) | Time (h) | Conv.b (%) |
M
n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c (g mol−1) c (g mol−1) |
Đ (Mw/Mn) |
v
app![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d (mol L−1 h−1) d (mol L−1 h−1) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Performed on an aluminum block under an argon atmosphere. CH2Cl2 was used as the reaction solvent. b Monomer conversion was calculated from the sum of the weights of the hexane-insoluble and hexane-soluble parts. c Number-averaged molecular weight (Mn) and dispersity (Đ) were determined using conventional GPC against PSt standards in CHCl3. d Apparent rate of monomer consumption during an initial period (vapp) was calculated using the first data point for each condition. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 2.0 | 0.0050 | 0.0050 | 8 | 11.0 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.17 | 0.0275 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 24 | 27.2 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.14 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 72 | 53.5 | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
1.29 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 168 | 54.8 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.32 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 2.0 | 0.0100 | 0.0050 | 8 | 18.1 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.16 | 0.0453 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 24 | 47.5 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.14 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 72 | 83.2 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
1.27 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 168 | 83.5 | 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 2.0 | 0.0200 | 0.0050 | 3 | 17.9 | 4100 | 1.20 | 0.1195 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 7 | 40.6 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.17 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 16 | 89.1 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.17 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 24 | 100.0 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
1.14 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | 48 | 99.9 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
1.14 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | 72 | 100.0 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
1.16 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | 1.5 | 0.0050 | 0.0050 | 8 | 17.0 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
1.16 | 0.0319 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | 24 | 39.9 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
1.11 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | 72 | 65.1 | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.25 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | 168 | 64.6 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
1.28 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | 1.0 | 0.0050 | 0.0050 | 4 | 15.9 | 6800 | 1.21 | 0.0398 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | 8 | 26.7 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | 24 | 63.2 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | 72 | 75.6 | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | 1.0 | 0.0025 | 0.0025 | 24 | 23.2 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
1.16 | 0.0097 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | 72 | 44.3 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
1.28 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | 168 | 46.5 | 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
1.34 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | 1.0 | 0.0025 | 0.0100 | 6 | 18.5 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
1.17 | 0.0308 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | 12 | 30.9 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
1.18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | 24 | 43.3 | 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
1.31 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | 72 | 46.3 | 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.36 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | 168 | 46.3 | 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
1.34 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | 1.0 | 0.0025 | 0.0400 | 3 | 24.6 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
1.19 | 0.0820 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | 6 | 38.2 | 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
1.19 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | 24 | 46.6 | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.33 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | 72 | 52.3 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.41 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | 168 | 47.6 | 57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.31 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Computational method
Theoretical calculations were performed using the Gaussian 09 software package.19 All the computations employed in this study were performed using density functional theory (DFT) with the B3LYP functional. Geometrical optimizations were performed using the 6-31G* basis set.20,21Results and discussion
GTP of crotonates using a silicon LA catalyst
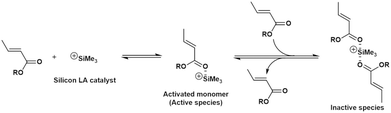
Fig. 1 shows a plausible polymerization mechanism for the GTP of crotonates using a silicon LA catalyst.8 First, a crotonate coordinates to a silicon LA catalyst, following which the activated monomer (active species) is generated. The activated monomer reacts with the initiator or the living polymer, which possesses a structure similar to that of the initiator at the polymer chain-end. Consequently, the polymer chain grows, and a silicon LA catalyst unit is released. The living polymer is elongated by repeating this process. The kinetic model in this study was constructed based on the pathway mentioned above but with the addition of new concepts, regarding the association between the monomer and the silicon LA catalyst as well as concerning the termination reactions.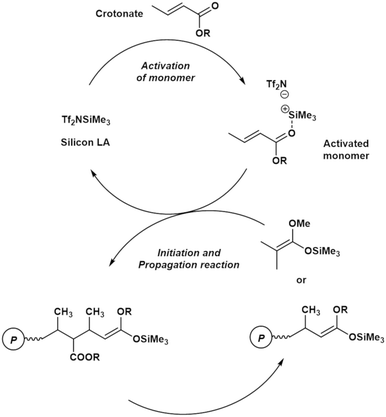 | ||
| Fig. 1 Plausible propagation pathway for the GTP of a crotonate using a silicon LA catalyst (reproduced from Takenaka and Abe8). | ||
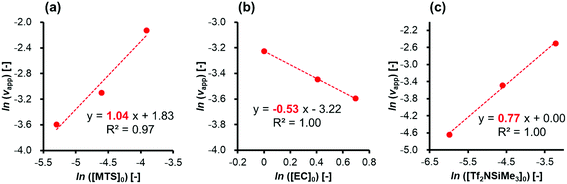
Determination of rate orders
First, experiments were conducted for the polymerization of EC using MTS as an initiator and Tf2NSiMe3 as the silicon LA catalyst under various conditions at −40 °C to evaluate the individual effects of concentrations of the monomer, initiator, and silicon LA catalyst. Table 1 lists the monomer conversions and the apparent rates of monomer consumption in an initial period (vapp) under various conditions.In order to investigate the reaction order for each concentration of the initiator, monomer, and silicon LA catalyst, double-logarithmic plots of vappversus [MTS]0, [EC]0, and [Tf2NSiMe3]0 were fit to straight lines (Fig. 2(a)–(c)). For the initiator, the slope of the straight line drawn using three data points ([MTS]0 = 0.0050, 0.010, and 0.020 M; [EC]0 = 2.0 M; [Tf2NSiMe3]0 = 0.0050 M) (entries 1, 5, and 9 in Table 1) was 1.04 (R2 = 0.97). For the monomer, the slope of the straight line drawn using three data points ([MTS]0 = 0.0050 M; [EC]0 = 2.0, 1.5, and 1.0 M; [Tf2NSiMe3]0 = 0.0050 M) (entries 1, 15, and 19 in Table 1) was −0.53 (R2 = 1.00). For the silicon LA catalyst, the slope of the straight line drawn using three data points ([MTS]0 = 0.0025 M; [EC]0 = 1.0 M; [Tf2NSiMe3]0 = 0.0025, 0.010, and 0.040 M) (entries 23, 26, and 31 in Table 1) was 0.77 (R2 = 1.00). The value of the slope corresponds to the reaction order of each component in the initial period.
 | ||
| Fig. 2 Double-logarithmic plots of apparent rates of monomer consumption during an initial period (vapp) as a function of (a) the initiator, (b) monomer, and (c) silicon LA catalyst. | ||
The slope of the plot of ln[vapp] vs. ln[MTS]0 in Fig. 2(a) (1.04) suggests that the initial polymerization rate is almost of first order with respect to the initiator concentration. As shown in Fig. 1, this result implies that an initiator or a living polymer chain-end group undergoes a first-order reaction with an activated monomer generated by the coordination of a monomer to a silicon LA catalyst.
A notable feature of this polymerization system, observed from the analysis of the double-logarithmic plots of the apparent rates of the monomer consumption during the initial period, is that the polymerization rate order calculated with respect to the monomer concentration (slope, −0.53) is negative. Furthermore, the rate order with respect to the silicon LA catalyst concentration (slope, 0.77) is less than one, although this polymerization rate should be of first order when considering only the active-species formation from the reaction between one monomer and one catalyst molecule. These peculiar results for the rate orders with respect to both the monomer and silicon LA catalyst concentrations suggest that the monomer reduces the polymerization rate while the silicon LA catalyst is somehow involved in this reduction. As shown in Scheme 1, we can express these peculiar rate orders with respect to the monomer and silicon LA catalyst concentrations by considering that one more monomer can coordinate with the activated monomer (active species) formed by the association of one silicon LA catalyst with one monomer, which leads to the formation of the inactive species.
Evidence for the formation of a monomer/silicon LA catalyst (2/1) adduct
A theoretical study was conducted to confirm that the generation of an inactive species, a monomer/silicon LA catalyst (2/1) adduct, is applicable to the present system. Fig. 3(a) and (b) show the structures of adduct A (active species, EC/+SiMe3 = 1/1) and adduct B (EC/+SiMe3 = 2/1) computed at the B3LYP/6-31G* level of theory, respectively. As shown in Fig. 3(a), the length of the bond between the silicon Si(1a) and oxygen O(1a) atoms was 1.805 Å for adduct A; whereas, for adduct B, as shown in Fig. 3(b), the lengths of the bonds between the silicon atom Si(1b) and the oxygen atoms O(1b) and O(2b) were 2.037 Å and 2.078 Å, respectively.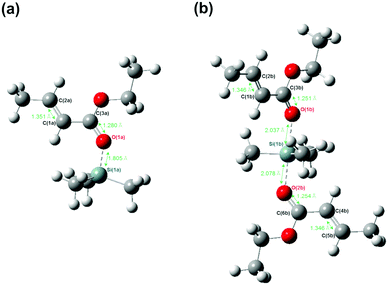 | ||
| Fig. 3 Computed structures of (a) adduct A (EC/+SiMe3 = 1/1) and (b) adduct B (EC/+SiMe3 = 2/1) at the B3LYP/6-31G* level. | ||
This result suggests that, in both adduct A and adduct B, the silicon atom of the silicon LA catalyst and the lone pair on the oxygen atoms of the carbonyl groups interact via the transfer of an electron because the bond lengths between them are sufficiently short.22,23 Therefore, this result can be considered as evidence for the presence of adduct B and adduct A. In addition, because the bond lengths between the silicon and oxygen atoms of adduct B are longer than those between the silicon and oxygen atoms of adduct A, the monomer activation degree of adduct B is lower than that of adduct A. The length of the vinyl bonds of EC in adduct B (C(1b)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(2b) and C(4b)
C(2b) and C(4b)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(5b), 1.346 Å) is less than that in adduct A (C(1a)
C(5b), 1.346 Å) is less than that in adduct A (C(1a)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(2a), 1.351 Å), although it is slightly longer than that in free EC, unbound to the silicon LA catalyst (1.339 Å). In addition, the length of the carbonyl bonds of EC in adduct B (C(3b)
C(2a), 1.351 Å), although it is slightly longer than that in free EC, unbound to the silicon LA catalyst (1.339 Å). In addition, the length of the carbonyl bonds of EC in adduct B (C(3b)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1b) and C(6b)
O(1b) and C(6b)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(2b), 1.251 Å and 1.254 Å, respectively) is less than that in adduct A (C(3a)
O(2b), 1.251 Å and 1.254 Å, respectively) is less than that in adduct A (C(3a)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O(1a), 1.280 Å), although it is slightly longer than that in free EC (1.217 Å).
O(1a), 1.280 Å), although it is slightly longer than that in free EC (1.217 Å).
Termination reactions on GTP of EC using a silicon LA catalyst
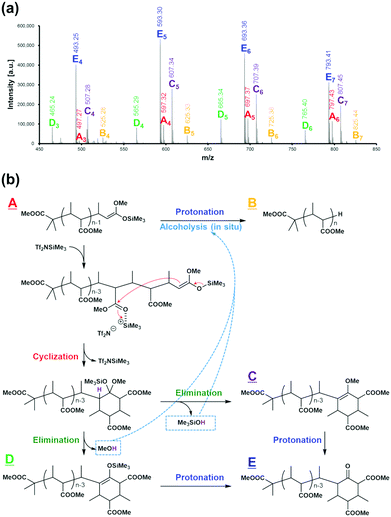
Despite the living-polymerization characteristics of a GTP system, the use of EC as a monomer substrate resulted in a decline of the propagation reaction, with unreacted monomer remaining in all cases, as summarized in Table 1, except for the case of a low feed ratio between the monomer and initiator (entries 9–14 in Table 1). Furthermore, a previous report8 stated that the GTP of alkyl crotonates generated not only polymers of a terminal cyclic form, via a well-known cyclization termination reaction, but also polymers of a linear form, via an acid treatment of a living polymer, as observed through the MALDI-TOF-MS analysis of the resulting polymers upon a halt of the polymerization reaction with unconsumed monomer remaining. This result suggests that some protic acids are produced in situ, which causes the protonation of a living polymer to occur in situ. In the present study, the termination mechanism was investigated in detail through a MALDI-TOF-MS analysis of the reaction mixture for the GTP of MC. The polymerization experiment was performed at 20 °C; at this temperature, termination reactions are promoted, with reduction of the monomer-to-initiator feed ratio for the ease of observation of products and/or intermediates.
Fig. 4(a) shows the MALDI-TOF-MS spectrum of the obtained reaction mixture. We can observe five series of mass ions (series A to E), all of which have mass-ion intervals corresponding to a repeat unit of m/z = 100 (in agreement with the molecular weight of MC). A detailed analysis of the mass spectrum reveals that the series A polymer corresponds to the structural formula (CH3)2[CH3OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)]C–(MC)n−1–CH(CH3)–HC
O)]C–(MC)n−1–CH(CH3)–HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(OCH3)(OSiMe3), and the series B polymer corresponds to the structural formula (CH3)2[CH3OC(
C(OCH3)(OSiMe3), and the series B polymer corresponds to the structural formula (CH3)2[CH3OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)]C–(MC)n–H. The former consists of linear living polymers possessing the chain-end structure of a silyl ketene acetal, and the latter consists of protonated forms of the linear living polymers (in addition to protonolysis during the polymerization, the protonated chain ends observed by MALDI-TOF-MS can result from post-polymerization protonolysis, which might occur because of the acidic compounds present in the form of the matrix (dithranol)). The series E polymer is observed as a major component, and it corresponds to the polymer structures shown in Fig. 4(b). The series E polymer is formed by the cyclization reaction of the linear living polymer (series A), a well-known termination reaction in GTP systems. In addition, 13C NMR studies suggest that such a cyclic structure could correspond to a keto-carbon, as shown in Fig. S1.† Furthermore, in the MALDI-TOF-MS spectrum, the series C and D polymers are also confirmed as intermediates of a transition from the series A to series E polymers.
O)]C–(MC)n–H. The former consists of linear living polymers possessing the chain-end structure of a silyl ketene acetal, and the latter consists of protonated forms of the linear living polymers (in addition to protonolysis during the polymerization, the protonated chain ends observed by MALDI-TOF-MS can result from post-polymerization protonolysis, which might occur because of the acidic compounds present in the form of the matrix (dithranol)). The series E polymer is observed as a major component, and it corresponds to the polymer structures shown in Fig. 4(b). The series E polymer is formed by the cyclization reaction of the linear living polymer (series A), a well-known termination reaction in GTP systems. In addition, 13C NMR studies suggest that such a cyclic structure could correspond to a keto-carbon, as shown in Fig. S1.† Furthermore, in the MALDI-TOF-MS spectrum, the series C and D polymers are also confirmed as intermediates of a transition from the series A to series E polymers.
These results reveal that the cyclization reaction of the linear living polymer proceeds with the formation of alcohols such as MeOH and Me3SiOH, which are protic acids, as shown in Fig. 4(b). In addition, the alcohols generated in situ react immediately with the linear living polymer, and the living chain-end is deactivated. This is probably the reason why the polymers observed when polymerization stopped include the polymer of a linear form.
Kinetic modeling
We propose an overall reaction pathway for the GTP of alkyl crotonates using a silicon LA catalyst from the knowledge obtained above. Scheme 2 shows the proposed elementary reactions of this polymerization system. With regard to the equilibrium between the monomer and silicon LA catalyst, the monomer (M) coordinates with the silicon LA catalyst (C) with the rate constant k1, and the activated monomer (M*) is generated. In the reverse reaction, the rate constant is expressed as k1/K1 using the equilibrium constant K1. Notably, we introduce one more equilibrium step, where one more monomer (M) coordinates with the activated monomer (M*), leading to the generation of the inactive species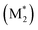 , with a decreased activation degree. In the latter equilibrium step, the rate constant and equilibrium constant are denoted as k2 and K2, respectively.
, with a decreased activation degree. In the latter equilibrium step, the rate constant and equilibrium constant are denoted as k2 and K2, respectively.
The initiation or propagation step proceeds with the activated monomer (M*) reacting with the initiator (I) or linear living polymer (PLn), respectively. For simplicity, the rate constants of the initiation and propagation reactions were considered to be similar because the structures of the initiator and the chain-end of the linear living polymer were almost the same; therefore, we treated each reaction as the propagation of a living species using the rate constant kp.
In the termination reaction in the presence of a silicon LA catalyst (C), the linear living polymer (PLn) was cyclized to a polymer having a terminal cyclic structure (PCn) with the formation of an alcohol (R′OH). The rate constant of the cyclization reaction is kc. Moreover, the generated alcohol (R′OH) reacts with the linear living polymer (PLn), and PLn is transformed to the deactivated form (PDn). The rate constant of the alcoholysis is ka. In this study, k1 and k2 were defined as k1 = k2 = 102kp, assuming that they were sufficiently large with respect to the polymerization reaction.
For each component, the rate law is expressed using a reaction time (t(s)) as follows (eqn (1)–(7)):
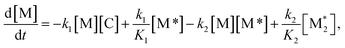 | (1) |
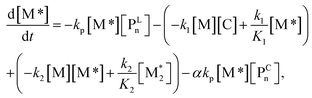 | (2) |
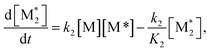 | (3) |
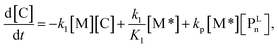 | (4) |
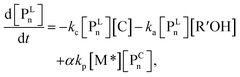 | (5) |
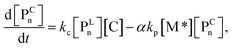 | (6) |
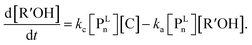 | (7) |
The parameter α, which is assumed to be zero in this study, is the relative value of the rate constant of the propagation reaction from the cyclic form (PCn) toward the propagation reaction from the linear living species (PLn). The seven ordinary differential equations generated were solved numerically for all the simulations in this study. Subsequently, the monomer conversion (x (%)) at t(s) was calculated as follows by using solved [M], and [M*] and 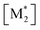 , which are recovered as free monomers after the polymerization is quenched with methanol, and the initial monomer concentration [M]0 (please note that [M*]0 and
, which are recovered as free monomers after the polymerization is quenched with methanol, and the initial monomer concentration [M]0 (please note that [M*]0 and 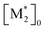 are zero):
are zero):
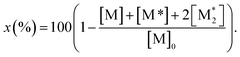 | (8) |
For further investigation of the alkyl crotonate GTP mechanism using a silicon LA catalyst, AdamsBDF curve-fitting analysis using Mathcad software was conducted using the monomer conversion data presented in Table 1, which were acquired under the following conditions: the initial monomer concentration was 1.0–2.0 M, the initial initiator concentration was 0.0025–0.020 M, and the initial silicon LA catalyst concentration was 0.0025–0.040 M. In this analysis, the kinetic parameters shown in Scheme 2 were optimized, as the simulated and experimental data are in good agreement.
Fig. 5 shows the agreement between the simulated and experimental data for the GTP of EC using MTS as the initiator and Tf2NSiMe3 as the silicon LA catalyst at −40 °C. The kinetic model constructed in this study agrees well with actual experiments in that despite the living-polymerization character of the GTP system, the propagation reaction declines, with unreacted monomer remaining. Table 2 summarizes the estimated kinetic parameters. Representative results are as follows: the rate constant of the propagation reaction kp was 0.94 L mol−1 s−1, and the rate constant of the cyclization reaction kc was 1.70 L mol−1 s−1.
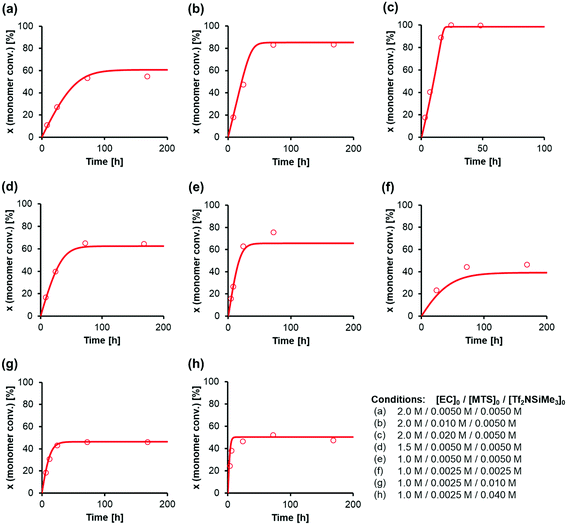 | ||
| Fig. 5 Curve-fitting calculations for the GTP of EC using MTS as the initiator and Tf2NSiMe3 as the catalyst in CH2Cl2 at −40 °C. The symbols represent the experimental data, and the lines represent the simulation results. The experimental data correspond to (a) entries 1–4, (b) entries 5–8, (c) entries 9–14, (d) entries 15–18, (e) entries 19–22, (f) entries 23–25, (g) entries 26–30, and (h) entries 31–35 in Table 1. | ||
| Kinetic parameter | Unit | Value | |
|---|---|---|---|
| Propagation | k p | L mol−1 s−1 | 0.94 |
| Cyclization | k c | L mol−1 s−1 | 1.70 |
| Alcoholysis | k a | L mol−1 s−1 | 0.01 |
| 1st equilibrium | K 1 | L mol−1 | 630 |
| 2nd equilibrium | K 2 | L mol−1 | 1.4 |
Temperature effect
Next, we attempted to estimate the activation energies for the propagation, cyclization, and alcoholysis reactions (Ep, Ec, and Ea), as well as the standard enthalpy changes for equilibrium in the formation of M* and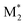 (ΔH1 and ΔH2). To confirm these parameters, polymerization experiments of EC were conducted using Tf2NSiMe3 and MTS under various temperature conditions (−10 °C, −20 °C, and −30 °C). Table 3 lists the monomer conversions under various temperature conditions. As the reaction temperature increased, polymerization stopped at a lower level of final monomer conversion. For example, the final monomer conversion at −10 °C was very low, 26% (entry 14 in Table 3). This result suggests that the termination reaction is significantly accelerated at higher temperatures, with the propagation reaction proceeding inferiorly.
(ΔH1 and ΔH2). To confirm these parameters, polymerization experiments of EC were conducted using Tf2NSiMe3 and MTS under various temperature conditions (−10 °C, −20 °C, and −30 °C). Table 3 lists the monomer conversions under various temperature conditions. As the reaction temperature increased, polymerization stopped at a lower level of final monomer conversion. For example, the final monomer conversion at −10 °C was very low, 26% (entry 14 in Table 3). This result suggests that the termination reaction is significantly accelerated at higher temperatures, with the propagation reaction proceeding inferiorly.
| Entry | Temperature (°C) | Time (h) | Conv.b (%) |
M
n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c (g mol−1) c (g mol−1) |
Đ (Mw/Mn) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Performed on an aluminum block under an argon atmosphere. CH2Cl2 was used as the reaction solvent. The conditions were as follows: [EC]0 = 2.0 M, [MTS]0 = 0.0050 M, and [Tf2NSiMe3]0 = 0.0050 M. b Monomer conversion was calculated from the sum of the weights of the hexane-insoluble and hexane-soluble parts. c Number-averaged molecular weight (Mn) and dispersity (Đ) were determined using conventional GPC against PSt standards in CHCl3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | −30 | 8 | 17.8 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 24 | 36.6 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
1.18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 48 | 41.3 | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
1.24 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 72 | 41.3 | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
1.24 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | −20 | 2.5 | 10.9 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
1.17 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 5 | 18.4 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
1.18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 10 | 27.7 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
1.23 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 24 | 32.6 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
1.32 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 72 | 32.3 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.31 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | −10 | 2.5 | 14.7 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
1.21 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 5 | 22.3 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | 10 | 24.9 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
1.32 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | 24 | 25.7 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
1.33 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | 72 | 25.6 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
1.32 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
AdamsBDF curve-fitting analysis with Mathcad software was conducted using the kinetic parameters estimated at −40 °C (Table 2) and the monomer conversion experimental data presented in Table 3. Using the rate constant estimated at −40 °C (k−40) and the activation energy (E), the rate constant at temperature T (kT) is expressed as kT = k−40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(E/R){(1/−40 °C) − (1/T)}], as per the Arrhenius equation. Using the equilibrium constant estimated at −40 °C (K−40) and the standard enthalpy change (ΔH), the equilibrium constant at the temperature T (KT) is expressed as KT = exp[(ΔH/R){(1/−40 °C) − (1/T)} + ln(K−40)], as per the van't Hoff equation. In this analysis, the activation energies (Ep, Ec, and Ea) and standard enthalpy changes (ΔH1 and ΔH2) were optimized, as the simulated and experimental data presented in Table 3 are in good agreement. Fig. 6 shows the agreement between the simulated and experimental data for the GTP of EC under various temperature conditions, and Table 4 lists the estimated parameters. Representative results are as follows: the activation energy of the propagation reaction Ep was 28.6 kJ mol−1, and the activation energy of the cyclization reaction Ec was 37.8 kJ mol−1. This result suggests that as the reaction temperature increased, the ratio of the reaction rate constants for the cyclization reaction toward the propagation reaction increased. Thus, the kinetic model constructed in this study can convincingly explain the actual polymerization behavior.
exp[(E/R){(1/−40 °C) − (1/T)}], as per the Arrhenius equation. Using the equilibrium constant estimated at −40 °C (K−40) and the standard enthalpy change (ΔH), the equilibrium constant at the temperature T (KT) is expressed as KT = exp[(ΔH/R){(1/−40 °C) − (1/T)} + ln(K−40)], as per the van't Hoff equation. In this analysis, the activation energies (Ep, Ec, and Ea) and standard enthalpy changes (ΔH1 and ΔH2) were optimized, as the simulated and experimental data presented in Table 3 are in good agreement. Fig. 6 shows the agreement between the simulated and experimental data for the GTP of EC under various temperature conditions, and Table 4 lists the estimated parameters. Representative results are as follows: the activation energy of the propagation reaction Ep was 28.6 kJ mol−1, and the activation energy of the cyclization reaction Ec was 37.8 kJ mol−1. This result suggests that as the reaction temperature increased, the ratio of the reaction rate constants for the cyclization reaction toward the propagation reaction increased. Thus, the kinetic model constructed in this study can convincingly explain the actual polymerization behavior.
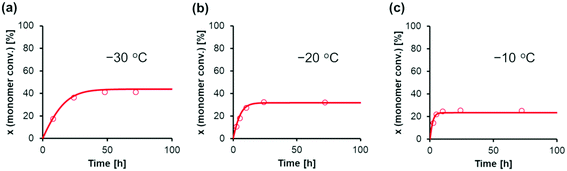 | ||
| Fig. 6 Curve-fitting calculations for the GTP of EC using MTS as the initiator and Tf2NSiMe3 as the catalyst in CH2Cl2 at various temperatures (a: −30 °C, b: −20 °C, and c: −10 °C). The conditions are as follows: [EC]0 = 2.0 M, [MTS]0 = 0.0050 M, and [Tf2NSiMe3]0 = 0.0050 M. The symbols represent experimental data, and the lines represent simulation results. The experimental data correspond to (a) entries 1–4, (b) entries 5–9, and (c) entries 10–14 in Table 3. | ||
| Kinetic parameter | Unit | Value | |
|---|---|---|---|
| Propagation | E p | kJ mol−1 | 28.6 |
| Cyclization | E c | kJ mol−1 | 37.8 |
| Alcoholysis | E a | kJ mol−1 | 29.8 |
| 1st equilibrium | ΔH1 | kJ mol−1 | −14.2 |
| 2nd equilibrium | ΔH2 | kJ mol−1 | −12.2 |
Substituent effect
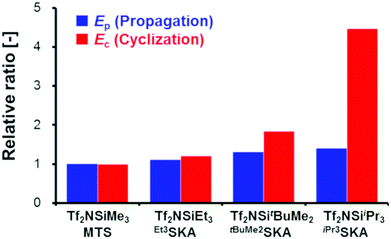
Next, we conducted the GTP of EC using various silicon LA catalysts (Tf2NSiR1R2R3) and SKAs (R1R2R3SKA) to examine the effect of the trialkylsilyl moiety. The kinetic parameters for the polymerization reactions using Tf2NSiEt3/Et3SKA, Tf2NSitBuMe2/tBuMe2SKA, and Tf2NSiiPr3/iPr3SKA were investigated. All experiments were performed in the same manner as the polymerization experiment using Tf2NSiMe3/MTS, except that the silicon LA catalysts were generated in situ by adding Tf2NH as a pre-catalyst to the corresponding SKAs (Scheme S1†). For the polymerization experiments using Tf2NSiiPr3/iPr3SKA, 1,2-dichloroethane, which has a higher boiling point (83.5 °C) than CH2Cl2 (39.8 °C), was used as the polymerization solvent. Table S1† lists the monomer conversions in the GTP under various conditions.In the kinetic analysis, a reference temperature (Tr), the temperature at which the monomer cannot be consumed fully, was first set for each system, because the kinetic model in this study includes both the propagation reaction and termination reaction, which significantly reduces the monomer consumption. The kinetic parameters (kp, kc, ka, K1, and K2) were estimated at the reference temperature (Tf2NSiEt3/Et3SKA, Tr = 10 °C; Tf2NSitBuMe2/tBuMe2SKA, Tr = 30 °C; Tf2NSiiPr3/iPr3SKA, Tr = 40 °C). AdamsBDF curve-fitting analyses using Mathcad software were conducted using the monomer conversion data presented in Table S1.† In the analyses, the parameter α was set to zero, except for the case of Tf2NSiiPr3/iPr3SKA (α = 0.1). The estimated kinetic parameters are listed in Table 5, and the curve-fitting results are shown in Fig. S2–S4.† In all cases, the simulations reproduced the experimental data well. Next, we attempted to estimate the activation energies of the propagation, cyclization, and alcoholysis reactions (Ep, Ec, and Ea), as well as the standard enthalpy changes for equilibrium in the formation of M* and 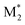 (ΔH1 and ΔH2) for each system. The analyses were conducted using the estimated kinetic parameters (kp, kc, ka, K1, and K2) at Tr and the monomer conversion data under various temperature conditions (entries 1–4 and 17–36 in Table S1† for Tf2NSiEt3/Et3SKA, entries 37–42 and 55–66 in Table S1† as for Tf2NSitBuMe2/tBuMe2SKA, and entries 67–73 and 86–102 in Table S1† as for Tf2NSiiPr3/iPr3SKA), in the manner described in the preceding subsection. The estimated kinetic parameters (Ep, Ec, Ea, ΔH1, and ΔH2) for each system are listed in Table 6, and the curve-fitting results are shown in Fig. S5–S7.†Fig. 7 shows the relative values of Ep and Ec for each system with respect to those for the Tf2NSiMe3/MTS system.
(ΔH1 and ΔH2) for each system. The analyses were conducted using the estimated kinetic parameters (kp, kc, ka, K1, and K2) at Tr and the monomer conversion data under various temperature conditions (entries 1–4 and 17–36 in Table S1† for Tf2NSiEt3/Et3SKA, entries 37–42 and 55–66 in Table S1† as for Tf2NSitBuMe2/tBuMe2SKA, and entries 67–73 and 86–102 in Table S1† as for Tf2NSiiPr3/iPr3SKA), in the manner described in the preceding subsection. The estimated kinetic parameters (Ep, Ec, Ea, ΔH1, and ΔH2) for each system are listed in Table 6, and the curve-fitting results are shown in Fig. S5–S7.†Fig. 7 shows the relative values of Ep and Ec for each system with respect to those for the Tf2NSiMe3/MTS system.
| Tf2NSiEt3/Et3SKA (Tr = 10 °C) | Tf2NSitBuMe2/tBuMe2SKA (Tr = 30 °C) | Tf2NSiiPr3/iPr3SKAa (Tr = 40 °C) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a The parameter α was set to 0.1 in the case of Tf2NSiiPr3/iPr3SKA. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Propagation | k p | L mol−1 s−1 | 4.49 | 6.20 | 1.80 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cyclization | k c | L mol−1 s−1 | 1.08 | 0.53 | 0.16 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Alcoholysis | k a | L mol−1 s−1 | 0.45 | 0.45 | 0.10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1st equilibrium | K 1 | L mol−1 | 130 | 81 | 71 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2nd equilibrium | K 2 | L mol−1 | 0.11 | 0.07 | 0.07 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tf2NSiEt3/Et3SKA | Tf2NSitBuMe2/tBuMe2SKA | Tf2NSiiPr3/iPr3SKAa | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a The parameter α was set to 0.1 in the case of Tf2NSiiPr3/iPr3SKA. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Propagation | E p | kJ mol−1 | 31.7 | 37.4 | 40.0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cyclization | E c | kJ mol−1 | 45.7 | 69.7 | 168.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Alcoholysis | E a | kJ mol−1 | 29.2 | 30.5 | 34.8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1st equilibrium | ΔH1 | kJ mol−1 | −13.6 | −14.0 | −14.7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2nd equilibrium | ΔH2 | kJ mol−1 | −12.2 | −11.6 | −9.6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In all cases, Ec was large with respect to Ep, indicating that the acceleration of the cyclization reaction rate with increasing polymerization temperature is greater than that of the propagation reaction. Furthermore, the values of both Ep and Ec increase in the order Tf2NSiiPr3/iPr3SKA > Tf2NSitBuMe2/tBuMe2SKA > Tf2NSiEt3/Et3SKA > Tf2NSiMe3/MTS. The trialkylsilyl group steric hindrance has previously been reported to increase in the order iPr3Si > tBuMe2Si > Et3Si > Me3Si.24,25 Thus, the results of the present study confirm that the steric hindrance of the trialkylsilyl moiety of a silicon LA catalyst and an SKA can affect both the propagation and cyclization reactions of the GTP of alkyl crotonates. Notably, as shown in Fig. 7, the influence of the steric hindrance of the trialkylsilyl moiety is more pronounced for the cyclization reaction than for the propagation reaction. This result suggests that changing the trialkylsilyl moiety is an effective strategy to prioritize the propagation reaction over the termination reaction, which mainly consists of a cyclization reaction, in a certain temperature range. When the initial concentration of each component was fixed to [EC]0 = 2.0 M, [R1R2R3SKA]0 = 0.0050 M, and [Tf2NSiR1R2R3]0 = 0.0050 M, the monomer was fully consumed in the case of Tf2NSiEt3/Et3SKA at −10 °C (entry 32 in Table S1†), Tf2NSitBuMe2/tBuMe2SKA at 15 °C (entries 61 and 62 in Table S1†), and Tf2NSiiPr3/iPr3SKA at 40 °C (entry 73 in Table S1†). However, in the case of Tf2NSiMe3/MTS, full conversion of the monomer could not be achieved even at a low temperature of −40 °C (entry 4 in Table 1).
Conclusions
In conclusion, we demonstrated the first example of a kinetic model of the GTP of alkyl crotonates including both the propagation and termination reactions. The kinetic model employs a new concept related to the equilibrium between a monomer and a silicon LA catalyst. Furthermore, we suggested that an inactive species might be generated from the coordination of another monomer to the activated monomer. Moreover, the MALDI-TOF-MS analysis of the reaction mixture revealed that the termination occurred both as a cyclization reaction of the linear living polymer and as an alcoholysis (in situ) of the linear living polymer, via the alcohols generated from the cyclization reaction.The constructed kinetic model can convincingly reproduce the experimentally observed polymerization behavior. In addition, the examination of a trialkylsilyl moiety effect on the silicon LA catalyst and initiator revealed that the steric hindrance of the trialkylsilyl moiety strongly affected the elementary reactions, particularly the propagation and cyclization reactions, in this GTP system.
Further investigations on not only the steric factor but also the electronic factor of various silyl moieties of the silicon LA catalyst and initiator are necessary to establish an optimized, efficient, and manageable GTP system for alkyl crotonates.
Author contributions
M. I. and Y. T. designed, performed the experiments and analyzed the data. M. I. and Y. T. co-wrote the paper. All the authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Toshifumi Nishida and Satoshi Ishida of the analysis technology center at Nippon Shokubai Co., Ltd for assistance with the preparation of the computational results. This research was financially supported by JSPS KAKENHI Grant Numbers 26410199 and 18K05210. This paper is based on results obtained with the support of the RIKEN-AIST Joint Research Fund (Full research).Notes and references
- K. Weissermel and H. J. Arpe, Industrial Organic Chemistry, Wiley-VCH, Weinheim, 2003 Search PubMed.
- J. Blumenstein, J. Albert, R. P. Schulz and C. Kohlpaintner, Crotonaldehyde and Crotonic Acid in ULLMANN'S Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 2015 Search PubMed.
- M. L. Miller and J. Skogman, J. Polym. Sci., Part A: Gen. Pap., 1964, 2, 4551 CrossRef CAS.
- T. Makimoto, K. Tanabe and T. Tsuruta, Makromol. Chem., 1966, 99, 279 CrossRef CAS.
- T. Tsuruta, T. Makimoto and T. Miyazako, Makromol. Chem., 1967, 103, 128 CrossRef CAS.
- R. K. Graham, J. E. Moore and J. A. Powell, J. Appl. Polym. Sci., 1967, 11, 1797 CrossRef CAS.
- T. Tsuruta, T. Makimoto and K. Tanabe, Makromol. Chem., 1968, 114, 182 CrossRef CAS.
- Y. Takenaka and H. Abe, Macromolecules, 2019, 52, 4052 CrossRef CAS.
- Y. Takenaka and H. Abe, Jpn. Pat, 6342699, June 13, 2018 Search PubMed.
- K. Matyjaszewski and N. V. Tsarevsky, J. Am. Chem. Soc., 2014, 136, 6513 CrossRef CAS.
- N. J. Treat, H. Sprafke, J. W. Kramer, P. G. Clark, B. E. Barton, J. R. Alaniz, B. P. Fors and C. J. Hawker, J. Am. Chem. Soc., 2014, 136, 16096 CrossRef CAS.
- W. J. Brittain and I. B. Dicker, Macromolecules, 1989, 22, 1054 CrossRef CAS.
- W. J. Brittain and I. B. Dicker, Makromol. Chem., Macromol. Symp., 1993, 67, 373 CrossRef CAS.
- K. Takata, K. Fuchise, Y. Chen, T. Satoh and T. Kakuchi, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 3560 CrossRef.
- K. Ute, T. Tarao, S. Nakao and T. Kitayama, Polymer, 2003, 44, 7869 CrossRef CAS.
- A. Zheng, L. Su, Z. Li, G. Zou, X. Xu and Y. Guan, RSC Adv., 2017, 7, 53996 RSC.
- Z. Li, J. Chen, G. Zou, T. Zhang, D. Wei, X. Xu, Y. Guan and A. Zheng, J. Polym. Sci., Part A: Polym. Chem., 2019, 57, 1130 CrossRef CAS.
- J. M. Wieting, T. J. Fisher, A. G. Schafer, M. D. Visco, J. C. Gallucci and A. E. Mattson, Eur. J. Org. Chem., 2015, 525 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- C. Chuit, R. J. P. Corriu, C. Reye and J. C. Young, Chem. Rev., 1993, 93, 1371 CrossRef CAS.
- M. G. Voronkov, E. A. Zel'bst, Y. V. Katkevich, A. A. Kashaev, V. S. Fundamenskii, Y. I. Bolgova, O. M. Trofimova, N. F. Chernov, A. I. Albanov, Y. I. Baukov and V. A. Pestunovich, Dokl. Chem., 2005, 402, 77 CrossRef CAS.
- N. Shimizu, N. Takesue, S. Yasuhara and T. Inazu, Chem. Lett., 1993, 22, 1807 CrossRef.
- N. Shimizu, N. Takesue, A. Yamamoto, T. Tsutsumi, S. Yasuhara and Y. A. Tsuno, Chem. Lett., 1992, 21, 1263 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0py00353k |
| This journal is © The Royal Society of Chemistry 2020 |