Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning magnetic anisotropy by the π-bonding features of the axial ligands and the electronic effects of gold(I) atoms in 2D {Co(L)2[Au(CN)2]2}n metal–organic frameworks with field-induced single-ion magnet behaviour†
María A.
Palacios
a,
Ismael F.
Díaz-Ortega
ab,
Hiroyuki
Nojiri
*b,
Elizaveta A.
Suturina
 *c,
Mykhaylo
Ozerov
*c,
Mykhaylo
Ozerov
 d,
J.
Krzystek
*d and
Enrique
Colacio
d,
J.
Krzystek
*d and
Enrique
Colacio
 *a
*a
aDepartamento de Química Inorgánica, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain. E-mail: ecolacio@ugr.es
bInstitute for Materials Research, Tohoku University, Katahira, Sendai, 980-8577, Japan
cDepartment of Chemistry, University of Bath, Wessex House 1.28, University of Bath, Claverton Down, Bath BA2 7AY, UK
dNational High Magnetic Field Laboratory, Florida State University, Tallahassee, Florida 32310, USA
First published on 1st October 2020
Abstract
The assembly of a Co(II) salt with two [Au(CN)2]− anions and ancillary ligands L afforded 2D complexes of the general formula {Co(L)2[Au(CN)2]2}n (where L = DMSO (1), DMF (2), Py (3) and PyPhCO (4); PyPhCO is benzoylpyridine). The structure of these complexes consists of parallel sheets, which are built from edge-sharing slightly distorted square-planar {NC–Au–CN–Co}4 units with the Co(II) ions located at the corners and the [Au(CN)2]− bridging anions at the edges. Co(II) atoms exhibit a slightly tetragonally distorted CoN4X2 coordination sphere (X = O, N), where the L molecules occupy the axial positions. These molecules are oriented in such a way that they penetrate the holes of neighbouring layers, giving rise in the case of 1, 2 and 4 to AB bilayers held together by Au⋯Au aurophilic interactions, whereas in 3, there are no aurophilic interactions between neighbouring layers, so they are not arranged in pairs but equally separated. Dc magnetic properties, HFEPR (high-frequency and -field EPR) and FIRMS (far-infrared magnetic spectroscopy) measurements and ab initio calculations demonstrate that Co(II) ions in compounds 1–4 possess large and positive D values (≳+70 cm−1). The experimental D values follow the same order as that established from ab initio calculations including gold(I) atoms: D (2) > D (4) > D (3) > D (1), which highlights the important role of Au(I) in determining the anisotropy of the Co(II) ions. All the complexes show field-induced slow relaxation of magnetization through a predominant Raman mechanism above 3 K. Neither the anisotropy order nor the Co(II)⋯Co(II) distances are clearly correlated with the phenomenological Ueff parameter (or the Raman parameters). This fact suggests that other factors, such as the flexibility of the axial ligands, could significantly contribute to the fast relaxation observed for these complexes.
Introduction
Discrete mono- or polynuclear coordination compounds exhibiting Single-Molecule Magnet (SMM) behaviour have been profusely investigated during the last two decades, because they show both classical properties (slow relaxation of magnetization and magnetic hysteresis, like bulk magnets) and quantum properties (quantum tunnelling of magnetization, QTM, quantum phase interference and quantum coherence).1 This combination of classical/quantum properties makes SMMs hopeful candidates not only for understanding the quantum phenomena at the mesoscopic level but also for potential upcoming applications, among other areas, in ultra-high density magnetic information storage2 and molecular spintronics,3 and as qubits for quantum computing at the molecular level.4 The origin of the SMM behaviour is associated with the existence of an energy barrier (U) for magnetization reversal within the bistable magnetic ground state.1 This energy barrier, which primarily depends on magnetic anisotropy,5,6h allows blocking of magnetization either parallel or antiparallel to the magnetizing field when this is removed below the so-called blocking temperature, TB, thus promoting the appearance of slow relaxation of magnetization.1 Among SMMs, those mononuclear in nature (also called Single-Ion Magnets, SIMs) have recently attracted enormous interest, because they can exhibit much stronger anisotropy than their polynuclear counterparts.6 This approach has revealed to be very convenient to achieve SMMs with improved properties, as shown by the fact that DyIII-based SIMs exhibit TB as high as 80 K.7 The superiority of SIMs over polynuclear SMMs lies in the fact that the anisotropy of the former can be finely regulated by controlling the electronic configuration of the metal centers, which depends on factors such as type and oxidation state of the metal ion, coordination number and geometry and ligand field strength.6h Although the highest values of U and TB have been reached with lanthanide-based SIMs,6c,d,i,l in the last decade the search for new SIMs has been expanded to transition metal ions.6g,i,k More specifically, that search was prompted by the discovery of a Fe(II) complex with trigonal pyramidal geometry exhibiting SIM behaviour with a very high effective energy barrier (Ueff).8 The most appropriate metal complexes for exhibiting SIM behaviour are those possessing: (a) low coordination numbers and oxidation states, because they exhibit weak ligand fields that favour sizable values of the orbital angular momentum (a large value of the angular momentum leads to a strong first-order spin–orbit coupling and consequently to a strong magnetic anisotropy9), and (b) non-integer spin metal ions (Kramers ions), because, in the absence of a magnetic field, neither direct phonon-induced nor QTM transitions between the MS states of the ground doublet can be induced by the modulation of the crystal field (van Vleck cancellation).10 Therefore, in principle, and conversely to that occurring in integer spin systems, the under-the-barrier tunnelling mechanism should not be operative in Kramers metal ions at zero field. The absence of fast QTM favours the observation of Orbach and Raman thermally activated relaxation processes.1 In light of the above concerns, and because Co(II) ions possess a non-integer spin ground state and can have strong magnetic anisotropy,6h,k the predominance of Co(II)-based SIMs, with a variety of geometries and coordination numbers (ranging from two to eight), is not unexpected.6e–g,k The strategy of using Co(II) metal ions with low coordination numbers to improve the SIM properties has been recently validated by the two-coordinated linear Co(II) complexes recently reported by Gao et al.11a and Long et al.11b The former complex of the formula [(NHC)Co(NDmp)] (NHC = N-heterocyclic carbene; Dmp = dimesitylphenyl)11a has been reported to have a relaxation barrier as high as 413 cm−1, whereas the second complex of the formula Co(C(SiMe2ONaph)3)2 (where Me is methyl and Naph is a naphthyl group)11b exhibits an unquenched orbital moment (L = 3) and an MJ = ±9/2 ground state and the highest effective energy barrier (Ueff = 450 cm−1) ever observed for a 3d-SIM.Ideal octahedral complexes also have strong magnetic anisotropy arising from the 4T1g crystal field ground term with L = 1 first order angular momentum. Moreover, small distortions of the Oh symmetry along four-fold and three-fold axes, leading to tetragonal (D4h) or trigonal (C3v) symmetries, can fully quench the first-order angular momentum.11a,b In this situation, magnetic anisotropy can arise from the second-order spin–orbit coupling leading to the development of zero field splitting (ZFS), which is characterized by the axial and rhombic anisotropy parameters D and E, respectively. It is worth noting that SIM behaviour has been observed not only for six-coordinated Co(II) complexes with D < 0 (easy-axis anisotropy)12 but also with D > 0 (easy-plane anisotropy).13 Nevertheless, the former are limited to a few examples, which, with one exception,12d present slow magnetization relaxation at zero dc field above 2 K,12 while the latter require the application of a magnetic field to show SIM behaviour (field-induced SIMs). Theoretical studies using basic principles have established that, at zero field, the electronuclear spin states arising from hyperfine interactions in six-coordinated Co(II) complexes with D > 0 have a negligible magnetic moment and, as a result, in no case SIM behaviour can be observed.14 However, in the presence of an applied magnetic field, the electronuclear spin states gradually attain a non-zero magnetic moment due to the Zeeman interactions, and then slow relaxation of magnetization can appear. It is worth mentioning that, in some cases, even in the presence of a dc field, six-coordinated Co(II) complexes with D > 0 do not show slow magnetization relaxation above 2 K.13d This fact can be due, among other reasons, to the existence of intermolecular dipolar interactions, which create an internal transverse magnetic field that favours under-the-barrier fast quantum tunnelling of magnetization (QTM) relaxation. Nevertheless, owing to the fact that the fast relaxation through QTM requires the existence of a thermal energy barrier, which is not possible for D > 0, some authors have suggested that the fast interconversion within the ground Kramers state at low temperature takes place through a zero-order temperature-independent direct process that is part of the intra-Kramers transition.15 In such cases, the use of magnetically diluted Co(II) complexes (prepared by cocrystalization with an isostructural ZnII compound) could eliminate the intermolecular dipolar interactions to an extent that “hidden SIM” behaviour could emerge.13b
Although numerous examples of structurally and magnetically characterized mononuclear isolated Co(II)-based SIMs have been reported so far, the number of extended Co(II) coordination polymers with SIM behaviour is limited to a few examples, most of them containing distorted octahedral metal ions.16 This is in a certain sense unexpected, because coordination polymers (CPs) are of great interest not only because they can exhibit exciting physical and chemical properties, particularly porous metal–organic frameworks (MOFs), but also because of their aesthetically fascinating structures.17 The combination of CPs and Co(II)-based SIMs in the same extended structure could present the following advantages: (i) the construction of Co(II)-based SIMs with different ligands in the axial positions is often easier to attain in the nodes of CPs with a 2D rigid scaffolding than in mononuclear systems. This is an invaluable tool for studying how the modification of the electronic effects of the axial ligands affects the magnetic anisotropy and SIM behaviour; (ii) the rigidity of the structural skeleton in CPs can reduce the spin–phonon coupling and consequently the relaxation rate, thus favouring the appearance of SIM behaviour; (iii) the magnitude of the dipolar/exchange magnetic interactions and, consequently, their effect on the SIM behavior can be tuned by playing with the length of the spacer ligand and (iv) they form an appropriate platform to analyse how the change of the exchangeable guest molecules in porous CPs affects the SIM properties.
It is well known that 2D square-grid heterometallic MII–AuI complexes can be obtained by assembling transition metal cations and dicyanoaurate anions.18 In these compounds, transition metal ions generally exhibit axially distorted octahedral geometries, with the same coordination environment in the equatorial plane and different neutral ligands in the axial positions and show, in some cases, interesting magnetic, vapochromic and luminescence properties.16c,d,f Some of the Co(II)-containing complexes, of the general formula {Co(L)2[Au(CN)2]2} (L = DMSO, DMF, Py), were prepared either by reacting the vapochromic complex {Co(μ-OH2)2[Au(CN)2]2} with certain VOCs (volatile organic compounds) containing nitrogen- or oxygen-donors in the solid state (Py, DMSO)18c or by reacting K[Au(CN)2] and Co(Ac)2·4H2O in DMF.18f Only in the case of the DMF counterpart, its X-ray single-crystal structure and dc magnetic properties were previously reported.18b,f In this paper, we report the synthesis, X-ray crystal structures, high-frequency and -field EPR spectroscopy (HFEPR), far-infrared magnetic spectroscopy (FIRMS), detailed dc and ac magnetic properties and theoretical calculations of the 2D square-grid heterometallic CoII–AuI cyanide-bridged complexes of the general formula {Co(L)2[(Au(CN)2]2}n, where L = DMSO, DMF, Py and PyPhCO (PyPhCO is benzoylpyridine). In these compounds, the Co(II) ions exhibit axially distorted octahedral geometries with the same coordination environment in the equatorial plane and different neutral ligands in the axial positions. The aim of this work is fourfold: (i) to analyse the role of the σ/π-bonding electronic effects of the axial ligands on the magnetic anisotropy. This analysis can be appropriately performed in the {Co(L)2[Au(CN)2]}n complexes, because the 2D framework is essentially preserved, so the bonding effects of axial ligands are essentially the only factor affecting the magnetic anisotropy. As far as we know, only one paper concerning the influence of the axial ligands on the magnetic anisotropy in 2D Co(II)-CPs has been reported so far. In that paper, the 2D skeleton of the reported complexes is made of a neutral spacer, whereas the axial ligands are anionic in nature.16n The results of these studies either did not reach any clear correlation between the magnetic anisotropy and the nature of the axial ligands or indicate that the magnetic anisotropy decreases with the distortion of the Co(II) coordination sphere from an ideal octahedron. Therefore, a methodical investigation of the influence of the σ/π electronic effects of the axial ligands on the magnetic anisotropy has not been reported yet; (ii) to study if the electronic effects of the diamagnetic Au(I) atoms connected by cyanate-bridging ligands to the Co(II) ions would have any effect on the magnetic anisotropy; and (iii) to learn if the long separation between Co(II) ions enforced by the dicyanoaurate ligand spacers (which prevents any magnetic exchange interaction between the Co(II)-based SIM nodes through the dicyanoaurate spacer) and the rigidity of the 2D framework would favour the observation of SIM behaviour.
Experimental
Synthetic procedures
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 991, 947, ν(S
N); 991, 947, ν(S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O).
O).
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1652, ν(C
N); 1652, ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1426, 1376, ν(CN).
O); 1426, 1376, ν(CN).
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1602, 1481, 1440, ν(C
N); 1602, 1481, 1440, ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) and ν(CN).
C) and ν(CN).
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N); 1662, ν(C
N); 1662, ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O); 1595, 1548, 1452, 1441, ν(C
O); 1595, 1548, 1452, 1441, ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) and ν(CN).
C) and ν(CN).
Physical measurements
Elemental analyses were performed at the “Centro de Instrumentacion Cientifica” (University of Granada) on a Fisons-Carlo Erba analyser model EA 1108. IR spectra were recorded on a Bruker Tensor 27 spectrophotometer by using ATR detection.Variable-temperature (2–300 K) magnetic susceptibility measurements were carried out on polycrystalline samples of 1–4 under an applied field of 1000 Oe using a Quantum Design SQUID MPMS XL-5 device. Alternating-current (ac) susceptibility measurements under different applied static fields were performed using an oscillating ac field of 3.5 Oe and ac frequencies in the 10–1500 Hz range. The experimental susceptibilities were corrected for the sample holder and diamagnetism of the constituent atoms using Pascal's tables. Pellets of the samples cut into very small pieces were placed in the sample holder to prevent any torquing of the microcrystals.
FIRMS experiments were performed at the National High Magnetic Field Laboratory using a Bruker Vertex 80v FT-IR spectrometer coupled with a 17 T vertical-bore superconducting magnet in a Voigt configuration (light propagation perpendicular to the external magnetic field). The experimental setup employs broadband terahertz radiation emitted by an Hg arc lamp. The radiation transmitted through the sample was detected using a composite silicon bolometer (Infrared Laboratories) mounted at the end of the quasioptical transmission line. Both the sample and bolometer were cooled by a low-pressure helium gas to a temperature of 4.6 K. The intensity spectra of the microcrystalline powder sample (∼7 mg) bonded by n-eicosane were measured in the spectral region between 14 and 730 cm−1 (0.42–22 THz) with a resolution of 0.3 cm−1 (9 GHz). To discern the magnetic absorptions, the spectra were divided by the reference spectrum, which is the average spectrum for all magnetic fields. Such normalized transmittance spectra are only sensitive to transmission changes induced by the magnetic field and therefore obscure nonmagnetic contribution to the intensity spectrum. All data analysis routine was implemented using an in-house written MATLAB code and the EPR simulation software package EasySpin.19 HFEPR spectra of 1–4 were recorded at 7 K on polycrystalline samples (20–25 mg) using a homodyne spectrometer at the EMR facility associated with a 15/17 T superconducting magnet and a frequency range from 52 to 426 GHz. Detection was provided with an InSb hot electron bolometer (QMC Ltd, Cardiff, UK). The magnetic field was modulated at 50 kHz for detection purposes. A Stanford Research Systems SR830 lock-in amplifier converted the modulated signal to dc voltage. The single-frequency spectra and their dependencies on the frequency were simulated using the SPIN software from A. Ozarowski.
Pulsed magnetization measurements
Low-temperature magnetization measurements were performed at IMR, Tohoku University, by means of a conventional inductive probe in pulsed magnetic fields. The temperature reached was as low as 0.4 K using a 3He cryostat.20 Polycrystalline specimens were mounted in a capillary tube made of polyimide. Samples of approximately 20 mg were not fixed within the sample tube so they aligned along the magnetic field direction. Subsequently, the magnetic field was applied several times until the orientation effect was saturated and the magnetization curves obtained in further shots were found to be identical.Powder diffraction measurements
The X-ray powder diffraction (XRPD) spectra of complexes 1–4 (Fig. S1†) were recorded on a (2θ) Bruker D2-PHASER system using CuKα (λ = 1.5418 Å) radiation and a LINXEYE detector, from 5 to 50° (2θ) at a scanning rate of 0.5° 2θ min−1. Fig. S1† also shows the comparison between the XRPD patterns of the bulk samples used for magnetic measurements and for recording HFEPR and FIRMS spectra and those derived from the X-ray crystal structures of 1–4.Single-crystal structure determination
Suitable crystals of 1, 3–4 were mounted on a glass fibre and used for data collection. X-ray diffraction data were collected using a Bruker D8 Venture diffractometer (MoKα radiation, λ = 0.71073 Å) fitted with a CCD area detector and equipped with an Oxford Cryosystems 700 series Cryostream device. Unit-cell parameters were determined and refined on all observed reflections using APEX2 software.21 Corrections for Lorentz polarization and absorption were applied using SAINT and SADABS programs, respectively.22,23The structures were solved by direct methods and refined by the full-matrix least-squares method on F2 using the OLEX2 program.24 All non-hydrogen atoms were refined anisotropically. Hydrogen atom positions were calculated and isotropically refined as riding models to their parent atoms. A summary of selected data collection and refinement parameters can be found in the ESI (Table S1†) and CCDC (2020915–2020918†).
Computational methodology
The electronic structure and magnetic properties have been computed using relativistic CASSCF/NEVPT2 methods25 with the def2-TZVP basis set,26 including the auxiliary basis sets for correlation and Coulomb fitting for all the atoms.27 Splitting of the d-orbitals was obtained with a new ab initio ligand field theory that was recently developed.28 The splitting of d-orbitals due to the ligand field has been computed with the ab initio ligand field theory using 10 quartet and 40 doublet states. All calculations were performed using the ORCA 4.0.1 quantum chemistry program.29 Spin Hamiltonian parameters (D, E and g-tensor) were computed using the effective Hamiltonian S = 3/2. In this case, spin–orbit effects were included using the quasi-degenerate perturbation theory (QDPT)30 and scalar relativistic effects were taken into account using the DKH (Douglas–Kroll–Hess) procedure.31 In both cases, the employed active space includes seven electrons in five 3d orbitals of Co(II) CAS (7,5). We have included all 10 states for the 2S + 1 = 4 (quartet) states arising from the 4F and 4P terms of Co(II), and all the 40 states for the respective 2S + 1 = 2 (doublet) states arising from the 2P, 2D (twice), 2F, 2G and 2H terms of the Co(II) ion.Results and discussion
2D complexes of the general formula {Co(L)2[Au(CN)2]2}n (where L = DMSO (1), DMF (2), Py (3) and PyPhCO (4); PyPhCO is benzoylpyridine) were obtained by the assembly a Co(II) salt and [Au(CN)2]− anions in the presence of the ligand L (coming from the solvent in conventional solution methods or from the corresponding reactive, py or PyPhCO, in hydrothermal methods). Specifically, compound 1 was prepared by the reaction of a solution of Co(BF4)2·6H2O with K[Au(CN)2] in DMSO and using a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Co/Au molar ratio. The same reaction but using Co(ClO4)2 as a cobalt salt and DMF as a solvent afforded 2. Complexes 3 and 4 were obtained by hydrothermal methods using the same Co/Au molar ratio and reagents as for 1, and pyridine (in excess) or 4-benzoylpyridine (in a 1
2 Co/Au molar ratio. The same reaction but using Co(ClO4)2 as a cobalt salt and DMF as a solvent afforded 2. Complexes 3 and 4 were obtained by hydrothermal methods using the same Co/Au molar ratio and reagents as for 1, and pyridine (in excess) or 4-benzoylpyridine (in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio). In all cases, pink crystals were obtained. The IR spectra of these compounds present ν(CN) stretching bands at ∼2170 cm−1, clearly indicating the bridging nature of the dicyanoaurate building blocks in 1–4 and their bidimensional nature. The X-ray crystal structures confirm the 2D nature of these complexes.
2 molar ratio). In all cases, pink crystals were obtained. The IR spectra of these compounds present ν(CN) stretching bands at ∼2170 cm−1, clearly indicating the bridging nature of the dicyanoaurate building blocks in 1–4 and their bidimensional nature. The X-ray crystal structures confirm the 2D nature of these complexes.
X-ray structures
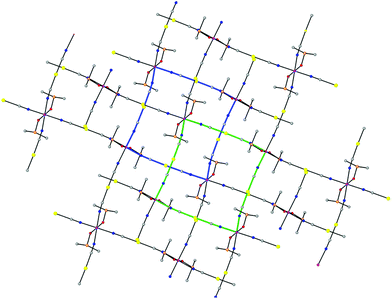
Compound 1 had already been reported but its X-ray crystal structure had not been solved. We have succeeded in obtaining a suitable crystal for X-ray crystal structure determination. The structure of 1 is made of parallel sheets lying in the bc plane, which are built from edge-sharing slightly distorted square-planar {NC–Au–CN–Co}4 units with the Co(II) ions located at the corners and the [Au(CN)2]− bridging anions at the edges (Fig. 1). Within each square unit, the Co(II)–Co(II) distances between diagonally opposite atoms are 14.368 Å and 14.900 Å, whereas those involving atoms connected by [Au(CN)2]− groups along the edges are 10.344 Å and 10.355 Å. The Co(II) ions exhibit a slightly tetragonally compressed CoN4O2 coordination sphere, which is formed by the coordination of four nitrogen atoms coming from the [Au(CN)2]− anions in the equatorial plane with Co–N distances in the range of 2.116 Å–2.134 Å, and two oxygen atoms belonging to the DMSO molecules in the axial positions with shorter Cu–O distances of 2.084 Å and 2.076 Å. The cis and trans angles are found to be in the ranges of 88.1°–91.2° and 176.3°–179.5°, respectively. Analysis of the six-coordination Co(II) coordination polyhedron by the continuous shape measure (CShM) method showed that the geometry of the CoN4O2 coordination environment is very close to an ideal Oh, as indicated by the very low value (SOh = 0.038) of the continuous shape measure parameter (the values for six-coordinated ideal polyhedra other than Oh are larger than 16, see Table S2†).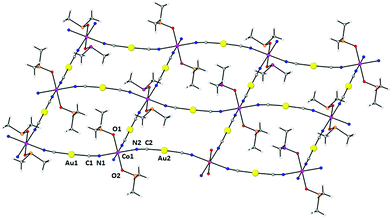 | ||
| Fig. 1 Perspective view of a fragment of the 2D structure of 1, together with the atom labelling scheme. Colour code: Au (yellow), Co (pink), N (blue), C (grey), O (red) and S (orange). | ||
The Co–NC–Au–CN–Co edges are not linear but slightly bent and located above and below the plane of the Co(II) ions (Fig. 1) with CN–Co and NC–Au angles in the ranges of 169.8°–171.2° and 175.2°–175.7°, respectively. As expected, the two crystallographically independent [Au(CN)2]− anions are almost linear with C–Au–C angles of 176.25° and 177.60°. The edges at the opposite sides of each {NC–Au–CN–Co}4 unit have different concavities (one is upward and the other downward) and the CoN4 planes of diagonally opposite Co(II) atoms are parallel, whereas the angle between the planes of neighboring Co(II) atoms connected by [Au(CN)2]− anions is 37.14°. As a result, the edge-sharing [Co–NC–Au–CN–Co]n chains along the b and c directions have a wave shape and the layers show some kind of “egg-carton” pattern.
Layers stack in such a way that each of them shifts with regard to the next-neighbouring ones so the Co(II) atoms of one layer lie above and below the centers of the square units of the neighbouring layers, giving rise to an ABAB… sequence pattern (Fig. 2).
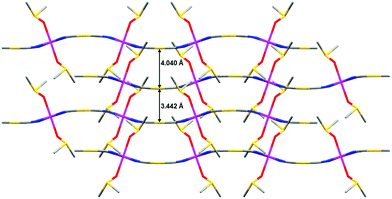
The Au⋯Au distance inside each AB pair of layers is 3.442 Å, whereas the Au⋯Au distance between pairs of AB layers is 4.040 Å. Therefore, the layers of each AB pair are held together by aurophilic interactions (see Fig. 3). The DMSO molecules are oriented in such a way that they penetrate the holes of neighbouring layers, which allow short interlayer distances. It is worth mentioning that the shortest interlayer Co(II)⋯Co(II) distance of 7.401 Å, occurring between the atoms of the two layers of the AB bilayer, is shorter than the shortest intralayer Co(II)⋯Co(II) distance of 10.344 Å.
The structure of 2 was previously reported18b and it is very similar to that of compound 1. The main differences between their structures are as follows: (i) the average Co–O and Cu–N distances in 2 of 2.090 Å and 2.096 Å are slightly larger and shorter, respectively, than those for compound 1 of 2.08 Å and 2.124 Å. Moreover, the distortion of the CoN4O2 coordination environment from Oh is slightly larger for 2 (SOh = 0.103). (ii) The CN–Co and NC–Au angles for 2 (with values in the ranges of 168.6–173.5 and 173.8–177.8°, respectively) are slightly larger and the dihedral angle between neighbouring CoN4 equatorial coordination planes (24.29°) is lower than those observed for 1 (see above). These structural features lead to more planar layers for 2 than for 1. (iii) The Co–O–S–C torsional angle of 1 is somewhat smaller than the Co–O–C–C torsional angle of 2, so the DMF molecules are able to penetrate to a larger extent in the holes of the neighbouring layer forming the AB pair, leading to a shorter Au⋯Au distance of 3.195 Å. As a result, the Au⋯Au distance between two pairs of AB layers for 2 (5.345 Å) is significantly larger than that for 1. (iv) The Co⋯Co interlayer distance is slightly larger for 2 (7.557 Å).
The structure of the compound {Co(pyridine)2[Au(CN)2]2}n (3) was previously solved from a model based on the X-ray structures of the compounds {Co(DMF)2[Au(CN)2]2}n and Cu[Au(CN)2]2(pyridine)2. The resolution was accomplished using a simulated annealing algorithm to maximize the agreement between the experimental and calculated X-ray powder diffractograms. In this way, it was possible to obtain the coordinates of the building block atoms but not the orientation of the pyridine molecules. In this case, we succeeded in obtaining suitable single crystals for X-ray crystallography. The structure of 3 is almost coincident with that determined from the X-ray powder data and similar to those of compounds 1 and 2 (Fig. 4). The most important differences with the structures of 1 and 2 are: (i) in 3, the cobalt atom is located on a center of symmetry and its tetragonally compressed octahedral CoN6 coordination sphere is less distorted than in 1 and 2, as indicated by the continuous shape measure parameter (SOh = 0.003); (ii) the Co–X axial and equatorial distances are longer for 3 (Co–N1 = 2.153 Å, Co–N2 = 2.149 Å and Co–N3 = 2.131 Å); (iii) the dihedral angle between neighbouring equatorial planes for 3 is only 4.5°, leading to almost planar square-grid layers; (iv) in contrast to 1 and 2, the layers are not arranged in pairs and are equally separated with an Au⋯Au distance of 4.213 Å. Therefore, there are no aurophilic interactions between the gold atoms; and (v) the pyridine molecules penetrate the neighbouring layers so there exist π⋯π interactions between the pyridine rings above one layer and below the next-neighbouring layer with a centroid–centroid distance of 3.398 Å. The shortest Co⋯Co distance of 7.135 Å corresponds to atoms located in neighbouring layers.
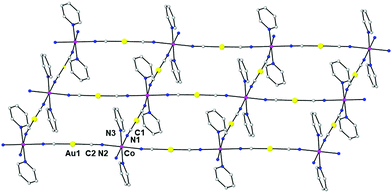 | ||
| Fig. 4 Perspective view of a fragment of the 2D structure of 3, together with the atom labelling scheme. Colour code: Au (yellow), Co (pink), N (blue) and C (grey). | ||
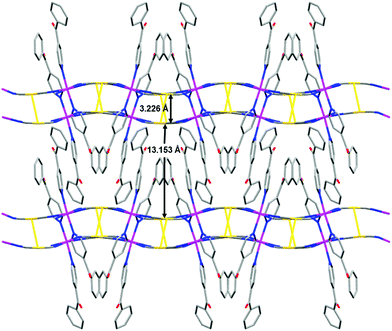
The structure of 4 is very similar to that of 1 in that (i) the Co–NC–Au–CN–Co fragments are bent and adopt an analogous configuration around the Co(II) ions; (ii) the angle between the CoN4 equatorial plane (formed by the cyanide nitrogen atoms) is 32.38° and the layers assume an egg-carton like pattern; and (iii) the layers are held together in pairs by strong aurophilic interactions (3.226 Å) forming bilayers (Fig. 5). However, there are significant differences, such as: (i) the CoN6 coordination sphere in not tetragonally compressed but tetragonally elongated. The mean value of the axial Co–N distances (2.194 Å) is larger than that corresponding to the Co–N equatorial ones (2.105 Å) and SOh = 0.126. (ii) As the PyPhCO ligand is long and there exist π⋯π interactions involving the pyridine ring and the phenyl ring of the PyPhCO molecules coordinated to neighbouring bilayers (with a centroid–centroid distance of 3.77 Å), these are rather well separated (13.153 Å). As expected, the shortest Co(II)⋯Co(II) distance (7.436 Å) occurs between the atoms of the two layers of the bilayer.
Electronic structure calculations
The continuous shape measures (see Table S2†) indicate that these compounds present a very small angular distortion from an ideal octahedron, as the shape measure SOh values are in the 0.003–0.126 range. If the radial distortion is taken into account, then these compounds could be considered as possessing compressed or elongated tetragonal geometries. Nevertheless, when SOh values are very small, like in 1–4, the axial distortion must be very small too. The distortion is a result of different factors such as the Jahn–Teller distortion associated with the 4T1g ground state of the ideal Oh symmetry, binding anisotropy and solid state effects. The tetragonal distortion splits the 4T1g ground term of the ideal Oh symmetry into the 4A2g (in D4h notation) and 4Eg terms separated by an energy gap, Δ, which increases with tetragonality. For tetragonal compression, Δ is positive and the 4A2g crystal field term is at a lower energy (easy-plane anisotropy), whereas for tetragonal elongation, Δ is negative and the ground term is 4Eg (easy-axis anisotropy). For the former case, the second-order spin–orbit coupling (SOC) splits the ground 4A2g term and the 4Eg term into two and four Kramers doublets (KDs), respectively, and this situation can be treated in a simple way as zero-field splitting (ZFS) within the spin Hamiltonian formalism (Fig. S2†).6h For tetragonal elongation, the ground crystal-field term 4Eg carries first-order orbital contribution. In this case, the simple ZFS approach is generally no longer applicable to analyse the electronic properties and consequently the Figgis–Griffith approach should be used.32For heteroleptic complexes, such as 1–4, the Co–Npy distances are generally longer than the Co–O distances. In spite of this, the former atoms produce larger crystal field effects than the latter atoms. In these circumstances, the determination of the effective distortion and the nature of the ground term is a rather difficult task. In view of this, and in order to analyse properly the magnetic properties and electronic structure of compounds 1–4, we have performed ab initio CASSCF/NEVPT2 calculations using the ORCA program.29 We have used the ab initio ligand field theory (AILFT)28 to calculate the splitting of d-orbitals provoked by the ligand field (see Fig. S3 and S4†). These calculations have been carried out excluding and including the Au(I) atoms. The ligand field parameters obtained from these calculations are presented in Table 1.
| Compound | B, cm−1 | C/B | Zeta, cm−1 | Relative orbital energies, cm−1 | |||
|---|---|---|---|---|---|---|---|
| Excluding gold(I) atoms | |||||||
| 1 | 1057 | 3.79 | 526(4) | 419 | 680 | 7380 | 9724 |
| 2 | 1060 | 3.76 | 525(4) | 125 | 613 | 7385 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420 420 |
| 3 | 1057 | 3.76 | 525(5) | 469 | 1140 | 9320 | 9742 |
| 4 | 1061 | 3.72 | 524(5) | 244 | 1269 | 8065 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 109 109 |
| Including gold(I) atoms | |||||||
| 1 | 1048 | 3.85 | 526(5) | 646 | 1174 | 8673 | 8887 |
| 2 | 1048 | 3.84 | 526(5) | 674 | 911 | 8926 | 9370 |
| 3 | 1056 | 3.76 | 525(5) | 46 | 654 | 8051 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 343 343 |
| 4 | 1047 | 3.82 | 525(5) | 58 | 445 | 9292 | 9475 |
As it can be observed, all complexes have a quartet ground state emphasizing the weak ligand field Dq/B ∼ 1. The ligand field strength calculated as the energy gap between the barycenters of the orbitals arising from the splitting of the eg and t2g sets in Oh symmetry increases for both calculations (excluding and including gold(I) atoms) in the order: 4 ≥ 3 > 2 > 1 (see Table 1 and Fig. 6). This order is not unexpected because: (i) the N-coordinated pyridine derivatives are better σ-donor ligands than the O-coordinated DMF and DMSO ligands, and (ii) DMSO and DMF are very weak π-donors when coordinated through the oxygen atom, whereas pyridine derivatives are weak π-acceptors. Both points favour the existence of a stronger ligand field for 4 and 3 than for 1 and 2.
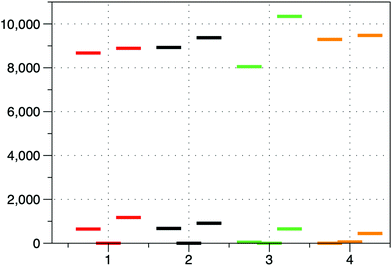 | ||
| Fig. 6 Splitting of the d-orbitals for compounds 1–4 using the ab initio ligand field theory (AILFT) including gold(I) atoms. | ||
When gold(I) atoms were excluded from calculations, the d-orbital energy diagrams indicate that complexes 1–4 exhibit a 4A2g ground state and therefore the spin Hamiltonian shown below can be used:6h
| H = D[Sz2 − S(S + 1)/3] + E(Sx2 − Sy2) + gμBHS | (1) |
The sign and magnitude of D can be rationalized by evaluating the Dii components (i = x, y, z), which depend on the excitation energies, as well as on the ml values of the orbitals implicated in the lowest energy transition.6h Thus, when the excitation energy involves two orbitals with Δml = ±1, Ms = ±1/2 KD is found at a lower energy and the contribution to D is positive (easy-plane anisotropy). However, when the excitation between d orbitals does not involve the change of ml, Ms = ±3/2 KD is stabilized and a negative contribution to D is obtained (easy-axis anisotropy). For complexes 1–4, the lowest energy transition involves the dyz and dxy orbitals with ml = ±1 and ±2, respectively, and therefore D must be positive. The CASSCF/NEVPT2 calculations using an effective spin Hamiltonian (eqn (1)) confirm this prediction. Thus, excluding gold(I) atoms, both calculations afford large positive D values (see Table 2) for 1–4. The D values corresponding to compounds 1 and 2 are significantly larger than those found for compounds 3 and 4. This result is not unexpected because the energy gap between dyz (highest double-occupied orbital) and dxy (lowest single-occupied orbital), which is proportional to the difference in the strength of π-interactions between the axial and equatorial ligands, is larger for 3 and 4 than for 1 and 2 and, therefore, smaller D values are expected for the former than for the latter.
| Compound | D, cm−1 | E/D | g 1 | g 2 | g 3 |
|---|---|---|---|---|---|
| 1 | 114 | 0.179 | 1.810 | 2.924 | 2.374 |
| +Au | 80 | 0.203 | 1.918 | 2.437 | 2.795 |
| 2 | 131 | 0.039 | 1.650 | 2.686 | 2.383 |
| +Au | 111 | 0.253 | 1.683 | 2.198 | 2.989 |
| 3 | 89 | 0.170 | 1.853 | 2.470 | 2.804 |
| +Au | 85 | 0.095 | 1.938 | 2.578 | 2.713 |
| 4 | 86 | 0.117 | 1.866 | 2.551 | 2.763 |
| +Au | 99 | 0.053 | 1.926 | 2.551 | 2.701 |
Although there exist contributions to D other than those coming from the low-lying spin–orbit free excited quartet states (those arising from the 4T1g term in an ideal Oh symmetry), the latter should be by far the most important, because Q1 and Q2 are those closest in energy to the ground quartet state. This expectation is confirmed by NEVPT2 calculations, which show that the largest positive contribution to D comes from the two first excited quartet states, Q1 and Q2 (see Table 3). As expected, the largest contributions from these excited quartet states occur in 1 and 2, which have the excited quartet states at lower energy than 3 and 4. As we can see from Table 3, the splitting of the ground 4T1 term essentially determines the magnetic anisotropy, whereas contributions from other states to ZFS are no more than 30%.
| Compound | EQ1 | Contribution to D | EQ2 | Contribution to D |
|---|---|---|---|---|
| Excluding gold(I) atoms | ||||
| 1 | 312 | 57 | 664 | 35 |
| 2 | 278 | 58 | 388 | 54 |
| 3 | 608 | 40 | 1150 | 24 |
| 4 | 794 | 38 | 1163 | 27 |
| Including gold(I) atoms | ||||
| 1 | 648 | 38 | 1346 | 22 |
| 2 | 215 | 56 | 1029 | 26 |
| 3 | 694 | 34 | 800 | 38 |
| 4 | 502 | 44 | 635 | 37 |
In view of the above considerations, it is reasonable to assume that in octahedral Co(II) complexes with weak σ-donor N-cyanide ligands33 in the equatorial plane, the substitution in the axial positions of weak σ-donor/weak π-donor ligands, such as DMF or DMSO, by intermediate σ-donor/weak π-acceptor ligands produces a decrease in the D value.
The rhombicity parameter E depends on the splitting of dxz and dyz orbitals. There are two sources of non-zero rhombicity; one is the asymmetry in the equatorial plane, since the Co–NC bond lengths are slightly different. Another source is the anisotropy of the π-donor orbitals in the xz and yz planes. The energy gap between dxz and dyz orbitals is relatively small and consequently the complexes exhibit small to intermediate E/D parameters.
After including gold(I) atoms, the energies of the d-orbitals undergo significant changes with respect to those calculated when gold(I) atoms are excluded (see Fig. 6 and Table 1). Thus, the energy gap between the highest double-occupied and the lowest single-occupied orbitals decreases for 2 and 4, whereas it increases dramatically for 1 and slightly for 3. This results in a significant decrease of D for 1 and a modest increase for 4, whereas 3 varies into a much lesser extent. Unexpectedly, 2 undergoes a considerable decrease in its D value after including gold(I) atoms in the calculations. For 1, D decreases to such an extent that it becomes lower than those for complexes 3 and 4, leading to the following anisotropy order: D (2) > D (4) > D (3) > D (1). Large rhombicity values (E/D ∼ 1/3) as observed for 2 lead to the mixing of the |Ms| = 3/2 and |Ms| = 1/2 wavefunctions, which can inverse the sign of D (the effective g-tensor of the ground KD exhibits easy-axis anisotropy) or loses its physical meaning. Complexes 1 and 2 have the largest splitting between double-occupied orbitals and consequently exhibit the largest E/D parameters.
In view of the above theoretical results including gold(I) atoms, we can conclude that the presence of very heavy metal atoms, like gold(I), connected to the cobalt(II) ions through bridging ligands, can significantly modify the energy of d-OA, which ultimately affects the D values and rhombicity of axially distorted CoII complexes. This effect is likely to be due to a redistribution of the electron density through the covalent cyanide bridges. As far as we know, there are no other reported examples of theoretical calculations on the influence of diamagnetic electron-rich 5d closed shell ions/atoms, M, on the magnetic anisotropy of the CoII ion in CoII–CN–M systems. However, ab initio calculations on CoII–CN–WV systems showed that the magnetic anisotropy of the cobalt(II) atom was also affected by the inclusion or exclusion of W.34
Static magnetic properties
The dc magnetic properties of 1–4 have been studied in the 2–300 K temperature range under an applied magnetic field of 1000 Oe, and are given in the form of the temperature dependence of χMT (χM is the molar magnetic susceptibility) in Fig. 7 (the plot for complex 1 is given as an example) and Fig. S5–S7† (for compounds 2–4, respectively).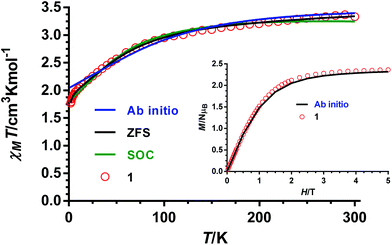 | ||
| Fig. 7 Temperature dependence of χMT for compound 1 (red circles). Black and green solid lines represent the best fit to eqn (1) and (2), respectively. Blue solid line generated from the ab initio calculated energy levels. | ||
The χMT values at room temperature for complexes 1–4 of 3.33, 3.035, 3.090 and 3.083 cm3 mol−1 K, respectively, are larger than the expected value for an orbitally non-degenerate ground state with S = 3/2 of 1.875 cm3 mol−1 K, which is due to the unquenched orbital contribution of the Co(II) ion in a slightly distorted octahedral geometry. By lowering the temperature, the χMT product diminishes first slightly from room temperature to around 100 K and then in a deeper manner to reach values of 1.77, 1.81, 1.64 and 1.79 cm3 mol−1 K at 2 K for 1–4, respectively. The decrease of χMT until 10 K is mainly due to spin–orbit coupling (SOC) effects, whereas below this temperature, the faster diminution of χMT is due to both the single-ion anisotropy and weak intermolecular antiferromagnetic interactions. The latter are not unexpected in view of the fact that the shortest intermolecular cobalt–cobalt distances are found to be in the range of 7.1–7.6 Å. The field dependence of the magnetization at 2 K is almost saturated at 5 T reaching values in the 2.31–2.37μB range. These values are significantly lower than the value expected for an S = 3/2 ground state with g = 2, thus indicating the presence of significant anisotropy.
The data for the temperature dependence of χMT and the field dependence of the magnetization at 2 K for 1–4 were simultaneously fitted with the ZFS Hamiltonian of eqn (1) (it has been assumed, according to theoretical calculations indicated above, a 4A2g ground term for these complexes), using the PHI program (Fig. 7 and Fig. S5–S7†).35 This approach is appropriate because the two low-lying KDs arising from the 4A2g ground term by second-order SOC are almost the only populated below ∼50 K. A TIP term has to be included to account for the thermal depopulation of the higher energy Kramers doublets. It is worth noting that this strategy is always valid below 100 K and frequently up to room temperature. Finally, a mean field term was also introduced to take into account the intermolecular interactions. It should be mentioned that this approach leads to large g values (∼2.5). As the fittings of the magnetic data are not sensitive to the E value, this parameter was fixed to zero and isotropic g tensors were used to avoid overparametrization. The following magnetic parameters were obtained from the fits: D = +68(1) cm−1, g = 2.610(7), zJ = −0.024(2) cm−1 and TIP = 620(6) × 10−6 cm3 mol−1 for 1, D = +90(2) cm−1, g = 2.687(6), zJ = −0.0291(2) cm−1 and TIP = 477 (3) × 10−6 cm3 mol−1 for 2, D = +75(2) cm−1, g = 2.531(7), zJ = −0.0362(3) cm−1 and TIP = 778(1) × 10−6 cm3 mol−1 for 3 and D = +80(1) cm−1, g = 2.605(1), zJ = −0.019(2) cm−1 and TIP = 90(4) × 10−6 cm3 mol−1 for 4. It is worth noting that virtually the same quality fits and parameters were obtained for negative D values. Nevertheless, based on theoretical calculations the D values must be positive.
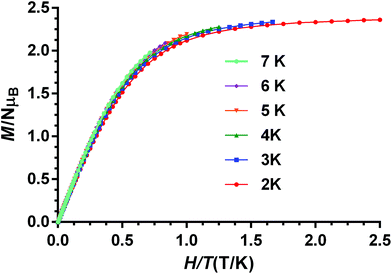
The fact that the M vs. H/T isotherms for compounds 1–4 depend only slightly on the temperature (the changes of the thermal depopulation of the two Kramers doublets below 7 K are almost negligible) and practically superimpose in a single master curve (see Fig. 8 for compound 1 and Fig. S8–S10† for compounds 2–4) confirm that ZFS is very large for these compounds.
The D values experimentally obtained from the magnetic data do not follow the same order as those calculated theoretically excluding gold(I) atoms (Table 2), but they do follow the order of the D values calculated including gold(I) atoms. However, as usual, the theoretical values are overestimated with regard to the experimental ones. The difference between the experimental and calculated D values is most likely due, among other reasons, to limitations inherent to the theoretical methods, certain inaccuracy of the magnetic data, and the use of isolated mononuclear models for calculations when the real structure is extended.
In order to confirm the sign and magnitude of Δ, and therefore the nature of the ground term for these compounds, the magnetic susceptibility data for 1–4 were also analysed with a Figgis–Griffith Hamiltonian that takes into account: (i) the first order SOC effects associated with the 4T1 ground term of the octahedral Co(II) ion, using the T,P isomorphism with an effective orbital moment L = 1; (ii) an axial distortion of the octahedral geometry and (iii) Zeeman interactions. The corresponding Hamiltonian can be written as:32
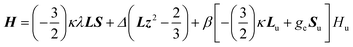 | (2) |
In view of this, the use of the phenomenological approach based on the zero-field splitting Hamiltonian for 2 and 4 is more than questionable and therefore the experimentally and calculated D values for these compounds could be taken with caution.
FIRMS/HFEPR
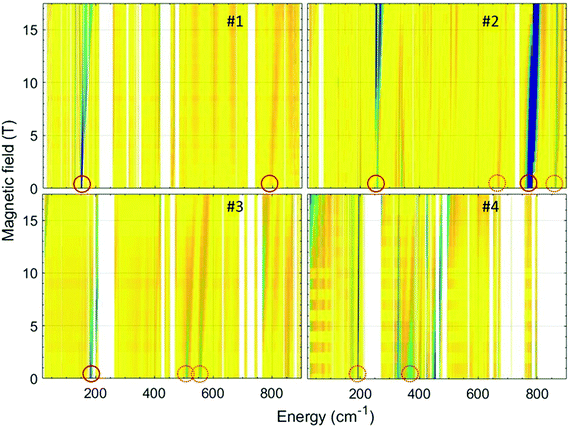
In order to accurately determine the magnitude of the ZFS in the current series of compounds, we used FIRMS. This technique allows one to directly assess the zero-field (zf) energy gap(s) between the lowest-energy Kramers doublets (KDs) in an S = 3/2 spin system. However, no information on the rhombicity of the ZFS can be obtained for KDs. For that purpose, a combination of FIRMS with HFEPR (vide infra), whenever applicable, is optimal. The combined maps of FIRMS turning points of compounds 1–4 are shown in Fig. 9.As it can be observed in Fig. 9 (top left), a zf magnetic transition is clearly recognizable at 151.2 cm−1 in the spectrum of compound 1, which readily yields the value of the energy gap between the ground and first excited KD arising from the 4A2g terms, δ (δ = 2(D2 + 3E2)1/2). The same complex produced satisfactory HFEPR spectra characteristics for an S = 3/2 spin state with positive D (Fig. S11 and Table S5†). From these spectra, we were able to obtain through simulations an estimate of the ZFS tensor rhombicity (E/D up to 0.17) and the following g-values: gx = 2.47, gy = 2.48, gz = 2.10. Using the E/D ratio determined by HFEPR, one can separate δ into D = 71.8 cm−1 and E = 12.4 cm−1 with a caveat that the value for E represents a maximum rather than a fixed number. These FIRMS/HFEPR results are quite similar to those obtained for other cobalt(II) complexes with a distorted octahedral CoN4O2 environment.38 It is worth mentioning that the obtained D value is very close to that obtained from dc magnetic measurements of 68 cm−1. The FIRMS spectra also reveal another magnetic transition at 793 cm−1, which corresponds to the excited Kramers doublet next to the S = 3/2 level. This energy is in excellent agreement with the value 785 cm−1 calculated using the spin–orbital coupling correction.
The FIRMS spectrum of compound 2 (Fig. 9, top right) shows a strong zf magnetic transition at 258 cm−1 and another very intense one at 777 cm−1. In addition, at least two weaker transitions appear at 665 and 863 cm−1. In this case, the observed transitions cannot be related to ZFS parameters as Δ is negative leading to a 4Eg ground term. The observed spectrum is therefore more likely due to transitions between KDs arising from the 4Eg term with a rhombic splitting. Correspondingly, the HFEPR spectra cannot be simulated using S = 3/2 spin Hamiltonian parameters and were simulated using instead effective spin S = 1/2 parameters (Fig. S12 and Table S4†). It is worth mentioning that the g values obtained from this simulation (gx = 2.65, gy = 2.95 and gz = 7.363) are close to those obtained for the ground Kramers doublet from CASSCF calculations (Table S3†) and magnetic measurements (eqn (2)) and support the easy-axis axial anisotropy (Δ < 0) of this complex. The CASSCF calculations using spin–orbital coupling correction provide good agreement for the first excited KD (255 cm−1), whereas the next high-energy KDs at 447 cm−1 and 834 cm−1 disagree with the experimental observations.
In the FIRMS spectrum of compound 3 (Fig. 9, bottom left), there appears a zf magnetic transition at 183 cm−1, which readily yields the value of δ. A transition within the ground MS = ± 1/2 KD shows up at a high magnetic field and low energy (upper left corner of the map), confirming the positive sign of D. In addition, there are also two weak zf magnetic transitions at 510 and 577 cm−1. The HFEPR spectra can be tentatively simulated with an S = 3/2 spin Hamiltonian. Using the E/D value estimated from HFEPR (Fig. S11 and Table S5†), the following parameters were obtained from the lowest energy zf FIRMS transition: D = 91.3 cm−1 and E = 3.7 cm−1. The D value is larger than but not too far from that obtained from the dc magnetic data of 75 cm−1.
The FIRMS for compound 4 (Fig. 9, bottom right), unexpectedly, does not reveal clearly any zf magnetic transition, although a remarkable spectral feature is observed at 193 cm−1. This feature shifts only slightly with full magnetic field sweep (∼1 cm−1/17 T) and preserves the intensity from spreading in the high-field range. Such behaviour is untypical of an anisotropic ZFS transition and is attributed to a magneto-elastic coupling with a phonon mode at 193.3 cm−1. Noticeably, CASSF calculations indicate the first excited KD to appear at the energy of 199 cm−1. However, we assume that the zf transition is located in the spectral range between 210 and 270 cm−1, which is non-transparent for the far-IR radiation and, therefore, hinders its direct observation. The evidence of this hypothesis is evolving of the absorption in the vicinity of 270 cm−1 at high magnetic fields (Fig. 9). There is another weak magnetic feature at 367 cm−1, which can be associated with high-energy Kramers doublets.
The HFEPR spectra of 4 cannot be simulated using S = 3/2 spin Hamiltonian parameters and were simulated using instead effective spin S = 1/2 parameters (Fig. S12 and Table S4†). A summary of experimental and calculated spin Hamiltonian parameters is presented in Table S5.†
Dynamic magnetic properties
Temperature and frequency dependence studies of the dynamic ac magnetic susceptibility measurements were performed under a 3.5 Oe alternating field at low temperature on complexes 1–4 with the aim of knowing if they show slow magnetization relaxation and, if so, to accomplish a comparative study of their dynamic magnetic properties. Unfortunately, none of the compounds show out-of-phase signals (χ′′M) above 2 K at zero applied dc field. This fact is not unexpected because for a Kramers ion like Co(II) with D > 0, the electronuclear spin states emerging as a consequence of the hyperfine interactions have, if any, negligible magnetic moments in the absence of a magnetic field, and therefore does not present slow magnetization relaxation. In contrast, the application of an applied dc field makes the electronuclear spin states gain magnetic moments and consequently slow relaxation could be observed if the compound behaves as a SMM.14 In view of the above considerations, we have analysed the field dependence of the ac magnetic susceptibility at T = 2 K for complexes 1–4 and for dc magnetic fields varying between 0.025 and 0.3 T. The goal of this study is threefold: (i) to learn if these compounds exhibit field induced slow magnetization relaxation, (ii) to investigate how the magnetization relaxation changes with the applied magnetic field and (iii) to choose the optimal field at which the relaxation is the slowest. The application of a dc magnetic field induces a clear frequency dependency of the in-phase (χ′M) and out-of-phase signals below 8 K for 1 and 3 and below 6 K for 2 and 4 (Fig. S13, S15, S19 and S23†), thus indicating the existence of slow magnetization relaxation. It is worth noting that below 0.1 T only one relaxation process appears, whereas for Hdc > 0.1 T, a second and slower relaxation process begins to emerge. This slow field induced relaxation process is rather common for Co(II) SIMs that are subjected to a magnetic field and has its origin in either: (i) a spin–phonon direct relaxation process stimulated by the split of the Kramers degeneration under the applied magnetic field (as the energy gap between the two MS ground states increases with the field, the phonon density also increases with an energy equal to this gap)39 or (ii) intermolecular interactions.40The relaxation times (τ) for the fast relaxation process at 2 K and at different fields were obtained from fitting the frequency dependence of the out-of-phase signal to the Debye model (Fig. 10 and Fig. S13 and S22†). As it can be observed in Fig. 10 and Fig. S14,† for complexes 1 and 2, 1/τ remains almost constant for fields below 0.1 T and then exponentially increases with the field, which is characteristic of a direct process. For complex 3, the field dependence of the ac data could not be correctly fitted to the Debye model because the peaks lie above the studied frequency range (Fig. S18†). For complex 4, the field dependence of τ−1 (Fig. S22†) shows that for fields below 0.1 T, τ−1 decreases as the field increases, which indicates the progressive quenching of either QTM or zero-order direct processes.15 For Hdc > 0.1, τ−1 strongly increases as the field increases, pointing out the predominance of a direct relaxation process.
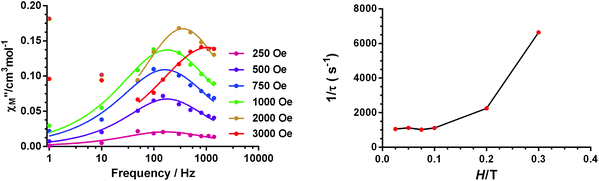 | ||
| Fig. 10 Field dependence of the out-of-phase signal (χ′′M) at 2 K for 1 (left). Field dependence of the relaxation times (right). | ||
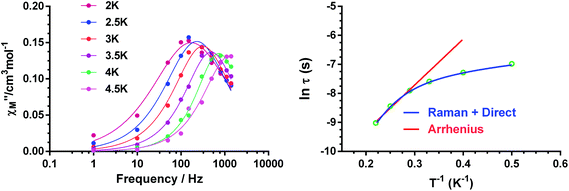
In view of the above facts, it appears that at very low temperature, complexes 1 and 2 show a predominant direct relaxation process with a very small contribution of QTM (or zero-order direct process). We carried out field- and frequency-dependent ac susceptibility measurements below 10 K at 0.1 T, because at this field the signals exhibit the strongest intensity for the slowest relaxation. For 3, we decided to perform the ac susceptibility measurements at 0.075 T because the intensity of the signal is large and the field-induced slow relaxation process is still rather small. Finally, for 4, field- and frequency-dependent ac susceptibility measurements were performed at 0.1 T, because this field leads to the slowest relaxation. Among these compounds, only 1 exhibited enough maxima in the χ′′M signals, which appeared in the 2.5 K (300 Hz)–4.5 K (1488 Hz) region (Fig. 11) to obtain the temperature dependence of the relaxation times using the Debye model.
The high-temperature obtained relaxation times for compound 1 were fitted to the Arrhenius expression:
| τ−1 = τ0−1e−Ueff/kBT | (3) |
| τ−1 = AT + BTn, | (4) |
For complexes 2–4, the ac data could not be fitted to the Debye model because all peaks or the majority of them appear above the studied frequency range (Fig. S16, S18, S20 and S24†). To overcome this problem, we have applied an alternative approach to obtain the relaxation parameters from the ac data. This approach consists of considering that the ratio between the out-of-phase and in-phase components of the ac susceptibility can be expressed in an approximate manner as13k
| χ′′M/χ′M = 2πfτ | (5) |
The substitution in this equation of the relaxation time (τ) by its expression for each relaxation mechanism (Orbach or Raman) permits the determination of the respective relaxation parameters. If we assume that hypothetically the relaxation occurs entirely through an Orbach relaxation mechanism, for which τ = τ0exp(−Ueff/kBT), the equation becomes as follows:
| ln(χ′′M/χ′M) = ln(2πfτ0) − Ueff/kBT | (6) |
The effective energy barrier Ueff could be approximately assessed by fitting the experimental χ′′/χ′ data in the high frequency region to this equation. In order to compare the parameters obtained using both methods, we have used this method not only for 2–4, but also for compound 1 (Fig. 12 left). The obtained parameters are presented in Table 4. As in the case of 1, the obtained Ueff values for complexes 2–4 are much lower than the energy gap (δ) obtained from static susceptibility measurements and ab initio theoretical calculations. This result once again ratifies the hypothesis that the magnetization relaxation for field-induced distorted octahedral Co(II) SIMs with D > 0 should not occur through an Orbach process but through direct and Raman processes. The direct process dominates at very low temperature (below ∼3 K), whereas the Raman process dominates at higher temperatures.
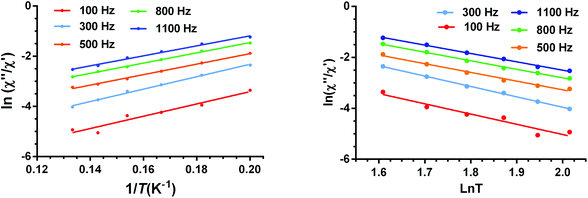 | ||
| Fig. 12 Temperature dependence of the ratio of the in-phase and out-of-phase ac components at different frequencies under a magnetic field of 0.1 T for 1. Solid lines correspond to the fit of the experimental data to eqn (6) (left) and eqn (7) (right). | ||
Bearing in mind that at high temperatures the magnetization relaxation is likely to occur through a Raman process, we have fitted the χ′′/χ′ data to the following equation:
ln(χ′′M/χ′M) = ln(2πfC) − n(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T) T) | (7) |
From the results presented in Table 4, the following conclusions can be drawn: (i) the Ueff value obtained from eqn (5) for 1 is higher (∼6 K) and the τ0 values are lower than those obtained from the Arrhenius plot. (ii) In all cases, the relatively short intermolecular Co(II)⋯Co(II) distances (in the range of 7.135 Å–7.557 Å), which involve Co(II) atoms of neighbouring sheets, lead to non-negligible dipolar interactions that favour QTM and reduce the magnitude of the phenomenologically obtained Ueff values even in the presence of the applied field. In fact, mononuclear complexes13 and 2D SIM-MOFs16f with larger Co(II)⋯Co(II) distances (typically higher than 10 Å) generally exhibit larger Ueff values. Good supporting evidence of the role played by dipolar interactions in six-coordinated Co(II) complexes with D > 0 is provided by the fact that, in some cases, even in the presence of a dc field, this type of complex does not show slow magnetization relaxation above 2 K and to observe it magnetic dilution with an isostructural diamagnetic complex is required (hidden SIM behavior).13b (iv) The Raman mechanism is predominant above 3 K for the fast relaxation process. (v) Neither the shortest Co(II)⋯Co(II) distances nor the dihedral angles between neighboring CoN4 equatorial planes (which are related to the angle between neighbouring anisotropy axes) are clearly correlated with the phenomenological Ueff parameter (or the Raman parameters). In view of the above concerns, it is reasonable to assume that, in addition to the presumable role played by the dipolar interactions, other factors, such as the flexibility of the axial ligands, could significantly contribute to the fast relaxation observed for complexes 1–4. In this regard, it has been recently shown that the temperature dependence of the spin relaxation not only depends on the electronic structure but also on the vibrational characteristics of the specific SMM.43 This is because the relaxation time strongly depends on the frequency and lifetime of phonons together with spin–phonon coupling coefficients. Consequently, internal vibrations play a crucial role in associating the spin states and phonons that contribute to the spin-relaxation pathways. Nevertheless, at low temperature, only a scarce number of local vibrational modes (those with the lowest frequencies) are active. Recent theoretical calculations of the lowest energy vibrational modes for two field-induced distorted octahedral Co(II) SIMs have demonstrated that their energies are close to the experimental thermal energy barriers for Orbach relaxation mechanisms.38 This fact led to a suggestion that the thermal energy barrier is tied to the lowest vibrational modes of the metal complex, so when these vibrational modes are thermally populated, the magnetization reversal becomes faster, promoting the elimination of the magnetization blocking. Moreover, it has been suggested that the direct relaxation between two quasi-degenerate ground states is accelerated in structurally flexible SMMs.43b Although the 2D dicyanoaurate-bridged scaffolding is rather rigid in complexes 1–4, the flexibility of ligands in the axial positions could increase the relaxation rate. Therefore, the observed magnetization relaxation in these complexes could take place through a two-phonon mechanism (predominantly through a Raman mechanism though an Orbach mechanism tied to the energy of the low vibrational modes cannot be ruled out) with the involvement of dipolar (and hyperfine) interactions and the lowest thermally populated vibrational modes, which accelerate magnetic relaxation.
Pulsed magnetization
Magnetization curves in a full cycle pulsed magnetic field at 0.4 K,44 measured on a polycrystalline sample under adiabatic conditions to ease the suppression of population on thermally activated states, are presented in Fig. 13 for 1 and Fig. S26–S29† for 2–4, respectively. We worked with different applied maximum fields that ranged between 1.8 T and ∼15 T with a sweep rate that depends on the maximum pulsed field, being the highest for the highest maximum applied field (0.6 T ms−1 to ∼5.5 T ms−1). Besides, the magnetic field strength is not symmetric for the magnet between the positive and negative directions during the pulsing. Magnetization curves show small hysteresis loops for these compounds that increase with increasing magnetic sweep rate, which is typical of SMM compounds, and saturation at a higher field with values in accordance with those observed in static magnetization isotherms and a small slope due to the low anisotropy of the system. In the down-sweep from the highest field, a gradual decrease of magnetization is found with its value being higher than that of the first quarter up cycle due to the competition between the thermal relaxation and the fast change of the magnetic field. Also, the sharp reversal around zero indicates that there is an adiabatic magnetization reversal most probably caused by QTM.20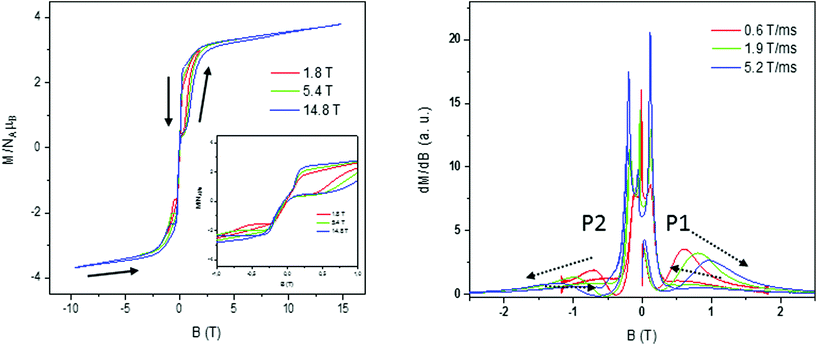 | ||
| Fig. 13 Pulsed-field (left) and differential (right) magnetization curves for 1 at 0.4 K and at different scan field rates. | ||
In order to obtain further information and to analyse the origin of the loop, the differential magnetization dM/dB vs. B was plotted for compounds 1–4 (Fig. 13 right for 1 and Fig. S27–S29† for 2–4, respectively). For all the cobalt complexes, in the initial up-sweep, the magnetization first increases slowly showing one peak, P1, corresponding to a magnetization step in the magnetization. The position of this peak shifts as a function of the sweep rate, probably caused by a nonadiabatic effect. In the down-sweep from the maximum magnetic field to the zero field, dM/dB is very small and the magnetization curve is nearly flat until near zero field, where we observe fine magnetization jumps in the range of 0.10 to 0.15 T (Fig. 13 right) with no field dependence. This observed behaviour at low T is related to QTM caused by the level crossing among excited states, characteristic of SMM.45 We can also find nearly symmetric fine magnetization jumps in the negative field when we sweep from the zero field to the negative maximum at around −0.10 to −0.15 T. Finally, a second step, P2, is found in dM/dB slightly shifted from its counterpart at the positive field indicating the presence of a dipolar-coupling bias that affects the field at which QTM occurs.
The slight sweep rate dependence of the peak field P1–P2 observed for all compounds indicates that the magnetization behavior is symmetric for the magnetic field reversal, as is found in the magnetization curve (Fig. S24†). This is presumably caused by the balance between the thermal relaxation time and the short sweeping time.
Conclusions
Four 2D {Co(L)2[Au(CN)2]2}n (L = DMSO, DMF, Py, 4-benzoylpyridine) metal–organic frameworks have been easily obtained by assembling Co(II) nodes, [Au(CN)2]− spacers and L molecules. These compounds are made of parallel sheets built from edge-sharing slightly distorted square-planar {NC–Au–CN–Co}4 units with the Co(II) ions located at the corners and the [Au(CN)2]− bridging anions at the edges. The parallel stacking of layers is favoured by aurophilic and/or aromatic π⋯π interactions. The Co(II) nodes exhibit a slightly tetragonally distorted CoN4X2 (X = O, N) octahedral coordination sphere, with the donor atoms X of the L molecules occupying trans axial positions. The change of the ligand L in the axial positions not only modifies the CoN4X2 coordination sphere, the packing and intermolecular exchange and dipolar interactions, but also the ligand field strength, the splitting of the d orbitals and consequently the anisotropy of the Co(II) ion. In this context, ab initio theoretical calculations show that the ligand field strength follows the order: 4 ≥ 3 > 2 > 1, which agrees with the electronic effects of the L ligands. Thus, the larger σ-donor ability of the N-coordinated pyridine derivatives, together with their weak π-acceptor properties, leads to a larger field strength for complexes 3 and 4 than for 1 and 2, which contain O-coordinated DMF and DMSO ligands with π-donor properties. Magnetic, FIRMS and HFEPR results point out that the D values for the reported compounds are all positive and larger than ∼+70 cm−1, and follow the order 2 > 4 > 3 > 1. Interestingly, this order of D values can be reproduced when gold(I) atoms are included in the theoretical model, thus indicating the essential role played by the electronic effect of the heavy gold(I) atoms in determining Co(II) magnetic anisotropy.In all these complexes, CoN4X2 nodes exhibit field-induced mononuclear SIM behaviour with slow relaxation of the magnetization occurring at very low temperatures, mainly through a Raman relaxation process, which is dominant above 3 K. Therefore, the D and E values seem not to play a relevant role in the slow magnetization relaxation process. The origin of the modest SIM behaviour for these compounds could be due to the relatively short intermolecular Co(II)⋯Co(II) distances (in the range of 7.135 Å–7.557 Å), which involve Co(II) atoms of neighbouring sheets, leading to non-negligible dipolar interactions that favour QTM. The fact that there is no correlation between the shortest Co(II)⋯Co(II) distances and the phenomenological Ueff parameters for complexes 1–4 suggests that, in addition to the presumable role played by the dipolar interactions, other factors, such as the flexibility of the axial ligands, could significantly contribute to the fast relaxation observed for complexes.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support was provided by the Ministerio de Economía y Competitividad (MINECO) for Project CTQ2014-56312-P and the Ministerio de Educación, Cultura y Deporte for Project PGC2018-102052-B-C21 and Junta de Andalucía (FQM-195) and Project A-FQM-172-UGR18 and the University of Granada. Part of this work was performed at the NHMFL, which is funded by the National Science Foundation (Cooperative Agreement DMR 1644779) and the State of Florida. The authors thank Dr A. Ozarowski (NHMFL) for his EPR software SPIN. HN and IFDO acknowledge GIMRT and ICC-IMR.References
- (a) D. Gatteschi and R. Sessoli, Quantum tunneling of magnetization and related phenomena in molecular materials, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS; (b) D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press, Oxford, 2006 CrossRef; (c) J. Bartolomé, F. Luis and J. F. Fernández, Molecular magnets: physics and applications, Springer-Verlag, Berlin-Heidelberg, 2014 CrossRef; (d) S. Gao, Molecular nanomagnets and related phenomena, in Structure and Bonding, Springer-Verlag, Berlin-Heidelberg, 2015, vol. 164 CrossRef; (e) J. J. Baldovi, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, Rational design of single-ion magnets and spin qubits based on mononuclear lanthanoid complexes, Inorg. Chem., 2012, 51, 12565–12574 CrossRef CAS; (f) S. T. Liddle and J. van Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M. A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Magnetic memory of a single-molecule quantum magnet wired to a gold surface, Nat. Mater., 2009, 8, 194–197 CrossRef CAS.
- (a) A. R. Rocha, V. M. García-Suárez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Towards molecular spintronics, Nat. Mater., 2005, 4, 335–339 CrossRef CAS; (b) L. Bogani and W. Wernsdorfer, Molecular spintronics using single-molecule magnets, Nat. Mater., 2008, 7, 179–186 CrossRef CAS; (c) R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Electronic read-out of a single nuclear spin using a molecular spin transistor, Nature, 2012, 488, 357–360 CrossRef CAS; (d) M. Ganzhorn, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Strong spin–phonon coupling between a single-molecule magnet and a carbon nanotube nanoelectromechanical system, Nat. Nanotechnol., 2013, 8, 165–169 CrossRef CAS; (e) M. Jenkins, T. Hümmer, M. J. Marínez-Pérez, J. García-Ripoll, D. Zueco and F. Luis, Coupling single-molecule magnets to quantum circuits, New J. Phys., 2013, 15, 095007 CrossRef; (f) E. Coronado and M. Yamashita, Molecular spintronics: the role of coordination chemistry, Dalton Trans., 2016, 45, 16553–16555 RSC; (g) E. Coronado, Molecular magnetism: from chemical design to spin control in molecules, materials and devices, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- (a) M. N. Leuenberger and D. Loss, Quantum computing in molecular magnets, Nature, 2001, 410, 789–793 CrossRef CAS; (b) A. Ardavan, O. Rival, J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Will spin-relaxation times in molecular magnets permit quantum information processing?, Phys. Rev. Lett., 2007, 98, 057201 CrossRef; (c) M. J. Martínez-Pérez, S. Cardona-Serra, C. Schlegel, F. Moro, P. J. Alonso, H. Prima-García, J. M. Clemente-Juan, M. Evangelisti, A. Gaita-Ariño, J. Sesé, J. Van Slageren, E. Coronado and F. Luis, Gd-based single-ion magnets with tunable magnetic anisotropy: molecular design of spin qubits, Phys. Rev. Lett., 2012, 108, 247213 CrossRef; (d) M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Structural effects on the spin dynamics of potential molecular qubits, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS; (e) L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Quantum coherence in a processable vanadyl complex: new tools for the search of molecular spin qubits, Chem. Sci., 2016, 7, 2074–2083 RSC.
- (a) F. Neese and D. A. Pantazis, What is not required to make a single molecule magnet, Faraday Discuss., 2011, 148, 229 RSC; (b) O. Waldmann, A Criterion for the Anisotropy Barrier in Single-Molecule Magnets, Inorg. Chem., 2007, 46, 10035 CrossRef CAS.
- Some reviews: (a) G. Aromi and E. K. Brechin, Synthesis of 3d metallic single-molecule magnets, in Structure and Bonding, ed. R. Winpenny, Springer-Verlag, Berlin-Heidelberg, 2006, vol. 122, pp. 1–67 Search PubMed; (b) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide single-molecule magnets, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS; (c) R. Layfield and M. Murugesu, Lanthanides and actinides in molecular magnetism, Wiley-VCH, Weinheim, 2015 Search PubMed; (d) J. Tang and P. Zhang, Lanthanide single molecule magnets, Springer-Verlag, Berlin Heidelberg, 2015 Search PubMed; (e) J. M. Frost, K. L. M. Harriman and M. Murugesu, The rise of 3-d single-ion magnets in molecular magnetism: towards materials from molecules?, Chem. Sci., 2016, 7, 2470–2491 RSC; (f) A. K. Bar, C. Pichon and J. P. Sutter, Magnetic anisotropy in two- to eight-coordinated transition–metal complexes: recent developments in molecular magnetism, Coord. Chem. Rev., 2016, 308, 346–380 CrossRef CAS; (g) G. A. Craig and M. Murrie, 3d single-ion magnets, Chem. Soc. Rev., 2015, 44, 2135–2147 RSC; (h) S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Large magnetic anisotropy in mononuclear metal complexes, Coord. Chem. Rev., 2015, 289–290, 379–392 CrossRef; (i) M. Feng and M. L. Tong, Single ion magnets from 3d to 5f: developments and strategies, Chem. – Eur. J., 2018, 24, 7574–7594 CrossRef CAS; (j) D. Maniaki, E. Pilichos and S. P. Perlepes, Coordination clusters of 3d-metals that behave as single-molecule magnets (SMMs): synthetic routes and strategies, Front. Chem., 2018, 6, 461–469 CrossRef CAS; (k) S. Tripathi, A. Dey, M. Shanmugam, R. S. Narayanan and V. Chandrasekhar, Cobalt(II) Complexes as Single-Ion Magnets, Top. Organomet. Chem., 2018, 64, 35–75 CrossRef; (l) Z. Zhu and J. Tang, Geometry and Magnetism of Lanthanide Compounds, Top. Organomet. Chem., 2019, 64, 191–226 CrossRef CAS.
- (a) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442 CrossRef CAS; (b) F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, A dysprosium metallocene single-molecule magnet functioning at the axial limit, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS; (c) F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403 CrossRef CAS.
- D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, Slow magnetic relaxation in a high-spin iron(II) complex, J. Am. Chem. Soc., 2010, 132, 1224–1225 CrossRef CAS.
- S. Gómez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, Mononuclear single-molecule magnets: tailoring the magnetic anisotropy of first-row transition-metal complexes, J. Am. Chem. Soc., 2013, 135, 7010–7018 CrossRef.
- J. H. Van Vleck, Paramagnetic relaxation times for titanium and chrome alum, Phys. Rev., 1940, 57, 426–447 CrossRef CAS.
- (a) X. N. Yao, J. Z. Du, Y. Q. Zhang, X. B. Leng, M. W. Yang, S. D. Jiang, Z. X. Wang, Z. W. Ouyang, L. Deng, B. W. Wang and S. Gao, Two-coordinate Co(II) imido complexes as outstanding single-molecule magnets, J. Am. Chem. Soc., 2017, 139, 373–380 CrossRef CAS; (b) P. C. Bunting, M. Atanasov, E. Damgaard-MØller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, A linear cobalt(II) complex with maximal orbital angular momentum from a non-Aufbau ground state, Science, 2018, 362, 7319 CrossRef.
- (a) A. A. Pavlov, Y. V. Nelyubina, S. V. Kats, L. V. Penkova, N. N. Efimov, A. O. Dmitrienko, A. V. Vologzhanina, A. S. Belov, Y. Z. Voloshin and V. V. J. Novikov, Polymorphism in a cobalt-based single-ion magnet tuning its barrier to magnetization relaxation, Phys. Chem. Lett., 2016, 7, 4111–4116 CrossRef CAS; (b) Y. Y. Zhu, Y. Q. Zhang, T. T. Yin, C. Gao, B. W. Wang and S. Gao, A family of CoIICoIII3 single-ion magnets with zero-field slow magnetic relaxation: fine tuning of energy barrier by remote substituent and counter cation, Inorg. Chem., 2015, 54, 5475–5486 CrossRef CAS; (c) Y. Y. Zhu, C. Cui, Y. Q. Zhang, J. H. Jia, X. Guo, C. Gao, K. Qian, S. D. Jiang, B. W. Wang, Z. M. Wang and S. Gao, Zero-field slow magnetic relaxation from single Co(II) ion: a transition metal single-molecule magnet with high anisotropy barrier, Chem. Sci., 2013, 4, 1802–1806 RSC; (d) T. J. Ozumerzifon, I. Bhowmick, W. C. Spaller, A. K. Rappé and M. P. Shores, Toward steric control of guest binding modality: a cationic Co(II) complex exhibiting cation binding and zero-field relaxation, Chem. Commun., 2017, 53, 4211–4214 RSC; (e) Y. Peng, T. Bodenstein, K. Fink, V. Mereacre, C. E. Anson and A. K. Powell, Magnetic anisotropy of a CoII single ion magnet with distorted trigonal prismatic coordination: theory and experiment, Phys. Chem. Chem. Phys., 2016, 18, 30135–30143 RSC; (f) B. Yao, Y. F. Deng, T. Li, J. Xiong, B. W. Wang, Z. Zheng and Y. Y. Zhang, Construction and magnetic study of a trigonal-prismatic cobalt(II) single-ion magnet, Inorg. Chem., 2018, 57, 14047–14051 CrossRef CAS; (g) V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M. E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, A trigonal prismatic mononuclear cobalt(II) complex showing single-molecule magnet behaviour, J. Am. Chem. Soc., 2015, 137, 9792–9795 CrossRef CAS; (h) A. A. Pavlov, D. Y. Aleshin, S. A. Savkina, A. S. Belov, N. N. Efimov, J. Nehrkorn, M. Ozerov, Y. Z. Voloshin, Y. V. Nelyubina and V. V. Novikov, A trigonal prismatic cobalt(II) complex as a single molecule magnet with a reduced contribution from quantum tunnelling, ChemPhysChem, 2019, 20, 1001–1005 CrossRef CAS.
- Some examples: (a) J. Vallejo, I. Castro, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, G. De Munno, W. Wernsdorfer and E. Pardo, Field-induced slow magnetic relaxation in a six-coordinate mononuclear cobalt(II) complex with a positive anisotropy, J. Am. Chem. Soc., 2012, 134, 15704–15707 CrossRef CAS; (b) E. Colacio, J. Ruiz, E. Ruiz, E. Cremades, J. Krzystek, S. Carretta, J. Cano, T. Guidi, W. Wernsdorfer and E. K. Brechin, Slow magnetic relaxation in a CoII–YIII single-ion magnet with positive axial zero-field splitting, Angew. Chem., Int. Ed., 2013, 52, 9130–9134 CrossRef CAS; (c) A. V. Palii, D. V. Korchagin, E. A. Yureva, A. V. Akimov, E. Y. Misochko, G. V. Shilov, A. D. Talantsev, R. B. Morgunow, S. M. Aldoshin and B. S. Tsukerblat, Single-ion magnet Et4N[CoII(hfac)3] with nonuniaxial anisotropy: synthesis, experimental characterization, and theoretical modelling, Inorg. Chem., 2016, 55, 9696–9706 CrossRef CAS; (d) M. A. Palacios, J. Nehrkorn, E. A. Suturina, E. Ruiz, S. Gómez-Coca, K. Holldack, A. Schnegg, J. Krzystek, J. M. Moreno and E. Colacio, Analysis of magnetic anisotropy and the role of magnetic dilution in triggering single–molecule magnet (SMM) behavior in a family of CoIIYIII dinuclear complexes with easy–plane anisotropy, Chem. – Eur. J., 2017, 23, 11649–11661 CrossRef CAS and references therein; (e) L. Váhovská, S. Vitushkina, I. Potočňák, Z. Trávníček and R. Herchel, Effect of linear and non-linear pseudohalides on the structural and magnetic properties of Co(II) hexacoordinate single-molecule magnets, Dalton Trans., 2018, 47, 1498–1512 RSC; (f) S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Origin of slow magnetic relaxation in Kramers ions with non-uniaxial anisotropy, Nat. Commun., 2014, 5, 4300 CrossRef; (g) L. Rigamonti, N. Bridonneau, G. Poneti, L. Tesi, L. Sorace, D. Pinkowicz, J. Jover, E. Ruiz, R. Sessoli and A. Cornia, A Pseudo-octahedral cobalt(II) complex with bispyrazolylpyridinel ligands acting as a zero-field single-molecule magnet with easy axis anisotropy, Chem. – Eur. J., 2018, 24, 8857–8868 CrossRef CAS; (h) Y. Wu, D. Tian, J. Ferrando-Soria, J. Cano, L. Yin, Z. Ouyang, Z. Wang, S. Luo, X. Liu and E. Pardo, Modulation of the magnetic anisotropy of octahedral cobalt(II) single-ion magnets by fine-tuning the axial coordination microenvironment, Inorg. Chem. Front., 2019, 6, 848–856 RSC; (i) D. Sertphon, K. S. Murray, W. Phonsri, J. Jover, E. Ruiz, S. G. Telfer, A. Alkas, P. Harding and D. J. Harding, Slow relaxation of magnetization in a bis-mer-tridentate octahedral Co(II) complex, Dalton Trans., 2018, 47, 859–867 RSC; (j) H. H. Cui, Y. Q. Zhang, X. T. Chen, Z. Wang and Z. L. Xue, Magnetic anisotropy and slow magnetic relaxation processes of cobalt(II)-pseudohalide complexes, Dalton Trans., 2019, 48, 10743–10752 RSC; (k) Y. P. Tupolova, I. N. Shcherbakov, L. D. Popov, V. E. Lebedev, V. V. Tkachev, K. V. Zakharov, A. N. Vasiliev, D. V. Korchagin, A. V. Palii and S. M. Aldoshin, Field-induced single-ion magnet behaviour of a hexacoordinated Co(II) complex with easy-axis-type magnetic anisotropy, Dalton Trans., 2019, 48, 6960–6970 RSC; (l) R. Modak, B. Mondal, Y. Sikdar, J. Banerjee, E. Colacio, I. Oyarzabal, J. Cano and S. Goswami, Slow magnetic relaxation and water oxidation activity of dinuclear CoIICoIII and unique triangular CoIICoIICoIII mixed-valence complexes, Dalton Trans., 2020, 49, 6328–6340 RSC; (m) A. Masegosa, M. A. Palacios, E. Ruiz, S. Gómez-Coca, J. Krzystek, J. M. Moreno and E. Colacio, Dinuclear CoIIYIIIvs. tetranuclear CoII2YIII2 complexes: the effect of increasing molecular size on magnetic anisotropy and relaxation dynamics, Dalton Trans., 2019, 48, 14873–14884 RSC.
- S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Origin of slow magnetic relaxation in Kramers ions with non-uniaxial anisotropy, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- P. Paul, M. Viciano-Chumillas, H. Puschmann, J. Cano and S. C. Manna, Field-induced slow magnetic relaxation in mixed valence di- and tri-nuclear CoII–CoIII complexes, Dalton Trans., 2020, 49, 9516–9528 RSC.
- (a) Y. Y. Zhu, M. S. Zhu, T. T. Yin, Y. S. Meng, Z. Q. Wu, Y. Q. Zhang and S. Gao, Cobalt(II) coordination polymer exhibiting single-ion-magnet-type field-induced slow relaxation behaviour, Inorg. Chem., 2015, 54, 3716–3718 CrossRef CAS; (b) A. E. Ion, S. Nica, A. M. Madalan, S. Shova, J. Vallejo, M. Julve, F. Lloret and M. Andruh, Two-dimensional coordination polymers constructed using, simultaneously, linear and angular spacers and cobalt(II) nodes. New examples of networks of single-ion magnets, Inorg. Chem., 2015, 54, 16–18 CrossRef CAS; (c) J. Palion-Gazda, T. Klemens, B. Machura, J. Vallejo, F. Lloret and M. Julve, Single ion magnet behaviour in a two-dimensional network of dicyanamide-bridged cobalt(II) ions, Dalton Trans., 2015, 44, 2989–2992 RSC; (d) Y.-L. Wang, L. Chen, C.-M. Liu, Y.-Q. Zhang, S.-G. Yin and Q.-Y. Liu, Field-Induced Slow Magnetic Relaxation and Gas Adsorption Properties of a Bifunctional Cobalt(II) Compound, Inorg. Chem., 2015, 54, 11362–11368 CrossRef CAS; (e) X. Liu, L. Sun, H. Zhou, P. Cen, X. Jin, G. Xie, S. Chen and Q. Hu, Single-ion-magnet behavior in a two-dimensional coordination polymer constructed from CoII nodes and a pyridylhydrazone derivative, Inorg. Chem., 2015, 54, 8884–8886 CrossRef CAS; (f) A. Switlicka-Olszewska, J. Palion-Gazda, T. Klemens, B. Machura, J. Vallejo, J. Cano, F. Lloret and M. Julve, Single-ion magnet behaviour in mononuclear and two-dimensional dicyanamide-containing cobalt(II) complexes, Dalton Trans., 2016, 45, 10181–10193 RSC; (g) J. Vallejo, F. R. Fortea-Pérez, E. Pardo, S. Benmansour, I. Castro, J. Krzystek, D. Armentano and J. Cano, Guest-dependent single-ion magnet behaviour in a cobalt(II) metal–organic framework, Chem. Sci., 2016, 7, 2286–2293 RSC; (h) Z. X. Wang, L. F. Wu, X. Zhang, F. Xing and M. X. Li, Structural diversity and magnetic properties of six cobalt coordination polymers based on 2,2′-phosphinico-dibenzoate ligand, Dalton Trans., 2016, 45, 19500–19510 RSC; (i) Y.-L. Wang, L. Chen, C.-M. Liu, Z.-Y. Du, L.-L. Chen and Q.-Y. Liu, 3D chiral and 2D achiral cobalt(II) compounds constructed from a 4-(benzimidazole-1-yl)benzoic ligand exhibiting field-induced single-ion-magnet type slow magnetic relaxation, Dalton Trans., 2016, 45, 7768–7775 RSC; (j) A. K. Mondal, S. Khatua, K. Tomar and S. Konar, Field-Induced Single-Ion-Magnetic Behavior of Octahedral CoII in a Two-Dimensional Coordination Polymer, Eur. J. Inorg. Chem., 2016, 3545–3552 CrossRef CAS; (k) R. Ma, Z. Chen, F. Cao, S. Wang, X. Huang, Y. Li, J. Lu, D. Li and J. Dou, Two 2-D multifunctional cobalt(II) compounds: field-induced single-ion magnetism and catalytic oxidation of benzylic C–H bonds, Dalton Trans., 2017, 46, 2137–2145 RSC; (l) G. Brunet, D. A. Safin, J. Jover, E. Ruiz and M. Murugesu, Single-molecule magnetism arising from cobalt(II) nodes of a crystalline sponge, J. Mater. Chem. C, 2017, 5, 835–841 RSC; (m) L. Shi, D. Shao, H. Y. Wei and X. Y. Wang, Two interpenetrated cobalt(II) metal–organic frameworks with guest-dependent structures and field-induced single-ion magnet behaviors, Cryst. Growth Des., 2018, 18, 5270–5278 CrossRef CAS; (n) L. Shi, F. X. Shen, D. Shao, Y. Q. Zhang and X. Y. Wang, Syntheses, structures, and magnetic properties of three two-dimensional cobalt(II) single-ion magnets with a CoIIN4X2 octahedral geometry, CrystEngComm, 2019, 21, 3176–3185 RSC; (o) P. Mondal, B. Dey, S. Roy, S. P. Bera, R. Nasani, A. Santra and S. Konar, Field-induced slow magnetic relaxation and anion/solvent dependent proton conduction in cobalt(II) coordination polymers, Cryst. Growth Des., 2018, 18, 6211–6220 CrossRef CAS; (p) A. Switlicka, B. Manchura, R. Kruszynski, J. Cano, L. M. Toma, F. Lloret and M. Julve, The influence of pseudohalide ligands on the SIM behaviour of four-coordinate benzylimidazole-containing cobalt(II) complexes, Dalton Trans., 2018, 47, 5831–5842 RSC; (q) X. Liu, X. Ma, P. Cen, F. An, Z. Wang, W. Song and Y. Q. Zhang, One-dimensional cobalt(II) coordination polymer featuring single-ion-magnet-type field-induced slow magnetic relaxation, New J. Chem., 2018, 42, 9612–9619 RSC; (r) P. Konieczny, A. B. González-Guillén, K. Luberda-Durnas, E. Cizmár, R. Pelka, M. Oszajca and W. Lasocha, 1D coordination polymer (OPD)2Co IISO4 showing SMM behaviour and multiple relaxation modes, Dalton Trans., 2019, 48, 7560–7570 RSC; (s) D. Ma, G. Peng, Y. Y. Zhang and B. Li, Field-induced slow magnetic relaxation in two-dimensional and three-dimensional Co(II) coordination polymers, Dalton Trans., 2019, 48, 15529–15536 RSC; (t) A. Switlicka, B. Machura, M. Penkala, A. Bienko, D. C. Bienko, J. Titis, C. Rajnak, R. Boca and A. Ozarowski, Slow magnetic relaxation in hexacoordinated cobalt(II) field-induced single-ion magnets, Inorg. Chem. Front., 2020, 7, 2637–2650 RSC; (u) H. Wu, L. Gao, J. Zhang, L. Zhai, T. Gao, X. Niu and T. Hu, Syntheses, characterization, and slow magnetic relaxation or luminescence properties of three new 2D coordination polymers, J. Mol. Struct., 2020, 1219, 128613 CrossRef CAS.
- (a) H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, The Chemistry and Applications of Metal-Organic Frameworks, Science, 2013, 341, 1230444 CrossRef; (b) G. Ferey, Hybrid porous solids: past, present, future, Chem. Soc. Rev., 2008, 37, 191–214 RSC; (c) O. K. Farha and J. T. Hupp, Rational Design, Synthesis, Purification, and Activation of Metal–Organic Framework Materials, Acc. Chem. Res., 2010, 43, 1166–1175 CrossRef CAS; (d) S. Horike, S. Shimomura and S. Kitagawa, Soft porous crystals, Nat. Chem., 2009, 1, 695 CrossRef CAS; (e) T. Kitao, Y. Zhang, S. Kitagawa, B. Wang and T. Uemura, Hybridization of MOFs and polymers, Chem. Soc. Rev., 2017, 46, 3108 RSC; (f) S. Yuan, L. Feng, K. Wang, J. Pang, M. Bosch, C. Lollar, Y. Sun, J. Qin, X. Yang, P. Zhang, Q. Wang, L. Zou, Y. Zhang, L. Zhang, Y. Fang, J. Li and H. C. Zhou, Stable Metal–Organic Frameworks: Design, Synthesis, and Applications, Adv. Mater., 2018, 30, 1704303 CrossRef.
- (a) G. Agustí, M. C. Muñoz, A. B. Gaspar and J. A. Real, Spin-crossover behavior in cyanide-bridged iron(II)–gold(I) bimetallic 2D hofmann-like metal–organic framework, Inorg. Chem., 2008, 47, 2552–2561 CrossRef; (b) E. Colacio, F. Lloret, R. Kivekäs, J. Ruiz, J. Suárez-Varela and M. R. Sundberg, Aurophilicity as a cofactor in crystal engineering. Dicyanoaurate(I) anion as a building block in a novel Co(II)–Au(I) bimetallic assembly, Chem. Commun., 2002, 592–593 RSC; (c) J. Lefebvre, R. J. Batchelor and D. B. Leznoff, Cu[Au(CN)2]2(DMSO)2: golden polymorphs that exhibit vapochromic behaviour, J. Am. Chem. Soc., 2004, 126, 16117–16125 CrossRef CAS; (d) M. J. Katz, T. Ramnial, H. Z. Yu and D. B. Leznoff, Polymorphism of Zn[Au(CN)2]2 and its luminescent sensory response to NH3 vapor, J. Am. Chem. Soc., 2008, 130, 10662–10673 CrossRef CAS; (e) C. Jobbágy, T. Tunyogi, G. Pálinkás and A. Deák, A versatile solvent-free mechanochemical route to the synthesis of heterometallic dicyanoaurate-based coordination polymers, Inorg. Chem., 2011, 50, 7301–7308 CrossRef; (f) J. Lefebvre, J. L. Korčok, M. J. Katz and D. B. Leznoff, Vapochromic behaviour of M[Au(CN)2]2-based coordination polymers (M = Co, Ni), Sensors, 2012, 12, 3669–3692 CrossRef CAS.
- S. Stoll and A. Schweiger, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS.
- H. Nojiri, K. Y. Choi and N. Kitamura, Manipulation of the quantum tunneling of nanomagnets by using time-dependent high magnetic fields, J. Magn. Magn. Mater., 2007, 310, 1468–1472 CrossRef CAS.
- APEX2, Bruker AXS, Madison, WI, 2010 Search PubMed.
- SAINT, Version 8.30a, Bruker AXS, Madison, WI, 2013 Search PubMed.
- G. M. Sheldrick, SADABS, Version 2004/1, Bruker AXS, Madison, WI, 2008 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- (a) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, Introduction of n-electron valence states for multireference perturbation theory, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS; (b) C. Angeli, R. Cimiraglia and J. P. Malrieu, N-electron valence state perturbation theory: a fast implementation of the strongly contracted variant, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS; (c) C. Angeli and R. Cimiraglia, Multireference perturbation configuration interaction V. Third-order energy contributions in the Møller–Plesset and Epstein–Nesbet partitions, Theor. Chem. Acc., 2002, 107, 313–317 Search PubMed; (d) C. Angeli, R. Cimiraglia and J. P. Malrieu, n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- (a) F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC; (b) A. Schaefer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef CAS; (c) A. Schaefer, C. Huber and R. Ahlrichs, Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef CAS.
- (a) K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Auxiliary basis sets for main row atoms and transition metals and their use to approximate Coulomb potentials, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed; (b) K. Eichkorn, O. Treutler, H. öhm, M. Haser and R. Ahlrichs, Auxiliary basis sets to approximate Coulomb potentials, Chem. Phys. Lett., 1995, 240, 283–289 CrossRef CAS.
- J. Jung, M. Atanasov and F. Neese, Ab initio ligand-field theory analysis and covalency trends in actinide and lanthanide free ions and octahedral complexes, Inorg. Chem., 2017, 56, 8802–8816 CrossRef CAS.
- F. Neese, Software update: The ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- (a) D. Ganyushin and F. Neese, A fully variational spin-orbit coupled complete active space self-consistent field approach: Application to electron paramagnetic resonance g-tensors, J. Chem. Phys., 2013, 138, 104113 CrossRef; (b) D. Ganyushin and F. Neese, First-principles calculations of zero-field splitting parameters, J. Chem. Phys., 2006, 125, 024103 CrossRef; (c) R. Maurice, R. Bastardis, C. D. Graaf, N. Suaud, T. Mallah and N. Guihéry, Universal theoretical approach to extract anisotropic spin hamiltonians, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS.
- M. Douglas and N. M. Kroll, Quantum electrodynamical corrections to the fine structure of helium, Ann. Phys., 1974, 82, 89–155 CAS.
- F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Magnetic properties of six-coordinated high-spin cobalt(II) complexes: Theoretical background and its application, Inorg. Chim. Acta, 2008, 361, 3432–3445 CrossRef CAS.
- (a) K. R. Dunbar and R. A. Heintz, Chemistry of transition metal cyanide complexes, modern perspectives, Prog. Inorg. Chem., 1997, 45, 283–291 CAS; (b) A. Cano, L. Reguera, M. Avila, D. Velasco-Arias and E. Reguera, Eur. J. Inorg. Chem., 2020, 1, 137–145 CrossRef.
- S. Clima, M. F. A. Hendrickx, L. F. Chibotaru, A. Soncini, V. Mironov and A. Ceulemans, Effect of the Metal Environment on the Ferromagnetic Interaction in the Co–NC–W Pairs of Octacyanotungstate(V)–Cobalt(II) Three-Dimensional Networks, Inorg. Chem., 2007, 46, 2682–2690 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: a powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS.
- (a) D. V. Korchagin, A. V. Palii, E. A. Yureva, A. V. Akimov, E. Y. Misochko, G. V. Shilov, A. D. Talantsev, R. B. Morgunov, A. A. Shakin, S. M. Aldoshin and B. S. Tsukerblat, Evidence of field induced slow magnetic relaxation in cis-[Co(hfac)2(H2O)2] exhibiting tri-axial anisotropy with a negative axial component, Dalton Trans., 2017, 46, 7540–7548 RSC; (b) E. A. Buvaylo, V. N. Kokozay, O. Y. Vassilyeva, B. W. Skelton, A. Ozarowski, J. Titiš, B. Vranovičová and R. Boča, Field-assisted slow magnetic relaxation in a six-coordinate Co(II)–Co(III) complex with large negative anisotropy, Inorg. Chem., 2017, 56, 6999–7009 CrossRef CAS.
- H. Sakiyama, Development of MagSaki(A) software for the magnetic analysis of dinuclear high-spin cobalt(II) complexes considering anisotropy in exchange interaction, J. Comput. Chem., Jpn., 2007, 6, 123–134 CrossRef CAS.
- J. Vallejo, M. Viciano-Chumillas, F. Lloret, M. Julve, I. Castro, J. Krzystek, M. Ozerov, D. Armentano, G. De Munno and J. Cano, Coligand effects on the field-induced double slow magnetic relaxation in six-coordinate cobalt(II) single-ion magnets (SIMs) with positive magnetic anisotropy, Inorg. Chem., 2019, 58, 15726–15740 CrossRef CAS.
- (a) A. Arauzo, A. Lazarescu, S. Shova, E. Bartolomé, R. Cases, J. Luzón, J. Bartolomé and C. Turta, Structural and magnetic properties of some lanthanide (Ln = Eu(III), Gd(III) and Nd(III)) cyanoacetate polymers: field-induced slow magnetic relaxation in the Gd and Nd substitutions, Dalton Trans., 2014, 43, 12342–12356 RSC; (b) H. X. Zhang, S. Y. Lin, S. F. Xue, C. Wang and J. K. Tang, Employment of triketones to construct a dysprosium(III) single-molecule magnet, Dalton Trans., 2015, 44, 4648–4654 RSC.
- (a) F. Habib, I. Korobkov and M. Murugesu, Exposing the intermolecular nature of the second relaxation pathway in a mononuclear cobalt(II) single-molecule magnet with positive anisotropy, Dalton Trans., 2015, 44, 6368–6373 RSC; (b) Z. B. Hu, Z. Y. Jing, M. M. Li, L. Yin, Y. D. Gao, F. Yu, T. P. Hu, Z. Wang and Y. Song, Important role of intermolecular interaction in cobalt(II) single-ion magnet from single slow relaxation to double slow relaxation, Inorg. Chem., 2018, 57, 10761–10767 CrossRef CAS; (c) J. Li, Y. Han, F. Cao, R. M. Wei, Y. Q. Zhang and Y. Song, Two field-induced slow magnetic relaxation processes in a mononuclear Co(II) complex with a distorted octahedral geometry, Dalton Trans., 2016, 45, 9279–9284 RSC; (d) I. Potoèòák, K. Ráczová, E. Èižmár, L. Váhovská, O. Bukrynov, S. Vitushkina and L. Findoráková, Low-dimensional compounds containing cyanido groups. Part XXXII. Field-induced multiple slow magnetic relaxation in [CoII(dcnm)(H2O)(phen)2](dcnm) complex with dominant easy-plane anisotropy (dcnm = dicyanonitrosomethanide), Polyhedron, 2017, 137, 112–121 CrossRef.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon Press, Oxford, 1970 Search PubMed.
- (a) A. Singh and K. N. Shrivastava, Optical–acoustic two–phonon relaxation in spin systems, Phys. Status Solidi B, 1979, 95, 273–277 CrossRef CAS; (b) K. N. Shirivastava, Theory of Spin–Lattice Relaxation, Phys. Status Solidi B, 1983, 117, 437–458 CrossRef.
- (a) D. H. Moseley, S. E. Stavretis, K. Thirunavukkuarasu, M. Ozerov, Y. Cheng, L. L. Daemen, J. Ludwig, Z. Lu, D. Smirnov, C. M. Brown, A. Pandey, A. J. Ramirez-Cuesta, A. C. Lamb, M. Atanasov, E. Bill, F. Neese and Z. L. Xue, Spin–phonon couplings in transition metal complexes with slow magnetic relaxation, Nat. Commun., 2018, 9, 2572 CrossRef; (b) A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, The role of anharmonic phonons in under-barrier spin relaxation of single molecule magnets, Nat. Commun., 2017, 8, 14620 CrossRef; (c) A. Lunghi and S. Sanvito, How do phonons relax molecular spins?, Sci. Adv., 2019, 5, eaax7163 CrossRef CAS.
- K. Saito and S. Miyashita, Magnetic Foehn effect in adiabatic transition, Phys. Soc. Jpn., 2001, 70, 3385–3390 CrossRef CAS.
- A. Okazawa, T. Nogami, H. Nojiri and T. Ishida, Exchange Coupling and Energy-Level Crossing in a Magnetic Chain [Dy2Cu2]n Evaluated by High-Frequency Electron Paramagnetic Resonance, Chem. Mater., 2008, 20, 3110–3119 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2020915–2020918. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0qi00996b |
| This journal is © the Partner Organisations 2020 |