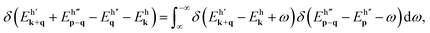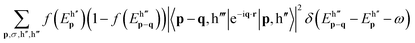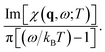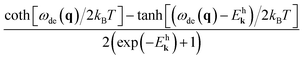Open Access Article
Open Access ArticleCoulomb decay rates in monolayer doped graphene
Chih-Wei Chiu *a,
Yue-Lin Chunga,
Cheng-Hsueh Yangb,
Chang-Ting Liua and
Chiun-Yan Lin*b
*a,
Yue-Lin Chunga,
Cheng-Hsueh Yangb,
Chang-Ting Liua and
Chiun-Yan Lin*b
aDepartment of Physics, National Kaohsiung Normal University, Kaohsiung 824, Taiwan. E-mail: giorgio@mail.nknu.edu.tw
bDepartment of Physics, National Cheng Kung University, Tainan 701, Taiwan. E-mail: cylin@mail.ncku.edu.tw
First published on 13th January 2020
Abstract
Excited conduction electrons, conduction holes, and valence holes in monolayer electron-doped graphene exhibit unusual Coulomb decay rates. The deexcitation processes are studied using the screened exchange energy. They might utilize the intraband and interband single-particle excitations, as well as the plasmon modes, depending on the quasiparticle states and the Fermi energies. The low-lying valence holes can decay through the undamped acoustic plasmon, so that they present very fast Coulomb deexcitations, nonmonotonous energy dependence, and anisotropic behavior. However, the low-energy conduction electrons and holes are similar to those in a two-dimensional electron gas. The higher-energy conduction states and the deeper-energy valence ones behave similarly in the available deexcitation channels and have a similar dependence of decay rate on the wave vector.
1 Introduction
There are some theoretical1–13 and experimental16–32 studies on the decay rates of the quasiparticle states in layered graphenes, Bernal graphite, and carbon nanotubes. The electron–electron (e–e) Coulomb scatterings,1,2,4,5,33 as well as the electron–phonon (e–ph) scatterings,1,4,13–18,26,28,29,33 play critical roles in the decay rates (the mean free paths) of the excited electron/hole states, especially for the former. By using the self-energy method34 and the Fermi-golden rule, the theoretical predictions of Coulomb decay rates in monolayer graphene clearly show that they purely come from the T-created intraband e–h excitations, and the dependence on temperature and wave vector is very strong.1,4 The Coulomb decay rate is much faster than the electron–phonon scattering rate. A 2D monolayer graphene sharply contrasts with a 2D electron gas33 or a 1D carbon nanotube4 in electronic excitations and deexcitations. The 2D superlattice model, corresponding to the effective-mass model of monolayer graphene, is utilized to evaluate the Coulomb decay rates and quasiparticle energies in the 2D doped graphene and the 3D graphite intercalation compounds.44,45 It should be noticed that the state energies of quasiparticles can only be evaluated by the self-energies.48 In addition to the interband excitations, the doping-induced intraband excitations and acoustic/optical plasmons are very effective deexcitation channels.1,4 For donor-type systems with EF ∼ 1 eV, the excited valence bands present the oscillatory energy dependence, in which the largest energy widths even achieve the order of 0.1 eV because of the strong plasmon decay channels. The highly anisotropic behavior is revealed under the calculations of the tight-binding model, such as, the direction-dependent Coulomb decay rates in doped graphene,1,43,46 silicene and germanene at large wave vectors. There exist certain important differences among these three systems, being attributed to the very different hopping integrals.There are four kinds of experimental methods in measuring the quasiparticle decay rates/lifetimes of carbon-related sp2-bonding systems. The femtosecond pump-probe spectroscopies are very powerful tools in exploring the ultrafast relation of photoexcited electrons. They cover the time-resolved photoemission spectroscopy,16–18,26,27,30,31 absorption/transmission/reflectivity,19–25,32 and fluorescence spectroscopies,11,12 in which their measurements are very useful in understanding the quasiparticle behaviors of the excited conduction electrons. Moreover, the energy distributions of the ARPES measurements could provide the inelastic scattering rates of the excited valence holes. From the experimental measurements on graphite by the first equipment,30 the quasiparticles above the Fermi level are identified to exhibit the 3D metallic behavior, being consistent with the layer electron gas theory.49 The generation, relaxation, and recombination of non-equilibrium electronic carriers are clearly observed by the second tool.32 Furthermore, the fourth method is utilized to confirm the pronounced temperature-dependent decay rate for the excited electrons near EF. As to carbon nanotubes, the measurements of the first method show the carrier relaxation of the excited electrons in metallic single-walled and multiwalled systems. The measured decay rate is ∼1 meV for the low energy excited states.26,27 The second19,21 and third11,12 methods are made on bundled and isolated single-walled carbon nanotubes. The decay rate of the first (second) conduction band is ∼1–5 meV (∼0.5–3 meV), which depends on the nanotube.5 The first geometry, or energy gap is deduced to come from the intraband carrier deexcitations. The first conduction band also shows a smaller decay rate about several percentages of the large one.5 This is attributed to the interband recombination or the defect trapping. The temperature-dependent photoluminescence spectra are measured for a very small (6, 4) nanotube between 48 K and 182 K. The non-exponential behavior might be associated with the non-radiative decay of excitations. The high-resolution ARPES spectra of doped graphene systems (e.g., potassium-adsorbed graphenes) have confirmed the strong and non-monotonous dependence on wave vector/energy, mainly owing to the isotropic Dirac-cone band structure and the prominent Coulomb interactions of free conduction electrons.16–18
2 Theories
The doping-dependent Coulomb decay rates of monolayer graphene/a single-walled carbon nanotube could also be calculated from the Fermi-golden rule.1 The bare and screened Coulomb potentials are the critical mechanisms in understanding the electronic excitations and deexcitations. The square of the bare Coulomb interaction, which includes the band-structure effect, is expressed as| |V(k, q, p, h, h′, h′′, h′′′)|2 = vq2|〈k + q, h′|eiq·r|k, h〉〈p − q, h′′′|e−iq·r|p, h′′〉|2, | (1) |
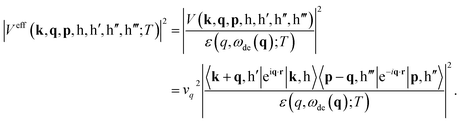 | (2) |
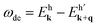 is the deexcitation energy from the initial |k, h〉 state to the final |k + q, h′〉 state through the intraband or interband process. Such potential is sensitive to the Fermi level, the direction and magnitude of the transferred momentum.
is the deexcitation energy from the initial |k, h〉 state to the final |k + q, h′〉 state through the intraband or interband process. Such potential is sensitive to the Fermi level, the direction and magnitude of the transferred momentum.
The effective e–e interactions could be utilized to explore the decay rate due to the inelastic Coulomb scatterings. From the Fermi golden rule, the quasiparticle decay rates of the excited |k, h)} state at any temperature is (ℏ = 1)
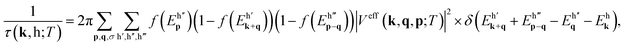 | (3) |
eqn (3) becomes
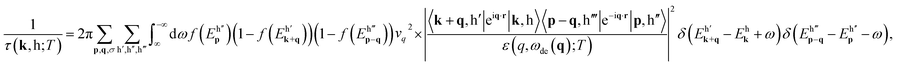 | (4) |
can be derived as
After the integral of ω is performed, one obtains the deexcitation energy from the delta function. eqn (4) becomes
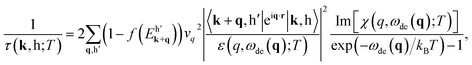 | (5) |
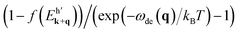 and vqIm[χ(q, ωde(q); T)]/|ε(q, ωde(q); T)|2 can be, respectively, derived as
and vqIm[χ(q, ωde(q); T)]/|ε(q, ωde(q); T)|2 can be, respectively, derived asand Im[−1/ε(q, ωde(q); T)]. Finally, the summation of q in eqn (5) is transformed into an integral form, and then the Coulomb decay rate is given by
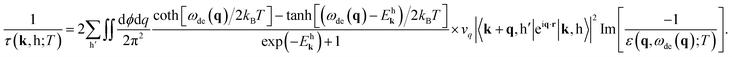 | (6) |
The Coulomb decay rate is determined by the Fermi–Dirac distribution of the final electronic state (the first term) and the energy loss function (the second term). In this work, we only focus on the zero-temperature condition. The Coulomb decay rate at T = 0 K is reduced to
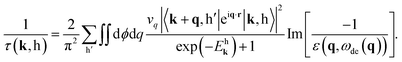 | (7) |
3 Results
3.1 Band structures and deexcitation channels
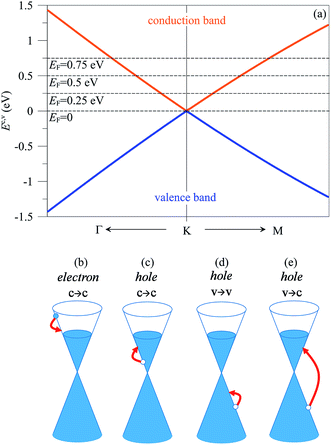
Carbon atom has six electrons, two of them forming a closed 1s2 shell and four filling 2s and 2p states. In monolayer graphene, only three outer electrons participate in the covalent bonds to form the sp2 hybrid orbitals, and the other outer electron with the 2pz orbital causes the feature-rich band structure. The linear Dirac-cone bands are isotropic for the low doping (EF ≤ 1 eV), while they gradually become parabolic at higher/deeper state energies [Fig. 1(a)]. The Fermi energy/free carrier density determines the main features of electronic excitations and thus dominate the Coulomb decay channels. When the Fermi level is situated at the gapless Dirac points, the excited electrons/holes at zero temperature could decay into conduction/valence band states only by utilizing the interband single-particle excitations. The increment of EF creates the intraband e–h excitations & plasmon modes, and induces the drastic changes in the interband single-particle excitations. Such EF-induced Coulomb excitations greatly diversify the decay channels. As for the excited conduction electrons above the Fermi level, the final states during the Coulomb deexcitations only lie between the initial states and the Fermi momentum [a red arrow in Fig. 1(b)], according to the Pauli exclusion principle and the conservation of energy and momentum. The available deexcitation channels, the intraband e–h excitations, make the most important contributions to the Coulomb decay rates for the low-lying conduction electrons, corresponding to the orange part in Fig. 2(a). But when the initial state energy is high, the interband single-particle excitations might become the effective deexcitation mechanisms [discussed later in Fig. 2(b)]. Concerning the excited holes in the conduction band, they could be de-excited to the conduction states [a blue arrow in Fig. 1(c)] through the intraband e–h excitations because of the low deexcitation energies and transferred momenta. On the other hand, the valence holes present two kinds of decay processes: v → v and v → c in Fig. 1(d) and (e), respectively. Their available decay channels, respectively, cover [intraband & interband e–h excitations] and [interband single-particle excitations & acoustic plasmon modes], corresponding to the blue arrow in Fig. 1(d) and red arrow in Fig. 1(e). Specifically, the latter has the large deexcitation energies at small momenta and is thus expected to exhibit the efficient and unusual Coulomb decay rates.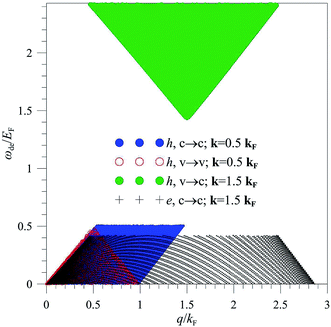 | ||
| Fig. 2 The relations between the deexcitation energies and transferred momenta for the specific excited states; conduction holes [Fig. 1(c)], valence holes [Fig. 1(d) and (e)], and conduction electrons [Fig. 1(b)]. | ||
3.2 Coulomb decay rates
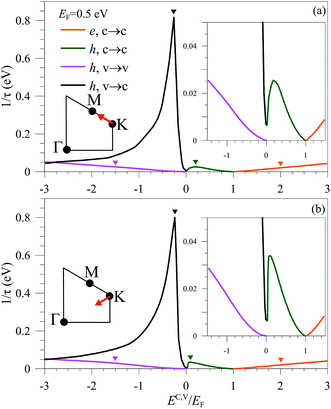
The Coulomb decay rates strongly depend on the quasiparticle states of (k, h). Concerning the excited conduction electrons near the Fermi momenta, the c → c intraband decay processes are the only deexcitation channels; that is, the intraband single-particle excitations make the main contributions to such processes (the orange part in Fig. 2); therefore, the Coulomb decay rates monotonously grow with Ec − EF, as indicated in Fig. 3(a) and (b) by the orange curves. Apparently, the zero decay rates (the infinite lifetimes) appear at the Fermi-momentum states because of the step-like Fermion distribution function at zero temperature. Furthermore, those of the neighboring excited states [|Ec,v − EF| < 0.5EF] are roughly proportional to (Ec,v − EF)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln|Ec,v − EF|, purely according to the numerical fitting. Also, the analytic derivations have been done for graphite intercalation compounds.35 Such an energy dependence is characteristic of a 2D electron gas.33,50 This is not surprising, since, when Ec,v → EF, the deexcitation energy is essential linear in q whether the energy band has a linear quadratic energy dispersion. Furthermore, the low momentum-frequency intraband single-particle are the only deexcitation channels. It is for such reasons that the widths of the doped graphene and electron gas near the Fermi level share a common character. The similar results are revealed in doped silicene and germanene.46 In addition, for the Fermi-momentum states, the temperature-dependent Coulomb decay rates display the T2
ln|Ec,v − EF|, purely according to the numerical fitting. Also, the analytic derivations have been done for graphite intercalation compounds.35 Such an energy dependence is characteristic of a 2D electron gas.33,50 This is not surprising, since, when Ec,v → EF, the deexcitation energy is essential linear in q whether the energy band has a linear quadratic energy dispersion. Furthermore, the low momentum-frequency intraband single-particle are the only deexcitation channels. It is for such reasons that the widths of the doped graphene and electron gas near the Fermi level share a common character. The similar results are revealed in doped silicene and germanene.46 In addition, for the Fermi-momentum states, the temperature-dependent Coulomb decay rates display the T2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[T] behavior, as observed in a 2D electron gas.51
ln[T] behavior, as observed in a 2D electron gas.51
The Coulomb decay rates of the higher-energy conduction electrons are sensitive to the anisotropic energy bands [Fig. 1(a)]. Along both the KM and KΓ directions [Fig. 3(a) and (b)], [1/τ]e,c→c grows with the increase of |Ec − EF|. The energy dependence on the two high-symmetry directions lies in whether the interband single-particle excitations become the effective deexcitation channels. The higher-energy electronic states have the stronger energy dispersions along KΓ [Fig. 1(a)]; therefore, their deexcitation energies at large transferred momenta are consistent with those of the interband e–h excitations. For example, the conduction state of Ec = 3EF along KΓ presents a plenty of deexcitation channels, as indicated by the orange curves in Fig. 4(a) at θq = 0°. Similar results are revealed in different momentum directions, e.g., θq = 30° in Fig. 4(c). The effective deexcitation channels cover the intraband and interband e–h excitations. The latter accounts responsible for the enhanced Coulomb decay rates in the high-energy conduction states.
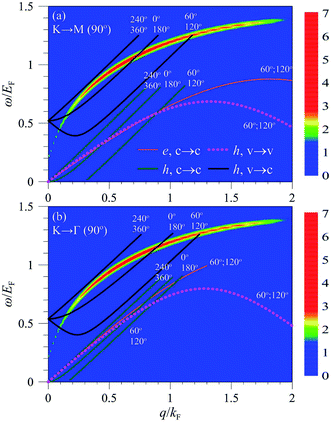 | ||
| Fig. 4 The available deexcitation spectra due to the specific states indicated by the arrows in Fig. 3(a) and (b) are displayed for (a) θq = 0° and (b) θq = 30°. The curves are defined by the conservation of energy and momentum. | ||
The deexcitation behaviors of the excited holes strongly depend on whether they belong to the conduction or valence states. Concerning the conduction holes, the Coulomb decay rates are almost isotropic, as indicated by the approximately identical [1/τ]h,c along KM and KΓ [green curves in Fig. 3(a) and (b)]. Furthermore, the energy dependence is similar to that of the low-lying conduction electrons (2D electron gas). Such results directly reflect the fact that the intraband single-particle excitations are the only available deexcitation channels, e.g., the pink curves related to the states very close to the conduction Dirac point [Fig. 4(a)–(d)]. As a result of the distorted linear dispersion, the finite decay rate at the Dirac point is different from the zero decay derived from the effective-mass model.35 Specifically, the Coulomb decay rate is local minimum at the K point, indicating that the Dirac-point state is the most stable among all the excited conduction holes [green curves in Fig. 3(a) and (b)].
On the other hand, the decay rates of the valence holes display the unique k dependence. The valence states slightly below the Dirac point have significant decay rates [purple arrow in Fig. 3(b)], approaching to those from above the conduction ones. They present only the v → c decay process, in which the deexcitation channels mainly come from the interband single-particle excitations and the undamped acoustic plasmon modes, as indicated by the black and brown symbols in Fig. 4(a) and (c). They create the important difference above and below the Dirac point. With the increasing valence-state energy, two decay channels, v → c and v → v, contribute to the Coulomb decay rates simultaneously. Concerning the former, the available range of the strong acoustic plasmon grows and then declines quickly for the low-lying valence holes, leading to an unusual peak structure in [1/τ]h,v→c at small Ev's [the red curve in Fig. 3(a) and (b)]. For example, the Ev = 0.9EF valence state along KM possesses the widest plasmon-decay range, associated with the black and brown curves in Fig. 4(a) and (c), so it could show the fast Coulomb decay [blue arrow in Fig. 3(a)]. The plasmon-induced deexcitations almost disappear for the deeper valence states, e.g., their absence under Ev < −1.5EF along the KM direction. The interband e–h excitations also make part of contributions to [1/τ]h,v→c, and they dominate the Coulomb decay rates of the deeper-energy valence holes, e.g., the red curves along KM and KΓ at Ev < −1.5EF. Specifically, for the v → v process, the excited valence holes [the blue curves in Fig. 3(a) and (b)] behave as the excited conduction electrons (the orange curves) in terms of the k dependence and the deexcitation channels. The intraband single-particle excitations are the dominating mechanisms in determining [1/τ]h,v→v of the low-lying valence states. They are substituted by the intraband and interband e–h excitations for the deeper valence holes along KΓ. This is responsible for the anisotropic Coulomb decay rates under the specific KΓ and KM directions.
The effective deexcitation channels is worthy of a detailed investigation. Each excited state experiences the inelastic e–e Coulomb scatterings along any directions, as clearly indicated by the summation of q in eqn (1), where the transferred momentum is a function of q (magnitude) and θq (azimuthal angle in the range of 2π). Through the specific excitation spectra, it might exhibit several dispersion relations (less than six) in the q-dependent deexcitation energies for a fixed θq. The main reason is that both Coulomb excitations and energy bands possess the hexagonal symmetry; that is, the excitation spectra are identical for θq, θq + π/3, θq + 2π/3, θq + π, θq + 4π/3, and θq + 5π/3. For example, the excited valence hole state, with the highest Coulomb decay rate along KM (KΓ), displays three (four) independent dispersive functions (blue curves) for θq = 0° (θq = 30°). The other excited states in Fig. 4(a) and (c) exhibit the similar behaviors. The total deexcitation regions cover the θq-dependent dispersion relations; that is, they strongly depend on the direction and magnitude of q, as expected from the basic scattering pictures.
3.3 Dependence of 1/τ on wave vector and Fermi level
Fig. 5–7 clearly illustrate the wave-vector- and Fermi-level-dependent Coulomb scattering rates. The decay rates of the valence holes exhibit non-monotonous energy dependence along any wave-vector directions, since the composite deexcitation channels cover the intraband & interband e–h excitations, and the damped & undamped acoustic plasmons. The strongest Coulomb scatterings, which are dominated by the undamped/damped collective excitations, come to exist for the valence states below the Dirac point [Fig. 5(d), 6(d), and 7(d)]. The valence-state decay rate strongly depends on the direction of k; the anisotropic decay is more obvious for the Fermi states. This is closely related to the strong anisotropy of the deeper valence band [Fig. 1(a)]. As for conduction holes and electrons, the Coulomb scattering rates, as measured from that of the Fermi-momentum states, present different behaviors. The former possesses nearly isotropic Coulomb decay rate in the phase diagram due to the low-energy isotropic Dirac cones. However, the latter exhibit monotonous energy dependence and the anisotropic deexcitations appear only for the high doping cases.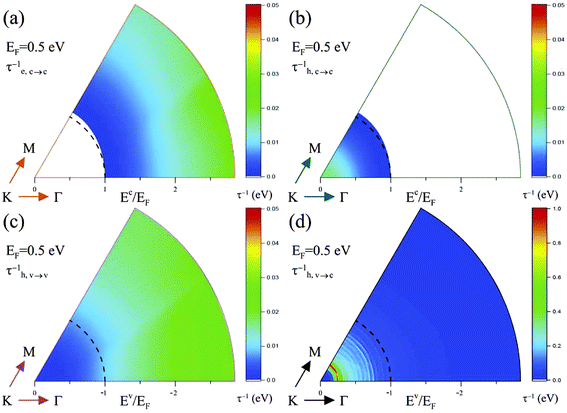 | ||
| Fig. 5 The wave-vector-dependent Coulomb scattering rates of (a) conduction electrons, (b) conduction holes, and valence holes with the (c) intraband and (d) interband decays at EF = 0.5 eV. | ||
It would be relatively easy to observe the oscillatory energy dependence and the anisotropic behavior under higher Fermi energies. Electronic excitations and Coulomb decay rates are very sensitive to the changes in the free-carrier densities with the variation of EF. The (q, ω)-phase diagram of 1/τ is drastically altered, as clearly shown in Fig. 5–7. For example, the less-damped acoustic plasmon and the almost isotropic excitations are revealed at a sufficiently low Fermi level, e.g., excitation spectra at EF ≤ 0.5 eV. These are directly reflected in the Coulomb decay rates [Fig. 5 and 6]. For the higher Fermi levels, the available momentum–frequency deexcitation ranges of the strongest acoustic plasmons and the interband single-particle excitations are greatly enhanced, since they could coexist together [Fig. 7]. This leads to the stronger dependence of decay rates on the state energy and direction of k, such as, a detailed comparison among those in Fig. 5(d) at EF = 0.5 eV, Fig. 6(d) at EF = 0.25 eV and Fig. 7(d) at EF = 0.75 eV. The EF-induced significant differences are further illustrated by the Coulomb decay rates of the specific states. For example, the largest decay rates come from the interband hole channels; the efficient decay is mainly contributed by the plasmons. Furthermore, the stability of the conduction/valence Dirac-point states is held even under heavy dopings, e.g., EF = 0.75 eV in Fig. 7.
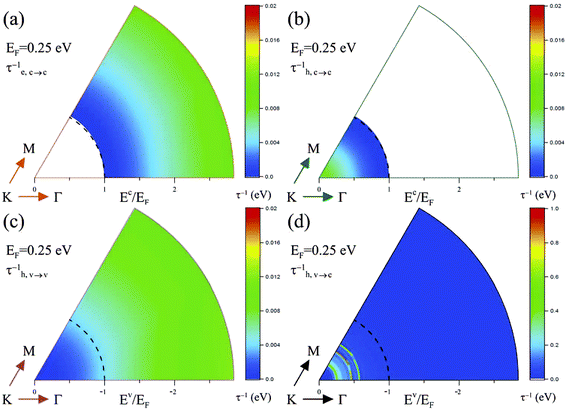 | ||
| Fig. 6 The wave-vector-dependent Coulomb scattering rates of (a) conduction electrons, (b) conduction holes, and valence holes with the (c) intraband and (d) interband decays at EF = 0.25 eV. | ||
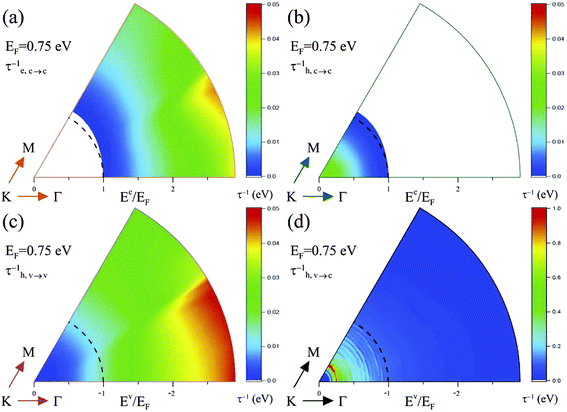 | ||
| Fig. 7 The wave-vector-dependent Coulomb scattering rates of (a) conduction electrons, (b) conduction holes, and valence holes with the (c) intraband and (d) interband decays at EF = 0.75 eV. | ||
3.4 Comparisons
The Coulomb decay rates of excited conduction and valence states in monolayer germanene have been thoroughly investigated in ref. 46, as done for graphene systems. The screened exchange self-energy is suitable for the inelastic Coulomb scatterings in monolayer germanene and silicene with the spin-orbital interactions; that is, the similar calculations could be finished under the accurate framework of the theoretical mode. It should be noticed that the spin-orbital couplings result in the superposition of the spin-up and the spin-down components. However, it does not need to deal with the spin-up- and spin-down-dependent Coulomb decay rates separately, because they only make the same contribution because of the conservation of spin configurations during the Coulomb scatterings. It is sufficient in exploring the wave-vector-, conduction-/valence- and energy-dependent self-energy. The effective deexcitation channels, which are diversified by the composite effects due to the spin-orbital couplings and carrier doping, are predicted to cover the intraband & interband e–h excitations, and the second, third & fourth kinds of plasmon modes. On the theoretical side, the RPA self-energy will be greatly modified under an external electric/magnetic field, mainly owing to the spin-split energy bands and wave functions. This is worthy of a complete investigation on the theoretical models and the electric-field- and magnetic-field-dependent Coulomb decay rates, being never studied in the previous calculations.Besides the electron–electron interactions, the electron–phonon interactions are also the effective deexcitation processes. In the study by Jiang et al.,13 the inverse of the relaxation time (1/τ) by means of the electron–phonon interactions is about 0.1–1 meV in the graphene-related system. The ratio of the electron–electron 1/τ in this work to the electron–phonon 1/τ roughly equals 2–3 orders of magnitude. The Coulomb decay rate is much faster than the electron–phonon scattering rate. However, the importance of the factors influencing the two kinds of the decay processes is different. In condensed-matter systems, phonons are quanta of lattice-vibration modes, which are regarded as quasiparticles and obey Bose–Einstein statistics.33 Previous works showed that the deexcitations from the electron–electron interactions become significant in extrinsic graphene with doping increase, while those from the electron–phonon interactions usually manifest at temperatures above room temperature.13–15
Monolayer germanene, silicene, and graphene, with the hexagonal symmetries, exhibit the pz-orbital-dominated low-lying band structures. The first system possesses the weakest nearest-neighbor hopping integral and the largest spin-orbital couplings, so that the essential properties are relatively easily tuned by the external factors, such as, the carrier doping, electric field, and magnetic field. Apparently, graphene shows the strongest hopping integral (∼2.6 eV) because of the smallest C–C bond length. This high-symmetry system presents a pair of linearly intersecting valence and conduction band at the gapless Dirac points under the negligible spin-orbital interactions, in which the isotropic Dirac-cone structure is further used to investigate the rich and unique physical properties. However, there are important differences between germanene and graphene in electronic excitations and Coulomb decay rates. Germanene is predicted to display the strongly anisotropic excitation/deexcitation behaviors, the second and third kinds of plasmons (the available decay channels), the e–h boundaries due to the spin-orbital couplings, and the F-induced splitting of excitation spectra. Such features are absent in graphene. The theoretical calculations have been done for the excited conduction and valence electrons in graphene, indicating the isotropic deexcitation behaviors under the low doping and a vanishing Coulomb decay rate at the Dirac point.1 The predicted Coulomb decay rates in monolayer germanene, silicene and graphene could be directly verified from the high-resolution ARPES measurements on the energy widths of quasiparticle state at low temperatures.16–18,26,27
Up to now, no theoretical models can deal with the complicated dynamic charge screenings using the fully exact manners. The extra comments on the random-phase approximation are useful in understanding the theoretical progress. The RPA is frequently utilized to explore the Coulomb excitations and deexcitations of condensed-matter systems, especially for the high carrier densities in 3D, 2D and 1D materials.1,5,41,42,45,47 This method might cause the poor results at low free carrier densities in certain many-particle properties, mainly owing to the insufficient correlation effects. A plenty of approximate models have been proposed to address/modify the electron–electron Coulomb interactions, e.g., the Hubbard52 and Singwi–Sjolander models53,54 for electronic excitation spectra, and the Ting–Lee–Quinn model for Coulomb decay rates.55 Concerning the time-dependent first-principles numerical calculations, accompanied with the Bethe–Salpeter equation, are further developed to investigate the electronic excitations and Coulomb decay rates in detail.10,28 Such calculations could account for the experimental measurements on excitation spectra and energy widths only under the large energy & momentum scales. However, it would be very difficult to provide much information about the critical mechanisms and physical pictures in determining the significant bare polarization functions, energy loss spectra, and Coulomb decay rates. Whether the calculated results within RPA are suitable and reliable at low energy is worthy of a systematic study.
It is also worthy to compare the decay rates of quasiparticles between monolayer graphene and 2D Fermi liquids through three kinds of deexcitation channels: i.e., via intraband & interband single-particle excitations and plasmon modes. These distinct deexcitation processes are explored in detail under the influences of electron dopings and energy band effects. It is shown that for the low-lying quasiparticles under zero or low doping, the decay rate in monolayer graphene is similar to that of 2D electron systems with parabolic energy dispersion.1,50 This is not surprising, since the available deexcitation channels mainly arise from low-energy single-particle excitations, and the corresponding deexcitation energies are essentially linear in q in the long-wavelength limit whether the energy band dispersion is linear or quadratic. However, this work demonstrates that, in general, doped graphene is non-Fermi liquid, once plasmons or high-energy single-particle excitations dominate the deexcitation processes. The important result indicates that the effects due to anisotropic screening and lattice structure play an important role in graphenes and other condensed-matter materials.46,56,57
Interatomic or intermolecular coulomb decay phenomenon is significant to chemical bonding in atoms and molecules. A monolayer doped graphene provides an ideal platform to study coulomb decay rate due to graphene. Its unique sp2 hybrid orbital and π-bonding orbital present in honeycomb carbon atoms arrangement. As monolayer doped graphene is irradiated, plasmons and excitons are generated and an Auger-like decay could occur, which is also refer as interatomic Coulomb decay. The higher energy generated via irradiation could be passed on to several electrons between neighbor carbon atoms in the graphene, affect bonding stabilizability, and cause single or double bonds breaks. Therefore, via doped monolayer graphene, Coulomb decay rate becomes an important and critical concept to understand how plasmons, excitons, electron energy, and 2p-electron status related to exchange and direct contribution between neighbor atoms. Coulomb decay rates in monolayer doped graphene can provide significant chemical bonding information and intermolecular interaction from simple graphene extend to complex biomolecules from chemistry aspect.58,59
4 Conclusions
The tight-binding model, the random phase approximation, and the Fermi-golden rule are respectively utilized to study the band structures and the dielectric functions, and the decay rates of monolayer electron-doped graphene. In conclusion, it can be said that four kinds of the deexcitation processes, due to the nonzero Fermi energy, including excited conduction electrons to conduction states, conduction holes to conduction states, valence holes to conduction states, and valence holes to valence states in monolayer electron-doped graphene exhibit unique Coulomb decay rates. These decays might be by means of the intraband e–h excitations, the interband e–h excitations, and the plasmon modes, which are dominated by the quasiparticle states and the Fermi energies. The low-lying valence hole states have the largest decay rate or the shortest lifetime, since they can decay through the undamped acoustic plasmon. They also show the nonmonotonous energy dependence and anisotropic behavior. On the other hand, the energy-dependent decay rate of the low-energy conduction electrons and holes are similar to those in a two-dimensional electron gas. As for the higher-energy conduction states and the deeper-energy valence states, the similar available deexcitation channels cause a similar dependence of decay rate on the wave vector.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to acknowledge the financial support from the Ministry of Science and Technology of the Republic of China (Taiwan) under Grant No. MOST 107-2112-M-017-001.References
- J. H. Ho, C. P. Chang, R. B. Chen and M. F. Lin, Electron decay rates in a zero-gap graphite layer, Phys. Lett. A, 2006, 357, 401 CrossRef CAS
.
- H. Zhao and S. Mazumdar, Electron–Electron Interaction Effects on the Optical Excitations of Semiconducting Single-Walled Carbon Nanotubes, Phys. Rev. Lett., 2004, 93, 157402 CrossRef PubMed
.
- C. W. Chiu, S. H. Lee and M. F. Lin, Inelastic Coulomb scatterings of doped armchair carbon nanotubes, J. Nanosci. Nanotechnol., 2010, 10, 2401–2408 CrossRef CAS PubMed
.
- C. W. Chiu, Y. H. Ho, S. C. Chen, C. H. Lee, C. S. Lue and M. F. Lin, Electronic decay rates in semiconducting carbon nanotubes, Phys. E, 2006, 34, 658–661 CrossRef CAS
.
- C. W. Chiu, F. L. Shyu, C. P. Chang, D. S. Chuu and M. F. Lin, Coulomb scattering rates of excited carriers in moderate-gap carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235407 CrossRef
.
- Q. Li and S. D. Sarma, Finite temperature inelastic mean free path and quasiparticle lifetime in graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085406 CrossRef
.
- J. Gonzalez, F. Guinea and M. A. H. Vozmediano, Unconventional Quasiparticle Lifetime in Graphite, Phys. Rev. Lett., 1996, 77, 3589 CrossRef CAS PubMed
.
- C. D. Spataru, M. A. Cazalilla, A. Rubio, L. X. Benedict, P. M. Echenique and S. G. Louie, Anomalous Quasiparticle Lifetime in Graphite: Band Structure Effects, Phys. Rev. Lett., 2001, 87, 246405 CrossRef CAS PubMed
.
- C.-H. Park, F. Giustino, C. D. Spataru, M. L. Cohen and S. G. Louie, Inelastic carrier lifetime in bilayer graphene, Appl. Phys. Lett., 2012, 100, 032106 CrossRef
.
- C.-H. Park, F. Giustino, C. D. Spataru, M. L. Cohen and S. G. Louie, First-Principles Study of Electron Linewidths in Graphene, Phys. Rev. Lett., 2009, 102, 076803 CrossRef PubMed
.
- A. Hagen, M. Steiner, M. B. Raschke, C. Lienau, T. Hertel, H. Qian, A. J. Meixner and A. Hartschuh, Exponential Decay Lifetimes of Excitons in Individual Single-Walled Carbon Nanotubes, Phys. Rev. Lett., 2005, 95, 197401 CrossRef PubMed
.
- F. Wang, G. Dukovic, L. E. Brus and T. F. Heinz, Time-Resolved Fluorescence of Carbon Nanotubes and Its Implication for Radiative Lifetimes, Phys. Rev. Lett., 2004, 92, 177401 CrossRef PubMed
.
- J. Jiang, A. Grüneis, G. Dresselhaus and M. S. Dresselhaus, Chem. Phys. Lett., 2004, 392, 383 CrossRef CAS
.
- D. K. Efetov and P. Kim, Controlling Electron–Phonon Interactions in Graphene at Ultrahigh Carrier Densities, Phys. Rev. Lett., 2010, 105, 256805 CrossRef PubMed
.
- P. J. Hale, S. M. Hornett, J. Moger, D. W. Horsell and E. Hendry, Hot phonon decay in supported and suspended exfoliated graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 121404(R) CrossRef
.
- T. Valla, J. Camacho, Z.-H. Pan, A. V. Fedorov, A. C. Walters, C. A. Howard and M. Ellerby, Anisotropic Electron–Phonon Coupling and Dynamical Nesting on the Graphene Sheets in Superconducting CaC6 using Angle-Resolved Photoemission Spectroscopy, Phys. Rev. Lett., 2009, 102, 107007 CrossRef CAS PubMed
.
- A. V. Fedorov, N. I. Verbitskiy, D. Haberer, C. Struzzi, L. Petaccia, D. Usachov, O. Y. Vilkov, D. V. Vyalikh, J. Fink, M. Knupfer, B. Buchner and A. Gruneis, Observation of a universal donor-dependent vibrational mode in graphene, Nat. Commun., 2014, 5, 3257 CrossRef CAS PubMed
.
- A. Bostwick, T. Ohta, T. Seyller, K. Horn and E. Rotenberg, Quasiparticle dynamics in graphene, Nat. Phys., 2007, 3, 36 Search PubMed
.
- J.-S. Lauret, C. Voisin, G. Cassabois, C. Delalande, Ph. Roussignol, O. Jost and L. Capes, Ultrafast Carrier Dynamics in Single-Wall Carbon Nanotubes, Phys. Rev. Lett., 2003, 90, 057404 CrossRef PubMed
.
- O. J. Korovyanko, C.-X. Sheng, Z. V. Vardeny, A. B. Dalton and R. H. Baughman, Ultrafast Spectroscopy of Excitons in Single-Walled Carbon Nanotubes, Phys. Rev. Lett., 2004, 92, 017403 CrossRef CAS PubMed
.
- G. N. Ostojic, S. Zaric, J. Kono, M. S. Strano, V. C. Moore, R. H. Hauge and R. E. Smalley, Interband Recombination Dynamics in Resonantly Excited Single-Walled Carbon Nanotubes, Phys. Rev. Lett., 2004, 92, 117402 CrossRef CAS PubMed
.
- L. Huang, H. N. Pedrosa and T. D. Krauss, Ultrafast Ground-State Recovery of Single-Walled Carbon Nanotubes, Phys. Rev. Lett., 2004, 93, 017403 CrossRef
.
- Y. Bai, J.-H. Olivier, G. Bullard, C. Liu and M. J. Therien, Dynamics of charged excitons in electronically and morphologically homogeneous single-walled carbon nanotubes, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 674 CrossRef CAS PubMed
.
- K. Maekawa, K. Yanagi, Y. Minami, M. Kitajima, I. Katayama and J. Takeda, Bias-induced modulation of ultrafast carrier dynamics in metallic single-walled carbon nanotubes, Phys. Rev. B, 2018, 97, 075435 CrossRef CAS
.
- X.-P. Tang, A. Kleinhammes, H. Shimoda, L. Fleming, K. Y. Bennoune, S. Sinha, C. Bower, O. Zhou and Y. Wu, Electronic Structures of Single-Walled Carbon Nanotubes Determined by NMR, Science, 2000, 288, 492–494 CrossRef CAS PubMed
.
- T. Hertel and G. Moos, Electron–Phonon Interaction in Single-Wall Carbon Nanotubes: A Time-Domain Study, Phys. Rev. Lett., 2000, 84, 5002 CrossRef CAS PubMed
.
- M. Ichida, Y. Hamanaka, H. Kataura, Y. Achiba and A. Nakamura, Ultrafast Relaxation Dynamics of Photoexcited Carriers in Metallic and Semiconducting Single-walled Carbon Nanotubes, J. Phys. Soc. Jpn., 2004, 73, 3479 CrossRef CAS
.
- L. Luer, C. Gadermaier, J. Crochet, T. Hertel, D. Brida and G. Lanzani, Coherent Phonon Dynamics in Semiconducting Carbon Nanotubes: A Quantitative Study of Electron–Phonon Coupling, Phys. Rev. Lett., 2009, 102, 127401 CrossRef PubMed
.
- J. Y. Park, S. Rosenblatt, Y. Yaish, V. Sazonova, H. Ustunel, S. Braig, T. A. Arias, P. W. Brouwer and Pa. L. McEuen, Electron–Phonon Scattering in Metallic Single-Walled Carbon Nanotubes, Nano Lett., 2004, 4, 517 CrossRef CAS
.
- S. Xu, J. Cao, C. C. Miller, D. A. Mantell, R. J. D. Miller and Y. Gao, Energy Dependence of Electron Lifetime in Graphite Observed with Femtosecond Photoemission Spectroscopy, Phys. Rev. Lett., 1996, 76, 483 CrossRef CAS PubMed
.
- G. Moos, C. Gahl, R. Fasel, M. Wolf and T. Hertel, Anisotropy of Quasiparticle Lifetimes and the Role of Disorder in Graphite from Ultrafast Time-Resolved Photoemission Spectroscopy, Phys. Rev. Lett., 2001, 87, 267402 CrossRef CAS PubMed
.
- K. Seibert, G. C. Cho, W. Kutt, H. Kurz, D. H. Reitze, J. I. Dadap, H. Ahn, M. C. Downer and A. M. Malvezzi, Femtosecond carrier dynamics in graphite, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 2842 CrossRef CAS PubMed
.
- G. D. Mahan, Many-Particle Physics, Plenum, New York, 1990 Search PubMed
.
- J. H. Ho, C. W. Chiu and M. F. Lin, Phys. E, 2006, 35, 212 CrossRef CAS
.
- K. W.-K. Shung, Lifetime effects in low-stage intercalated graphite systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34(2), 1264 CrossRef CAS PubMed
.
- M. F. Lin and D. S. Chuu, Elementary excitations in a carbon nanotube, J. Phys. Soc. Jpn., 1997, 66, 757 CrossRef CAS
.
- Y. C. Chuang, J. Y. Wu and M. F. Lin, Dynamical Conductivity and Zero-Mode Anomaly in Honeycomb Lattices, J. Phys. Soc. Jpn., 2002, 71, 1318 CrossRef
.
- Y. C. Chuang, J. Y. Wu and M. F. Lin, Analytical Calculations on Low-Frequency Excitations in AA-Stacked Bilayer Graphene, J. Phys. Soc. Jpn., 2012, 81, 124713 CrossRef
.
- M. F. Lin, Y. C. Chuang and J. Y. Wu, Electrically tunable plasma excitations in AA-stacked multilayer graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125434 CrossRef
.
- Y. C. Chuang, J. Y. Wu and M. F. Lin, Electric-field-induced plasmon in AA-stacked bilayer graphene, Ann. Phys., 2013, 339, 298 CAS
.
- J. H. Ho, C. L. Lu, C. C. Hwang, C. P. Chang and M. F. Lin, Coulomb excitations in AA- and AB-stacked bilayer graphites, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 085406 CrossRef
.
- J. H. Ho, C. P. Chang and M. F. Lin, Electronic excitations of the multilayered graphite, Phys. Lett. A, 2006, 352, 446 CrossRef CAS
.
- J. Y. Wu, S. C. Chen and M. F. Lin, Temperature-dependent Coulomb excitations in silicene, New J. Phys., 2014, 16, 125002 CrossRef
.
- M. F. Lin, C. S. Huang and D. S. Chuu, Plasmons in graphite and stage-1 graphite intercalation compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 13961 CrossRef CAS
.
- K. W.-K. Shung, Dielectric function and plasmon structure of stage-1 intercalated graphite, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 979 CrossRef CAS PubMed
.
- P. H. Shih, C. W. Chiu, J. Y. Wu, T. N. Do and M. F. Lin, Coulomb scattering rates of excited states in monolayer electron-doped germanene, Phys. Rev. B, 2018, 97, 195302 CrossRef CAS
.
- F. L. Shyu and M. F. Lin, Loss spectra of graphite-related systems: a multiwall carbon nanotube, a single-wall carbon nanotube bundle, and graphite layers, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8508 CrossRef
.
- M. F. Lin and K. W.-K. Shung, The self-energy of electrons in graphite intercalation compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 1109–1118 CrossRef CAS PubMed
.
- P. Hawrylak, Effective mass and lifetime of electrons in a layered electron gas, Phys. Rev. Lett., 1987, 59, 485 CrossRef CAS PubMed
.
- G. F. Giuliani and J. J. Quinn, Lifetime of a quasiparticle in a two-dimensional electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 4421 CrossRef CAS
.
- C. P. Weber, N. Gedik, J. E. Moore, J. Orenstein, J. Stephens and D. D. Awschalom, Observation of spin Coulomb drag in a two-dimensional electron gas, Nature, 2005, 437, 1330–1333 CrossRef CAS PubMed
.
- J. Hubbard, The description of collective motions in terms of many-body perturbation theory. II. The correlation energy of a free-electron gas, Proc. R. Soc. London, Ser. A, 1963, 276, 238–257 CrossRef
.
- K. S. Singwi, M. P. Tosi, R. H. Land and A. Sjolander, Electron Correlations at Metallic Densities, Phys. Rev., 1968, 176, 589 CrossRef CAS
.
- P. Vashishta and K. S. Singwi, Electron Correlations at Metallic Densities. V, Phys. Rev. B: Solid State, 1972, 6, 875 CrossRef CAS
.
- C. S. Ting, T. K. Lee and J. J. Quinn, Effective Mass and g Factor of Interacting Electrons in the Surface Inversion Layer of Silicon, Phys. Rev. Lett., 1975, 34, 870 CrossRef CAS
.
- B. Kiraly, E. J. Knol, K. Volckaert, D. Biswas, A. N. Rudenko, D. A. Prishchenko, V. G. Mazurenko, M. I. Katsnelson, P. Hofmann, D. Wegner and A. A. Khajetoorians, Anisotropic Two-Dimensional Screening at the Surface of Black Phosphorus, Phys. Rev. Lett., 2019, 123, 216403 CrossRef PubMed
.
- C.-Y. Lin, B.-L. Huang, C.-H. Ho, G. Gumbs and M.-F. Lin, Geometry-diversified Coulomb excitations in trilayer AAB stacking graphene, Phys. Rev. B, 2018, 98, 195442 CrossRef CAS
.
- C. A. Schmuttenmaer, Exploring Dynamics in the Far-Infrared with Terahertz Spectroscopy, Chem. Rev., 2004, 104, 1759 CrossRef CAS PubMed
.
- F. Krausz and M. Ivanov, Attosecond physics, Rev. Mod. Phys., 2009, 81, 163 CrossRef
.
| This journal is © The Royal Society of Chemistry 2020 |