Open Access Article
Open Access ArticleMulti-ionization of the Cl2 molecule in the near-infrared femtosecond laser field
Jian Zhanga,
Zhipeng Lib and
Yan Yang *b
*b
aKey Laboratory of Science and Technology of Eco-Textiles, Ministry of Education, College of Chemistry, Chemical Engineering and Biotechnology, Donghua University, Shanghai 201620, China
bDepartment of Physics, State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, People's Republic of China. E-mail: yyang@lps.ecnu.edu.cn
First published on 2nd January 2020
Abstract
The multi-electron ionization and subsequent dissociation of the Cl2 molecule in a near-infrared femtosecond laser field was investigated via the dc-sliced ion imaging technique. The single charged molecular ions, Cl2+, dissociate from two excited states, 2Πu and 2Σg+, with the electrons ionized from the HOMO−1 and HOMO−2 orbital, respectively. For the multi-charged molecular ions, Cl2n+ (n = 2–8), our results showed that the stretch of the inter-nuclear distance benefitted the ionization of the electrons to produce highly-charged molecular ions. In addition, compared with the traditional charge resonance enhanced ionization (CREI) model, the critical distance (Rc) for the Cl2 molecule in our experiment was a short range that depended on the charge state rather than a single point.
Introduction
Diatomic molecules, which are exposed to a femtosecond laser field with an intensity over 1014 W cm−2, always undergo multi-electron dissociative ionization, followed by the explosion of molecular ions into ionic fragments with characteristic kinetic energy releases (KERs).1–8Recently, multi-electron ionization in an intense field has drawn extensive attention. At the same time, some theoretical models have been proposed to illustrate the dynamical process. The multi-electron dissociative ionization (MEDI) model showed that the femtosecond laser field can quickly strip several electrons off at the equilibrium nuclear distance. The subsequent dissociation of the charged molecular ion was influenced by the repulsive Coulomb energy. However, the energy defect, namely, the kinetic energy releases (KERs) was always smaller than the theoretical prediction for all of the charged states of the molecular ions, is still indistinct and unresolved. For last two decades, several models have been proposed to explain this issue. The post-dissociative ionization (PDI) model showed that the fragment ions could be ionized for the second time after the dissociation process.9 This model explained the origin of high charged fragmental ions with small kinetic energy. S. Chelkowski and A. D. Bandrauk proposed a two-step model in which the molecule loses electrons and coulomb explosions occur twice, at their equilibrium distance and critical distance.10 This model explains the energy defect problem from the starting point of the Coulomb explosion. Bandrauk et al. proposed a charge resonance enhanced ionization (CREI) model11 and showed that there exists a pair of charge-resonant states that are strongly coupled to the laser field at a critical distance, Rc, where photoionization can be greatly enhanced. Based on this model, the energy defect ratio of all of the charged-state molecular ions is nearly the same. Researchers found that for a given molecule, the Rc is nearly the same for all charge states and is appropriately 1–2 times larger than the equilibrium internuclear distance of the neutral molecule.9,12
Until now, the CREI model has been proved to be an appropriate explanation for highly charged molecular ions. However, George N. Gibson et al.13,14 proposed that CREI experience a sequential ionization process where electrons are successively stripped in one laser pulse and the nuclear stretch cannot be avoided. The kinetic energy (KE) obtained from each channel also included the energy accumulated from the previous ionization step. Therefore, the Rc should change along with the charge states rather than having a fixed value for all of the charge states for a given molecule. In addition, the ionization process is greatly influenced by the intensity and the duration of the laser pulse.
The existence of the Rc can resolve the energy deficit problem for the Coulomb explosion (CE) process. However, the driving force of these dissociation processes and how the KE accumulated in the molecules before dissociation is still worth researching. In this work, we studied the dissociative ionization and CE of a Cl2 molecule irradiated by an 800 nm femtosecond laser field using a de-sliced ion imaging technique. By measuring the KE of the fragment ions, we found that the molecular ions, Cl2+, dissociated from two excited states, 2Πu and 2Σg+, with the electrons being respectively excited from the HOMO−1 and HOMO−2 orbital. For multi-charged molecular ions, Cl2n+ (n = 2–8), an energy defect also existed in our experimental results, which could be explained by the CREI model. The measured KER of each channel for the Cl2 Coulomb explosion was around 48–66% of the theoretical calculation. Our results showed that the stretch of the internuclear distance benefitted the ionization of the electrons to produce highly-charged molecular ions. In addition, other than the traditional CREI process, the critical distance, Rc, for the Cl2 molecule in femtosecond laser fields was not a single point, but a short range that depended on the charge state.
Experimental and theoretical methods
The photodissociative ionization of the Cl2 molecule in a near-infrared femtosecond laser field was performed in a home-made DC-sliced-velocity-imaging system, which has been described in detail elsewhere.15 Briefly, the linearly polarized femtosecond laser pulse (70 fs FWHM, center wavelength: 800 nm) was focused into a custom DC-sliced imaging spectrometer by a biconvex lens with 40 cm focal length. The gaseous chlorine molecules that were seeded into helium (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) were ejected into the reaction chamber (∼4.0 × 10−9 mbar) by a pulse valve (General valve, Parker) with a repetition rate of 100 Hz and a duration of 150 μs. The laser beam interacted with a supersonic molecular beam at a right angle. The produced ions passing through the velocity mapping lens, during which momentum focusing was maintained and every individual ion-cloud was stretched to meet the slice condition, were detected by a pair microchannel plates (MCP) coupled with a P47 phosphor screen. The 2D momentum images of each fragment were the central slice (around pz = 0) of the corresponding 3D momentum distribution and were obtained by a charge coupled device camera (PI-MAXII, Princeton Instrument) with a 5 ns time resolution. The laser intensity in the focal volume was estimated to be between 7 × 1013 to 1.0 × 1015 W cm−2, which was calibrated by the relationship of the Ar2+/Ar+ yield ratio and the laser intensity proposed by Guo et al.16
10) were ejected into the reaction chamber (∼4.0 × 10−9 mbar) by a pulse valve (General valve, Parker) with a repetition rate of 100 Hz and a duration of 150 μs. The laser beam interacted with a supersonic molecular beam at a right angle. The produced ions passing through the velocity mapping lens, during which momentum focusing was maintained and every individual ion-cloud was stretched to meet the slice condition, were detected by a pair microchannel plates (MCP) coupled with a P47 phosphor screen. The 2D momentum images of each fragment were the central slice (around pz = 0) of the corresponding 3D momentum distribution and were obtained by a charge coupled device camera (PI-MAXII, Princeton Instrument) with a 5 ns time resolution. The laser intensity in the focal volume was estimated to be between 7 × 1013 to 1.0 × 1015 W cm−2, which was calibrated by the relationship of the Ar2+/Ar+ yield ratio and the laser intensity proposed by Guo et al.16
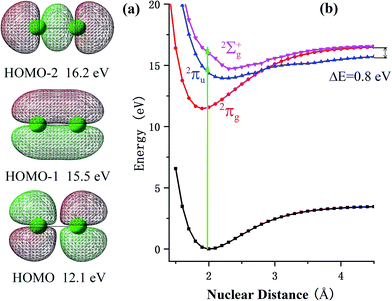
To better illustrate the ionization and dissociation process of the Cl2 molecule, theoretical calculations were performed using the Gaussian 09 software package.17 The potential energy surface (PES) was calculated with an equation-of-motion couple cluster singles and doubles (EOM-CCSD)18–20 level of theory using an aug-cc-pvtz basis set.21 The equation-of-motion couple cluster method has been identified to be an accurate method to calculate the energy of the excited states and has generally been used in singles and doubles excitation approximations. To verify the accuracy of this method, we compared the equilibrium distance of the ground state, 2Πg, and excited states, 2Πu and 2Σg+, of the Cl2+ ions as well as the energy gaps between them. The calculated equilibrium distance of the 2Πg and 2Πu states were 1.9 and 2.3 Å, respectively, which were in accordance with the reported data in ref. 22 (1.9 and 2.3 Å). The calculated energy gaps of these states were around 2.78 and 1.63 eV, which were very close to the same data (2.75 and 1.79 eV).22 Therefore, the good agreement between our computation and previous results demonstrated the feasibility of the theoretical methodology used in this paper.
Results
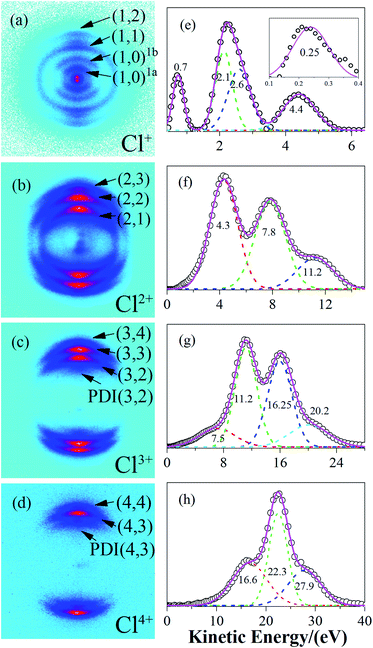
The raw DC-sliced ion images of Cln+ (n = 1–4) are shown in Fig. 1(a)–(d). Clearly, the multi-ring structure provided intuitive evidence that the fragment ions with the same charge state were from different reaction channels. The corresponding KE values were extracted and are shown in Fig. 1(e)–(h). The circles ( ) denote the experiment data. The short dashed lines (
) denote the experiment data. The short dashed lines ( ) are the fitting peaks and the solid line (
) are the fitting peaks and the solid line ( ) is the simulated distribution. The label/channel (p, q) corresponds to the estimated dissociation process, Cl2(p+q)+ → Clp+ + Clq+.
) is the simulated distribution. The label/channel (p, q) corresponds to the estimated dissociation process, Cl2(p+q)+ → Clp+ + Clq+.
Based on the two-body CE model, the exploded two fragment ions should have met the momentum conservation requirements. Therefore, the relationship of the KERs and mass can be written as
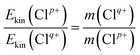 | (1) |
| Dissociation channels | KERs | |
|---|---|---|
| (1, 0)1a | Cl2+ → Cl+ + Cl | 0.5 |
| (1, 0)1b | Cl2+ → Cl+ + Cl | 1.4 |
| (1, 1) | Cl22+ → Cl+ + Cl+ | 4.8 |
| (2, 1) | Cl23+ → Cl2+ + Cl+ | 8.7 |
| (2, 2) | Cl24+ → Cl2+ + Cl2+ | 15.6 |
| (3, 2) | Cl25+ → Cl3+ + Cl2+ | 22.4 |
| PDI(3, 2) | Cl25+ → Cl3+ + Cl2+ | 15.0 |
| (3, 3) | Cl26+ → Cl3+ + Cl3+ | 32.5 |
| (4, 3) | Cl27+ → Cl4+ + Cl3+ | 42.5 |
| PDI(4, 3) | Cl27+ → Cl4+ + Cl3+ | 33.8 |
| (4, 4) | Cl28+ → Cl4+ + Cl4+ | 55.8 |
Discussion
(1) Dissociative ionization of the (1, 0) channel
At a relatively lower laser intensity, the single ionization dominated the ionization process of the Cl2 molecule and the subsequent dissociation produced one Cl+ ion and one neutral Cl atom. Two dissociation channels with different KERs for the Cl2+ dissociation were observed and marked as channel (1, 0)1a and channel (1, 0)1b. As shown in Table 1, because the KERs of the above two channels were much smaller than those from the CE channels, these Cl+ ions could not be produced by the CE process of the multi-charged molecular ions. In addition, the energy difference of these two channels was 0.9 eV, which was far beyond our experimental systematic error. Therefore, the two channels should have given rise to the dissociation process of the Cl2+ ions with different excited electronic states. To further understand the dissociation process, the PES of the Cl2+ ion was calculated and is shown in Fig. 2.Fig. 2 shows the PES of the Cl2+ ions by removing one electron from the HOMO, HOMO−1 and HOMO−2 orbital of the Cl2 molecule, respectively. After removing one electron from the HOMO, the molecule was excited to the 2Πg state. Considering HOMO is an anti-bonding π orbital, the equilibrium inter-nuclear distance of the Cl2+ ion (1.90 Å) was shorter than that of the Cl2 molecule (1.98 Å). The interaction of the two Cl atoms became stronger as shown in Fig. 2b and the potential well became deeper. The situation was the opposite when the removed electron was from the HOMO−1 and the molecular ion was excited to the 2Πu state. The HOMO−1 was a bonding orbital. Removing one electron from the bonding orbital made the equilibrium internuclear distance longer to 2.3 Å. The interaction of the two Cl atoms weakened and the potential well became shallower. The removed electron could have also come from the σg orbital (HOMO−2) to form the 2Σg+ state. The PES of this state was similar to the 2Πu state with a long equilibrium internuclear distance and weak interactions.
The dissociative ionization started from the neutral Cl2 molecule being vertically ionized at the equilibrium internuclear distance (green region in Fig. 2b) to produce the Cl2+ ion. The 2Πg state was right in its potential well, where the molecular ions were barely able to dissociate into fragments. Our experimental results, in which no fragments dissociated from the 2Πg state, also support this point.
Actually, the Cl2+ ions were easy to populate in the Cl2+ ion state 2Πg due to the low exciting energy and bounding character. The molecular ion on this state may not have dissociated directly, but these ions may have been further excited to a higher state and produced multi-charge fragment ions, which we discussed in previous reports.23
When the Cl2+ ions are vertically excited to 2Πu and 2Σg+ states, during which the electrons are respectively taken away from the HOMO−1 and HOMO−2 orbital, the molecular ions populate on high vibrationally excited states that have enough energy to overcome the potential well. Therefore, they have the chance to dissociate into fragments. There were only two channels observed for Cl2+ dissociation and the measured energy difference of these two channels was 0.9 eV (0.5 eV and 1.4 eV). Therefore, they dissociated from the two states with an energy gap around 0.9 eV. By observing the PES of the two states, we found that the energy gap of the 2Πu and 2Σg+ states was 0.8 eV, which was similar to our experimental results. Considering the experimental systematic error, we concluded that channel 1a and channel 1b dissociated from the 2Πu and 2Σg+ states of the Cl2+ ions, respectively.
(2) CE of multi-charged molecular ions Cl2n+ (n = 2–8)
When the Cl2 molecule was irritated by an intense femtosecond laser field, several electrons may be peeled off to produce the multi-charged molecular ions Cl2n+ (n = 2–8). The repulsion of the multiple charges drove the dissociation process for the Cl2n+ (n = 2–8) ions. For the diatomic molecule CE channels Cl2(p+q)+ → Clp+ + Clq+, the possible dissociation pathways of the multi-charged parent ions included a charge symmetry dissociation (CSD) where |p − q| ≤ 1, and a charge asymmetric dissociation (CAD) where |p − q| > 1. According to our experimental results, the latter case was not observed and it is likely that the CAD process was not involved in our experiment.In classic CE model, the total KERs of one CE channel are expressed as:
| KER = 14.4 pq/r | (2) |
Using the PES of the parent ions Cl2n+ (n = 2–8), the critical distance, Rm,n, was calculated as follows. The relationship of the experimentally measured KERs, Em,n, and the potential energy for the (m, n) channel, Vm,n(Rm,n), was used. They should meet the following relationship:14,15
| Eexpm,n = Vm,n(Rm,n) − V(∞) | (3) |
| Eexpm,n = Vm,n(Rm,n) + Eaccm,n | (4) |
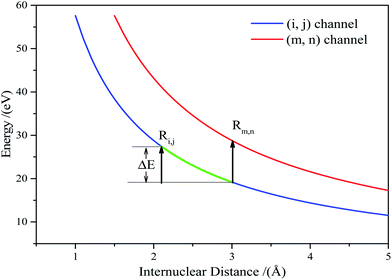
For any ionization from (i, j) to (m, n), the KERs increment can be expressed as:
| Eexpm,n − Eexpi,j = Vm,n(Rm,n) + Eaccm,n − Vi,j(Ri,j) − Eacci,j | (5) |
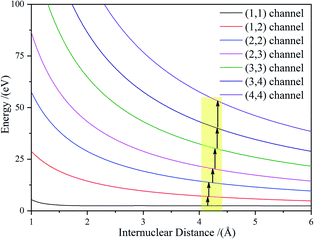
The accumulated energy increase from (i, j) to (m, n) can be seen in Fig. 3(the green line).
| ΔE = Eaccm,n − Eacci,j = Vi,j(Ri,j) − Vi,j(Rm,n) | (6) |
Substituting eqn (6) into eqn (5), we arrived at:
| Eexpm,n − Eexpi,j = Vm,n(Rm,n) − Vi,j(Rm,n) | (7) |
Vm,n(Rm,n) can be calculated according to Coulomb's law. Thus, eqn (7) can be written as:
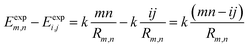 | (8) |
We applied eqn (7) to our measured KERs data and the calculated Rc for each channel is listed in Table 2. For comparison, the traditional method (eqn (2)) was used to calculate the critical distance and the results are also listed as 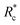 in the table. We found that the values of
in the table. We found that the values of 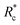 were always smaller than those of Rc.
were always smaller than those of Rc.
Considering the molecular Cl2 experience, a sequential ionization process where the electrons are successively stripped, all of the dissociation channels were charge symmetric. The only possible ionization step was (1, 1) → (1, 2) → (2, 2) → (2, 3) → (3, 3) → (3, 4) → (4, 4). The (1, 1) channel was produced by the Cl2+ ion, which further ionized to Cl22+. According to our experimental results and the theoretical calculation, the CE of Cl22+ started at Rc = 3 Å and produced Cl+ fragment ions with the KERs of the channel mainly distributed around 4.8 eV. During the nuclear distance stretch, Cl22+ was ionized to Cl23+ at Rc = 4.15 Å. Then, some of the Cl23+ ions exploded to produce Cl2+ and Cl+ ions with a 8.7 eV KER. The measured KER included the potential energy change and the accumulated energy from the Cl22+ stretching process. The other Cl23+ ions reduplicated the above process at 4.17 Å for further ionization to Cl24+ ions. If the laser pulse intensity was high enough, Cl2n+ (n = 3–8) ions were successfully produced, resulting in the generation of the CE channels listed in Table 2 and Fig. 4. We found that all of the high charged molecular ions were produced at Rc around 4.2 Å, which was consistent with the enhanced ionization mechanism. The difference was that the Rc was not a single point, but a small range.
Once these ionization and dissociation processes were determined, it was important to know whether the pulse duration was long enough to cover these multi-electron ionization process. We calculated the time it took (Tij–mn) to travel from Ri,j to Rm,n on the Vi,j(r) potential energy curve using eqn (9):
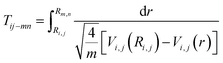 | (9) |
The travel time from the (1, 1) to (1, 2) channel was 19.8 fs, which was much longer than the further ionization process. The whole process from (1, 1) to (4, 4) was less than 30 fs. Considering that the (0, 1) to (1, 1) channel also took some time, the whole CE process was finished in one laser pulse duration of 70 fs.
(3) Post dissociation ionization
In Fig. 1c, we observed one component with the KER at 7.5 eV (the first peak in Fig. 1c), which we could not find a corresponding component to match. Considering that the whole CE process could be finished in one laser pulse and the experimental systemic error could not be so large, this low KE component may have been from the post-dissociation ionization9 of the (2, 2) channel, which exploded to a Cl2+ ion first. The laser field was still present after the dissociation. Then, some Cl2+ ions with a 7.8 eV KE were further ionized to Cl3+ ions before they left the interaction zone. To verify our assumption, we compared the KE and angular distribution of this component and the Cl2+ ion in the (2, 2) channel. The 7.5 eV KE was very close to the 7.8 eV KE component in the (2, 2) channel. The 0.3 eV error may have been caused by the data collection process or an experimental systemic error. In addition, as shown in Fig. 5, the angular distribution of the two components is exactly the same, proving that the low KE Cl3+ ion was ionized from the Cl2+ ion. This same situation also took place in the Cl4+ ion, where the low 16.9 eV KE component was from the ionization of an exploded Cl3+ ion. This phenomenon indicated that the CE process was very fast and could take place in one laser pulse, which was 70 fs under our experimental conditions.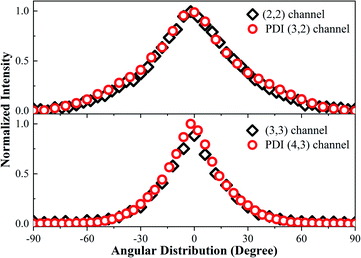 | ||
| Fig. 5 The angular distribution of the (2, 2) channel, PDI (3, 2) channel, (3, 3) channel, and PDI (4, 3) channel. | ||
Conclusions
We studied the dissociative ionization and CE of a Cl2 molecule in a near-infrared femtosecond laser field using a dc-sliced ion velocity imaging technique. We found that Cl2+ dissociates from two excited states, 2Πu and 2Σg+, with electrons respectively from the HOMO−1 and HOMO−2 orbital. For the Cl2n+ (n = 2–8) molecular ions, their precursor started to expend at the equilibrium internuclear distance, Re, and ionized at the critical distance, Rc, to explode into ionic fragments. The accumulated KERs were also included to calculate the final KERs. The Rc for these molecular ions was not a single point, but a small region around 4.2 Å. The dissociation time was calculated, which was within one pulse duration. This was further proved by observing the post dissociation ionization channels.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work was supported by the Natural Science Foundation of Shanghai (No. 16ZR1448100), the “Chenguang Program” by the Shanghai Education Development Foundation and Shanghai Municipal Education Commission (No. 16CG38), and the National Natural Science Foundation of China (No. 11604046).References
- Z. Wu, C. Wu, X. Liu, Y. Deng and Q. Gong, J. Phys. Chem. A, 2010, 114, 6751 CrossRef CAS PubMed.
- V. Tagliamonti, H. Chen and G. N. Gibson, Phys. Rev. A, 2011, 84, 043424 CrossRef.
- H. Sakai, H. Stapelfeldt, E. Constant, M. Y. Ivanov, D. R. Matusek, J. S. Wright and P. B. Corkum, Phys. Rev. Lett., 1998, 81, 2217 CrossRef CAS.
- R. J. Verver, D. R. Matusek, J. S. Wright, G. N. Gibson, R. Bhardwaj, S. Aseyev, D. M. Villeneuve, P. B. Corkum and M. Y. Ivanov, J. Phys. Chem. A, 2001, 105, 2435 CrossRef CAS.
- T. Seideman, M. Y. Ivanov and P. B. Corkum, Phys. Rev. Lett., 1995, 75, 2819 CrossRef CAS PubMed.
- F. Rosca-Pruna, E. Springate, H. L. Offerhaus, M. Krishnamurthy, N. Farid, C. Nicole and M. J. J. Vrakking, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 4919 CrossRef CAS.
- P. A. Hatherly, M. Stankiewiczt, K. Codling, L. J. Frasinski and G. M. Cross, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 2993 CrossRef CAS.
- J. McKenna, et al., Phys. Rev. A, 2006, 73, 043401 CrossRef.
- M. Schmidt, D. Normand and C. Cornaggia, Phys. Rev. A, 1994, 50, 5037 CrossRef CAS PubMed.
- S. Chelkowski and A. D. Bandrauk, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, L723 CrossRef CAS.
- T. Zuo and A. D. Bandrauk, Phys. Rev. A, 1995, 52, R2511 CrossRef CAS PubMed.
- J. H. Posthumusy, A. J. Gilesy, M. R. Thompsony, W. Shaikhz, A. J. Langleyz, L. J. Frasinskiy and K. Codling, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, L525 CrossRef.
- J. P. Nibarger, S. V. Menon and G. N. Gibson, Phys. Rev. A, 2001, 63, 053406 CrossRef.
- S. V. Menon, J. P. Nibarger and G. N. Gibson, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 2961 CrossRef CAS.
- Y. Yang, et al., J. Chem. Phys., 2011, 135, 064303 CrossRef PubMed.
- C. Guo, M. Li, J. P. Nibarger and G. N. Gibson, Phys. Rev. A, 1998, 58, R4271 CrossRef CAS.
- M. J. Frischet al., Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029 CrossRef CAS.
- M. Caricato, J. Chem. Phys., 2013, 139, 114103 CrossRef PubMed.
- M. Kállay and J. Gauss, J. Chem. Phys., 2004, 121, 9257 CrossRef PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1992, 98, 1358 CrossRef.
- S. D. Peyerimhoff and R. J. Buenker, Chem. Phys., 1981, 57, 279 CrossRef CAS.
- J. Zhang, Y. Yang, Z. Li, H. Sun, S. Zhang and Z. Sun, Phys. Rev. A, 2018, 98, 043402 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |