Open Access Article
Open Access ArticlePhonon transport and thermal conductivity of diamond superlattice nanowires: a comparative study with SiGe superlattice nanowires
Xilong Qu * and
Jinjie Gu
* and
Jinjie Gu
Hunan Provincial Key Laboratory of Finance & Economics Big Data Science and Technology, School of Information Technology and Management, Hunan University of Finance and Economics, Changsha 410205, P. R. China. E-mail: quxilong_hufe@sina.com
First published on 8th January 2020
Abstract
Due to the coupling of a superlattice's longitudinal periodicity to a nanowire's radial confinement, the phonon transport properties of superlattice nanowires (SLNWs) are expected to be radically different from those of pristine nanowires. In this work, we present the comparative investigation of phonon transport and thermal conductivity between diamond SLNWs and SiGe SLNWs by using molecular dynamics simulations. In the case of period length ∼ 25 Å, the thermal conductivities of diamond SLNWs and SiGe SLNWs both increase linearly with increasing the period number, which implies the wave-like coherent phonons dominate the heat transport of SLNWs. In the case of period length ∼ 103 Å, the thermal conductivity of SiGe SLNWs is length-independent with increasing the period number, indicating that the particle-like incoherent phonons in SiGe SLNWs control the heat transport, because the phonon–phonon scattering causes phonons to not retain their phases and the coherence is destroyed before the reflection at interfaces. However in diamond SLNWs the coherent phonons still dominate heat conduction and the thermal conductivity is length-dependent, because the mean free path of phonon–phonon scattering in diamond SLNWs is much longer. The spatial distribution of phonon localized modes further supports these opinions. These results are helpful not only to understand the coherent and incoherent phonon transport, but also to modulate the thermal conductivity of SLNWs.
1. Introductions
Diamond is the stiffest material in nature, and has extremely high thermal conductivity which can exceed 2000 W m−1 K−1 at room temperature. The thermal transport properties of pristine diamond,1 diamond nanothread,2 isotope-doped diamond3 and diamond composites4 have been widely investigated. It is well known that diamond has hexagonal and cubic structures. Tanigaki et al.5 reported that a nanopolycrystalline diamond was synthesized from graphite by a direct-conversion method. They found that nanopolycrystalline diamond was a superlattice-like twinned structure composed of hexagonal and cubic diamonds. Meanwhile, by ab initio-calculations they demonstrated that the nanopolycrystalline diamond was stiffer than the natural and synthesized monocrystal diamond. Plenitudinous studies focused on the structures and mechanical properties of nanopolycrystalline diamond,6–9 however the research of phonon transport properties of this novel structure is still scarce so far.Phonon transport and thermal conductivity of nanomaterials have attracted considerable research effort due to their unique properties and potential applications,10–20 such as thermoelectric generators and thermal management devices. Generally, there are two contrasting pictures to describe phonon transport in nanostructures, the one is particle-like incoherent phonons, and the other is wave-like coherent phonons.21 Recently, the influence of coherent and incoherent scattering mechanisms on thermal conductivity of periodic structures, such as superlattices and nanomeshes, is one of the hottest topics in the field of nanoscale heat transport.22–31 In periodic nanostructures, if the mean free path of phonons is longer than the period length of structures, coherent phonon transport occurs due to the constructive interference of incident and reflected phonon waves at the interfaces.32,33 At room temperature, phonons in diamond have long mean free path, because C–C bond is very strong and the phonon–phonon Umklapp scattering in diamond is weak.34 Therefore, superlattice-like structures of diamond, such as nanopolycrystalline diamond, are beneficial for investigating coherent phonon transport mechanism.
In this work, we demonstrate the strongly length-dependent thermal conductivity of diamond SLNWs constructed from hexagonal and cubic diamond by non-equilibrium molecular dynamics (NEMD) simulation at room temperature, which implies coherent phonon transport. There are many factors that affect the phonon coherence in superlattice structures, and the interface is one of the most important. In order to investigate the coherent and incoherent phonon transport at the interface, the thermal conductivities of diamond SLNWs and SiGe SLNWs are comparatively studied. The calculation results show that the thermal conductivities of diamond SLNWs and SiGe SLNWs have the same linearly increasing trend with the number of period, when the period length is ∼25 Å. The localization effect of phonons is not observed at the interfaces of both SLNWs. When the period length is ∼103 Å, the thermal conductivity of diamond SLNWs still increases with the number of period. No localized effect of phonons is observed at the interface. However, the thermal conductivity of SiGe SLNWs converges to a constant, and obvious phonon localization effect is observed at the interface. This indicates that phonon transport is still coherent in diamond SLNWs, while it is incoherent in SiGe SLNWs.
2. Models and methods
Fig. 1(a) shows the structure of diamond SLNW, A′ and B′' are the structure of hexagonal diamond, the A, B and C are the structure of cubic diamond. The diamond SLNW is composed of cubic and hexagonal diamond alternately stacked in the z-axis direction. The lattice constant is 2.058 Å. Fig. 1(b) shows the cross-section of diamond SLNW, and Fig. 1(c) shows the model of diamond SLNW. In Fig. 1(b) and (c), the red part represents cubic diamond, and the blue part represents hexagonal diamond. The ratio of hexagonal diamond to cubic diamond is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Ls is the period length of SLNW in Fig. 1(c).
1. Ls is the period length of SLNW in Fig. 1(c).
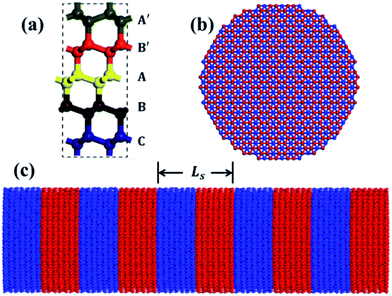 | ||
| Fig. 1 (a) The structure of diamond SLNW. (b) The cross section of diamond SLNW. (c) The vertical axis plane of diamond SLNW. | ||
In this work, the non-equilibrium molecular dynamics (NEMD) simulation method is used to calculated the thermal conductivity of SLNWs. We adopt the Tersoff potential35 for both carbon, silicon, and germanium atoms. All simulations are performed using the LAMMPS36 code with a time step of 0.5 fs. As shown in Fig. 2, we divide the sample into three parts: fixed wall at each end of the sample, thermostat area adjacent to the fixed wall, and the free part in the center. An fixed wall is used to make the atoms in the thermostat areas steady, and equalize the force applied on them. Free boundary conditions are used in all directions.
In our simulations, using a Nosé–Hoover thermostat37,38 we firstly equilibrate this system at 300 K for 5 ns with the walls moving freely in the longitudinal direction, corresponding to zero pressure. After the NPT relaxation, the optimized structure is obtained, we fix the atoms at the ends of the sample and run the system in the constant volume and constant temperature ensemble (NVT) for 2 ns. After the NVT, the system continues to be simulated in the constant volume and constant energy ensemble (NVE) for 2 ns. After these running, to obtain steady heat flux, the temperature of hot and cold Nosé–Hoover thermostat is set as 320 K and 280 K respectively. Due to the existence of temperature difference, heat flows from the hot bath to the cold bath across the sample. The steady state is reached after this NEMD is performed for 5 ns. The simulation of final 2 ns is to get the heat flux and calculate the thermal conductivity. The temperature gradient (dT/dz) is obtained by fitting the linear portion of temperature profile, and the heat flux (Jz) is calculated using:
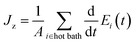 | (1) |
| κ = −Jz/(dT/dz) | (2) |
3. Results and discussions
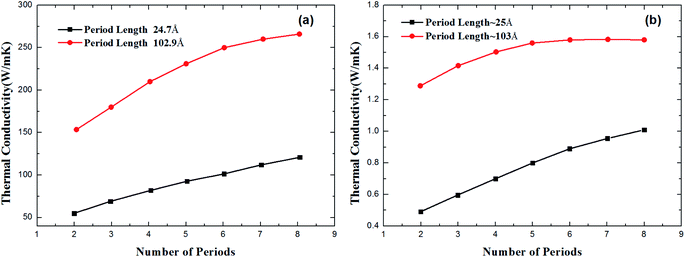
The thermal conductivities of the diamond SLNWs as a function of the number of periods are shown in Fig. 3(a). In the case of short period length such as Ls = 24.7 Å. The thermal conductivity is almost linearly proportional to the number of periods. This ballistic transport across the whole thickness implies coherent heat conduction in the diamond SLNWs. The nonlinear dependence of thermal conductivity on the number of periods in the case of long period length Ls = 102.9 Å suggests the increasing influence of incoherent effects. However, the thermal conductivity is still obviously increasing with the increase of period number, therefore coherent phonons still dominate the heat conduction in diamond SLNWs.For comparison, we also calculate the thermal conductivities of the SiGe SLNWs with the same period length as a function of their number of periods, which is shown in Fig. 3(b). It is evident that the thermal conductivity of SiGe SLNWs with Ls of ∼25 Å increases almost linearly with the number of periods, implying coherent phonon transport characteristics. However, in the case of long period length ∼ 103 Å, the situation is quite different. When the number of periods is larger than 5, the thermal conductivity of SiGe SLNWs is length-independent, indicating that the incoherent phonons dominate the thermal transport.
In order to further reveal the difference of phonon transport mechanisms between diamond SLNWs and SiGe SLNWs, we investigate the localization effect of the phonon modes at the interface in these two types of SLNWs with the Ls of ∼103 Å. The position of localized phonons can be described clearly by the spatial distribution of localized modes Γ = {λ:pλ < pc}. The spatial distribution of localized modes is expressed by
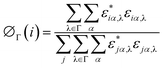 | (3) |
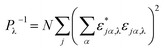 | (4) |
The normal-mode eigen frequencies and their corresponding eigenvector components are gotten via solving the lattice dynamical equation expressed by
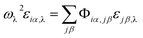 | (5) |
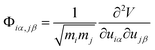 | (6) |
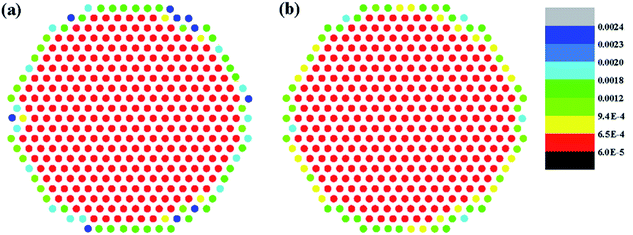
Fig. 4(a) and (b) demonstrate the spatial distribution of localized phonon modes in diamond SLNWs within Γ = {λ:pλ < 0.2} at the interface and non-interface atom layers, respectively. It is obvious that no matter interface or non-interface, the localized phonon modes locate in the surface region of diamond SLNWs. Chen et al. found that because the dangling bond atoms on the surface break the perfect lattice periodicity, phonon modes are localized on the surface of nanowires.41 Except for atoms in the surface region, the inner atoms have ultralow value of ∅Γ, and there are no significant differences for the spatial distribution of localized modes between the interface and non-interface atom layers. This implies that the phonons are not localized at the interface, and the coherent phonons transport through the interface in the diamond SLNWs with Ls of ∼103 Å. The analysis agrees well with the theoretical and experimental results,32,42,43 in which coherent phonons maintain their phase when they cross multiple interfaces in a superlattice, and the superlattice can be considered as a homogeneous material with its own primitive cell and phonon spectra.
The spatial distribution of localized phonon modes for SiGe SLNWs within Γ = {λ:pλ < 0.2} at the interface and non-interface atom layer is shown in Fig. 5(a) and (b) respectively. The spatial distribution of localized modes at the interface and non-interface layer is quite different. Despite the surface region, phonons propagate through the non-interface layer, but they are strongly localized at the interface layer of SiGe SLNWs. From Fig. 4(b) and 5(b), we consider that there are two competing mechanisms controlling the heat transport in SLNWs, which are particle-like interface scattering and wave-like interference effect. The thermal conductivity of diamond is ultra-high. According to the kinetic theory 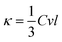 Che et al. derived the phonon mean free path l = 494 nm at room temperature.44 Due to the large mean free path, phonon–phonon Umklapp scattering is scarce between the reflection at atomically smooth interfaces, a majority of phonons in diamond SLNWs can maintain their phases, and the wave-like interference effect dominates heat conduction in diamond SLNWs. However, the thermal conductivity of silicon and germanium is much lower than diamond and accordingly the phonon mean free path of silicon is much shorter. The frequent phonon–phonon scattering make phonons not retain their phases and the coherence is destroyed before the reflection at interfaces, therefore phonons in SiGe SLNWs are particle-like, and the interface scattering mechanism is much stronger than the coherent transport mechanism. It is worth noting that in the case of very short period length, phonon–phonon Umklapp scattering is scarce between the reflection at interfaces, therefore coherent transport mechanism is dominant in SiGe SLNWs, and the thermal conductivity is evidently length-dependent, shown by the black line in Fig. 3(b).
Che et al. derived the phonon mean free path l = 494 nm at room temperature.44 Due to the large mean free path, phonon–phonon Umklapp scattering is scarce between the reflection at atomically smooth interfaces, a majority of phonons in diamond SLNWs can maintain their phases, and the wave-like interference effect dominates heat conduction in diamond SLNWs. However, the thermal conductivity of silicon and germanium is much lower than diamond and accordingly the phonon mean free path of silicon is much shorter. The frequent phonon–phonon scattering make phonons not retain their phases and the coherence is destroyed before the reflection at interfaces, therefore phonons in SiGe SLNWs are particle-like, and the interface scattering mechanism is much stronger than the coherent transport mechanism. It is worth noting that in the case of very short period length, phonon–phonon Umklapp scattering is scarce between the reflection at interfaces, therefore coherent transport mechanism is dominant in SiGe SLNWs, and the thermal conductivity is evidently length-dependent, shown by the black line in Fig. 3(b).
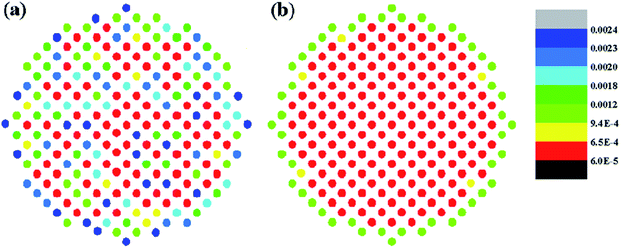 | ||
| Fig. 5 Spatial distribution of localized phonon modes in SiGe SLNWs at the interface atom layer (a), and at the non-interface atom layer (b). | ||
4. Conclusions
In summary, we calculate the thermal conductivities of diamond SLNWs and SiGe SLNWs by performing the non-equilibrium molecular dynamics simulations, and investigate the phonon transport mechanisms in SLNWs. We find that there are two competing mechanisms controlling the heat transport in SLNWs, which are particle-like interface scattering and wave-like interference effect. Which mechanism is dominant depends on the relationship between phonon–phonon scattering mean free path and period length of SLNWs. In the case of short period length (∼25 Å), the phonon–phonon scattering mean free paths of both SLNWs are longer than the period length, the phonons can retain their phases and wave nature, therefore the heat transport is coherent, and the thermal conductivities are linearly length-dependent. In the case of long period length (∼103 Å), a majority of phonons in SiGe SLNWs can not maintain their phases because of frequent phonon–phonon scattering, and the coherence is destroyed. Phonons are strongly localized at the interface layer of SiGe SLNWs, indicating that the particle-like interface scattering mechanism is dominant, and the interfaces significantly hinder the heat conduction, therefore the thermal conductivities are length-independent. However, due to the ultra-long phonon–phonon scattering mean free path of diamond SLNWs, in this case (period length ∼ 103 Å), the wave-like interference effect still dominates the heat conduction, and the phonon transport is quasi-ballistic. Our findings are helpful not only for understanding the coherent and incoherent phonon transport mechanism, but also for manipulating the thermal conductivity of SLNWs.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the Research Project of Education Department of Hunan Province (No. 18A441, 18C0958), and the Open Research Fund of Hunan Provincial Key Laboratory of Network Investigational Technology (No. 2017WLZC006), and the Key Project of Educational Planning of Hunan Province (No. XJK18DJA1).References
- G. A. Slack, Thermal conductivity of pure and impure silicon, silicon carbide, and diamond, J. Appl. Phys., 1964, 35, 3460–3466 CrossRef CAS.
- H. Zhan, G. Zhang, Y. Zhang, V. B. C. Tan, J. M. Bell and Y. Gu, Thermal conductivity of a new carbon nanotube analog: the diamond nanothread, Carbon, 2016, 98, 232–237 CrossRef CAS.
- W. L. Liu, M. Shamsa, I. Calizo, A. A. Balandin, V. Ralchenko, A. Popovich and A. Saveliev, Thermal conduction in nanocrystalline diamond films: effects of the grain boundary scattering and nitrogen doping, Appl. Phys. Lett., 2006, 89, 171915 CrossRef.
- S. Kidalov and F. Shakhov, Thermal conductivity of diamond composites, Materials, 2009, 2, 2467–2495 CrossRef CAS.
- K. Tanigaki, H. Ogi, H. Sumiya, K. Kusakabe, N. Nakamura, M. Hirao and H. Ledbetter, Observation of higher stiffness in nanopolycrystal diamond than monocrystal diamond, Nat. Commun., 2013, 4, 2343 CrossRef PubMed.
- H. Sumiya and T. Irifune, Indentation hardness of nano-polycrystalline diamond prepared from graphite by direct conversion, Diam. Relat. Mater., 2004, 13, 1771–1776 CrossRef CAS.
- H. Couvy, D. Lahiri, J. Chen, A. Agarwal and G. Sen, Nanohardness and Young's modulus of nanopolycrystalline diamond, Scr. Mater., 2011, 64, 1019–1022 CrossRef CAS.
- H. Sumiya, K. Hamaki and K. Harano, Note: evaluation of microfracture strength of diamond materials using nano-polycrystalline diamond spherical indenter, Rev. Sci. Instrum., 2018, 89, 056102 CrossRef CAS PubMed.
- S. V. Erohin and P. B. Sorokin, Elastic properties of nanopolycrystalline diamond: the nature of ultrahigh stiffness, Appl. Phys. Lett., 2015, 107, 121904 CrossRef.
- K. Novoselov, A. Mishchenko, A. Carvalho and A. C. Neto, 2D materials and van der Waals heterostructures, Science, 2016, 353, 9439 CrossRef PubMed.
- X. L. Wei, Y. C. Wang, Y. L. Shen, G. F. Xie, H. P. Xiao, J. X. Zhong and G. Zhang, Phonon thermal conductivity of monolayer MoS2: a comparison with single layer graphene, Appl. Phys. Lett., 2014, 105, 103902 CrossRef.
- L. P. Tang, L. M. Tang, H. Geng, Y. P. Yi, Z. M. Wei, K. Q. Chen and H. X. Deng, Tuning transport performance in two-dimensional metal-organic framework semiconductors: role of the metal d band, Appl. Phys. Lett., 2018, 112, 012101 CrossRef.
- W. X. Zhou and K. Q. Chen, Enhancement of thermoelectric performance in β-graphyne nanoribbons by suppressing phononic thermal conductance, Carbon, 2015, 85, 24–27 CrossRef CAS.
- Y. Y. Liu, Y. J. Zeng, P. Z. Jia, X. H. Cao, X. W. Jiang and K. Q. Chen, An efficient mechanism for enhancing the thermoelectricity of nanoribbons by blocking phonon transport in 2D materials, J. Phys. Condens. Matter, 2018, 30, 275701 CrossRef PubMed.
- X. L. Zhu, P. F. Liu, G. F. Xie, W. X. Zhou, B. T. Wang and G. Zhang, Thermoelectric Properties of Hexagonal M2C3 (M = As, Sb, and Bi) Monolayers from First-Principles Calculations, Nanomaterials, 2019, 9, 597 CrossRef CAS PubMed.
- X. L. Zhu, P. F. Liu, J. R. Zhang, P. Zhang, W. X. Zhou, G. F. Xie and B. T. Wang, Monolayer SnP3: an excellent p-type thermoelectric material, Nanoscale, 2019, 11, 19923 RSC.
- W. X. Zhou and K. Q. Chen, First-Principles Determination of Ultralow Thermal Conductivity of monolayer WSe2, Sci. Rep., 2015, 5, 15070 CrossRef CAS PubMed.
- G. F. Xie, Y. Guo, X. L. Wei, K. W. Zhang, L. Z. Sun, J. X. Zhong, G. Zhang and Y. W. Zhang, Phonon mean free path spectrum and thermal conductivity for Si1−xGex nanowires, Appl. Phys. Lett., 2014, 104, 233901 CrossRef.
- D. F. Li, J. He, G. Q. Ding, Q. Q. Tang, Y. Ying, J. He, C. Y. Zhong, Y. Liu, C. B. Feng, Q. L. Sun, H. B. Zhou, P. Zhou and G. Zhang, Stretch-Driven Increase in Ultrahigh Thermal Conductance of Hydrogenated Borophene and Dimensionality Crossover in Phonon Transmission, Adv. Funct. Mater., 2018, 28, 1801685 CrossRef.
- J. H. Zou, Z. Q. Ye and B. Y. Cao, Phonon thermal properties of graphene from molecular dynamics using different potentials, J. Chem. Phys., 2016, 145, 134705 CrossRef.
- G. F. Xie, D. Ding and G. Zhang, Phonon coherence and its effect on thermal conductivity of nanostructures, Adv. Phys.: X, 2018, 3, 1480417 Search PubMed.
- S. Alaie, D. F. Goettler, M. Su, Z. C. Leseman, C. M. Reinke and I. El-Kady, Thermal transport in phononic crystals and the observation of coherent phonon scattering at room temperature, Nat. Commun., 2015, 6, 7228 CrossRef CAS PubMed.
- N. Zen, T. A. Puurtinen, T. J. Isotalo, S. Chaudhuri and I. J. Maasilta, Engineering thermal conductance using a two-dimensional phononic crystal, Nat. Commun., 2014, 5, 3435 CrossRef PubMed.
- X. K. Chen, J. Liu, Z. X. Xie, Y. Zhang, Y. X. Deng and K. Q. Chen, A local resonance mechanism for thermal rectification in pristine/branched graphene nanoribbon junctions, Appl. Phys. Lett., 2018, 113, 121906 CrossRef.
- J. Maire, R. Anufriev, R. Yanagisawa, A. Ramiere, S. Volz and M. Nomura, Heat conduction tuning by wave nature of phonons, Sci. Adv., 2017, 3, 1700027 CrossRef PubMed.
- X. K. Chen, Z. X. Xie, W. X. Zhou, L. M. Tang and K. Q. Chen, Thermal rectification and negative differential thermal resistance behaviors in graphene/hexagonal boron nitride heterojunction, Carbon, 2016, 100, 492–500 CrossRef CAS.
- M. R. Wagner, B. Graczykowski, J. S. Reparaz, A. E. Sachat, M. Sledzinska, F. Alzina and C. M. S. Torres, Two-dimensional phononic crystals: disorder matters, Nano Lett., 2016, 16, 5661–5668 CrossRef CAS PubMed.
- M. Hu and D. Poulikakos, Si/Ge superlattice nanowires with ultralow thermal conductivity, Nano Lett., 2012, 12, 5487–5494 CrossRef CAS PubMed.
- A. Jain, Y. J. Yu and A. J. H. McGaughey, Phonon transport in periodic silicon nanoporous films with feature sizes greater than 100 nm, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195301 CrossRef.
- G. F. Xie, Z. F. Ju, K. K. Zhou, X. L. Wei, Z. X. Guo, Y. Q. Cai and G. Zhang, Ultra-low thermal conductivity of two-dimensional phononic crystals in the incoherent regime, npj Comput. Mater., 2018, 4, 21 CrossRef.
- J. Lee, W. Lee, G. Wehmeyer, S. Dhuey, D. L. Olynick, S. Cabrini, C. Dames, J. J. Urban and P. D. Yang, Investigation of phonon coherence and backscattering using silicon nanomeshes, Nat. Commun., 2017, 8, 14054 CrossRef CAS PubMed.
- M. N. Luckyanova, J. Garg and K. Esfarjani, et al., Coherent phonon heat conduction in superlattices, Science, 2012, 338, 936–939 CrossRef CAS PubMed.
- M. Maldovan, Phonon wave interference and thermal bandgap materials, Nat. Mater., 2015, 14, 667 CrossRef CAS PubMed.
- A. Ward, D. A. Broido, D. A. Stewart and G. Deinzer, Ab initio theory of the lattice thermal conductivity in diamond, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125203 CrossRef.
- J. Tersoff, Modeling solid-state chemistry: interatomic potentials for multicomponent systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5566 CrossRef.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Canonical dynamics: equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef PubMed.
- H. S. Zhang, T. Zhou, G. F. Xie, J. X. Cao and Z. Q. Yang, Thermal transport in folded zigzag and armchair graphene nanoribbons, Appl. Phys. Lett., 2014, 104, 241908 CrossRef.
- Y. Wang, B. Qiu and X. Ruan, Edge effect on thermal transport in graphene nanoribbons: a phonon localization mechanism beyond edge roughness scattering, Appl. Phys. Lett., 2012, 101, 013101 CrossRef.
- J. Chen, G. Zhang and B. Li, A universal gauge for thermal conductivity of silicon nanowires with different cross sectional geometries, J. Chem. Phys., 2011, 135, 204705 CrossRef PubMed.
- X. Mu, T. Zhang, D. B. Go and T. F. Luo, Coherent and incoherent phonon thermal transport in isotopically modified graphene superlattices, Carbon, 2015, 83, 208–216 CrossRef CAS.
- Z. T. Tian, K. Esfarjani and G. Chen, Green's function studies of phonon transport across Si/Ge superlattices, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235307 CrossRef.
- J. Che, T. Çağın, W. Deng and W. A. Goddard III, Thermal conductivity of diamond and related materials from molecular dynamics simulations, J. Chem. Phys., 2000, 113, 6888–6900 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |