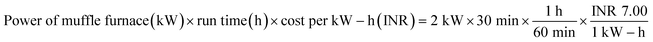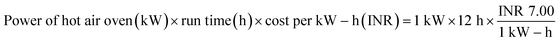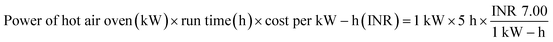DOI:
10.1039/C9RA08995K
(Paper)
RSC Adv., 2020,
10, 1204-1218
The biosorptive uptake of enrofloxacin from synthetically produced contaminated water by tamarind seed derived activated carbon
Received
31st October 2019
, Accepted 17th December 2019
First published on 8th January 2020
Abstract
The veterinary antibiotic enrofloxacin (ENR), an emerging contaminant, poses great concern due to its ubiquitous nature. Efforts have been made to eliminate ENR from synthetic aqueous solutions through applying an adsorption process, using tamarind-seed-derived carbon chemically activated with 85% (w/w) ortho-phosphoric acid (ACTS) as an adsorbent. ACTS was characterized via BET studies, SEM, EDX spectroscopy, FT-IR spectroscopy, etc. Parametric optimization was performed with the aid of a Taguchi L16 orthogonal array approach, aimed at maximizing the ENR percentage removal (% R). Analysis of variance (ANOVA) results revealed that temperature, chosen as one of the process parameters, had insignificant effects. % R was found to be maximum (95.11%) at a contact time of 15 h, a pH of 8, an ACTS dose of 8 g L−1 and an initial ENR concentration of 10 mg L−1. Equilibrium and kinetics studies revealed that the adsorption process followed a Redlich–Peterson isotherm model and a pseudo-second-order kinetics model. Reusability studies were performed, which showed that the developed adsorbent is reusable and regenerable. ACTS is also cost-effective, as the laboratory preparation of ACTS incurred a cost of INR 246. Finally, the ENR-laden ACTS was safely disposed of following WHO guidelines.
1. Introduction
In recent years, the pollution of the environment with pharmaceutical products has developed into an area of great concern. Because of their numerous adverse effects on living beings and their ubiquitous nature, many such products have been designated as emerging contaminants, which can pose a serious threat if not taken care of properly. Enrofloxacin (ENR) is one such emerging contaminant, which has been reported in soil, ground water, river water, pharmaceutical plant effluent, municipality sewage treatment plant effluent, etc.1–4 ENR, a type of fluoroquinolone, is a veterinary antibiotic, widely applied in the treatment of infections of the skin, bones, urinary tract, respiratory tract, etc. Besides pharmaceutical plant effluent, effluent laden with incompletely metabolized antibiotics from poultry and animal farms is also responsible for surface water, soil and ground water contamination. Looking at the severe side effects and the development of antibiotic resistance in bacteria, it is extremely crucial to eliminate ENR from water media.
Several works regarding the removal of ENR using different techniques have been reported by researchers. Advance oxidation processes, such as ozonation, Fenton oxidation, electrochemical oxidation,5 photo-degradation,6 micellar-enhanced ultrafiltration,7 and microbial remediation,8 have been employed by researchers to eliminate ENR from wastewater. The major issues connected with these techniques are that they are either time-consuming or have the potential to produce secondary pollutants. Adsorption is one frequently used technique for domestic and large-scale water treatment. Some literature reports can be found where clay materials,9 carboxylic graphene/titanium nanotubes,10 natural zeolites,11 etc. have been used as adsorbents to remove ENR. Activated carbon has been proved to have excellent adsorption properties, as it possesses a high pore volume and specific surface area. In India, tamarind (Tamarindus indica) is widely produced and consumed. According to the National Horticulture Board, India produced 192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 metric tons of tamarind in the year 2015–16. It is also a matter of fact that, globally, a large amount of tamarind seed is discarded as agricultural waste. The use of tamarind seed as an adsorbent has been reported by some researchers for dye and chromium(VI) removal.28,29 Looking at its waste utilization potential, in the present study, waste tamarind seed has been utilized to develop activated carbon (ACTS) that can be applied to the removal of ENR via an adsorption technique.
000 metric tons of tamarind in the year 2015–16. It is also a matter of fact that, globally, a large amount of tamarind seed is discarded as agricultural waste. The use of tamarind seed as an adsorbent has been reported by some researchers for dye and chromium(VI) removal.28,29 Looking at its waste utilization potential, in the present study, waste tamarind seed has been utilized to develop activated carbon (ACTS) that can be applied to the removal of ENR via an adsorption technique.
Parametric optimization is very much needed to determine the optimum conditions under which maximum throughput can be obtained. Conventionally, one factor at a time (OFAT) can be applied for this purpose, but it requires a substantial number of experimental runs, increasing the length and expense of research work. Several researchers have used Box–Behnken, Central Composite Design (CCD), etc. for parametric optimization. However, the Taguchi method is an efficient optimization tool that can be used to determine the significant parameters, identify the insignificant ones, and optimize the process, with a far lower number of experimental runs and less computational expense.12
In the current research work, activated carbon was developed from tamarind seed. This activated carbon was applied to remove ENR from water via adsorption. Five parameters, namely the pH, initial ENR concentration, ACTS dose, temperature and contact time, were selected to observe the influence of these on adsorption. Mathematical modelling was performed via a Taguchi L16 array approach, and the use of analysis of variance (ANOVA) helped to adjudge the relevancy of the model and the parameters involved. Parametric optimization was also carried out with the aim of obtaining the maximum removal of ENR. A kinetics study, an equilibrium study, and an analysis of the cost of the development of ACTS were also conducted. The reusability potential of the developed adsorbent was observed experimentally. Finally, in order to make the process eco-friendly, the ENR-laden adsorbent was safely disposed. Therefore, the novelty of the study is in the preparation of a cost-effective adsorbent from a natural waste material like tamarind seed, with parametric optimization using the Taguchi L16 method, cost analysis and the safe disposal of the adsorbent.
2. Materials and methods
2.1. Materials
The tamarind seeds that were employed for making the adsorbent were collected from a marketplace located at Durgapur, West Bengal, India. Vinipul Inorganics Pvt. Ltd, India, supplied the ortho-phosphoric acid (industrial grade; purity: 90%; density: 1.73 g mL−1) at a concentration of 85% (w/v). 37% hydrochloric acid and sodium hydroxide pellets were bought from Merck, India. Enrofloxacin (ENR) with a purity of >98.0% (HPLC) and a MW of 359.39 g mol−1 was bought from Sigma-Aldrich Co., St. Louis, MO. The molecular structures of ENR are illustrated in Fig. 1.7 Deionized water was purchased from ARKRAY Healthcare Pvt. Ltd, Gujarat, India.
 |
| | Fig. 1 The molecular structures of ENR. | |
2.2. Preparation of the stock solution
An aqueous 100 mg L−1 stock solution of ENR was prepared in a volumetric flask. The stock solution was kept in a cool and dark place so that degradation could be avoided.
2.3. Preparation of the adsorbent
Raw tamarind seeds were first washed well, and then dried under the sun for 5 days. Thereafter, the dried tamarind seeds were crushed manually and then carbonized at 400 °C using a laboratory muffle furnace.28 A heating rate of 10 °C min−1 was maintained and after reaching the required temperature, the sample was kept for 1 h at a constant temperature. The produced biochar was cooled, keeping it inside a desiccator. Then, the biochar was cleaned with deionized water and kept at 100 °C for 12 h inside an air oven. The developed biochar was named as char from tamarind seed (CTS).
2.4. Activation of the adsorbent
Dried tamarind seed biochar was taken from the air oven and permeated with 85% (w/w) ortho-phosphoric acid. Ortho-phosphoric acid and tamarind seed biochar were mixed at a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (w/w) ratio, so that the bio-char could be immersed in the solution. This solution was maintained under continuous stirring for 24 hours at 35 °C.15 Then, applying Whatman 42 filter paper, the slurry of carbonized tamarind seed and ortho-phosphoric acid was filtered. The residue was then washed with deionized water until the pH achieved a constant value of 7. Then, the carbon was exposed to a hot air oven for drying at 85 °C for 5 h; thereafter, it was kept inside a desiccator. The obtained material was used as an adsorbent and it was named activated carbon derived from tamarind seeds (ACTS). From 1 kg of dry tamarind seeds, around 450 g of ACTS was generated.
2 (w/w) ratio, so that the bio-char could be immersed in the solution. This solution was maintained under continuous stirring for 24 hours at 35 °C.15 Then, applying Whatman 42 filter paper, the slurry of carbonized tamarind seed and ortho-phosphoric acid was filtered. The residue was then washed with deionized water until the pH achieved a constant value of 7. Then, the carbon was exposed to a hot air oven for drying at 85 °C for 5 h; thereafter, it was kept inside a desiccator. The obtained material was used as an adsorbent and it was named activated carbon derived from tamarind seeds (ACTS). From 1 kg of dry tamarind seeds, around 450 g of ACTS was generated.
2.5. Characterization
In order to visualize the surface characteristics, the Brunauer–Emmett–Teller (BET) specific surface areas and cumulative pore volumes of CTS and ACTS (before adsorption) were found using a Quantachrome instrument (USA). To determine the functional groups, ACTS pre- and post-adsorption was analyzed using Fourier transform infrared (FTIR) spectroscopy using a PerkinElmer FT-IR C109292 spectrometer (USA). In this study, the background was first scanned using a pellet of powdered potassium bromide (KBr); thereafter, test samples were scanned after making pellets constituted of a tiny pinch of test sample and KBr. To check the surface morphologies, scanning electron microscope (SEM) images were taken after coating the samples with gold. SEM images of CTS and ACTS before and after the adsorption of ENR were taken using a scanning electron microscope (Model SEI, 15 kV). EDX analysis of the biochar derived from tamarind seed was carried out before and after activation.
2.6. Design of the experiments
To design the experiments and optimize the process, the Taguchi method was applied. The process parameters that may influence the adsorption process and their levels, as illustrated in Table 1, were selected on the basis of previous experiments and a literature survey.13–15 In the present study, five process parameters were selected: initial ENR concentration; temperature; pH; contact time; and ACTS dose. Using Design Expert 10 software (Stat-Ease USA), by applying a Taguchi L16 orthogonal array approach, an experimental matrix was generated, which is depicted in Table 2. Changes in pH were made by adding aqueous 0.1 M HCl solution and/or 0.1 M NaOH solution. All lab-scale experiments were carried out in a 100 mL Erlenmeyer flask containing 30 mL of working solution. After a certain period of incubation, the working solutions were centrifuged using Ultra-centrifuge apparatus (Sigma) at a speed of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 minutes. After centrifugation, the supernatant was subjected to UV-vis spectrophotometry (Shimadzu UV 1800, Japan) to evaluate the ENR concentration at a wavelength of 271 nm.15 Each of the experiments was run in triplicate and the arithmetic means of the experimental outcomes are reported.
000 rpm for 10 minutes. After centrifugation, the supernatant was subjected to UV-vis spectrophotometry (Shimadzu UV 1800, Japan) to evaluate the ENR concentration at a wavelength of 271 nm.15 Each of the experiments was run in triplicate and the arithmetic means of the experimental outcomes are reported.
Table 1 The process parameters and their levels
| Process parameter |
Unit |
Symbol |
Level |
| 1 |
2 |
3 |
4 |
| Initial ENR concentration |
mg L−1 |
A |
5 |
10 |
15 |
20 |
| pH |
|
B |
6 |
7 |
8 |
9 |
| ACTS dose |
g L−1 |
C |
2 |
4 |
6 |
8 |
| Temperature |
°C |
D |
20 |
25 |
30 |
35 |
| Contact time |
h |
E |
9 |
12 |
15 |
18 |
Table 2 The experiment designs
| Std |
Run |
ENR conc. (mg L−1) |
pH |
ACTS dose (g L−1) |
Temperature (°C) |
Time (h) |
% R |
| 12 |
1 |
15 |
9 |
4 |
20 |
15 |
45.12 |
| 1 |
2 |
5 |
6 |
2 |
20 |
9 |
49.92 |
| 9 |
3 |
15 |
6 |
6 |
35 |
12 |
48.08 |
| 15 |
4 |
20 |
8 |
4 |
35 |
9 |
46.15 |
| 3 |
5 |
5 |
8 |
6 |
30 |
15 |
80.85 |
| 5 |
6 |
10 |
6 |
4 |
30 |
18 |
64.88 |
| 2 |
7 |
5 |
7 |
4 |
25 |
12 |
61.07 |
| 11 |
8 |
15 |
8 |
2 |
25 |
18 |
43.91 |
| 14 |
9 |
20 |
7 |
6 |
20 |
18 |
54.66 |
| 10 |
10 |
15 |
7 |
8 |
30 |
9 |
51.21 |
| 16 |
11 |
20 |
9 |
2 |
30 |
12 |
42.08 |
| 13 |
12 |
20 |
6 |
8 |
25 |
15 |
54.69 |
| 7 |
13 |
10 |
8 |
8 |
20 |
12 |
94.1 |
| 6 |
14 |
10 |
7 |
2 |
35 |
15 |
70.3 |
| 8 |
15 |
10 |
9 |
6 |
25 |
9 |
78.96 |
| 4 |
16 |
5 |
9 |
8 |
35 |
18 |
72.69 |
The percentage removal (% R), considered as a response from the analysis, was calculated using eqn (1):16
| |
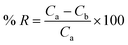 | (1) |
where
Ca denotes the initial concentration of ENR (mg L
−1) and
Cb denotes the concentration of ENR (mg L
−1) after adsorption.
The adsorption capacity of the adsorbent may be defined as the quantity of ENR removed per unit weight of ACTS. Eqn (2) was employed to quantify the adsorption capacity (qe) of ACTS:16
| |
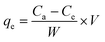 | (2) |
where
qe is the adsorption capacity (mg g
−1) of ACTS,
Ce denotes the ENR concentration (mg L
−1) at equilibrium, and
W and
V denote the weight of ACTS and the working volume of ENR solution, respectively.
2.7. Equilibrium study
Equilibrium studies of processes related to chemical engineering are very essential, as a lot of useful information can be extracted for an equilibrium study, such as the maximum adsorption capacity of the adsorbent, the extent of adsorption possible for a particular adsorbate concentration, etc.; this type of information is highly crucial for designing equipment and accessories. In the current study, the equilibrium data were fitted into some established isotherm models, such as the Langmuir, Freundlich, Temkin, and Redlich–Peterson isotherm models.
The Langmuir, Freundlich, Temkin, and Redlich–Peterson isotherm models in linear form can be formulated using eqn (3), (4), (5) and (6), respectively:15,30
| |
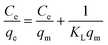 | (3) |
| |
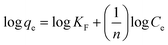 | (4) |
| |
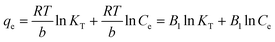 | (5) |
| |
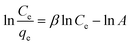 | (6) |
where
Ce designates the final ENR concentration at equilibrium (mg L
−1), and
qe denotes the adsorption capacity of ACTS at equilibrium (mg g
−1).
In eqn (3), KL represents the adsorption equilibrium constant (L mg−1) and qm is the maximum adsorption capacity of ACTS (mg g−1). qm and KL can be enumerated by drawing a linear plot of 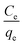 vs. Ce.
vs. Ce.
In eqn (4), KF and n denote the proportionality constant (mg L(1/n) g−1 mg(−1/n)) and exponential constant, respectively, and these parameters can be calculated from a linear plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. log
qe vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce.
Ce.
In eqn (5), KT and b represent the equilibrium binding constant (L mg−1) and adsorption energy (J mol−1), respectively, and R and T denote the universal gas constant (J mol−1 K−1) and temperature (K), respectively. Here, if a plot of qe vs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce plot is made, then KT and b can be calculated.
Ce plot is made, then KT and b can be calculated.
In eqn (6), β is an exponent and A is the Redlich–Peterson isotherm constant (L g−1). Therefore, a plot of ln(Ce/qe) vs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce will give the values of β and A.
Ce will give the values of β and A.
2.8. Kinetics study
For the industrial application of any process, it is necessary to establish the kinetics of the process, since necessary design information, such as the time needed for one batch, the size of the equipment, etc., can be determined from a kinetics study. There are various established kinetics models that are often used for determining the kinetics parameters of adsorption processes. In the present study, the kinetics data obtained from experiments were fitted into some built-in models, viz., Elovich, intra-particle diffusion, pseudo-first-order and pseudo-second-order models. The linear forms of the pseudo-first-order and pseudo-second-order models can be expressed via eqn (7) and (8), respectively:17| |
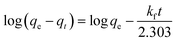 | (7) |
| |
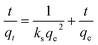 | (8) |
where qe is the adsorption capacity (mg g−1) of ACTS at equilibrium, qt is the adsorption capacity (mg g−1) of ACTS at a particular time, t denotes the time (h), and kf and ks represent the pseudo-first-order rate constant (h−1) and pseudo-second-order rate constant (g mg−1 h−1), respectively.
Eqn (9) represents the linear form of the Elovich model, which is a popular way to illustrate the kinetics of chemisorption:
| |
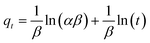 | (9) |
where
qt is the adsorption capacity (mg g
−1) of ACTS at a particular time,
t denotes the time (h), and
α and
β stand for the rate of chemisorption (mg L
−1 h
−1) at zero coverage and the desorption constant (g mg
−1), related to surface analysis and activation energy analysis for chemisorption, respectively.
18
The values of α and β can be derived from a plot of qt vs. ln(t).
| |
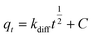 | (10) |
Eqn (10) represents the intra-particle diffusion model, in which
C is a constant (mg g
−1) and
kdiff denotes the intra-particle diffusion rate constant (mg g
−1 h
−1/2).
15 kdiff can be estimated from a linear plot of
qt vs. t1/2.
3. Results and discussion
3.1. Characterization
3.1.1. Proximate analysis. Proximate analysis shows that the weight percentages of fixed carbon, moisture, ash and volatile matter in the raw tamarind seeds were 19.25%, 5.2%, 2.83% and 72.15%, respectively, whereas the values of the same components in ACTS were 72.3%, 4.88%, 10.62% and 12.20%, respectively. Proximate analysis shows that most of the volatile matter was lost during carbonization, making the fixed carbon content of ACTS high. As the fixed carbon content of ACTS was on the higher side, it was selected as an adsorbent for the removal of ENR.
3.1.2. SEM analysis. Scanning electron micrographs of CTS (raw carbon derived from tamarind seeds), and ACTS (activated carbon from tamarind seeds) before and after adsorption are shown in Fig. 2(a–c), respectively. If Fig. 2(b) is compared with Fig. 2(a), it is clearly observed that after chemical activation the smooth surface texture of the particles changed to a surface with many micropores. This is obvious, since at the time of activation the surface of CTS was impregnated with ortho-phosphoric acid, and during drying some ortho-phosphoric acid evaporated, generating pores in the surface. The formation of a porous structure may also be due to the elimination of a few organic particles from the carbonized biomass skeleton as a consequence of hydrolysis reactions occurring in CTS during acid treatment. The transformation of the smooth surface to a rough surface caused a higher surface area and higher porosity, along with an increase in the number of active binding sites and the accessibility; this promotes better biosorption. From Fig. 2(c), under high magnification, it can be observed that the porosity decreases because of the adsorption of ENR onto the surface of ACTS. When a finite number of ACTS active sites are occupied by ENR following the adsorption process, the accessibility drops resulting in a lack of penetrating sites.
 |
| | Fig. 2 SEM micrographs of (a) CTS, (b) pre-adsorption ACTS and (c) post-adsorption ACTS. | |
3.1.3. Surface characteristics. The Brunauer–Emmett–Teller (BET) specific surface areas of CTS and ACTS before adsorption were calculated to be 560 m2 g−1 and 962 m2 g−1, respectively, while the cumulative pore volumes of CTS and ACTS before adsorption were calculated to be 0.365 cm3 g−1 and 0.568 cm3 g−1, respectively. Therefore, it can be inferred that morphological modification took place in CTS at the time of chemical activation, leading to an increase in the porosity and specific surface area.
3.1.4. EDX analysis. Fig. 3(a) and (b) show EDX spectra demonstrating the elemental compositions of CTS and ACTS. From Fig. 3(a) it can be seen that before activation, the bio-char contained only C and O atoms, however, after activation, the presence of phosphorous atoms, as shown in Fig. 3(b), clearly signifies the impregnation of ortho-phosphoric acid into the biochar; besides, a decrease in the O atom abundance, although by a very small amount, proves the release of organic O atoms, increasing the surface area and porosity and in turn increasing the number of active adsorption sites in ACTS.
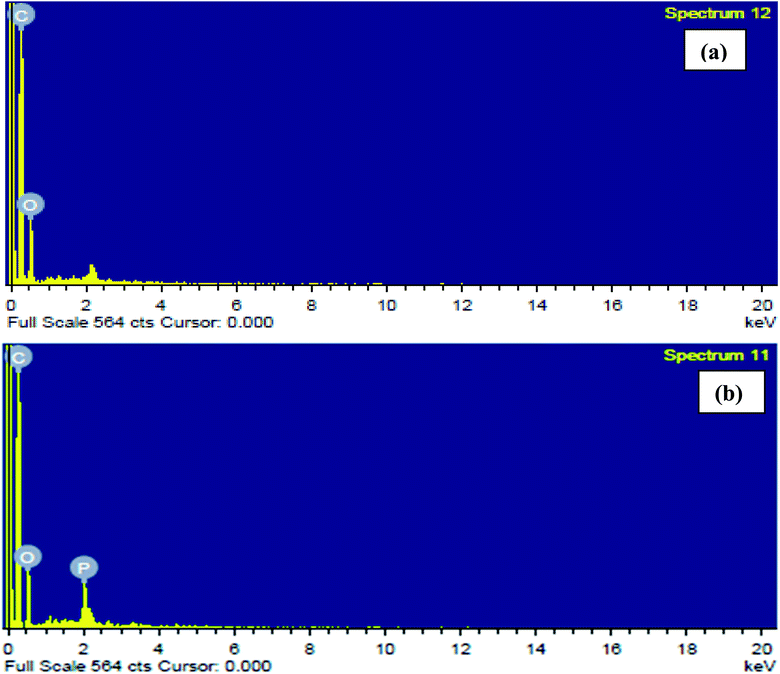 |
| | Fig. 3 EDX spectra of (a) CTS and (b) ACTS. | |
3.1.5. FTIR analysis. Usually, FTIR analysis is performed to investigate the functional groups present. In Fig. 4, the transmittance bands at wavenumber values of 866 cm−1, 1465 cm−1, 1786 cm−1 and 3672 cm−1 demonstrate the existence of C–H bending, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching, C
C stretching, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching (carboxylic acid groups) and alcoholic O–H groups,13,25,27 respectively, in ACTS before adsorption. After adsorption, the existence of new bands at wavenumber values of 1122 cm−1, 1640 cm−1, 1782 cm−1 and 3441 cm−1 feasibly implies the appearance of C–N stretching, N–H bending, C
O stretching (carboxylic acid groups) and alcoholic O–H groups,13,25,27 respectively, in ACTS before adsorption. After adsorption, the existence of new bands at wavenumber values of 1122 cm−1, 1640 cm−1, 1782 cm−1 and 3441 cm−1 feasibly implies the appearance of C–N stretching, N–H bending, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching (ketone group) and N–H stretching,15,25,26 respectively. Since in the structure of ENR, as shown in Fig. 1, N–H bonds, C–N bonds and carboxylic acid groups are present, the FT-IR spectra provide evidence in favour of the adsorption of ENR by ACTS. It is suitably confirmed from the transformation of the IR bands that, due to the penetration of ENR molecules into the active sites and the porous structure of ACTS through the adsorption process, the N atoms within ENR were captured and encapsulated within the adsorbent, which certified the success of the process.
O stretching (ketone group) and N–H stretching,15,25,26 respectively. Since in the structure of ENR, as shown in Fig. 1, N–H bonds, C–N bonds and carboxylic acid groups are present, the FT-IR spectra provide evidence in favour of the adsorption of ENR by ACTS. It is suitably confirmed from the transformation of the IR bands that, due to the penetration of ENR molecules into the active sites and the porous structure of ACTS through the adsorption process, the N atoms within ENR were captured and encapsulated within the adsorbent, which certified the success of the process.
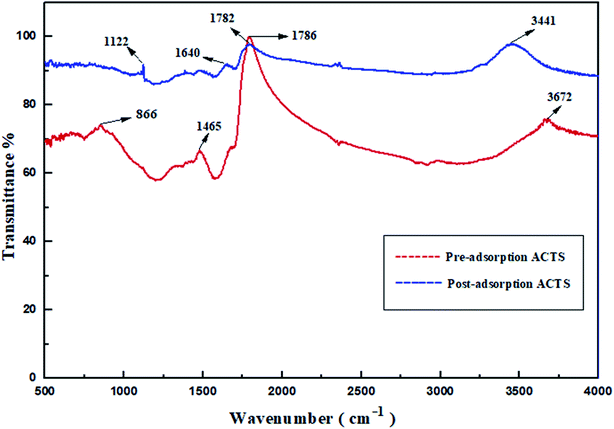 |
| | Fig. 4 The FTIR spectra of pre- and post-adsorption ACTS. | |
3.1.6. Point of zero charge (pHzc). The determination of the point of zero charge (pHzc) of an adsorbent is important as it gives an idea about the surface chemistry of adsorption. pHzc is the pH at which the adsorbent has zero charge. To determine pHzc values, solutions of different pH from 1 to 14 were prepared. Then in 30 mL of each solution in an Erlenmeyer flask, 0.5 g of ACTS was added, and the mixtures were kept for 24 h under continuous agitation. It was observed after 24 h that the pH of all the solutions changed, except for the solution with an initial pH of 6. Therefore, it may be inferred that the point of zero charge (pHzc) of ACTS is 6.
3.2. Statistical analysis of the adsorption process
3.2.1. Analysis of variance (ANOVA). ANOVA was applied to explore the significance of the developed Taguchi L16 mathematical model and the model terms. The ANOVA findings are illustrated in Table 3. A clear perspective of the relevancy of the model and the model parameters can be obtained from the sum of squares (SS), F- and p-values. The model and the model parameters can be decided to have higher significance on the basis of higher SS and F-values and a lower p-value.19 It is evident from Table 3 that the developed model possesses a large SS value (3613.77) and F-value (147.12), and the p-value of 0.000815 points out the fact that there is only a 0.08% chance of obtaining the large F-value due to noise. Therefore, it may be concluded that the developed model is significant and can be used for the prediction of adsorption performance. Among the model terms, temperature (D) is proved to be an insignificant parameter and, hence, temperature has been discarded for building up the model. To experimentally verify whether temperature is an insignificant parameter, adsorption experiments were carried out, varying the temperature in the range of 20 °C to 35 °C and keeping the ENR concentration at 10 mg L−1, the pH at 8, the ACTS dose at 8 g L−1 and the contact time at 12 h. Only very slight fluctuations in the percentage removal were observed. Hence, it can be said that temperature (D) is an insignificant parameter. All the remaining parameters, viz. ENR concentration (A), pH (B), ACTS dose (C) and contact time (E), are significant in nature since for all these parameters, the p-values are lower than 0.05 and the SS and F-values of these parameters are reasonably large. Among the significant parameters, the ENR concentration has the highest SS value; therefore, it can be inferred that the ENR concentration has the highest influence on the % R of ENR.
Table 3 The analysis of variance (ANOVA) results
| Source |
Sum of squares |
df |
Mean square |
F-Value |
p-Value prob > F |
|
| Model |
3613.77 |
12 |
301.15 |
147.12 |
0.000815 |
Significant |
| A: ENF concentration |
2432.06 |
3 |
810.69 |
396.04 |
0.000214 |
|
| B: pH |
284.27 |
3 |
94.76 |
46.29 |
0.005187 |
|
| C: adsorbent dose |
809.35 |
3 |
269.78 |
131.79 |
0.001107 |
|
| E: time |
88.08 |
3 |
29.36 |
14.34 |
0.027688 |
|
| Residual |
6.14 |
3 |
2.05 |
|
|
|
| Cor total |
3619.90 |
15 |
|
|
|
|
3.2.2. Regression coefficients. By analysing the regression coefficients and other statistical parameters, such as adequate precision (AP), standard deviation (SD), coefficient of variance (CV), etc., the extent of the fitting of experimental data to the developed model has been determined. From Table 4, it is evident that the regression coefficient, R2, is very close to 1 and the difference between the adjusted regression coefficient and predicted regression coefficient is much less than 0.2. The adjusted regression coefficient indicates the goodness-of-fit for regression models, whereas the predicted regression coefficient determines how well a regression model makes predictions. From these two results, it may be inferred that the developed model is very much efficient at predicting % R over different sets of process conditions. The obtained value of AP (39.41), being far greater than 4, indicates that an adequate signal was obtained with small noise. The lower SD value (1.43) indicates that the experimental findings are in close proximity to the predicted values. CV represents the reproducibility of the model; in the present study CV was 2.39%, which is on the lower side, and thus the reproducibility of the model can be confirmed.20
Table 4 The fit statistics of the model
| Std dev. |
1.43 |
R-squared |
0.998 |
| Mean |
59.92 |
Adj R-squared |
0.991 |
| CV% |
2.39 |
Pred R-squared |
0.952 |
| PRESS |
174.67 |
Adeq precision |
39.41 |
−2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log likelihood log likelihood |
30.08 |
BIC |
66.13 |
| AICc |
238.08 |
3.3. Derivation of the model equation
From the ANOVA results obtained for the response, viz. the percentage removal, it is clear that the initial ENR concentration (A), pH (B), ACTS dose (C) and contact time (E) are significant parameters and temperature (D) is an insignificant parameter. Only the significant parameters were involved in the development of the model equation and the insignificant one was discarded. The model equation, which can be used for the prediction of % R through inputting values for the parameters, is as follows (eqn (11)):| | |
Percentage removal (%) = 59.917 + 6.216 × A[1] + 17.143 × A[2] − 12.837 × A[3] − 5.524 × B[1] − 0.607 × B[2] + 6.336 × B[3] − 8.364 × C[1] − 5.612 × C[2] + 5.721 × C[3] − 3.357 × E[1] + 1.416 × E[2] + 2.823 × E[3]
| (11) |
where A, B, C and E are the process parameters and the numbers in square parenthesis represent the levels of the corresponding parameters.
The experimental values and the predicted values obtained from the model equation are shown in Fig. 5. It is observable in Fig. 5 that a majority of points lie on the diagonal line of the plot, indicating that the predicted values are on par with the values obtained from experiments and that the established model equation is well-equipped to predict the response.
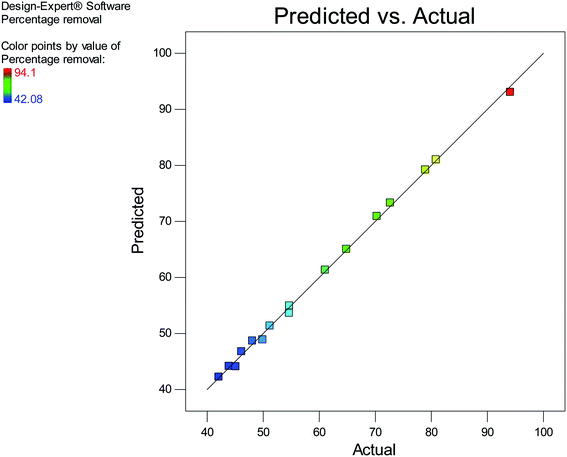 |
| | Fig. 5 A plot of predicted vs. actual values. | |
3.4. Influence of parameters on adsorption
3.4.1. Influence of pH. pH is a crucial parameter needing to be considered in adsorption processes. Fig. 6(a) depicts how % R changes with changes in pH when the other parameters, viz. contact time, ACTS dose and ENR concentration, remain constant at 15 h, 8 g L−1 and 10 mg L−1, respectively. In Fig. 6(a), when pH goes from 6 to 8, % R increases gradually, while at pH values beyond 8, % R decreases. The maximum removal is obtained at pH 8. This trend can be explained with the help of the point of zero charge (pHzc) of ACTS and the molecular structure of ENR. The pHzc of ACTS is 6; this indicates that when the pH of the environment is below 6, ACTS is positively charged and when pH of the environment is above 6, ACTS is negatively charged. Also, the pKa values of ENR are 6.09 and 7.91,21 substantiating the fact that when the pH of the environment is below 6.09, most ENR molecules remain in cationic form, and when the pH is above 7.91, a majority of ENR molecules remain in the anionic form; in between 6.09 and 7.91, a large number of ENR molecules adopt a zwitterionic structure (Fig. 1).14 At pH values in the range of 7–8, there are electrostatic attractive forces between the positive sites of zwitterionic ENR and the negatively charged adsorbent; this results in higher removal percentages. On the other hand, electrostatic repulsion between negatively charged ACTS and anionic ENR exists at higher pH values; also, at lower pH values, electrostatic repulsion exists between positively charged ACTS and cationic ENR. That is why at lower and higher pH values, comparatively lower % R values were obtained.
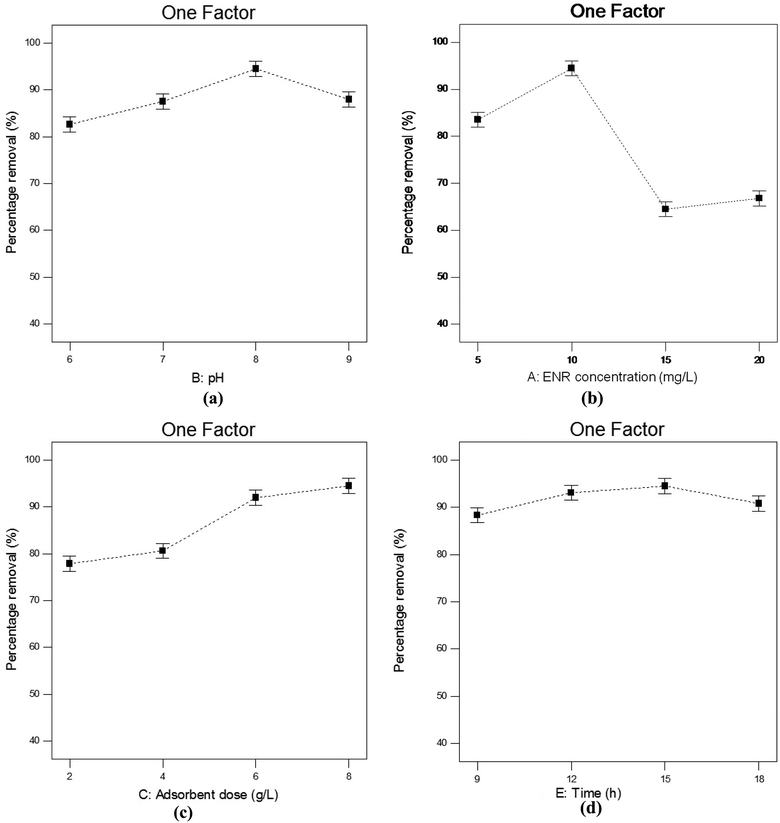 |
| | Fig. 6 The influences of (a) pH, (b) ENR concentration, (c) adsorbent dose and (d) contact time on the percentage removal of ENR. | |
3.4.2. Influence of ENR concentration. The changes in % R with changing ENR concentration in the range of 5–20 mg L−1 can be observed in Fig. 6(b), where the pH remains at 8, the ACTS dose at 8 g L−1 and the contact time at 15 h. It is observable from Fig. 6(b) that the highest % R value was obtained at an ENR concentration of 10 mg L−1, whereas below and above 10 mg L−1, % R is lower. At a lower ENR concentration, there is a lower concentration gradient, which reduces the driving force for adsorption;15 as a result, lower % R values are obtained at lower ENR concentrations. At a certain ENR concentration, all possible adsorbent active sites are filled with ENR molecules and in this saturated condition, a further increase in the ENR concentration leads to over-crowdedness in the system, which results in lower ENR % R values.22
3.4.3. Influence of adsorbent dose. The adsorbent dose is also one of the significant parameters that affects the adsorption process. In Fig. 6(c), it is clear that at pH 8, an initial ENR concentration of 10 mg L−1 and a contact time of 15 h, when the ACTS dose is increased from 2 to 6 g L−1, % R increases sharply; with a further increase in the adsorbent dose, % R slowly increases. The highest removal percentage was obtained at an adsorbent dose of 8 g L−1. It is obvious that when the adsorbent dose increases, the number of active sites increases, which results in an increase in % R.23 But above a certain dose, % R does not increase sharply and instead becomes nearly constant. This is because when the adsorbent dose increases above a certain limit, the adsorbent agglomerates and, as a result, the diffusion paths become longer and there is higher mass transfer resistance for ENR molecules to diffuse into the pores.24
3.4.4. Influence of contact time. Fig. 6(d) depicts the effects of contact time on the ENR % R value when the pH, initial ENR concentration and ACTS dose were kept at 8, 10 mg L−1 and 8 g L−1, respectively. It can be observed that when the contact time increases from 9 to 15 h, % R increases, but when the contact time increases further, % R decreases. The increase in % R with an increase in contact time may be because the adsorbent has more time to adsorb ENR molecules. The decrease in % R with a further increase in contact time may be due to the desorption of ENR from the adsorbent.
3.5. Optimization of the percentage removal and experimental validation
The present study aims at finding the optimal conditions under which % R becomes maximum. Table 5 depicts the optimal process parameters: the maintaining of these leads to the maximum % R value being achieved. At an ENR concentration of 10 mg L−1, a pH of 8, an ACTS dose of 8 g L−1 and a contact time duration of 15 h, the maximum % R value of 94.474% can be predicted. To validate the optimal conditions experimentally, experiments were carried out in triplicate, maintaining the above process conditions; temperature, as an insignificant parameter, was maintained at 20 °C. It can be witnessed from Table 5 that the experimentally found % R values from the first, second and third runs are 95.11%, 94.75% and 94.15%, which are in close proximity to the predicted values, proving the predictive nature of the model.
Table 5 The optimization and validation of the process parameters
| Sr. no. |
pH |
Initial ENR concentration (mg L−1) |
Adsorbent dose (g L−1) |
Contact time (h) |
Percentage removal (%) |
| Actual |
Predicted |
| 1 |
8 |
10 |
8 |
15 |
95.11 |
94.474 |
| 2 |
8 |
10 |
8 |
15 |
94.75 |
94.474 |
| 3 |
8 |
10 |
8 |
15 |
94.15 |
94.474 |
3.6. Equilibrium studies
Equilibrium studies were performed at different initial ENR concentrations, at a constant pH of 8, an adsorbent dose of 8 g L−1 and a contact time of 15 h. As depicted in Fig. 7, the obtained experimental values were fed into Langmuir, Freundlich, Temkin and Redlich–Peterson isotherm models.
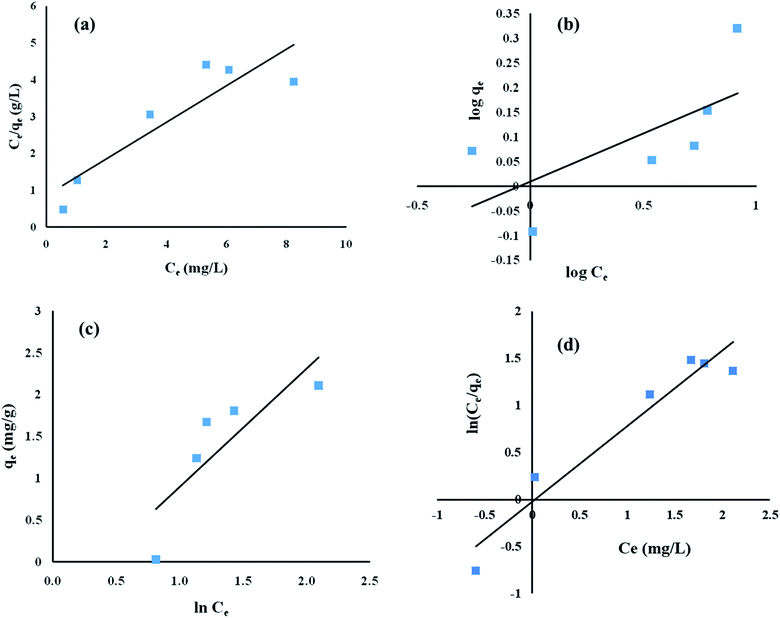 |
| | Fig. 7 Adsorption equilibrium studies of ENR removal using (a) Langmuir isotherm, (b) Freundlich isotherm, (c) Temkin isotherm, and (d) Redlich–Peterson isotherm models. | |
The regression coefficient (R2) values obtained using the Langmuir, Freundlich, Temkin and Redlich–Peterson isotherm models are 0.81, 0.46, 0.69 and 0.94, respectively (Table 6). Therefore, looking at the highest R2 value, it can be inferred that the adsorption of ENR by ACTS followed the Redlich–Peterson isotherm model. The maximum adsorption capacity (qm) was calculated to be 2.02 mg g−1. The parameters for the different isotherm models are summarized in Table 6. As the Redlich–Peterson model combines Langmuir and Freundlich models, it may be concluded that the adsorption process does not adhere to an ideal monolayer concept.30,31
Table 6 The parameters of the isotherm models
| Langmuir isotherm model |
| qm (mg g−1) |
KL (L mg−1) |
R2 |
| 2.02 |
0.58 |
0.81 |
| Freundlich isotherm model |
| KF (mg L(1/n) g−1 mg(−1/n)) |
n |
R2 |
| 1.02 |
5.12 |
0.46 |
| Temkin isotherm model |
| b (J mol−1) |
KT |
R2 |
| 1753.29 |
0.69 |
0.69 |
| Redlich–Peterson isotherm model |
| β |
A |
R2 |
| 0.80 |
1.02 |
0.94 |
3.7. Kinetics studies
To obtain the kinetics data, the contact time duration for adsorption was varied while the other parameters, namely pH, initial ENR concentration and adsorbent dose, remained constant at 8, 10 mg L−1 and 8 g L−1, respectively. The obtained kinetics data was fed into pseudo-first-order, pseudo-second-order, Elovich, and intra-particle diffusion models (Fig. 8).
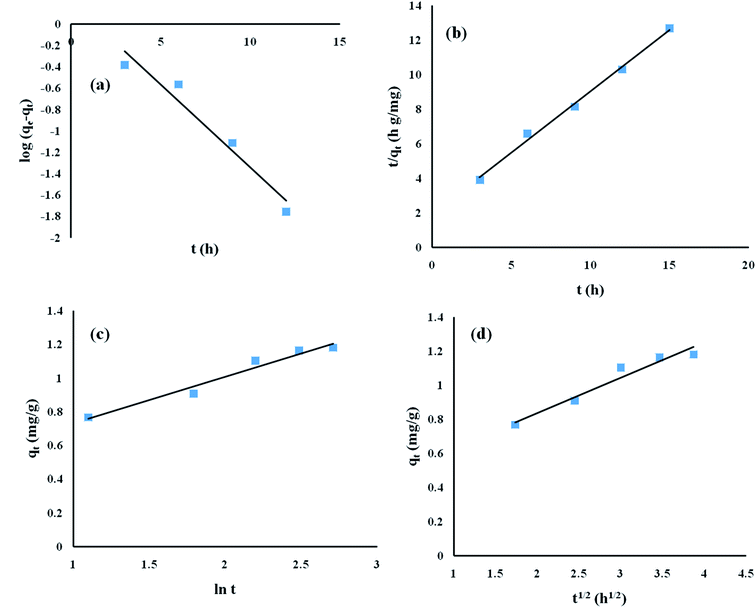 |
| | Fig. 8 Adsorption kinetics studies of ENR removal: (a) pseudo-first-order model; (b) pseudo-second-order model; (c) Elovich model; and (d) intra-particle diffusion model. | |
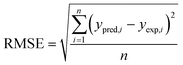
The obtained R2 values for the pseudo-first-order, pseudo-second-order, Elovich, and intra-particle diffusion models are 0.95, 0.99, 0.97 and 0.95, respectively (Table 8). As the R2 values of the different kinetics models are close to each other, error analysis was performed in which the statistical error parameters of root mean square error (RMSE) and average absolute deviation (AAD%) were calculated; these are tabulated in Table 8. The formulas for RMSE and AAD% are depicted in eqn (12) and (13), respectively. It is clear from Table 8 that although the RMSE and AAD% values of the Elovich model are the lowest, the R2 value of the Elovich model is lower than that of the pseudo-second order kinetics model; based on the R2 value, it is believed that the adsorption process might follow pseudo-second-order kinetics. As the adsorption process follows pseudo-second-order kinetics, it may be concluded that chemical interactions between the adsorbent and adsorbate take place.31 The rate constant for the pseudo-second-order kinetics model was evaluated to be 0.368 g mg−1 h−1. The parameters of the different kinetics models are depicted in Table 7.
| |
 | (12) |
| |
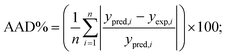 | (13) |
ypred,i is the predicted response obtained from the model and
yexp,i is the actual response obtained from experiment;
n denotes the total number of runs.
Table 7 Parameters of the kinetic models
| Pseudo-first-order model |
| kf (h−1) |
| 0.358 |
| Pseudo-second-order model |
| ks (g mg−1 h−1) |
| 0.368 |
| Elovich model |
| α (mg L−1 h−1) |
β (g mg−1) |
| 1.411 |
3.59 |
| Intra-particle diffusion model |
| kdiff (mg g−1 h−1/2) |
C (mg g−1) |
| 0.208 |
0.42 |
3.8. Reusability of the developed adsorbent
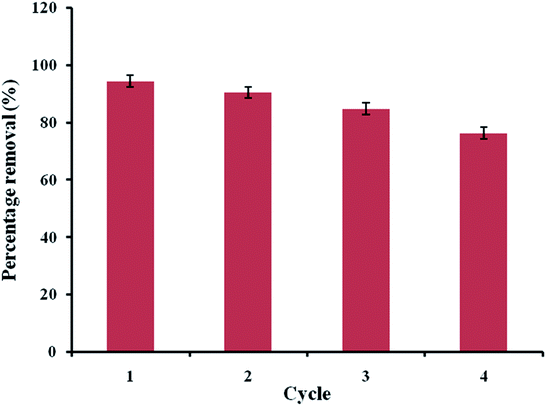
An adsorbent can be designated as suitable for industrial or large-scale applications if it has the potential to be reused. Industrial adsorbents are generally used, regenerated via suitable techniques, and reused further over multiple cycles; this reusability potential lowers the operating costs. To investigate the reusability of ACTS, it was first used under the optimal process conditions obtained above and, after centrifugation, the spent ACTS was collected and poured into 40% (w/w) ethanol solution under constant stirring for 5 hours. Desorption of ENR, i.e., mass transfer of ENR from ACTS to the ethanol solution, takes place and then the free ACTS was collected, dried and used again for the further adsorption of ENR. This procedure was repeated for up to 4 cycles. From Fig. 9, it is clear that after 4 cycles of use, the ENR % R values had not decreased by more than 18.5%; this substantiates the fact that the developed adsorbent has reusability potential.
 |
| | Fig. 9 Reusability study of the adsorbent. | |
3.9. The safe disposal of spent ACTS
One of the drawbacks of using adsorption as a water treatment method is that, although the contaminants are transferred from aqueous media to the surface of the adsorbent used, it is extremely necessary to dispose the contaminant-laden adsorbent in such a manner that no further contamination takes place. In the present research work, following the rules mentioned in the “Guidelines for the Safe Disposal of Unwanted Pharmaceuticals In and After Emergencies” published by the World Health Organization (WHO), the ENR-laden ACTS was immobilized via an inertization technique. First, the spent ACTS was encapsulated in a mixture of lime, cement and water and, after drying, the hard mixture was buried underground.
3.10. Analysis of the cost of preparation of the adsorbent
Analysis of the cost of preparation of an adsorbent is important as, apart from other operating costs, a large portion of the overall cost of large-scale adsorption processes lies in purchasing the adsorbents. Therefore, it is necessary to make the adsorbent cost-effective. A detailed cost break-down for the laboratory preparation of 1 kg of ACTS is illustrated in Table 9. From Table 9, it is clear that the developed adsorbent incurs a cost of approximately INR 246 kg−1 for its preparation.
Table 8 Error analysis of the kinetics models
| Kinetics model |
RMSE |
AAD% |
R2 |
| Pseudo-first-order model |
0.062 |
3.514 |
0.95 |
| Pseudo-second-order model |
0.033 |
2.967 |
0.99 |
| Elovich model |
0.029 |
2.633 |
0.97 |
| Intra-particle diffusion model |
0.037 |
3.064 |
0.95 |
Table 9 A cost break-down for the preparation of ACTS
| Activity |
Sub-section |
Break-down |
Cost (INR) |
| Processing of raw materials |
Raw material cost |
Raw tamarind seeds collected free of charge |
0.0 |
| Raw material drying cost |
Dried under the sun |
0.0 |
| Preparation of biochar (CTS) |
Carbonization cost |
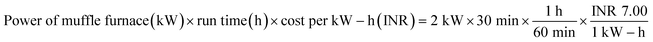 |
7.00 |
| Drying after washing |
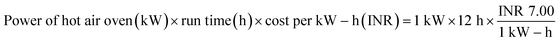 |
84.00 |
| Chemical activation |
Ortho-phosphoric acid |
 |
97.50 |
| Washing cost |
Distilled water received from laboratory set up |
0.0 |
| Drying cost |
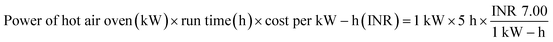 |
35.00 |
| Net cost |
|
|
223.5 |
| Other overhead costs |
|
10% of net cost |
22.35 |
| Total cost |
|
Net cost + overhead costs |
245.85 |
4. Conclusions
Chemically activated biochar was produced from tamarind seeds in the current investigation, and this activated carbon was employed for the removal of enrofloxacin from aqueous solution. The Taguchi L16 process was applied in order to optimize the process conditions, aimed at maximizing the percentage removal. The highest removal of 95.11% was achieved when the contact time, pH, ENR concentration and ACTS dose were 15 h, 8, 10 mg L−1 and 8 g L−1, respectively. The adsorption of ENR onto ACTS followed the Redlich–Peterson isotherm model and a pseudo-second-order kinetics model. The preparation of 1 kg of ACTS incurred a cost of INR 246, as revealed through a cost analysis. The advantages of the developed adsorbent are that it is cost-effective, it is reusable, and it has the potential to adsorb enrofloxacin from aqueous media. The research work is limited to the laboratory scale and the scale-up of the process and an estimation of the overall cost of the process may be future directions for this work.
Conflicts of interest
There are no conflicts to declare.
References
- A. Karcı and I. K. Balcıoğlu, Investigation of the tetracycline, sulfonamide, and fluoroquinolone antimicrobial compounds in animal manure and agricultural soils in Turkey, Sci. Total Environ., 2009, 407, 4652–4664 CrossRef.
- Yiruhan, Q. J. Wang, C. H. Mo, Y. W. Li, Y. P. Tai, Y. Zhang, Z. L. Ruan and J. W. Xu, Determination of four fluoroquinolones antibiotics in tap water in Guangzhou and Macao, Environ. Pollut., 2010, 158, 2350–2358 CrossRef CAS PubMed.
- C. Tong, X. Zhuo and Y. Guo, Occurrence and risk assessment of four typical fluoroquinolone antibiotics in raw and treated sewage and in receiving waters in Hangzhou, China, J. Agric. Food Chem., 2011, 59, 7303–7309 CrossRef CAS.
- M. Seifrtová, A. Pena, C. M. Lino and P. Solich, Determination of fluoroquinolone antibiotics in hospital and municipal wastewaters in Coimbra by liquid chromatography with a monolithic column and fluorescence detection, Anal. Bioanal. Chem., 2008, 391, 799–805 CrossRef PubMed.
- E. Guinea, E. Brillas, F. Centellas, P. Cañizares, M. A. Rodrigo and C. Sáez, Oxidation of enrofloxacin with conductive-diamond electrochemical oxidation, ozonation and Fenton oxidation. A comparison, Water Res., 2009, 43, 2131–2138 CrossRef CAS PubMed.
- Y. Li, J. Niu and W. Wang, Photolysis of enrofloxacin in aqueous systems under simulated sunlight irradiation: kinetics, mechanism and toxicity of photolysis products, Chemosphere, 2011, 85, 892–897 CrossRef CAS PubMed.
- S. Chowdhury, G. Halder, T. Mandal and J. Sikder, Cetylpyridinium bromide assisted micellar-enhanced ultrafiltration for treating enrofloxacin-laden water, Sci. Total Environ., 2019, 687, 10–23 CrossRef CAS.
- J. Q. Xiong, M. B. Kurade and B. H. Jeon, Ecotoxicological effects of enrofloxacin and its removal by monoculture of microalgal species and their consortium, Environ. Pollut., 2017, 226, 486–493 CrossRef CAS.
- E. Rivagli, A. Pastorello, M. Sturini, F. Maraschi, A. Speltini, L. Zampori, M. Setti, L. Malavasi and A. Profumo, Clay minerals for adsorption of veterinary FQs: behavior and modelling, J. Environ. Chem. Eng., 2014, 2, 738–744 CrossRef CAS.
- T. S. Anirudhan, F. Shainy and J. Christa, Synthesis and characterization of polyacrylic acid-grafted-carboxylic graphene/titanium nanotube composite for the effective removal of enrofloxacin from aqueous solutions: adsorption and photocatalytic degradation studies, J. Hazard. Mater., 2017, 324, 117–130 CrossRef CAS PubMed.
- D. Ašperger, I. Varga, S. Babić and L. Ćurković, Adsorption of enrofloxacin on natural zeolite–clinoptilolite, Holist. Approach Environ., 2014, 4, 3–15 Search PubMed.
- S. H. Dhawane, S. Chowdhury and G. Halder, Lipase immobilised carbonaceous catalyst assisted enzymatic transesterification of Mesua ferrea oil, Energy Convers. Manage., 2019, 184, 671–680 CrossRef CAS.
- S. Sayen, M. Ortenbach-López and E. Guillon, Sorptive removal of enrofloxacin antibiotic from aqueous solution using a ligno-cellulosic substrate from wheat bran, J. Environ. Chem. Eng., 2018, 6, 5820–5829 CrossRef CAS.
- M. Wan, Z. Li, H. Hong and Q. Wu, Enrofloxacin uptake and retention on different types of clays, J. Asian Earth Sci., 2013, 77, 287–294 CrossRef.
- S. Chowdhury, J. Sikder, T. Mandal and G. Halder, Comprehensive analysis on sorptive uptake of enrofloxacin by activated carbon derived from industrial paper sludge, Sci. Total Environ., 2019, 665, 438–452 CrossRef CAS.
- P. Chakraborty, S. Show, S. Banerjee and G. Halder, Mechanistic insight into sorptive elimination of ibuprofen employing bidirectional activated biochar from sugarcane bagasse: performance evaluation and cost estimation, J. Environ. Chem. Eng., 2018, 6, 5287–5300 CrossRef CAS.
- J. P. Simonin, On the comparison of pseudo-first order and pseudo-second order rate laws in the modeling of adsorption kinetics, Chem. Eng. J., 2016, 300, 254–263 CrossRef CAS.
- S. Chen, J. Zhang, C. Zhang, Q. Yue, Y. Li and C. Li, Equilibrium and kinetic studies of methyl orange and methyl violet adsorption on activated carbon derived from Phragmites australis, Desalination, 2010, 252, 149–156 CrossRef CAS.
- B. Karmakar, S. H. Dhawane and G. Halder, Optimization of biodiesel production from castor oil by Taguchi design, J. Environ. Chem. Eng., 2018, 6, 2684–2695 CrossRef CAS.
- S. Chakraborty, J. Dasgupta, U. Farooq, J. Sikder, E. Drioli and S. Curcio, Experimental analysis, modelling and optimization of chromium(VI) removal from aqueous solutions by polymer-enhanced ultrafiltration, J. Membr. Sci., 2014, 456, 139–154 CrossRef CAS.
- E. Jiménez-Lozano, I. Marqués, D. Barrón, J. L. Beltrán and J. Barbosa, Determination of pKa values of quinolones from mobility and spectroscopic data obtained by capillary electrophoresis and a diode array detector, Anal. Chim. Acta, 2002, 464, 37–45 CrossRef.
- S. Banerjee, S. Mukherjee, A. Lamin Ka-ot, S. R. Joshi, T. Mandal and G. Halder, Biosorptive uptake of Fe2+, Cu2+ and As5+ by activated biochar derived from Colocasiaesculenta: isotherm, kinetics, thermodynamics, and cost estimation, J. Adv. Res., 2016, 7, 597–610 CrossRef CAS PubMed.
- A. K. Meena, G. K. Mishra, P. K. Rai, C. Rajagopal and P. N. Nagar, Removal of heavy metal ions from aqueous solutions using carbon aerogel as an adsorbent, J. Hazard. Mater., 2005, 122, 161–170 CrossRef CAS PubMed.
- V. K. Garg, R. Kumar and R. Gupta, Removal of malachite green dye from aqueous solution by adsorption using agro-industry waste: a case study of Prosopis cineraria, Dyes Pigm., 2004, 62, 1–10 CrossRef CAS.
- https://www.sigmaaldrich.com/technical-documents/articles/biology/ir-spectrum-table.html.
- P. Trivedi and D. Vasudevan, Spectroscopic investigation of ciprofloxacin speciation at the goethite–water interface, Environ. Sci. Technol., 2007, 41(9), 3153–3158 CrossRef CAS PubMed.
- W. Wang, X. Ma, J. Sun, J. Chen, J. Zhang, Y. Wang, J. Wang and H. Zhang, Adsorption of enrofloxacin on acid/alkali-modified corn stalk biochar, Spectrosc. Lett., 2019, 52(7), 367–375 CrossRef CAS.
- K. S. Shahul Hameed, P. Muthirulan and M. M. Sundaram, Adsorption of chromotrope dye onto activated carbons obtained from the seeds of various plants: equilibrium and kinetics studies, Arabian J. Chem., 2017, 10, S2225–S2233 CrossRef CAS.
- G. S. Agarwal, H. K. Bhuptawat and S. Chaudhari, Biosorption of aqueous chromium(VI) by Tamarindus indica seeds, Bioresour. Technol., 2006, 97, 949–956 CrossRef CAS PubMed.
- N. Nimibofa Ayawei, A. N. Augustus Newton Ebelegi and D. Donbebe Wankasi, Modelling and Interpretation of Adsorption Isotherms, J. Chem., 2017, 3039817, DOI:10.1155/2017/3039817.
- D. Bulgariu and L. Bulgariu, Potential use of alkaline treated algae waste biomass as sustainable biosorbent for clean recovery of cadmium(II) from aqueous media: batch and column studies, J. Clean. Prod., 2016, 112, 4525–4533 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 metric tons of tamarind in the year 2015–16. It is also a matter of fact that, globally, a large amount of tamarind seed is discarded as agricultural waste. The use of tamarind seed as an adsorbent has been reported by some researchers for dye and chromium(VI) removal.28,29 Looking at its waste utilization potential, in the present study, waste tamarind seed has been utilized to develop activated carbon (ACTS) that can be applied to the removal of ENR via an adsorption technique.
000 metric tons of tamarind in the year 2015–16. It is also a matter of fact that, globally, a large amount of tamarind seed is discarded as agricultural waste. The use of tamarind seed as an adsorbent has been reported by some researchers for dye and chromium(VI) removal.28,29 Looking at its waste utilization potential, in the present study, waste tamarind seed has been utilized to develop activated carbon (ACTS) that can be applied to the removal of ENR via an adsorption technique.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (w/w) ratio, so that the bio-char could be immersed in the solution. This solution was maintained under continuous stirring for 24 hours at 35 °C.15 Then, applying Whatman 42 filter paper, the slurry of carbonized tamarind seed and ortho-phosphoric acid was filtered. The residue was then washed with deionized water until the pH achieved a constant value of 7. Then, the carbon was exposed to a hot air oven for drying at 85 °C for 5 h; thereafter, it was kept inside a desiccator. The obtained material was used as an adsorbent and it was named activated carbon derived from tamarind seeds (ACTS). From 1 kg of dry tamarind seeds, around 450 g of ACTS was generated.
2 (w/w) ratio, so that the bio-char could be immersed in the solution. This solution was maintained under continuous stirring for 24 hours at 35 °C.15 Then, applying Whatman 42 filter paper, the slurry of carbonized tamarind seed and ortho-phosphoric acid was filtered. The residue was then washed with deionized water until the pH achieved a constant value of 7. Then, the carbon was exposed to a hot air oven for drying at 85 °C for 5 h; thereafter, it was kept inside a desiccator. The obtained material was used as an adsorbent and it was named activated carbon derived from tamarind seeds (ACTS). From 1 kg of dry tamarind seeds, around 450 g of ACTS was generated.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 10 minutes. After centrifugation, the supernatant was subjected to UV-vis spectrophotometry (Shimadzu UV 1800, Japan) to evaluate the ENR concentration at a wavelength of 271 nm.15 Each of the experiments was run in triplicate and the arithmetic means of the experimental outcomes are reported.
000 rpm for 10 minutes. After centrifugation, the supernatant was subjected to UV-vis spectrophotometry (Shimadzu UV 1800, Japan) to evaluate the ENR concentration at a wavelength of 271 nm.15 Each of the experiments was run in triplicate and the arithmetic means of the experimental outcomes are reported.
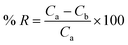
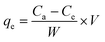
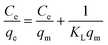
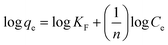
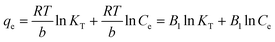
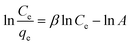
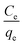 vs. Ce.
vs. Ce.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe vs. log
qe vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce.
Ce.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce plot is made, then KT and b can be calculated.
Ce plot is made, then KT and b can be calculated.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce will give the values of β and A.
Ce will give the values of β and A.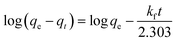
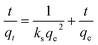
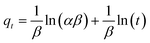
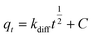
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching, C
C stretching, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching (carboxylic acid groups) and alcoholic O–H groups,13,25,27 respectively, in ACTS before adsorption. After adsorption, the existence of new bands at wavenumber values of 1122 cm−1, 1640 cm−1, 1782 cm−1 and 3441 cm−1 feasibly implies the appearance of C–N stretching, N–H bending, C
O stretching (carboxylic acid groups) and alcoholic O–H groups,13,25,27 respectively, in ACTS before adsorption. After adsorption, the existence of new bands at wavenumber values of 1122 cm−1, 1640 cm−1, 1782 cm−1 and 3441 cm−1 feasibly implies the appearance of C–N stretching, N–H bending, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching (ketone group) and N–H stretching,15,25,26 respectively. Since in the structure of ENR, as shown in Fig. 1, N–H bonds, C–N bonds and carboxylic acid groups are present, the FT-IR spectra provide evidence in favour of the adsorption of ENR by ACTS. It is suitably confirmed from the transformation of the IR bands that, due to the penetration of ENR molecules into the active sites and the porous structure of ACTS through the adsorption process, the N atoms within ENR were captured and encapsulated within the adsorbent, which certified the success of the process.
O stretching (ketone group) and N–H stretching,15,25,26 respectively. Since in the structure of ENR, as shown in Fig. 1, N–H bonds, C–N bonds and carboxylic acid groups are present, the FT-IR spectra provide evidence in favour of the adsorption of ENR by ACTS. It is suitably confirmed from the transformation of the IR bands that, due to the penetration of ENR molecules into the active sites and the porous structure of ACTS through the adsorption process, the N atoms within ENR were captured and encapsulated within the adsorbent, which certified the success of the process.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log likelihood
log likelihood