Open Access Article
Open Access ArticleTheoretical evaluation of inter-ion and intra-ion isotope effects in fragmentation: insights into chlorine and bromine isotope effects of halogenated organic compounds occurring in electron ionization mass spectrometry†
Caiming Tang *a,
Jianhua Tanb,
Yujuan Fanac,
Ke Zhengac,
Zhiqiang Yu
*a,
Jianhua Tanb,
Yujuan Fanac,
Ke Zhengac,
Zhiqiang Yu a and
Xianzhi Penga
a and
Xianzhi Penga
aState Key Laboratory of Organic Geochemistry, Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, Guangzhou 510640, China. E-mail: CaimingTang@gig.ac.cn
bGuangzhou Quality Supervision and Testing Institute, Guangzhou 510110, China
cUniversity of Chinese Academy of Sciences, Beijing 100049, China
First published on 4th April 2020
Abstract
Revelation of chlorine and bromine isotope effects in fragmentation is crucial for compound-specific isotope analysis of chlorine/bromine (CSIA-Cl/Br) using gas chromatography-electron ionization mass spectrometry (GC-EI-MS), but theoretical fundamentals of the isotope effects remain unclear. Herein, this study provides a theoretical basis for elucidating the details and implications of chlorine and bromine isotope effects occurring in dehalogenation reactions in EI-MS. Inter-ion and intra-ion isotope effects can occur in dehalogenation reactions in EI-MS, and affect chlorine/bromine isotope ratios. In a dehalogenation reaction, inter-ion isotope effects increase the isotope ratio of a precursor ion but decrease that of its product ion. On the other hand, intra-ion isotope effects can only affect (increase) the isotope ratio of a product ion, and have no effect on its precursor ion. The chlorine/bromine isotopologue distributions of ions measured by EI-MS are deduced to be non-binomial (nonrandom), regardless of the initial isotopologue distributions prior to fragmentation. The bulk chlorine/bromine isotope ratio of an ion cannot be exactly achieved with a calculation scheme using an arbitrary pair or pairs of neighboring chlorine/bromine isotopologues, but can be calculated with complete isotopologues of the ion. The isotope ratio of a compound calculated with a pair/pairs of neighboring isotopologues could not accurately reflect the trueness, even though it has been calibrated with external isotopic standard(s), due to different isotopologue distributions of the analyte and external isotopic standard(s). The conclusions derived from theoretical derivation have been experimentally proven with the isotopically distinct standards of tetrachloroethylene and trichloroethylene from different manufacturers. The findings of this study are conducive to CSIA-Cl/Br using GC-EI-MS to obtain high-quality data, and provide new insights into the actual chlorine/bromine isotopologue distributions of chlorinated/brominated organic compounds.
1 Introduction
During the last decade, gas chromatography electron ionization mass spectrometry (GC-EI-MS) has been increasingly applied to compound-specific isotope analysis of chlorine/bromine (CSIA-Cl/Br) for halogenated organic compounds (HOCs).1–4 GC-EI-MS can provide comparable precision and accuracy of CSIA-Cl compared with conventional offline isotope ratio MS (IRMS), and is much more efficient, more cost-effective and simpler.3,4 In addition, GC-EI-MS can be applied to CSIA-Cl for much more universal compounds compared with GC-IRMS, without converting analytes.5–7 As a result, CSIA-Cl/Br using GC-EI-MS has been raising concern recently.3,4,8Offline IRMS converts all chlorine atoms of analytes into singly chlorinated molecules such as CH3Cl and CsCl for performing CSIA-Cl,9–13 whereas CSIA-Cl using GC-EI-MS measures isotope ratios by calculation with molecular and/or fragmental ions.1 In GC-EI-MS, fragmentation occurs during ionization process in ion source and metastable-ion dissociation in mass analyzer. It has been reported that “staggering large” hydrogen/deuterium isotope effects could be present in fragmentation in EI-MS,14 with the kinetic isotope effects (KIEs) reaching up to 102 to 103.15,16 Both inter-ion and intra-ion KIEs can be present in fragmentation, and the latter can be approximately evaluated with relative abundances of fragmental ions.14 In our recent studies, we observed chlorine and bromine isotope effects of HOCs occurring in both separation on GC and fragmentation in EI-MS.6,7,17,18 Isotope effects in EI-MS could affect CSIA results, and thus external isotopic standards structurally identical to analytes are necessary.17 Up to now, it remains unclear how chlorine and bromine isotope effects in EI-MS influence relative abundances of chlorine and bromine isotopologues, and thereby raw isotope ratios measured by GC-EI-MS. Furthermore, at present, impacts of the in-fragmentation isotope effects on isotopologue distributions of ions on EI-MS has not been revealed, neither the exact properties of the isotopologue distributions (binomial or non-binomial). The properties of isotopologue distributions are vital for the CSIA-Cl/Br methods which apply an arbitrary pair or pairs of neighboring isotopologues of ion(s) to calculation of isotope ratios, due to that this isotopologue-pair scheme is based on the binomial theorem and assuming that the complete isotopologues of individual ions conform to binomial distribution (stochastic distribution).1,2,8 However, none of the reported CSIA-Cl/Br studies has seriously taken the facticity of the assumption into account, not to mention questioning it.
The main objectives of this study are (1) to theoretically evaluate the impacts of the in-fragmentation chlorine and bromine isotope effects on measured relative abundances of isotopologues of individual ions and on CSIA-Cl/Br results; and (2) to prove the validity of two isotope-ratio calculation schemes that use pair(s) of neighboring isotopologues and complete isotopologues of individual ions, respectively. Some strategies are proposed for obtaining precise and accurate CSIA-Cl/Br data, e.g., using the complete molecular isotopologue scheme of isotope-ratio calculation involving all molecular isotopologues of individual analytes, and applying calibration with external isotopic standards. This study can benefit CSIA-Cl/Br to achieve precise and accurate results, and provides new understandings in the real chlorine and bromine isotopologue distributions of HOCs.
2 Inter-ion isotope effects
Actually, isotope effects occurring in EI-MS are relevant to ions rather than molecules. In this context, we therefore use the terms “inter-ion” and “intra-ion”, instead of “intermolecular” and “intramolecular” as used in the literature,14 for describing the isotope effects. In this section, we do not take intra-ion isotope effects into account for explicitly elucidating inter-ion isotope effects.We hypothesize that dehalogenation reactions of HOCs in fragmentation in EI-MS are stepwise and follow the following sequence: molecular ion → losing Cl/Br atoms one by one → product ions containing successive numbers of Cl/Br atom(s).17,18 We define an ion with n Cl/Br atoms as the precursor ion of an ion with n − 1 Cl/Br atom(s), which stem from the same compound and keep unchanged carbon skeletons; and the latter is defined as the product ion of the former. Specifically, we define a precursor ion that finally transforms to its product ion as the parent ion of the product ion. Both chlorine and bromine have two stable isotopes with a mass difference of 2 u in the nature (35Cl vs. 37Cl, and 79Br vs. 81Br), and isotopologue distributions and dehalogenation processes of organochlorines and organobromines in EI-MS are similar.17 Therefore, organochlorines and organobromines may exhibit similar characteristics of chlorine/bromine isotope effects in fragmentation in EI-MS.17 In this study, to simplify expression, we hence principally concern chlorine isotope effects and use organochlorines to conduct theoretical derivation for elucidating the in-fragmentation isotope effects in EI-MS. In principle, the theoretical derivation results for chlorine isotope effects of organochlorines are also applicable for bromine isotope effects of organobromines.
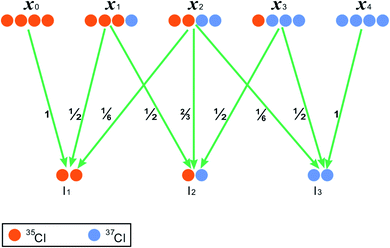
We hypothesize a compound harboring four chlorine atoms on structurally equivalent positions (RCl4) and then take it for example to elucidate the inter-ion chorine isotope effects (Fig. 1). Moreover, after the loss of one or two Cl atoms from RCl4, we hypothesize that the remaining Cl atoms on the dechlorination fragment are still position-equivalent. RCl4 has five chlorine isotopologues in theory, whose formulas are shown as 35Cl4, 35Cl337Cl, 35Cl237Cl2, 35Cl37Cl3 and 37Cl4, with the omission of carbon and other unconcerned elements, such as hydrogen and oxygen (Fig. 1). If intra-ion isotope effects are not considered and the dechlorination reactions shown in Fig. 1 are neither isotope-selective nor position-selective, then the corresponding probabilities for generating the product isotopologues can be theoretically calculated (Fig. 1).
For a compound with n Cl atoms (Cln), if a molecular isotopologue has i 37Cl atom(s), then the generating probability (P) of a product isotopologue produced in dechlorination reaction(s) of the molecular isotopologue by losing r Cl atom(s) and in possession of t 37Cl atom(s) is:
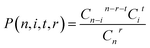 | (1) |
Specifically, as for the compound RCl4 (Fig. 1), the probability of a product isotopologue possessing t 37Cl atom(s) generated from the molecular ion by losing two Cl atoms is:
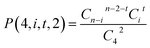 | (2) |
According to the derivation shown as eqn (S1)–(S5), we obtained an exemplary equation:
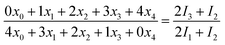 | (3) |
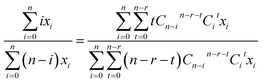 | (4) |
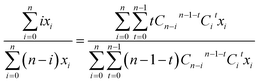 | (5) |
The left algebraic fraction of eqn (5) is actually the chlorine isotope ratio (37Cl/35Cl) of a parent ion, and the right is that of its product ion. This equation demonstrates that the isotope ratios of the parent ion and product ion are equal, provided that intra-ion isotope effects in the dechlorination reaction are nonexistent or not taken into account. As the lighter isotopologues of a precursor ion are more liable to lose a 35Cl atom than the heavier ones to lose a 37Cl atom, the heavy isotope (37Cl) thus accumulates in the remaining isotopologues of the precursor ion, and attenuates in the isotopologues of the product ion. Therefore, inter-ion isotope effects can increase the isotope ratio of a precursor ion, but decrease the isotope ratio of its product ion. Accordingly, the measured isotope ratio of the amount of a detected molecular ion (viz. non-fragmented molecular ion) is deduced to be higher than that of the total amount of the molecular ion comprising both fragmented and non-fragmented fractions (viz. the total amount of the molecular ion prior to fragmentation). In addition, the isotope ratio of the total amount of the molecular ion is inferred to exceed that of the fragmented molecular ion. The isotope ratio of a product ion is impacted by two types of inter-ion isotope effects, one takes place in the dechlorination process from the parent ion to the product ion, and another occurs in the further dehalogenation process from the product ion to its product ion. The former type decreases the isotope ratio of this product ion, whereas the latter increases the isotope ratio.
For an asymmetric compound possessing identical chlorine isotope ratios on individual Cl-atom positions, if the dechlorination process from a parent ion to its product ion occurs on only one position, then the remaining Cl atoms on the dechlorination fragment have the isotope ratio equivalent to that of the total amount of the precursor ion consisting of both fragmented and non-fragmented fractions. The isotope ratio of the product ion is deduced to be lower than that of the detected precursor ion (non-fragmented fraction), but higher than that of the parent ion (fragmented fraction). As a result, the inter-ion isotope effects occurring under this condition increase the precursor ion's isotope ratio, but has no effect on the product ion's isotope ratio which is identical to the initial isotope ratio of the total amount of the precursor ion prior to fragmentation.
A prerequisite for inter-ion isotope effects to happen is that the total amount of the precursor ion before fragmentation should exceed the amount of the parent ion (fragmented fraction). In other words, the total amount of the precursor ion should not be completely transformed to its product ion in one-step dechlorination reaction. Otherwise, the isotope ratio of the product ion will be equal to that of the total amount of the precursor ion according to eqn (5). In this scenario, the precursor ion cannot be observed on EI-MS, hence neither the inter-ion isotope effects for the precursor ion.
3 Intra-ion isotope effects
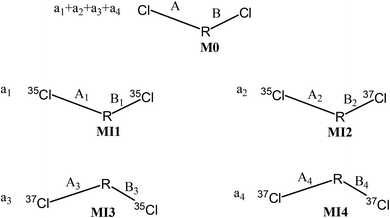
We create an imaginary molecule (M0) containing two Cl atoms as illustrated in Fig. 2. The symmetry between bond A and bond B of M0 is undetermined. M0 has four possible molecular isotopomers entitled as MI1, MI2, MI3 and MI4, whose isotopomeric structures are depicted in Fig. 2. The molar amount of M0 is a1 + a2 + a3 + a4, and those of MI1, MI2, MI3 and MI4 were a1, a2, a3, and a4, respectively. The chemical bonds involving chlorine isotopes of the four isotopomers are marked as A1, B1, A2, B2, A3, B3, A4, and B4, respectively (Fig. 2).M0 has three theoretical isotopologues, and the isotopomers MI2 and MI3 share the same isotopologue (35Cl37Cl, unconcerned elements omitted), while the isotopologues of MI1 and MI4 are 35Cl2 and 37Cl2, respectively.
The prerequisites for the occurrence of intra-ion isotope effects are (1) the isotopologue formula of a parent ion should possess both light and heavy isotopes (35Cl and 37Cl); (2) at least two dechlorination reactions can happen synchronously and alternatively on two reacting positions; and (3) the amount of any reacting C–Cl bond should not be entirely broken. In addition, the reacting positions can be structurally identical or different, given that the reactions can take place synchronously and alternatively.
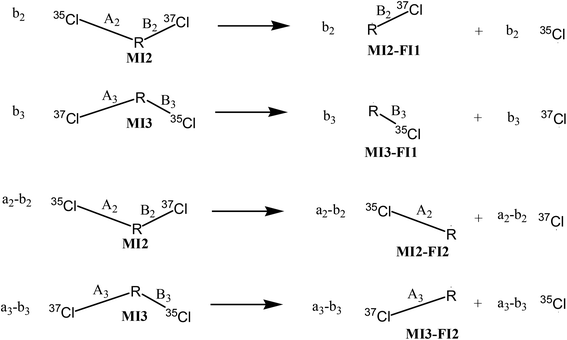
As shown in Fig. 3, the four possible fragments stemming from MI2 and MI3 are named as MI2-F1, MI3-F1, MI2-F2 and MI3-F2, with molar amounts of b2, b3, a2–b2, and a3–b3, respectively. According to the quasiequilibrium theory (QET),19 if internal energy and detection timescale of a compound on EI-MS are fixed, then fractions of all ions stemming from the compound are predicable, indicating that relative abundances of all the ions can reach an equilibrium state. Therefore, the equilibrium (quasiequilibrium) constant between the cleavages of bond A2 and bond A3 can be expressed as:
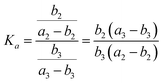 | (6) |
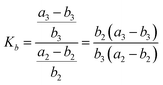 | (7) |
Therefore, Ka = Kb. Similarly, the equilibrium constant (K2) between the cleavages of bond A2 and bond B2, and that (K3) between bond A3 and bond B3 can be respectively expressed as:
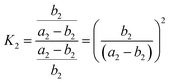 | (8) |
 | (9) |
The chlorine isotope ratio of the parent ion derived from MI2 and MI3 (Rpar(a2a3)) is
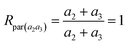 | (10) |
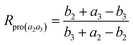 | (11) |
According to the derivation shown as eqn (S15)–(S26), we obtain the following inferences. When K3 = 0, Rpro(a2a3) has the minimum:
| Rpro(a2a3) = 1 = Rpar(a2a3) | (12) |
When K3 = Ka, Rpro(a2a3) has the maximum:
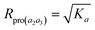 | (13) |
When K3 approaches infinity, Rpro(a2a3) reaches the limit equal to 1. Then for K3 ∈ (0, ∞), we have
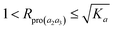 | (14) |
Thus, the isotope ratio of a product ion is higher than that of its parent ion. The physicochemical meanings for the cases of K3 = 0, K3 → ∞ and K3 = Ka are proposed as the following. K3 = 0: the amounts of bonds A2 and A3 are completely broken, whereas those of bonds B2 and B3 are completely unbroken. In this case, the isotope ratio of the product ion equals that of the parent ion, indicating no intra-ion isotope effect taking place. This scenario is probably existent for asymmetric molecules. If the critical energies of the asymmetric C–Cl bonds are different enough, so that the amount of a bond can be completely cleaved and that of another bond is completely non-cleaved or negligibly cleaved.17 K3 → ∞: this case is in fact equivalent to the case of K3 = 0. K3 = Ka: if the bonds A2, B2, A3 and B3 are structurally identical, then the amounts of all the bonds are partially broken and the amounts of C–35Cl bonds are broken more relative to those of C–37Cl bonds, indicating the presence of intra-ion isotope effects. With regard to other scenarios, intra-ion isotope effects can take place, and the isotope ratio of the product ion is higher than 1 but lower than 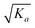 .
.
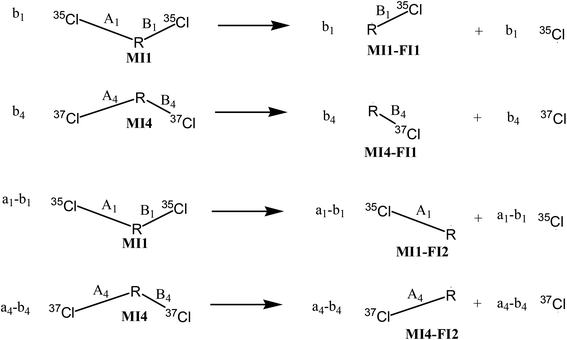
According to the reaction pathways illustrated in Fig. 3 and 4, the chlorine isotope ratio of complete isotopologues of the product ion (apparent isotope ratio, Rpro(app)) of the imaginary compound is
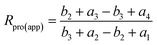 | (15) |
And the isotope ratio of the parent ion involving MI1, MI2, MI3 and MI4 (Rpar) is
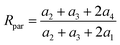 | (16) |
If the bonds A2, B2, A3 and B3 are structurally identical, then we have a2 = a3, and thus eqn (16) simplifies to
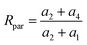 | (17) |
Based on the derivation displayed by eqn (S28)–(S34), the following conclusions can be obtained. When Ka = 1, we obtain
| Rpro(app) = Rpar | (18) |
When Ka > 1, we have
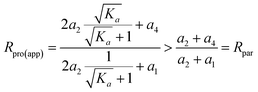 | (19) |
Thus, the apparent isotope ratio of the product ion is always higher than that of the parent ion, only if Ka > 1.
For asymmetric molecules, substituting Rpro(a2a3) with Ku, then we have 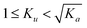 . On the basis of the derivation shown as eqn (S35)–(S43), the Rpro(app) can be expressed as:
. On the basis of the derivation shown as eqn (S35)–(S43), the Rpro(app) can be expressed as:
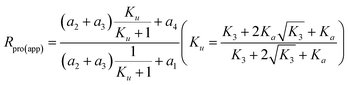 | (20) |
In addition, for K3 ∈ (0, ∞), we have the following inequation:
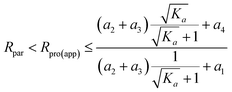 | (21) |
Thus, the apparent isotope ratio of a product ion is always higher than that of its parent ion, indicating enhancement of isotope ratio for the product ion caused by the intra-ion isotope effects occurring in EI-MS. Since both inter-ion and intra-ion isotope effects are taken into consideration in eqn (20), the total isotope effects are deduced to increase the isotope ratio of the product ion, although the inter-ion isotope effects present in the dechlorination from the parent ion to the product ion decrease the isotope ratio, provided that intra-ion isotope effects indeed exist in the dechlorination reaction.
4 Impacts on isotopologue distribution and implications to isotope-ratio calculation schemes
4.1 Scenario of symmetric compounds
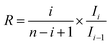 | (22) |
In previous studies, we developed an isotope-ratio calculation scheme using complete isotopologues of individual molecular ions.6,7 This complete molecular isotopologue scheme can be expressed as follows:
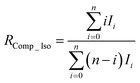 | (23) |
We hypothesize that the molecular isotopologues of an organochlorine comply with binomial distribution. In fact, this is a very rare and unrealistic scenario, unless the organochlorine is synthesized at an extremely high temperature. In addition, we further hypothesize no isotope effect present in the ionization process (excluding fragmentation process) in EI-MS, which is reasonable in principle. Therefore, the total amount of molecular ion comprising both fragmented and non-fragmented fractions, as well as the initial molecules prior to ionization have the same binomial distribution of chlorine isotopologues. The chlorine isotope ratio of the total amount of molecular ion (Rall) can thus be calculated as:
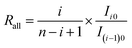 | (24) |
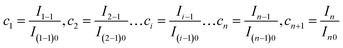 | (25) |
Then according to eqn (22) and (25), for a random pair of neighboring isotopologues containing i − 1 and i 37Cl atoms, respectively, we have
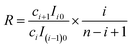 | (26) |
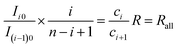 | (27) |
Similarly, for the pair of isotopologues possessing i and i + 1 37Cl atoms, respectively, we obtain
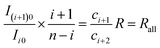 | (28) |
If the detected molecular isotopologues comply with binomial distribution, then the isotope ratios calculated with all pairs of neighboring isotopologue ions are equal. Therefore, for the isotope ratios calculated with random three neighboring isotopologues, we have
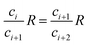 | (29) |
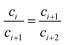 | (30) |
This equation demonstrates that the progression (c1, c2 … ci, ci+1 … cn, cn+1) is geometric, or in other words,
| ci = c1qi−1 | (31) |
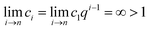 | (32) |
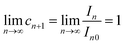 | (33) |
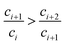 | (34) |
According to eqn (27) and (28), we have
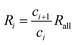 | (35) |
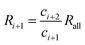 | (36) |
Therefore, Ri > Ri+1 can be obtained. The isotope ratio calculated with I0 and I1 (R1) is the highest among all the isotope ratios calculated with pairs of neighboring isotopologues, and higher than that calculated with complete molecular isotopologues by the complete molecular isotopologue scheme.
4.2 Scenario of asymmetric compounds
We hypothesize that the isotopologues of an asymmetric organochlorine containing n Cl atoms comply with binomial distribution which is expressed as:| f0(n) = (α0 + β0)n | (37) |
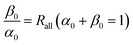 | (38) |
If the compound loses a Cl atom from only one specific position in EI-MS, then the chlorine isotope ratio on this position of the detected molecular ion becomes higher than the initial isotope ratio prior to fragmentation. However, the isotope ratios on the rest positions are unchanged. If the Cl atom on the specific position are not taken into account, then the isotopologues of the detected molecular ion still comply with binomial distribution, viz. the isotopologues of the dechlorination product ion are binomially distributed. When incorporating the Cl atom on the specified position into consideration, we can express the distribution of the isotopologues as:
| f(n) = (α + β)(α0 + β0)n−1 | (39) |
We define the isotope ratios calculated with the molecular isotopologue-pair scheme using two adjacent pairs of neighboring isotopologues of the molecular ion as Ri+1 and Ri+2, respectively. According to the derivation displayed as Eqs/Ineqs (S54)–(S76), we obtain the following inequation:
| Ri+1 > Ri+2 (i = 0,1,2…n) | (40) |
Hence, with regard to asymmetric organochlorines, the isotope ratios calculated with pairs of neighboring isotopologues monotonically decrease with the increase of 37Cl atoms of the isotopologues. As a result, the isotope ratio calculated with the first pair of neighboring molecular isotopologues (I0 and I1) of an asymmetric organochlorine (R1) is the largest, and higher than that calculated by the complete molecular isotopologue scheme using all the isotopologues.
4.3 Effects of initial distribution of molecular isotopologues
The theoretical deduction provided above is based on the assumption that the molecular isotopologues of individual organochlorines comply with binomial distribution. If the initial distribution of the molecular isotopologues is non-binomial, how does it affect the distribution of the detected molecular isotopologues on EI-MS? Obviously, if the initial molecular isotopologues are non-binomially distributed, the detected molecular isotopologues are extremely unlikely to conform to binomial distribution, and the initial distribution can somewhat impact that of the detected molecular isotopologues. As a consequence, the isotope ratios calculated with the molecular isotopologue-pair scheme may not absolutely gradually decrease as 37Cl atoms increase, and that calculated with the first pair of neighboring isotopologues may not always be the largest. Certainly, the isotope ratio calculated with the first pair of neighboring isotopologues cannot reflect the bulk isotope ratio of an organochlorine compound.4.4 Concerns for product ions
For a product ion, due to further inter-ion isotope effects in next-step dechlorination reaction, all the isotopologues of the detected product ion thus never comply with binomial distribution, which is similar to the molecular ion scenario discussed above. Similarly, the chlorine isotope ratios calculated with pairs of neighboring isotopologues of the product ion may gradually decrease with the increasing 37Cl atoms. Therefore, the isotope ratio of the product ion calculated with the first pair of neighboring isotopologues (R1) may be the highest, and anticipated to exceed that calculated by the complete molecular isotopologue scheme using all the isotopologues of the product ion. However, if the isotopologues of the initial product ion before further dechlorination are non-binomially distributed, then the isotope ratios calculated with pairs of neighboring isotopologues may not always gradually decrease with the increase of 37Cl atoms, but could be more susceptible to the initial isotopologue distribution prior to further dechlorination. In addition, if intra-ion isotope effects are present in a dechlorination reaction from a parent ion to its product ion, then the isotopologues of the detected product ion more likely tend to be non-binomially distributed, in contrast with the scenario of a dechlorination reaction without intra-ion isotope effects.5 Implications to CSIA-Cl/Br study
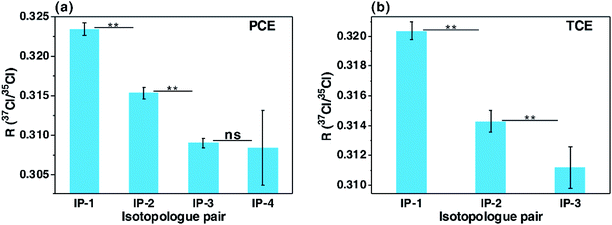
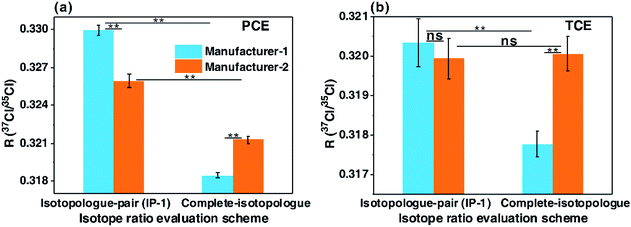
Because of inter-ion isotope effects inevitably occurring in EI-MS, detected molecular and product isotopologues never exactly comply with binomial distribution, or may only approximately follow binomial distribution. Up to now, we have not found any organochlorine standard whose molecular and/or product isotopologues strictly complied with binomial distribution, consistent with the theoretical inferences in this study. In our experimental study, the chlorine isotope ratios measured by GC-EI-high resolution MS (GC-EI-HRMS) with the calculation schemes using isotopologue pairs or complete molecular isotopologues have proven the theoretical inferences mentioned above from an experimental perspective. As indicated in Fig. 5, the isotope ratios of tetrachloroethylene (PCE) and trichloroethylene (TCE) calculated with the pairs of neighboring molecular isotopologues gradually decreased with the increase of 37Cl atoms of isotopologues (Fig. 5). This result agreed well with the above-mentioned inference that chlorine isotopologues of individual organochlorines are not binomially distributed and isotope ratios calculated with lighter isotopologue pairs are higher than those calculated with heavier ones. In addition, the isotope ratios of the two PCE standards and the TCE standard from manufacturer-1 calculated with the first isotopologue pairs are significantly higher than those calculated with the complete molecular isotopologue scheme (P < 0.01, paired-samples T test, Fig. 6). This finding accorded well with the aforementioned theoretical conclusion that chlorine isotope ratios calculated with the first isotopologue pairs are higher than the bulk isotope ratios calculated with the complete molecular isotopologues for individual organochlorines, demonstrating non-binomial (or non-stochastic) distributions of chlorine isotopologues of organochlorine compounds. Moreover, in our recent study, we observed the inconsistent carbon isotope compositions of chlorine isotopologues of individual organochlorines, which also experimentally proved the above theoretical inference that distributions of chlorine isotopologues of individual organochlorines are nonrandom.20Since chlorine isotopologue distributions of individual organochlorines are non-stochastic, chlorine isotopologue distribution modes of different organochlorines may be different. Therefore, if the chlorine isotopologue distributions of an analyte and its external isotopic standard(s) are different, then the chlorine isotope ratio of the analyte calculated by the molecular isotopologue-pair scheme may be inaccurate, despite of the utilization of external isotopic standard(s). This inference has been experimentally proven in our CISA-Cl study by analyzing the standards of PCE and TCE from different manufacturers (manufacturer-1 and manufacturer-2, Fig. 6). The chlorine isotope ratio of the PCE standard from manufacturer-1 calculated with the first pair of neighboring molecular isotopologues was significantly higher than that of the standard from manufacturer-2 (P < 0.01, independent-samples T test, Fig. 6a), while those of the TCE standards from the two manufacturers were insignificantly different (p > 0.2, Fig. 6b). However, the isotope ratios of the two standards from manufacturer-1 calculated by the complete molecular isotopologue scheme were significantly lower than those from manufacturer-2 (P < 0.01, Fig. 6).
The chlorine isotope ratios calculated with the complete molecular isotopologue scheme conceptually reflected the bulk isotope ratios of the detected molecular ions of the compounds, demonstrating the accurate raw isotope ratios. Yet the isotope ratios calculated with the molecular isotopologue-pair scheme only reflected the idealized isotope ratios with the assumption that the molecular isotopologues of individual compounds conform to binomial distribution. We postulate that the real isotope ratios, anchored to the scale of Standard Mean Ocean Chlorine (SMOC), of the two standards from manufacturer-1 are known, and then can use them as the external isotopic standards for those from manufacturer-2 in CSIA-Cl study. Therefore, the real isotope ratios of the standards from manufacturer-2 can be obtained by calibration with the external isotopic standards (standards from manufacturer-1). As shown in Fig. 6, the scale orders of isotope ratios of individual standards from the two manufacturers calculated with the molecular isotopologue-pair scheme were completely different from those with the complete molecular isotopologue scheme. As a consequence, the calibrated isotope ratios of the standards from manufacturer-2 calculated with the molecular isotopologue-pair scheme cannot exactly reflect the actual isotope ratios of the standards. However, using the complete molecular isotopologue scheme together with external isotopic standards can help to obtain actual chlorine isotope ratios of analytes.
6 Conclusions
This study proposes a solid theoretical basis for elucidating the chlorine and bromine isotope effects taking place in fragmentation in EI-MS. Both inter-ion and intra-ion isotope effects can be present in dehalogenation reactions in EI-MS. Generally, inter-ion isotope effects increase chlorine/bromine isotope ratios of precursor ions but decreases those of their product ions. The isotope ratios of molecular ions are affected (increased) by only one type of inter-ion isotope effects in the dehalogenation from the molecular ions to their product ions. Whereas product ions can be impacted by two types of inter-ion isotope effects, i.e., the inter-ion isotope effects in the dehalogenation from their parent ions to the product ions (causing enhancement of isotope ratios) and that from the product ions to their further dehalogenation product ions (causing reduction of isotope ratios). Intra-ion isotope effects increase the isotope ratios of product ions but has no effect on their precursor ions. Because inter-ion isotope effects are inherently present in dehalogenation reactions in fragmentation, the chlorine/bromine isotopologues of detected individual precursor ions never conform to binomial distribution, no matter whether the initial isotopologue distributions prior to fragmentation are binomial or not. Therefore, the bulk isotope ratio involving all the isotopologues of an ion cannot be obtained by the isotopologue-pair scheme of isotope-ratio calculation which is derived from the binomial theorem and based on the assumption that all the isotopologues of each ion are binomially distributed. However, the bulk isotope ratio of an ion can be calculated with the complete isotopologue scheme using all the isotopologues of the ion. Application of the complete molecular isotopologue scheme and calibration with external isotopic standards can help to obtain accurate isotope ratios of analytes. The results of this study are conducive to CSIA-Cl/Br for achieving precise and accurate data, and provide new cognitions in actual distributions of chlorine and bromine isotopologues of HOCs.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors sincerely appreciate the assistance from Mr Ruotai Li (The School of Mathematical Sciences at Peking University, China) and Mr Xianda Sun (Rongxin Power Electronic Co., Ltd., China) in checking the mathematical derivation. This work was partially supported by the National Natural Science Foundation of China (Grant No. 41603092).References
- B. Jin, C. Laskov, M. Rolle and S. B. Haderlein, Environ. Sci. Technol., 2011, 45, 5279–5286 CrossRef CAS PubMed.
- Y. Zakon, L. Halicz, O. Lev and F. Gelman, Rapid Commun. Mass Spectrom., 2016, 30, 1951–1956 CrossRef CAS PubMed.
- T. C. Schmidt and M. A. Jochmann, Annu. Rev. Anal. Chem., 2012, 5, 133–155 CrossRef CAS PubMed.
- A. Cincinelli, F. Pieri, Y. Zhang, M. Seed and K. C. Jones, Environ. Pollut., 2012, 169, 112–127 CrossRef CAS PubMed.
- O. Shouakar-Stash, R. J. Drimmie, M. Zhang and S. K. Frape, Appl. Geochem., 2006, 21, 766–781 CrossRef CAS.
- C. Tang, J. Tan, S. Xiong, J. Liu, Y. Fan and X. Peng, J. Chromatogr. A, 2017, 1514, 103–109 CrossRef CAS PubMed.
- C. Tang and J. Tan, Anal. Chim. Acta, 2018, 1039, 172–182 CrossRef CAS PubMed.
- X. Liu, L. Li, Y. Chi and Z. Zhang, J. Chin. Mass Spectrom. Soc., 2016, 37, 10–16 Search PubMed.
- N. Jendrzejewski, H. G. M. Eggenkamp and M. L. Coleman, Anal. Chem., 1997, 69, 4259–4266 CrossRef CAS.
- K. C. Westaway, T. Koerner, Y. R. Fang, J. Rudzinski and P. Paneth, Anal. Chem., 1998, 70, 3548–3552 CrossRef CAS PubMed.
- B. D. Holt, L. J. Heraty and N. C. Sturchio, Environ. Pollut., 2001, 113, 263–269 CrossRef CAS PubMed.
- B. D. Holt, N. C. Sturchio, T. A. Abrajano and L. J. Heraty, Anal. Chem., 1997, 69, 2727–2733 CrossRef CAS.
- M. Numata, N. Nakamura, H. Koshikawa and Y. Terashima, Environ. Sci. Technol., 2002, 36, 4389–4394 CrossRef CAS PubMed.
- P. J. Derrick, Mass Spectrom. Rev., 1983, 2, 285–298 CrossRef CAS.
- C. Z. Ottinger, Z. Naturforsch., A: Phys. Sci., 1965, 20, 1232–1234 Search PubMed.
- U. Löhle and C. Ottinger, J. Chem. Phys., 1969, 51, 3097–3104 CrossRef.
- C. Tang, J. Tan, Z. Shi, Y. Fan, Z. Yu and X. Peng, J. Chromatogr. A, 2019, 1603, 278–287 CrossRef CAS PubMed.
- C. Tang, L. Peng, J. Tan, Y. Guan, Q. Huang, Z. Yu and X. Peng, Int. J. Mass Spectrom., 2020, 447, 116238 CrossRef.
- L. H. Eyring, S. H. Lin and S. M. Lin, Basic chemical kinetics, John Wiley and Sons, New York, 1980 Search PubMed.
- C. Tang, J. Tan, Y. Fan, K. Zheng, Q. Huang and X. Peng, Observation of inconsistent carbon isotope compositions of chlorine-isotopologue pairs of individual organochlorines on gas chromatography-high resolution mass spectrometry, Int. J. Environ. Anal. Chem., 2020 DOI:10.1080/03067319.2019.1699550 , in press.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra09155f |
| This journal is © The Royal Society of Chemistry 2020 |