Open Access Article
Open Access ArticleThe influence of molecular vicinity (expressed in terms of dielectric constant) on the infrared spectra of embedded species in ices and solid matrices
Pilling S. * and
Bonfim V. S.
* and
Bonfim V. S.
Universidade do Vale do Paraíba – UNIVAP, Laboratório de Astroquímica e Astrobiologia – LASA, Av. Shishima Hifumi, 2911, Urbanova, São José dos Campos, SP, Brazil. E-mail: sergiopilling@yahoo.com.br
First published on 3rd February 2020
Abstract
In this theoretical work we evaluate how the chemical environment influences some features presented in the infrared spectrum, such as band intensities and band location of embedded species in icy matrices. The calculations were performed employing the Polarized Continuum Model (PCM) approach with the second-order Møller–Plesset perturbation theory (MP2) level using the Gaussian 09 package. Here, we simulate the effects of molecular vicinity around embedded species in terms of the effects of the dielectric constant (ε) of the icy and solid samples. Gas phase calculation was also performed for comparison purpose. The investigated embedded single molecules were CO, CO2, CH4, NH3, SO2 HCOOH, CH3OH and also H2O. The results suggest that for most vibrational modes, the strengths of IR bands show an increase with ε, which implies they also decrease with respect to porosity. The frequency shifts showed opposite behavior in relation to the band strengths, with few exceptions. A correlation between calculated band intensities with the band strengths A (taken from literature) was determined and described by a linear function I ∼ 6 × 1018 A [km mol−1], with A in unity of cm per molecule. In addition, an associative exponential function was adjusted to the studied dataset to characterize the evolution of frequency-shift and intensity-shift and band strength ratio as function of the dielectric constant. Since astrophysical ice mantles over cold dust grains can vastly vary in composition in space (having different dielectric constants) they are a challenge to be well characterized. Therefore, this work can help the astrochemistry community to better understand astrophysical ices and its observations in the infrared.
1 Introduction
The molecular abundances in solid phase observed in cold astrophysical environments (e.g. dense molecular clouds, inner part of protoplanetary disks, obscured regions of young stellar objects (YSOs), comets, and frozen surfaces of solar system) are mainly determined by measuring the area of specific peaks in emission or absorption (the latter is more frequent) in the infrared (IR) spectra which are related to a given molecular vibrational modes.1–3 However, the procedure requires an accurate value of a molecular (physicochemical) parameter called band strength A (sometimes also called the A-value in the literature) ordinarily measured in the laboratory during ice simulation at low temperatures.4–7 Additionally, it has been reported in the literature that the molecular band strength and peak position in the IR spectrum may vary depending on the sample temperature and chemical environment.7–13Considering that in cold space environments, the ices may contain different chemical compositions in a water-ice matrix (embedded molecules lie in different chemical environments), different temperatures and porosity degree, the employment of laboratory values of band strength (and also peak locations) derived for pure samples, or for simple mixtures, can introduce errors in the determination of real molecular abundances and also molecular identification in astronomical observations. In attempt to better handle and quantify molecular abundances of frozen species in the IR spectra of cold astrophysical environments, we performed a theoretical/computational work to evaluate, through vibrational analysis from ab initio calculations, how the chemical environment influences features in the spectrum, specifically, the peak positions and their respective intensities (here described in terms of band strengths).
Here, we simulate the effects of chemical environment in single molecular species embedded in an icy matrix by considering the net effect of a surrounding average electric field, parameterized by the dielectric constant (ε) of the medium. This level of description was achieved employing Polarized Continuum Model (PCM),14 which is implemented in several computational quantum chemistry packages.15 This approach has been used to model the average icy matrix effect on the embedded molecule reactivity.16–20 The studied embedded species in this manuscript were CO, CO2, CH4, NH3, SO2, HCOOH (“trans” conformer), CH3OH and H2O.
Section 2 presents, with details, the employed computational methodology with the description of the approximations and considerations used in the work. The results are listed in Section 3 with focus on the changes in the infrared features of the embedded selected species as function of dielectric constant of icy matrix. Conclusion and final remarks are given in Section 4.
2 Methodology
In this work we investigate through theoretical/computational analysis how cold chemical environments (astrophysical ice analogs) influence changes (e.g. peak positions and intensities) in the IR spectrum of single embedded species. Here we investigate eight different molecules (polar and non-polar ones): CO, CO2, CH4, NH3, SO2, HCOOH, CH3OH and also H2O. Such species are observed in several space environments.21,22The PCM approach is here implemented via its “integral equation formalism” version, and employing the Gaussian 09 program.15,23,24 The PCM solvation method is a good approximation to simulate the implicit solvation (sometimes termed continuum solvation). As it is a method to represent solvent as a continuum medium instead of individual “explicit” solvent molecules, it has been employed for liquids representation in molecular dynamics as well as good for simulating amorphous ices.16,18–20 In the case of crystalline ices (not studied in this work) the explicit solvation would be more appropriated due to the system symmetry around the embedded molecule (unit cell) which may play a major influence on the molecular vibrations. The cavity model used here was the default available in the Gaussian 09 program.24
All calculations have been performed at second-order Møller–Plesset perturbation theory (MP2) level, with the correlation consistent triple zeta basis set, or just cc-pVTZ.25 The number of electrons of the studied system varies quite well among the molecules investigated here, and also a larger set of molecules on which calculations are in progress. Thus, for reasons of computational convenience, we have used the MP2/cc-pVTZ calculation level for all the electronic structure calculations of the current work. Every chemical species had the equilibrium geometry confirmed for each ε value (varying from 1 to 180) by applying harmonic vibrational analysis, which has also provided the desired output data. Here, ε = 1 explicitly indicates molecules in gas-phase (vacuum), low values of ε also indicate molecules embedded in “very cold” ices (porous or not), and ε = 180 indicates molecules embedded in “hot” water-rich ices (see Aragones et al.27), as we will discuss further. The calculated molecular infrared spectra of the studied species in the current work, including the assignment of molecular vibration (vibration modes), band intensities as well as the band locations (frequency or wavenumber) were performed using the Gaussian 09 package.24
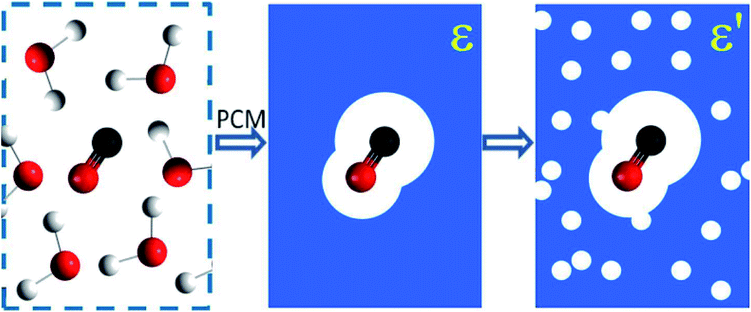
In the adopted effective-medium approach context, we can use the link between dielectric constant ε and other physical–chemical properties of the bulk ice to probe how they influence the IR spectra of the embedded molecules. For practical means, it may be assumed that variations in such properties, such as ice temperature, are dominated by changes in the solid water matrix, and consequently in the corresponding ε values. Fig. 1 presents an illustration of the PCM approximation employed (individual molecules are replaced by an average field represented by the dielectric constant). As discussed previously in this approach the molecular environment (force filed) is represented by its dielectric constant ε. The amount of polarization which occurs when a certain voltage (or electric potential) is applied to an object influences the amount of electrical energy that is stored in the electric field. This is described by the dielectric constant of the material. As discussed by Silla et al.26 and Aragones et al.,27 and references therein in both works, the dielectric constant (or relative permittivity) of materials is also very dependent on chemical composition (diversity of polarity in molecules), sample temperature and degree of compaction (or its porosity). This figure also illustrates the porous sample approximation employed in this work (solid matrix filled with holes containing vacuum) in which the value of dielectric constant is lower as the amount of pores increases.
It is important to note that, a given dielectric constant might be associated with several types of ices/solid matrices (with different chemical composition, porosity degree and temperature). For this reason, we prefer to make all the calculations here in terms of the dielectric constant to make the manuscript as general as possible for the astrochemistry community. In future work we consider the explicit dependence of the dielectric constant with sample temperature and porosity and how this can influence spectral features of embedded molecules, following the directions already pointed out in the literature.17,28
Considering as an approximation that band area S is proportional to band intensity (S ∝ I), particularly good for symmetric band profiles, the relationship between the band intensity I and band strength (A-value) can be seen from the equation:
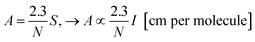 | (1) |
Assuming the change in the band area (S) is very little affected by the enlargement or narrowing of the peak, eqn (1) states that the variations in the ratio between two different A values (e.g. A1 and A2) will be equivalent to the ratio between to different intensities I values (e.g. I1 and I2) when we compare systems in three different situations: (1) two different samples (1 and 2) containing the same amount of molecules or column density N; (2) two different IR bands (i and j) of the same molecular species; (3) the same species in two different environments (embedded into different media with different dielectric constants related with different temperatures, porosity or chemical composition). This methodology is very helpful since it avoids any systematic errors in the determination of individual values of band intensities due to the use of a given level of theory. Therefore, the prediction value for the ratio of two bands strengths (comparing two vibration modes of a single molecule or single vibration mode for same molecule in different environments) gets us as close as possible from connections with observational and/or experimental data.
It is important to note that, in an attempt not to be strongly affected by the level of calculation/theory, the current methodology focus on the relative values rather the absolute values. Here we always make a comparison (subtraction or a division) of calculated quantifies with some reference calculated value and identify the main changes/differences from such comparison.
As it will be described in the following sections, in this manuscript we will consider the third situation listed above to describe, for each studied species, the dependence of IR band intensities (written in terms of I/I0) and IR bands strengths (written in terms of A/A0) as a function of different dielectric constants (ε).
3 Results and discussion
The evaluated IR spectrum features (peak location and intensities) have presented considerable variations with the systematic changes of ε. As pointed out previously, a variation in the ratio of band intensities is proportional to the change on the ratio of band strengths for the same species in two different environments (for example, considering different dielectric constants). In this section we will present such variations for the studied embedded species (CO, CO2, CH4, NH3, SO2, HCOOH, CH3OH and also H2O).As pointed out by Mate30 the molecular band strengths are intrinsic properties of the material, and as the dielectric constants do, vary significantly with the temperature due to morphology and phase changes. Additionally, the band strength values are also different in ice mixtures as compared with pure species, due to the interaction between the different kinds of molecules within the ice. The intensity variations are usually accompanied with frequency shifts of the IR absorptions. Both modifications must be taken into account for a proper description of the composition of ice samples. The chemical environments expressed in terms of the different type of neighbor molecules around a given embedded species and its influence on IR profiles were also discussed by Schimitt et al.31 Similarly, the changes in the band strengths with chemical composition were extensively investigated experimentally in the literature.32–35 As the surrounded species changes, the electric field and dielectric constant of the medium change, and this affects the molecular orbital and atom configuration of the embedded species (as well as electric dipole moments) which interact differently with the incoming electromagnetic field. These changes result, as a consequence, changes in the molecular band strength for a given energy transition (or vibration mode). For example, Bouwman et al.32 show that most bands of water (stretch, bend and librations modes) decreases as the water species is surrounded by CO molecules. A similar behavior for the water bands was also observed by Öberg et al.33 as the embedded water molecules are being surrounded by CO2 molecules.
Table 1 lists the selected IR bands analyzed in this manuscript. The theoretical peak positions (in units of wavenumbers and micrometers) calculated for ice samples at 10 K (cold ice with ε = 3) and at gaseous-phase (ε = 1) are given. For comparison purpose, we also present some experimental values of band location and band strengths, taken from literature for pure ices at low temperature.6,8,36–39
| Selected vibrational modes | MP2(fu)/cc-pVTZ (this work) | Experimental data (literature) | ||||||
|---|---|---|---|---|---|---|---|---|
| Cold ice (10 K; ε = 3) | Gas-phase (vacuum; ε = 1) | Cold pure ices (ε = unknown) | ||||||
| Molecule | Mode assignment | ν# | ν (cm−1) | λ (μm) | ν (cm−1) | λ (μm) | ν (cm−1) | A (molecule per cm) |
| a At 25 K; Bouilloud et al.36b At 90 K; Khanna et al.37c At 16 K; Garozzo et al.38d At 10 K; Hudgins et al.8e At 10 K (presumably); Sandford and Allamandola.39f At 10 K; D'Hendecourt and Allamandola.6 | ||||||||
| CO | Stretching | ν1 | 2145 | 4.661 | 2139 | 4.675 | 2139 | 1.1 × 10−17a |
| CO2 | Bending | ν2 | 659 | 15.19 | 661 | 15.13 | 665 | 1.2 × 10−17a |
| Asymmetric stretching | ν3 | 2427 | 4.120 | 2440 | 4.098 | 2342 | 7.6 × 10−17a | |
| CH4 | Asymmetric bending | ν4 | 1352 | 7.394 | 1358 | 7.364 | 1302 | 8.0 × 10−18a |
| Asymmetric stretching | ν3 | 3214 | 3.112 | 3216 | 3.109 | 3010 | 1.1 × 10−17a | |
| SO2 | Bending | ν2 | 503 | 19.85 | 504 | 19.84 | 530 | 4.8 × 10−18b |
| Symmetric stretching | ν1 | 1125 | 8.903 | 1120 | 8.929 | 1149 | 2.2 × 10−18c | |
| Asymmetric stretching | ν3 | 1333 | 7.495 | 1337 | 7.479 | 1335 | 1.5 × 10−17c | |
| H2O | Bending | ν2 | 1645 | 6.080 | 1650 | 6.061 | 1659 | 9.0 × 10−18a |
| Symmetric stretching | ν1 | 3864 | 2.588 | 3872 | 2.583 | 3298 | 1.7 × 10−16d | |
| Asymmetric stretching | ν3 | 3977 | 2.515 | 3993 | 2.504 | 3257 | 1.5 × 10−16a | |
| NH3 | Symmetric bending | ν2 | 1098 | 9.111 | 1077 | 9.285 | 1069 | 1.6 × 10−17a |
| Asymmetric bending | ν4 | 1683 | 5.943 | 1691 | 5.914 | 1624 | 4.7 × 10−18e | |
| Symmetric stretching | ν1 | 3533 | 2.831 | 3542 | 2.823 | 3375 | 2.2 × 10−17f | |
| Asymmetric stretching | ν3 | 3666 | 2.728 | 3680 | 2.717 | 3376 | 2.3 × 10−17a | |
| HCOOH | Out of plane O–H bond bending | ν5 | 685 | 14.67 | 692 | 14.45 | 929 | 6.4 × 10−17a |
| Out of plane C–H bond bending | ν8 | 1141 | 8.774 | 1143 | 8.749 | 1064 | 3.1 × 10−19a | |
| Carbonyl group stretching | ν3 | 1819 | 5.514 | 1830 | 5.46 | 1708 | 5.4 × 10−17a | |
| O–H bond stretching | ν1 | 3772 | 2.654 | 3781 | 2.64 | 2586 | 1.4 × 10−16a | |
| CH3OH | Methyl group torsion | ν12 | 306 | 32.70 | 309 | 32.36 | 694 | 1.4 × 10−17a |
| C–O bond stretching | ν8 | 1067 | 9.368 | 1073 | 9.320 | 1031 | 1.1 × 10−17a | |
| C–H bond sym. stretching | ν3 | 3076 | 3.251 | 3070 | 3.257 | 2700–3600 | 1.6 × 10−16a | |
| C–H bond asym. stretching | ν9 | 3132 | 3.192 | 3124 | 3.20 | 2700–3600 | 1.4 × 10−16a | |
As a summary of the results, for most vibration modes employed in this study, the band strengths have increased with ε, which also implies they have decreased with respect to porosity. The frequency shifts (in wavenumbers) have shown an opposite behavior in relation to the band strengths, with few exceptions. Moreover, all the trends here observed seem to be more pronounced in low temperature ices than in the higher temperature ones. Hopefully, this study will provide a better understanding of some astrophysical ices properties and their interaction with radiation, since from the IR spectral profile of diluted species, one could be able to infer physical and chemical properties of the surrounding medium. In the following section we go deeper into these findings for each studied species.
3.1 Influence of dielectric constant in infrared features (band location and intensity)
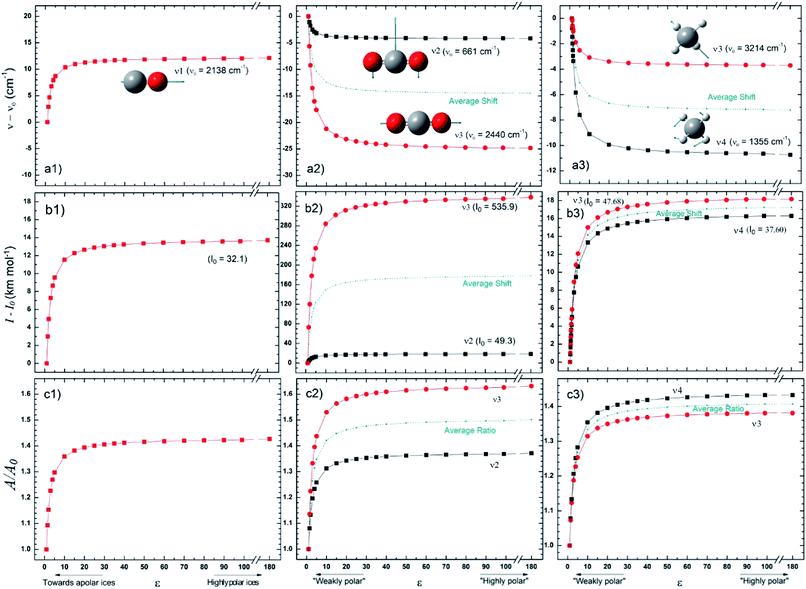
Fig. 2 presents the changes in the IR spectral features of the vibration modes of frozen CO, CO2 and CH4 molecules embedded in a solid matrix as a function of its dielectric constant ε displayed in three different views: (a) frequencies shifts, (b) intensities shifts and, (c) band strength ratio. The calculated values for ν0, I0, and A0 were performed considering ε0 = 1 (gas phase), as the reference. The results for these species clearly indicate that IR features seem to be much more dependent on the environment (expressed in terms of ε) for ε < 20 values. For dielectric constant higher than 50 it seems that band strength ratio A/A0, as well as band location and band intensity lose their dependencies with dielectric constant.The wavenumber of the CO vibrational mode showed an increase – blueshift in frequency – of up to 12 cm−1 (∼1%) over the studied interval. The variation calculated for the intensity, in turn, was numerically similar, around 14 km mol−1, but much larger in relative terms, increasing more than 40% over I0 (or A0). Since CO has no other vibrational modes, those results shall be compared with CO2 and CH4 ones, the two apolar (non-polar) molecules also studied in this work. Comparing the frequency variations for the three molecules we see that only for CO it occurs in the same way as the matrix ε changes. Despite this differentiation, there is an almost quantitative agreement with the laboratory data from Karssemeijer et al.40 These authors reported a higher shift by 12 cm−1, comparing the stretching of CO molecules trapped in H2O ice with that observed in a lower ε (pure CO) chemical environment. On the other hand, there are also recent studies in which the authors argue there is an increase in the wavenumber also of CO embedded in a matrix formed from nonpolar molecules.41 The results for CO2 molecule are, on average, of the same range of frequency variation as those seen for CO, which does not hold for intensities, because mode ν3 for CO2 is much more intense. In addition, the wavelength variation profile thus agrees with that reported by Pilling et al.,3 assuming that ε has increased throughout his pure CO2 ice irradiation experiment. The other nonpolar molecule, CH4, was studied by Boogert et al.,42 in which the authors compared the characteristics of the ν4 mode for some different chemical environments. The same authors found no direct correlation between band position and dipole moment (or polarity) of the predominant molecule in the solid matrix. Nevertheless, they found that the wavenumber of ν4 is lower in solid methane (ε = 1.766) than in gas, which agrees with the trend observed from this work calculations.
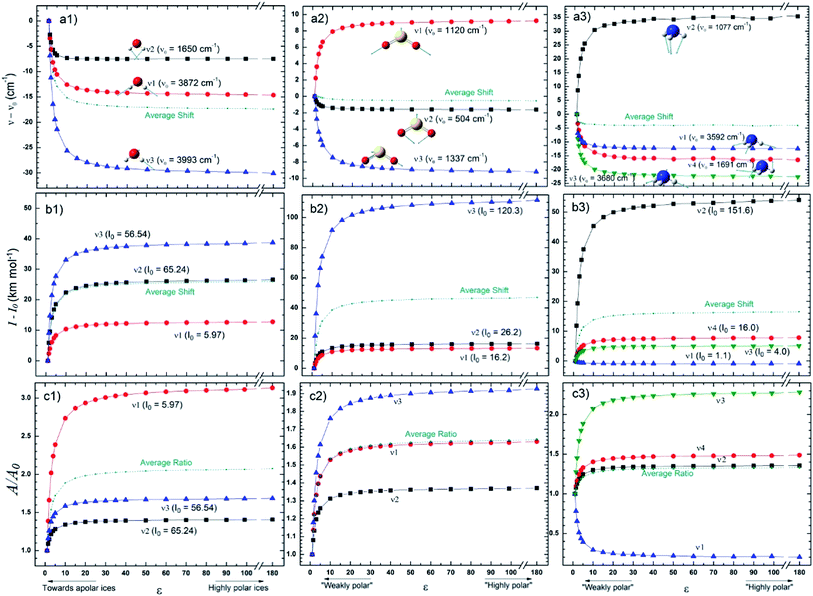
The changes in the IR spectral features of the vibrational mode of frozen H2O, SO2, and NH3 molecules embedded in solid matrix as a function of its dielectric constant is displayed in Fig. 3 at three different views: (a) frequencies shifts, (b) intensities shifts and, (c) band strength ratio. The calculated values for ν0, I0, and A0 were performed considering ε0 = 1 (gas phase), as the reference. In the case of water species ice we observed that all 3 studied vibrational modes decreases as the value of ε increases (more dramatic for ν3 vibrational mode). Curiously, some IR bands of SO2 and NH3 have different behavior as the dielectric constant increases, some bands presenting a blueshift and other ones a redshift. Additionally, some ammonia bands seem to be highly affected by the changes in ε (mainly between 5 < ε < 10), for example, the ν1 mode had a shift of about 35 cm−1 and the ν3 mode an opposite shift of roughly −22 cm−1 when compared with nominal values at gas phase. For ε > 50 it seems that the band center location is no more affected by the dielectric constant.
For the species shown in Fig. 3 the band intensities have presented and increase as function of dielectric constant (with the exception of ν1 of NH3). Curiously, some bands are much more sensitive to the dielectric constant (mainly between 5 < ε < 10) than others as the case of ν3 of SO2 (with an outstanding increase of roughly 120 km mol−1) and ν2 of NH3 (increase of roughly 55 km mol−1). These two bands, have also present the larger values of intensities calculated in the gaseous-phase and despite obvious explanation this might have some influence. The bands strengths ratio A/A0 (where A0 indicates the value calculated at gas-phase) presented in the panels c, indicate an clear increase with the dielectric constant (mainly below ε < 20) for the 3 frozen species H2O, SO2, and NH3 (with the exception of the ν1 NH3 vibration mode). As observed in Fig. 2, for ε > 50 (for highly polar ice matrix) it seems that the bands strengths ratio A/A0 lose its dependency with dielectric constant.
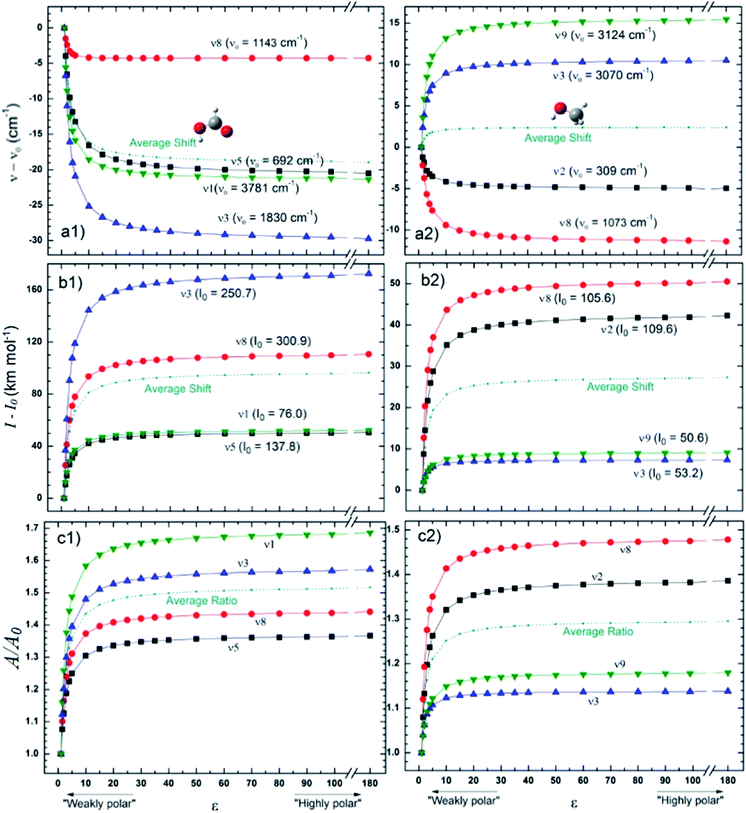
Fig. 4 presents the changes in the IR spectral features of the vibrational modes of frozen HCOOH and CH3OH molecules embedded in icy matrix as a function of its dielectric constant ε displayed in three different views: (a) frequencies shifts, (b) intensities shifts and, (c) band strength ratio. All the studied frequencies of HCOOH have presented a redshift (in comparison with the reference values at gas-phase) as the increasing of dielectric constant. For CH3OH, only the frequencies ν12 and ν8 have presented such behavior, the frequencies ν3 and ν9 have presented a blueshift (in comparison with the reference values at gas-phase) with the increasing of dielectric constant. The two molecules have the intensities of its infrared band enhanced when the species are embedded in icy matrix in respect with the values at vacuum. Such behavior also suggests the enhancement of band strength as the dielectric constant increases, as it is observed in the panel c1 and c2, for HCOOH and CH3OH, respectively.
Fig. 5 presents average changes in the IR spectral features of vibrational modes of studied frozen molecules embedded in icy matrix as a function of its dielectric constant ε. Panels a, b and c indicates frequencies shifts, intensities shifts and band strength ratio, respectively. The calculation considered ε0 = 1 (gas phase) for ν0, I0, and A0. Table 2 presents the employed parameters for the associative exponential that best fit the average dataset. From Fig. 5a we observe that the shift in frequencies due to the presence of dielectric medium was more enhanced for CO molecule (average blueshift effect as ε increases) and HCOOH molecule (average redshift effect as ε increases). In addition, two groups of molecules are identified: (i) the species that blueshift its vibration frequencies as ε increases such as CO and CH3OH, and (ii) the species the redshift its vibration frequencies as ε increases such as SO2 (slightly affected), NH3, CH4, CO2, H2O and HCOOH. Such blueshift/redshif behavior as dielectric constant increases is still a mystery and might be related with cavity effects of PCM ice model employed. Future investigation will help to clarify this effect. Fig. 5b shows the influence of dielectric constant on band intensities for the studied species. We observe clearly that the presence of medium increase the band intensities and this dependence with dielectric constant could be described by an associative exponential function. The most affected species was CO2 and the less affected was the embedded CO species.
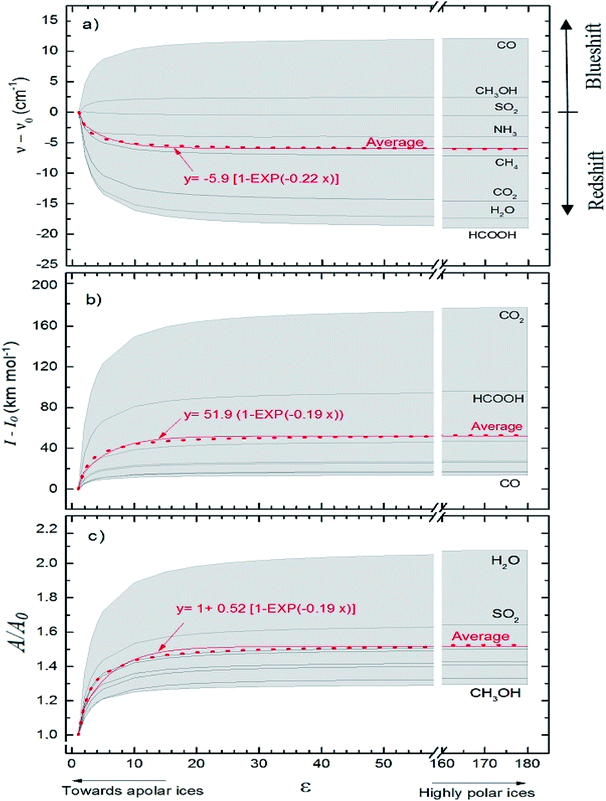 | ||
| Fig. 5 Average changes in the IR spectral features of vibrational modes of studied frozen molecules embedded in icy matrix as a function of its dielectric constant ε. Gas phase calculation is indicated by the data at ε = 1. (a) Frequencies shifts; (b) intensities shifts and (c) band strength ratio (considering ε0 = 1 (gas phase) for ν0, I0, and A0 calculations). The associative exponential that best fits the average dataset was also presented (see also Table 2). | ||
Curiously the average intensity of infrared bands of CO2 and HCOOH presents the higher enhancement with the increases of dielectric constant (indicating that such species might be easier to be detected in astrophysical environments in highly polar ices than in apolar ices). Fig. 5c shows the dependence on band strength ratio A/A0 as a function of the dielectric constant. The most affected species was the H2O embedded species and the less affected was the embedded CH3OH species. Considering the entire studied dataset, the band strength (the average value) of embedded species at dielectric constant of ε = 10 is 40% higher than the value calculated for the gaseous species or at ε ∼ 1. All panels in the Fig. 5 suggest that variation ε in apolar ices induce much more changes than variation of ε in polar ices (compared with the IR features in the gas-phase). This reinforces the concern on the effects of medium in the infrared properties of embedded species in space environments since its contain a variety of frozen species at different temperatures and porosity degrees.
3.2 Correlation between band strengths and band intensities
The band intensities observed in the infrared spectrum, as parameterized by the Lambert-beer law, is mainly related with the number of molecules (oscillators) in the line of sight and a quantum property related with the specific molecule (plus the vicinity) with take into an account how much the incoming radiation is affected by the molecular vibration in a given frequency (ruled by the band strength or A-value). In the current calculation, the infrared intensity (absorption) was determined by the amount of variation of the electric dipole, of a specific vibration mode, of a single molecular species embedded in an electric field descried by the given dielectric constant.The correlation between calculated band intensities (calculated at epsilon equal to 3, expected for cold ices at ∼10 K)43,44 with band strengths (taken from literature mostly at temperatures below 25 K) for the studied vibration modes (listed in Table 1) is shown in Fig. 6. The vertical lines over each black circle represents calculated values ranging from ε = 1 (for the gas-phase) to 180 (higher value in the figure). For the most part of the current studied vibration modes, the band intensities (I) is correlated with the band strength (A), in units of cm per molecule, by the linear function:
| I ∼ 6 × 1018 A [km mol−1 or D2 Å−1 u−1] | (2) |
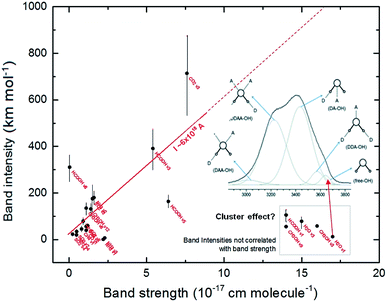 | ||
| Fig. 6 Correlation between calculated band intensities (calculated at epsilon equal to 3) and band strengths (taken from literature) for the studied vibration modes. The vertical lines over each black circle represents calculated values ranging from ε = 1 (for the gas-phase) to 180 (higher value in the figure). The values inside the box in right-bottom corner indicate the vibration modes in which the calculated intensities do not have a correlation with band strengths and might be related with molecular cluster within the ice. Figure inset with band profile is taken from Choe et al.46 and illustrates the influence of water molecular cluster in the H2O ν1 band. See details in text. | ||
However, for some vibration modes (e.g. H2O ν3 and ν1, HCOOH ν1 and CH3OH ν9) the calculated intensities does not follow the linear tendency described by eqn (2). These vibration modes have, in the literature, large value of band strengths (∼1.5 × 10−16 cm per molecule) and have presented very low values of calculated band intensities. One suggestion in attempt to explain such behavior might be the influence of the vibration of molecular clusters (molecules linked by hydrogen bonds) in the infrared band of ice associated with of such vibration mode. Such behavior might also be related with asymmetric band profiles of such vibration modes in the ices.45–48 The inset figure, with the spectrum profile, in the right part of Fig. 6 illustrates the influence of water molecular cluster in the H2O ν1 band of typical water ice or liquid (taken from Choe et al.46).
The current investigation shows that the PCM approach can be valid for ices with low dielectric constants (apolar ices, very cold ices or for porous ices). Whereas, if there are other bonding considerations that may alter the IR intensities or A-values then the PCM approach may not be valid (the species shown in the gray box of Fig. 6 are examples of these). Bennett et al.51 presented some examples of how PCM may be valid for ices of low dielectric values but did also note its failing for species such as H2O in some cases.
3.3 Overview of changes in band strengths compared with typical of cold ice as function of degree of polarity
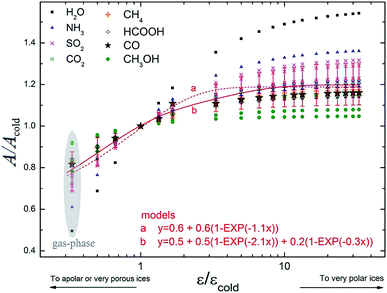
Fig. 7 presents the variation in the band strength of selected vibrational modes as a function dielectric constant normalized by its typical value for cold ice, characterized by a compact water-like matrix at 10 K (εcold = 3).28,43 As two of the studied molecules, methanol and formic acid, have much more complex IR spectrum than the other ones, the intensities shown in this figure correspond to the four most intense modes in vacuum, while simpler molecules had all modes presented. A special exception was made for the ammonia molecule, because it showed one vibration mode (∼3337 cm−1) with a decreasing behavior of A/Acold with the enhancement of ε/εcold, contrary to the other values in the dataset, and so it was omitted in order to facilitate visualization of the whole set of modes behavior. In this figure we also present two different models, employing associative exponential functions, that best fit the calculated dataset of band strengths ratio. The apolar (and porous ices) are indicated by ε/εcold < 1, very polar ices are expected to be at ε/εcold < 5–10. We observe in this figure a decrease up to 20% for the values of band strength towards very porous ices (or highly apolar) and an increase of 20% for polar ices in comparison with the typical value of compact cold ice at 10 K.The A/A0 value for the H2O symmetric stretching mode varied by more than 50% with the change from ε = 3.0 (expected for cold ices around 10 K; Tsekouras et al.;43 Ruepp44) to ε = 180 (expected for hot water-rich ices; Aragones et al.27). Considering that the determination of molecular abundances is highly dependent on the band strength, it is therefore very important to better precise such value (and its dependence with temperature, porosity degree and chemical environment) to obtain more accurate molecular abundances of astrophysical ices.
Finally, we would like to point out that besides the employ of PCM be a good approximation to simulate the effects solid/icy matrices around embedded species, there are some works in the literature that addressed some deficiencies of the this approach towards predicting IR intensities.49,50 Additionally, as pointed out by Bennett et al.51 the PCM approach would likely provide good estimates of the band intensities (and band strengths) in ices with low dielectric constants (apolar ices, very cold ices or porous ices), however if there are other bonding considerations that may alter the IR intensities or A-values then the PCM approach may not be valid, for example when molecular clusters might exist within the ice.
Finally, following the ideas of Bonfim and Pilling,28 the approach performed in the current work is likely to be better applicable to the very cold astrophysical ices where the dielectric constant is the dominant effect such as the case of apolar ices at very low temperatures (<50 K) and ices with some degree of porosity, and should be employed with caution for weakly-bounded very porous ices (ε ∼ 1) and very polar ices (ε ≫ 10).
4 Conclusions
In this work, we computationally simulate and investigate, through vibrational analysis, how the chemical environment influences some molecular properties in the IR spectra such as band position and intensities (linked with absorption cross section), of individual species embedded in the solid phase water-like matrix employing the Polarized Continuum Model (PCM) approach. The solid phase was simulated using different values of dielectric constant representing different types of matrix containing the studied molecules at PCM approach. The studied molecules employed in this research were CO, CO2, CH4, NH3, SO2, HCOOH, CH3OH and also H2O.Our main conclusions are listed bellow:
(i) In respect of frequency shift (in units of cm−1) two groups of molecules are identified: (1) molecular species that blueshift their vibration frequencies as ε increases such as CO and CH3OH, and (2) molecular species the redshift their vibration frequencies as ε increases such as SO2 (slightly affected), NH3, CH4, CO2, H2O and HCOOH. The shift in frequencies due to the presence of dielectric medium was more enhanced for CO molecule (average blueshift effect as ε increases) and HCOOH molecule (average redshift effect as ε increases).
(ii) We observe clearly that the presence of medium increases the band intensities and this dependence on dielectric constant could be described by an associative exponential function. The most affected species was CO2 and the less affected was the embedded CO species. Curiously the average intensity of infrared bands of CO2 and HCOOH presents the higher enhancement with the increases of dielectric constant (indicating that such species might be easier to be detected in astrophysical environments in highly polar ices than in apolar ices).
(iii) In respect of the dependence on band strength ratio A/A0 as a function of dielectric constant we observe that the most affected species was the H2O embedded species and the less affected was the embedded CH3OH species. The A/A0 value for the H2O symmetric stretching mode varied by more than 50% with the change from ε = 3.0 to ε = 180. Considering the entire studied dataset, the band strength (the average value) of embedded species at dielectric constant of ε = 10 is 40% higher than the value calculated for the gaseous species or at ε ∼ 1. The results also suggest that variation ε in apolar ices induce much more changes than variation of ε in polar ices. This reinforces the concern on the effects of medium (icy matrix) in the infrared properties of embedded species in space environments since it contains a variety of frozen species at different temperatures and porosity degrees.
(iv) A correlation between calculated band intensities with the band strengths (taken from literature) were determined and described by a linear function I ∼ 6 × 1018 A [km mol−1], with A in unity of cm per molecule. In addition, an associative exponential functions were adjusted to the studied datasets to characterize the evolution of frequency-shift and intensity-shift and band strength ratio as function of dielectric constant. We hope the tendencies and behavior that we pointed out here in this manuscript might be better characterized in future works employing high precision quantum chemistry calculation methods.
Considering that the determination of molecular abundances is highly dependent on the band strength and that it can be affected by the dielectric constant of the medium (molecular environment), this study helps us to better characterize solid samples in the infrared, specially, for astrophysical ices monitored by infrared observations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Brazilian agencies FAPESP (#JP2009/18304-0), CAPES and CNPq (#306145/2015-4; #302985/2018-2).References
- A. C. A. Boogert and P. Ehrenfreund, ASP Conf. Ser 309, Astrophysics of Dust, ed. A. N. Witt, G. C. Clayton and B. T. Draine, ASP, San Francisco, 2004, p. 547 Search PubMed.
- E. L. Gibb, D. C. B. Whittet and J. E. Chiar, Astrophys. J., 2001, 558, 702 CrossRef CAS.
- S. Pilling, E. Seperuelo Duarte, A. Domaracka, H. Rothard, P. Boduch and E. F. da Silveira, Astron. Astrophys., 2010, 523, A77 CrossRef.
- P. A. Gerakines, W. A. Schutte, J. M. Greenberg and E. F. van Dishoeck, Astron. Astrophys., 1995, 296, 810 CAS.
- O. Kerkhof, W. A. Schutte and P. Ehrenfreund, Astron. Astrophys., 1999, 346, 990 CAS.
- L. B. D'Hendecourt and L. J. Allamandola, Astron. Astrophys., Suppl. Ser., 1986, 64, 453 Search PubMed.
- P. A. Gerakines, J. J. Bray, A. Davis and C. R. Richey, Astrophys. J., 2005, 620, 1140 CrossRef CAS.
- D. M. Hudgins, S. A. Sandford, L. J. Allamandola and A. G. G. M. Tielens, Astrophys. J., Suppl. Ser., 1993, 86, 713 CrossRef CAS PubMed.
- D. Fulvio, B. Sivaraman, G. A. Baratta, M. E. Palumbo and N. J. Mason, Spectrochim. Acta, Part A, 2009, 72, 1007 CrossRef CAS PubMed.
- R. L. Hudson, P. A. Gerakines and R. F. Ferrante, Spectrochim. Acta, Part A, 2018, 193, 33 CrossRef CAS PubMed.
- R. L. Hudson, R. F. Ferrante and M. H. Moore, Icarus, 2014, 276, 287 Search PubMed.
- M. H. Moore, R. F. Ferrante, W. J. Moore and R. L. Hudson, Astrophys. J., Suppl. Ser., 2010, 191, 96 CrossRef CAS.
- K. I. Öberg, H. J. Fraser and A. C. A. Boogert, et al., Astron. Astrophys., 2007, 462, 1187 CrossRef.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117 CrossRef.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032 CrossRef.
- V. S. Bonfim, R. B. Castilho, L. Baptista and S. Pilling, J. Phys.: Conf. Ser., 2015, 635, 102012 CrossRef.
- V. S. Bonfim, R. B. Castilho, L. Baptista and S. Pilling, Phys. Chem. Chem. Phys., 2017, 19, 26906 RSC.
- J. Y. Park and D. E. Woon, J. Phys. Chem. A, 2004, 108, 6589 CrossRef CAS.
- S. Pilling, L. Baptista, H. M. Boechat-Roberty and D. P. P. Andrade, Astrobiology, 2011, 11, 883 CrossRef CAS PubMed.
- D. E. Woon and J.-Y. Park, Astrophys. J., 2004, 607, 342 CrossRef CAS.
- P. Ehrenfreund and S. B. Charnley, Annu. Rev. Astron. Astrophys., 2000, 38, 427 CrossRef CAS.
- P. Ehrenfreund and W. A. Schutte, Infrared Observations of Interstellar Ices, in Astrochemistry: From Molecular Clouds to Planetary Systems, Proceedings of IAU Symposium 197, ed. Y. C. Minh and E. F. van Dishoeck, 2000, p. 135 Search PubMed.
- R. Cammi and J. Tomasi, J. Comput. Chem., 1995, 16, 14498 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria and M. A. Robb, et al., Gaussian 09 (Revision B.01), 2010 Search PubMed.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- E. Silla, et al., Fundamental principles governing Solvents Use, in Handbook of Solvents, ed. G. Wypych, ChemTec Publishing, 2nd edn, 2014, pp. 11–72, ISBN 9781895198645, DOI:10.1016/B978-1-895198-64-5.50004-0.
- J. L. Aragones, L. G. Macdowell and C. Vega, J. Phys. Chem. A, 2011, 115, 5745 CrossRef CAS PubMed.
- V. S. Bonfim and S. Pilling, Proc. Int. Astron. Union, 2017, 13(S332), 346–352 CrossRef CAS.
- S. Pilling, E. S. Duarte, A. Domaracka, H. Rothard, P. Boduch and E. F. da Silveira, Phys. Chem. Chem. Phys., 2011, 13, 15755 RSC.
- B. Mate, in Infrared optical constants and Band Strengths of ices, Laboratory Astrophysics, Astrophysics and Space Science Library 451, ed. G. M. Munoz-Caro and R. Escribano, Springer, 2018, pp. 71–86, DOI:10.1007/978-3-319-90020-9_5.
- B. Schimitt, E. Quirico, F. Trotta and W. M. Grundy, in Optical properties of ices form UV to infrared, Solar System Ices, ed. B. Schmitt, et al., Kluwer Academic Publishers, Netherlands, 1998, pp. 199–204 Search PubMed.
- J. Bouwman and L. Wiebke, et al., Astronomy & Astrophysics, 2007, 476, 995 Search PubMed.
- K. I. Öberg, H. J. Fraser and A. C. A. Boogert, et al., Astronomy & Astrophysics, 2007, 462, 1187 Search PubMed.
- R. Luna and G. Molpeceres, et al., Astronomy & Astrophysics, 2018, 617, A116 Search PubMed.
- S. E. Bisschop, et al., Astronomy & Astrophysics, 2007, 470, 749 Search PubMed.
- M. Bouilloud, N. Fray, Y. Bénilan, H. Cottin, M. C. Gazeau and A. Jolly, Mon. Not. R. Astron. Soc., 2015, 451, 2145 CrossRef CAS.
- R. K. Khanna, G. Zhao, M. J. Ospina and J. C. Pearl, Spectrochim. Acta, Part A, 1988, 44, 581–586 CrossRef.
- M. Garozzo, D. Fulvio, O. Gomis, M. E. Palumbo and G. Strazzulla, Planet. Space Sci., 2008, 56, 1300–1308 CrossRef CAS.
- S. A. Sandford and L. J. Allamandola, Astrophys. J., 1993, 417, 815 CrossRef CAS PubMed.
- L. J. Karssemeijer, S. Ioppolo, M. C. van Hemert, A. van der Avoird, M. A. Allodi, G. A. Blake and H. M. Cuppen, Astrophys. J., 2014, 781, 16 CrossRef.
- A. C. A. Boogert, P. A. Gerakines and D. C. B. Whittet, Annu. Rev. Astron. Astrophys., 2015, 53, 541–581 CrossRef CAS.
- A. C. A. Boogert, W. A. Schutte, F. P. Helmich, A. G. G. M. Tielens and D. H. Wooden, Astron. Astrophys., 1997, 317, 929–941 CAS.
- A. A. Tsekouras, M. J. Iedema and J. P. Cowin, Phys. Rev. Lett., 1998, 80, 5798 CrossRef CAS.
- R. Ruepp, Physics and chemistry of ice. Papers presented at the Symposium on the Physics and Chemistry of Ice, Ottawa-Canada, 14–18 August 1972, ed. E. Whalley, S. J. Jones and L. W. Gold, Royal Society of Canada, Ottawa, 1973, pp. 179–86, ASIN: B007ETWNK0 Search PubMed.
- J. O. Daldrop, M. Saita and M. Heyden, et al., Nat. Commun., 2018, 9, 311 CrossRef PubMed.
- C. Choe, J. Lademann and M. E. Darvin, Analyst, 2016, 141, 6329 RSC.
- D. A. Schmidt and K. Miki, J. Phys. Chem. A, 2007, 111, 10119 CrossRef CAS PubMed.
- N. A. Chumaevskii and M. N. Rodnikova, J. Mol. Liq., 2003, 106, 167 CrossRef CAS.
- S. A. Katyuba, E. E. Zvereva and T. I. Burganov, J. Phys. Chem. A, 2013, 117, 6664 CrossRef PubMed.
- A. Gladney, C. Qin and H. Tamboue, Open J. Phys. Chem., 2012, 2, 117 CrossRef CAS.
- C. J. Bennett, P. Courtney and R. I. Kaiser, Astrophys. J., 2014, 782, 63 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |