Sr₉In(VO₄)₇ as a model ferroelectric in the structural family of β-Ca₃(PO₄)₂-type phosphates and vanadates

Abstract

Sr₉In(VO₄)₇ was prepared by a solid-state method at 1270 K in air. This vanadate has the β-Ca₃(PO₄)₂-type structure and crystallizes in polar space group R3c. The structural parameters of Sr₉In(VO₄)₇ were refined by the Rietveld method from laboratory powder X-ray diffraction data (XRD): the lattice parameters are a = 11.18016(9) Å and c = 39.6170(3) Å with Z = 6. In³⁺ cations occupy the octahedral M5 site, Sr²⁺ cations occupy the M1, M2, and M3 sites of the β-Ca₃(PO₄)₂-type structure, and the M4 site remains vacant. Sr₉In(VO₄)₇ was characterized by differential thermal analysis (DTA), optical second-harmonic generation (SHG), high-temperature XRD, and dielectric measurements. All these methods prove the existence of a ferroelectric–paraelectric phase transition at T_c = 974 K. This transition is compared with a similar transition in Ca₉In(PO₄)₇ with lower T_c = 902 K. The polar-to-centrosymmetric phase transition in such compounds has a quite unique mechanism of the order–disorder type. The structural transition involves slight shifts of the M1, M2, M3 cations and the E2O₄, E3O₄ tetrahedra, while half of the E1O₄ tetrahedra (E = P or V) statistically reverse their orientation along the three-fold axis, so that the centre of symmetry appears in the structure as a whole. To invert the E1O₄ tetrahedron, one oxygen anion should pass a large neighbouring cation (Sr²⁺ or Ca²⁺) that is only possible when intense rotational vibrations of the tetrahedra are excited at high temperatures. The lower Curie temperature in Ca₉In(PO₄)₇ corresponds to the smaller rotational vibration amplitude of the P1O₄ tetrahedron required to reverse this tetrahedra at T_c in comparison with V1O₄ in Sr₉In(VO₄)₇.

---

1 Introduction

Phosphates and vanadates with the β-Ca₃(PO₄)₂-type (β-TCP-type) structure¹ are of great interest now mainly due to their potential use as efficient phosphors in light-emitting diode (LED) devices.^2–6 They also have other interesting properties, such as being ferroelectric,^7–9 antiferroelectric,^10,11 nonlinear optical,^12–14 and catalytic,^15,16 and have properties related to bio-applications due to their biocompatibility.^17,18 They were suggested to be host materials for Tm³⁺ and Yb³⁺ luminescent ions in lasers including those with self-doubling frequency.^19,20

Ca²⁺ ions in β-TCP-type structure are located in five quite different positions. The M1, M2, and M3 sites are large sites with eight-to-nine oxygen coordination, the M5 site is a small octahedral site, and the M4 site is a very extended site or a cavity formed by 15 oxygen atoms.²¹ This unique structure allows different isovalent and aliovalent substitutions, including the introduction of a large strontium cation.²² The β-TCP-type materials with two- and three-valent luminescent ions, substituting for calcium in various positions, are very promising to be used together with light-emitting diodes (LED) in spectra-controlled luminous sources. As the incorporation of Sr²⁺ cations into the structure is usually accompanied by noticeable changes of luminescence spectra it is interesting to design Sr-based β-TCP-type structural analogues and compare their basic properties with known ferroelectrics, non-linear optical materials, calcium-ion conductors, and luminophores in the family of calcium-containing β-TCP-type phosphates and vanadates. The attempt is encouraged by the fact that in the solid solutions of β-Ca_3−xSr_x(PO₄)₂, Sr²⁺ replaces Ca²⁺ in a wide range of compositions with 0 ≤ x ≤ 16/7,²³ and this substitution leads to noticeable changes of the luminescent properties and symmetry. For example, emission color in Ca_3−xSr_x(PO₄)₂:Eu²⁺ changes from blue to green and to green-yellow.²⁴ In addition, as a result of changes in symmetry (R3c ↔ R3̄m) ferroelectric properties change to paraelectric.²³ In some cases, the luminescence intensity noticeably increases with strontium content, for example, in (Ca,Sr)₁₀Li(PO₄)₇:Ce³⁺, Mn²⁺, Eu²⁺.^25,26

In case of β-TCP-type phosphates, Ca- and Sr-containing phosphates are known with small substituting cations M²⁺/M³⁺, for example, Ca₉M(PO₄)₇ and Sr₉M(PO₄)₇ (where M = Al, Sc, Cr, Fe, Ga, and In),^27,28 Ca_9+xM_1.5−x(PO₄)₇,²³ Sr_9+xNi_1.5−x(PO₄)₇,²⁹ Sr_9+xCo_1.5−x(PO₄)₇,³⁰ and Sr₉Fe_1.5(PO₄)₇,³¹ and also with large rare-earth R³⁺ cations, for example, Ca₉R(PO₄)₇ (R = RE).³² On the other hand, in case of β-TCP-type vanadates, Ca- and Sr-containing vanadates are known only with large dopant rare-earth R³⁺ cations or Bi³⁺, for example, Ca₉R(VO₄)₇,³³ Ca_9−xSr_xBi(VO₄)₇,²¹ and Sr₉R(VO₄)₇ (R = Tm, Yb, and Lu).³⁴ These compounds are noncentrosymmetric and shows ferroelectric and non-linear optical properties. In this paper, we describe the first β-TCP-type vanadate containing small In³⁺ cation, Sr₉In(VO₄)₇. Calcium phosphates with a similar composition with small cations (Fe³⁺ or In³⁺) were previously obtained.^37,41 Phosphates Ca₉R(PO₄)₇ (R = Fe³⁺ or In³⁺) are ferroelectrics and a reversible ferroelectric/paraelectric phase transition is realized in their crystal structures. However, the phase transition mechanism in these phosphates has not been discussed. In present work we report on the synthesis, crystal structure refinement and description of new Sr₉In(VO₄)₇, its ferroelectric phase transition, and a detailed structural analysis of the order–disorder mechanism of the phase transformation.

2 Experimental section

Sr₉In(VO₄)₇ was prepared by a conventional solid state method from a stoichiometric mixture of SrCO₃ (99.99%), V₂O₅ (99.9%), and In₂O₃ (99.9%). All reagents were purchased from Sigma-Aldrich. The mixture was placed in an alumina crucible and first heated in 15 h to 923 K and annealed at 923 K for 30 h. Then the mixture was reground and annealed at 1073 K for 200 h with several intermediate grindings. Finally, the mixture was pressed into pellets and annealed on Pt foil at 1273 K for 100 h with several intermediate grindings. The obtained hard pellets and crashed powder were light yellow.

Laboratory powder X-ray diffraction (XRD) data for phase analysis and structure refinements were collected at room temperature (RT) and high temperatures (from 360 to 1190 K) on a Rigaku RINT 2500 diffractometer (40 kV, 300 mA) using CuK_α radiation (2θ range of 8–100°, a step width of 0.02° and a counting time of 1 s per step for phase analysis and high temperatures; 2θ range of 8–150°, a step width of 0.02°, and a counting time of 12 s per step for the structure analysis). Structure parameters were refined with the Rietveld method using Jana-2006.³⁵

Thermogravimetry (TG) and differential thermal analysis (DTA) were carried out in air on a MacScience TG-DTA 2000 instrument between 290 and 1273 K at a heating–cooling rate of 10 K min⁻¹ using a Pt holder. Three runs were performed to check the reproducibility. After TG-DTA experiments, the sample remained single-phased as examined with XRD.

Second-harmonic generation (SHG) responses of powder samples (grain size of about 3 μm) were measured in a reflection scheme using a Q-switch pulsed YAG:Nd laser operated at a wavelength, λ_ω, of 1064 nm. The SHG signals were registered in reference to α-SiO₂ (grain size 3–5 μm) kept at RT. Temperature dependence of the SHG signals of the sample was measured between 300 and 1000 K.

To measure the dielectric permittivity (ε) and loss tangent (tan δ) we used ceramic disks of Sr₉In(VO₄)₇, approximately 1 mm thick and 5 mm in diameter. Commercial Pt paste was put on both flat surfaces of the disks, and then they were heated to 923 K to produce metal electrodes. Temperature dependences of ε and tan δ were registered between 300 and 1070 K with computer-controlled ac-bridges R5083 and E7-12 at electric-field frequencies between 1 kHz and 1 MHz.

3 Results

3.1. XRD studies

The X-ray diffraction study at T = 293 K was carried out on the powder and ceramic samples. The XRD data on the powder and ceramic samples did not differ from each other. The structural parameters of Sr₉Lu(VO₄)₇ with space group R3c³⁴ were used as the initial ones in the structural refinement of Sr₉In(VO₄)₇. It has been confirmed that the M1, M2, and M3 sites are occupied solely by Sr²⁺ cations, the M5 site is occupied by In³⁺ cations, and the M4 site is vacant. A fragment of the experimental, calculated, and difference XRD patterns for Sr₉In(VO₄)₇ are given in Fig. 1. This figure also illustrates that the sample was single-phase. The final fractional coordinates and U values, final R factors, lattice parameters, and other refinement parameters are listed in Table S1 of the ESI.† Main interatomic distances, bond valence sums (BVS)³⁶ for Sr₉In(VO₄)₇ are listed in Table S2 of the ESI.†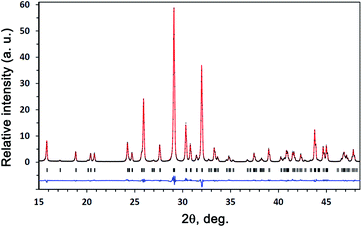

Fig. 1 A fragment of the experimental (black crosses), calculated (red line), and difference (blue line) XRD patterns for Sr₉In(VO₄)₇ at room temperature.

Fig. 2 shows the temperature dependence of the lattice parameters for Sr₉In(VO₄)₇. The phase transition is marked by discontinuity in all temperature dependences of a, c and V. The a lattice parameter demonstrates a drop at the phase transition temperature, while the c parameter shows a jump. The resultant unit cell volume shows a small drop at the phase transition temperature. In general, there is a slight increase in the cell volume of Sr₉In(VO₄)₇ (2.5%) upon heating from 297 K to 970 K. A similar increase in cell volume was also observed in Ca₉In(PO₄)₇ (2.7%).³⁷

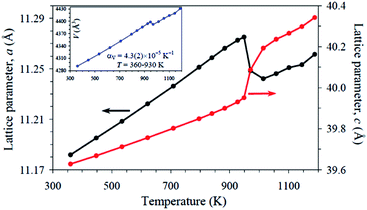Fig. 2 Temperature dependence of the a and c lattice parameters of Sr₉In(VO₄)₇. The inset shows temperature dependence of the unit-cell volume. α_V is the volumetric coefficient of thermal expansion.

3.2. DTA and TG measurements

A fragment (between 900 and 1000 K) of the heating/cooling DTA curves of Sr₉In(VO₄)₇ are given in Fig. 3. One peak was observed at 972 K (the position of the peak maximum) on heating and at 960 K (the position of the peak maximum) on cooling (Fig. 3), and a very good reproducibility was observed on heating/cooling cycling. This indicates that the phase transition is of the first order, and fully reversible. No other anomalies were detected on the DTA and TG curves between 290 and 1273 K.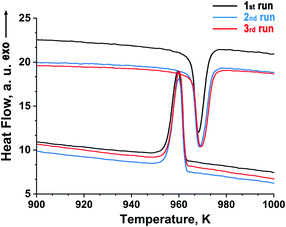

Fig. 3 Fragments of heating/cooling DTA curves of Sr₉In(VO₄)₇ (the heating/cooling rate was 10 K min⁻¹). Three heating/cooling cycles were run to verify the reproducibility.

3.3. Second-harmonic generation (SHG)

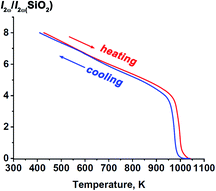
At room temperature, the SHG response from Sr₉In(VO₄)₇ powder was 8 times that of the SiO₂ standard powder sample, thus reliably indicating a noncentrosymmetric structure. Also, a noncentrosymmetric and polar structure was earlier established in Ca₉In(PO₄)₇.³⁷ The temperature dependence of the SHG signal of Sr₉In(VO₄)₇ is shown in Fig. 4. During heating up to ∼950 K the SHG signal decreases twofold almost linearly with temperature, and then it drops rapidly to null in between 950 and 970 K. Disappearance of the SHG indicates that above 970 K the structure becomes centrosymmetric. On cooling the SHG appears again and reaches the initial intensity with small temperature hysteresis. These results indicate the reversible nature of the phase transition in Sr₉In(VO₄)₇. One may conclude that gradual weakening of the SHG on heating indicates progressive changes in the crystal towards the centrosymmetric structure. The step-like disappearance of the SHG at T = T_c indicates an abrupt change in the crystal structure, that corresponds to the first-order phase transition between structures with- and without center of symmetry, respectively, in the high- and low-temperature regions.

Fig. 4 Temperature dependence of the SHG signal from Sr₉In(VO₄)₇ on heating and cooling.

3.4. Dielectric measurements

The temperature dependence of dielectric permittivity (ε) for Sr₉In(VO₄)₇ is shown in Fig. 5. Sharp peaks were observed on the ε(T) curves at 972 K (on heating) and 961 K (on cooling). The positions of maxima on the ε(T) curves were frequency independent. The positions of the anomalies on the ε(T) curves were close to the temperature positions of the DTA anomalies and to the temperature of the disappearance of the SHG signal. Similar maxima on dielectric constant are known to appear in both ferroelectric³⁷ and antiferroelectric^10,11 compounds. In the case of Sr₉In(VO₄)₇, the results of the dielectric measurements coupled with the results of the SHG measurements unambiguously prove that a ferroelectric-type phase transition takes place.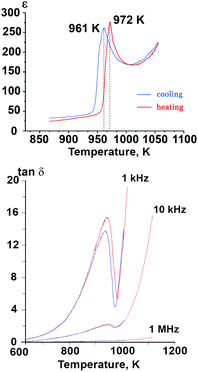

Fig. 5 Temperature dependence of dielectric constant (ε) at 300 kHz frequency and dielectric loss tangent (tan δ) in Sr₉In(VO₄)₇.

A further classification of ferroelectric phase transitions is possible using the Curie–Weiss law as discussed in ref. 38. With this approach, the inverse dielectric constant in a ferroelectric material can be approximated by a straight line above T_c, as it was done for Sr₉In(VO₄)₇ in Fig. 6. The slope of this linear approximation defines the Curie–Weiss constant, C_C–W. Values of C_C–W vary between 10³–10⁵ K for different ferroelectric materials. The lower values of C_C–W are typical for ferroelectrics with the “order–disorder” type of a ferroelectric transition, while the larger values of C_C–W (∼10⁵ K) are usually observed in ferroelectrics with the “displacive” mechanism of a ferroelectric transition. In case of Sr₉In(VO₄)₇ the estimated value of C_C–W = 1.35 × 10³ K corresponds to the “order–disorder” type of a ferroelectric transition. It means that a structural unit in Sr₉In(VO₄)₇ should have a strictly defined non-centrosymmetric position below the temperature transitions, while above this temperature it is ambiguously distributed in a number of positions. According to the available structural data, only the oxygen tetrahedral group E1O₄ (E = P or V) meets this requirement in the β-TCP-type ferroelectrics. The O11 atoms of the E1O₄ tetrahedra lie on the polar c axis and are all oriented along one direction below T_c, while above T_c half of the E1O₄ tetrahedra are randomly turned in the opposite direction.³⁷

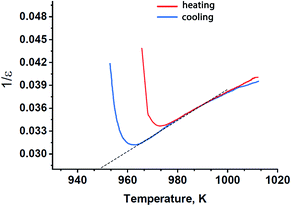Fig. 6 Reciprocal dielectric constant in Sr₉In(VO₄)₇ on heating and cooling with the Curie–Weiss fit in the high-temperature region (broken line).

4 Discussion

In Sr₉In(VO₄)₇ vanadate a reversible ferroelectric phase transition was detected at T_c = 974 K. In the isostructural phosphate Ca₉In(PO₄)₇ a similar, but less pronounced transition, was previously detected at T_c = 902 K.³⁷ Using high-temperature X-ray powder diffraction, electron diffraction and high-resolution electron microscopy it was shown that the ferroelectric-type transformation in Ca₉In(PO₄)₇ was realized between polar and centrosymmetry phases (R3c ↔ R3̄c).³⁷ As crystal structures and properties of Ca₉In(PO₄)₇ and Sr₉In(VO₄)₇ are very similar, we can assume that the symmetry change R3c↔ R3̄c also occurs in Sr₉In(VO₄)₇ at T_c = 974 K.

In the detailed consideration of structure–properties correlations in the β-TCP-type substances it is necessary to keep in mind that in the group of isostructural compositions Ca₉R(XO₄)₇ (X = P or V, and R – trivalent metal) the ferroelectric Curie temperatures, T_c, are 200–300 K regularly higher in the vanadates (1000–1220 K) in comparison with the phosphates (800–892 K).^8,9,39,40 This correlates with larger size of the V⁵⁺ cation and VO₄³⁻ tetrahedron as a whole against the P⁵⁺ cation and PO₄³⁻ tetrahedron, respectively. Evidently, the smaller size of PO₄³⁻ tetrahedra favors the decrease of the transition temperature in calcium phosphates versus calcium vanadates but does not explain the comparable transition temperatures in Ca₉In(PO₄)₇ and Sr₉In(VO₄)₇ (T_c = 902 and 974 K, respectively). Starting from the comparison of the crystal structure of Ca₉In(PO₄)₇ at room temperature and above T_c and the similarity of its RT crystal structures with that of Sr₉In(VO₄)₇ it is naturally to suppose that in these compounds all cations and anions (except oxygen atoms O11) are close to the centrosymmetric positions.³⁷ During the ferroelectric–paraelectric transition, all cations and V2O₄³⁻ and V3O₄³⁻ ions should only slightly shift. The largest changes occur in the V1O₄³⁻ position. The half of V1O₄³⁻ tetrahedra changes their orientation to the opposite.³⁷ Such overturn of the voluminous oxygen tetrahedron without changing the rest of the crystal lattice meets spatial obstacles which require more detailed consideration.

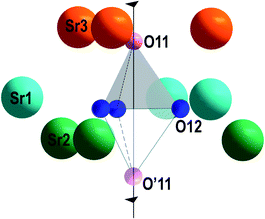
In β-TCP-type structure, the O11 oxygen atom (hereinafter the apical oxygen atom on the three-fold c axis) and E cation (E = P, V) are located in 6a site on the three-fold axis. Three other O12 oxygen atoms of the E1O₄ tetrahedron are connected by the three-fold axis (Fig. 7). In Sr₉In(VO₄)₇ structure, V1O₄³⁻ tetrahedron forms bonds with nine strontium cations (3Sr1 + 3Sr2 + 3Sr3) at distances d_Sr–O = 2.488–2.68 Å (Fig. 7). The apical O11 oxygen atom is connected with three Sr3 cations at distances 2.69 Å. Each O12 atom is connected with two strontium cations: Sr1 (d_Sr1–O12 = 2.68 Å) and Sr2 (d_Sr2–O12 = 2.488 Å). Also, there are three Sr3 cations at a longer distance (d_Sr3–O12 = 3.01 Å) from the O12 atom. A similar position of calcium cations around the P1O₄³⁻ tetrahedron is also realized in the structure of Ca₉In(PO₄)₇.³⁷ From the analysis it follows that the V1O₄³⁻ tetrahedron in β-TCP-type structure has a symmetric environment from the alkaline earth element cations in Sr3, Sr2 and Sr1 sites (Fig. 7).

Fig. 7 The environment of V1O₄³⁻ tetrahedron by Sr1, Sr2 and Sr3 cations in Sr₉In(VO₄)₇. Tetrahedron V1O₄³⁻ before (upper) and after (lower) rotation during the ferroelectric–paraelectric phase transition.

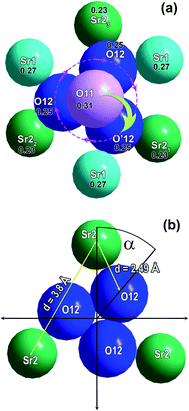
Nevertheless, with increasing temperature, such a tetrahedron changes its orientation to the opposite at ferroelectric–paraelectric phase transition temperature (Fig. 7). The distance between the two extreme positions of oxygen atoms on the three-fold axis in the polar O11 and nonpolar O′11 phases is ∼3.2 Å. Reversal of the V1O₄³⁻ tetrahedron may be achieved by simultaneous moving the O11 atom to the O′12 position, and the O′12 atom to the O′11 atom position (Fig. 8a). In this case, as a result of thermal vibrations, bonds between the Sr3–O11, Sr2–O12, and Sr1–O12 atoms should be broken. In any case, the O12 oxygens of V1O₄³⁻ tetrahedron have to overcome the bottleneck between the two neighboring cations Sr2₁–Sr2₂ (d = 3.8 Å) (Fig. 8b). If the O′12 oxygen atom moves in the direction of the O′11 position, then the Sr2₁ cation, which is slightly lower than the O′12 atom (Fig. 8a), impedes this movement. To overcome this obstacle, the O′12 atom must first shift toward the Sr2₂ cation and then toward the O′11 position (Fig. 8a). After such a shift, there are no obstacles to the movement of the O′12 atom to the O′11 position, and the O11 atom to the O′12 atom position (Fig. 8a). Such a displacement becomes possible only at high temperature, when the rotational vibrational mode of the oxygen tetrahedron rotates its base by some angle (α) (Fig. 8b). This angle will be sufficient for the passage of the oxygen between the two neighboring Sr2 cations (Fig. 8b). Similar transitions are also realized in the structure of Ca₉In(PO₄)₇.

Fig. 8 The O1 and O12 oxygen atom displacement scheme of the V1O₄³⁻ tetrahedron during a ferroelectric/paraelectric phase transition (a). Inside the atoms, their z-axis heights are given. The arrows on the circle indicate the possible movement of oxygen atoms O12. The required angle of rotation (α) of the O12–O12–O12 basis of the V1O₄³⁻ tetrahedron during phase transition (b).

The rotation through this angle α is sufficient to allow the oxygen O′12 atom of the tetrahedron to move in O′11 position. Its value depends on the crystal chemical sizes of the ions constituting the structure. At 297 K it is 38.1° for Ca₉In(PO₄)₇ and 38.9° for Sr₉In(VO₄)₇. Rotation at such an angle can be performed only with the accumulation of sufficient thermal energy of the tetrahedron: W_v ∼ k_BT. With increasing temperature, the amplitude of the rotational vibration of the tetrahedron is also rising. Moreover, the proximity of the α angles of phosphate and vanadate is consistent with their close values of the phase transformation temperatures, T_c. A little bit lower Curie temperature in the case of Ca₉In(PO₄)₇ agrees with slightly smaller angle of rotation of P1O₄ tetrahedron required to turning over this tetrahedra at T_c in comparison with V1O₄ in Sr₉In(VO₄)₇.

5 Conclusions

A new ferroelectric Sr₉In(VO₄)₇ was obtained, and its crystal structure was refined by the Rietveld method. It exhibits a ferroelectric–paraelectric phase transition at T_c = 974 K. In³⁺ cations occupy the octahedral M5 site, Sr²⁺ cations occupy the M1, M2, and M3 sites of the β-TCP-type structure, and the M4 site remains vacant. Sr₉In(VO₄)₇ was characterized by differential thermal analysis (DTA), optical second-harmonic generation (SHG), high-temperature XRD, and dielectric measurements. All these methods prove the existence of a reversible ferroelectric–paraelectric phase transition at T_c = 974 K. It has been suggested that a ferroelectric transition of the “order–disorder” type is realized in Sr₉In(VO₄)₇. A structural model of ferroelectric–paraelectric phase transition has been proposed.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by Russian Science Foundation (Grant 16-13-10340).

Notes and references

1. B. Dickens, L. W. Schroeder and W. E. Brown, J. Solid State Chem., 1974, 10, 232–248.
2. H. Ji, Z. Huang, Z. Xia, M. S. Molokeev, V. V. Atuchin, M. Fang and S. Huang, Inorg. Chem., 2014, 53, 5129–5135.
3. S. Liang, P. Dang, G. Li, M. S. Molokeev, Y. Wei, Y. Wei, H. Lian, M. Shang, A. A. Al Kheraif and J. Lin, J. Mater. Chem. C, 2018, 6, 6714–6725.
4. Y. Chen, Q. Guo, L. Liao, M. He, T. Zhou, L. Mei, M. Runowski and B. Ma, RSC Adv., 2019, 9, 4834–4842.
5. J. Qiao, Z. Xia, Z. Zhang, B. Hu and Q. Liu, Sci. China Mater., 2018, 61, 985–992.
6. Q. Zhang, X. Wang, X. Ding and Y. Wang, Dyes Pigm., 2018, 149, 268–275.
7. H. Ning, H. Yan and M. J. Reece, Ferroelectrics, 2015, 487, 94–100.
8. B. I. Lazoryak, A. A. Belik, S. Y. Stefanovich, V. A. Morozov, A. P. Malakho, O. V. Baryshnikova, I. A. Leonidov and O. I. Leonidova, Dokl. Phys. Chem., 2002, 384, 144–148.
9. B. I. Lazoryak, S. M. Aksenov, S. Y. Stefanovich, N. G. Dorbakov, D. A. Belov, O. V. Baryshnikova, V. A. Morozov, M. S. Manylov and Z. Lin, J. Mater. Chem. C, 2017, 5, 2301–2310.
10. A. A. Belik, V. A. Morozov, D. V. Deyneko, A. E. Savon, O. V. Baryshnikova, E. S. Zhukovskaya, N. G. Dorbakov, Y. Katsuya, M. Tanaka, S. Y. Stefanovich, J. Hadermann and B. I. Lazoryak, J. Alloys Compd., 2017, 699, 928–937.
11. D. V. Deyneko, V. A. Morozov, E. S. Zhukovskaya, I. V. Nikiforov, D. A. Spassky, A. A. Belik and B. I. Lazoryak, J. Alloys Compd., 2020, 815, 152352.
12. X. Hu, X. Chen, N. Zhuang, R. Wang and J. Chen, J. Cryst. Growth, 2008, 310, 5423–5427.
13. N. Zhuang, X. Liu, Q. Xu, X. Chen, B. Zhao, X. Hu and J. Chen, J. Alloys Compd., 2014, 595, 113–119.
14. S. Sun, L. Zhang, Y. Huang, Z. Lin and G. Wang, J. Cryst. Growth, 2014, 392, 98–101.
15. A. Legrouri, S. S. Romdhane, J. Lenzi, M. Lenzi and G. Bonel, J. Mater. Sci., 1996, 31, 2469–2473.
16. A. Benarafa, M. Kacimi, G. Coudurier and M. Ziyad, Appl. Catal., A, 2000, 196, 25–35.
17. M. Frasnelli and V. M. Sglavo, Acta Biomater., 2016, 33, 283–289.
18. R. K. Singh, M. Srivastava, N. K. Prasad, S. Awasthi, A. Dhayalan and S. Kannan, Mater. Sci. Eng., C, 2017, 78, 715–726.
19. Z. Zhang, P. Loiko, H. Wu, X. Mateos, J. M. Serres, H. F. Lin, W. D. Chen, G. Zhang, L. Z. Zhang, F. Díaz, M. Aguiló, V. Petrov, U. Griebner, Y. C. Wang, E. Vilejshikova, K. Yumashev and Z. B. Lin, Opt. Mater. Express, 2017, 7, 484.
20. H. Wu, F. Yuan, S. Sun, Y. Huang, L. Zhang, Z. Lin and G. Wang, J. Rare Earths, 2015, 33, 239–243.
21. A. P. Malakho, K. K. Kobyletskii, O. V. Baryshnikova, V. A. Morozov, S. Y. Stefanovich and B. I. Lazoryak, Russ. J. Inorg. Chem., 2003, 48, 1700–1712.
22. D. V. Deyneko, V. A. Morozov, J. Hadermann, A. E. Savon, D. A. Spassky, S. Y. Stefanovich, A. A. Belik and B. I. Lazoryak, J. Alloys Compd., 2015, 647, 965–972.
23. A. A. Belik, F. Izumi, T. Ikeda, V. A. Morozov, R. A. Dilanian, S. Torii, E. M. Kopnin, O. I. Lebedev, G. Van Tendeloo and B. I. Lazoryak, Chem. Mater., 2002, 14, 4464–4472.
24. B. Li, H. Zhang, A. Lan and H. Tang, Superlattices Microstruct., 2015, 86, 425–429.
25. X. Zhang, J. Xu, Z. Guo and M. Gong, Ind. Eng. Chem. Res., 2017, 56, 890–898.
26. J. Zhang, Z. Hua and S. Wen, J. Alloys Compd., 2015, 637, 70–76.
27. A. A. Belik, F. Izumi, T. Ikeda, M. Okui, A. P. Malakho, V. A. Morozov and B. I. Lazoryak, J. Solid State Chem., 2002, 168, 237–244.
28. S. Y. Stefanovich, A. A. Belik, M. Azuma, M. Takano, O. V Baryshnikova, V. A. Morozov, B. I. Lazoryak, O. I. Lebedev and G. Van Tendeloo, Phys. Rev. B, 2004, 70, 172103.
29. A. A. Belik, F. Izumi, T. Ikeda, A. P. Malakho and B. I. Lazoryak, J. Mater. Chem., 2002, 12, 3803–3808.
30. A. A. Belik, A. P. Malakho, P. S. Salamakha and B. I. Lazoryak, J. Solid State Chem., 2006, 179, 161–168.
31. A. A. Belik, B. I. Lazoryak, K. V. Pokholok, T. P. Terekhina, I. A. Leonidov, E. B. Mitberg, V. V. Karelina and D. G. Kellerman, J. Solid State Chem., 2001, 162, 113–121.
32. V. N. Golubev and B. I. Lazoryak, Russ J. Inorg Mater., 1991, 27, 480–483.
33. B. I. Lazoryak, L. O. Dmitrienko and S. V. Grechkin, Russ. J. Inorg. Chem., 1990, 35, 1095–1099.
34. A. A. Belik, M. Takano, M. V Boguslavsky, S. Y. Stefanovich and B. I. Lazoryak, Chem. Mater., 2005, 17, 122–129.
35. V. Petrícek, M. Dušek and L. Palatinus, Z. Kristallogr., 2014, 229, 345–352.
36. N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197.
37. V. A. Morozov, A. A. Belik, S. Y. Stefanovich, V. V. Grebenev, O. I. Lebedev, G. Van Tendeloo and B. I. Lazoryak, J. Solid State Chem., 2002, 165, 278–288.
38. F. Jona and G. Shirane, Ferroelectric crystals, Pergamon Press, 1962.
39. B. I. Lazoryak, D. V. Deyneko, S. M. Aksenov, S. Y. Stefanovich, E. A. Fortalnova, D. A. Petrova, O. V. Baryshnikova, M. B. Kosmyna and A. N. Shekhovtsov, Z. für Kristallogr. – Cryst. Mater., 2018, 233, 453–462.
40. A. V. Teterskii, V. A. Morozov, S. Y. Stefanovich and B. I. Lazoryak, Russ. J. Inorg. Chem., 2005, 50, 986–989.
41. B. I. Lazoryak, V. A. Morozov, A. A. Belik, S. Yu. Stefanovich, V. V. Grebenev, I. A. Leonidov, E. B. Mitberg, S. A. Davydov, O. I. Lebedev and G. Van Tendeloo, Solid State Sci., 2004, 6, 185–195.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10336h

---