Electronic transitions and ESIPT kinetics of the thienyl-3-hydroxychromone nucleobase surrogate in DNA duplexes: a DFT/MD-TDDFT study

Abstract

The fluorescent nucleobase surrogate M (2-thienyl-3-hydroxychromone fluorophore) when imbedded in DNA opposite an abasic site exhibits a two colour response highly sensitive to environment changes and base composition. Its two colour emission originates from an excited state intramolecular proton transfer (ESIPT), which converts the excited normal N* form into its T* tautomer. To get deeper insight on the spectroscopic properties of M in DNA duplexes, quantum chemical calculations were performed on M stacked with different base pairs in model trimers extracted from MD simulations. The photophysics of M in duplexes appeared to be governed by stacking interactions as well as charge and hole transfer. Indeed, stacking of M in DNA screens M from H-bonding with water molecules, which favours ESIPT and thus, the emission of the T* form. With A and T flanking bases, the electronic densities in the frontier MOs were localized on M, in line with its effective absorption and emission. In addition, reduction of the free rotation between the thienyl and chromone groups together with the shielding of the dye from water molecules largely explain its enhanced quantum yield in comparison to the free M in solution. By contrast, the localisation of the electron density on the flanking G residues in the ground state and the energetically favorable hole transfer from M to G in the excited state explains the reduced quantum yield of M sandwiched between CG pairs. Finally, the much higher brightness of M as compared to 2-aminopurine when flanked by A and T residues could be related to the much stronger oscillator strength of its S₀ → S₁ transition and the ineffective charge transfer from M to A or T residues.

---

Introduction

Site-specific fluorescent DNA labels are of high demand in order to sense DNA hybridization, conformation changes and activities of DNA-binding proteins and enzymes.^1–8 Valuable information can be obtained from these labels by analysing their fluorescence intensity, anisotropy, excited state lifetime and emission band position. Among the different types of fluorescent labels, the environment-sensitive ones that minimally perturb the structure and function of DNA are of upmost interest. As a typical example, 2-aminopurine (2AP) a popular adenine fluorescent analogue has been successfully used in a large range of applications. However, 2AP is limited by its extremely low quantum yield when incorporated in oligonucleotides (ODNs).⁹ This low quantum yield results from both static quenching due to electron delocalization in the ground state with weak oscillator strength and dynamic quenching through efficient non-radiative relaxation to a charge transfer state.^10,11

More recently, the 2-thienyl-3-hydroxychromone (3HC) dye (Fig. 1), referred to as M in this manuscript, has been introduced as a new nucleobase surrogate for DNA labelling, which could replace 2AP and other fluorescent nucleoside analogues.^{1,2,6–8,13,14} M is highly attractive because it is a rather flat molecule and its size corresponds well to the size of an AT or GC base pair. The excellent stacking properties of M with its neighboring base pairs as well as its preferential syn–anti conformation in DNAs were recently evidenced by NMR and MD simulations.¹⁵

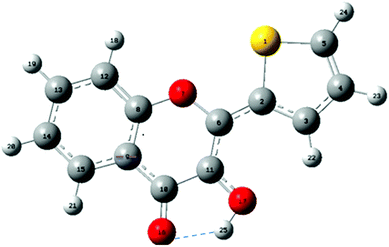Fig. 1 Structure and atom numbering of 2-thienyl-3HC (M). The intramolecular H-bond between O16 and H25 is drawn as a dashed line.

The spectroscopic properties of M in solvents and oligonucleotides (ODN) have also been extensively studied.^7,16–18 This dye undergoes an excited state intramolecular proton transfer (ESIPT) between the 3-hydroxyl and 4-carbonyl groups. As a result, M exhibits two fluorescent bands in the visible region that are sensitive to hydration and polarity; the short-wavelength band being attributed to the normal form (N*) and the long-wavelength band to the tautomer form (T*), the product of the ESIPT reaction.^7,11

The quantum yield (QY) of M in labelled ODNs⁷ is remarkably enhanced as compared to that of the free dye M when sandwiched by AT pairs. This increase in QY is accompanied by a strong decrease in the N*/T* intensity ratio (I_N*/I_T*) and a red shift of the T* band. The behaviour of M was noticeably different when sandwiched between CG pairs, showing a lower QY and a higher N*/T* intensity ratio. Interestingly, the QY of this probe is about 2–25-fold larger than that of 2AP in corresponding ODN sequences. Since M absorbs two times more, it thus appears up to 50-fold brighter than 2AP in ODNs.^11,18

In this work, the structural and spectroscopic properties of the ESIPT M dye as a free probe and included in M-containing trimers were investigated by combining quantum mechanics (QM) calculations and molecular dynamics (MD) simulations to understand how the electronic properties of M are influenced in DNA duplexes. A deeper insight in the photophysics of M in DNA is mandatory for interpreting protein/DNA interactions and designing new 3HC derivatives with optimized photophysical properties. MD and QM are powerful tools for unravelling the complex interplay between fluorescent nucleoside analogues or intercalating agents and DNA^19–21 and clarifying the contribution of the surrounding nucleotides to the photophysics of the fluorescent reporter. The MD/QM approach was applied with success to single band emitters such as 2AP and 8-vinyl-deoxyadenosine;^5,9,10 but to the best of our knowledge, application to a dual emissive fluorescent dye, such as the ESIPT dye M, is unprecedented. The most stable conformations of M in protic and aprotic media as well as in the ODN context were investigated. The absorption and emission wavelengths of M and the energy diagram of the different states that intervene in its photophysics were calculated by using the dispersion-corrected PCM-DFT and PCM-TDDFT. Calculations on M-containing trimers extracted from MD simulations frames were found to correlate well with previously reported experimental data of a series of 15-mer ODNs differing by the nature of the base pairs flanking the central M opposite an abasic site.

Computational details

In solution, the electronic properties of M were investigated by using a dispersion-corrected density functional theory²² at PBE0-D/TZVP level. The dispersion corrections are mandatory to correctly handle the electronic transitions with CT. The solvent effect was taken into account by the PCM solvation theory. The PBE0 functional was chosen because it gives a good performance in the calculations with H-bonding systems^23,24 and the prediction of vertical transition energies.^25,26 The TZVP basis set from the Ahlrichs group is well adapted for the investigation of nonbonding interactions and electronic properties of synthetic DNA nucleoside.²⁷ The transition state of M was optimised by a procedure developed by Ayala and Schlegel.²⁸ A similar procedure with different functionals and basis sets was also used by Yamazaki and Taketsugu.²⁹ To account for the impact of H-bonding in water, a complex of M in interaction with explicit water molecules was considered. The most stable conformation of M was then retrieved and used for the TDDFT calculation of the electronic transitions with the same hybrid functional and basis set. For our calculations, different 3-HC forms were considered in both ground and excited states. For each state, we considered the normal (N) and tautomer (T) forms, as well as their corresponding hydrated species (NH and TH). Taking into account that the ESIPT reaction (>10 ps) is much slower than the solvent relaxation processes (<1 ps),^30,31 we assumed that the ESIPT reaction occurs between solvent-relaxed excited states. All calculations were performed on g16.³²

In the DNA context, MD simulation was used to sample the possible conformations of the M labelled duplexes. Their photophysics was calculated by collecting an equilibrium MD simulation and then by post processing the resulting trajectory similarly to the work of Furse and Corcelli.³³ To obtain the labelled duplexes, we started from regular B-form duplexes with the sequence d(CGT TTT XMX TTT TGC) where X = A, T or C are the flanking bases of M. The complementary sequence contains the central motif YAbY, where Y = T, A or G corresponds to the base complementary to X and Ab is the abasic site opposite M. The duplexes were built starting with an AT central base pair by using the NAB module of AMBER14 package.³⁴ The central base A was manually replaced by the most stable ground state of M in water optimised at the D-PBE0/TZVP level. Finally, T opposite M was cut out, and only the sugar was left in order to obtain an abasic site and maintain the DNA double helix. The restrained electrostatic potential (RESP)^35–37 was used to derive the partial charges on M in the ground state in order to reproduce its DFT electrostatic potential. This approach was proven to satisfactorily describe dynamic processes in DNA.³³ The Na⁺ counter ions were placed around the ODNs to neutralise the negative charges of the phosphate backbone, and the whole system was solvated with a box of 10 Å TIP3 water molecules. The ff99SB force field was used for DNA natural bases, while the GAFF force field was used for M. Water molecules were energy minimized for 500 steps using the Steepest Descent algorithm (SD) and further 1500 steps using the Conjugate Gradient algorithm (CG), while keeping the solute as frozen. Then, the solvated solute was energy minimized for 1000 steps using the SD and 1500 steps using the CG before being heated from 0 to 300 K during 10 ps in the NVT (constant number of particles N, volume V and temperature T) ensemble, T is regulated via a Langevin thermostat. A density equilibration was carried out for 100 ps in the NPT (constant number of particles N, pressure P and temperature T) ensemble, before running the production of 100 ns MD trajectories in the ground state. Their structural parameters were obtained from web 3DNA program³⁸ and the relative enthalpy change ΔH values were calculated by solving the Poisson–Boltzmann equation (PBE) and the General Born Model (GBM) by using an approach combining MM energies with continuum solvent approaches commonly referred to as (MM-PBSA) and (MM-GBSA) for the two methods, respectively.^39,40 The wavelength positions of the N* and T* emissions were estimated by using the above mentioned functional and basis sets. The relative energy between these states was obtained from single point calculation on these structures.

Electronic transitions in duplexes generally occur between molecular orbitals (MOs) that are either localised on the fluorescent probe or delocalised on the flanking nucleobases.^10,11 As a consequence, the trimer supermolecule approach⁴¹ was adopted to predict the photophysics of M in the duplexes. For each considered duplex, a trimer composed of the central motif XMX + YAbY was excised in order to calculate the electronic transitions of M in a DNA. The dispersion corrected functional PBE0-D was used at this purpose to properly describe the stacking interactions that occur when M is embedded in a DNA duplex. To characterize the excited-state transitions, a localized orbital picture was used in which transitions were described as linear combinations of localized (excitonic) and intermolecular (CT) transitions. In the present study, we have focused the calculations only on singlet transitions that occur at low energy (E < 3.3 eV; λ > 350 nm).

Results and discussion

Calculation of the geometry and photophysics of free M in acetonitrile and water

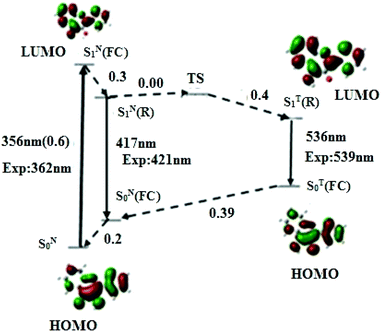
To rationalise the photophysics of M in DNA duplexes, we first investigated the electronic transitions and relative energies of its different states in the free (non-incorporated) dye in acetonitrile and water, taken as models of polar aprotic and protic media, respectively.

Representative geometric parameters obtained in acetonitrile from the DFT calculations at PBE0-D/TZVP level for the most stable conformation of M in its S₀ ground and relaxed S^N₁(R) and S^T₁(R) excited states, are given in Table 1. Though M adopts a planar conformation in both states, significant differences in the interatomic distances can be observed between the two states. The most prominent are the shortening of the C(2)–C(6) bond joining the thienyl ring to the chromone and the C(11)–O(17) bond of the hydroxyl group by 0.04 and 0.03 Å, respectively, as well as the lengthening of the C(6)–C(11) bond by 0.04 Å. Noticeably, the affected bonds are consecutive. This behaviour suggests an electron delocalisation from the thienyl ring and proton donor oxygen O17 to the proton acceptor O16, as already mentioned in other 3HC derivatives.⁴² This electron delocalisation is thought to render O17H more acidic (as supported by the Mulliken charge variation, Δq = +0.06 a.u) and O16 more basic (Δq = −0.06 a.u), thus favouring the ESIPT. Interestingly, the distance between the transferring proton and the carbonyl oxygen is 1.976 Å, thus supporting the formation of an intramolecular H-bond (Fig. 1) which is known to facilitate the proton transfer from the donor O(17) to the acceptor O(16). The excited T* form shows a remarkable shortening of the C(11)–O(17) bond by 0.075 Å, and a lengthening of the C(10)–O(16) bond by 0.092 Å, which are involved in the proton transfer process. The geometry modifications between N* and T* forms indicate that M undergoes structural rearrangement during the ESIPT process. PCM-TDDFT calculations with the PBE0-D functional on the TZVP optimised geometry further predict the S₀ → S₁ absorption peak (and oscillator strength) at 356 nm (0.6), the N* emission band at 417 nm, and the T* emission at 536 nm, respectively (Fig. 2). The predicted transitions are close to the previously reported experimental values.¹²

Table 1 Bond length and bond angle of M in its ground state and first relaxed excited state in the normal and tautomer forms obtained from DFT and TDDFT calculations at PBE0-D/TZVP level in bulk acetonitrile

Bonds	Bonds lengths			Angles	Bonds angles
	S0	S^N1(R)	S^T1(R)		S0	S^N1(R)	S^T1(R)
S(1)–C(2)	1.740	1.768	1.764	C(2)–S(1)–C(5)	91	91	91
S(1)–C(5)	1.717	1.720	1.718	S(1)–C(2)–C(3)	111	113	110
C(2)–C(3)	1.377	1.410	1.402	S(1)–C(2)–C(6)	119	120	119
C(2)–C(6)	1.437	1.390	1.395	C(3)–C(2)–C(6)	127	130	129
C(3)–C(4)	1.411	1.390	1.396	C(2)–C(3)–C(4)	113	113	112
C(4)–C(5)	1.364	1.383	1.377	C(3)–C(4)–C(5)	112	113	113
C(6)–O(7)	1.350	1.360	1.367	S(1)–C(5)–C(4)	112	114	112
C(6)–C(11)	1.374	1.405	1.433	C(2)–C(6)–O(7)	112	115	114
O(7)–C(8)	1.350	1.376	1.365	C(2)–C(6)–C(11)	126	127	126
C(8)–C(9)	1.394	1.410	1.413	O(7)–C(6)–C(11)	121	118	119
C(8)–C(12)	1.392	1.376	1.377	C(6)–O(7)–C(8)	121	122	122
C(9)–C(10)	1.450	1.428	1.400	O(7)–C(8)–C(9)	121	122	121
C(9)–C(15)	1.404	1.407	1.412	O(7)–C(8)–C(12)	117	116	116
C(10)–C(11)	1.440	1.452	1.433	C(9)–C(8)–C(12)	122	122	121
C(10)–O(16)	1.248	1.258	1.330	C(8)–C(9)–C(10)	119	119	117
C(11)–O(17)	1.344	1.314	1.262	C(8)–C(9)–C(15)	119	118	118
C(12)–C(13)	1.380	1.405	1.396	C(10)–C(9)–C(15)	122	123	124
C(13)–C(14)	1.405	1.390	1.393	C(9)–C(10)–C(11)	125	116	121
C(14)–C(15)	1.375	1.384	1.381	C(9)–C(10)–O(16)	116	128	122
				C(11)–C(10)–O(16)	121	116	116
				C(6)–C(11)–C(10)	121	123	118
				C(6)–C(11)–O(17)	119	123	124

---

Fig. 2 Energy levels and frontier molecular orbitals involved in the photophysics of M in acetonitrile, generated by PBE0-D/TZVP calculations. Upward arrow: absorption; downward arrow: emission; dashed arrow: non radiative relaxation. FC denotes the Franck–Condon state and R the relaxed excited states. The subscripts N and T denote the normal and tautomer forms, respectively. The radiative transitions energies are expressed in nm and non radiative transitions in eV.

The S₀ → S₁ excitation corresponds to the transition of one electron from HOMO (Highest Occupied Molecular Orbital) to LUMO (Lowest Occupied Molecular Orbital). In accordance with the above mentioned charge delocalisation, this transition is assigned to a ππ* character, featuring an appreciable charge displacement from the thienyl group to the rest of the molecule, as the Mulliken charge of this group obtained by PBE0-D/TZVP calculation varies from −0.49 a.u. in the ground state to +1.42 a.u. in the S₁ state. This assignment was further confirmed with M06-2X/TZVP calculation, taken as control method. Concomitantly, the magnitude of the molecular dipole moment varies from 3.94 D in the ground state to 7 D in the S₁ excited state. A charge displacement from an aryl group is common for ESIPT dyes,^42,43 and is responsible of the strongly increased dipole moment of N* as compared to N.⁴⁴

To understand the mechanism that governs the ESIPT reaction in acetonitrile, we have calculated the energies of the transition state (TS) and all the other states that likely intervene in the photophysics of M (Fig. 2). From the absorption and fluorescence energies given by the PBE0-D/TZVP calculation, and the 0.2 eV energy gap between S^N₀ and S^N₀(FC) obtained from a single point energy calculation, the energy gap between S^N₁(FC) and S^N₁(R) was estimated to be 0.30 eV. Moreover, the energy gap between S^N₁(R) and TS states, corresponding to the activation barrier to the ESIPT reaction, was estimated to be 0.00 eV. By using the TDDFT data on the T* form, an energy difference of 0.4 eV between S^N₁(R) and S^T₁(R) was obtained, indicating that S^T₁(R) is energetically favourable. Thus, the T* state is expected to be predominantly populated, in line with the experimental dominant contribution of the T* band to the emission spectrum (I_N*/I_T* = 0.13).¹¹ Taken together, our data suggest a very fast ESIPT reaction, facilitated by the absence of activation barrier, the relative low energy of the S^T₁(R) state with respect to S^N₁(R), and the pre-existing intramolecular H-bond.

The ESIPT reaction is an environment sensitive process, which is influenced by specific solute–solvent interactions like H bonding.^45,46 To examine how H-bonds with solvent affect the ESIPT reaction, we considered M in water. Only the first shell of solvent molecules was taken into account. The number of water molecules H-bonded to M was estimated from 100 ns of MD simulations. In this respect, the pair distribution function g(r) between the M carbonyl oxygen (Oa) and water oxygen (O) was plotted for the ground state (Fig. S1A†). g(r) measures the probability of finding O at a distance r from Oa, relative to that for an ideal gas. The g(r) curve presents a profile similar to that obtained experimentally for the O–O radial distribution of water oxygen atoms⁴⁷ (Fig. S1†), featuring strong peaks around 3 and 5 Å, attributed to the first and second solvent shells. The number n of water molecules in the vicinity of M in the first solvent shell was obtained from the area under the first peak of g(r) at 3.45 Å.⁴⁷ A value of 3.62 was obtained for n at the first minimum, indicating that about 3 water molecules are in the first solvent shell.

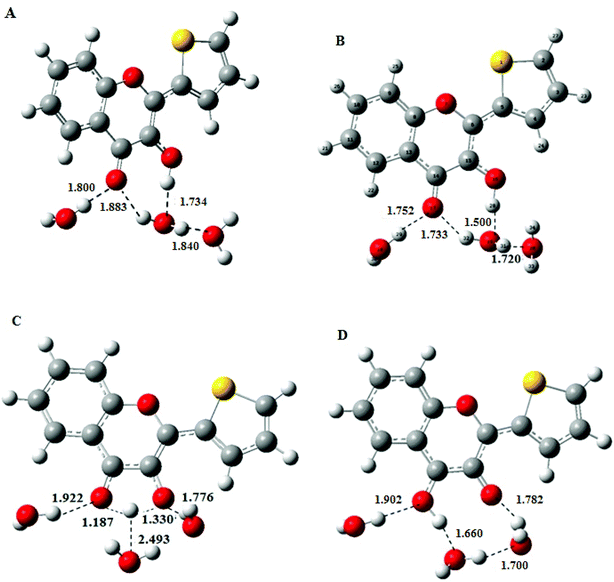
Consequently, a superstructure of M in complex with three water molecules was considered and optimised to obtain the most stable conformation of NH, the hydrated N form in the ground state, by using the DFT at PBE0-D/TZVP level. The geometry of NH retrieved from these calculations was further used as a starting structure in TDDFT calculations to obtain the geometry of the excited-state N*H and T*H complexes (Fig. 3B and D). Comparison of NH and N*H complexes (Fig. 3A and B) reveals that the conversion from NH to N*H is accompanied by a shortening of the intermolecular H-bond. Moreover, the transition state (Fig. 3C) is characterised by an appreciable lengthening of the distance between the transferring proton and the closest water molecule that increases from 1.50 to 2.493 Å. This result is consistent with the weakening or disruption of the intermolecular H-bond prior to the ESIPT reaction.^30,31

Fig. 3 Structure of the M-water complexes for (A) the normal NH form, (B) the relaxed N*H form, (C) the transition state and (D) the tautomer T*H form. The possible H-bonds and the interatomic distances (in Å) obtained from PCM-DFT PBE0-D/TZVP calculations are shown.

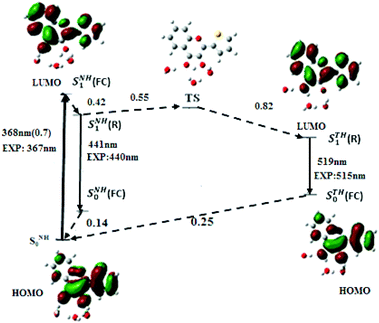
From the optimised geometries of NH and N*H and T*H complexes, the electronic transitions of M in water were calculated. As in acetonitrile, the PBE0-D functional along with the TZVP atomic basis set (Fig. 4) positions the S₀ → S₁ absorption maximum of NH in water at 368 nm (f = 0.7), and the N*H and T*H emission at 441 and 519 nm, close to the experimental values.¹² Our calculations further predict that the S₀ → S₁ transition arises from an electron promotion between HOMO and LUMO. Moreover, a comparison of M with the popular 2AP shows that the oscillator strength of S₀ → S₁ transition in M (0.7) is about five times that of 2AP (0.127), thus explaining the superior absorptivity of M in solution.¹¹

Fig. 4 Energy levels and frontier molecular orbitals involved in the photophysics of M in water, generated by PBE0-D/TZVP calculations. Upward arrow: absorption; downward arrow: emission; dashed arrow: non radiative transition. (FC) and (R) denote the Franck–Condon and relaxed excited states, respectively. The superscripts NH and TH denote respectively the hydrated normal and tautomer forms. The radiative transitions energies are expressed in nm and non radiative transitions in eV.

The solvatochromism observed on going from acetonitrile to water suggests that H-bonds and the dielectric constant play a major role in M photophysics. To distinguish the general solvent effects from specific solute–solvent effects, the electronic transitions of M were also calculated in bulk water. The positions of the lowest energy absorption band, and of the N* and T* emission bands obtained by PBE0-D/TZVP method are at 354, 424 and 540 nm, respectively. This shows that, the dielectric constant alone has a negligible effect on the absorption position maximum but dramatically affects the quality of the predictions for the positions of the emission bands as evidenced by the large shifts with respect to the experimental data (16 and 25 nm for the N* and T* bands, respectively). These results highlight the key importance of specific intermolecular H-bonding with water molecules to account for the photophysics of M in aqueous media, a behaviour already observed with other 3HC derivatives.⁴²

To get insight into the kinetics of the ESIPT reaction in water, the conformation and energy of the transition state (TS) were calculated. The energy of the TS state was found 0.55 eV above the S^NH₁(R) state, so that the activation barrier to the ESIPT reaction is very high. Nevertheless, ESIPT is thermodynamically favoured, as the emissive state of S^TH₁(R) is 0.27 eV below S^NH₁(R). From the energy diagram of M in water (Fig. 4), it may be inferred that after excitation from the S^NH₀ ground state, the S^NH₁(FC) relaxes to S^NH₁(R) and returns to the ground state by fluorescence emission or non-radiative process. However, a small population of M likely crosses the activation barrier and undergoes ESIPT to reach the S^TH₁(R) state, explaining the observation of the low energy emission band and the high value (1.72) of the experimental I_N*/I_T* ratio.⁷

Geometries of M-labelled DNA duplexes with an abasic site

To characterize M inserted in ODN duplexes, 100 ns of MD simulations were performed in the ground state. The nucleoside analogue, M connected to 2′-deoxyribose was analysed and geometrically optimized with the DFT. Starting from the main conformation of M in the duplex,¹⁵ the three other possible conformations differing by the torsion angles of the glycosidic bond and the thienyl group with respect to the chromone moiety were built on. The calculated energies of the four conformations (Fig. S2†) show that the syn–anti conformation is the most stable. Noticeably, this conformation was similar to the one adopted by M in the resolved NMR structure.¹⁵ To monitor the geometry convergence, the root-mean-square deviation (RMSD) of the duplexes with respect to the average structure along the MD trajectories was followed. In Fig. S3,† the RMSD of duplexes bearing M in its syn–anti conformation indicates that their structures were stable during the simulation, with a mean RMSD of 6, 5.5 and 5.2 Å respectively for AMA + TAbT, TMT + AAbA and CMC + GAbG duplexes. The average structures along the 100 ns MD simulations of these duplexes are presented in Fig. S4.† The obtained structures and structural parameters are very close to those of the normal B-form DNA (Tables S3 and S4†),⁴⁸ explaining the limited decrease of the thermodynamic stability of the M labelled duplexes. Finally, the radial distribution function g(r) (Fig. S5†) showed no significant peak, indicating that M is screened from water molecules in the ground state.

Next, the photophysics of M in each of the three duplexes was investigated using ten structures extracted each 10 ns of the 100 ns simulation. To calculate the behaviour of M in the excited state, we replaced the ground-state structure of M in each of the selected MD frame by the S^N₁(R), TS and S^T₁(R) structures obtained from DFT/TDDFT geometry optimisation of the free probe in water. Then, the XMX + YAbY trimers were excised from the duplexes obtained by MD calculations.

Electronic properties and transitions in DNA duplexes containing M and an abasic site

The average absorption electronic transitions wavelength calculated on the trimers extracted from MD simulations are reported in Table 2.

Table 2 Electronic transitions along with their MOs contributions, calculated by using the TDDFT at PBE0-D/TZVP level on 10 structures extracted each 10 ns from the 100 ns MD trajectories. H is the HOMO and L the LUMO

Sequence	Abs. (nm)	f	Transitions	Sequence	Abs. (nm)	f	Transitions	Sequence	Abs. (nm)	f	Transition
AMA + TAbT-1	366	0.37	H → L	TMT + AAbA-1	366	0.33	H → L	CMC + GAbG-1	409	0.016	H → L
									395	0.012	H−1 → L
									376	0.34	H−2 → L
AMA + TAbT-2	371	0.35	H → L	TMT + AAbA-2	369	0.36	H → L	CMC + GAbG-2	404	0.012	H → L
									394	0.016	H−1 → L
									370	0.33	H−2 → L
AMA + TAbT-3	367	0.38	H → L	TMT + AAbA-3	374	0.35	H → L	CMC + GAbG-3	419	0.004	H → L
									389	0.04	H−1 → L
									368	0.39	H−2 → L
AMA + TAbT-4	383	0.31	H → L	TMT + AAbA-4	383	0.41	H → L	CMC + GAbG-4	407	0.007	H → L
									388	0.022	H−2 → L
									367	0.37	H−1 → L
AMA + TAbT-5	386	0.27	H → L	TMT + AAbA-5	371	0.37	H → L	CMC + GAbG-5	412	0.03	H → L
									396	0.054	H−1 → L
									356	0.33	H−2 → L
AMA + TAbT-6	381	0.34	H → L	TMT + AAbA-6	377	0.33	H → L	CMC + GAbG-6	421	0.04	H → L
									413	0.01	H−1 → L
									357	0.35	H−2 → L
AMA + TAbT-7	373	0.36	H → L	TMT + AAbA-7	387	0.24	H → L	CMC + GAbG-7	417	0.006	H → L
									390	0.004	H−1 → L
									367	0.40	H−2 → L
AMA + TAbT-8	370	0.40	H → L	TMT + AAbA-8	382	0.3	H → L	CMC + GAbG-8	402	0.024	H → L
									383	0.01	H−1 → L
									346	0.14	H−2 → L
AMA + TAbT-9	375	0.37	H → L	TMT + AAbA-9	382	0.40	H → L	CMC + GAbG-9	407	0.024	H → L
									400	0.014	H−1 → L
									358	0.33	H−2 → L
AMA + TAbT-10	373	0.32	H → L	TMT + AAbA-10	370	0.25	H → L	CMC + GAbG-10	405	0.01	H → L
									390	0.0006	H−1 → L
									363	0.370	H−2 → L
Average value	375	0.35	H → L		376	0.31	H → L		410	0.018	H → L
									392	0.018	H−1 → L
									363	0.33	H−2 → L

---

M flanked with AT base pairs. Our PBE0-D/TZVP calculations revealed that the S₀ → S₁ absorption wavelength of the AMA + TAbT trimers was predicted at 375 nm (f = 0.35), close to the experimental value (377 nm). The average values of the N* and T* emission wavelengths, obtained with the same method were at 435 nm and 547 nm, respectively, very close to the experimental values of 437 and 542 nm, respectively. These data suggest that the geometry of M* in the DNA duplex is not markedly modified as compared to the most stable conformation of M* free in solution. The S₀ → S₁ transition arises exclusively from the promotion of one electron from HOMO to LUMO. The electron distribution in these two orbitals (Fig. 5A) was located on M in both ground and excited states, indicating that the MOs involved in M excitation were not perturbed by the two flanking base pairs. The calculated red-shift (7 nm) of this transition in comparison to M in water is in agreement with the experimental one (10 nm). This red-shift likely results from the interaction of M with the neighboring base pairs^1,49,50 that lowers the energy of M in the excited state and decreases the oscillator strength of the absorption band. The energy diagram (Fig. 5A) of the trimer revealed that the emissive S^T₁(R) state was lower in energy than S^N₁(R) by 0.27 eV and the energy barrier between the S^N₁(R) and TS states was low (0.13 eV). Both observations suggest a fast ESIPT process and an efficient accumulation of the T* state, in line with the low experimental intensity ratio (I_N*/I_T* = 0.07) of M in AMA + TAbT.

Fig. 5 Energy diagrams and frontier molecular orbitals involved in the photophysics of M in (A) AMA + TAbT, (B) TMT + AAbT and (C) CMC + GAbG trimers, as generated by PBE0-D/TZVP calculations. Upward arrow: absorption; downward arrow: emission; dashed arrow: non-radiative transition. (FC) and (R) denote the Franck–Condon and relaxed excited states, respectively. The superscripts N and T denote respectively the normal and tautomer forms. The radiative transitions energies are expressed in nm and non radiative transitions in eV.

M flanked with TA base pairs. PBE0-D/TZVP calculations predicted the S₀ → S₁ absorption in the TMT + AAbA trimers (Fig. 5B) to be at 376 nm (f = 0.31), in agreement with the experimental value (373 nm). This transition also received its major contribution from HOMO to LUMO, with the two orbitals located on M. Emission wavelengths of N* and T* were predicted at 424 and 547 nm, respectively. These values are in reasonable agreement with the experimental values (433 and 541 nm). Interestingly the FC absorption was very similar for AMA + TAbT and TMT + AAbA (375 nm and 376 nm) but the S₁ minima were not (435 nm and 424 nm). This behaviour is probably the consequence of nonbonding dispersive (induced dipole-induced dipole) interactions between A and M in the relaxed S₁ state when they stack, due to the relatively high molecular polarizability of A (purine) in comparison to T and C (pyrimidine), which is closely related to the number of conjugated π electrons. Indeed the molecular polarizability of M, A, T and C is respectively 25, 16, 10 and 11 ų dispersive interactions are attractive and thus contribute to the stabilisation of the S₁ state.

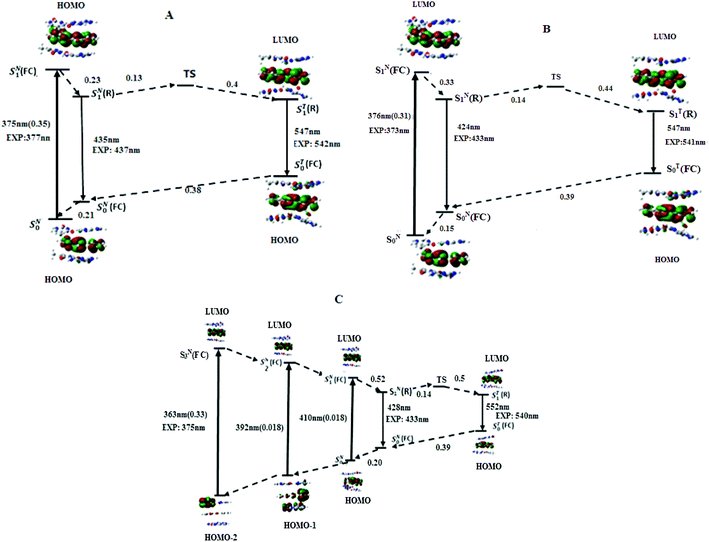
According to the energy diagram (Fig. 5B), S^T₁(R) was 0.30 eV below S^N₁(R) and the transition state TS was 0.14 eV above S^N₁(R). As for the AMA + TAbT trimer, the ESIPT reaction is thus expected to be fast and lead to an efficient accumulation of T*, in line with the low experimental value (0.08) of the I_N*/I_T* ratio.

M flanked with CG base pairs. When M was sandwiched between two CG base pairs in the CMC + GAbG trimer (Fig. 5C), the electronic transitions were predicted at 410 nm (f = 0.018), 392 nm (f = 0.018) and 363 nm (f = 0.33) for the S₀ → S₁, S₀ → S₂ and S₀ → S₃ singlet excitation, respectively. The S₀ → S₁ transition receives contribution from the promotion of one electron from HOMO to LUMO, while the S₀ → S₂ and S₀ → S₃ transition are due to one electron promotion from HOMO-1 to LUMO, and HOMO-2 to LUMO respectively. In HOMO and LUMO, the electron density was concentrated on M, while in HOMO-1 and HOMO-2, it was either partially or fully delocalised over one of the two guanines of the adjacent CG base pairs (Fig. 5C). According to the f values, the dominant electronic transition comes from the S₀ → S₃ transition, which has mostly G character in the ground state and M character in the excited state. This attribution is further substantiated by the predicted wavelength of the S₀ → S₃ transition that matched well with the experimental value of the absorption maximum (375 nm). Little fluorescence is expected from the S₃ → S₀ transition because of the mixed ground state configuration. The calculated emissions for N* (428 nm) and T* (552 nm) were also close to the experimental values (433 and 540 nm). The energy diagram (Fig. 5C) of the trimer revealed a 0.14 eV barrier opposed to ESIPT reaction and a 0.36 eV difference between S^N₁(R) and S^T₁(R). These values are close to those obtained with the two other trimers, in line with an efficient ESIPT reaction as well in this trimer and the low experimental I_N*/I_T* ratio (0.39).⁷

To get a deeper insight on the origin of the quenching of M when sandwiched by CG base pairs, its ionization potential IP (eV) and electronic affinity EA (eV) as well as the energies of HOMO and LUMO were calculated at the DFT/PBE0-D/TZVP level, using the adiabatic approach.⁵¹ 2AP as well as A, C, G, T were used as references for comparison (Table 3). The G HOMO appears higher in energy (0.05 eV, 4.8 kJ mol⁻¹) than the M and 2AP ones. As a result, the supermolecule HOMO is highly localized on the G.¹⁰ Moreover the IP of G (5.85 eV) is comparatively small as compared to M (5.93 eV), which may facilitate the hole transfer to this nucleobase during the excitation process. Another remarkable result is the very low energy level of the LUMO in M (−2.28 eV), as compared to 2AP (−1.1 eV) and other natural bases. This probably explains the localization of the LUMO on M in the CMC-GAbG trimer, and the photo-induced electron transfer (PET) from G to M in the excited state, further contributing to M quenching.

Table 3 Computed DFT/PBE0-D/TZVP adiabatic ionization potential, electronic affinity and HOMO and LUMO energy

Bases	IP (eV)	AE (eV)	HOMO (eV)	LUMO (eV)
Adenine	6.28	−1.17	−6.55	−0.71
Cytosine	6.71	−1.46	−6.96	−0.96
Guanine	5.85	−0.93	−6.23	−0.35
Thymine	6.70	−1.68	−6.99	−1.2
M	5.93	−2.64	−6.28	−2.28
2AP	6.05	−1.52	−6.28	−1.1

---

Our calculations can also rationalize the observed differences in the spectroscopic properties of 2AP and M in the same ODNs. In the T2APT trimer, the oscillator strength of the S₀ → S₁ transition is only 0.012 (ref. 9) and thus, 40-fold less than in the TMT trimer. In addition, the close energy level of the LUMOs in 2AP (−1.1 eV), T (−1.2 eV) and A (−0.71 eV) likely favours CT from 2AP to T or A, whereas in M the gap between the LUMOs of M (−2.28 eV) and T (−1.2 eV) or A (−0.71 eV) is higher than 1 eV, thus precluding CT to T. Altogether the superior oscillator strength in absorption and the unfavourable CT mechanism are consistent with the superior brightness of M when it is intercalated between A and T nucleobases in duplexes. In contrast, the higher ionisation potentials of M (5.93 eV) and 2AP (6.05 eV) as compared to G (5.85 eV) well explain the pronounced CT of both 2AP and M to G in the ground state, and thus, the low quantum yield of both probes when close to G.

Influence of thienyl torsional motion on M electronic transitions

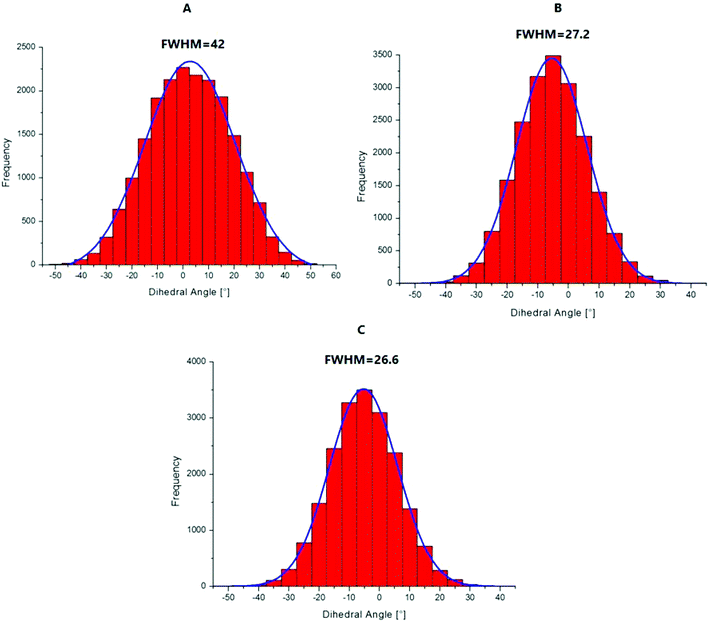
To explain the high quantum yield of M when flanked by AT and TA base pairs in DNA duplexes as compared to the free probe in solution,⁷ one likely hypothesis is that the DNA context restricts the rotation of the thienyl and chromone moieties of M around the C2–C6 single bond, thus favouring the radiative deactivation channel.¹³ To check this hypothesis, we examined the torsional motion of the two moieties by monitoring the dihedral angle formed by the C3, C2, C6 and C11 atoms during 10 ns of molecular dynamics in the ground state, both for the free probe and the probe in DNA. For the free probe, the rotational motion of the thienyl group around the C2–C6 bond is symmetrical and can be described by a Gaussian distribution with a full width at half maximum (FWHM) value of 42°. In the DNA context, the FWHM decreases to 27.2° and 26.6° for AMA + TAbT and TMT + AAbA, respectively (see Fig. 6). This restricted motion of the thienyl group favours a more planar conformation of M in the DNA, which increases the conjugation of the π electrons of the thienyl group with the rest of the molecule. This in turn is thought to increase the oscillator strength of the transitions localised on M and presenting a CT from thienyl. This increase in the oscillator strength accompanied by a concomitant red shift of the S₀ → S₁ wavelength position with a maximum for a fully planar conformation (dihedral angle of 0°) was clearly confirmed by our calculations (Fig. 7).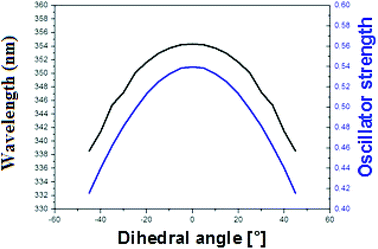

Fig. 6 Histograms of the distribution of the dihedral angle C3–C2–C6–C11 describing the torsional motion of the thienyl group with respect to the chromone moiety in the ground state for the free probe in solution (A), and for M in AMA-TAbT (B) and TMT-AAbA (C).

Fig. 7 Variation of the S₀ → S₁ wavelength position (black) and oscillator strength (blue) with the value of the dihedral angle C3–C2–C6–C11 in acetonitrile.

Conclusion

In the present study, the electronic transitions and the energy of the states involved in the absorption and emission processes of M free in solution and inserted in DNA were investigated. The most stable conformations of M were retrieved from DFT calculations for the free probe in solution and MD simulations for M in the DNA context, and further used to calculate the electronic transitions. The accessibility of the transferring proton to the surrounding water molecules was monitored by considering the pair radial distribution function in the ground and excited states. Taken together, our calculations show that ESIPT is slow in buffer because of a high energy barrier that results from the intermolecular H-bonding of both the transferring proton and acceptor oxygen with surrounding water molecules. This consequently disrupts the pre-existing intramolecular H-bond, which favours ESIPT. In the DNA context, the transferring proton of M is screened from H-bonding with water molecules by its flanking nucleobases in the ground state. The electronic properties of M were described using the trimer supermolecule approach. In AMA + TAbT and TMT + AAbA trimers, the electronic density in the frontier MOs was localised on M. In addition, the screening of M from water molecules and the prevention of free rotation between the thienyl and chromone groups probably decrease the non radiative pathways and hence increase the fluorescence quantum yield. The small energy barrier for the ESIPT process is consistent with an efficient accumulation of the T* state, in line with experimental fast ESIPT kinetics and low intensity ratio (I_N*/I_T*) of M. Differently, in the CMC + GAbG trimer, the electronic density was shifted to the neighbouring G in the ground state and localized to M in the excited state. The very low quantum yield observed for M in this trimer is probably the consequence of the mixed ground state configuration favouring hole transfer to G.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

C. A. K. acknowledges the Abdus Salam Inter-national Centre for Theoretical Physics (ICTP) for its support to CEPAMOQ through the OEA-AC-71 project and the High Performance Computing Center of the University of Strasbourg for supporting this work by providing scientific support and access to computing resources. Part of the computing resources was funded by the Equipex Equip@Meso project (Programme Investissements d'Avenir). YM and AB thank ANR Fluometadn, ANR Pico2 and the FRM for financial support. YM is grateful to the Institut Universitaire de France (IUF) for support and providing additional time to be dedicated to research.

References

1. A. S. Klymchenko, V. V. Shvadchak, D. A. Yushchenko, N. Jain and Y. Mély, J. Phys. Chem. B, 2008, 112, 12050.
2. V. V. Shvadchak, A. S. Klymchenko, H. de Rocquigny and Y. Mély, Nucleic Acids Res., 2009, 37, e25.
3. S. V. Avilov, E. Piémont, V. Shvadchak, H. de Rocquigny and Y. Mély, Nucleic Acids Res., 2008, 36, 885.
4. J. Godet, C. Kenfack, F. Przybilla, L. Richert, G. Duportail and Y. Mély, Nucleic Acids Res., 2013, 41, 5036.
5. C. A. Kenfack, E. Piémont, N. Ben Gaied, A. Burger and Y. Mély, J. Phys. Chem. B, 2008, 112, 9736.
6. A. A. Kuznetsova, N. A. Kuznetsov, Y. N. Vorobjev, N. P. F. Barthes, B. Y. Michel, A. Burger and O. S. Fedorova, PLoS One, 2014, 9, e10007.
7. D. Dziuba, V. Y. Postupalenko, M. Spadafora, A. S. Klymchenko, V. Guérineau, Y. Mély, R. Benhida and A. Burger, J. Am. Chem. Soc., 2012, 134, 10209.
8. W. Xu, K. M. Chan and E. T. Kool, Nat. Chem., 2017, 9, 1043.
9. N. Ben Gaied, N. Glasser, N. Ramalanjaona, H. Beltz, P. Wolff, R. Marquet, A. Burger and Y. Mély, Nucleic Acids Res., 2005, 33, 1031.
10. J. M. Jean and K. B. Hall, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 37.
11. J. M. Jean and K. B. Hall, Biochemistry, 2002, 41, 13152.
12. M. Spadafora, V. Y. Postupalenko, V. V. Shvadchak, A. S. Klymchenko, A. Burger and Y. Mély, Tetrahedron, 2009, 65, 7809.
13. R. W. Sinkeldam, N. J. Greco and Y. Tor, Chem. Rev., 2010, 110, 2579.
14. L. M. Wilhelmsson, Q. Rev. Biophys., 2010, 43, 159.
15. L. Zargarian, A. Ben Imeddourene, K. Gavvala, N. P. F. Barthes, B. Y. Michel, C. A. Kenfack, N. Morellet, B. René, P. Fossé, A. Burger, Y. Mély and O. Mauffret, J. Phys. Chem. B, 2017, 121, 11249.
16. V. Kilin, K. Gavvala, N. P. Barthes, B. Y. Michel, D. Shin, C. Boudier, O. Mauffret, V. Yashchuk, M. Mousli, M. Ruff, F. Granger, S. Eiler, C. Bronner, Y. Tor, A. Burger and Y. Mély, J. Am. Chem. Soc., 2017, 139, 2520.
17. D. Dziuba, J. A. Karpenko, N. P. F. Barthes, B. Y. Michel, A. S. Klymchenko, R. Benhida, A. P. Demchenko, Y. Mély and A. Burger, Chem.–Eur. J., 2014, 20, 1998.
18. (a) K. Gavvala, N. P. F. Barthes, D. Bonhommes, A. S. Dabert-Guy, D. Debayle, B. Y. Michel, A. Burger and Y. Mély, RSC Adv., 2016, 6, 87142; (b) S. Lobsiger, S. Blaser, R. K. Sinha, H.-M. Frey and S. Leutwyler, Nat. Chem., 2014, 6, 989.
19. T. Liu and J. K. Barton, J. Am. Chem. Soc., 2005, 127, 10160.
20. J. C. Genereux and J. K. Barton, Chem. Rev., 2010, 110, 1642.
21. T. Very, S. Despax, P. Hebraud, A. Monari and X. Assfield, Phys. Chem. Chem. Phys., 2012, 14, 12496.
22. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
23. B. Santra, A. Michaelides and M. Scheffler, J. Chem. Phys., 2007, 127, 184104.
24. B. Wang, W. Jiang and R.-Q. Zhang, Sci. Rep., 2016, 6, 22099.
25. D. Jacquemin, V. Wathelet, E. A. Perpete and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420.
26. D. Jacquemin, J. Preat, M. Charlot, V. Wathelet, J. M. Andre and E. A. Perpete, J. Chem. Phys., 2004, 121, 1736.
27. (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297; (b) J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305.
28. P. Y. Ayala and H. B. Schlegel, J. Chem. Phys., 1997, 107, 375.
29. S. Yamazaki and T. Taketsugu, Phys. Chem. Chem. Phys., 2012, 14, 8866.
30. R. Das, A. S. Klymchenko, G. Duportail and Y. Mély, Photochem. Photobiol. Sci., 2009, 8, 1583.
31. A. J. G. Strandjord and P. F. Barbara, J. Phys. Chem., 1985, 89, 2355.
32. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 16, Gaussian, Inc., Pittsburgh, PA, 2016, licence g16.
33. K. E. Furse and S. A. Corcelli, J. Chem. Theory Comput., 2009, 5, 1959.
34. D. A. Pearlman, D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham, S. De Bolt, D. Fergurson, G. Seibel and P. A. Kollman, Comput. Phys. Commun., 1995, 91, 1.
35. C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269.
36. P. Cieplak, W. D. Cornell, C. I. Bayly and P. A. Kollman, J. Comput. Chem., 1995, 16, 1357.
37. W. D. Cornell, P. Cieplak, C. I. Bayly and P. A. Kollman, J. Am. Chem. Soc., 1993, 115, 9620.
38. G. Zheng, X.-J. Lu and W. K. Olson, Nucleic Acids Res., 2009, 37, 240.
39. A. Onufriev, D. Bashford and D. A. Case, Proteins: Struct., Funct., Genet., 2004, 55, 383.
40. F. Fogolari, A. Brigo and H. Molinari, J. Mol. Recognit., 2002, 15, 377.
41. G. Ricciardi, A. Rosa, S. J. A. Van Gisbergen and E. J. Baerends, J. Phys. Chem. A, 2000, 104, 635.
42. C. A. Kenfack, A. S. Klymchenko, G. Duportail, A. Burger and Y. Mély, Phys. Chem. Chem. Phys., 2012, 14, 8910.
43. A. D. Roshal, J. A. Organero and A. Douhal, Chem. Phys. Lett., 2003, 379, 53.
44. N. A. Nemkovich, W. Baumann and V. G. Pivovarenko, J. Photochem. Photobiol., A, 2002, 153, 19–24.
45. A. P. Demchenko, K. C. Tang and P.-T. Chou, Chem. Soc. Rev., 2013, 42, 1379.
46. A. S. Klymchenko, C. Kenfack, G. Duportail and Y. Mély, J. Chem. Sci., 2007, 119, 83.
47. G. N. I. Clark, C. D. Cappa, J. D. Smith, R. J. Saykally and T. Head-Gordon, Mol. Phys., 2010, 108, 1415.
48. (a) V. A. Bloomfield, D. M. Crothers, and I. Tinoco Jr, Nucleic Acids, Structure, Properties, and Function, University Science Books, California, USA, 2000; (b) R. E. Dickerson, M. Bansal, C. R. Calladine, S. Diekmann, W. N. Hunter, O. Kennard, E. Von Kitzing, R. Lavery, H. C. M. Nelson and W. K. Olson, J. Mol. Biol., 1989, 205, 781.
49. A. East and E. C. Lim, J. Chem. Phys., 2000, 113, 8981.
50. I. Tinoco Jr, J. Am. Chem. Soc., 1960, 82, 4786.
51. E. Cauet, D. Dehareng and J. Liévin, J. Phys. Chem. A, 2006, 110, 9200.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10419d

---