B₁₂-containing volleyball-like molecule for hydrogen storage

Abstract

A stable core–shell volleyball-like structure of B₁₂@Li₂₀Al₁₂ has been proposed using first-principles calculations. This structure with T_h symmetry is constructed with a core structure of I_h-B₁₂ and a volleyball-like shell of Li₂₀Al₁₂. Frequency analysis and molecular dynamics simulations demonstrate the exceptional stability of B₁₂@Li₂₀Al₁₂. The chemical bonding analysis for B₁₂@Li₂₀Al₁₂ is also conducted to confirm its stability and 46 multi-center two-electron σ bonds are observed, which are widely distributed throughout the core–shell structure. For the hydrogen storage capacity of the B₁₂@Li₂₀Al₁₂, our calculated results indicate that about 58 H₂ molecules can be absorbed at most, leading to a gravimetric density of 16.4 wt%. The exceptionally stable core–shell volleyball-like B₁₂@Li₂₀Al₁₂ combined with its high hydrogen storage capacity indicates that it can be one of the outstanding hydrogen storage materials of the future.

---

Introduction

Since the experimental observation of C₆₀,¹ more and more attention has been paid to research of novel cage-like structures, including the Met-Cars,^2–4 hollow gold cages,^5–9 hollow boron cages,^10–17 hollow silicon cages with transition metals embedded^18–21 and so on. Recently, a volleyball-shape cage-like structure with an extremely high stability of Sc₂₀C₆₀, called “volleyballene”, was proposed.²² Soon after, another two new volleyballenes of Y₂₀C₆₀ and La₂₀C₆₀ were also reported.²³ The theoretical prediction of volleyballenes, on the one hand, enriches the cage-like structure library, and on the other hand, opens a new gate to construct other stable volleyball-shape structures.

Among all these cage-like structures, hollow boron cages have drawn our attention due to their unique electronic structure (multi-center two-electron bonds) and widespread potential applications in many fields. Up to now, a large variety of boron cages, like B₂₈,¹⁰ B₃₈,¹¹ B₃₉⁻,¹² B₄₀⁻ (ref. 13) and B₈₀,^14–16 has been theoretical identified. For the B₈₀ structure, it has been proved that core–shell structure (I_h-B₁₂ containing structure of B₁₂@B₆₈)¹⁶ has higher stability than the buckyball-like¹⁴ and volleyball-like¹⁵ structures. Besides, some other I_h-B₁₂ containing structures of B₈₄ and B₉₈–B₁₀₂ are also predicted to have high stability.¹⁷ For the icosahedral B₁₂, many early literatures have proved that most of the boron allotropes are mainly taking it as a building block. These boron allotropes, accompanied with the B-rich compounds composed by the icosahedral B₁₂, are often called boron-icosahedral cluster solids (B-ICSs).²⁴ Up to now, many B-ICSs have been proposed, such as boron nitride nanostructures,²⁵ B₁₂X₂ (X = As, P, O)^26–28 and boron carbide.²⁹ These results indicate that I_h-B₁₂ structure is one of promising building blocks to construct varieties of boron-based structures.

Nowadays, with the increasing energy shortage and environmental problems, searching for an alternate energy has become more and more emergent. Hydrogen is one of the promising candidates due to its wide distribution, renewables and environmental protection. However, how to storage hydrogen effectively is still an open problem. Compared with the hydrogen storage technologies of high pressure tank and liquid state storage, which are limited by the large size and weight of the tank and the high cost for liquefaction, the solid state storage has become a popular technology which can storage hydrogen by providing storage mediums and release it without changing the structure of mediums. A large amount of work has proved that carbon nanostructures (including carbon fullerenes, carbon nanotubes and graphyne), which decorated by the alkali metal atoms,^30–34 alkaline-earth metal atoms^35–38 and transition-metal atoms,^39–44 can be the promising hydrogen storage mediums. Similarly, boron nanostructures decorated by the metal atoms can also be applied in hydrogen storage. For example, researches have shown that B₈₀ fullerene decorated by the metal atoms, forming B₈₀M₁₂ (M = Na, K),⁴⁵ B₈₀Ca₁₂,⁴⁶ B₈₀Sc₁₂ (ref. 47) and B₈₀Mg₁₂,⁴⁸ can be applied in hydrogen storage. More recently, two types of I_h-B₁₂ containing structures of B₁₂@Mg₂₀B₁₂ (ref. 49) and B₁₂@Mg₂₀Al₁₂ (ref. 50) with high hydrogen storage capacities have been proposed. The widespread I_h-B₁₂ structures and the superior hydrogen storage performance of boron nanostructures functionalized by the metal atoms motivate us to investigate more metals-decorated I_h-B₁₂ structures and their hydrogen storage capacities.

In this paper, considering the wide existence of the I_h-B₁₂ structure in boron-based structure and the exceptional stability of volleyballenes, we constructed a new stable core–shell volleyball-like B₁₂@Li₂₀Al₁₂ structure. Different from the pentakis dodecahedron of B₁₂@Mg₂₀B₁₂ and B₁₂@Mg₂₀Al₁₂, the B₁₂@Li₂₀Al₁₂ with T_h symmetry has a volleyball-like shape, which is similar with the Sc₂₀C₆₀ volleyballene. We further investigated its stability by vibrational frequency analysis and molecular dynamics (MD) simulations. Besides, the chemical bond, which determines the structures and dynamics of molecules, was also explored by chemical bonding analysis to evaluate the stability of the B₁₂@Li₂₀Al₁₂. The interaction between H₂ molecules and the B₁₂@Li₂₀Al₁₂ was also investigated to measure the hydrogen storage capacity of B₁₂@Li₂₀Al₁₂.

Calculation details

In our calculations, the exchange–correlation potential was described by the Perdew–Burke–Ernzerhof version (PBE) of the general gradient approximation (GGA).⁵¹ The double-numerical basis plus polarized functions (DNP)⁵² was chosen without spin restrictions. The geometric optimizations were performed with unrestricted symmetry. The core electrons treatment was all-electron. For the MD simulations, we chose the NVE ensemble (NVE: number of particles N, volume V and energy E are constant) to carry out and the total time was 5.0 ps with a time step of 1.0 fs. As for the adsorption of hydrogen molecules on the core–shell B₁₂@Li₂₀Al₁₂, it is necessary to take the van der Waals (vdW) interactions, which are crucial for the formation, stability and function of molecules, into account. Here, we chose hybrid semi empirical dispersion-correction approach of Tkatchenko and Scheffler (TS) scheme⁵³ to describe the vdW interactions. In order to measure the effects of temperature on the hydrogen desorption, we also conducted the MD simulations for the B₁₂@Li₂₀Al₁₂ with H₂ absorbed using the NVT ensemble (NVT: number of particles N, volume V and temperature T are constant). The total time was 0.5 ps and the time step was 0.1 fs. The chemical bonding analysis via adaptive natural density partitioning (AdNDP) method⁵⁴ and localized orbital locator (LOL) were carried out in Gaussian 09 package.⁵⁵

Results and discussions

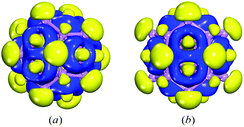
The core–shell volleyball-like B₁₂@Li₂₀Al₁₂ structure was constructed based on the icosahedral I_h-B₁₂ structure. As for the shell structure, it consisted of six Al₂Li₈ structures, forming the shape of a volleyball. After energy minimization, we got the stable core–shell volleyball-like B₁₂@Li₂₀Al₁₂ structure, as shown in Fig. 1. Taking further consideration into the relationship between core structure and shell structure, it can be found that 12 Al atoms are located above the center of 12 triangular faces of B₁₂ icosahedron, every Al atom connects with three B atoms in B₃ triangle. For the 20 Li atoms, there are two different positions: eight top locations above the center of the rest triangular faces of B₁₂ icosahedron (Li^I), every Li^I atom connects with three B atoms in B₃ triangle just like Al atom, and twelve top locations above the B atoms of the B₁₂ icosahedron (Li^II), every Li^II atom connects with one B atom. As for connections between Li and Al atoms, they can be classified as two types as shown in Fig. S1.† Besides, the detail construction process of the core–shell volleyball-like B₁₂@Li₂₀Al₁₂ is also given in Fig. S1, Tables S1 and S2† also list the average distances of all type of connections and the charge partitioning of the core–shell volleyball-like B₁₂@Li₂₀Al₁₂.

Fig. 1 The optimized core–shell volleyball-like B₁₂@Li₂₀Al₁₂ structure viewed from the structure line of the volleyball (a) and the top of the Al₂Li₈ subunit (b). The highlighted region represents one of the Al₂Li₈ subunits and six Al₂Li₈ subunits form the shell structure of Li₂₀Al₁₂. (Large ball: Li atom; small ball: Al atom; inside ball: B atom).

To explore the relative stability of the core–shell B₁₂@Li₂₀Al₁₂, we adjusted three different positions of the core B₁₂ icosahedron inside the Li₂₀Al₁₂; besides, we select some low-energy isomers during the MD simulations. After energy minimization, all the structures revert to core–shell volleyball-like B₁₂@Li₂₀Al₁₂ we proposed, as shown in Fig. S2,† indicating that the core–shell volleyball-like B₁₂@Li₂₀Al₁₂ is an energy minimum within the scope of our research.

Considering the similarity between the B₁₂@Li₂₀Al₁₂ and the B₈₀M₁₂ (M = Li, Na, Mg, K, Ca and Sc), the relative stability of them are compared by calculating the average adsorption energy of per metal atom (E_b) and corresponding results are listed in Table S3.† The higher value of E_b, the stronger interaction between metal atoms and B atoms. The calculated results indicate that the E_b of B₁₂@Li₂₀Al₁₂ is up to 2.78 eV, higher than the E_b of B₈₀M₁₂ (M = Li, Na, Mg, K and Ca), except for the extremely high value of E_b (4.06 eV) for B₈₀Sc₁₂. These results indicate that metal atoms have stronger connection with B atoms in B₁₂@Li₂₀Al₁₂.

Vibrational frequency analysis is conducted to check the kinetic stability of the core–shell volleyball-like B₁₂@Li₂₀Al₁₂. The frequency range is between 89.9 cm⁻¹ and 583.1 cm⁻¹ and no imaginary frequencies are found, indicating that this core–shell structure has good kinetic stabilities. Besides, we also list several vibrational frequency modes as shown in Fig. S3,† which can be used to evaluate the distribution of vibration of different atoms at different frequencies. We further simulated the Raman spectrum of the core–shell volleyball-like B₁₂@Li₂₀Al₁₂ and list several peaks, as shown in Fig. 2. This may provide a theoretical basis for future experimental synthesis and observation.

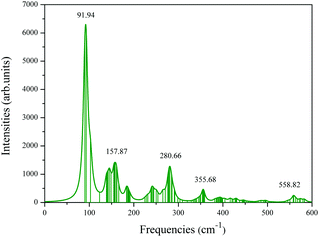Fig. 2 Simulated Raman spectrum for the core–shell volleyball-like B₁₂@Li₂₀Al₁₂. The assumed temperature and incident light are 300 K and 488.00 nm, respectively.

The thermodynamic stability of core–shell volleyball-like B₁₂@Li₂₀Al₁₂ was further checked by ab initio NVE MD simulations. The initial temperatures were set to be 1600 K, 1800 K, 2000 K and 2200 K, corresponding to the effective temperatures of 785 K, 876 K, 930 K and 993 K, respectively, as shown in Fig. S4.† It can be inferred that the core–shell volleyball-like B₁₂@Li₂₀Al₁₂ configuration can be well-kept during the simulations at 2000 K, corresponding to the effective temperature of 930 K. When the initial temperature increases, such as 2200 K, corresponding to the effective temperature of 993 K, the structure collapses and part of the inner B atoms appears in the shell structure.

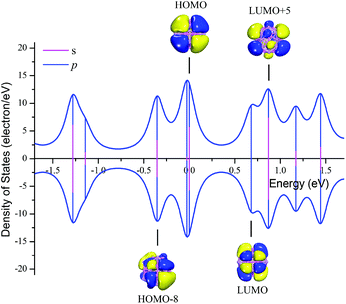
The deformation electron density (Fig. 3) and partial density of states (PDOS) (Fig. 4) were carried out to investigate the electronic structure of core–shell volleyball-like B₁₂@Li₂₀Al₁₂. The deformation electron density, which can be described as the difference between total cluster electron density and the electron density of isolated atoms, can be of great help in indicating the bonds formation. To be specific, the charge depletes on both Al and Li atoms; while the charge gathers into two rings on each Al₂Li₈ subunit rather than the bond position between two bonding atoms, indicating that there may be multi-center two-electron bonds. Further AdNDP analysis confirm that all the σ bonds found in B₁₂@Li₂₀Al₁₂ are multi-center two-electron bonds. As for the PDOS curve accompanied with some selected frontier molecular orbitals, it is found that the profile of HOMO orbital represents the characters of s–p hybridization, which is also coincident with the PDOS curve. The LUMO orbital is mainly composed of the 2p electrons from the Al atoms in the shell. Besides, both HOMO−8 and LUMO+5 orbitals represent the characters of s–p hybridization, which can also be proved by the PDOS curve.

Fig. 3 Deformation electron density viewed from the structure line of the volleyball (a) and the top of the Al₂Li₈ subunit (b) for the core–shell volleyball-like B₁₂@Li₂₀Al₁₂. Specifically, the blue and yellow parts present the charge accumulation and depletion respectively and the isosurface is set to be 0.01 e Å⁻³.

Fig. 4 Partial density of states (PDOS) for the core–shell volleyball-like B₁₂@Li₂₀Al₁₂. The positive and negative DOSs represent spin up and down, the magenta lines and blue lines represent s electrons and p electrons respectively. Some selected frontier orbitals corresponding to related orbital energy levels are also listed, with isosurface of 0.01 e Å⁻³.

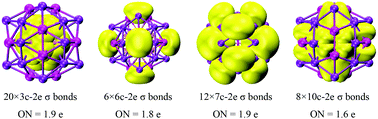
The chemical bonding analysis for core–shell volleyball-like B₁₂@Li₂₀Al₁₂ by AdNDP method is shown in Fig. 5. There are 92 valence electrons in total, forming 46 multi-center two-electron σ bonds. Of all the multi-center two-electron σ bonds, 20 three-center two-electron (3c-2e) σ bonds are observed on the icosahedral B₁₂; 6 six-center two-electron (6c-2e) σ bonds are observed among two inner B atoms, two outer Al atoms and two outer Li^II atoms; 12 seven-center two-electron (7c-2e) σ bonds are observed among one inner B atom, one outer Al atom and five outer Li atoms (two Li^I atoms and three Li^II atoms); 8 ten-center two-electron (10c-2e) σ bonds are observed among three inner B atoms, three outer Al atom and four outer Li atoms (every 10c-2e σ bond located on the region centered on Li^I atom with surrounding three Li^II atoms, three Al atoms and three inner B atoms). The fully covered σ bonds of the B₁₂@Li₂₀Al₁₂, which are also coincident with the characters of the localized orbital locator (LOL) as shown in Fig. S5,† are the powerful illustration of structural stability.

Fig. 5 Results of the chemical bonding characters by AdNDP methods for the core–shell volleyball-like B₁₂@Li₂₀Al₁₂. Of all 46 multi-center two-electron σ bonds, 20 three-center two-electron (3c-2e) σ bonds are observed on the core structure of icosahedral B₁₂, 6 six-center two-electron (6c-2e) σ bonds are observed among 2B–2Li–2Al, 12 seven-center two-electron (7c-2e) σ bonds are observed among B–5Li–Al, 8 ten-center two-electron (10c-2e) σ bonds are observed among 3B–4Li–3Al. Their occupied numbers are also listed.

Before evaluating the hydrogen storage properties of the B₁₂@Li₂₀Al₁₂, we research its stability under ambient conditions. For this purpose, we analysis the electron localization function (ELF) of B₁₂@Li₂₀Al₁₂ as shown in Fig. S5.† It can be concluded that electrons gather on both Li atoms and inner B atoms, indicating Li atoms have strong connection with B atoms. Besides, we also investigated the oxygen absorption of B₁₂@Li₂₀Al₁₂. The results indicate that O atom tends to be absorbed at the bridge position between Li^I and Al and connects with three Li atoms and one Al atom with an average adsorption energy of 1.10 eV. After O atom absorbed, the configuration of the B₁₂@Li₂₀Al₁₂ does not change, indicating O atom has little influence on the structure of B₁₂@Li₂₀Al₁₂, which can be proof of its stability under ambient conditions.

The interaction between the core–shell volleyball-like B₁₂@Li₂₀Al₁₂ and hydrogen molecules was investigated to explore the potential application in hydrogen storage. Several possible absorbed locations of H₂ molecule are given in Fig. S6,† corresponding distance of H₂ to the nearest metal atoms (d_H–M), adsorption energies (E_ad) and the desorption temperature (T_d) of H₂ molecule on the eleven specific adsorption locations are also listed in Table S4.† Here, the E_ad was defined as E_ad = E[B₁₂@Li₂₀Al₁₂(H₂)] − E(B₁₂@Li₂₀Al₁₂) − E(H₂) and the T_d was calculated using T_d = (E_ad/k_B)(ΔS/R − ln P)⁻¹ (Van't Hoff equation), where the E_ad = adsorption energy, k_B = Boltzmann constant, P = pressure (1 atm), R = gas constant and ΔS is the change in H₂ entropy from gas to liquid phase. It is found that all absolute values of adsorption energies of absorbed H₂ molecule on the eleven specific adsorbed locations lie in the range of 0.10–0.60 eV, which is flexible for hydrogen molecules to be absorbed and released. Especially, the adsorption energy of absorbed H₂ molecule on T₁ adsorbed location is up to −0.32 eV, corresponding to a desorption temperature of 408 K. Further analysis indicates that the existence of chemical bond between H₂ molecule and Li^II atom is the main contributor to high adsorption energy. The wide distribution of adsorbed locations suggests that the B₁₂@Li₂₀Al₁₂ may be the potential hydrogen storage material.

To further explore the chemical bonding properties between H₂ molecules and Li^II atoms, we evenly added 12 H₂ molecules on the top positions of 12 Li^II atoms, and calculated deformation electron density of the B₁₂@Li₂₀Al₁₂–12H₂ as shown in Fig. S7.† Besides, partial density of states (PDOS) of H atoms in 12 isolated H₂ molecules, H atoms in B₁₂@Li₂₀Al₁₂–12H₂, Al (Li) atoms in B₁₂@Li₂₀Al₁₂ and Al (Li) atoms in B₁₂@Li₂₀Al₁₂–12H₂ were also calculated and shown in Fig. S8.† From the deformation electron density, we can clearly observe that there are charge transfer from Li^II atoms to the H₂ molecules. The charge analysis indicates that every H atom gets 0.04 e on average. As for the PDOS curve, we can conclude from Fig. S8(a) and (b)† that the PDOS of H atoms in B₁₂@Li₂₀Al₁₂–12H₂ almost retains the same shape as that of 12 isolated H₂ even though being pushed to lower energy states. Besides, we also observed a tiny peak near Fermi level for the PDOS of H atoms in B₁₂@Li₂₀Al₁₂–12H₂, which further indicates that H atoms get electrons. The PDOS of Al atoms is basically unchanged after H₂ molecules absorbed, just as shown in Fig. S8(c) and (d),† indicating that there are no interactions between Al and H atoms. For Li atoms, at Fermi level, the PDOS of s electrons decreases to zero and the PDOS of p electrons also decreases after H₂ molecules absorbed. All the results are highly consistent with the results of charge analysis.

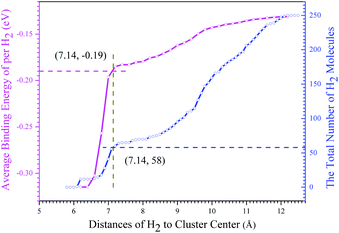
In order to further evaluate the hydrogen storage capacity of the core–shell volleyball-like B₁₂@Li₂₀Al₁₂, 250 H₂ molecules were placed around the structure. Subsequently, we counted the distances of different atoms to the cluster center and got the results as shown in Fig. 6 and 7. It can be clearly observed in Fig. 6 that H₂ molecules start to occupy the outer space at the distance of about 6.04 Å to the cluster center, corresponding to the distance of about 2.0 Å to the surface Li^II atoms, which is also consistent with chemical bond length (about 1.95 Å) between H₂ molecule and Li^II atom. The first layer of absorbed H₂ molecules ends at the distance of about 6.24 Å to the cluster center with 12 H₂ molecules absorbed by 12 Li^II atoms via forming chemical bonds, leading to a gravimetric density of 3.9 wt%. The average adsorption energy of per H₂ for the first layer of absorbed H₂ molecules is about −0.30 eV. Based on the Van't Hoff equation, the desorption temperature for the first layer of absorbed H₂ molecules is 402 K. The second layer of absorbed H₂ molecules is mainly distributed between 6.80 Å and 7.14 Å to the cluster center, about 0.83 Å to the first layer. The distance between the first and second layer of absorbed H₂ molecules is much shorter than the balance distance of two free H₂ molecules (about 2.70 Å), indicating that the absorption of the second layer of H₂ molecules is mainly from the B₁₂@Li₂₀Al₁₂, rather than the first layer of absorbed H₂ molecules. After the second layer of H₂ molecules being absorbed, there are about 58 absorbed H₂ molecules in total, with a gravimetric density of 16.4 wt%. The average adsorption energy of per H₂ is −0.19 eV, whose absolute value lies within the range of 0.1–0.6 eV; the desorption temperature is 242 K calculated by the Van't Hoff equation. As for the third layer of absorbed H₂ molecules, it is mainly distributed between 9.44 Å and 10.06 Å to the cluster center, about 2.78 Å (close to the 2.70 Å) to the second layer of absorbed H₂ molecules, which means that the absorbed H₂ molecules, not the cluster, absorb the third layer of H₂ molecules. Thus, about 58 H₂ molecules can be absorbed around the B₁₂@Li₂₀Al₁₂ with a hydrogen uptake of 16.4 wt% and an average adsorption energy of per H₂ of −0.19 eV, corresponding to a desorption temperature of 242 K.

Fig. 6 The statistical results of the distribution of different atoms to the core–shell volleyball-like B₁₂@Li₂₀Al₁₂ center. Specifically, the orange, magenta, violet and olive lines represent the number density of B atoms, Al atoms, Li atoms and H atoms, respectively. Besides, the distribution of the total number of H₂ molecules is also shown by the blue symbol line.

Fig. 7 Average adsorption energy of per H₂ (E_ad) and the distances of H₂ to the cluster center (d) for the core–shell volleyball-like B₁₂@Li₂₀Al₁₂ with 250 H₂ absorbed (E_ad = {E[B₁₂@Li₂₀Al₁₂(H₂)_n^6.0−d] − E(B₁₂@Li₂₀Al₁₂) − n × E(H₂)}/n). Here, we estimate the farthest distance of absorbed H₂ molecules to the cluster center, about 7.14 Å. The H₂ molecules whose distance to the cluster center lower than 7.14 Å can be considered as the absorbed H₂ molecules by the B₁₂@Li₂₀Al₁₂. Corresponding average binding energy of per H₂ and the total number of H₂ molecules are also marked.

After 58 H₂ absorbed by the B₁₂@Li₂₀Al₁₂, it is natural to investigate the mechanism of H₂ desorption. To this end, we conducted the MD simulations of the B₁₂@Li₂₀Al₁₂ with both 58 H₂ and 12 H₂ absorbed. We further counted the distances of the H₂ molecules to the cluster center and the results are shown in Fig. S9.† The H₂ molecules, whose distances to the cluster center are shorter than 7.14 Å, can be considered as being absorbed by the B₁₂@Li₂₀Al₁₂. Based on the statistical results, there are about 25 H₂ molecules absorbed by the B₁₂@Li₂₀Al₁₂ at the temperature of 300 K, leading to a gravimetric density of 7.8 wt%. As the temperature increases, such as 400 K and 500 K as shown in Fig. S9(a),† more and more H₂ molecules can be released and there are only 9 H₂ molecules being absorbed at the temperature of 600 K. In addition, we also investigated the desorption of the absorbed H₂ molecules in the first layer. The 12 H₂ molecules, which are absorbed by the B₁₂@Li₂₀Al₁₂ via forming chemical bonds with Li^II atoms, can also be released by heating. The results of MD simulations indicate that about 8 H₂ molecules can be still absorbed at the temperature of 300 K, while only about 3 H₂ molecules can be absorbed at the temperature of 600 K a shown in Fig. S9(b).†

Conclusions

In summary, we constructed a new stable core–shell volleyball-like B₁₂@Li₂₀Al₁₂ structure using the DFT calculations. The structure, which can be regarded as an icosahedron B₁₂ covered by a volleyball-like shell structure of Li₂₀Al₁₂, has a high symmetry of T_h. Calculation results demonstrate that the B₁₂@Li₂₀Al₁₂ has good kinetic stability and can maintain its original structure at the effective temperature of 930 K. The chemical bonding analysis of the B₁₂@Li₂₀Al₁₂ shows that the multi-center two-electron σ bonds exist all over the structure, which is of great importance for structural stability. The analysis in the hydrogen storage of the B₁₂@Li₂₀Al₁₂ indicates that about 58 H₂ can be absorbed by this structure with a gravimetric of 16.4 wt%, corresponding to an average adsorption energy of per H₂ of −0.19 eV, which is flexible for hydrogen molecules to be absorbed and released. All these outstanding results suggest that the new stable core–shell volleyball-like B₁₂@Li₂₀Al₁₂ structure may have potential application in hydrogen storage.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 11274089 and U1331116), the Natural Science Foundation of Hebei Province for Distinguished Young Scholars (Grant No. A2018205174), the Science Foundation of Hebei Education Department for Young Scholar (Grant No. QN2017086) and the Innovation Funding Project for Doctoral Students in Hebei Province (Grant No. CXZZBS2019080). We also acknowledge partially financial support from the 973 Project in China under Grant No. 2011CB606401.

References

1. H. M. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163.
2. J. S. Pilgrim and A. Duncan, J. Am. Chem. Soc., 1993, 115, 6958–6961.
3. B. C. Guo, S. Wei, J. Purnell, S. Buzza and A. W. Castleman Jr, Science, 1992, 256, 515–516.
4. S. Wei, B. C. Guo, J. Purnell, S. Buzza and A. W. Castleman Jr, J. Phys. Chem., 1992, 96, 4166–4168.
5. J. Li, X. Li, H. J. Zhai and L. S. Wang, Science, 2003, 299, 864–867.
6. M. P. Johansson, D. Sundholm and J. Vaara, Angew. Chem., Int. Ed., 2004, 43, 2678–2681.
7. D. Tian, J. Zhao, B. Wang and R. B. King, J. Phys. Chem. A, 2007, 111, 411–414.
8. A. J. Karttunen, M. Linnolahti, T. A. Pakkanen and P. Pyykkö, Chem. Commun., 2008, 465–467.
9. Y. Gao and X. C. Zeng, J. Am. Chem. Soc., 2005, 127, 3698–3699.
10. J. Zhao, X. Huang, R. Shi, H. Liu, Y. Su and R. B. King, Nanoscale, 2015, 7, 15086–15090.
11. J. Lv, Y. C. Wang, L. Zhu and Y. M. Ma, Nanoscale, 2014, 6, 11692–11696.
12. Q. Chen, W. L. Li, Y. F. Zhao, S. Y. Zhang, H. S. Hu, H. Bai, H. R. Li, W. J. Tian, H. G. Lu, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, ACS Nano, 2015, 9, 754–760.
13. H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731.
14. G. N. Szwacki, A. Sadrzadeh and B. I. Yakobson, Phys. Rev. Lett., 2007, 98, 166804.
15. X. Q. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 153409.
16. H. Li, N. Shao, B. Shang, L. F. Yuan, J. Yang and X. C. Zeng, Chem. Commun., 2010, 46, 3878–3880.
17. D. L. V. K. Prasad and E. D. Jemmis, Phys. Rev. Lett., 2008, 100, 165504.
18. H. Kawamura, V. Kumar and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 245433.
19. E. N. Koukaras, C. S. Garoufalis and A. D. Zdetsis, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235417.
20. J. Wang, Y. Liu and Y. C. Li, Phys. Chem. Chem. Phys., 2010, 12, 11428–11431.
21. J. Li, J. Wang, H. Y. Zhao and Y. Liu, J. Phys. Chem. C, 2013, 117, 10764–10769.
22. J. Wang, H. M. Ma and Y. Liu, Nanoscale, 2016, 8, 11441–11444.
23. J. Wang and Y. Liu, Sci. Rep., 2016, 6, 30875.
24. B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668.
25. J. Yin, J. D. Li, Y. Hang, J. Yu, G. A. Tai, X. M. Li, Z. H. Zhang and W. L. Guo, Small, 2016, 12, 2942–2968.
26. T. L. Aselage, D. R. Tallant and D. Emin, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 3122–3129.
27. D. Li and W. Y. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1451–1454.
28. S. Bakalova, Y. Gong, C. Cobet, N. Esser, Y. Zhang, J. H. Edgar, Y. Zhang, M. Dudley and M. Kuball, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075114.
29. M. M. Balakrishnarajan, P. D. Pancharatna and R. Hoffmann, New J. Chem., 2007, 31, 473–485.
30. G. E. Froudakis, Nano Lett., 2001, 1, 531–533.
31. Q. Sun, P. Jena, Q. Wang and M. Marquez, J. Am. Chem. Soc., 2006, 128, 9741–9745.
32. K. R. S. Chandrakumar and S. K. Ghosh, Nano Lett., 2008, 8, 13–19.
33. W. Liu, Y. H. Zhao, Y. Li, Q. Jiang and E. J. Lavernia, J. Phys. Chem. C, 2009, 113, 2028–2033.
34. C. R. Luna, P. Bechthold, G. Brizuela, A. Juan and C. Pistonesi, Appl. Surf. Sci., 2018, 459, 201–207.
35. M. Yoon, S. Yang, C. Hicke, E. Wang, D. Geohegan and Z. Zhang, Phys. Rev. Lett., 2008, 100, 206806.
36. H. Lee, J. Ihm, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115412.
37. S. Seenithurai, R. K. Pandyan, S. V. Kumar, C. Saranya and M. Mahendran, Int. J. Hydrogen Energy, 2014, 39, 11990–11998.
38. S. V. Hosseini, H. Arabi and A. Kompany, Int. J. Hydrogen Energy, 2017, 42, 969–977.
39. E. Durgun, S. Ciraci and T. Yildirim, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 085405.
40. B. Chakraborty, P. Modak and S. Banerjee, J. Phys. Chem. C, 2012, 116, 22502–22508.
41. Q. Sun, Q. Wang, P. Jena and Y. Kawazoe, J. Am. Chem. Soc., 2005, 127, 14582–14583.
42. P. Modak, B. Chakraborty and S. Banerjee, J. Phys.: Condens. Matter, 2012, 24, 185505.
43. A. Gangan, B. Chakraborty, L. M. Ramaniah and S. Banerjee, Int. J. Hydrogen Energy, 2019, 44, 16735–16744.
44. A. Yadav, B. Chakraborty, A. Gangan, N. Patel, M. R. Press and L. M. Ramaniah, J. Phys. Chem. C, 2017, 121, 16721–16730.
45. Y. C. Li, G. Zhou, J. Li, B. L. Gu and W. H. Duan, J. Phys. Chem. C, 2008, 112, 19268–19271.
46. M. Li, Y. F. Li, Z. Zhou, P. W. Shen and Z. F. Chen, Nano Lett., 2009, 9, 1944–1948.
47. G. F. Wu, J. L. Wang, X. Y. Zhang and L. Y. Zhu, J. Phys. Chem. C, 2009, 113, 7052–7057.
48. J. L. Li, Z. S. Hu and G. W. Yang, Chem. Phys., 2012, 392, 16.
49. H. Y. Zhao, L. Y. Ai, H. M. Ma, J. J. Guo, J. L. Qiu, J. Wang and Y. Liu, J. Phys. Chem. C, 2019, 123, 17639.
50. J. J. Guo, H. Y. Zhao, L. Y. Ai, J. Wang and Y. Liu, Int. J. Hydrogen Energy, 2019, 44, 28235–28241.
51. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
52. B. Delley, J. Chem. Phys., 1989, 92, 508–517.
53. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
54. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
55. G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G.-A. Petersson, et al., Gaussian 09, revision C.01, Gaussian, Inc., Wallingford, CT, 2010.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10491g

---