Open Access Article
Open Access ArticleNew wide-stability four-ring azo/ester/Schiff base liquid crystals: synthesis, mesomorphic, photophysical, and DFT approaches†
Nagwa H. S. Ahmeda,
Gamal R. Saad*b,
Hoda. A. Ahmed *b and
Mohamed Hagar
*b and
Mohamed Hagar c
c
aHigher Institute of Engineering and Technology, Department of Mathematics and Physical Science, New Cairo Academy, 5th Settlement, New Cairo City, Egypt
bFaculty of Science, Department of Chemistry, Cairo University, Giza 12631, Egypt. E-mail: grsaad@sci.cu.edu.eg; ahoda@sci.cu.edu.eg
cFaculty of Science, Chemistry Department, Alexandria University, Alexandria, Egypt
First published on 6th March 2020
Abstract
New four-groups-based azo/ester/Schiff base liquid crystals, ((4-substitutedphenylimino)methyl)phenyl 4-[2-(4-alkoxyhenyl)diazenyl]benzoate, Ina–d, were synthesized and analyzed for their mesomorphic stability and optical activity. In these compounds, a terminal alkoxy group of variable chain length from n = 6 to n = 16 carbons is attached to the end of a phenylazo benzoate moiety and the other end of the molecules is connected to a different polar compact substituent X (CH3O, CH3, H, and Cl). FT-IR, 1H NMR, mass spectroscopy and elemental analysis were carried out for molecular structure confirmation of the prepared compounds. The mesomorphic properties were confirmed using a combination of differential scanning calorimetry (DSC) and polarized light microscopy (PLM). The photophysical property was studied by UV-vis spectroscopy. All the prepared homologous series exhibited high thermal stability with a wide-temperature mesomorphic range. The thermal and geometrical parameters of the investigated compounds were estimated by density functional theory (DFT). The results revealed that all the compounds were not completely planar with a relatively high twisting moiety at the CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N part and their twist angles were affected by the electronic nature of the attached X group. Moreover, the calculated quantum chemical parameters as determined by the DFT approach of the investigated compounds were related to the experimentally determined values of the mesophase thermal stability (Tc) and mesophase temperature ranges (ΔTSmA and ΔTN) as well as the type of the mesophase.
N part and their twist angles were affected by the electronic nature of the attached X group. Moreover, the calculated quantum chemical parameters as determined by the DFT approach of the investigated compounds were related to the experimentally determined values of the mesophase thermal stability (Tc) and mesophase temperature ranges (ΔTSmA and ΔTN) as well as the type of the mesophase.
1. Introduction
Achievement of the proper characteristics for new device applications requires structure–activity relationship tools to design suitable materials.1–4 Optical devices and temperature/humidity sensors are important applications in the field of liquid crystal (LC) instrumentation.5–9 Thus, liquid-crystal molecular structures are constructed based on the factors and principles of anisotropic mesogenic shapes. To understand the relationship between the molecular geometry of mesogens and their mesomorphic properties, many Schiff base/ester liquid crystals based on two or three ring compounds have been investigated and their optical behaviors studied.10–14 Moreover, low molar mass liquid crystal compounds comprising just a single mesogenic unit1,15–17 exhibit behavior significantly different from molecules having two or more mesogenic groups.14,18–21 Thus, the addition of new mesogens or aromatic rings as well as different terminal substituents (compact group or alkoxy/alkyl chains) will impact the molecular geometry and offer wide thermal stability ranges of the designed materials.22 Further, slight changes in the molecular architecture can lead to considerable changes in the mesomorphic transitions and play an important role in the formation, type, and stability of the observed mesophase.14,18–20,23–28 Recently, the design of molecular deformation architectures that influence the mesophase formation have been studied,29–32 e.g., lattices with free space, fibers in the twist-bend nematic phase,33,34 and oligomers.1,35–37 Many of these studies have involved an investigation of the impact of the terminal groups on the phase-transition temperatures.38 Also, the incorporation of –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– linkages to rigid phenyl rings provides a stepped core shape and helps retain the linearity of the molecular structure. Thus, this can enhance the stability of the formed mesophases.39 Azo group (–N
N– linkages to rigid phenyl rings provides a stepped core shape and helps retain the linearity of the molecular structure. Thus, this can enhance the stability of the formed mesophases.39 Azo group (–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–) linkages can lead to marked changes in the photophysical and photochemical properties of such prepared materials. Consequently, in designing new thermotropic LCs with a mesogenic core, the terminal groups and a flexible chain are the essential specifications.40 To ensure the molecules have structural linearity and a large molecular polarizability a para-substituted phenyl ring is typically used.41 Moreover, the use of theoretical calculations to estimate the thermal and geometrical parameters for predicting the molecular geometry and correlating the calculated data with experiment values is one of our interests.19,20,42–51 Because of their interesting properties and the considerable temperature range of azo/ester LCs, several compounds bearing different terminal groups have been prepared and their mesomorphic properties studied.25–28 Substituents with different polarities residing at both terminals along the molecular axis of a mesogenic compound have been known to either promote or suppress their mesophase thermal transitions. The high dipole moment due to the attachment of polar substituents improves the stability of the lattice. The introduction of a Schiff base mesogenic core in the three rings azo/ester system plays an important role in the mesomorphic behavior. The alteration of the molecular polarizability and the resultant magnitudes of the anisotropic forces of attractions could lead to an enhancement of the thermal stability of the mesophase. The careful selection of the molecular geometry of prepared compounds to modify their mesomorphic behavior is one of our interests.14,19,20
N–) linkages can lead to marked changes in the photophysical and photochemical properties of such prepared materials. Consequently, in designing new thermotropic LCs with a mesogenic core, the terminal groups and a flexible chain are the essential specifications.40 To ensure the molecules have structural linearity and a large molecular polarizability a para-substituted phenyl ring is typically used.41 Moreover, the use of theoretical calculations to estimate the thermal and geometrical parameters for predicting the molecular geometry and correlating the calculated data with experiment values is one of our interests.19,20,42–51 Because of their interesting properties and the considerable temperature range of azo/ester LCs, several compounds bearing different terminal groups have been prepared and their mesomorphic properties studied.25–28 Substituents with different polarities residing at both terminals along the molecular axis of a mesogenic compound have been known to either promote or suppress their mesophase thermal transitions. The high dipole moment due to the attachment of polar substituents improves the stability of the lattice. The introduction of a Schiff base mesogenic core in the three rings azo/ester system plays an important role in the mesomorphic behavior. The alteration of the molecular polarizability and the resultant magnitudes of the anisotropic forces of attractions could lead to an enhancement of the thermal stability of the mesophase. The careful selection of the molecular geometry of prepared compounds to modify their mesomorphic behavior is one of our interests.14,19,20
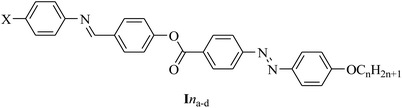
The present work was focused on the synthesis of a new series of four-ring liquid-crystalline compounds, Ina–d, and an investigation of their thermal, mesomorphic, and optical behaviors. Such investigations included the effect of the terminal alkoxy chain length (n = 6 to 16 carbons) and the polarity of the small compact substituent (X = OCH3, CH3H, and Cl) on the thermal stability of the mesophase transitions and type. Moreover, a comparison between the present four-ring compounds and previously prepared three-ring system, IIna–d, was made and is discussed herein. Further, several theoretical parameters were estimated from density functional theory (DFT) calculations for the prepared compounds and the results correlated with the experimental results.
Ina, X = CH3O; Inb, X = CH3; Inc, X = H and, Ind; X = Cl, n = 6, 8, 10, 12, 14, and 16.
2 Experimental
2.1. Preparation of Ina–d
The Ina–d compounds were prepared according to Scheme 1. | ||
| Scheme 1 Synthesis of (4-substituted phenylimino)methyl)phenyl 4-[2-(4-alkoxyphenyl)diazenyl]benzoate, Ina–d. | ||
2.2. Preparation of ((4-substitutedphenylimino)methyl)phenyl 4-[2-(4-alkoxyphenyl)diazenyl]benzoate, Ina–d
Molar equivalents of 4-[2-(4-methoxyphenyl)diazenyl]benzoic acid (An) and (4-substitutedphenylimino)methyl)phenol (Cn) (0.01 mol each) were dissolved in 25 ml dry methylene chloride (DCM). To the resulting mixture, N,N′-dicyclohexylcarbodiimide, DCC, (0.02 mol) and a few crystals of 4-(dimethylamino) pyridine (DMAP), as a catalyst, were added and the solution left to stand for 72 h at room temperature with continuous stirring. The solid separated was then filtered off and the solution evaporated. The solid residue obtained was recrystallized twice from acetic acid and twice from ethanol. The purity of the prepared samples was checked with TLC using TLC sheets coated with silica gel (E Merck), and CH2Cl2/CHOH (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) as the eluent, whereby only one spot was detected by a UV-lamp.
1) as the eluent, whereby only one spot was detected by a UV-lamp.
2.3. (4-Methoxyphenylimino)methyl)phenyl 4-[2-(4-dodecyloxyphenyl)diazenyl]benzoate, I12a
Yield: 93.7%; mp 155.0 °C, FTIR (![[small upsilon, Greek, dot above]](https://www.rsc.org/images/entities/char_e158.gif) , cm−1): 2927, 2857 (CH2 stretching), 1733 (C
, cm−1): 2927, 2857 (CH2 stretching), 1733 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1596 (C
O), 1596 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N), 1468 (C–OAsym), 1255 (C–OSym).1HNMR (300 MHz, CDCl3):δ = 0.90 (t, 3H, CH3(CH2)9CH2CH2, J = 5.1 Hz), 1.29–1.55 (m, 12H, CH3(CH2)9CH2CH2), 1.84 (q, 2H, J = 7.0 Hz, CH3(CH2)9CH2CH2), 4.08 (t, 2H, CH3(CH2)9CH2CH2, J = 6.1 Hz), 6.94 (d, 2H, J = 8.7 Hz, Ar–H), 7.02 (d, 2H, J = 9.0 Hz, Ar–H), 7.25–7.26 (m, 2H, Ar–H), 7.37 (d, 2H, J = 8.4 Hz, Ar–H), 7.96–8.01 (m, 4H, Ar–H), 8.34 (d, 2H, J = 8.8 Hz, Ar–H), 8.52 (s, 1H, CH
N), 1468 (C–OAsym), 1255 (C–OSym).1HNMR (300 MHz, CDCl3):δ = 0.90 (t, 3H, CH3(CH2)9CH2CH2, J = 5.1 Hz), 1.29–1.55 (m, 12H, CH3(CH2)9CH2CH2), 1.84 (q, 2H, J = 7.0 Hz, CH3(CH2)9CH2CH2), 4.08 (t, 2H, CH3(CH2)9CH2CH2, J = 6.1 Hz), 6.94 (d, 2H, J = 8.7 Hz, Ar–H), 7.02 (d, 2H, J = 9.0 Hz, Ar–H), 7.25–7.26 (m, 2H, Ar–H), 7.37 (d, 2H, J = 8.4 Hz, Ar–H), 7.96–8.01 (m, 4H, Ar–H), 8.34 (d, 2H, J = 8.8 Hz, Ar–H), 8.52 (s, 1H, CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N). Elemental analyses: found (Calc.): C, 75.55 (75.58); H, 7.29 (7.32); N, 6.76 (6.78).
N). Elemental analyses: found (Calc.): C, 75.55 (75.58); H, 7.29 (7.32); N, 6.76 (6.78).
2.4. (4-Methylphenylimino)methyl)phenyl 4-[2-(4-dodecyloxyphenyl)diazenyl]benzoate, I12b
Yield: 94.0%; mp 155.0 °C, FTIR (![[small upsilon, Greek, dot above]](https://www.rsc.org/images/entities/char_e158.gif) , cm−1): 2932, 2863 (CH2 stretching), 1735 (C
, cm−1): 2932, 2863 (CH2 stretching), 1735 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1600 (C
O), 1600 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N), 1486 (C–OAsym), 1248 (C–OSym). 1HNMR (300 MHz, CDCl3):δ = 0.90 (t, 3H, CH3(CH2)9CH2CH2, J = 6.6 Hz), 1.29–1.56 (m, 12H, CH3(CH2)9CH2CH2), 1.85 (q, 2H, J = 6.6 Hz, CH3(CH2)9CH2CH2), 2.40 (s, 3H, CH3), 4.08 (t, 2H, CH3(CH2)9CH2CH2, J = 6.6 Hz), 7.03 (d, 2H, J = 9.0 Hz, Ar–H), 7.15 (d, 2H, J = 8.1 Hz, Ar–H), 7.21–7.27 (m, 4H, Ar–H), 7.37 (d, 2H, J = 8.6 Hz, Ar–H), 7.97–8.02 (m, 4H, Ar–H), 8.34 (d, 2H, J = 8.4 Hz, Ar–H), 8.50 (s, 1H, CH
N), 1486 (C–OAsym), 1248 (C–OSym). 1HNMR (300 MHz, CDCl3):δ = 0.90 (t, 3H, CH3(CH2)9CH2CH2, J = 6.6 Hz), 1.29–1.56 (m, 12H, CH3(CH2)9CH2CH2), 1.85 (q, 2H, J = 6.6 Hz, CH3(CH2)9CH2CH2), 2.40 (s, 3H, CH3), 4.08 (t, 2H, CH3(CH2)9CH2CH2, J = 6.6 Hz), 7.03 (d, 2H, J = 9.0 Hz, Ar–H), 7.15 (d, 2H, J = 8.1 Hz, Ar–H), 7.21–7.27 (m, 4H, Ar–H), 7.37 (d, 2H, J = 8.6 Hz, Ar–H), 7.97–8.02 (m, 4H, Ar–H), 8.34 (d, 2H, J = 8.4 Hz, Ar–H), 8.50 (s, 1H, CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N). 13C NMR (101 MHz, CDCl3) δ 170.87, 158.23, 154.78, 148.45, 135.89, 131.20, 129.9, 129.72, 125.26, 122.50, 122.07, 120.75, 119.50, 114.78, 68.41, 31.85, 29.53, 29.30, 29.10, 25.94, 22.62, 20.96, 14.10. Elemental analyses: found (Calc.): C, 77.56 (77.58); H, 7.49 (7.51); N, 6.95 (6.96).
N). 13C NMR (101 MHz, CDCl3) δ 170.87, 158.23, 154.78, 148.45, 135.89, 131.20, 129.9, 129.72, 125.26, 122.50, 122.07, 120.75, 119.50, 114.78, 68.41, 31.85, 29.53, 29.30, 29.10, 25.94, 22.62, 20.96, 14.10. Elemental analyses: found (Calc.): C, 77.56 (77.58); H, 7.49 (7.51); N, 6.95 (6.96).
2.5. Phenyliminomethyl)phenyl 4-[2-(4-dodecyloxyphenyl)diazenyl]benzoate, I12c
Yield: 91.0%; mp 129.0 °C, FTIR (![[small upsilon, Greek, dot above]](https://www.rsc.org/images/entities/char_e158.gif) , cm−1): 2927, 2861 (CH2 stretching), 1733 (C
, cm−1): 2927, 2861 (CH2 stretching), 1733 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1595 (C
O), 1595 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N), 1457 (C–OAsym), 1256 (C–OSym). 1HNMR (300 MHz, CDCl3):δ = 0.90 (t, 3H, CH3(CH2)9CH2CH2, J = 5.1 Hz), 1.29–1.55 (m, 12H, CH3(CH2)9CH2CH2), 1.89 (q, 2H, J = 7.2 Hz, CH3(CH2)9CH2CH2), 3.86 (s, 3H, OCH3), 4.08 (t, 2H, CH3(CH2)9CH2CH2, J = 6.0 Hz), 7.03 (d, 2H, J = 9.0 Hz, Ar–H), 7.17 (d, 2H, J = 8.6 Hz, Ar–H), 7.37–7.41 (m, 4H, Ar–H), 7.97–8.01 (m, 4H, Ar–H), 8.34 (d, 2H, J = 8.6 Hz, Ar–H), 8.47 (s, 1H, CH
N), 1457 (C–OAsym), 1256 (C–OSym). 1HNMR (300 MHz, CDCl3):δ = 0.90 (t, 3H, CH3(CH2)9CH2CH2, J = 5.1 Hz), 1.29–1.55 (m, 12H, CH3(CH2)9CH2CH2), 1.89 (q, 2H, J = 7.2 Hz, CH3(CH2)9CH2CH2), 3.86 (s, 3H, OCH3), 4.08 (t, 2H, CH3(CH2)9CH2CH2, J = 6.0 Hz), 7.03 (d, 2H, J = 9.0 Hz, Ar–H), 7.17 (d, 2H, J = 8.6 Hz, Ar–H), 7.37–7.41 (m, 4H, Ar–H), 7.97–8.01 (m, 4H, Ar–H), 8.34 (d, 2H, J = 8.6 Hz, Ar–H), 8.47 (s, 1H, CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N). 13C NMR (101 MHz, CDCl3) δ 170.89, 162.23, 154.12, 153.81, 146.71, 138.08, 127.58, 125.07, 122.63, 119.45, 114.75, 68.40, 32.30, 31.88, 30.73, 29.62, 29.55, 29.34, 26.20, 25.96, 25.30, 25.20, 24.47, 22.65, 14.10. Elemental analyses: found (Calc.): C, 77.37 (77.39); H, 7.32 (7.35); N, 7.10 (7.12).
N). 13C NMR (101 MHz, CDCl3) δ 170.89, 162.23, 154.12, 153.81, 146.71, 138.08, 127.58, 125.07, 122.63, 119.45, 114.75, 68.40, 32.30, 31.88, 30.73, 29.62, 29.55, 29.34, 26.20, 25.96, 25.30, 25.20, 24.47, 22.65, 14.10. Elemental analyses: found (Calc.): C, 77.37 (77.39); H, 7.32 (7.35); N, 7.10 (7.12).
2.6. (4-Chlorophenylimino)methyl)phenyl 4-[2-(4-dodecyloxyphenyl)diazenyl]benzoate, I12d
Yield: 94.0%; mp 140.0 °C, FTIR (![[small upsilon, Greek, dot above]](https://www.rsc.org/images/entities/char_e158.gif) , cm1): 2928, 2862 (CH2 stretching), 1733 (C
, cm1): 2928, 2862 (CH2 stretching), 1733 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1594 (C
O), 1594 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N), 1471 (C–OAsym), 1251 (C–OSym). 1HNMR (300 MHz, CDCl3):δ = 0.90 (t, 3H, CH3(CH2)9CH2CH2, J = 5.1 Hz), 1.29–1.55 (m, 12H, CH3(CH2)9CH2CH2), 1.89 (q, 2H, J = 7.2 Hz, CH3(CH2)9CH2CH2), 3.86 (s, 3H, OCH3), 4.08 (t, 2H, CH3(CH2)9CH2CH2, J = 6.0 Hz), 7.03 (d, 2H, J = 9.0 Hz, Ar–H), 7.17 (d, 2H, J = 8.6 Hz, Ar–H), 7.37–7.41 (m, 4H, Ar–H), 7.97–8.01 (m, 4H, Ar–H), 8.34 (d, 2H, J = 8.6 Hz, Ar–H), 8.47 (s, 1H, CH
N), 1471 (C–OAsym), 1251 (C–OSym). 1HNMR (300 MHz, CDCl3):δ = 0.90 (t, 3H, CH3(CH2)9CH2CH2, J = 5.1 Hz), 1.29–1.55 (m, 12H, CH3(CH2)9CH2CH2), 1.89 (q, 2H, J = 7.2 Hz, CH3(CH2)9CH2CH2), 3.86 (s, 3H, OCH3), 4.08 (t, 2H, CH3(CH2)9CH2CH2, J = 6.0 Hz), 7.03 (d, 2H, J = 9.0 Hz, Ar–H), 7.17 (d, 2H, J = 8.6 Hz, Ar–H), 7.37–7.41 (m, 4H, Ar–H), 7.97–8.01 (m, 4H, Ar–H), 8.34 (d, 2H, J = 8.6 Hz, Ar–H), 8.47 (s, 1H, CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N). 13C NMR (101 MHz, CDCl3) δ 1l70.61, 162.43, 153.45, 152.78, 145.70, 131.84, 131.21, 129.16, 125.32, 122.55, 121.75, 114.81, 68.45, 32.31, 31.89, 29.61, 29.34, 29.13, 26.20, 25.97, 25.30, 25.20, 24.47, 22.67, 14.11. Elemental analyses: found (Calc.): C, 73.10 (73.12); H, 6.77 (6.78); N, 6.70 (6.73); Cl, 5.67 (5.68).
N). 13C NMR (101 MHz, CDCl3) δ 1l70.61, 162.43, 153.45, 152.78, 145.70, 131.84, 131.21, 129.16, 125.32, 122.55, 121.75, 114.81, 68.45, 32.31, 31.89, 29.61, 29.34, 29.13, 26.20, 25.97, 25.30, 25.20, 24.47, 22.67, 14.11. Elemental analyses: found (Calc.): C, 73.10 (73.12); H, 6.77 (6.78); N, 6.70 (6.73); Cl, 5.67 (5.68).
3 Results and discussion
3.1. Molecular structure characterization
The IR spectra, 1H NMR, mass, and elemental analyses for the compounds investigated were consistent with the molecular structures assigned. The analysis data of the investigated compounds are given as supplemental materials (Fig. S1–S4†). The 1H NMR results showed the expected integrated aliphatic to aromatic proton ratios in all the compounds. The FT-IR results showed that the length of the alkoxy chain and polarity of the compact substituent X group did not extensively impact the position of the absorption bands of the main characteristic functional groups. The mass spectra and elemental analyses confirmed the molecular structure and the purity of the materials investigated.3.2. TG analysis
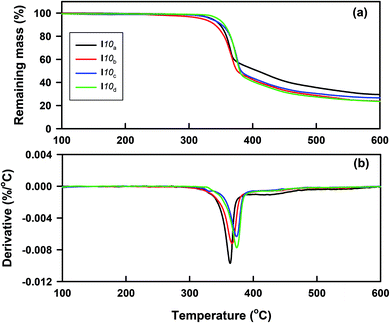
The thermal stability of all the prepared homologues series Ina–d were studied by thermogravemetric analysis (TG). The typical TG curves and their corresponding derivatives (DTG) of the compounds I10(a–d), as examples, are shown in Fig. 1. The thermal degradation parameters, such as Tonset (the temperature at which the thermal degradation starts), Tmax (the temperature at which the thermal degradation rate is at the maximum), and m% (the mass percentage loss recorded in each stage), are given in Table 1. As can be seen from Fig. 1 and Table 1, the thermal decomposition occurred through two degradation steps with various mass losses, depending on the chemical structure. The first main step occurred in the temperature range 320–395 °C and started at 336 °C, 321 °C, 334 °C, and 346 °C, with maximum degradation rates (Tmax) at 364 °C, 367 °C, 374 °C, and 376 °C for I10a, I10b, I10c, and I10d, respectively; indicating that the thermal stability increased in the following order: I10d > I10a > I10c > I10b. While the second one with a low mass loss took place between 395 °C and 465 °C with the maximum degradation rate almost independent of the substituent X. Additionally, the degradation was not complete up to 600 °C, and the amount of residue left over was found to be between 23% and 29%. Based on the previous studies,52–58 the suggested degradation of azo-based materials occurs through the cleavage of the azo bond by reductive processes. The larger conjugation of the I10d and I10a with Cl and –OCH3 substituents, respectively, through resonance from the delocalization of the non-bonding electron pairs of the substituent and π electrons of the aromatic rings and azo bonds, may enhance the thermal stability. These results revealed that the compounds under investigation possessed a high thermal stability up to 316–341 °C, which covers the temperature window where the mesophase transitions were detected calorimetry, except for the compounds with short alkoxy terminal groups (I6a–b and I8a–b), where the isotropic transition could not observed by DSC and was detected only with PLM.| Compound | Thermal degradation stages | Tonset (°C) | Tmax. (°C) | Residue (%) | Mass (%) |
|---|---|---|---|---|---|
| I10a | I | 336 | 364 | 29.4 | 60 |
| II | 384 | 428 | 21 | ||
| Residue | — | — | 29 | ||
| I10b | I | 321 | 367 | 23.7 | 50 |
| II | 383 | 430 | 26 | ||
| Residue | — | — | 24 | ||
| I10c | I | 334 | 374 | 26.6 | 52 |
| II | 392 | 430 | 21 | ||
| Residue | — | — | 27 | ||
| I10d | I | 346 | 376 | 23.5 | 48 |
| II | 398 | 432 | 29 | ||
| Residue | — | — | 23 |
3.3. Mesophase behavior
The DSC thermograms of some selected compounds, namely I14a–d, during both heating and cooling scans are shown in Fig. 2. It is clearly shown that upon heating, all the compounds (Fig. 2a) showed three endotherms characteristic of the crystal-SmA, SmA–N, and N-isotropic transitions. While, during the cooling cycle, all the compounds exhibited a nematic and SmA phase, but their transitions were shifted to lower temperatures compared with those observed through the heating cycle. The PLM measurements revealed textures that confirmed the SmA and N mesophases (Fig. 3). The SmA phase showed a focal conic fan texture and N had a threaded/schlieren texture. This indicated that these compounds possessed enantiotropic dimorphic properties. Details of the transition temperatures and the associated enthalpies of all the investigated homologues in the Ina–d series, as derived from DSC measurements, are summarized in Table 2. The transition temperatures of all the investigated derivatives are represented graphically in Fig. 4 in order to evaluate the effect of the terminal alkoxy-chain length on the mesophase behavior in each series having a different terminal compact substituent X.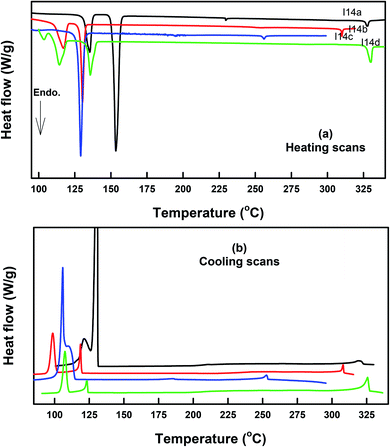 | ||
| Fig. 2 DSC thermograms of some representative compounds: (a) recorded from second heating and (b) from cooling at a rate of ±10 °C min−1. | ||
 | ||
| Fig. 3 PLM textures of: (a) the nematic phase of I12b at 240.0 °C upon cooling; (b) smectic A phase of I16d at 299.0 °C upon heating; (c) smectic A phase of I16d at 280.0 °C upon cooling. | ||
| Compounds | TCr–SmA | TCr–N | TSmA–N | TSmA–I | TN–I | ΔSSmA–N/R | ΔSSmA–I/R | ΔSN–I/R |
|---|---|---|---|---|---|---|---|---|
| a Cr–SmA denotes transition from solid to the SmA phase. Cr–N denotes transition from solid to the N phase. SmA–N denotes transition from SmA to the N phase. SmA–I denotes transition from SmA to the isotropic phase. N–I denotes transition from nematic to the isotropic phase.b Values detected by PLM only. | ||||||||
| I6a | 165.9(51.31) | 369.0b | — | |||||
| I8a | 161.4(44.67) | 352.0b | ||||||
| I10a | 157.5(50.46) | 185.1(0.33) | 348.0b | 0.087 | ||||
| I12a | 155.4(50.08) | 211.4(0.40) | 339.6(3.60) | 0.098 | 0.707 | |||
| I14a | 153.4(77.32) | 229.6(0.55) | 327.4(3.98) | 0.132 | 0.797 | |||
| I16a | 151.7(47.09) | 242.9(0.64) | 314.4(4.23) | 0.149 | 0.880 | |||
| I6b | 149.3(24.83) | 366.0b | ||||||
| I8b | 153.8(21.95) | 188.1(0.41) | 355.4(1.37) | 0.110 | 0.460 | |||
| I10b | 152.5(35.95) | 220.8(0.59) | 338.3(2.69) | 0.143 | 0.530 | |||
| I12b | 155.1(38.91) | 240.0(0.68) | 327.0(3.39) | 0.160 | 0.680 | |||
| I14b | 130.3(26.31) | 252.3(0.96) | 310.0(3.88) | 0.220 | 0.800 | |||
| I16b | 122.4(62.38) | 257.0(1.10) | 298.1(4.23) | 0.250 | 0.890 | |||
| I6c | 156.5(30.56) | 211.7(0.87) | 323.5(2.88) | 0.220 | 0.580 | |||
| I8c | 145.4(19.21) | 234.9(1.01) | 305.7(2.93) | 0.240 | 0.610 | |||
| I10c | 135.7(44.37) | 245.3(1.64) | 290.1(3.23) | 0.380 | 0.690 | |||
| I12c | 129.0(37.57) | 249.2(1.78) | 276.8(3.38) | 0.410 | 0.740 | |||
| I14c | 129.6(57.78) | 249.3(1.85) | 265.0(3.53) | 0.426 | 0.790 | |||
| I16c | 129.2(59.05) | 245.4(1.94) | 254.3(3.81) | 0.450 | 0.870 | |||
| I6d | 168.7(29.47) | 319.0(0.83) | 370.0b | 0.170 | — | |||
| I8d | 146.1(20.34) | 335.9(1.40) | 360.0b | 0.280 | — | |||
| I10d | 143.8(21.28) | 338.5(2.19) | 350.5(3.01) | 0.430 | 0.580 | |||
| I12d | 137.9(21.98) | 336.6(4.26) | 340.2(3.16) | 0.840 | 0.620 | |||
| I14d | 135.7(22.57) | 330.2(8.09) | 2.950 | |||||
| I16d | 133.9(19.23) | 322.9(8.97) | 3.340 | |||||
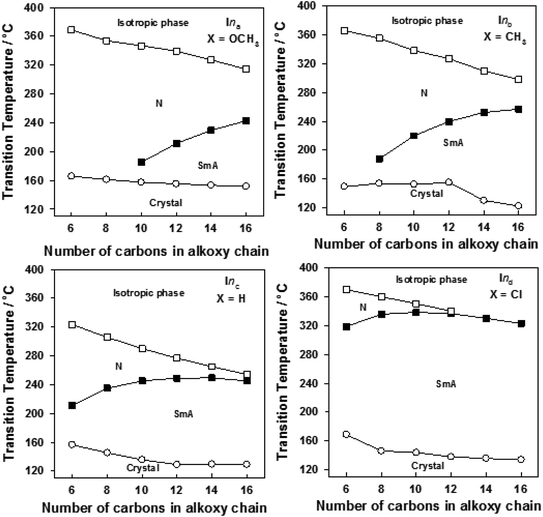 | ||
| Fig. 4 Effect of the alkoxy-chain length on the mesophase behavior of the individual homologous series of Ina–d. | ||
The data in Table 2 and Fig. 4 revealed that the melting temperatures of (Cr–N/SmA) for the methoxy, unsubstituted, and chloro derivatives slightly declined with increasing the alkoxy chain length from n = 6 up to 16, except for the methyl derivatives, which showed an irregular trend. The melting point increased as the polarizability of the compounds within the same series increased. However, the obtained current trend was not in agreement with this common rule. Additionally, all the members of the homologous series were enantiotropic with a high mesophase thermal stability and broad temperature mesomorphic range. For the electron-donating terminal CH3O group (Ina), their compounds were dimorphic, exhibiting enantiotropic SmA and N phases, except for the short chains n = 6 and n = 8, which were purely nematogenic. The SmA range (ΔTSmA = TSmA − Tcr) increased from 27.6 °C to 91.2 °C with increasing the alkoxy chain length from n = 10 up to 16, while the N phase range (ΔTN = Tiso − TSmA) decreased from 203.1 °C to 71.5 °C as the alkoxy chain length n ascended from 6 to 16. Compounds with the terminal CH3 substituent (Inb) were also found to be dimorphic, possessing SmA and N mesophases, except I6b, which was purely nematogenic. ΔTSmA increased from 34.3 °C to 134.6 °C with increasing n from 8 to 16, while ΔTN was reduced from 167.3 °C to 41.1 °C as n increased from 6 to 16. For X = H (Inc series), all the compounds exhibit dimorphic SmA and N phases, irrespective of the alkoxy chain length, with a relatively low thermal stability compared with the Ina and Inb series. ΔTSmA was enhanced from 54.4 °C to 116.2 °C, while ΔTN was reduced from 112.6 °C to 8.9 °C. The electron-withdrawing Cl derivatives had the highest broad mesomorphic range. Compounds of the Inc series with the electron-withdrawing group Cl possessed an SmA phase, with high thermal stability and a wide range, and N phases for alkoxy chain lengths up to n = 12; then with increasing the length of the terminal alkoxy chain (n = 14 and 16), the phase became purely smectogeic (SmA). ΔTSmA increased from 150.3 °C to 189.0 °C with increasing n from 8 to 16, while ΔTN was reduced from 51.0 °C to 3.6 °C as n increased from 6 to 12. For all the series, irrespective of the polarity of the substituent X, the stability of the nematic phase decreased while the SmA phase increased, as usual, with increasing the terminal alkoxy chain length.59,60 The descending trend in the thermal transition of the N phase could be ascribed to the dilution of the rigid mesogenic core. Nevertheless, the appearance of SmA phase depressed the nematic phase range as the alkoxy chain length increased. This was probably due to increase in the van der Waals attractions forces between the long alkoxy chains, leading to their intertwining and facilitating the lamellar packing, which is of crucial importance for the occurrence of the smectic phase.
Based on the above data, the thermal stability of the N phase (N-isotropic transition), at a given alkoxy chain, declined in the following order: Cl > CH3O > CH3 > H, while the thermal stability of the SmA phase (Tcry–TSmA transition) increased in the order: Cl > CH3 > CH3O > H. The increment of the SmA mesophase range (ΔTSmA) followed the order: Cl > CH3 > CH3O > H and the reduction in the N range (ΔTN) in the order: Cl > CH3O > CH3 > H. In general, the polarity of the substituent groups, polarizability, aspect ratio, rigidity, and architecture of the molecule are considered important factors that are responsible for the stability of the formed mesophases and their textures. These factors contribute to different extents to the mesophase behavior. It was already known that the stability of a mesophase of a given mesomorphic compound is increased by any enhancement in the polarity and/or polarizability of the mesogenic core of the molecule, which is affected by the polarity of the substituent, which would consequently affect the polarity of the whole molecular structure. Also, increasing van der Waals attractions, which increase with increasing the terminal alkoxy group, enhance the stability of the SmA phase by favoring lamellar packing. On the other hand, it suppresses the nematic phase range. These factors that affect the stability of the mesophases and their types are discussed and correlated with the molecular geometries and quantum chemical parameters studied by DFT calculations in the next section.
The entropy change of mesophase transitions (ΔS/R) was estimated for the investigated compounds and the results are included in Table 2. Independent of the terminal alkoxy-chain length of molecules (n), an irregular trend and small magnitudes of the ΔS/R associated with the SmA–N, N-isotropic were observed. However, the obtained small values in all the derivatives might probably be due to the somewhat molecular biaxiality induced by the ester linkage group and the relatively high values of the clearing temperatures, which in turn reduces the SmA–N, N-isotropic entropy changes.61–63 However; the variation and complexity in the entropy change with a compact terminal group X and alkoxy chain length may be attributed to a change in the molecular interactions between molecules, which are affected by the dipole moment, polarizability, rigidity, aspect ratio (length/breadth ratio), and geometrical shape of molecules. These factors may contribute to the conformational, orientational, and translational entropies of the molecule to different extents. Although, the increment of the alkoxy chain length has a dilution effect on core–core interactions, it increases the polarizability of the whole molecule, which increases the intermolecular adhesion forces between adjacent molecules that promote the degree of molecular ordering. The increase in ΔS/R values with increasing the number of carbons in the alkoxy chain is probably due to the disappearance of the long orientational order and the increase in the number of conformational distributions in mesophase transitions.
The terminally substituted polarizable –Cl group leads to an increase in the dipole moment of the molecule, which enhances the lateral interaction and consequently allows the molecules to pack more efficiently in the liquid-crystal phase, resulting in a higher ΔS/R magnitude, which is especially associated with SmA-isotropic transitions, as in the case here with the I14d and I16d derivatives.
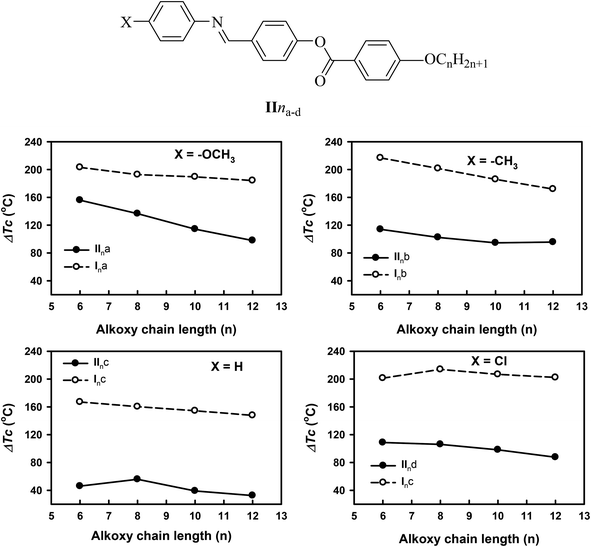
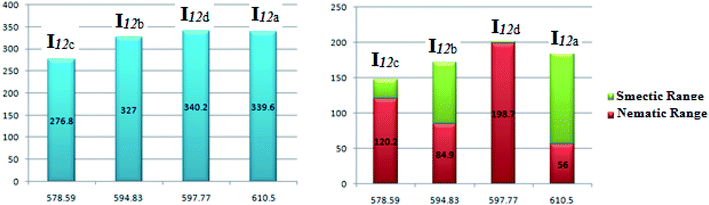
In order to investigate the effect of the addition of an extra phenylazo group moiety into the previously investigated three-ring analogues20 with –COO– and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– connecting units (IIna–d) to give Ina–d20 on the mesophase thermal stability range (ΔTc), a comparison was made with the data reported before20 and the results are illustrated in Fig. 5. As can be seen from Fig. 4, the addition of the extra phenylazo group into the three Schiff base/ester compounds resulted in a great increase in the Tc values and their ranges. The ΔTc values were found to be increased in the range of 101.1–116.5 °C, 116.8–97.1 °C, 46.0–32.5 °C, and 108.7–87.6 °C for methoxy, methyl, unsubstituted, and chloro derivatives. These increment were attributed to the increase in polarizability of the whole molecule as well as the increase in rigidity and the aspect ratio, which in turn lead to an increase in the intermolecular interactions between molecules.
N– connecting units (IIna–d) to give Ina–d20 on the mesophase thermal stability range (ΔTc), a comparison was made with the data reported before20 and the results are illustrated in Fig. 5. As can be seen from Fig. 4, the addition of the extra phenylazo group into the three Schiff base/ester compounds resulted in a great increase in the Tc values and their ranges. The ΔTc values were found to be increased in the range of 101.1–116.5 °C, 116.8–97.1 °C, 46.0–32.5 °C, and 108.7–87.6 °C for methoxy, methyl, unsubstituted, and chloro derivatives. These increment were attributed to the increase in polarizability of the whole molecule as well as the increase in rigidity and the aspect ratio, which in turn lead to an increase in the intermolecular interactions between molecules.
3.4. DFT calculations and conformational analysis
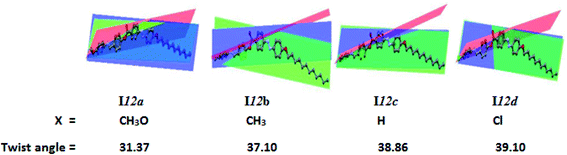
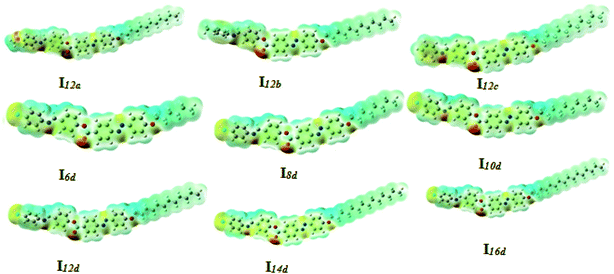
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N unit. The electronic nature of the polar compact terminal group has a high impact on the twist angle; however, the length of the terminal alkoxy chains almost has no significant effect on the aromatic rings planarity. Our group reported that21,23 the planarity of the mesogenic core of the LC molecules was enhanced by the mesomeric nature of the polar terminal substituent, where the higher donation of electrons by the substituent to the conjugated π-cloud, the greater the enforcement of the system to be planar. This phenomena could explain the lowest twist angle of the methoxy derivative (I12a) of 31.57°. On the other hand, the chloro-substituted derivative (I12d) of the negative inductive effect of the chloro group and its lower donating ability showed the highest twist angle of 39.52° (Table 3).
N unit. The electronic nature of the polar compact terminal group has a high impact on the twist angle; however, the length of the terminal alkoxy chains almost has no significant effect on the aromatic rings planarity. Our group reported that21,23 the planarity of the mesogenic core of the LC molecules was enhanced by the mesomeric nature of the polar terminal substituent, where the higher donation of electrons by the substituent to the conjugated π-cloud, the greater the enforcement of the system to be planar. This phenomena could explain the lowest twist angle of the methoxy derivative (I12a) of 31.57°. On the other hand, the chloro-substituted derivative (I12d) of the negative inductive effect of the chloro group and its lower donating ability showed the highest twist angle of 39.52° (Table 3).
| Parameter | I12a | I12b | I12c | I6d | I8d | I10d | I12d | I14d | I16d | |
|---|---|---|---|---|---|---|---|---|---|---|
| a ZPVE: sum of electronic and zero-point energies; Etot: sum of electronic and thermal energies; H: sum of electronic and thermal enthalpies; G: sum of electronic and thermal free energies. | ||||||||||
| Ecorr | 0.7671 | 0.7625 | 0.735129 | 0.553804 | 0.610854 | 0.667968 | 0.725161 | 0.782295 | 0.839413 | |
| ZPVE | −1977.50 | −1902.30 | −1863.04 | −2086.95 | −2165.52 | −2244.09 | −2322.65 | −2401.22 | −2479.79 | |
| Etot | −1977.50 | −1902.28 | −1863.00 | −2086.92 | −2165.48 | −2244.05 | −2322.61 | −2401.17 | −2479.74 | |
| H | −1977.50 | −1902.28 | −1863.00 | −2086.92 | −2165.48 | −2244.04 | −2322.61 | −2401.17 | −2479.74 | |
| G | −1977.60 | −1902.42 | −1863.13 | −2087.03 | −2165.60 | 2244.17 | −2322.74 | −2401.31 | −2479.89 | |
| Total dipole moment | 6.93 | 6.85 | 7.21 | 9.42 | 9.47 | 9.50 | 9.51 | 9.52 | 8.67 | |
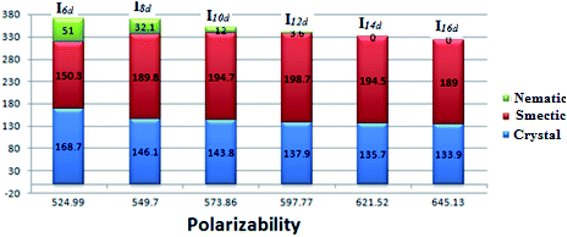
| Polarizability α | 610.52 | 594.83 | 578.59 | 524.99 | 549.70 | 573.86 | 597.77 | 621.52 | 645.13 | |
| Twist angles | A–B | 31.57 | 37.26 | 38.86 | 39.10 | 39.33 | 39.50 | 39.52 | 39.49 | 39.47 |
| B–C | 12.93 | 2.24 | 7.61 | 1.22 | 1.08 | 2.04 | 2.42 | 2.24 | 2.27 | |
 | ||
| Fig. 7 Relation of the mesophase thermal stability and the mesophase range of the homologues series I12a–d with their calculated polarizability. | ||
Fig. 8 shows the relation of the mesophase thermal stabilities and the mesophases temperature ranges of the homologues series I12a–d with their calculated twist angle between aromatic rings A–B connected with imine group. It can be clearly seen that as the twist angle increases, the chance for packing the molecules decreases, and consequently, there is a decrement in the mesophase stability and its range, except for the chloro derivative (I12d). This result is taken as evidence that the mesophase stability and its range is caused by an accumulation of factors not only one. Moreover, it is obvious that the less planar the molecules, the higher the range of a more ordered smectic phase, and the lower the range of the nematic mesophase. This might be attributed to the competitive interaction between the lateral and the terminal interaction that is affected by the planarity of the molecules.
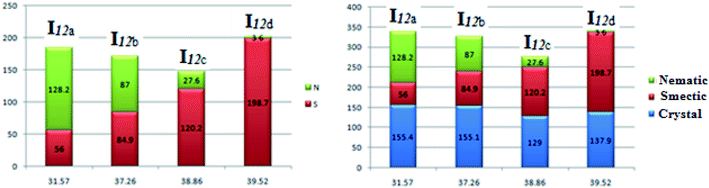 | ||
| Fig. 8 Relation of the mesophase stability and the mesophase range of the homologues series I12a–d with their calculated twist angle between rings A–B. | ||
Fig. 9 emphasizes that the dipole moment of the investigated compounds significantly affects the mesophase type, mesophase stability, and its range. As the dipole moment increases, the parallel interaction increases to form a highly ordered smectic mesophase; however, the lower dipole moment enhances the nematic mesophase formation by enforcing the terminal attraction.
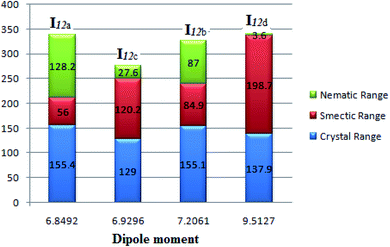 | ||
| Fig. 9 Dependence of the mesophase stability of the homologues series I12a–d with the calculated dipole moment. | ||
One of the important parameters affecting the liquid-crystal behavior is the aspect ratio (molecular length to the width ratio). This is a structural feature that is relevant in the formation of liquid crystals. The melting of the liquid-crystal material makes the solid diminish because of the increasing molecular fluctuations and rotations, whereby the smectic and nematic phases gain from the retention of positional and orientational ordering due to the lateral and terminal interactions, respectively.20,23,24,42,64–68 The dependence of the mesophase stabilities and their ranges on the calculated aspect ratio (L/D) of Ind is given in Table 4 and represented graphically (Fig. 10). Increasing the aspect ratio leads to a significant increase in the thermal stability of the smectic A and its range up to an alkoxy chain length of n = 12 and then declines while the thermal stability of the nematic phase and its range then decreases. As expected, as the aspect ratio of the molecule increases, the more side–side interactions there are to enhance the smectic mesophase rather than the less ordered nematic phase. However, at an alkoxy chain length longer than 12 carbon atom, the lateral attraction of the chains shows a less pronounced effect to increase the nematic range but not to such a large extent. Moreover, the increment of the alkoxy chains strengthens the end–end interaction with respect to the π–π stacking of the benzene rings.
| Compound | Width (D) Å | Length (L) C Å | Aspect ratio (L/D) |
|---|---|---|---|
| I6d | 4.97 | 35.54 | 7.15 |
| I8d | 5.98 | 38.10 | 6.37 |
| I10d | 5.00 | 40.63 | 8.13 |
| I12d | 5.03 | 43.14 | 8.58 |
| I14d | 5.09 | 45.62 | 8.96 |
| I16d | 5.31 | 48.06 | 9.05 |
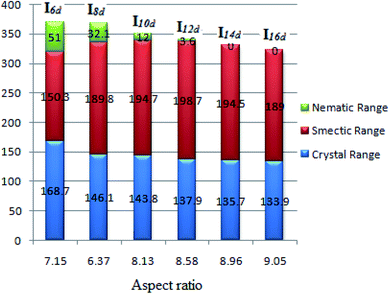 | ||
| Fig. 10 Dependence of the mesophase stabilities and their ranges of Ind on the calculated aspect ratio. | ||
The effect of the polarizability of the alkoxy chain length on the thermal stabilities and their ranges for Ind is shown in Fig. 11. The results reveal that the effect of polarizability on the mesophase stabilities and their ranges follows the same trend as the effect of the aspect ratio. However, the presence of a nematic mesophase (less ordered) with the shorter alkoxy chains and a smectic phase (more ordered) for the longer chain lengths could be explained in the term of the increment of the polarizability with increasing the alkoxy chain length. There is greater lateral interaction aggregation of the alkoxy chains in the ordered smectic phase as the alkoxy chain length increases.
 | ||
| Fig. 12 Calculated ground-state isodensity surface plots for the Frontier molecular orbitals of I12a–d. | ||
 | ||
| Fig. 13 Calculated ground-state isodensity surface plots for the Frontier molecular orbitals of Ind. | ||
| Compound | EHOMO (a.u) | ELUMO (a.u) | ΔE(ELUMO − EHOMO) (a.u) | η = ΔE(ELUMO − HOMO)/2 | S = 1/ΔE = (1/2η) |
|---|---|---|---|---|---|
| I12a | −0.20951 | −0.10377 | 0.10574 | 0.05287 | 9.45716 |
| I12b | −0.21870 | −0.10426 | 0.11444 | 0.05722 | 8.73820 |
| I12c | −0.22405 | −0.10493 | 0.11912 | 0.05956 | 8.39490 |
| I6d | −0.23005 | −0.10720 | 0.12285 | 0.06143 | 8.14001 |
| I8d | −0.22998 | −0.10718 | 0.12280 | 0.06140 | 8.14332 |
| I10d | −0.22997 | −0.10716 | 0.12281 | 0.06141 | 8.14266 |
| I12d | −0.22995 | −0.10714 | 0.12281 | 0.06141 | 8.14266 |
| I14d | −0.22995 | −0.10713 | 0.12282 | 0.06141 | 8.14200 |
| I16d | −0.22996 | −0.10712 | 0.12284 | 0.06142 | 8.14067 |
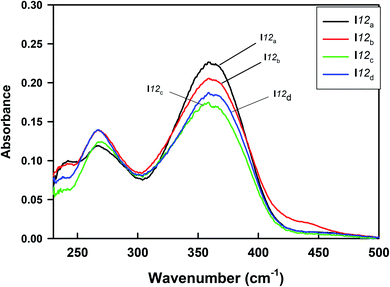
The UV-vis absorption spectra of the homologues series of the I12a–d compounds are shown in Fig. 14, and the data are tabulated in Table 6. As can be seen from Fig. 14, the present compounds with N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, COO, and –N
N, COO, and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– linkages exhibited two absorption bands at 267 nm and ≈364 nm. The more intense peak observed at ≈364 nm may be assigned to π–π* transition in the π-electronic system throughout the whole aromatic rings and connecting units, with a suitable charge-transfer (CT) property,63–65 while the weak absorption band that appeared around 267 nm may be related to n-π* transition of the azobenzene moiety.
CH– linkages exhibited two absorption bands at 267 nm and ≈364 nm. The more intense peak observed at ≈364 nm may be assigned to π–π* transition in the π-electronic system throughout the whole aromatic rings and connecting units, with a suitable charge-transfer (CT) property,63–65 while the weak absorption band that appeared around 267 nm may be related to n-π* transition of the azobenzene moiety.
| Compound | X | Peak 1 | Peak 2 |
|---|---|---|---|
| I12a | CH3O | 267 | 364 |
| I12b | CH3 | 267 | 363 |
| I12c | H | 267 | 361 |
| I12d | Cl | 267 | 363 |
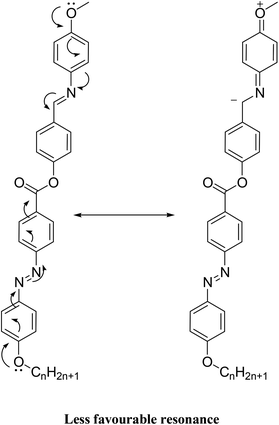
It is noteworthy that there was somewhat of an effect on the absorption peaks position of these compounds under investigation. This result could be explained in terms of the estimated data by DFT calculations, Table 5. The change in the polarity of the terminal substituent X impacted the HOMO–LUMO energy gaps of the molecules, as shown in Fig. 12. Moreover, the terminal methoxy group of I12a had no pronounced effect, as expected, on the energy difference between the Frontier molecular orbitals (FMOs); this could be explained in terms of the resonance effect of the terminal methoxy group of the imino part opposite the alkoxy chain of the azo moiety (Fig. 15).
4. Conclusion
A new four-ring series of compounds with –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–, –COO– and –CH
N–, –COO– and –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– connecting units, (4-substitutedphenylimino)methyl)phenyl 4-[2-(4-alkoxyhenyl)diazenyl]benzoate, were successfully synthesized and their molecular structures confirmed via FT-IR, 1H-NMR, 13C-NMR, mass spectra and elemental analyses. Their thermotropic and optical behaviours were studied and correlated with theoretical parameters derived from DFT calculations.
N– connecting units, (4-substitutedphenylimino)methyl)phenyl 4-[2-(4-alkoxyhenyl)diazenyl]benzoate, were successfully synthesized and their molecular structures confirmed via FT-IR, 1H-NMR, 13C-NMR, mass spectra and elemental analyses. Their thermotropic and optical behaviours were studied and correlated with theoretical parameters derived from DFT calculations.
The study revealed that:
(1) All the prepared compounds exhibited high thermal stability with broad enantiotropic temperature mesomorphic ranges.
(2) The geometrical parameters of the prepared compounds were highly affected by the electronic nature of the terminal substituent X as well as the alkoxy chain length.
(3) The twist angle of the non-coplanar geometry impacted the mesophase type, stability and its range.
(4) As the dipole moment increased, the smectic mesophase was enhanced by enforcing the lateral attraction.
(5) Increasing the aspect ratio of Ind led to significant increases in the thermal stability of the smectic A and its range up to C12 and then declined, while the thermal stability of the nematic phase and its range decreases.
(6) The results revealed that the effect of the calculated polarizability of the same compounds Ind on the mesophase stabilities and their ranges followed the same trend as the effect of the aspect ratio.
(7) The FMOs' energy gap and global softness (S) were impacted by the electronic nature of the terminal substituent.
Conflicts of interest
There are no conflicts to declare.References
- C. T. Imrie, P. A. Henderson and G.-Y. Yeap, Liq. Cryst., 2009, 36, 755–777 CrossRef CAS.
- G.-Y. Yeap, H.-C. Lee, W. A. K. Mahmood, C. T. Imrie, D. Takeuchi and K. Osakada, Phase Transitions, 2011, 84, 29–37 CrossRef CAS.
- G.-Y. Yeap, F. Osman and C. T. Imrie, Liq. Cryst., 2015, 42, 543–554 CrossRef CAS.
- G.-Y. Yeap, T.-C. Hng, S.-Y. Yeap, E. Gorecka, M. M. Ito, K. Ueno, M. Okamoto, W. A. K. Mahmood and C. T. Imrie, Liq. Cryst., 2009, 36, 1431–1441 CrossRef CAS.
- A. Pramanik, M. K. Das, B. Das, M. Żurowska and R. Dąbrowski, Liq. Cryst., 2015, 42, 412–421 CrossRef CAS.
- G. H. Heilmeier and L. Zanoni, Appl. Phys. Lett., 1968, 13, 91–92 CrossRef CAS.
- G. H. Heilmeier, L. A. Zanoni and L. A. Barton, Proc. IEEE, 1968, 56, 1162–1171 Search PubMed.
- J. Goodby, Ferroelectricity and related phenomena, Gordon and Breach Science publishers, New York, 1991, vol. 7, ch. 2, p. 99 Search PubMed.
- R. J. Carlton, J. T. Hunter, D. S. Miller, R. Abbasi, P. C. Mushenheim, L. N. Tan and N. L. Abbott, Liq. Cryst. Rev., 2013, 1, 29–51 CrossRef CAS PubMed.
- B. N. Veerabhadraswamy, D. S. S. Rao and C. V. Yelamaggad, Chem.–Asian J., 2018, 13, 1012–1023 CrossRef CAS PubMed.
- C.-C. Huang, C.-C. Hsu, L.-W. Chen and Y.-L. Cheng, Soft Matter, 2014, 10, 9343–9351 RSC.
- J. L. Segura, M. J. Mancheño and F. Zamora, Chem. Soc. Rev., 2016, 45, 5635–5671 RSC.
- A. Gowda, L. Jacob, N. Joy, R. Philip, R. Pratibha and S. Kumar, New J. Chem., 2018, 42, 2047–2057 RSC.
- M. Hagar, H. Ahmed and G. Saad, Liq. Cryst., 2018, 45, 1324–1332 CrossRef CAS.
- H. A. Ahmed, M. Hagar and O. A. Alhaddad, Crystals, 2019, 9, 133 CrossRef.
- C. T. Imrie and P. A. Henderson, Curr. Opin. Colloid Interface Sci., 2002, 7, 298–311 CrossRef CAS.
- C. T. Imrie and P. A. Henderson, Chem. Soc. Rev., 2007, 36, 2096–2124 RSC.
- H. Ahmed, M. Hagar, T. El-Sayed and R. B. Alnoman, Liq. Cryst., 2019, 1–11 Search PubMed.
- M. Hagar, H. Ahmed and G. Saad, J. Mol. Liq., 2019, 273, 266–273 CrossRef CAS.
- H. Ahmed, M. Hagar and G. Saad, Liq. Cryst., 2019, 1–10 Search PubMed.
- S. S. Nafee, M. Hagar, H. A. Ahmed, O. A. Alhaddad, R. M. El-Shishtawy and B. M. Raffah, J. Mol. Liq., 2019, 112161, DOI:10.1016/j.molliq.2019.112161.
- H. Gulbas, D. Coskun, Y. Gursel and B. Bilgin-Eran, Adv. Mater., 2014, 5, 333–338 Search PubMed.
- S. S. Nafee, M. Hagar, H. A. Ahmed, R. M. El-Shishtawy and B. M. Raffah, Molecules, 2019, 24, 3032 CrossRef PubMed.
- R. Alnoman, H. A. Ahmed and M. Hagar, Molecules, 2019, 24, 4293 CrossRef PubMed.
- H. Ahmed and G. Saad, Liq. Cryst., 2015, 42, 1765–1772 CrossRef CAS.
- N. E. Mahmoud, G. R. Saad, A. A. Fahmi and M. M. Naoum, Liq. Cryst., 2018, 45, 1711–1722 CrossRef CAS.
- G. R. Saad, N. H. Ahmed, A. A. Fahmi, M. M. Kaddah and M. M. Naoum, Liq. Cryst., 2019, 1–13 Search PubMed.
- N. H. Ahmed, G. R. Saad and M. M. Naoum, Liq. Cryst., 2019, 1–12 Search PubMed.
- C. Tschierske, Liq. Cryst., 2018, 45, 2221–2252 CrossRef CAS.
- J. W. Goodby, Liq. Cryst., 2017, 44, 1755–1763 CAS.
- C. Zannoni, Liq. Cryst., 2018, 45, 1880–1893 CrossRef CAS.
- M. Hagar, H. A. Ahmed, S. S. Nafee, R. M. El-Shishtawy and B. M. Raffah, Molecules, 2019, 24, 3032 CrossRef PubMed.
- V. Prasad, N. Nagendrappa Gowdru and M. Manjunath, Liq. Cryst., 2018, 45, 666–679 CrossRef CAS.
- D. A. Paterson, R. Walker, J. P. Abberley, J. Forestier, W. T. Harrison, J. M. Storey, D. Pociecha, E. Gorecka and C. T. Imrie, Liq. Cryst., 2017, 44, 2060–2078 CAS.
- A. Nesrullajev and B. Bilgin-Eran, Mater. Chem. Phys., 2005, 93, 21–25 CrossRef CAS.
- O. Yasa-Sahin, O. Yazici, B. Karaagac, D. Sakar, O. Cankurtaran, B. Bilgin-Eran and F. Karaman, Liq. Cryst., 2010, 37, 1111–1118 CrossRef CAS.
- N. Y. Canli, S. Günes, A. Pivrikas, A. Fuchsbauer, D. Sinwel, N. Sariciftci, Ö. Yasa and B. Bilgin-Eran, Sol. Energy Mater. Sol. Cells, 2010, 94, 1089–1099 CrossRef.
- G. Bhola and U. Bhoya, Mol. Cryst. Liq. Cryst., 2016, 630, 188–196 CrossRef CAS.
- H. Kelker and B. Scheurle, Angew. Chem., Int. Ed., 1969, 8, 884–885 CrossRef CAS.
- G. W. Gray, Thermotropic liquid crystals, John Wiley & Sons Inc, 1987 Search PubMed.
- P. J. Collings and M. Hird, Introduction to liquid crystals: chemistry and physics, CRC Press, 2017 Search PubMed.
- H. Ahmed, M. Hagar and O. Alhaddad, Liq. Cryst., 2019, 1–10 Search PubMed.
- M. Hagar, H. A. Ahmed and O. A. Alhaddadd, Crystals, 2018, 8, 359 CrossRef.
- M. Hagar, H. A. Ahmed and G. R. Saad, J. Mol. Liq., 2019, 273, 266–273 CrossRef CAS.
- H. Ahmed, M. Hagar, M. Alaasar and M. Naoum, Liq. Cryst., 2019, 46, 550–559 CrossRef CAS.
- M. Hagar, H. Ahmed and O. Alhaddadd, Crystals, 2018, 8, 359 CrossRef.
- M. Hagar, S. M. Soliman, F. Ibid and H. El Sayed, J. Mol. Struct., 2013, 1049, 177–188 CrossRef CAS.
- S. M. Soliman, M. Hagar, F. Ibid and H. El Sayed, Spectrochim. Acta, Part A, 2015, 145, 270–279 CrossRef CAS PubMed.
- M. Hagar, S. M. Soliman, F. Ibid and H. El Sayed, J. Mol. Struct., 2016, 1108, 667–679 CrossRef CAS.
- A. Aboelnaga, M. Hagar and S. M. Soliman, Molecules, 2016, 21, 848 CrossRef PubMed.
- M. Hagar, H. Ahmed and G. Saad, Liq. Cryst., 2018, 45, 1324–1332 CrossRef CAS.
- M. Gür, H. Kocaokutgen and M. Taş, Dyes Pigm., 2007, 72, 101–108 CrossRef.
- H. Kocaokutgen and I. Gümrükçüoğlu, J. Therm. Anal. Calorim., 2003, 71, 675–679 CrossRef CAS.
- D. F. DeTar and A. R. Ballentine, J. Am. Chem. Soc., 1956, 78, 3916–3920 CrossRef CAS.
- A. Andrei, A. Moanţă, M. Dumitru, H. O. Manolea, A. Andrei, M. Dinescu and C. Goldner-Constantinescu, J. Therm. Anal. Calorim., 2017, 128, 89–105 CrossRef.
- A. Rotaru, C. Constantinescu, P. Rotaru, A. Moanţâ, M. Dumitru, M. Socaciu, M. Dinescu and E. Segal, J. Therm. Anal. Calorim., 2008, 92, 279 CrossRef CAS.
- A. Rotaru, G. Brătulescu and P. Rotaru, Thermochim. Acta, 2009, 489, 63–69 CrossRef CAS.
- A. Rotaru and M. Dumitru, J. Therm. Anal. Calorim., 2017, 127, 21–32 CrossRef CAS.
- C. Imrie and L. Taylor, Liq. Cryst., 1989, 6, 1–10 CrossRef CAS.
- C. T. Imrie, Liq. Cryst., 2006, 33, 1449–1485 CrossRef CAS.
- T. Donaldson, H. Staesche, Z. Lu, P. Henderson, M. Achard and C. Imrie, Liq. Cryst., 2010, 37, 1097–1110 CrossRef CAS.
- P. A. Henderson, O. Niemeyer and C. T. Imrie, Liq. Cryst., 2001, 28, 463–472 CrossRef CAS.
- P. A. Henderson and C. T. Imrie, Liq. Cryst., 2011, 38, 1407–1414 CrossRef CAS.
- O. Alhaddad, H. Ahmed and M. Hagar, Molecules, 2020, 25, 365 CrossRef CAS.
- S. S. Nafee, H. Ahmed and M. Hagar, Liq. Cryst., 2020, 1–12 Search PubMed.
- S. S. Nafee, M. Hagar, H. A. Ahmed, O. Alhaddad, R. M. El-Shishtawy and B. M. Raffah, J. Mol. Liq., 2019, 112161 Search PubMed.
- S.-T. Ha and T.-L. Lee, ISRN Mater. Sci., 2014, 2014, 1–7 CrossRef.
- T. Wöhrle, I. Wurzbach, J. Kirres, A. Kostidou, N. Kapernaum, J. Litterscheidt, J. C. Haenle, P. Staffeld, A. Baro, F. Giesselmann and S. Laschat, Chem. Rev., 2016, 116, 1139–1241 CrossRef PubMed.
- I.-C. Khoo and S.-T. Wu, Optics and nonlinear optics of liquid crystals, World Scientific, 1993 Search PubMed.
- D. S. Chemla, Nonlinear optical properties of organic molecules and crystals, Elsevier, 2012 Search PubMed.
- G. R. Meredith, J. VanDusen and D. J. Williams, Macromolecules, 1982, 15, 1385–1389 CrossRef CAS.
- M. Hagar, H. A. Ahmed and O. A. Alhaddad, Liq. Cryst., 2019, 1440–1451, DOI:10.1080/02678292.2019.1581290.
- M. Hagar, H. Ahmed and O. Alhaddad, Liq. Cryst., 2019, 1–12 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10499b |
| This journal is © The Royal Society of Chemistry 2020 |