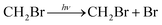DOI:
10.1039/C9RA10511E
(Paper)
RSC Adv., 2020,
10, 24308-24318
Computational study on the mechanisms and kinetics of the CH2BrO2 + ClO reaction in the atmosphere†
Received
14th December 2019
, Accepted 4th February 2020
First published on 25th June 2020
Abstract
The singlet and triplet potential energy surfaces for the CH2BrO2 + ClO reaction are studied at the CCSD(T)/cc-pVTZ//B3LYP/6-311++G(d,p) level. CH2BrO2 is revealed to react with ClO through two kinds of mechanisms on the triplet potential energy surface (PES), namely, SN2 displacement and H-abstraction, and the production of P3 (CHBrO2 + HOCl) via H-abstraction is the dominant channel. Addition/elimination and SN2 displacement mechanisms exist on the singlet PES and are more complicated. The RRKM calculations of the mechanism and product distribution in the CH2BrO2 + ClO reaction show that the stabilization of IM1 (CH2BrOOOBr) is dominant at T ≤ 600 K, while the pathway of producing P1 (CHBrO + HO2 + Cl) occupies the entire reaction at T > 600 K. The total rate constants are independent of pressure, while the individual rate constants are sensitive to pressure. The lifetime of CH2BrO2 in the presence of ClO is estimated to be 20.27 h. Moreover, time-dependent density functional theory (TDDFT) calculations suggest that IM1 (CH2BrOOOCl), IM2 (CH2BrOOClO) and IM3 (CH2BrOClO2) will photolyze under the sunlight.
1. Introduction
Owing to the significant contribution of halogens to stratospheric ozone depletion, the atmospheric oxidation of halogens has been extensively studied in the past decades. In recent years, the oxidation process of halogenated compounds was investigated in the atmosphere because these compounds are conducive to the conversion of halogens in the stratosphere.1,2 Significant attention has been focused on chlorine compounds, which have a huge impact on the atmosphere. Although the concentration of bromine is very low, it can deplete the stratospheric ozone very effectively; thus, it plays an important role in stratospheric chemistry.3,4 The oxidation process of brominated compounds has aroused the interest of researchers in recent years. The CH2Br radical is obtained either by CH3Br reacting with OH/Cl, which abstracts an H atom from CH3Br, or the photolysis of C–Br bonds in CH2Br2; the CH2Br radical further reacts with ambient O2 to produce CH2BrO2:5
| CH3Br + OH/Cl → CH2Br + H2O/HCl |
Because of the significant role of halogens in the stratosphere and troposphere, more and more attention has been focused on them in recent years. For instance, the reactions of ClO with the organic peroxy radicals such as HO2, CH3O2, CF3O2, CFCl2O2 CFCl2CH2O2 and CH3CFClO2 have been reported experimentally and theoretically.6–16 However, no studies have been reported for the CH2BrO2 + ClO reaction that, in principle, may contribute to the removal of CH2BrO2 and ClO and thereby impact stratospheric ozone depletion. Therefore, we first reported the mechanisms of CH2BrO2 + ClO, and the possible product channels are presented in Scheme 1. The present theoretical study aims at providing a description of the mechanism and kinetics of the multiple channel reaction and supply data about the gas phase reaction of CH2BrO2 + ClO by employing high-level quantum chemical methods and RRKM-TST theory,17 which has been successfully used with complex reactions.18–23 In the present kinetic calculations, we used a modified computer program written for the C2H5CO + O2 reaction by Hou and Wang.19
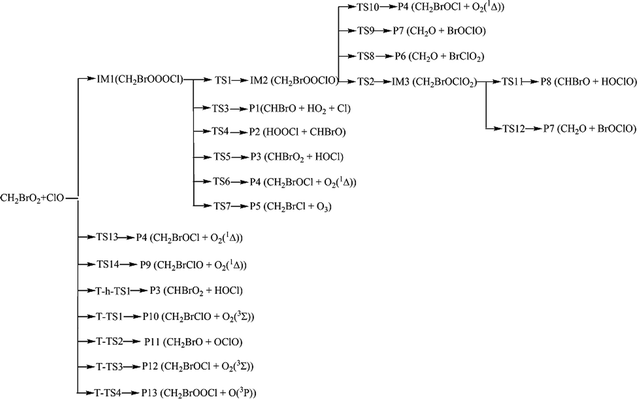 |
| | Scheme 1 The reaction pathways of the CH2BrO2 + ClO reaction on the singlet and triplet PESs. | |
2. Computational methods
2.1 Electronic structure calculations
Full geometry optimizations (including reactants, intermediates, transition states and products) were carried out at the B3LYP24,25 level of theory using the 6-311++G(d,p) basis set. The B3LYP method has been proven to be an economical and accurate computational model for predicting electronic structures and has been employed widely.26,27 Compared with other levels of theory, it was found to be sufficiently accurate for predicting the reliable geometries of the stationary points. At the same time, it is not expensive computationally for scanning the potential energy surface. Moreover, B3LYP theory can effectively suppress the problem of spin contaminants. At the same level of geometry optimization, all stationary points were characterized by harmonic vibrational frequency analysis (the number of imaginary frequencies, NIMAG, 0 for minima and 1 for transition state). To confirm that a transition state connects the right reactants and products, the intrinsic reaction coordinate (IRC)28,29 path was performed at the B3LYP/6-311++G(d,p) level of theory. Based on the B3LYP/6-311++G(d,p) level optimized geometries, the single-point energies of all the species were refined by coupled cluster theory with single and double with perturbative triple excitations CCSD(T)30 with the cc-pVTZ basis set. To ensure that all stationary points were treated with a single-reference based wave function, the T1-diagnostic was evaluated for each point using CCSD(T)/cc-pVTZ. The T1 diagnostic value gives a qualitative assessment of the significance of non-dynamic correction. For closed-shell systems, values exceeding 0.02 are suspect. However, Lee et al.31 suggested that T1-diagnostic values for open-shell systems may be larger. A number of studies have shown that the multireference wave function is significant if the T1 diagnostic value calculated is greater than 0.045.31–34 The T1 values of the closed-shell and open-shell species in our system are smaller than 0.02 and 0.045, except for TS6, TS13, TS14, T-TS2, and T-TS4. Fortunately, the five species are not important on the triplet and singlet potential energy surfaces and do not affect the reaction mechanism and dynamic behavior. All the calculations were carried out using the GAUSSIAN 09 program package.35
2.2 Calculations of rate constants
The microcanonical rate constant was calculated using the RRKM theory as follows:
| ki(E) = αiCiNi(E≠i)/hρj(Ej) |
In the above equation, αi is the statistical factor (degeneracy) for the ith reaction path. Ni(E≠i) is the number of states at the energy above the barrier height for transition state i; ρj(Ej) is the density of states at energy Ej of the intermediate. The density of states and the number of states were calculated using the extended Beyer–Swinehart algorithm.36,37
3. Results and discussion
The corresponding equilibrium structures of the intermediates and transition states are depicted in Fig. 1, and all the reactants and products are depicted in Fig. 2, with the corresponding limited experimental data.38 The computational bond lengths of CH2O, OClO, HOCl, HO2, ClO, HCl, O2(3Σ) and O3 are in good agreement with the corresponding experimental values. To clarify the reaction mechanism, the relevant pathways of the singlet and triplet PESs for the CHBr2O2 + ClO reaction at the CCSD(T)/cc-pVTZ//B3LYP/6-311++G(d,p) level are depicted in Fig. 3. Table S1† summarizes the relative energies including the ZPE corrections of the stationary points. The Z-matrix Cartesian coordinates of all species found on the singlet and triplet PESs are shown in Table S2.† Table S3† displays the harmonic vibrational frequencies and the moment of inertia of all the intermediate and transition states along with available experimental values.
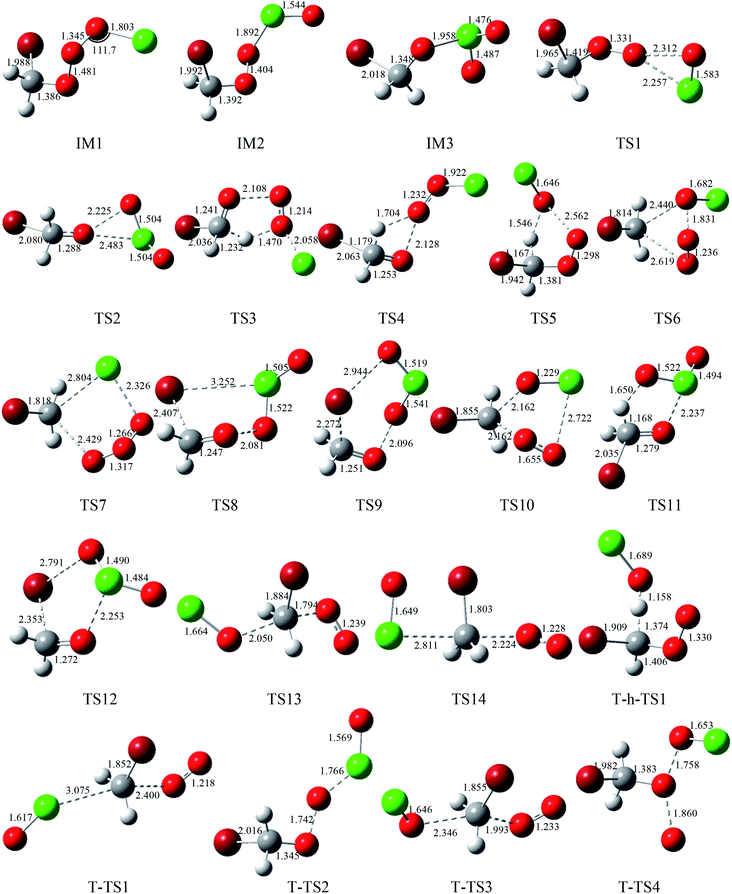 |
| | Fig. 1 Optimized geometries (length in Å and angle in degree) for all the intermediates and transition states at the B3LYP/6-311++G(d,p) level. | |
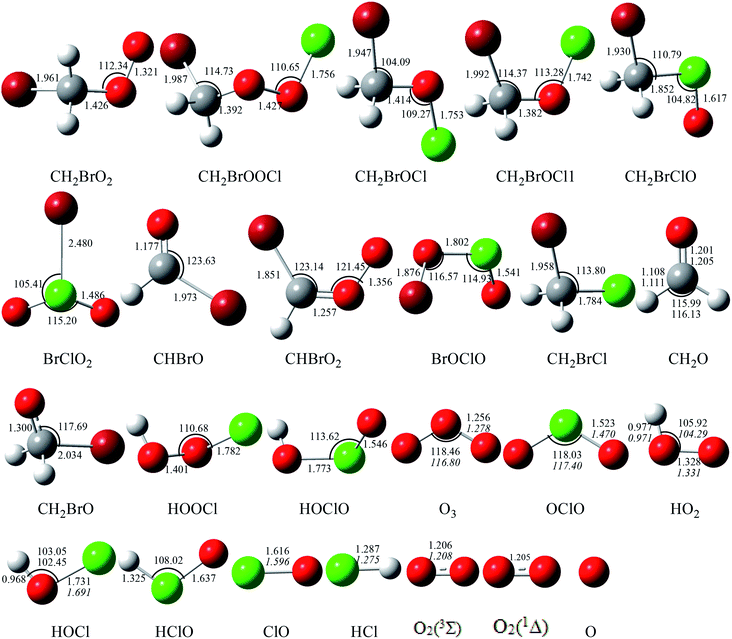 |
| | Fig. 2 Optimized geometries (length in Å and angle in degree) for all the reactants and products at the B3LYP/6-311++G(d,p) level. The values in italics are experimental data from ref. 38. | |
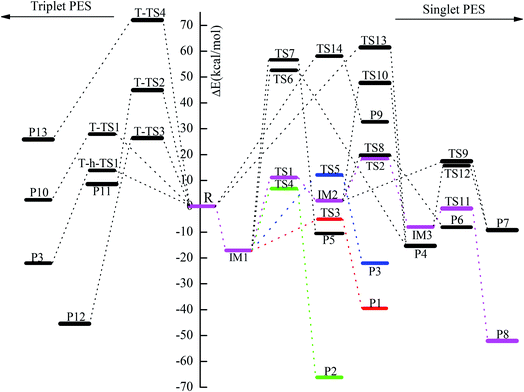 |
| | Fig. 3 Potential energy diagram of the reaction channels for the reaction of CH2BrO2 with ClO at the CCSD(T)/cc-pVTZ//B3LYP/6-311++G(d,p) level. | |
For the title reaction, our results indicate that addition/elimination and SN2 displacement mechanisms take place on the singlet PES, while SN2 displacement and H-abstraction mechanisms occur on the triplet PES. Next, we will provide a detailed discussion of these processes.
3.1 The mechanism on the singlet PES
3.1.1 The production of adducts on the singlet PES. On the singlet surface, the most significant characteristic of the potential energy surface (PES) of the CH2BrO2 + ClO reaction is the ability to form the minimum peroxide compound IM1 (CH2BrOOOCl) with no barrier. The newly formed O–O bond is 1.345 Å, the other O–O and C–Br bonds are somewhat longer, and the C–O bond is somewhat smaller than those in the CH2BrO2 radical. The isomer IM2 (CH2BrOOClO) is more unstable than IM1 (CH2BrOOOCl) and may be formed passing through the isomerization transition state TS1. TS1 presents a OOCl three-center geometry, which is formed by migration of the Cl atom to the middle-O atom, accompanied with cleavage of the O–O bond. The migrating chlorine is found 2.257 Å away from the shifting end-O by decreasing the OOCl angle from 111.7° to 68.9° and the breaking O–O bond is 2.312 Å. The barrier for IM1 (CH2BrOOOCl) → TS1 → IM2 (CH2BrOOClO) is 28.2 kcal mol−1, and IM2 (CH2BrOOClO) is still 2.2 kcal mol−1 higher than the separate molecular CH2BrO2 + ClO, so the isomerization process may be possible at high temperatures. Subsequently, IM2 (CH2BrOOClO) can surmount the TS2 barrier, leading to IM3 (CH2BrOClO2), where the –ClO is transferred to the middle-O atom of the COO– skeleton, and the simultaneous breakage of the O–O bond occurs. The O–O bond breaking in the triangular TS2 is stretched to 2.225 Å and the formed Cl–O bond is 2.483 Å long. The magnitude of the imaginary frequency for TS2 is 140i cm−1. The barrier for the IM2 (CH2BrOOClO) → TS2 → IM3 (CH2BrOClO2) process is 16.3 kcal mol−1. In any case, the isomerization of IM2 → TS2 → IM3 is energetically more favorable than the isomerization of IM1 → TS1 → IM2 by 11.9 kcal mol−1. Therefore, once IM2 (CH2BrOOClO) is formed, IM1 can easily convert to IM3. At the CCSD(T)//B3LYP level, the energy of IM1 (CH2BrOOOCl), IM2 (CH2BrOOClO) and IM3 (CH2BrOClO2) are −17.1, 2.2 and −8.0 kcal mol−1 relative to CH2BrO2 + ClO, respectively, which may involve various dissociation processes, and will be discussed below.
3.1.2 Decomposition channels from IM1 (CH2BrOOOCl) on the singlet PES. The energy-rich addition complex IM1 (CH2BrOOOCl) could decompose to various products. Through TS3, with the 1,4-H shift and the breaking of the O–O bond of the nearly planar HCOOO ring, associated with the breakage of the isolated O–Cl bond (pointed out of the plane), the product P1 (CHBrO + HO2 + Cl) is formed, which is the most feasible pathway in energy. The barrier for the IM1 → TS3 → P1 process is 12.1 kcal mol−1. The elimination channel is the most exothermic (ΔH = 32.9 kcal mol−1), and the relative Gibbs free energy (ΔG) is −47.5 kcal mol−1 (Table S1†), indicating that the decomposition pathway to P1 (CHBrO + HO2 + Cl) is spontaneous and contributes more to the reaction under certain conditions.The second route involves the HOOCl-elimination through TS4, with one of the hydrogen atoms in the –CH2Br group moving to the middle-O atom of the –OOO– skeleton. The breaking C–H and O–O bonds in the HCOO four-center structure TS4 are stretched to 1.179 and 2.128 Å, and the forming O–H bond is 1.704 Å long. Although the whole R (CH2BrO2 + ClO) → IM1 (CH2BrOOOCl) → TS4 → P2 (HOOCl + CHBrO) reaction is highly exothermic by about 60.6 kcal mol−1, and the relative Gibbs free energy (ΔG) is −66.7 kcal mol−1 (Table S1†), the barrier for the IM1 → TS4 → P2 process is 24.0 kcal mol−1, indicating that this HOOCl-elimination process is spontaneous and may be efficient in the high temperature region.
The production of the P3 (CHBrO2 + HOCl) channel from IM1 (CH2BrOOOCl) takes place via an HCOOO five-centered-ring. As shown in Fig. 1, TS5 occurs via the migration of one of the hydrogen atoms in the –CH2Br group to the middle-O atom of the –OOCl skeleton accompanied by cleavage of the O–O bond. In the five-center HCOOO structure, the length of the H atom to either the C atom or the O atom is 1.167 or 1.546 Å, respectively, and the broken O–O bond is 2.562 Å. The IM1 (CH2BrOOOCl) → TS5 → P3 (CHBrO2 + HOCl) reaction is moderately exothermic by 16.4 kcal mol−1, and the HOCl-elimination barrier is predicted to be 29.2 kcal mol−1, which are 17.1 and 5.2 kcal mol−1 higher than the processes of IM1 → TS3 → P1 and IM1 → TS4 → P2, respectively, suggesting that the HOCl-elimination pathway is less competitive with the production of the P1 (CHBrO + HO2 + Cl) and P2 (HOOCl + CHBrO) pathways, and may be unimportant for the CH2BrO2 + ClO reaction.
In addition, the –ClO group or Cl atom shifting from IM1 (CH2BrOOOCl) respectively undergoes the COOO four-center transition state TS6 or COOOCl five-center transition state TS7 to produce P4 (CH2BrOCl + O2(1Δg)) and P5 (CH2BrCl + O3). In TS6, the C–O and O–O bonds that will be broken and the C–O bond that will be formed are extremely long at 2.619, 1.831, and 2.440 Å, respectively. In TS7, the breaking C–O and O–Cl bonds and the forming C–Cl bond are 2.429, 2.326, and 2.804 Å, respectively. The vibrational frequency analysis of TS6 and TS7 suggest only one imaginary frequency of 378i and 461i cm−1, respectively. The energy barriers for the dissociation of IM1 (CH2BrOOOCl) → TS6 → P4 (CH2BrOCl + O2 (1Δg)) and IM1 (CH2BrOOOCl) → TS7 → P5 (CH2BrCl + O3) are extremely high, 69.7 and 73.7 kcal mol−1, respectively, and thus these two dissociation channels may be excluded judging from the higher barrier heights.
3.1.3 Decomposition channels from IM2 (CH2BrOOClO) on the singlet PES. When we considered the decomposition channels from IM2 (CH2BrOOClO), it could undergo respective O–O bond breaking associated with the 1,4-Br shift or 1,5-Br shift from the C to the Cl atom or the terminal-O atom of the –OClO skeleton (i.e., TS8 and TS9) to yield the final product P6 (CH2O + BrClO2) and P7 (CH2O + BrOClO). In TS8 and TS9, the loose COOClBr five-membered ring and COOClOBr six-membered ring are non-planar, respectively. In TS8, the Cl–Br bond that will be formed and the C–Br and O–O bonds that will be broken are as long as 3.252, 2.407, and 2.081 Å, respectively. In TS9, the breaking O–O and C–Br bonds and the forming Br–O bond are 2.096, 2.272, and 2.944 Å, respectively. The barrier heights for the channels of IM2 (CH2BrOOClO) → TS8 → P6 (CH2O + BrClO2) and IM2 (CH2BrOOClO) → TS9 → P7 (CH2O + BrOClO) are 17.6 and 15.2 kcal mol−1, which are 1.3 kcal mol−1 higher and 1.1 kcal mol−1 lower than the process of IM2 → TS2 → IM3, suggesting that these three channels could be competitive with each other.P4 (CH2BrOCl + O2(1Δg)) could also be produced from IM2 (CH2BrOOClO) via transition state TS10 involving the terminal-O atom migrating to the carbon atom, associated with the C–O and Cl–O bonds breaking. The located loose COOClO five-centered-ring is non-planar in TS10. In comparison with the production channels of P6 (CH2O + BrClO2) and P7 (CH2O + BrOClO) from IM2 (CH2BrOOClO), the pathway of IM2 (CH2BrOOClO) → TS10 → P4 (CH2BrOCl + O2) has a higher dissociation barrier (45.6 kcal mol−1), meaning this decomposition pathway may not be plausible for the title reaction.
3.1.4 Decomposition channels from IM3 (CH2BrOClO2) on the singlet PES. Two possible decomposition channels from IM3 (CH2BrOClO2) are the elimination of the HOClO or BrOClO to form CHBrO or CH2O, respective with either the H atom or Br atom in the –CH2Br group shifting to the O atom, associated with the O–Cl bond cleavage. The BrOClO-elimination is not important compared with the HOClO-eliminations, as the BrOClO-elimination barrier is 16.6 kcal mol−1 higher than the HOClO-elimination. Moreover, the overall exothermicity of the IM3 → TS11 → P8 (CHBrO + HOClO) and IM3 → TS12 → P7 (CH2O + BrOClO) reactions are 46.3 and 3.0 kcal mol−1, implying that P8 (CHBrO + HOClO) is easily produced once IM3 (CH2BrOClO2) is produced.
3.1.5 SN2 displacement channels on the singlet PES. The O atom or the Cl atom in the ClO radical could attack the C site of CH2BrO2, kicking off the O2 (1Δg) and producing the CH2BrOCl or CH2BrClO, respectively. The transition states involved in these two substitution steps are TS13 and TS14, respectively. The forming and breaking C–O bond in TS13 are 2.050 and 1.794 Å, meanwhile the forming C–Cl bond and breaking C–O bond in TS14 are 2.811 and 2.224 Å, respectively. The barrier heights for these two channels, 61.5 and 58.1 kcal mol−1, are rather high, therefore, these two elementary substitution channels are prohibited for the title reaction.
3.2 The mechanisms on the triplet PES
H-abstraction and SN2 displacement reaction mechanisms are presented on the triplet surface. The P3 (CHBrO2 + HOCl) products on the triplet PES, exothermic by 16.4 kcal mol−1, can be achieved by the O atom of the ClO radical directly abstracting from the –CH2Br group through T-h-TS1. The barrier of CH2BrO2 + ClO → T-h-TS1 → P3 (CHBrO2 + HOCl) is 13.9 kcal mol−1, which involves the lowest barrier on the PES. Four SN2 displacement reaction channels between CH2BrO2 and ClO could take place on the triplet PES. The Cl atom of the ClO radical could attack the carbon atom or the terminal oxygen atom of the CH2BrO2, kicking off the O2 (3Σ) or CH2BrO to give CH2BrClO or OClO via T-TS1 or T-TS2, or the oxygen atom of the ClO radical could attack the carbon atom or the middle oxygen atom of the CH2BrO2, simultaneously with the departure of O2(3Σ) and O(3P), leading to CH2BrOCl or CH2BrOOCl via T-TS3 or T-TS4, respectively. The predicted heat of reaction for the production of P10 (CH2BrClO + O2(3Σ)), P11 (CH2BrO + OClO), P12 (CH2BrOCl + O2(3Σ)) and P13 (CH2BrOOCl + O(3P)) is 8.5, 14.1, −39.6 and 31.7 kcal mol−1, respectively. The above four substituent channels involve high barriers (28.0, 45.0, 26.4 and 72.0 kcal mol−1) with respect to the reactants, which are 14.1, 31.1, 12.5 and 58.1 kcal mol−1 higher than that of the H-abstraction pathway, thus, these four substituent routes on the triplet are not competitive with the H-abstraction pathway.
3.3 Rate constant calculations
As discussed above, for the reaction pathways producing P1, P2, P3, P6, P7 and P8 (Scheme 1), the reaction energy barriers are lower and the reactions are exothermic, so these reaction pathways are involved in the kinetics calculations. However, the reaction pathways producing P4, P5, P9, P10, P11, P12 and P13 with higher energy barriers are less competitive in energy, and their contribution to the total reaction is negligible.
Temperature- or pressure-dependent rate constants for the important pathways (Scheme 2) of the CH2BrO2 + ClO reaction were calculated at 200–3000 K and 10−10 to 1010 atm using RRKM theory, based on the optimized geometries, moment of inertia and frequencies obtained at the B3LYP/6-311++G(d,p) level, and the energies were obtained at the CCSD(T)/cc-pVTZ level.
 |
| | Scheme 2 The dominant channels for the CH2BrO2 + ClO reaction. | |
The steady-state approximation for all energized intermediates (IM1*, IM2* and IM3*) leads to the following expressions:
| |
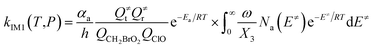 | (1) |
| |
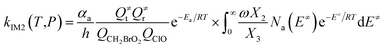 | (2) |
| |
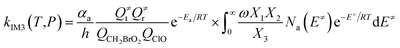 | (3) |
| |
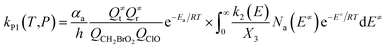 | (4) |
| |
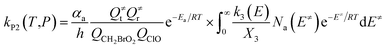 | (5) |
| |
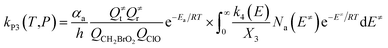 | (6) |
| |
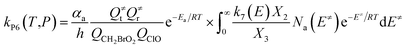 | (7) |
| |
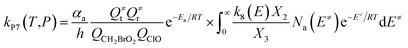 | (8) |
| |
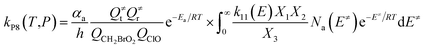 | (9) |
with the following definitions:
| X1 = k9(E)/(k10(E) + k11(E) + ω) |
| X2 = k5(E)/(k6(E) + k7(E) + k8(E) + k9(E) + ω − k10(E)X1) |
| X3 = k1(E) + k2(E) + k3(E) + k4(E) + k5(E) + ω − k6(E)X2 |
In the above equations, αa is the statistical factor for the reaction path a, and Ea is the energy barrier for the reaction step a. QClO and QCH2BrO2 are the total partition functions of ClO and CH2BrO2, respectively; Q≠tand Q≠r are the translational and rotational partition functions of the entrance transition state, respectively; Na(E≠) is the number of states for the association transition state with excess energy E≠ above the association barrier. ki(E) is the energy-specific rate constant for the ith channel and Ci is the ratio of the overall rotational partition function of the TSi and IMj.
Based on the above thermodynamic results obtained at the CCSD(T)//B3LYP level, the kinetic calculations were performed for the dominant addition/elimination channels (on the singlet PES) and the direct H-abstraction channel (on the triplet PES) using RRKM theory. The temperature dependence of the total and individual rate constants at a selected temperature range of 200–3000 K are shown in Fig. 4. The rate constants for IM1 (CH2BrOOOCl), IM2 (CH2BrOOClO), IM3 (CH2BrOClO2), P1 (CHBrO + HO2 + Cl), P2 (CHBrO + HOOCl), P3 (CHBrO2 + HOCl), P6 (CH2O + BrClO2), P7 (CH2O + BrOClO), and P8 (CHBrO + HOClO) and the rate constants of the H-abstraction channel on the triplet PES are labeled as kIM1, kIM2, kIM3, kP1, kP2, kP3, kP6, kP7, kP8 and kT-h-TS1, respectively. The overall rate constant for the CH2BrO2 + ClO reaction is denoted as kover, where kover = kIM1 + kIM2 + kIM3 + kP1 + kP2 + kP3 + kP6 + kP7 + kP8 + kT-h-TS1.
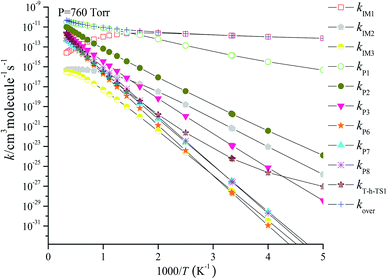 |
| | Fig. 4 Predicted rate coefficients of total and individual primary pathways at 760 torr, N2 in the temperature region of 200–3000 K for the CH2BrO2 + ClO reaction. | |
Fig. 4 reveals the contributions of IM1, IM2, IM3, P1, P2, P3, P6, P7, P8 and the H-abstraction channel on the triplet PES to the CH2BrO + ClO reaction versus 1000/T between 200 and 3000 K. Fig. 4 indicates that kIM1 reveals weak temperature dependence at T ≤ 600 K first and then decreases with increasing temperature, and the rate constants for other pathways exhibit a positive temperature dependence at 200–3000 K. The contribution of IM1 (CH2BrOOOCl) takes over the reaction below 600 K. Meanwhile, the contribution of P1 (CHBrO + HO2 + Cl) becomes more important than that of other products at T > 600 K. For example, the values of kIM1/kover are 1.00 at 200 K and 0.62 at 600 K (Fig. 5), respectively. However, as the temperature increases, the channel of production of P1 (CHBrO + HO2 + Cl) overcomes IM1 (CH2BrOOOCl) and becomes predominant, and the ratios of kP1/kover are 0.56 at 600 K, 0.94 at 1400 K and 0.66 at 3000 K (Fig. 5).
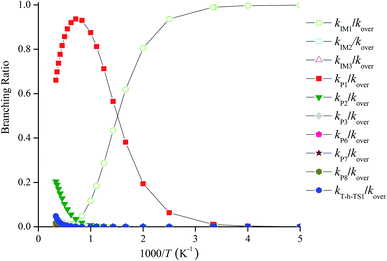 |
| | Fig. 5 Forecasted branching ratios for the CH2BrO2 + ClO reaction at 760 torr. | |
RRKM calculated the overall high-pressure limit rate constants kinf(over) and the individual high-pressure limit rate constants kinf(IM1), kinf(IM2), kinf(IM3), kinf(P1), kinf(P2), kinf(P3), kinf(P6), kinf(P7), kinf(P8) and kinf(T-h-TS1) in the temperature range of 200–3000 K are illustrated in Fig. 6. kinf(IM1) is equal to kinf(over), which implies that the most favorable channel is the stabilization of IM1 (CH2BrOOOCl) at 200–3000 K. For the main emphasis is on atmospheric applications, the three-parameter Arrhenius fits the total high-pressure limit rate constants kinf(over) (in units of cm3 per molecule per s) within 200–3000 K as follows:
kinf(over) = 2.20 × 10−16T1.54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.54/T)(200 ≤ T ≤ 3000 K) exp(−0.54/T)(200 ≤ T ≤ 3000 K) |
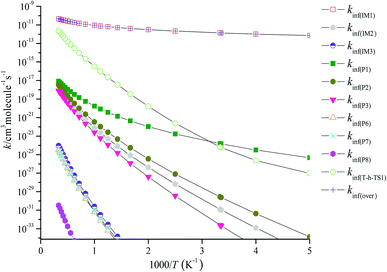 |
| | Fig. 6 Predicted high-pressure limit rate coefficients of total and individual primary pathways at high pressure in the temperature region of 200–3000 K. | |
We also investigated the pressure effect of the total and branching reaction rate constants at selected temperatures of 298, 500, 1000 and 3000 K (Fig. 7) and a pressure range of 10−10 to 1010 torr. Obviously, the overall rate constants are not subject to pressure. At 298, 500, 1000 and 3000 K, the stabilization of the IM1 (CH2BrOOOCl) is the significant channel at P ≥ 101, P ≥ 102, P ≥ 104 and P ≥ 106 torr, respectively; at lower pressure, the production of P1 (CHBrO + HO2 + Cl) is the dominant reaction channel.
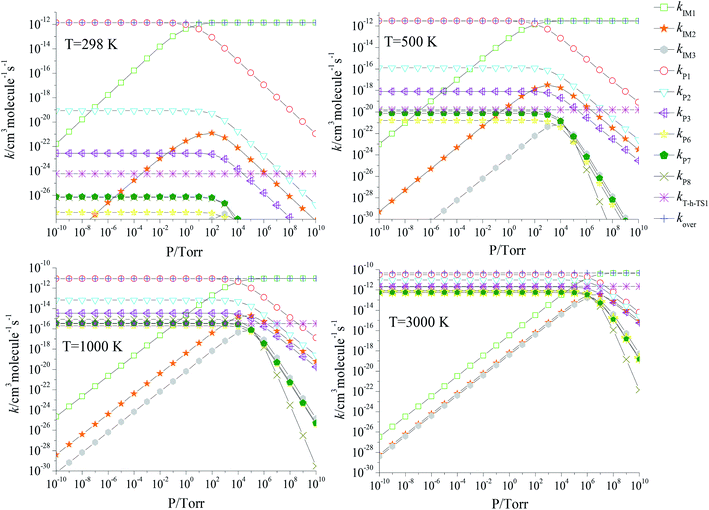 |
| | Fig. 7 Predicted rate coefficients of total and individual primary pathways at high pressures in the temperature region of 200–3000 K. | |
3.4 Vertical excitation energy of IM1 (CH2BrOOOCl), IM2 (CH2BrOOClO) and IM3 (CH2BrOClO2)
The photo-oxidation of compounds containing bromine and chlorine is significant for Br and Cl atmospheric chemistry, which as sources of Br and Cl, the photolysis might affect the stratosphere and troposphere. To gain new insights into the photolytic stability of the Br and Cl containing compounds, the vertical excitation energy (TV) of the first ten excited states for IM1 (CH2BrOOOCl), IM2 (CH2BrOOClO) and IM3 (CH2BrOClO2) were calculated by the TDDFT method using B3LYP/6-311++G(d,p), and the results comprising wavelength (λ), excitation energy (TV) and oscillator strength (f) are listed in Table 1. Compounds will be considered to photolyze if the TV value is smaller than 4.1 eV or the wavelength is longer than 300 nm.39,40 From Table 1, it is seen that the TV value of the first three excited states of IM1 (CH2BrOOOCl) and IM3 (CH2BrOClO2) are 382 nm (3.2 eV), 340 nm (3.6 eV), and 329 nm (3.7 eV) and 482 nm (2.5 eV), 465 nm (2.6 eV), and 410 nm (3.0 eV), respectively, and their oscillator strengths are 0.0014, 0.0003, and 0.0168, and 0.0021, 0.0202, and 0.0035. The first four excited states of IM2 (CH2BrOOClO) are 684 nm (1.8 eV), 374 nm (3.3 eV), 364 nm (3.4 eV) and 331 nm (3.7 eV), and the oscillator strengths are 0.0001, 0.0082, 0.0075, and 0.0041, respectively, indicating the possibility of photolysis of IM1 (CH2BrOOOCl), IM2 (CH2BrOOClO) and IM3 (CH2BrOClO2) under sunlight, which will cause them to be an origin of reactive bromine and chlorine species in the atmosphere.
Table 1 The excitation energy TV (in eV), oscillator strength f (in atomic units) and wavelength λ (in nm) of the first five excited states of IM1 (CH2BrOOOCl), IM2 (CH2BrO2ClO) and IM3 (CH2BrOClO2) at the TD-B3LYP/6-311++(d,p) level of theory
| Excited states |
IM1 (CH2BrOOOCl) |
IM2 (CH2BrOOClO) |
IM3 (CH2BrOClO2) |
| TV |
F |
λ |
TV |
f |
λ |
TV |
f |
λ |
| 1 |
3.2 |
0.0014 |
382.37 |
1.8 |
0.0001 |
684.81 |
2.5 |
0.0021 |
482.56 |
| 2 |
3.6 |
0.0003 |
340.18 |
3.3 |
0.0082 |
374.45 |
2.6 |
0.0202 |
465.33 |
| 3 |
3.7 |
0.0168 |
329.99 |
3.4 |
0.0075 |
364.59 |
3.0 |
0.0035 |
410.05 |
| 4 |
4.2 |
0.0003 |
294.26 |
3.7 |
0.0041 |
331.18 |
4.1 |
0.0518 |
299.90 |
| 5 |
4.4 |
0.0095 |
277.97 |
4.2 |
0.1482 |
289.55 |
4.3 |
0.0018 |
286.12 |
| 6 |
5.1 |
0.0037 |
239.07 |
4.8 |
0.0014 |
253.87 |
5.4 |
0.2292 |
229.05 |
| 7 |
5.2 |
0.0199 |
234.54 |
5.4 |
0.0297 |
226.09 |
5.4 |
0.0293 |
226.33 |
| 8 |
5.45 |
0.0592 |
227.54 |
5.6 |
0.0049 |
217.93 |
5.6 |
0.0007 |
219.90 |
| 9 |
5.6 |
0.0084 |
220.97 |
5.8 |
0.0002 |
211.35 |
5.8 |
0.0018 |
212.98 |
| 10 |
5.6 |
0.0882 |
218.85 |
6.1 |
0.0077 |
202.31 |
5.9 |
0.0013 |
206.78 |
3.5 Atmospheric lifetime of CH2BrO2
The atmospheric lifetime of CH2BrO2 can be calculated using the following formula: 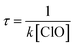 . Using the total rate constants, 1.37 × 10−12 cm3 per molecule per s for the CH2BrO2 + ClO reaction at 298 K and the global atmospheric ClO concentrations 1 × 107 molecules per cm3,41 the lifetime of CH2BrO2 was estimated to be 20.27 h, which suggests that the reaction of CH2BrO2 + ClO plays an important role in some special areas and the marine boundary layer.
. Using the total rate constants, 1.37 × 10−12 cm3 per molecule per s for the CH2BrO2 + ClO reaction at 298 K and the global atmospheric ClO concentrations 1 × 107 molecules per cm3,41 the lifetime of CH2BrO2 was estimated to be 20.27 h, which suggests that the reaction of CH2BrO2 + ClO plays an important role in some special areas and the marine boundary layer.
3.6 Atmospheric implications of CHBrO
With the concentration of around 107 molecules per cm3 in the stratosphere, OH/ClO radicals play a significant role in the degradation processes of many molecules.42 Thus, the formation of CHBrO as a major product in the title reaction could lead to further reactions with OH and ClO, respectively. To be thorough, the CHBrO + ClO/OH reactions were studied by the same methods, and the corresponding PESs are depicted in Fig. 8a and b, as well. According to the calculations, two channels were located via different transition states for these two reactions. The first scenario starts from transition states TS-ClO or TS-OH surmounting the barrier of 16.55 or 8.00 kcal mol−1, leading to the final products HCOOCl + Br or HCOOH + Br, respectively. Moreover, the hydrogen atom in CHBrO could be abstracted by OH/ClO radicals via h-TS-ClO or h-TS-OH. The IRC calculation confirms that the corresponding product is BrCO + HOCl or BrCO + H2O. The barrier height of h-TS-ClO and h-TS-OH is about 25.46 and −1.36 kcal mol−1. Thus, the OH-initiated reaction might be one of the main removal pathways for CHBrO.
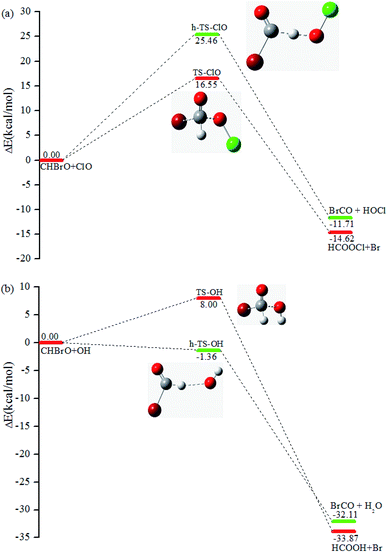 |
| | Fig. 8 Reaction channels and relative energy (unit: kcal mol−1) at the CCSD(T)/cc-pVTZ//B3LYP/6-311++G(d,p) level. (a) The energetic profile of the CHBrO with ClO reaction. (b) The energetic profile of the CHBrO with OH reaction. | |
3.7 Comparisons with the similar reaction of CH3O2 + ClO
In order to gain a deeper understanding of the reaction of CH2BrO2 + ClO, it is very important to compare the mechanism and kinetics between the title reaction and a similar system (CH3O2 + ClO).43 It is concluded that the addition/elimination and SN2 displacement mechanisms are found both on the singlet PES of the above two reactions. On the triplet PES, H-abstraction and SN2 displacement mechanisms are found for the CH2BrO2 + ClO reaction and only addition/elimination is identified for the CH3O2 + ClO reaction. By comparing the two reactions, we find that the most favorable channel is the oxygen atom in ClO attacking the terminal-O atom in CH2BrO2 and CH3O2, forming the intermediate CH2BrOOOCl and CH3OOOCl, and then decomposition to the final products CHBrO + HO2 + Cl and CH2O + HOOCl. The Br-substituted effect could be speculated to be of no significant role in the reactions of CH2BrO2 and CH3O2 with ClO in the atmospheric conditions. Also, no kinetic behaviors were discovered for the CH3O2 + ClO reaction theoretically. The total rate constants show temperature dependence and pressure independence for the reaction between CH2BrO2 and ClO.
4. Conclusions
The atmospheric oxidation process of CH2BrO + ClO was studied at the CCSD(T)//B3LYP level of theory. H-abstraction and SN2 displacement mechanisms on the triplet PES, and addition/elimination and SN2 displacement mechanisms on the singlet PES were identified, respectively. The dominant reaction mechanism on the triplet PES is H-abstraction, and on the singlet PES, addition/elimination. The rate constants of the title reaction at 200–3000 K have been calculated employing a Fortran code based on RRKM theory. According to the obtained kinetics data, the ClO-addition to the terminal-O of CH2BrO2 producing IM1 (CH2BrOOOCl) dominates the title reactions at T ≥ 600 K on the singlet PES, and the O atom of ClO abstracting one of the H atoms in CH2BrO2 dominates the whole reaction at T > 600 K on the triplet PES. The atmospheric lifetime of CH2BrO2 in the presence of ClO is predicted to be 20.27 h. IM1 (CH2BrOOOCl), IM2 (CH2BrOOClO) and IM3 (CH2BrOClO2) will photolyze under sunlight, which might be one source of Br and Cl containing species in the atmosphere.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Natural Science Foundations of China (No. 21707062 & 41775119), Scientific Research Starting Foundation of Mianyang Normal University (No. QD2016A007).
References
- B. Finlayson-Pitts and J. N. Pitts Jr, Chemistry of the Upper and Lower Atmosphere, Academic Press, New York, 1999 Search PubMed.
- R. P. Wayne, Chemistry of Atmospheres, Oxford University Press, Oxford, 3rd edn, 2000 Search PubMed.
- D. L. Albritton and R. T. Watson, Methyl Bromide: Its Atmospheric Science, Technology and Economics, Montreal Protocol Assessment Supplement. UNEP, Nairobi, Kenya, 1993 Search PubMed.
- S. A. Montzka and S. Reimann, et al., Ozone-depleting substances (ODSs) and related chemicals. Scientific Assessment of Ozone Depletion: 2010, Global Ozone Research and Monitoring Project Report No. 52, World Meteorological Organization, Geneva, Switzerland, ch. 1, 2011 Search PubMed.
- W. S. McGivern, H. Kim, J. S. Francisco and S. W. North, J. Phys. Chem. A, 2004, 108, 7247–7252 CrossRef CAS.
- K. M. Hickson, L. F. Keyser and S. P. Sander, J. Phys. Chem. A, 2007, 111, 8126–8138 CrossRef CAS PubMed.
- S. L. Nickolaisen, S. M. Roehl, L. K. Blakely, R. R. Fridel, J. S. Francisco, R. F. Liu and S. P. Sander, J. Phys. Chem. A, 2000, 104, 308–319 CrossRef CAS.
- G. P. Knight, T. Beiderhase, F. Helleis, G. K. Moortgat and J. N. Crowley, J. Phys. Chem. A, 2000, 104, 1674–1685 CrossRef CAS.
- Z. F. Xu, R. S. Zhu and M. C. Lin, J. Phys. Chem. A, 2003, 107, 3841–3850 CrossRef CAS.
- E. Drougas, A. F. Jalbout and A. M. Kosmas, J. Phys. Chem. A, 2003, 107, 11386–11390 CrossRef CAS.
- F. Helleis, J. N. Crowley and G. K. Moortgat, J. Phys. Chem., 1993, 97, 11464–11473 CrossRef CAS.
- F. Helleis, J. N. Crowley and G. K. Moortgat, Geophys. Res. Lett., 1994, 21, 1795–1798 CrossRef CAS.
- A. S. Kukui, T. P. W. Jungkamp and R. N. Schindler, Ber. Bunsen Phys Chem., 1994, 98, 1298–1302 CrossRef CAS.
- Y. Z. Tang, H. F. Sun, J. Y. Sun, Y. J. Zhang and R. S. Wang, Atmos. Environ., 2014, 92, 367–375 CrossRef CAS.
- A. Horowitz, G. Schuster and G. K. Moortgat, Int. J. Chem. Kinet., 1992, 24, 255–269 CrossRef CAS.
- F. X. Wu and R. W. Carr, J. Phys. Chem., 1995, 99, 3128–3136 CrossRef CAS.
- K. A. Holbrook, M. J. Pilling and S. H. Robertson, Unimolecular Reactions, J. Wiley, Chichester, UK, 1996 Search PubMed.
- H. Hou, B. S. Wang and Y. S. Gu, J. Phys. Chem. A, 2000, 104, 320–328 CrossRef CAS.
- H. Hou and B. S. Wang, J. Chem. Phys., 2007, 127, 054306 CrossRef PubMed.
- J. A. Manion and I. A. Awan, Int. J. Chem. Kinet., 2018, 50, 225–242 CrossRef CAS.
- Y. Z. Tang, C. G. Lu and J. Y. Sun, et al, Environ. Sci. Pollut. Res., 2019, 26, 2345–2352 CrossRef CAS PubMed.
- S. H. Mousavipour, S. Ramazani and Z. Shahkolahi, J. Phys. Chem. A, 2009, 113, 2838 CrossRef CAS PubMed.
- Y. J. Zhang, J. Y. Sun, W. Q. Zhang, Y. Z. Tang and R. S. Wang, J. Comput. Chem., 2014, 35, 1646–1656 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS PubMed.
- J. Zhao and R. Y. Zhang, Atmos. Environ., 2008, 42, 5849–5858 CrossRef CAS.
- Y. Z. Tang and C. J. Nielsen, Atmos. Environ., 2012, 55, 185–189 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., 1989, 23, 199 CAS.
- J. Peiró-García and I. Nebot-Gil, ChemPhysChem, 2003, 4, 843 CrossRef PubMed.
- J. Peiró-García and I. Nebot-Gil, J. Comput. Chem., 2003, 24, 1657 CrossRef PubMed.
- J. C. Rienstra-Kiracofe, W. D. Allen and H. F. Schaefer X, J. Phys. Chem. A, 2000, 104, 9823 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian, Inc, Wallingford CT, 2009.
- S. E. Stein and B. S. Rabinovitch, J. Chem. Phys., 1973, 58, 2438–2445 CrossRef CAS.
- D. C. Astholz, J. Troe and W. Wieters, J. Chem. Phys., 1979, 70, 5107–5116 CrossRef CAS.
- NIST Computational Chemistry Comparison and Benchmark Database, http://srdata.nist.gov/cccbdb/.
- Y. Z. Tang, H. F. Sun, J. Zhao, J. H. Liu and R. S. Wang, Atmos. Environ., 2013, 65, 164–170 CrossRef CAS.
- Y. Z. Tang, H. F. Sun, J. Y. Sun, Y. J. Zhang and R. S. Wang, Atmos. Environ., 2014, 92, 367–375 CrossRef CAS.
- C. T. Chang, T. H. Liu and F. T. Jeng, Environ. Res., 2004, 94, 67–74 CrossRef CAS PubMed.
- J. G. Anderson, Geophys. Res. Lett., 1976, 3, 165–168 CrossRef CAS.
- A. M. Kosmas and E. Drougas, Chem. Phys., 2009, 358, 230–234 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10511e |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Yizhen Tangb and
Bing Hec
*a,
Yizhen Tangb and
Bing Hec



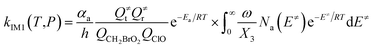
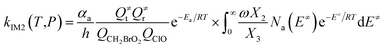
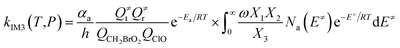
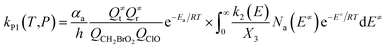
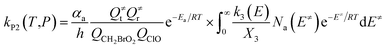
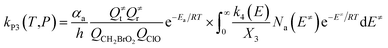
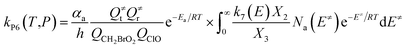
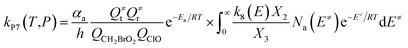
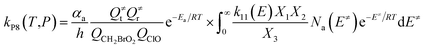

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.54/T)(200 ≤ T ≤ 3000 K)
exp(−0.54/T)(200 ≤ T ≤ 3000 K)

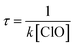 . Using the total rate constants, 1.37 × 10−12 cm3 per molecule per s for the CH2BrO2 + ClO reaction at 298 K and the global atmospheric ClO concentrations 1 × 107 molecules per cm3,41 the lifetime of CH2BrO2 was estimated to be 20.27 h, which suggests that the reaction of CH2BrO2 + ClO plays an important role in some special areas and the marine boundary layer.
. Using the total rate constants, 1.37 × 10−12 cm3 per molecule per s for the CH2BrO2 + ClO reaction at 298 K and the global atmospheric ClO concentrations 1 × 107 molecules per cm3,41 the lifetime of CH2BrO2 was estimated to be 20.27 h, which suggests that the reaction of CH2BrO2 + ClO plays an important role in some special areas and the marine boundary layer.