Open Access Article
Open Access ArticleThe tesseract in two dimensional materials, a DFT approach†
Long Zhoua,
Guanglong Zhanga,
Fangyuan Xiub,
Shuwei Xia *a and
Liangmin Yua
*a and
Liangmin Yua
aKey Laboratory of Marine Chemistry Theory and Technology, Ministry of Education, College of Chemistry and Chemical Engineering, Ocean University of China, Qingdao 266100, China. E-mail: shuweixia@ouc.edu.cn
bMolecular Nanofabrication Group, MESA+ Institute for Nanotechnology, University of Twente, Enschede, 7522 NB, Netherlands
First published on 27th February 2020
Abstract
A series of novel two-dimensional materials inspired from a 4D polytope, tesseract, have been proposed by density functional theory (DFT) based computations. Both C24X12 and C16X16 (X = O, S and Se) are found to have great thermodynamic and dynamic stabilities, and C24X12 exhibited excellent thermal stability up to 1000 K. All these 2D crystals are semiconductors with 2.17 eV to 3.35 eV band gaps at the HSE06 theoretical level, except for C24S12 (4.14 eV energy gap). Moreover, the intrinsic pore sizes of C24Se12 are suitable to sieve He from the He/CH4 mixture, with over 80% separation ratio and nearly 100% selectivity. Our findings not only enlarged the boundary of the 2D family, but also offered another potential method to recover helium from natural gas at ambient conditions.
Introduction
Elements of mathematics are widely adopted as the foundation of natural science. In the realm of chemistry, however, geometry owns a non-replaceable position, since all the crystal structures or structural units can find their geometrical analogs.Inspired by the aesthetics of geometry, chemists and material scientists have long been looking for analogic figures in compounds or crystals. From hexagon to benzene, from truncated icosahedron to fullerene, from honeycomb to graphene, significant breakthroughs in chemistry are tightly connected to those highly symmetric figures. Thus, it has become a competition for scientists to synthesize special morphological materials or design new materials from some attractive patterns.
For example, a Bi2WO6 flower nanostructure grown on conductive wire mesh substrates was successfully synthesized as a photocatalyst to improve the separation of photo-generated electron–hole pairs;1 the large specific surface area (331.3 m2 g−1) and low over-potential of the flower-like FeNi@OCNF nanostructure made it an excellent candidate as a catalyst for the oxygen evolution reaction (OER).2 Moreover, thistle-shaped nano-composites were found to have high performance as microwave absorbers with broad band features.3–8 Besides, nanotubes,9–13 nanowires,14–17 nanosheets,18–21 and arrays22–25 were also fabricated to enlarge the boundary.
With the development of density functional theory (DFT) calculations, efforts have been focused on the prediction of novel structures based on geometric patterns. Though 16 different isohedral convex pentagonal tilings have been discovered so far,26 less than one third of them are predicted in two-dimensional (2D) materials.27–31 Among them, perfect band edge position and high carrier mobilities guarantee A2B (A = P, As, Sb; B = C, Si) family members potential applications in photocatalytic water splitting and 2D devices.32,33
Till now, this competition is limited below three dimensions. However, polyhedrons of higher dimensions have been predicted for a long time,34–36 though they are difficult to imagine. Compared with the stereographic projection to map a sphere into the plane, 4D structures can also be understood in a XYZ system.37
Among these fascinating polytopes, the tesseract (or called hypercube) has attracted considerable attention since it is much easier to comprehend, compared to the others. In geometry, it can be regarded as a result of moving a 3D cube one-unit-length into the fourth dimension (Fig. 1 is only the static structure), which contains eight 3D cubes. Although it is impossible to reproduce all the characters of a tesseract in our three-dimensional world, the basic double-shell cubic architecture may be acquired in the molecular level.
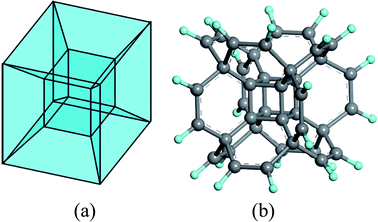 | ||
| Fig. 1 The structure of (a) tesseract and (b) hypercubane. H and C atoms are colored in cyan and grey. | ||
A theoretical study about supercubane in 1998 revealed the possibility to polymerize the molecular cubane groups together;38 later, a DFT investigation on a bonding cubane to create a covalent array in 2006![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39 via doping or substitution with donor/acceptor groups further proved the feasibility to expand such cubic frameworks. Based on these results, an Oh-symmetric hypercube structure was predicted by DFT calculations in 2014 (Fig. 1 (b)):40 the double-shell architectured hypercubane and its perfluorinated analog were proved to be stable, while the removal of the C8 core yielded a hollow hydrocarbon with a positive electron affinity. Later, the thermal character41 and substitution effects42 of the hypercubane, together with the mechanical properties43 of its variant, namely hypercubyne, were analyzed, which further demonstrated the stability of the tesseract structure at molecular level.
39 via doping or substitution with donor/acceptor groups further proved the feasibility to expand such cubic frameworks. Based on these results, an Oh-symmetric hypercube structure was predicted by DFT calculations in 2014 (Fig. 1 (b)):40 the double-shell architectured hypercubane and its perfluorinated analog were proved to be stable, while the removal of the C8 core yielded a hollow hydrocarbon with a positive electron affinity. Later, the thermal character41 and substitution effects42 of the hypercubane, together with the mechanical properties43 of its variant, namely hypercubyne, were analyzed, which further demonstrated the stability of the tesseract structure at molecular level.
The successful prediction of hypercubane also encouraged us to explore the tesseract in two dimensional materials. Since the experimental realization of graphene in 2004,44 the boundary of 2D materials realm extended at an amazing speed, and large numbers of novel nanosheets with atomic thickness were theoretically predicted and synthesized.45–51 We assume that the combination of attractive 4D polytopes and 2D materials may introduce some fascinating properties and further enlarge their applications.
Herein, by connecting the C8 core with the bridging VIA group atoms, five stable two-dimensional materials were predicted via DFT calculations: except for C24S12, other nanosheets exhibit semiconducting characters (Eg = 2.17–3.35 eV). Moreover, the perfect pore size of C24Se12 also guarantees its application as an excellent molecular sieve to separate He from He/CH4. Our predictions not only render a way to access the hypercube structure in two-dimensional world, but also highlight another possibility to recover helium under ambient conditions.
Computation methods
Our computations were performed by VASP (Vienna ab initio simulation package),52 where electron–ion interactions were described via projector-augmented plane wave;53 generalized gradient approximation (GGA)54 together with Perdew, Burke and Ernzerhof (PBE) were also utilized for the calculations. The DFT-D3 method was adopted for optimal performance.55The energy cutoff was set to 500 eV with 10−6 eV as the convergence tolerance for geometry optimizations and electronic property computations; 7 × 7 × 1 and 11 × 11 × 1 Monkhorst–Pack k-point meshes were utilized to sample a 2D Brillouin zone for geometry optimizations and band structure calculations, respectively. A 20 Å vacuum layer in the Z direction was set to eliminate significant interactions between adjacent layers.
To evaluate their dynamic stabilities, the phonon dispersions of a 3 × 3 × 1 supercell at the PBE level were calculated by CASTEP (Cambridge Sequential Total Energy Package).56 Ab initio molecular dynamics (AIMD) simulations were also performed to verify their thermal stabilities by the VASP code. PBE functional and NVT canonical ensemble57,58 were used to anneale these 2 × 2 × 1 supercell up to 1500 K for 10 ps with a time step of 1.0 fs.
Since the PBE functional tends to underestimate the band gaps of materials, we recomputed the band structures using the Heyd–Scuseria–Ernzerhof (HSE06)59 screened-hybrid functional, which has been proved to be a reliable method to predict electronic and optical properties. In the HSE06 hybrid functional, the expression for the exchange-correlation energy is given by:
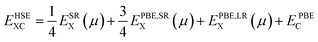 | (1) |
The possibilities for C24X12 as molecular sieve were determined via force field molecular dynamic simulations using Forcite code. A 25 Å gas chamber with a 2 × 2 × 1 supercell of C24X12 as the roof and graphene as the bottom was constructed, and a 35 Å vacuum layer was set upon C24X12 for penetrated gas to freely move. One hundred helium and methane molecules were placed into the chamber before MD simulations. Universal force field60,61 and NVT ensemble were utilized, and the slab was kept at 300 K, 400 K and 500 K for 2 ns with a time step of 1.0 fs.
Results and discussion
Geometric structures and chemical bonding analysis
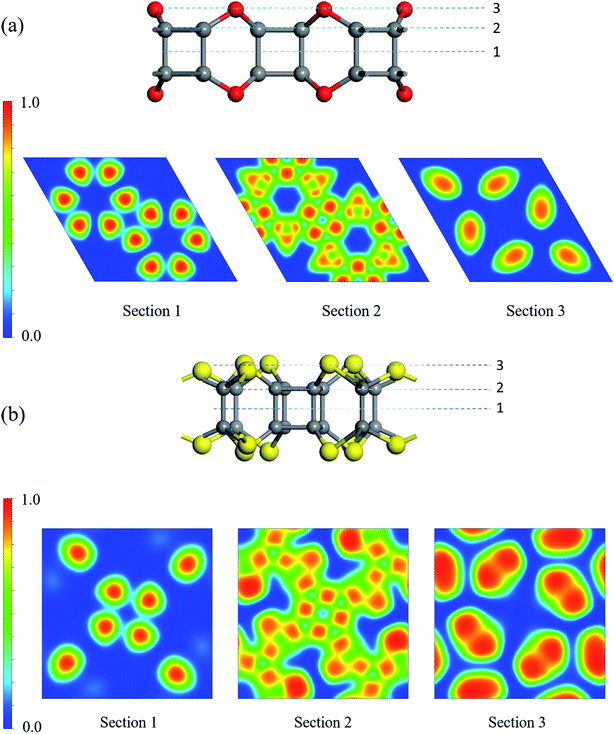
To realize the tesseract structure in two-dimension, we started from the dehydrogenated cubane (C8 core) and choose different bridging atoms to connect the vertices with another. Two factors were considered to select the bridging atoms: (1) the bridging atom should act as a vertex to form a polyhedron coordinated structure; (2) the bridged cubane can only be extended in planar. Thus, atoms with more than three coordination bonds will be sieved out from our list, since atoms with four or more coordination bonds could only be as the centroid rather than a vertex (for example, carbon atoms in methane); and a three-coordinated bridge atom, such as phosphorus, would make it less possible to extend the cubane in the XOY system. Therefore, VIA group atoms became our only choice.Two different types of nanosheets were constructed following the rule: C24X12 and C16X16 (X = O, S, and Se) (Fig. 2 and S1†). In C24X12, each C8 shared two bridge chalcogen atoms with an adjacent C8 core, and six-member rings (C4X2, X = O, S, and Se) were expected between the neighboring C8 units, forming P6/MMM symmetric 2D crystals. The lattice parameters of these monolayers are a = b = 8.85, 9.74 and 10.10 Å, for X = O, S, and Se, respectively. All the C24X12 nanosheets are porous structures: two types of crown-like pores, with D6h and D3h symmetries, are formed by three and six C8s (Table 1); in the Z direction, both the pores resulted from the alternating of six-member rings (C4X2) and four-member rings (C4). Different from the C24X12, an eclipsed ethane-like C2X6 unit assists the extension of C8: one pair of overlapping VIA atoms in the Z direction acting as bridging atoms connecting the C2X6 unit with the C8 core; while, the rest two pairs of X atoms are shared by another two adjacent C2X6 units, forming P4/m symmetry structures with a = b = 8.68 and 9.14 Å for C16S16 and C16Se16. Three C2X6 units are enclosed inside a D4h cage with diameters of 4.49 Å and 4.89 Å for X = S and Se, while surrounded by four C2h 14-member rings with d = 4.36 Å and 4.47 Å, respectively (these are the raw diameters of each pore, while results in Table 1 have taken the van der Waals radii of each atom into consideration).
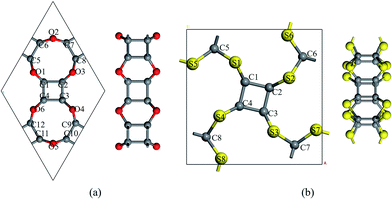 | ||
| Fig. 2 Snapshots of the optimized structures of (a) C24O12 and (b) C16S16. Oxygen and sulfur atoms are coloured in red and yellow, respectively. | ||
| C–C/Å | C–X/Å | C–C–X/° (along XOY direction) | C–C–X/° (along Z direction) | C–X–C/° | Pore size 1/Å | Pore size 2/Å | Eb eV per atom | |
|---|---|---|---|---|---|---|---|---|
| a Cubane, methyl ether, dimethylsulfide and methyl selenide were optimized under B3LYP/6-311G+ (d, p) theoretical level62,63 in Gaussian 09,64 van der Waals radius of corresponding atoms were taken into consideration to calculate pore sizes. | ||||||||
| C24O12 | 1.58 | 1.39 | 129.1 | 121.3 | 109.2 | 0.58 | 3.32 | 6.18 |
| C24S12 | 1.58 | 1.77 | 128.6 | 125.4 | 100.0 | 0.91 | 3.27 | 5.71 |
| C24Se12 | 1.57 | 1.93 | 127.9 | 126.9 | 97.4 | 0.90 | 3.20 | 5.38 |
| C16S16 | 1.59 | 1.85 | 130.0 | 124.5 | 106.6 | 0.90 | 0.71 | 4.97 |
| C16Se16 | 1.58 | 2.07 | 121.4 | 126.7 | 102.7 | 1.01 | 0.69 | 4.54 |
| Cubane | 1.57 | — | — | — | — | — | — | — |
| CH3OCH3 | — | 1.41 | — | — | 112.7 | — | — | — |
| CH3SCH3 | — | 1.81 | — | — | 108.7 | — | — | — |
| CH3SeCH3 | — | 1.94 | — | — | 110.3 | — | — | — |
After extending into two-dimension, the C–C bond in the C8 core is enlarged slightly from 1.57 Å of cubane (Table 1). This is mainly due to the stronger electron-withdrawing ability introduced by the higher electronegativity of oxygen and sulfur atoms. However, the C–C–C bond angle in all these nanosheets remained a perfect 90°, which is inherited from the stability of the cubane.65,66 Compared to their counterparts of dimethyl compounds, the corresponding C–X bonds shrink a little in C24X12, while elongate in C16X16, indicating the stronger bonding character of the former with better stability.
Though the bond lengths in C24X12 and C16X16 exhibited single bond character, electron localization function was also performed for better understanding of their binding nature (Fig. 3 and S2†). High ELF values between the adjacent carbon atoms and C/X atoms demonstrate significant single bond character (Section 2 in Fig. 3); relatively high ELF values around X atoms illustrate the existence of lone-pair electrons. Thus, all the atoms are sp3 hybridized with only σ bonds expected in these 2D monolayers.
Thermodynamic, dynamic and thermal stabilities
To examine the thermodynamic stability of C24X12 and C16X16, binding energies (Eb) were first calculated based on the following equation:| Eb = (nEC + mEX − ECnXm)/(m + n) | (2) |
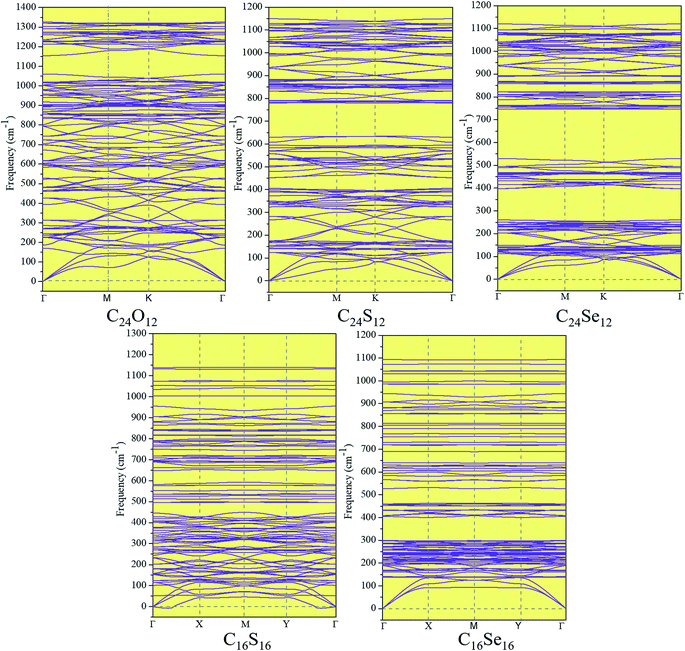
The kinetic stabilities of these monolayers were tested by phonon spectra (Fig. 4). No significant soft phonon modes are available in those spectra, demonstrating their excellent kinetic stabilities. Encouragingly, the highest frequencies of these monolayers are over 1000 cm−1, higher than most of the single element and bi-element 2D materials (except graphene (1600 cm−1) and h-BN (1350 cm−1)),69 such as MoS2 (473 cm−1), WS2 (∼450 cm−1),70 penta-P2C (∼800 cm−1),71 and phosphorene (450 cm−1),72 indicating their robust C–C and C–X bonds.
Moreover, their thermal stabilities were further evaluated via AIMD simulations. Three individual MD simulations were performed at the temperatures of 500 K, 1000 K and 1500 K with a 2 × 2 × 1 supercell (Fig. S3 and S4†). The C24X12 monolayers do not collapse under 10 ps simulations up to 1000 K, while huge defects emerge in the 14-member-ring for both the C16S16 and C16Se16 at 1000 K, demonstrating their inferior thermal stabilities, and this is also in accordance with the binding energy results. All those reveal that the tesseract containing 2D monolayers have relatively good thermal stabilities and can maintain their structural integrities under ambient conditions.
The above results demonstrate the excellent stabilities of C24X12 and C16X16, thermodynamically, kinetically and thermally; thus, these nanosheets are possible to be realized experimentally. Therefore, we also proposed several potential approaches to synthesize them (Table 2), expecting their successful experimental synthesis in the near future.
| Nanosheet | Possible realization approach |
|---|---|
| C24O12 | Laser irradiation of cubane under O2 atmosphere |
| C24S12 | Heat cubane with melt sulfur |
| C16S16 | Microwave heating the mixture of cubane, S/Se and carbon disulfide or carbon diselenide |
Electronic properties
To investigate their electronic properties, the band structures of C24X12 and C16X16 were first computed at the GGA/PBE theoretical level (Fig. S5†). All monolayers exhibited semiconducting characters with the C24Se12 and C16S16 having 2.25 and 1.70 eV indirect bandgaps, respectively, while the rest three nanosheets have 2.27 (C24O12), 3.02 eV (C24S12) and 1.17 eV (C16Se16) direct bandgaps. Both the valence band maximum (VBM) and conduction band minimum (CBM) for C24O12, C24S12 and C16Se16 are located at the Γ point; the VBM for C24Se12 is located at the K point, and CBM at Γ point, while the VBM for C16S16 is at the Γ point, and the CBM is located at the M point. The analysis of the partial density of states revealed that both the VBM and CBM for C24X12 are primarily contributed by the C-2p and X-p orbitals, while the VBMs for C16X16 are almost contributed by the X-p orbital, CBM by the C-2p and X-p orbitals.Since the GGA/PBE method trends to underestimate the bandgap of semiconductors, the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional is chosen to recalculate the band structure. Compared to GGA, the bandgap of all the five monolayers are enlarged (from 2.17 to 4.14 eV in Fig. 5), while no significant change in the band structures are observed, except for the VBM of C24Se12 moved from the K point to the middle of the K and Γ points.
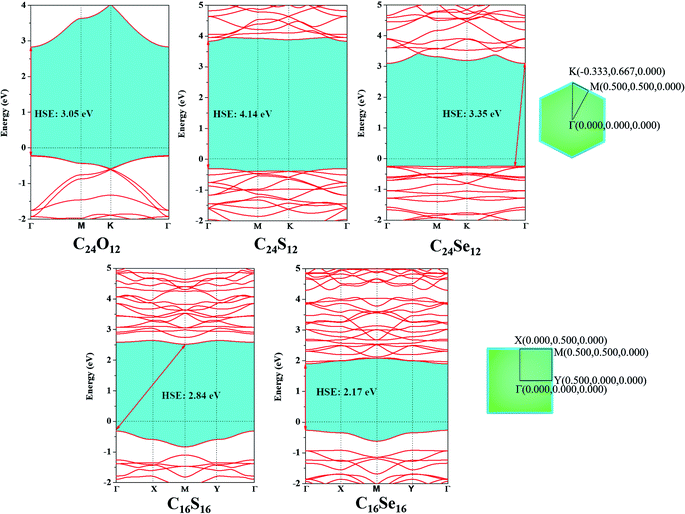 | ||
| Fig. 5 Band structures of C24X12 and C16X16 computed by HSE06 and corresponding Brillouin zone path. | ||
According to the bandgap results under the HSE06 level, the huge gap for C24X12 made it less possible to be effective electronic devices; though C16X16 have an appropriate bandgap, the fairly flat VBM and CBM will introduce huge effective mass of carriers, also making it unsuitable to be applied as electronic device or photocatalyst. Thus, another path for the application of these monolayers, molecular sieve, was considered.
Molecular sieve
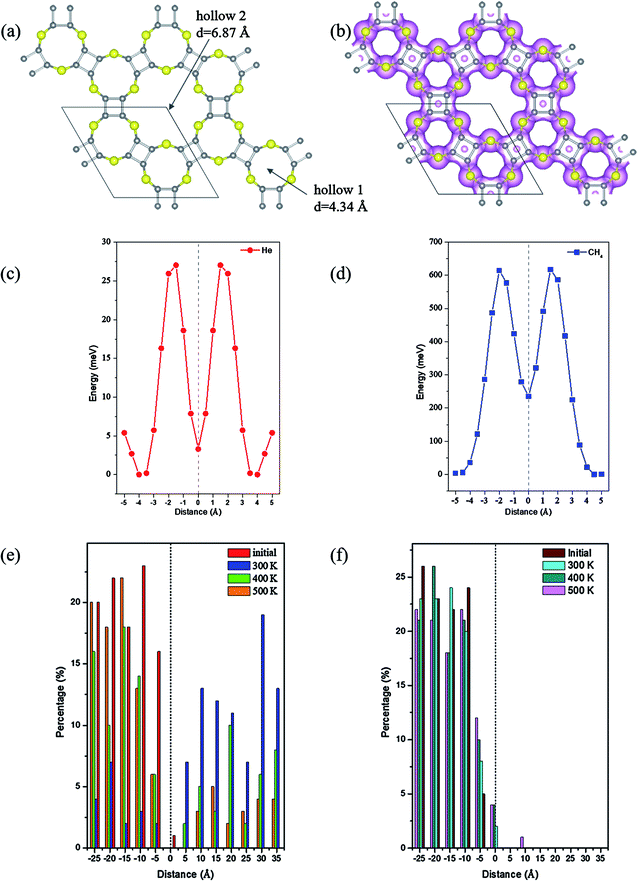
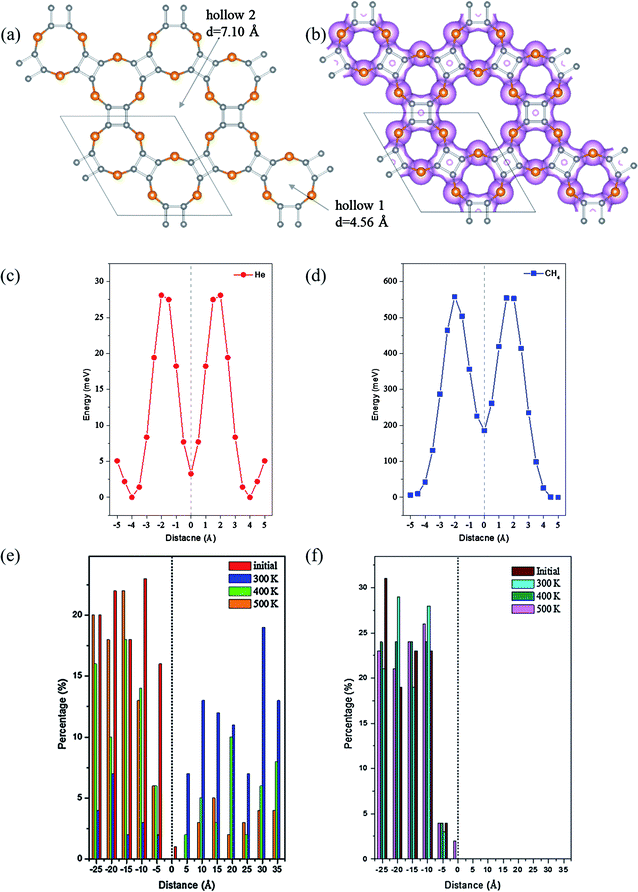
Due to the intrinsic porous structure of C24X12 and C16X16, their applications as molecular sieve were considered. For C24X12, the diameters of the smaller pores are ranged from 3.78 to 4.56 Å; though bigger than the majority of gas molecules, it is impossible for the molecules to pass through considering the electron densities around the pores (Fig. 6(b), 7(b) and S7(b),† iso value = 0.05), similar to the impenetrable nature of graphene.73–76 Thus, the C16X16 nanosheets are also beyond our considerations (Fig. S6†). Therefore, hollow 2 in C24X12 becomes the only possible channel.As one of the most valuable noble gas in the industry, helium is widely applied in the superconductor and space industries;77 He is also a critical resource for future controllable nuclear fusion. Though huge reserves have been prospected on the Moon,78–83 great challenges and expends still withdraw this inter-planet mining.84,85 Among its preparation methods available so far, the separation of He from natural gas is one of the best choices;86 however, such condensation approach is also greatly energy consuming. Thus, different membranes viz, polymeric87 or zeolite88 frameworks were developed to recover He from the natural gas under ambient conditions, but the toxicity of metal ions and less stability make them less favorable.
The possibilities for C24X12 to separate helium from methane were evaluated through energetic barrier and MD simulations. For C24O12, the energy barrier for He to penetrate hollow 2 is only 0.6 meV, while that for CH4 is 79 meV (Fig. S7(c) and (d)†). Though these values are incomparable, such small barriers would make both gas molecules easily pass through the pore. MD simulation results (Fig. S7(e), (f) and S8†) also revealed that it is impossible to separate the He/CH4 mixture upon C24O12.
Different from C24O12, the energetic barriers for He to pass the hole of C24S12 and C24Se12 are 25.9 and 28.1 meV, respectively, while those for CH4 are 617 and 554 meV (Fig. 6(c), (d), 7(c) and (d)), illustrating that tiny perturbation from the outer system will make He move from one side to another; however, much more energies would be required for CH4 to penetrate.
Since the possibilities to sieve He from the He/CH4 mixture were initially verified by energetic barriers, MD simulations were further utilized to evaluate the performance of the separation. The mixture of one hundred He and CH4 molecules were placed into a 25 Å height chamber 1 composed with C24X12 and graphene as its roof and bottom. After 2 ns MD simulations, almost pure helium could be expected in chamber 2 of C24S12 and C24Se12 under ambient conditions (Fig. S9 and S10†).
The separation ratios of He/CH4 upon C24S12 and C24Se12 were analyzed through the distribution of two types of molecules in the slab model (summarized in Table 3). For C24S12, the ratio of He in chamber 2 is largely reduced with the rise in temperature, while that for CH4 increases a little. Compared to that of C24S12, the ratio for He in chamber 2 of C24Se12 remains almost constant (over 80%) with the increase in temperature and the ratio for CH4 remains at zero.
| C24O12 | C24S12 | C24Se12 | ||||
|---|---|---|---|---|---|---|
| He | CH4 | He | CH4 | He | CH4 | |
| 300 K | 32% | 30% | 82% | 0% | 82% | 0% |
| 400 K | 68% | 42% | 36% | 0% | 85% | 0% |
| 500 K | 66% | 50% | 21% | 1% | 84% | 0% |
Two possible reasons could explain this phenomenon: considering the VDW (van der Waals) radius of sulfur (1.80 Å) and selenium (1.90 Å), the adjusted effective diameters of hollow 2 are 3.27 and 3.20 Å, respectively, for C24S12 and C24Se12. The bigger pore size of C24S12 will make the CH4 molecules easier to move into the center of the 18-member ring than C24Se12. However, the energy for CH4 to leave the center of C24S12 is 382 meV, 13 meV larger than that of C24Se12. Thus, though methane molecules can easily get into the cage of both C24S12 and C24Se12, it is more possible for CH4 to be trapped inside the hollow 2 of C24S12 (verified by more CH4 molecules in the center of the C24S12 holes after MD simulations (Fig. S9 and S10†)), forming a gas-host system. Moreover, the electronegativity of sulfur is bigger than that of selenium; therefore, stronger hydrogen bonds can be expected to stabilize the gas-host system for C24S12 than C24Se12 after the entrance of methane into the hole (Table S1,† acquired from the optimized structures of CH4@C24S12/C24Se12 in Fig. S11†), leading to the fixation of CH4 inside the pore rather than leaving or penetration.
Conclusion
We have proposed a series of 2D nanosheets containing the unit of 4D polytope, tesseract, namely C24X12 and C16X16 (X = O, S and Se). Thermodynamic, kinetic and thermal stabilities were verified by binding energies, phonon dispersion and MD simulations: their excellent stabilities were found to largely originate from the unusual stability of cubane. All these monolayers exhibited semiconducting characters with 2.17 to 3.35 eV bandgaps, except for the insulator nature of C24S12 (4.14 eV gap). The fairly flat VBM and CBM make these 2D crystals less probable in the applications of electronic devices and photocatalyst. However, over 80% separation ratio of He from the He/CH4 mixture upon C24Se12 and high selectivity will make it one of the best candidates as a molecular sieve. This study not only proved the possibility to design novel 2D materials from the prototype of 4D polytopes, extending the realm of the 2D family, but also explored their potential applications. We believe this work would motivate experimental pioneers to realize them in the very near future.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge financial supports from Natural Science Foundation (50673085) and the Ao Shan Talents Cultivation Program Supported by Qingdao National Laboratory for Marine Science and Technology (2017ASTCP-OS02).References
- C. Chang, J. Chen, K. Lin, Y. Wei, P. Chao and C. Huang, J. Alloys Compd., 2020, 813, 152186 CrossRef CAS.
- P. He, Y. Wu, H. Chen, Z. Zhu, H. Liu, J. Gao and H. Xu, J. Alloys Compd., 2020, 813, 152192 CrossRef CAS.
- L. Liu, N. He, T. Wu, P. Hu and G. Tong, Chem. Eng. J., 2019, 355, 103–108 CrossRef CAS.
- N. Zhang, Y. Huang, M. Wang, X. Liu and M. Zong, J. Colloid Interface Sci., 2019, 534, 110–121 CrossRef CAS PubMed.
- J. Ma, X. Wang, W. Cao, C. Han, H. Yang, J. Yuan and M. Cao, Chem. Eng. J., 2018, 339, 487–498 CrossRef CAS.
- X. Liu, J. Yu, C. Cui, Y. Sun, X. Li and Z. Li, J. Phys. D: Appl. Phys., 2018, 51, 265002 CrossRef.
- J. Deng, S. Li, Y. Zhou, L. Liang, B. Zhao, X. Zhang and R. Zhang, J. Colloid Interface Sci., 2018, 509, 406–413 CrossRef CAS PubMed.
- N. Wu, C. Liu, D. Xu, J. Liu, W. Liu, Q. Shao and Z. Guo, ACS Sustainable Chem. Eng., 2018, 6, 12471–12480 CrossRef CAS.
- J. Xu, L. Gao, J. Cao, W. Wang and Z. Chen, Electrochim. Acta, 2010, 56, 732–736 CrossRef CAS.
- J. Zou, J. Liu, A. S. Karakoti, A. Kumar, D. Joung, Q. Li, S. I. Khondaker, S. Seal and L. Zhai, ACS Nano, 2010, 4, 7293–7302 CrossRef CAS PubMed.
- B. J. Sanghavi and A. K. Srivastava, Electrochim. Acta, 2010, 55, 8638–8648 CrossRef CAS.
- P. Kar, S. Zeng, Y. Zhang, E. Vahidzadeh, A. Manuel, R. Kisslinger, K. M. Alam, U. K. Thakur, N. Mahdi, P. Kumar and K. Shankar, Appl. Catal., B, 2019, 243, 522–536 CrossRef CAS.
- M. Xu, D. N. Futaba, T. Yamada, M. Yumura and K. Hata, Science, 2010, 330, 1364–1368 CrossRef CAS PubMed.
- J. Kim, A. Mirzaei, H. W. Kim and S. S. Kim, Sens. Actuators, B, 2019, 285, 358–367 CrossRef CAS.
- P. Tan, B. Chen, H. Xu, W. Cai, W. He and M. Ni, Appl. Catal., B, 2019, 241, 104–112 CrossRef CAS.
- D. Su, Z. Tang, J. Xie, Z. Bian, J. Zhang, D. Yang, D. Zhang, J. Wang, Y. Liu, A. Yuan and Q. Kong, Appl. Surf. Sci., 2019, 469, 487–494 CrossRef CAS.
- Z. Wan, D. Lei, W. Yang, C. Liu, K. Shi, X. Hao, L. Shen, W. Lv, B. Li, Q. Yang, F. Kang and Y. He, Adv. Funct. Mater., 2019, 29, 1805301 CrossRef.
- Y. Li, X. Lv, J. Lu and J. Li, J. Phys. Chem. C, 2010, 114, 21770–21774 CrossRef CAS.
- H. Zhao, X. Mu, C. Zheng, S. Liu, Y. Zhu, X. Gao and T. Wu, J. Hazard. Mater., 2019, 366, 240–249 CrossRef CAS PubMed.
- A. Bafaqeer, M. Tahir and N. A. S. Amin, Appl. Catal., B, 2019, 242, 312–326 CrossRef CAS.
- R. Li, X. Zhu, Q. Fu, G. Liang, Y. Chen, L. Luo, M. Dong, Q. Shao, C. Lin, R. Wei and Z. Guo, Chem. Commun., 2019, 55, 2493–2496 RSC.
- X. Li, X. Chen, Z. Yi, Z. Zhou, Y. Tang and Y. Yi, Micromachines, 2019, 10, 164 CrossRef PubMed.
- Y. Lai, J. Huang, H. Zhang, V. Subramaniam, Y. Tang, D. Gong, L. Sundar, L. Sun, Z. Chen and C. Lin, J. Hazard. Mater., 2010, 184, 855–863 CrossRef CAS PubMed.
- D. Chao, C. R. Zhu, M. Song, P. Liang, X. Zhang, N. H. Tiep, H. Zhao, J. Wang, R. Wang, H. Zhang and H. J. Fan, Adv. Mater., 2018, 30, 1803181 CrossRef PubMed.
- N. Han, K. R. Yang, Z. Lu, Y. Li, W. Xu, T. Gao, Z. Cai, Y. Zhang, V. S. Batista, W. Liu and X. Sun, Nat. Commun., 2018, 9, 924 CrossRef PubMed.
- T. Sugimoto, Graph. Combinator., 2015, 31, 281–298 CrossRef.
- S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377 CrossRef CAS PubMed.
- H. L. Zhuang, Comput. Mater. Sci., 2019, 159, 448–453 CrossRef CAS.
- J. Li, X. Fan, Y. Wei and G. Chen, Sci. Rep., 2016, 6, 31840 CrossRef CAS PubMed.
- L. Liu, I. Kankam and H. L. Zhuang, Comput. Mater. Sci., 2018, 154, 37–40 CrossRef CAS.
- Z. Liu, H. Wang, J. Sun, R. Sun, Z. F. Wang and J. Yang, Nanoscale, 2018, 10, 16169–16177 RSC.
- S. Sun, F. Meng, Y. Xu, J. He, Y. Ni and H. Wang, J. Mater. Chem. A, 2019, 7, 7791–7799 RSC.
- M. Naseri, S. Lin, J. Jalilian, J. Gu and Z. Chen, Frontiers of Physics, 2018, 13, 138102 CrossRef.
- H. S. M. Coxeter, Proc. Lond. Math. Soc., 1938, 2–43, 33 CrossRef.
- R. V. B. Rucker, Geometry, Relativity, and the Fourth Dimension, Dover Pubns, 1977 Search PubMed.
- E. H. Neville, The Fourth Dimension, Merchant Books, 2007 Search PubMed.
- W. Armstrong and R. Burton, in Stereoscopic Displays & Applications, International Society for Optics and Photonics, 1990 Search PubMed.
- B. Winkler and V. Milman, Chem. Phys. Lett., 1998, 293, 284–288 CrossRef CAS.
- B. Herrera, F. Valencia, A. H. Romero, M. Kiwi, R. Ramírez and A. Toro-Labbé, J. Mol. Struct., 2006, 769, 183–187 CrossRef CAS.
- F. Pichierri, Chem. Phys. Lett., 2014, 612, 198–202 CrossRef CAS.
- M. M. Maslov and K. P. Katin, Chem. Phys. Lett., 2016, 644, 280–283 CrossRef CAS.
- F. Pichierri, Theor. Chem. Acc., 2017, 136, 114 Search PubMed.
- S. W. Cranford, Extreme Mechanics Letters, 2018, 22, 19–26 Search PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- M. Kawaguchi, S. Kuroda and Y. Muramatsu, J. Phys. Chem. Solids, 2008, 69, 1171–1178 CrossRef CAS.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tomanek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS PubMed.
- B. Aufray, A. Kara, S. Vizzini, H. Oughaddou, C. Leandri, B. Ealet and G. Le Lay, Appl. Phys. Lett., 2010, 96, 183102 CrossRef.
- R. S. Sundaram, M. Engel, A. Lombardo, R. Krupke, A. C. Ferrari, P. Avouris and M. Steiner, Nano Lett., 2013, 13, 1416–1421 CrossRef CAS PubMed.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS PubMed.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- B. Leimkuhler, E. Noorizadeh and F. Theil, J. Stat. Phys., 2009, 135, 261–277 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. K. Rappe, K. S. Colwell and C. J. Casewit, Inorg. Chem., 1993, 32, 3438–3450 CrossRef CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- R. C. Binning and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206–1216 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, 2009.
- P. E. Eaton, Angew. Chem., Int. Ed. Engl., 1992, 31, 1421–1436 CrossRef.
- K. F. Biegasiewicz, J. R. Griffiths, G. P. Savage, J. Tsanaktsidis and R. Priefer, Chem. Rev., 2015, 115, 6719–6745 CrossRef CAS PubMed.
- L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377 CrossRef CAS PubMed.
- L. Huang, P. Gong and Z. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 205433 CrossRef.
- H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- A. Molina-Sanchez and L. Wirtz, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155413 CrossRef.
- M. Naseri, S. Lin, J. Jalilian, J. Gu and Z. Chen, Frontiers of Physics, 2018, 13, 138102 CrossRef.
- G. Qin, Q. Yan, Z. Qin, S. Yue, M. Hu and G. Su, Phys. Chem. Chem. Phys., 2015, 17, 4854–4858 RSC.
- Y. Zhao, Y. Xie, Y. Y. Hui, L. Tang, W. Jie, Y. Jiang, L. Xu, S. P. Lau and Y. Chai, J. Mater. Chem. C, 2013, 1, 4956 RSC.
- R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva and A. K. Geim, Science, 2012, 335, 442–444 CrossRef CAS PubMed.
- J. S. Bunch, S. S. Verbridge, J. S. Alden, A. M. van der Zande, J. M. Parpia, H. G. Craighead and P. L. McEuen, Nano Lett., 2008, 8, 2458–2462 CrossRef CAS PubMed.
- X. Zheng, M. Zhang, X. Shi, G. Wang, L. Zheng, Y. Yu, A. Huang, P. K. Chu, H. Gao, W. Ren, Z. Di and X. Wang, Adv. Funct. Mater., 2015, 25, 1805–1813 CrossRef CAS.
- F. G. Kerry, Industrial Gas Handbook: Gas Separation and Purification, 2007 Search PubMed.
- G. I. Dimov, J. Fusion Energy, 2014, 33, 453–455 CrossRef CAS.
- F. H. Cocks, Icarus, 2010, 206, 778–779 CrossRef CAS.
- D. Li, H. Liu, W. Zhang, Y. Li and C. Xu, Sci. China: Earth Sci., 2010, 53, 1103–1114 CAS.
- Z. Wang, Y. Li, J. Jiang and D. Li, Sci. China: Earth Sci., 2010, 53, 1365–1378 CrossRef CAS.
- W. Fa and Y. Jin, Icarus, 2007, 190, 15–23 CrossRef CAS.
- J. R. Johnson, T. D. Swindle and P. G. Lucey, Geophys. Res. Lett., 1999, 26, 385–388 CrossRef CAS.
- J. C. Woods, J. Appl. Physiol., 2013, 114, 705–706 CrossRef CAS PubMed.
- U. Guven and P. Kuchhal, Appl. Mech. Mater., 2011, 110–116, 2054–2061 Search PubMed.
- S. Faramawy, T. Zaki and A. A. E. Sakr, J. Nat. Gas Sci. Eng., 2016, 34, 34–54 CrossRef CAS.
- C. Zhang, R. P. Lively, K. Zhang, J. R. Johnson, O. Karvan and W. J. Koros, J. Phys. Chem. Lett., 2012, 3, 2130–2134 CrossRef CAS PubMed.
- C. A. Scholes, G. W. Stevens and S. E. Kentish, Fuel, 2012, 96, 15–28 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10696k |
| This journal is © The Royal Society of Chemistry 2020 |