Open Access Article
Open Access ArticleFirst-principles calculations of electronic structure and optical and elastic properties of the novel ABX3-type LaWN3 perovskite structure†
Xing Liuab,
Jia Fu *a and
Guangming Chen
*a and
Guangming Chen c
c
aShaanxi Key Laboratory of Material Processing Engineering, School of Material Science and Engineering, Xi'an Shiyou University, Xi'an, 710065, China. E-mail: fujia@xsyu.edu.cn
bState Key Laboratory of Solidification Processing, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi'an 710072, PR China
cShenzhen Key Laboratory of Polymer Science and Technology, College of Materials Science and Engineering, Shenzhen University, Shenzhen, 518060, China
First published on 5th May 2020
Abstract
The development of ABX3-type advanced perovskite materials has become a focus for both scientific researchers and the material genome initiative (MGI). In addition to the traditional perovskite ABO3 and halide perovskite ABX3, LaWN3 is discovered as a new ABX3-type advanced perovskite structure. The elastic and optical properties of this novel LaWN3 structure are systematically studied via DFT. Based on the calculated elastic constants, the bulk modulus, shear modulus, Young's modulus and Pugh modulus ratio are precisely obtained. Results show that (1) LaWN3 is an indirect bandgap semiconductor with a hybrid occuring near the Fermi level and the main contributions are La-d, W-d and N-p. (2) LaWN3 has a certain ductility. The optical constants, such as absorption spectrum, energy-loss spectrum, conductivity, dielectric function, reflectivity and refractive index, are analyzed and the static dielectric constant is 10.98 and the refractivity index is 3.31. (3) The optical constants of LaWN3 are higher than those of other existing ABX3-type materials, showing very promising application as a functional perovskite in the future. The existence of this stable LaWN3 structure might widen the perovskite material's application, such as in photodetectors, light-emitting diodes, perovskite solar cells, fuel cells and so on.
1 Introduction
The ABX3-type advanced perovskite materials have become a research hotspot in recent years, including the traditional perovskite ABO3, organic–inorganic hybrid perovskite MAPbX3 (X = Cl, Br, and I), halide perovskite ABX3 (X = Cl, Br, and I). In recent years, perovskite materials ABX3, with their special structural characteristics, have been widely used in the fields of catalysis,1,2 piezoelectricity,3–5 solar cells,6,7 giant magnetoresistance,8–10 and light-emitting diode materials11–13 due to their unique physical structures. They have excellent physical–chemical properties, ferroelectric performance, ferromagnetic performance, superconductivity and fluorescence laser performance. The designed anisotropic single crystal at nano-scale as the instinct link helps to predict physical properties of larger structure at micro-scale and might be used to verify the isotropic properties of experimental phase using both experiment and simulation techniques.14 These basic investigation results can be applied in efficient solar modules coated by large-area perovskite films15 and organic solar cells.16The traditional perovskite ABO3, organic–inorganic hybrid perovskite MAPbX3 (X = Cl, Br, I) and halide perovskite ABX3 (X = Cl, Br, I)17 have been studied in theory and experiment. Liu et al.18 synthesized CH3NH3PbBr3 quantum dots with a tunable spectrum. The emission peak range is from green-blue to deep purple (523.6 nm and 432.9 nm, separately), which is wider than quantum dots made without changing the halide composition; thus the blue shift mechanism of the photoluminescence spectrum of CH3NH3PbBr3 quantum dots is clear. Su et al.19 realized a room temperature polarized laser in an experiment based on non-epitaxial all inorganic cesium lead perovskite microcavities. The polarized lasing is characterized by macroscopic ground state occupation, narrow linewidth and long-range spatial coherence accumulation. This significant work shows that the lead halide perovskites and doped perovskites have great application prospects in low cost, large area, high performance room temperature transistors or polarized light devices.20–22 Today, the maximum efficiency of crystalline silicon cells has exceeded 26% (its limiting efficiency is 29%)23 and the maximum efficiency of perovskite cells is higher than that of crystalline silicon cells. (The designed cell can theoretically reach an efficiency limit of 33% and the theoretical conversion limit of stacked cells is 43%.)24,25 Although the perovskite battery has a high energy-saving limit, simple process, rapid development, and impressive performance in the laboratory, there is still a long way to go for large-scale practical application.
For numerical simulation of ABX3 structures, Wang et al.26 found that ordered porous La0.6Sr0.4MnO3 perovskite arrays are decomposed into hexagonal mesoporous nanoparticles, thus revealing a new crystal plane that is more active in the catalytic combustion of methane. The first-principles calculations show that fractures at the weak joints of the 3DOM structure provide a large area of (001) plane surface, which indicates that the energy barrier of hydrogen extraction is reduced, thus promoting methane oxidation. Based on DFT calculations, Lu et al.27 found that there are three in-plane Fe states from different micro mechanisms, which revealed a new physical mechanism of 2D ferroelectricity in perovskite oxide films. Ryan et al.28 screened about 2145 different perovskite compositions for potential application as SOFC cathodes with high activity and stability and verified that the screening method qualitatively reproduced the stability and conductivity of the cathode materials. Lanthanide ions can improve perovskite film properties due to their unique photophysical properties, such as long excited state life, long wavelength emission in the near infrared or visible region, and linear emission band.29,30 With this background, LaWN3 perovskite material is found as a new ABX3-type advanced perovskite structure. The above published works focus on perovskite oxide (ABO3) or inorganic–organic halide perovskites (MAPbX3), while few studies have been found on the potential LaWN3 structure. For this newly discovered LaWN3 perovskite structure, the thermodynamic stability, mechanical stability and structural stability are studied and determined using the relevant theories of phonon dispersion,31 elastic constants,32 and tolerance factors,33,34 respectively.
Reviewing previous studies, their investigations of perovskites in experiment and theory have made great achievements; however, as a new ABX3-type material with perovskite structure, LaWN3 has been rarely studied. So far, we are one of the few research groups to find this substance, apart from Hiroki Moriwake's group in the Nanostructures Research Laboratory of the Japan Fine Ceramics Center (JFCC),35 and our group has systematically studied and confirmed that this stable structure has excellent comprehensive performance. The LaWN3 perovskite material is a new ABX3-type advanced perovskite structure. Therefore, the electronic structure, elasticity and optics of LaWN3 are studied using the first-principles method. This paper aims to study the LaWN3 electronic structure and optical and elastic properties based on DFT, which can provide theoretical parameters for experimentation and explore the significant value for applications of the designed perovskite with LaWN3 structure.
2 Modelling and computational details
The ionic radius matching in perovskite structure should fit the following relationship
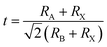 | (1) |
The tolerance factor of perovskite allows a variety of elements to meet the structural requirements, so the materials show good elemental adjustability. Generally, A-site elements play a supporting role in perovskite structure, B-site elements are catalytic active sites, and there is mutual influence and restriction between A-site and B-site. The charge balance is also a factor for structural stability. Theoretically, if the radii of A, B and X ions meet the structural tolerance factor 0.81 < t < 1.11, the typical perovskite crystal structure can exist stably.
For the LaWN3 structure, the ionic radii of La and W and N are RLa = 1.36 Å, RW = 0.66 Å and RN = 1.46 Å, respectively. The tolerance factor is calculated as 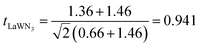 and the value of 0.941 is within the stability region of 0.81–1.11,33 showing that the structure of LaWN3 is relatively stable.
and the value of 0.941 is within the stability region of 0.81–1.11,33 showing that the structure of LaWN3 is relatively stable.
2.1 Structure model
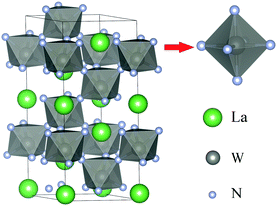
Fig. 1 shows the crystal structure of LaWN3. As can be seen from Fig. 1, LaWN3 can be seen as a WN6 octahedron connected at the top of the three-dimensional common angle. The A-site ions are located in the centre of the gap surrounded by BX6 octahedra. The lattice constants are a = b = 5.71 Å, c = 13.96 Å, α = β = 90°, and γ = 120° (hexagonal type), the density is 9.2122 g cm−3 and the space group is R3c with an H-lattice type.2.2 Methods of calculations
The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof functional is used to calculate the band structure and optical and elastic properties of LaWN3 in this work.36 The Cambridge Sequential Total Energy Package (CASTEP) is selected for calculation.37,38 The plane wave function is expanded from the base plane. An ultrasoft pseudopotential is adopted to describe the interaction between electrons and ions, as it helps to reduce the number of base planes in convergence calculations and save computational resources. The function forms of GGA and PBE are selected to be exchange correlation functions. In the LaWN3 structure, the La 5p65d16s2 electrons, W 5d46s2 electrons, and N 2s22p3 electrons are explicitly treated as valence electrons. The cut-off energy of the plane wave is taken as Ecut = 300 eV and Brillouin zone integration is performed over 3 × 3 × 2 grids using the Monkhorst–Pack method. The convergence thresholds for total energy, maximum force, maximum stress, maximum displacement and Hellmann–Feynman ionic force are respectively less than 5 × 10−7 eV per atom, 0.01 eV Å−1, 0.02 GPa, 5.0 × 10−4 Å and 1 meV Å−1.3 Results and discussion
3.1 Geometry optimization
Geometric optimization is essential for the theoretical study of this new ABX3-type LaWN3 material. The calculation parameters are optimized in order to find the stable state and the ground state. As LaWN3 research is rare, it is difficult to compare the optimization results with literature results. Therefore, different functional methods are used to optimize structural parameters of LaWN3, with the error less than 2% between the two nearest optimizations. That is to say, the structural model with the most unchanged parameters is the structure in the ground state.The stability of a crystal structure is related to its cohesive energy and formation heat, where the cohesive energy is often defined as the minimum work which is needed to decompose the crystal into single atoms. Generally, the larger the cohesive energy or the larger the negative value of the formation heat during the process of formation from its elements in exothermic reaction, the more stable the crystal structure is.39
The cohesive energy (Ecoh) of a given phase is a measure of the strength of the forces which bind the atoms together in the solid state. The cohesive energy (Ecoh) can be calculated by the standard relation40,41
| EABcoh = EAatom + EBatom − EABtotal | (2) |
Hence, by eqn (2), the cohesive energies of LaN, WN2 and LaWN3 are calculated to be −16.674 eV per atom, −18.331 eV per atom and −20.526 eV per atom, respectively. The formation enthalpy should be considered the energy per atom of the pure constituents (LaN and WN2) in their solid states. The formation enthalpy is determined to be about −14.4795 eV per f.u., which is lower than the result of Fang.35
Table 1 shows the structural parameters of the optimized LaWN3 structure calculated with different functional methods (GGA–PBE, GGA–PBESOL and GGA–PW91). It can be seen that the lattice constants of LaWN3 changed very little, with the relative error between lattice parameters within only 1%. Thus, we can infer that LaWN3 reaches a stable state and further research into related properties can be performed.
| Structural parameters | GGA | ||
|---|---|---|---|
| PBE | PBESOL | PW91 | |
| a | 5.7363 | 5.7080 | 5.7368 |
| b | 5.7363 | 5.7080 | 5.7368 |
| c | 14.0038 | 14.0349 | 13.9985 |
| α | 90 | 90 | 90 |
| β | 90 | 90 | 90 |
| γ | 120 | 120 | 120 |
3.2 Electronic structure
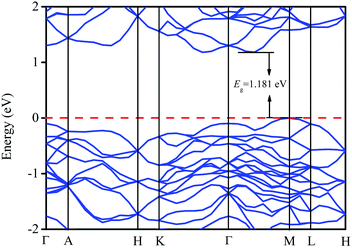
The solid energy band theory is used to determine the energy levels of electrons in solids, that is, energy bands can explain many basic physical properties of solids.42,43As seen in Fig. 2, the bottom of the conduction band is not the same as the top of the valence band, so LaWN3 is an indirect band gap semiconductor.35 The bandgap is calculated to be 1.181 eV.
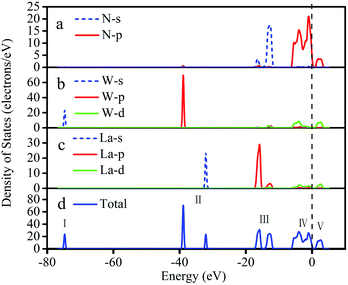
The density of states analysis is in Fig. 3; the whole DOS is divided into five parts, of which part I–part IV are mainly concentrated on the valence band, while part V appears in the conduction band. The low valence band (I) is mainly composed of W-s, with a bandwidth of 3.11 eV. The W-p and La-s orbitals contribute to part II, with a small amount of N-s contributing. Part III of the DOS has two peaks composed of the hybrid of L-p and N-s orbitals from −17.7 eV to −11.3 eV. On the left side of the Fermi level, part IV contains obvious hybridizations near the top of the valence band, with three elements (N-2p, La-5d, and W-5d orbitals) mainly contributing. For the conduction band region of part V, the orbitals of La-5d, W-5d and N-2p participate in the hybridization, thus forming a weak hybrid peak.
3.3 Phonon dispersion and molecular-orbital bonding
The stability of the perovskite material is key to its design and simulation. The phonon spectrum is closely related to the thermodynamic stability and can be used to verify an existing phase rather than a mesophase, which is beneficial to subsequent research and application in laboratory synthesis.44Phonon spectra represent the collective vibration modes of the atoms that make up the material. If the primitive cell of the material contains n atoms, the phonon spectrum has a total of 3n branches, including 3 acoustic branches and 3n − 3 optical branches. The acoustic branch represents the overall vibration of the cell and the optical branch represents the relative vibrations of the atoms in the cell.45–48 The vibration frequency is described as
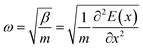 | (3) |
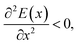 that is to say, when the atomic equilibrium position is located at the “mountain top” of energy (similar to the parabolic vertex), the atoms in this equilibrium position are obviously unstable.
that is to say, when the atomic equilibrium position is located at the “mountain top” of energy (similar to the parabolic vertex), the atoms in this equilibrium position are obviously unstable.
The relationship between the direction of atom displacement and the direction of lattice wave propagation should be considered in a three-dimensional lattice. If q moves along a symmetry axis of the crystal and the crystal rotates around this axis by π/2 (or π/3, 2π/3) in a symmetry operation, the lattice wave can be divided into a transverse wave and a longitudinal wave. The atomic displacement of the transverse wave is perpendicular to the propagation direction of the wave and contains two degenerate frequency waves. The phonon dispersion diagram for LaWN3 is shown in Fig. 4.
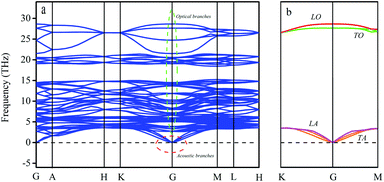 | ||
| Fig. 4 The (a) phonon dispersion curves and (b) transverse & longitudinal waves in optics and acoustics of the R3c LaWN3 structure. | ||
As in Fig. 4(a), there are five atoms in a cell of LaWN3, with 15 dispersion curves, 3 acoustic branches and 12 optical branches. The frequencies of the acoustic branches are lower than that of the optical branch, so the three acoustic branches degenerate to G (shown by the red ring), and the 12 optical branches have multiple splits (shown by the green ring). The calculated phonon spectra have no imaginary frequency, which indicates that LaWN3 is stable thermodynamically.
To clarify the relationship between the transverse and longitudinal waves, the phonon dispersion diagram is simplified, as seen in Fig. 4(b). It can be seen that there are four coloured curves, the longitudinal optical branch (LO), transverse optical branch (TO), longitudinal acoustic branch (LA) and transverse acoustic branch (TA). The transverse waves (TO and TA) are composed by wave degeneracy of the same frequency (shown by the green and orange curves).
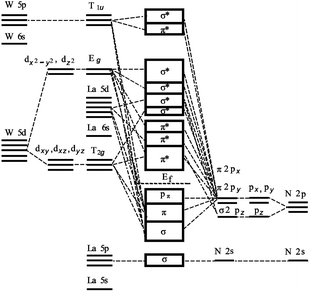
The molecular-orbital bonding of LaWN3 structure is shown in Fig. 5. Based on the theories of crystal-field and molecular-orbital bonding,49,50 the d-orbits of transition elements can be split in electrostatic fields with different symmetries. In LaWN3, the d-orbit of the W atom would be split and two crystal field split levels would be formed in the On field, which are Eg (dx2−y2, dz2) and T2g (dxy, dxz, dyz). A molecular orbital bonding diagram derived from the character of the states is presented in Fig. 5 to examine the chemical bonding of LaWN3. With an increase of energy, N-2s and Eg, σ2 pz and T1u, π2 (px + py) and T1u, σ2 pz and Eg, π2 (px + py) and T2g respectively, contribute to the bonding from the bottom to the Ef. The corresponding antibondings are presented in Fig. 5 from the Ef to the top.
3.4 Homogenized elastic moduli of LaWN3 structure
| Our work | Previous work | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| LaWN3 | CaCO3 | SrZrO3 | α-SrZrO3 | CaCO3 | SrZrO3 | α-SrZrO3 | |||
| PBE | PW91 | PBESOL | PBE | PBE | PBE | PBE | PBE | PBE | |
| C11 | 320.36 | 324.55 | 328.23 | 147.2 | 365.27 | 283.54 | 149.4 | 368.3 | 288.6 |
| C22 | — | — | — | — | — | 286.89 | — | — | 284.6 |
| C33 | 268.94 | 273.19 | 262.15 | 87.6 | 301.87 | 85.3 | — | 305.9 | |
| C12 | 134.61 | 135.70 | 139.81 | 56.1 | 72.69 | 128.32 | 57.9 | 77.3 | 131.5 |
| C13 | 80.30 | 83.17 | 81.95 | 55.3 | — | 104.96 | 53.5 | — | 102.5 |
| C23 | — | — | — | — | — | 87.47 | — | — | 91.4 |
| C44 | 44.13 | 50.37 | 44.47 | 33.7 | 77.52 | 91.96 | 34.1 | 76.6 | 95.6 |
| C55 | — | — | — | — | — | 82.89 | — | — | 86.2 |
| C66 | 92.88 | 94.43 | 94.21 | 47.8 | — | 103.47 | 45.75 | — | 105 |
From Table 2, the elastic constants of other ABX3 functional materials calculated by ab initio method are very close to those from previous works, showing that the calculation accuracy and DFT method are reasonable. Thus, we can safely say that the obtained elastic constants of LaWN3 are precise. Elastic moduli are important parameters that reflect the extent of a solid's resistance to both elastic and plastic deformation, using various simulation techniques.56
Mechanical stability is commonly based on Born's stability restrictions, which are as follows.57
| C44 > 0, C11 > |C12|, (C11 > 2C12)C33 > 2C132 | (4) |
As the elastic constants satisfy Born's stability restrictions, we can infer that LaWN3 is mechanically stable.
Bulk modulus and shear modulus are two parameters critical for describing the ability of a material to resist volume change and change of shape caused by shear force and bond angle, respectively. The bulk modulus and shear modulus can be obtained based on Cij. There exist two limit bounds: one is from Reuss and can calculate the grain boundary strain continuity; the other is the grain boundary stress continuity proposed by Voigt. Hill proves that the calculations of the Reuss and Voigt models are the upper and lower limits of the elastic constant, respectively. The expressions of homogenized elastic moduli can be calculated as follows:
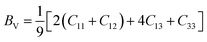 | (5) |
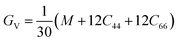 | (6) |
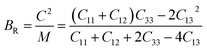 | (7) |
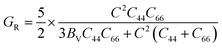 | (8) |
The Young's modulus E of a material can be expressed as
| E = 9BxGx/(Gx + 3Bx) | (9) |
The comparison of elastic moduli and available theoretical data for typical ABX3 functional materials is listed in Table 3. For LaWN3, the Young's modulus EH is smaller than in other functional materials.58–65 In our calculation of Bx/Gx, the Pugh values of LaWN3 are higher than the critical value of 1.75 proposed by Pugh,66 showing a certain ductility in LaWN3.
| B | G | Young's moduli | Pugh | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BV | BR | GV | GR | EV | ER | EH | BV/GV | BR/GR | BH/GH | |
| LaWN3(PBE) | 166.68 | 162.97 | 77.19 | 65.80 | 200.6 | 173.98 | 187.39 | 2.16 | 2.48 | 2.31 |
| LaWN3(PW91) | 169.60 | 166.04 | 80.38 | 71.45 | 208.25 | 187.46 | 197.90 | 2.11 | 2.32 | 2.21 |
| LaWN3(PBESOL) | 169.56 | 164.42 | 77.62 | 66.21 | 202.04 | 175.13 | 188.67 | 2.18 | 2.48 | 2.32 |
| SmAlO3 (ref. 58) | 194.42 | 194.42 | 148.96 | 148.19 | 134.71 | 120.91 | 107.12 | 1.31 | 1.31 | 1.31 |
| SmCoO3 (ref. 59) | 204.63 | 204.63 | 137.57 | 124.52 | 337.16 | 310.57 | 323.98 | 1.49 | 1.64 | 1.56 |
| CaCO3 (ref. 60–62) | 76 | 69.63 | 36 | 28.71 | 93.27 | 75.72 | 84.56 | 2.11 | 2.43 | 2.25 |
| 89.78 | 83.84 | 39.17 | 37.49 | 102.59 | 97.88 | 100.24 | 2.29 | 2.24 | 2.26 | |
| 77.81 | 71.55 | 36.72 | 35.08 | 95.19 | 90.46 | 92.83 | 2.12 | 2.04 | 2.08 | |
| SrZrO3 (ref. 63–65) | 160.2 | 160.2 | 99.72 | 92.75 | 247.75 | 233.24 | 240.54 | 1.61 | 1.73 | 1.66 |
| 192.83 | 192.83 | 97.94 | 91.08 | 251.28 | 236.07 | 243.71 | 1.97 | 2.12 | 2.04 | |
| 147.64 | 147.64 | 92.19 | 89.31 | 228.92 | 222.97 | 225.95 | 1.60 | 1.65 | 1.63 | |
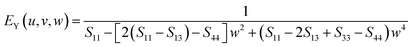 | (10) |
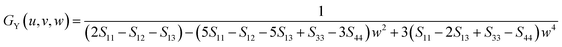 | (11) |
Similarly, for the Voigt bounds of hexagonal polycrystals, the Y-parameter containing the surface normal can be described as follows.60
| EY (u, v, w) = {[C11 + C12 + C13 − w2(C11 + C12 − C13 − C33)][2C11 − C12 − C13 − w2(5C11 − C12 − 5C13 + C33 − 12C44) + 3w4(C11 − 2C13 + C33 − 4C44]}/{2C11 + C12 + C13 − w2(3C11 + C12 − 3C13 − 4C44) + w4(C11 − 2C13 + C33 − 4C44)} | (12) |
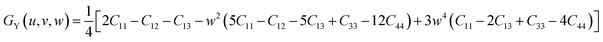 | (13) |
Based on the elastic compliance, the Young's modulus EΦ and shear modulus GΦ in either direction of the hexagonal crystal making an angle Φ with the c-axis can be described as67
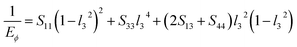 | (14) |
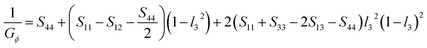 | (15) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ is the cosine of the normal orientation L3 within the crystal plane and Sij is the compliance coefficient.
θ is the cosine of the normal orientation L3 within the crystal plane and Sij is the compliance coefficient.
For a hexagonal structure, the relationships between elastic stiffness Cij and elastic compliance Sij are as follows.67
| S11 − S12 = (C11 − C12)−1 | (16) |
| S11 + S12 = C33/[C33(C11 + C12) − 2C132] | (17) |
| S13 = −C13/[C33(C11 + C12) − 2C132] | (18) |
| S33 = (C11 + C12)/[C33(C11 + C12) − 2C132] | (19) |
| S44 = C44−1 | (20) |
From eqn (10)–(13) and eqn (14)–(20), the elastic moduli of hexagonal LaWN3 can be calculated using the Y-parameter. The elastic moduli based on the Y-parameter can then be determined by the Reuss and Voigt models.
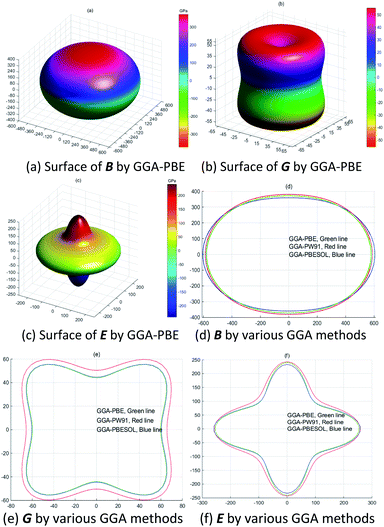
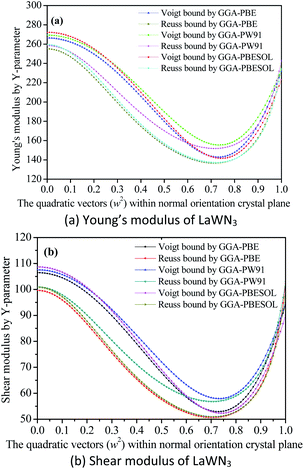
Fig. 6(a–c) show the anisotropy of the bulk modulus, shear modulus and Young's modulus. Meanwhile, the Young's modulus of LaWN3 in Fig. 6(c) has a great deviation in shape from a sphere, indicating that it shows great anisotropy. Fig. 6(d–f) clearly point out the projection curves of the three-dimensional diagrams from Fig. 6(a–c) when the value is zero in the Y-direction and we can see that the various GGA methods (GGA–PBE, GGA–PBESOL and GGA–PW91) have little effect on the curves, with the outer curve being the GGA–PW91 method.
As seen in Fig. 7(a and b), the Young's modulus of LaWN3 using various GGA methods is between 272.23 GPa and 141.58 GPa for the Voigt bounds and between 259.52 GPa and 136.65 GPa for the Reuss bounds as a function of the crystal plane orientation. The maximum value of the Young's modulus is 272.23 GPa and the minimum value is 136.65 GPa. The shear modulus of LaWN3 by Reuss and Voigt bounds of the Y-parameter is between 108.68 GPa and 50.65 GPa, with the Voigt in the region of 52.31–108.68 GPa and the Reuss in the region of 50.65–100.94 GPa. Moreover, in comparison, the Young's modulus and shear modulus of LaWN3 are very close to each other when using various exchange functions (GGA–PBE, GGA–PBESOL and GGA–PW91).
3.5 Optical properties
The reflection spectrum varies with the reflection of electromagnetic wave wavelength characteristics. Materials with different composition or surface structure contribute to the differences in reflection spectrum curves. Light absorption generally follows Beer–Lambert law, where the absorption coefficient is a constant and the symbol α is the absorption coefficient of the medium to monochromatic light. The energy level and intensity of the absorption peak are related to the imaginary part of the dielectric function. Meanwhile, the absorption coefficient is consistent with the corresponding electron transition probability, which can explain the transition of the electron well.The optical constants of LaWN3, including conductivity, dielectric constants, absorption spectra, refractive index, loss function and reflectivity, can be calculated by the following equations,
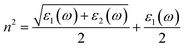 | (21) |
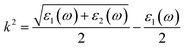 | (22) |
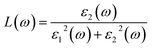 | (23) |
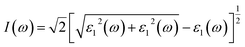 | (24) |
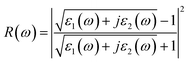 | (25) |
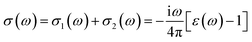 | (26) |
Generally, the appearance of peaks in the spectrum can be considered the result of plasma excitation, while the peak position indicates the frequency of the collective excitation of electrons.
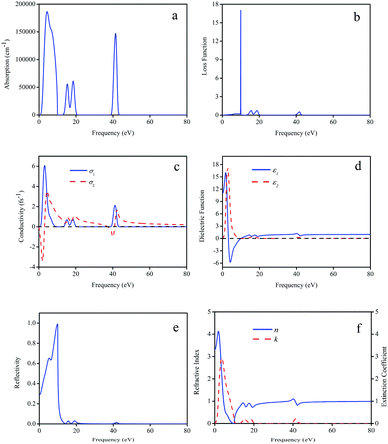
The optical constants of LaWN3, including the absorption spectrum, energy-loss spectrum, conductivity, dielectric function, reflectivity, refractive index and extinction coefficient, are calculated and shown in Fig. 8.
It is noted in Fig. 8(a) that there are three absorption regions (0–10.83 eV, 11.59–21.88 eV and 37.9–44.24 eV, respectively), due to the transition from the N-2p state at the top of the valence band to the unoccupied W-5d state at the bottom of the conduction band. The peak values of L(ω) correspond to the trailing edge of the reflection spectrum; 10 eV, 15.6 eV, 18.8 eV and 41.8 eV are the obvious peaks in Fig. 8(b). We can see that the energy loss near 10 eV is larger, while the energy loss in the other region is the smallest. The peak around 10 eV is very steep, indicating that the energy loss is too small, which is very beneficial to reduce loss and improve the storage efficiency. In Fig. 8(c), there are four obvious peaks, among which the strongest peak is located at 3.18 eV with a value of 6.05 fs−1 and the other three peaks are located at 15.12 eV, 18.35 eV and 41.21 eV.
As seen in Fig. 8(d), when the frequency is zero, the real part (ε1) of the dielectric function corresponds to the static dielectric constant and the calculated ε1 is about 10.98. It can be seen that there are three peaks (2.77 eV, 18.28 eV and 41.27 eV) from the imaginary part of the dielectric function and the strongest peak appears at 2.77 eV with the ε1 value of 17.14. These differences can be attributed to the N common -2p and W-5d transitions between the conduction band and the valence band.
In Fig. 8(e), as the optical reflection is an important optical loss, the reflection spectrum of LaWN3 is given, in which the positions of some peaks are consistent with the calculations of the energy-loss function. It can be seen that the crystal has high reflectivity in the energy region of 3.17–10 eV. Moreover, Fig. 8(f) shows the refractive index n(ω) and extinction coefficient k(ω) and the calculated static refractive index of n(0) is 3.31 at 0 eV. The maximum of the static refractive index is about 4.13 when the frequency is 1.89 eV and the minimum is about 0.75 at 15.23 eV.
In all, it is interesting to find that the spectral characteristics of n(ω) in Fig. 8(f) are very similar to the dielectric function ε1(ω) in Fig. 8(d), which means that the static dielectric constant ε1(0) corresponds to the static refractive index n(0). For the LaWN3 structure, the value of n(ω) arrives at a maximum value of 4.13 at the energy of 1.89 eV and then decreases gradually to the minimum value of zero at the energy of about 9.87 eV.
In summary, the high conductivities in the low frequency (3.18 eV) and medium frequency (41.21 eV) allow future possible application of LaWN3 in optical materials, such as optical fiber transmission to reduce the loss of light in long-distance transmission due to absorption and scattering. This work is meaningful in the synthesis of nitride perovskites for future application in modern optoelectronics devices.68,69
4 Conclusions
Based on DFT, the geometric parameters of LaWN3 were optimized. Then, the elastic constant, band structure, density of states, dielectric constant, refractive index, reflectivity, absorption coefficient and conductivity were calculated and analyzed. The results are as follows:(1) After geometric optimization with different functional methods, the ABX3-type LaWN3 structure is confirmed to be stable.
(2) From the calculation results of the phonon dispersion spectrum and elasticity criterion, LaWN3 is thermodynamically and mechanically stable.
(3) LaWN3 is an indirect band gap semiconductor (Eg = 1.181 eV) and a hybrid orbital is formed near the Fermi level by the contributions of N-2p and W-5d, as well as a small amount of La-5d.
(4) Through study of the elastic properties, LaWN3 produces deformation under stress and shows good ductility.
(5) As for the optical properties of LaWN3, the optical constants, i.e., dielectric constants and refractive index, are higher than those of other ABX3-type materials, which shows that LaWN3 is a very promising functional perovskite material.
The above results provide a theoretical basis to explain the relationship between the electronic structure and physical properties of LaWN3. For further research on LaWN3, surface adsorption, quantum dots, doping, thermodynamics, photocatalysis and piezoelectric properties will be investigated. Investigation of this novel LaWN3 ABX3-type material based on first principles can accelerate the future practical synthesis of the piezoelectric and ferroelectric properties of LaWN3 nitride perovskite using well-established design principles, such as increasing the piezoelectric response in nitride perovskites using morphotropic phase boundaries to better understand the boundary between the polar R3c LaWN3 and non-polar I4 LaWOxN3−x structures.70,71 In all, this investigation helps accelerate the practical synthesis of R3c LaWN3 and improve the efficiency by narrowing the scope of specific chemical reaction conditions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 51905427) and the Provincial Natural Science Foundation of Shaanxi Province (No. 2020JQ-769).Notes and references
- J. Hwang, R. R. Rao, L. Giordano, Y. Katayama, Y. Yu and Y. Shao-Horn, Science, 2017, 358, 751–756 CrossRef CAS PubMed.
- H. Najjar and H. Batis, Catal. Rev., 2016, 58, 371–438 CrossRef CAS.
- A. Gómez, Q. Wang, A. R. Goñi, M. Campoy-Quiles and A. Abate, Energy Environ. Sci., 2019, 12, 2537–2547 RSC.
- Y. B. Lu, X. Kong, X. Chen, D. G. Cooke and H. Guo, Sci. Rep., 2017, 7, 41860 CrossRef CAS PubMed.
- D. Ran, X. Zhang and W. S. Xiao, Adv. Funct. Mater., 2017, 27, 1702207 CrossRef.
- X. Zhang, R. Munir, Z. Xu, Y. Liu, H. Tsai, W. Nie, J. Li, T. Niu, D. M. Smilgies, M. G. Kanatzidis, A. D. Mohite, K. Zhao, A. Amassian and S. Liu, Adv. Mater., 2018, 30, 1707166 CrossRef PubMed.
- M. Kim, G. H. Kim, K. S. Oh, Y. Jo, H. Yoon, K. H. Kim, H. Lee, J. Y. Kim and D. S. Kim, ACS Nano, 2017, 11, 6057–6064 CrossRef CAS PubMed.
- T. Song, X. Cai, M. W.-Y. Tu, X. Zhang, B. Huang, N. P. Wilson, K. L. Seyler, L. Zhu, T. Taniguchi, K. Watanabe, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao and X. Xu, Science, 2018, 360, 1214–1218 CrossRef CAS PubMed.
- J. Fujioka, T. Okawa, A. Yamamoto and Y. Tokura, Phys. Rev. B, 2017, 95, 121102 CrossRef.
- L. Glasser, Inorg. Chem., 2017, 56, 8920–8925 CrossRef CAS PubMed.
- L. Zhang, X. Yang, Q. Jiang, P. Wang, Z. Yin, X. Zhang, H. Tan, Y. M. Yang, M. Wei, B. R. Sutherland, E. H. Sargent and J. You, Nat. Commun., 2017, 8, 15640 CrossRef CAS PubMed.
- S. Kumar, J. Jagielski, N. Kallikounis, Y.-H. Kim, C. Wolf, F. Jenny, T. Tian, C. J. Hofer, Y.-C. Chiu, W. J. Stark, T.-W. Lee and C.-J. Shih, Nano Lett., 2017, 17, 5277–5284 CrossRef CAS PubMed.
- H. Tsai, W. Nie, J. C. Blancon, C. C. Stoumpos, C. M. M. Soe, J. Yoo, J. Crochet, S. Tretiak, J. Even, A. Sadhanala, G. Azzellino, R. Brenes, P. M. Ajayan, V. Bulovic, S. D. Stranks, R. H. Friend, M. G. Kanatzidis and A. D. Mohite, Adv. Mater., 2018, 30, 1704217 CrossRef PubMed.
- F. Jia, K.-B. Siham, B. Fabrice and C. Marilyne, Composites, Part B, 2018, 151, 127–138 CrossRef.
- H. Chen, F. Ye, W. Tang, J. He, M. Yin, Y. Wang, F. Xie, E. Bi, X. Yang, M. Gratzel and L. Han, Nature, 2017, 550, 92 CrossRef CAS PubMed.
- M. Ans, J. Iqbal, A. I. A. Bhatti and K. Ayub, RSC Adv., 2019, 9, 34496–34505 RSC.
- N. Raja, D. Murali, S. V. M. Satyanarayana and M. Posselt, RSC Adv., 2019, 9, 34158–34165 RSC.
- Y. Liu, Q. Xu, S. Chang, Z. Lv, S. Huang, F. Jiang, X. Zhang, G. Yang, X. Tong, S. Hao and Y. Ren, Phys. Chem. Chem. Phys., 2018, 20, 19950–19957 RSC.
- R. Su, C. Diederichs, J. Wang, T. C. H. Liew, J. Zhao, S. Liu, W. Xu, Z. Chen and Q. Xiong, Nano Lett., 2017, 17, 3982–3988 CrossRef CAS PubMed.
- C. Tian, T. Guo, S. Zhao, W. Zhai, C. Ge and G. Ran, RSC Adv., 2019, 9, 35984–35989 RSC.
- Z. Xiao, Q. Wang, X. Wu, Y. Wu, J. Ren, Z. Xiong and X. Yang, Org. Electron., 2020, 77, 105546 CrossRef CAS.
- J. Bao and V. G. Hadjiev, Nano-Micro Lett., 2019, 11, 26 CrossRef CAS.
- K. Masuko, M. Shigematsu, T. Hashiguchi, D. Fujishima, M. Kai, N. Yoshimura, T. Yamaguchi, Y. Ichihashi, T. Mishima, N. Matsubara, T. Yamanishi, T. Takahama, M. Taguchi, E. Maruyama and S. Okamoto, IEEE J. Photovolt., 2014, 4, 1433–1435 Search PubMed.
- Y. Kato, S. Fujimoto, M. Kozawa and H. Fujiwara, Phys. Rev. Appl., 2019, 12, 024039 CrossRef CAS.
- L. Ba, H. Liu and W. Shen, Prog. Photovoltaics, 2018, 26, 924–933 CAS.
- Y. Wang, H. Arandiyan, H. A. Tahini, J. Scott, X. Tan, H. Dai, J. Gale, A. Rohl, S. C. Smith and R. Amal, Nat. Commun., 2017, 8, 15553 CrossRef CAS PubMed.
- J. Lu, W. Luo, J. Feng and H. Xiang, Nano Lett., 2017, 18, 595–601 CrossRef PubMed.
- R. Jacobs, T. Mayeshiba, J. Booske and D. Morgan, Adv. Energy Mater., 2018, 8, 1702708 CrossRef.
- S. S. Shin, E. J. Yeom, W. S. Yang, S. Hur, M. G. Kim, J. Im, J. Seo, J. H. Noh and S. I. Seok, Science, 2017, 356, 167–171 CrossRef CAS PubMed.
- M. S. Alkathy and K. C. J. Raju, J. Alloys Compd., 2018, 737, 464–476 CrossRef CAS.
- B. Huang and M. Kaviany, Acta Mater., 2010, 58, 4516–4526 CrossRef CAS.
- T. Fan, Q.-F. Zeng and S.-Y. Yu, Acta Phys. Sin., 2016, 65, 118102 Search PubMed.
- M. Ju, J. Dai, L. Ma and X. Zeng, Adv. Energy Mater., 2017, 7, 1700216 CrossRef.
- W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2016, 7, 4548–4556 RSC.
- Y. Fang, C. A. J. Fisher, A. Kuwabara, X. Shen, T. Ogawa, H. Moriwake, R. Huang and C. Duan, Phys. Rev. B, 2017, 95, 014111 CrossRef.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570 Search PubMed.
- R. Malik, L. Franke and A. Siebes, Thin Solid Films, 2001, 381, 176–182 CrossRef.
- V. I. Zubov, N. P. Tretiakov, J. N. Teixeira Rabelo and J. F. Sanchez Ortiz, Phys. Lett. A, 1994, 194, 223–227 CrossRef CAS.
- B. R. Sahu, Mater. Sci. Eng., B, 1997, 49, 74–78 CrossRef.
- M. G. Brik and C.-G. Ma, Comput. Mater. Sci., 2012, 51, 380 CrossRef CAS.
- L. J. Sham and M. Schlüter, Phys. Rev. Lett., 1983, 51, 1888–1891 CrossRef.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, Phys. Rev. Lett., 2007, 100, 146401 CrossRef PubMed.
- S. Sajid, A. M. Elseman, J. Ji, S. Dou, D. Wei, H. Huang, P. Cui, W. Xi, L. Chu, Y. Li, B. Jiang and M. Li, Nano-Micro Lett., 2018, 10, 51 CrossRef PubMed.
- F. Giustino, Rev. Mod. Phys., 2017, 89, 015003 CrossRef.
- D. M. Monahan, L. Guo, J. Lin, L. Dou, P. Yang and G. R. Fleming, J. Phys. Chem. Lett., 2017, 8, 3211–3215 CrossRef CAS PubMed.
- J. Iles-Smith, D. P. S. Mccutcheon, A. Nazir and J. Mork, Nat. Photonics, 2017, 11, 521–526 CrossRef CAS.
- I. Niehues, R. Schmidt, M. Drüppel, P. Marauhn, D. Christiansen, M. Selig and R. Bratschitsch, Nano Lett., 2018, 18, 1751–1757 CrossRef CAS PubMed.
- R. Y. Babkin, K. V. Lamonova, S. M. Orel, Yu. G. Pashkevich and V. F. Meshcheryakov, Opt. Spectrosc., 2012, 112, 438–442 CrossRef CAS.
- K. Matsunaga, Y. Iwamoto and H. Matsubara, J. Mater. Res., 2000, 15, 429–436 CrossRef CAS.
- S. Tennakoon, Y. Peng, M. Mookherjee, S. Speziale, G. Manthilake, T. Besara, L. Andreu and F. Rivera, Sci. Rep., 2018, 8, 1372 CrossRef PubMed.
- M. Zhong, Q. Liu, H. Qin, Z. Jiao, F. Zhao, H. Shang, F. Liu and Z. Liu, Eur. Phys. J. B, 2017, 90, 115 CrossRef.
- X. S. Cao, J. Low Temp. Phys., 2017, 189, 1–8 CrossRef.
- C. C. Chen, C. C. Lin, L. G. Liu, S. V. Sinogeikin and J. D. Bass, Am. Mineral., 2001, 86, 1525–1529 CrossRef CAS.
- Q. Liu, Z. Liu, L. Feng and H. Tian, J. Solid State Chem., 2012, 196, 425–434 CrossRef CAS.
- F. Jia, K.-B. Siham and B. Fabrice, Mol. Simul., 2018, 44, 285–299 CrossRef.
- M. Born, K. Huang and M. Lax, Am. J. Phys., 1954, 39, 113–127 Search PubMed.
- A. Afaq, A. Bakar, S. Anwar, W. Anwar and A. Fazal-e-Aleem, Int. J. Mod. Phys. B, 2018, 32, 1850362 CrossRef CAS.
- E. Olsson, X. Aparicio-Anglès and N. H. de Leeuw, J. Chem. Phys., 2016, 145, 224704 CrossRef PubMed.
- J. Fu, F. Bernard and S. Kamali-bernard, J. Phys. Chem. Solids, 2017, 101, 74–89 CrossRef CAS.
- Y. L. Page, P. Saxe and J. R. Rodgers, Phys. Status Solidi B, 2002, 229, 1155–1161 CrossRef.
- D. P. Dandekar, Phys. Rev., 1968, 172, 873–877 CrossRef CAS.
- R. Terki, H. Feraoun, G. Bertrand and H. Aourag, Phys. Status Solidi B, 2005, 242, 1054–1062 CrossRef CAS.
- I. R. Shein, K. I. Shein and A. L. Ivanovskii, J. Nucl. Mater., 2007, 361, 69–77 CrossRef CAS.
- L. Shi, Y. Duan, X. Yang and L. Qin, Chin. Phys. Lett., 2010, 27, 159–162 Search PubMed.
- S. F. Pugh, Philos. Mag., 2009, 45, 823–843 Search PubMed.
- J. Zhang and R. J. Reeder, Am. Mineral., 1999, 84, 861–870 CrossRef CAS.
- N. Pandey, A. Kumar and S. Chakrabarti, RSC Adv., 2019, 9, 29556–29565 RSC.
- F. Hao, C. C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Nat. Photonics, 2017, 8, 489–494 CrossRef.
- K. R. Talley, J. Mangum, C. L. Perkins, R. Woods-Robinson, A. Mehta, B. P. Gorman, G. L. Brennecka and A. Zakutayev, Adv. Electron. Mater., 2019, 5, 1900214 CrossRef.
- H. Liu, J. Chen, H. B. Huang, L. L. Fan, Y. Ren, Z. Pan, J. X. Deng, L. Q. Chen and X. R. Xing, Phys. Rev. Lett., 2018, 120, 055501 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10735e |
| This journal is © The Royal Society of Chemistry 2020 |