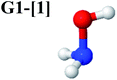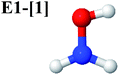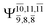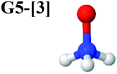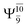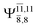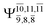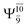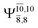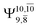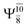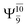Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Photolytic mechanisms of hydroxylamine†
Jittima Thisuwana,
Phorntep Prommab and
Kritsana Sagarik *b
*b
aDivision of Science, Faculty of Education, Nakhon Phanom University, Nakhon Phanom 48000, Thailand
bSchool of Chemistry, Institute of Science, Suranaree University of Technology, Nakhon Ratchasima 30000, Thailand. E-mail: kritsana@sut.ac.th; Fax: +66 44 224635; Tel: +66 44 224635
First published on 26th February 2020
Abstract
The photodissociation of small molecules has been extensively studied because of the increase in environmental problems related to the atmosphere of the Earth. In this work, the photodissociation mechanisms of hydroxylamine (NH2OH) as a model molecule in its lowest singlet-excited (S1) state were systematically studied using the complete active space second-order perturbation theory (CASPT2) and transition state theory (TST). In particular, this study focused on nonradiative relaxation processes that convert the S0 → S1 excited-state molecule to its products in their respective electronic ground states. The potential energy curves obtained from relaxed scans suggest that O–H dissociation is the preferred process in the S1 state. For the N–O and N–H dissociation pathways, thermally excited precursors were hypothesized to form in the S0 state to circumvent O–H dissociation. Thus, S0 → S1 vertical excitations lead to transition structures in the S1 state, which fragment to their respective electronic-ground-state products. The thermodynamic and kinetic results confirmed the precursor hypothesis, showing that the exothermic energy caused by the formation of HNO and H2 is sufficient to generate such precursors in the S0 state. Additionally, the TST confirmed that unimolecular isomerization–dissociation is a two-step process that generates products effectively by direct photolysis of the corresponding covalent bonds. In particular, the process consists of O–H bond dissociation, followed by spontaneous isomerization and formation of H2 in its electronic ground state, resulting in the high quantum yield observed in the UV absorption experiments in the preferential formation of HNO and H2. The configuration interaction coefficients of the characteristic structures on the potential energy curves revealed considerable changes in the multiconfigurational character of the wavefunctions, especially for the transition structures. These are characterized by the development of Rydberg orbitals, being produced at the intersection of the S0 and S1 states. The present study highlights the effects of thermal selectivity and the multiconfigurational character of the wavefunctions on photodissociation. Because detailed information on the photolytic mechanisms of isolated NH2OH is limited both theoretically and experimentally, these results provide fundamental insight into unimolecular photodissociation, posing ground for future studies on related systems.
Introduction
The photodissociation of small molecules has been extensively studied both theoretically and experimentally because environmental problems related to the atmosphere of the Earth are increasing.1 Because it has O–H and N–H groups, as well as lone-pair electrons, hydroxylamine (NH2OH) has often been employed as a prototypical molecule in mechanistic studies of gas-phase photodissociation processes.2–7 For isolated NH2OH, two types of unimolecular photodissociation mechanisms have been reported: (i) direct photolysis of the O–H, N–O, and N–H covalent bonds,3 which can generate the nitroxyl (NH2O), hydroxylamino (NHOH), amino (NH2), hydroxyl (OH) radical groups, and hydrogen (H); (ii) intramolecular isomerization/dissociation, which can produce, e.g., nitrosyl hydride (HNO)8–10 and ammonia oxide (NH3O).11–14In the direct photolysis pathway, ultraviolet (UV) absorption experiments have shown that the H-atom channel, in which two H atoms are generated with a quantum efficiency greater than one (1.7), is the preferred process at an absorption wavelength of 193 nm. In this pathway, N–O dissociation is a minor process, with a quantum efficiency of less than 0.1.5 Instead, photolysis by UV absorption at 240 nm leads mainly to the dissociation of N–O and formation of NH2 and OH in their electronic ground states.7 Thus, though the O–H dissociation was first proposed, both O–H and N–O dissociation have been reported as primary processes (representing 60% and 40%, respectively) in the direct photolysis of NH2OH vapor at 298 K, because of the possible thermal decomposition.3
Analysis of the H-atom Doppler profiles5 suggested that the only energetically accessible path to generate two H atoms is
| NH2OH + hν → H + HNO + H, | (1) |
| NH2OH + hν → H + NH2O → H + HNO + H | (2) |
| NH2OH + hν → H + NHOH → H + HNO + H. | (3) |
Although the final products of eqn (2) and (3) are identical, the intermediates are different. Therefore, it is necessary to determine which covalent bond, O–H or N–H, dissociates first. Limited evidence suggests that the N–H dissociation of eqn (3) occurs first.5
To study the photodissociation of NH2OH, ab initio calculations have been previously performed on low-lying singlet states using the complete active space self-consistent field (CASSCF) method.7 The potential energy curves obtained from the freeze-scan method, in which the remaining coordinates were fixed at their MP2/6-31G** equilibrium values in the electronic ground state, showed that excitations from the two lowest-lying singlet states (norb = 8 and 9) are possible and can lead to fragmentations through the H-atom, NH2, and OH channels. It was concluded that these two dissociation processes result from excitations with different wavelengths rather than different excitation mechanisms.7 This is consistent with other ab initio calculations based on the coupled electron pair approximation, which showed that the two highest occupied orbitals, 2a′′ and 7a′, are associated with the 2p lone-pair orbitals of the O and N atoms, respectively, with an energy difference of less than 1 eV.15
The end product of NH2OH photolysis at 193 nm (6.42 eV)5 is HNO, which is an important intermediate in the formation of NO by combustion16 and by the catalytic decomposition of ozone (O3) in the stratosphere and reaction with HNOH.17 HNO is a reactive radical with a rather long lifetime (0.1 s),18 and it has been studied extensively both experimentally and theoretically.8 Although computational studies have suggested the formation of triplet HNO (3HNO), the bent structure in the singlet state (1HNO) was concluded to be the most stable,19 with a singlet–triplet energy gap of 77 kJ mol−1.20 Using thermodynamic data, the threshold wavelength (λthres) for the formation of HNO and H2 after excitation of NH2OH by 193 nm-UV radiation was predicted to be 891 nm (1.39 eV).5
The interconversion between NH2OH and NH3O is a prototypical model for unimolecular chemical transformations (i.e., isomerization).11 Although the energy barrier associated with intramolecular hydrogen/proton transfer from the O atom to N is rather high in the electronic ground state of this system (∼234 kJ mol−1),11 mass spectroscopic experiments and ab initio calculations confirmed the existence of neutral NH3O in the gas phase,12 and structure–reactivity analysis of the equilibrium constants suggested that ∼20% of aqueous NH2OH solution is composed by NH3O.13
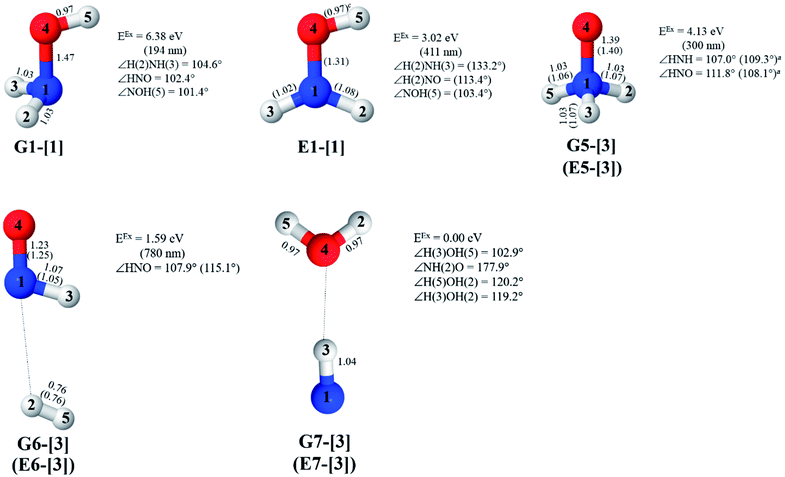
In this work, the photolytic mechanisms of a single NH2OH molecule in the lowest singlet-excited (S1) state were studied using ab initio calculations through the complete active space second-order perturbation theory (CASPT2) with the aug-cc-pVDZ basis set. Different from previous ones, this study focuses on nonradiative relaxation processes that convert the excited-state molecule to its electronic-ground-state products and on the effects of thermal energy on photodissociation. The structures and energetics of the precursors, and the transition structures of the seven dissociation channels, shown in Fig. 1, were studied in detail using the S0 and S1 potential energy curves obtained from CASPT2 and relaxed scans. To determine the contributions of the different electronic states to photodissociation, we analyzed the configuration interaction (CI) coefficients corresponding to the multiconfigurational character of each structure on the potential energy curves. Because of the limited theoretical and experimental information, the role of thermal energy in the photolytic mechanisms was discussed using the transition state theory (TST),21,22 considering the 200–1200 K temperature range.
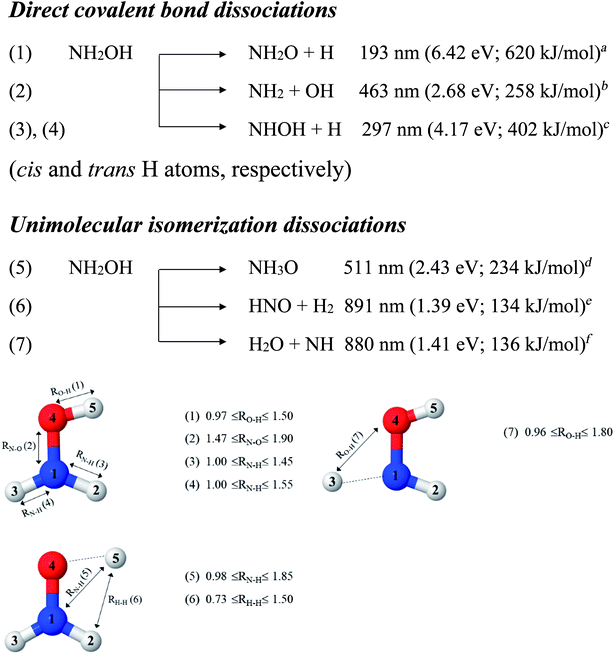 | ||
| Fig. 1 Direct covalent bond dissociations and unimolecular-isomerization dissociations for NH2OH in the gas phase suggested based on experiments and theories. Double sided arrows represent the degrees of freedom used in the calculations of the potential energy curves. Distances are in Å. (…) = dissociation channel. aUV absorption in ref. 5; bthe value reported in Table II of ref. 7 based on the analysis of the data in ref. 41; cthreshold energy for the photodissociation of NH3 into NH and H2 from photoemission in ref. 42; dab initio calculations in the electronic ground state in ref. 11; ethermodynamic data in ref. 5; fthermodynamic data and ab initio calculations in ref. 43. | ||
Computational methods
Ab initio calculations
Because the photodissociation of NH2OH involves fragmentation and formation of covalent bonds, closed- and open-shell configurations must be considered.23 To account for the multiconfigurational character of NH2OH photolysis, ab initio calculations were performed using CASPT2, which is a widely recognized method for excited-state calculations.24 It should be mentioned that although the multistate complete-active-space second-order perturbation (MS-CASPT2) method is more accurate, MS-CASPT2 calculations are computer intensive and therefore applicable only to small systems. In this work, because the energy gradients with respect to degrees of freedom and Hessian had to be computed extensively, the CASPT2 method was employed to optimize the computational resources.The electronic ground state of NH2OH in its equilibrium structure with Cs symmetry is represented by (1a′)2(2a′)2(3a′)2(4a′)2(1a′′)2(5a′)2(6a′)2(2a′′)2(7a′)2. The active space was defined by assigning ten electrons (n = 10) to nine active orbitals (m = 9), and hereafter abbreviated as the (10,9) active space. The remaining electrons were assigned to four doubly occupied orbitals (close = 4). For NH2OH, CASPT2(10,9) calculations involved 5292 CASSCF reference wavefunctions. The aug-cc-pVDZ basis set was satisfactorily used to optimize computational resources. Indeed, augmented basis sets with diffuse functions are reportedly suitable for singlet-state calculations,24 and in our previous study, CASPT2/aug-cc-pVDZ calculations were shown to yield reasonable potential energy curves and S0 → S1 vertical excitation energies for water clusters.25
The ab initio CI calculations in the CASSCF framework7 revealed that the first two electronic excited states involve excitations of a single electron from the two highest occupied orbitals, 2a′′ (norb = 8) and 7a′ (norb = 9), to the two lowest unoccupied ones, 8a′ (norb = 10) and 9a′ (norb = 11), and that these low-lying excited states possess Rydberg and dissociative-valence character, which results from adiabatic excitation.26 Because of this, the S1 state was calculated adiabatically. Schematic diagram showing doubly occupied and active spaces used in CASPT2(10,9) calculations and spatial distributions of the orbitals potentially involved in the S0 → S1 excitation of NH2OH are illustrated in Fig. S1.†
Additionally, because previous ab initio calculations suggested that the products of photodissociation forming at conical intersections do not necessarily have Cs symmetry,26 and because nonradiative relaxations of the excited structures are our primary interest, the CASPT2(10,9) geometry was optimized with no geometrical constraints (C1 symmetry). To study the effects of the multiconfigurational wavefunctions in the photolysis of NH2OH, the CI coefficients of the equilibrium, transition, and final structures on the potential energy curves were examined. The CASPT2(10,9) calculations were performed using the MOLPRO software package27,28 and applying the Werner–Meyer–Knowles nonlinear method in the orbital/state optimization.29–31
Potential energy curves and equilibrium structures
To obtain information on the equilibrium structures and elementary photodissociation steps, the potential energy curves of the direct O–H, N–O, and N–H dissociations were constructed as relaxed scans in the S1 state. Here, the structural parameters of the potential energy curves were optimized using the CASPT2(10,9) and quadratic steepest descent (QSD) methods,32 and the same geometries were used to calculate the energies of the S0 potential energy curves. All degrees of freedom used in these ab initio calculations are included in Fig. 1.Because our preliminary CASPT2(10,9) results showed that the O–H dissociation of channel (1) occurs preferentially along a purely repulsive potential energy curve in the S1 state, the S1 potential energy curves for the N–O and N–H dissociation of channels (2)–(4) were constructed by constraining the O–H(5) distance at the equilibrium value of the ground (S0) state (RO–H(5) = 0.97 Å). These calculated potential energy curves were used to characterize the potential precursors in their electronic ground state outside the Franck–Condon region of the equilibrium structure. From these, the S0 → S1 vertical excitations could provide the transition and final structures in their respective ground state.
Because mass spectroscopy measurements confirmed the existence of neutral NH3O in the gas phase,12 and because intramolecular isomerization is one of the most common radical reactions in electronic excited states, the unimolecular isomerization potential energy curve11 for the formation of ammonia oxide (NH2OH → NH3O) of channel (5) was constructed in the S1 state by transferring the dissociated H(5) atom of channel (1) to the N atom (Fig. 1). Similarly, because HNO and H2 are the dominant products of photolysis at the lowest absorption wavelength (193 nm),5 and because O–H dissociation is the primary process, an intramolecular isomerization that generates HNO and H2 (channel (6)) was assumed by transferring the dissociated H atom of channel (1) (H(5)) to one of the H atoms (H(2) or H(3)) of the NH2 group (Fig. 1). A high energy barrier caused by intramolecular rearrangement was assumed for the H2 generation mechanisms.7
Although NH was not detected during UV photolysis at 193 nm,7 it is interesting to calculate the transition structures and energetics of the H(2) → O and H(3) → O isomerization of channel (7) and compare them with those of the H(5) → N isomerization of channel (5). Similar to the approach used for N–O and N–H dissociation, the unimolecular isomerization–dissociation process that underlies the formation of NH and H2O was simulated by constraining the O–H(5) distance at 0.97 Å and transferring the dissociated H atom of channel (3) or (4) (H(2) or H(3)) to the O atom.
The effects of thermal energy on photodissociation
Because the potential energy curves obtained by CASPT2(10,9) calculations represent the reaction paths at 0 K, the effects of temperature must be incorporated in the model. The mechanisms represented in Fig. 1 involve covalent bond dissociation and isomerization of a single molecule. Therefore, unimolecular rate constants (k) were used, calculating them in the 200–1200 K temperature range according to TST,21,22 which can be applied when the energy barrier is higher than the thermal energy (kBT).33 Although some of the direct covalent bond dissociations involve transferring the H atom, the S0 and S1 potential energy curves evidenced that the S0 state has a broad energy barrier, whereas S1 is barrierless, implying that quantum mechanical tunneling has no significant role. Therefore, the classical (kClass) and quantized-vibrational (kQ-vib, which includes the zero-point vibrational energies) rate constants were initially computed. For the one-dimensional energy profile, the classical transition rate constant is expressed as34
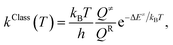 | (4) |
To calculate the rate constant with quantized vibrations, the barrier height obtained with the zero-point vibrational energy (ΔE≠ZPE) is used, and the partition functions are calculated in the harmonic oscillator approximation:
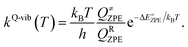 | (5) |
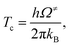 | (6) |
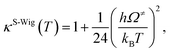 | (7) |
| kS-Wig(T) = κS-Wig(T)kQ-vib(T). | (8) |
Finally, the enthalpy changes (ΔH) in the elementary reactions were computed. For the reactions with energy barrier higher than kBT, the linear relationship between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQ-vib(T) and 1/T was used to calculate the activation enthalpy (ΔH≠) through the Eyring equation,34
kQ-vib(T) and 1/T was used to calculate the activation enthalpy (ΔH≠) through the Eyring equation,34
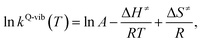 | (9) |
The results confirmed that, for direct covalent bond dissociation at 1200 K, kS-Wig is at most 8% higher than kQ-vib, confirming the applicability of kQ-vib to this system. All the transition state calculations were performed using the DL-FIND program37 included in the ChemShell package.38
Results and discussion
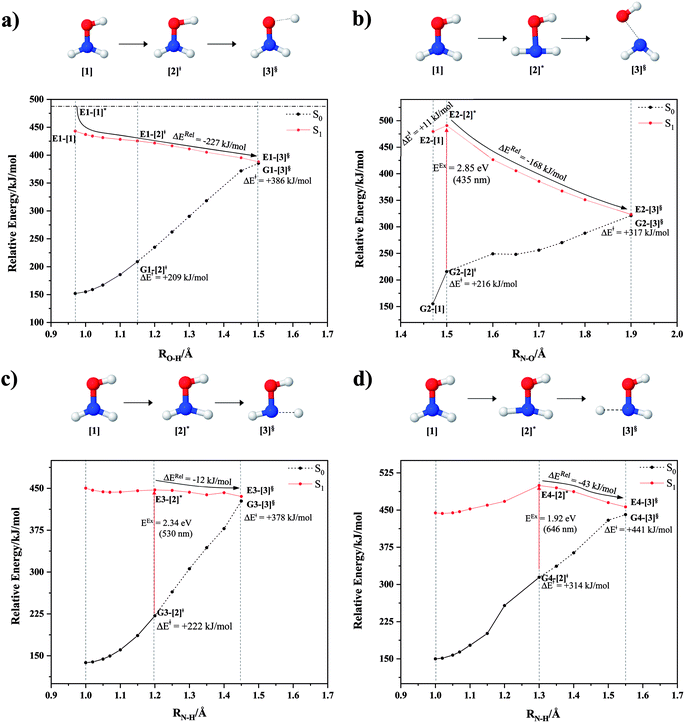
The characteristic structures of NH2OH, identified on the S0 and S1 potential energy curves, are labeled with a three-character code as Gk-[l], Ek-[l]≠, or Ek-[l]*, where G indicates a structure in the S0 state, E indicates one in the S1 state, and k indicates dissociation channels (1)–(7). Different NH2OH structures in the same dissociation channel are labeled [1], [2], etc. The *, §, and ≠ symbols denote vertically excited structures, those at the intersection of the S0 and S1 potential energy curves, and transition structures, respectively. For instance, structures G1-[1]* and E1-[1]* are identical structures (l = 1) computed in the S0 (G) and S1 (E) states, respectively, involved in channel (1) O–H dissociation (k = 1). Instead, E2-[2]* and E2-[4]§ are different structures (l = 2 and 4) on the S1 potential energy curve of N–O dissociation (k = 2); they are a vertically excited structure (*) and a structure at the S0–S1 state intersection (§), respectively.The equilibrium structures of NH2OH in the electronic ground (S0) and lowest singlet-excited (S1) states, obtained from CASPT2(10,9) geometry optimizations, are shown in Fig. 2. The relax-scan potential energy curves and proposed mechanisms for the direct covalent bond dissociations are shown in Fig. 3 and 4, respectively. The relax-scan potential energy curves and proposed mechanisms for the unimolecular-isomerization dissociations are illustrated in Fig. 5 and 6, respectively. The calculated CI coefficients are reported in Tables 1 and S1–S7 of the ESI.† Note that Ψ0 and C0 indicate the electronic ground state, Ψra and Cra indicate the a → r singly excited state (S-type), and Ψr,sa,b and Cr,sa,b indicate the a → r and b → s doubly excited state (D-type). Indices a/r and b/s correspond to occupied and virtual (or unoccupied) spin orbitals, respectively; the presence or absence of a bar denotes beta (β) or alpha (α) spin orbitals, respectively. The classical and quantum rate constants and relative Gibbs free energies of the elementary reactions are reported in Tables S8–S11.† The vertical excitation energies and corresponding oscillator strengths of characteristic structures are included in Table S12.†
Equilibrium structures
Five equilibrium structures were obtained from the CASPT2(10,9) geometry optimizations in the S0 and S1 states (Fig. 2). Structure G1-[1] has Cs symmetry with RN–O = 1.47 Å, RO–H = 0.97 Å, RN–H = 1.03 Å, ∠HNH = 104.6°, ∠HNO = 102.4°, and ∠NOH = 101.4°. These values are in excellent agreement with those obtained from previous ab initio calculations39 and microwave spectra (RN–O = 1.45 Å, RO–H = 0.96 Å, RN–H = 1.02 Å, ∠HNH = 107.1°, ∠HNO = 103.2°, and ∠NOH = 101.4°).40 For structure G1-[1], the CASPT2(10,9) method yields an S0 → S1 vertical excitation energy (EEx) of 6.38 eV (194 nm) with the highest oscillator strength compared with other characteristic structures (Table S12†). These results are in excellent agreement with the photodissociation of NH2OH caused by UV absorption at 193 nm (6.42 eV).5Although NH2OH is not stable in the S1 state and preferentially dissociates into NH2O and H, the CASPT2(10,9) geometry was optimized in this state, constraining the O–H distance to its ground state equilibrium value (0.97 Å), because the corresponding structural and energetic data can be used to understand the photodissociation mechanisms. Although the N–H and N–O distances do not change substantially, the three-dimensional (3-D) S0 structure G1-[1] is transformed into the planar (2-D) structure E1-[1] of Fig. 2, with a considerably lower vertical excitation energy (EEx) of 3.02 eV (411 nm). The change of the NH2OH equilibrium structure upon S0 → S1 excitation (3-D → 2-D) makes it unreasonable to use the freeze-scan method in the construction of the potential energy curves in the excited states.7
The CI coefficients of Table 1 evidence that, for structure G1-[1], the electronic ground state, Ψ0, dominates (C0 = 0.9727), with a small contribution from the doubly excited 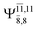 state
state 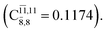 For comparison, the same structure in the S1 state is characterized by a singly excited
For comparison, the same structure in the S1 state is characterized by a singly excited 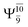 state
state 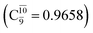 with a small contribution from the excitation of two electrons of the HOMO−1 orbital (norb = 8),
with a small contribution from the excitation of two electrons of the HOMO−1 orbital (norb = 8), 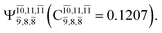 The interference of the primary electronic states with higher electronic excited states confirms the importance of describing the multiconfigurational character of NH2OH. For structure G1-[1], this interference is approximately 12% in both the S0 and S1 states.
The interference of the primary electronic states with higher electronic excited states confirms the importance of describing the multiconfigurational character of NH2OH. For structure G1-[1], this interference is approximately 12% in both the S0 and S1 states.
CASPT2(10,9) geometry optimizations reveal that NH3O with C3v symmetry is stable in both the S0 and S1 states. The S0 state of structure G5-[3], shown in Fig. 2, has RN–O = 1.39 Å, RN–H = 1.03 Å, ∠HNH = 107.0°, and ∠HNO = 111.8°, in excellent agreement with mass spectroscopic experiments and G2-like ab initio calculations (RN–O = 1.35 Å, RN–H = 1.03 Å, and ∠HNO = 113.7°).12 For structure G5-[3], the CASPT2(10,9) method yields a vertical excitation energy (EEx) of 4.13 eV (300 nm). The S0 → S1 excitation leads to structure E5-[3], with small changes in the covalent bond distances and angles: RN–O = 1.40 Å, RN–H = 1.07 Å, ∠HNH = 109.3°, and ∠HNO = 108.1°. Analysis of the CI coefficients listed in Table 1 shows an electronic state interference similar to the case of G1-[1]: structure G5-[3] is characterized by Ψ0 (C0 = 0.9729), with a small contribution from the doubly excited 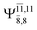 state
state 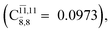 whereas, in the S1 state,
whereas, in the S1 state, 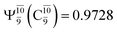 dominates, with a small contribution from
dominates, with a small contribution from 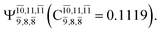
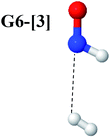
The CASPT2(10,9)-optimized structures of the HNO–H2 complex are nearly identical in the S0 and S1 states, as evidenced by structures G6-[3] and E6-[3] of Fig. 2: in the S0 state, RN–O = 1.23 Å, RN–H = 1.07 Å, and ∠HNO = 107.9°, with a vertical excitation energy (EEx) of 1.59 eV (780 nm); in the S1 state, RN–O = 1.25 Å, RN–H = 1.05 Å, and ∠HNO = 115.1°. The equilibrium geometries and EEx are compatible with the results obtained from absorption in the 650–770 nm range (RN–O = 1.21 Å, RN–H = 1.06 Å, ∠HNO = 109°, and EEx = 1.91–1.61 eV).18 The CI coefficients listed in Table 1 reveal that, in the S0 state, the electronic ground state Ψ0 (C0 = 0.9493) dominates with ∼21% contributions from the closed-shell excited 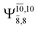 state
state 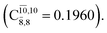 In the S1 state, the same structure is represented by
In the S1 state, the same structure is represented by 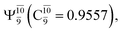 with a small contribution from
with a small contribution from 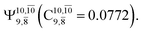 In this case, the patterns of the CI coefficients differ from those of the previously discussed structures: the primary electronic states interfere with excitations of two electrons from the lone-pair orbital of the O atom (norb = 8) to a dissociated-valence orbital (norb = 11).
In this case, the patterns of the CI coefficients differ from those of the previously discussed structures: the primary electronic states interfere with excitations of two electrons from the lone-pair orbital of the O atom (norb = 8) to a dissociated-valence orbital (norb = 11).
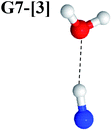
Excellent agreement with previous theoretical and experimental data is also found for the NH–H2O complex. In this case, the equilibrium geometries obtained from CASPT2(10,9) optimization in the S0 and S1 states are identical, as shown for structure G7-[3] in Fig. 2, with RN–H = 1.04 Å, RO–H = 0.97 Å, ∠HOH = 102.9°, and EEx = 0 eV. The patterns of the CI coefficients of structure G7-[3] are the same as those of structures G1-[1], E1-[1], and G5-[3].
Collectively, the structural results, the energetic ones, and the electronic states discussed above confirm the accuracy of the CASPT2(10,9)/aug-cc-pVDZ framework and its applicability to study the photodissociation of NH2OH in the S0 and S1 states.
O–H dissociation
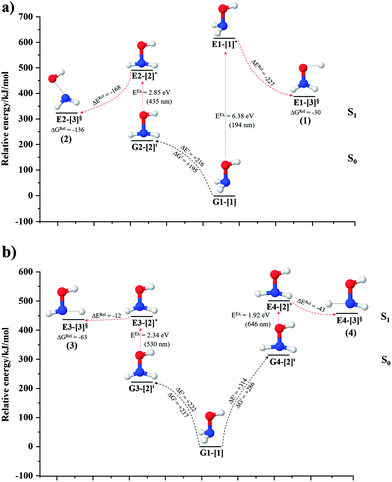
The O–H dissociation in the S1 state is represented by a purely repulsive potential energy curve, as shown in Fig. 3a. Assuming that NH2OH completely dissociates into NH2O and H in their electronic ground states at the intersection of the S0 and S1 states (structure E1-[3]§, with EEx ≈ 0 eV), the potential energy for the O–H dissociation relative to the vertically excited structure E1-[1]* is ΔERel = −227 kJ mol−1. Instead, in the S0 state, the energy barrier (ΔE≠) with respect to the ground-state equilibrium structure G1-[1] is 386 kJ mol−1. The rate constants and relative Gibbs free energies of Tables S8 and S9† confirm that NH2OH becomes a photoacid through S0 → S1 vertical excitation at 194 nm (6.38 eV), and that the nonradiative relaxation of excited NH2OH into ground-state NH2O and H is thermodynamically favorable: for instance, at 1200 K, ΔGRel = −30 kJ mol−1. Oppositely, the thermal dissociation of the O–H bond in the S0 state is thermodynamically and kinetically unfavorable: e.g., at 1200 K, ΔG≠ = 437 kJ mol−1 and kQ-vib = 2.46 × 10−6 s−1.Examination of the S0 and S1 potential energy curves reveals inflection points at O–H distance RO–H = 1.15 Å. Analysis of the CI coefficients of the characteristic structures (Table S1†) shows that, in the S0 state, the planar structure with RO–H = 0.97 Å is dominated by the electronic ground state Ψ0 (C0 = 0.9789), whereas the singly excited 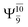 state
state 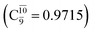 dominates the S1 state. As the O–H distance increases to RO–H = 1.15 Å, the electronic states associated with excitations of an electron of the O lone-pair orbital (norb = 8),
dominates the S1 state. As the O–H distance increases to RO–H = 1.15 Å, the electronic states associated with excitations of an electron of the O lone-pair orbital (norb = 8), 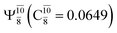 and
and 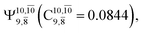 appear in the S0 and S1 states, respectively, having their maximum contribution at the intersection of the S0 and S1 states,
appear in the S0 and S1 states, respectively, having their maximum contribution at the intersection of the S0 and S1 states, 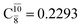 and
and 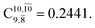 Therefore, structure E1-[2]≠ can be considered as a transition structure and RO–H = 1.15 Å as the threshold O–H distance for Rydberg orbital evolution,7 beyond which O–H in NH2OH dissociates. In this case, the Rydberg orbital (norb = 10) is the natural orbital related to the dissociated H atom. The Gibbs free energy barrier for the Rydberg orbital evolution in the S0 state at 1200 K is ΔG≠ = 210 kJ mol−1, with kQ-vib = 1.82 × 104 s−1 (Table S8†).
Therefore, structure E1-[2]≠ can be considered as a transition structure and RO–H = 1.15 Å as the threshold O–H distance for Rydberg orbital evolution,7 beyond which O–H in NH2OH dissociates. In this case, the Rydberg orbital (norb = 10) is the natural orbital related to the dissociated H atom. The Gibbs free energy barrier for the Rydberg orbital evolution in the S0 state at 1200 K is ΔG≠ = 210 kJ mol−1, with kQ-vib = 1.82 × 104 s−1 (Table S8†).
It is noteworthy that the conversion of the transition structure into the dissociated products is characterized by significant contributions from excitations of an electron in the lone-pair orbital of the O atom (norb = 8) to the Rydberg orbital (norb = 10). For example, in the S1 state, though the contribution of primary electronic state 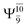 gradually decreases from
gradually decreases from 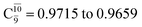 and 0.9463 for structures E1-[1], E1-[2]≠, and E1-[3]§, respectively, the contribution of the next excited state,
and 0.9463 for structures E1-[1], E1-[2]≠, and E1-[3]§, respectively, the contribution of the next excited state, 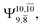 increases significantly from
increases significantly from 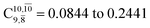 (nearly 300%) for transition structure E1-[2]≠ and product E1-[3]§. These values will be used as guidelines to discuss direct covalent bond dissociation and isomerization–dissociation.
(nearly 300%) for transition structure E1-[2]≠ and product E1-[3]§. These values will be used as guidelines to discuss direct covalent bond dissociation and isomerization–dissociation.
N–O dissociation
Fig. 3b shows the S1 potential energy curve obtained from the CASPT2(10,9) calculations. A maximum is seen at RN–O = 1.50 Å (structure E2-[2]*) with ΔE≠ = 11 and ΔERel = −168 kJ mol−1 at the intersection of the S0 and S1 states, resulting in structure E2-[3]§ and G2-[3]§ with RN–O = 1.90 Å. However, the energy barrier for G2-[3]§ formation through N–O dissociation in the S0 state is ΔE≠ = 317 kJ mol−1 (Fig. 3b). We recall that the S1 potential energy curve for N–O dissociation was calculated by constraining the O–H distance to 0.97 Å because, in the absence of this constraint, the reaction preferentially proceeds towards O–H dissociation. To confirm that structure E2-[2]* is the transition structure for N–O dissociation in the S1 state, CASPT2(10,9) geometrical optimizations were performed with no geometrical constraints and starting from slightly shifted RN–O values of 1.45 and 1.55 Å. For RN–O = 1.45 Å, the results show that structure E2-[2]* relaxes to structure E1-[3]§ (the O–H dissociated structure). Instead, for RN–O = 1.55 Å, N–O dissociation occurs, yielding NH2 and OH (structure E2-[3]§).Overall, these results imply that N–O dissociation cannot proceed directly through the S0 → S1 vertical excitation of structure G1-[1]. However, the S0 and S1 potential energy curves shown in Fig. 3b suggest an alternative pathway to avoid the O–H dissociation shown in Fig. 4a. In fact, equilibrium structure G1-[1] in the S0 state could be thermally excited and form a precursor in the S0 state, i.e., structure G2-[2]≠. This structure can be vertically excited to structure E2-[2]* with EEx = 2.85 eV (435 nm), nonradiatively relaxing along a purely repulsive potential energy curve into products NH2 and OH in their respective electronic ground states (structure E2-[3]§) with ΔGRel = −136 kJ mol−1 (Table S9†). Because the N–O dissociation of structure E2-[2]* is barrierless and spontaneous in the S1 state, the thermal excitation is the process that determines the rate of generation of structure G2-[2]≠; at 1200 K, ΔG≠ = 195 kJ mol−1 and kQ-vib = 7.75 × 104 s−1 (Table S8†). The photolytic mechanism of the N–O bond at 435 nm is supported by the value of the threshold wavelength that generates NH2 and OH from the photoexcitation of NH2OH, λthres = 463 nm (2.68 eV).7,41
The values of the CI coefficients listed in Table S2† for the N–O dissociation show multiconfigurational trends along the potential energy curves, similar to the O–H dissociation. For example, in the S1 state, as the contribution of the primary electronic excited 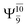 state gradually changes from
state gradually changes from 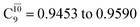 and 0.9312 for structures E2-[1], E2-[2]*, and E2-[3]§, respectively, the contributions arising from excitations of one or two electrons from the HOMO−1
and 0.9312 for structures E2-[1], E2-[2]*, and E2-[3]§, respectively, the contributions arising from excitations of one or two electrons from the HOMO−1 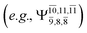 significantly increase when transition structure E2-[2]* with
significantly increase when transition structure E2-[2]* with 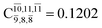 is converted into structure E2-[3]§ (the N–O dissociated structure) with
is converted into structure E2-[3]§ (the N–O dissociated structure) with 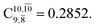 The finding that structure E2-[2]* (with RN–O = 1.50 Å) in the S1 state is represented by a slightly longer N–O distance than the equilibrium value (because of Rydberg orbital evolution at RN–O slightly longer than 1.47 Å) is consistent with previous ab initio calculations using the CASSCF method, which suggested that the Rydberg-valence intersection is close to the N–O equilibrium value.7
The finding that structure E2-[2]* (with RN–O = 1.50 Å) in the S1 state is represented by a slightly longer N–O distance than the equilibrium value (because of Rydberg orbital evolution at RN–O slightly longer than 1.47 Å) is consistent with previous ab initio calculations using the CASSCF method, which suggested that the Rydberg-valence intersection is close to the N–O equilibrium value.7
N–H dissociation
Two possible N–H dissociation pathways have been considered: N–H(2) and N–H(3), hereafter referred to as N–Hcis and N–Htrans dissociations, respectively. Fig. 3c shows that for the N–Hcis dissociation, the S1 potential energy curve with constrained O–H distance (RO–H(5) = 0.97 Å) has a maximum at RN–H(2) = 1.20 Å (structure E3-[2]*) with ΔERel = −12 kJ mol−1 at the intersection of the S0 and S1 states, yielding structure E3-[3]§ with RN–H(2) = 1.45 Å. In the S0 state, the energy barrier for the N–Hcis dissociation (structure G3-[3]§) is ΔE≠ = 378 kJ mol−1 (Fig. 3c). For the N–Htrans dissociation, the S1 potential energy curve with constrained O–H distance reveals a maximum at RN–H(3) = 1.30 Å (structure E4-[2]*) and ΔERel = −43 kJ mol−1, yielding structure E4-[3]§ with RN–H(3) = 1.55 Å. Similar to the case of the N–O dissociation, CASPT2(10,9) geometry optimizations confirmed that E3-[2]* and E4-[2]* are the transition structures for the N–H(2) and N–H(3) dissociation pathways, respectively, with threshold N–H distances of 1.20 and 1.30 Å.In the N–Hcis dissociation pathway, the S0 and S1 potential energy curves suggest the possibility to circumvent the O–H dissociation pathway shown in Fig. 4b by thermal excitation of structure G1-[1] to precursor structure G3-[2]≠ in the S0 state: at 1200 K, ΔG≠ = 217 kJ mol−1 and kQ-vib = 8.54 × 103 s−1 (Table S8†). Then, structure G3-[2]≠ is vertically excited to E3-[2]* with EEx = 2.34 eV (530 nm), and subsequently relaxes into ground-state NHOH and H (structure E3-[3]§): at 1200 K, ΔGRel = −63 kJ mol−1 (Table S9†). In the N–Htrans dissociation pathway (Fig. 4b), structure G1-[1] could be thermally excited to structure G4-[2]≠ with ΔG≠ = 286 kJ mol−1 and kQ-vib = 8.82 × 100 s−1 (Table S8†), and the S0 → S1 vertical excitation with EEx = 1.92 eV (646 nm) leads to structure E4-[2]* and subsequently to ground-state NHOH and H (structure E4-[3]§). Because the ΔG≠ for the formation of the precursor in the S0 state (structure G4-[2]≠) is rather high even at the highest temperature (1200 K), the N–Htrans dissociation is thermodynamically unfavorable. Therefore, the N–Hcis dissociation pathway is preferred, and structure E3-[3]§ can be hypothesized as a precursor for the isomerization–dissociation of channels (6) and (7).
Analysis of the main electronic states of the characteristic structures on the potential energy curves (Tables S3 and S4†) for N–H dissociation shows trends of the CI coefficients similar to the case of O–H dissociation. For N–Hcis dissociation, the electronic ground state Ψ0 dominates (C0 = 0.9807) the S0 state, whereas the singly excited 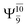 state
state 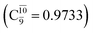 dominates the S1 state. As the N–H(2) distance increases to RN–H(2) = 1.20 Å, the electronic states associated with excitations of an electron from the HOMO−1 (norb = 8) to the LUMO (norb = 10),
dominates the S1 state. As the N–H(2) distance increases to RN–H(2) = 1.20 Å, the electronic states associated with excitations of an electron from the HOMO−1 (norb = 8) to the LUMO (norb = 10), 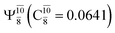 and
and 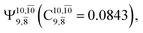 appear in the S0 and S1 states, respectively. Their respective maximum,
appear in the S0 and S1 states, respectively. Their respective maximum, 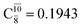 and
and 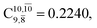 is observed at the intersection of the S0 and S1 states, corresponding to dissociated N–H(2). Therefore, E3-[2]≠ and RN–H = 1.20 Å are confirmed to be the transition structure and the threshold N–H(2) distance for the evolution of the Rydberg orbitals, respectively.
is observed at the intersection of the S0 and S1 states, corresponding to dissociated N–H(2). Therefore, E3-[2]≠ and RN–H = 1.20 Å are confirmed to be the transition structure and the threshold N–H(2) distance for the evolution of the Rydberg orbitals, respectively.
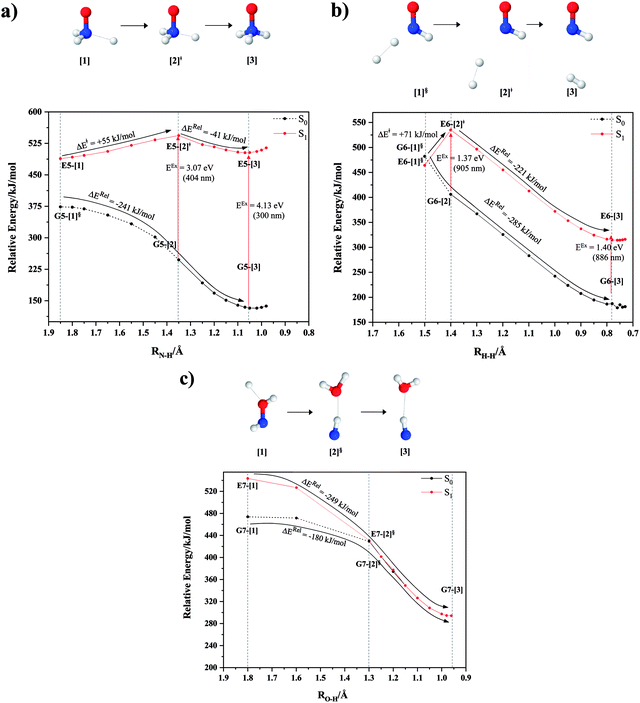
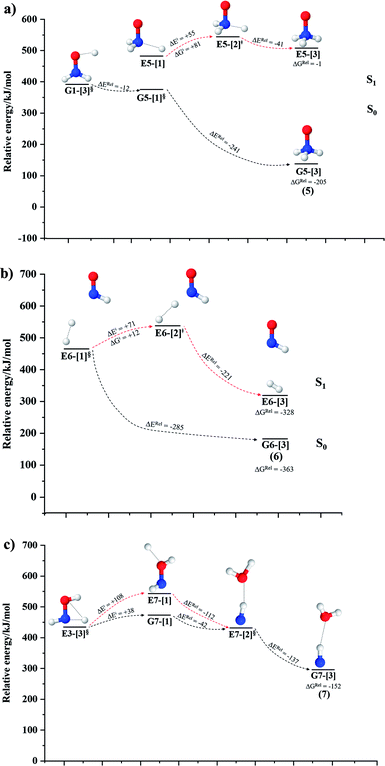
NH3O formation
The relaxed S1 potential energy scan suggests that, starting from the O–H dissociated E1-[3]§ structure, H(5) → N unimolecular isomerization occurs at RN–H(5) = 1.85 Å (structure E5-[1] in Fig. 5a). The results of ref. 11 showed that, in the S0 state, the one-step H(5) → N unimolecular isomerization has a high energy barrier (∼234 kJ mol−1). In contrast, we found that the formation of NH3O from the O–H dissociated structure is barrierless and spontaneous in the S0 state (ΔGRel = −205 kJ mol−1 at 1200 K, Table S10†), and mediated by transition structure E5-[2]≠ (ΔG≠ = 81 kJ mol−1 and kQ-vib = 7.55 × 109 s−1, Table S11†) in the S1 state. Because the total energies of structures E1-[3]§ and G5-[1] are similar (Fig. 6a), the two-step pathway involving E1-[3]§ as the precursor is the preferred mechanism.The CI coefficients listed in Table S5† reveal that, in the S0 state, the potential energy curve for the H(5) → N isomerization is purely repulsive because of an increase in the contribution of the electronic ground state, Ψ0: C0 = 0.6747, 0.9514, and 0.9715 for structures G5-[1]§, G5-[2], and G5-[3], respectively. The increase in C0 is accompanied by a significant decrease in the contribution of excitations from the HOMO−1. As an example, 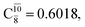
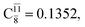 and
and 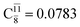 for G5-[1]§, G5-[2], and G5-[3], respectively. In the S1 state, the formation of NH3O is associated to an increasing energy because of an increase in the contributions of the singly excited
for G5-[1]§, G5-[2], and G5-[3], respectively. In the S1 state, the formation of NH3O is associated to an increasing energy because of an increase in the contributions of the singly excited 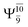 configuration:
configuration: 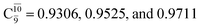 for structures E5-[1], E5-[2]≠, and E5-[3], respectively.
for structures E5-[1], E5-[2]≠, and E5-[3], respectively.
HNO and H2 formation
Intuitively, two precursors are possible for isomerization in channel (6), E1-[3]§ and E3-[3]§, i.e., the O–H(5) and N–H(2) dissociated structure, respectively. Starting from either structure and using RH(2)–H(5) = 1.50 Å, H(5) → H(2) isomerization readily occurs at the intersection of the S0 and S1 states, yielding structure E6-[1]§, as shown in Fig. 5b. This suggests that O–H dissociation occurs first. The potential energy curves for the H(5) → H(2) isomerization show two possibilities for the formation of HNO and H2, which are structures E6-[3] and G6-[3] in the S1 and S0 state, respectively. In the S1 state, E6-[3] can form with a low free energy barrier via transition structure E6-[2]≠ (ΔG≠ = 12 kJ mol−1, kQ-vib = 7.78 × 1012 s−1, and ΔGRel = −328 kJ mol−1 at 1200 K, Table S11†). The existence of E6-[3] as an equilibrium structure in the S1 state supports the experimental finding that the reactive HNO radical has a rather long lifetime (0.1 s) and is one of the dominant products in the gas-phase isolated system.18In contrast, the formation of HNO and H2 from structure G6-[1]§ is barrierless and spontaneous (ΔGRel = −363 kJ mol−1, Table S10†) in the S0 state, with structure G6-[3] (EEx = 1.40 eV, corresponding to 886 nm) as the product. The value of EEx is in excellent agreement with the threshold wavelength associated with the formation of HNO and H2, λthres = 891 nm (1.39 eV), which was obtained experimentally from the excitation of NH2OH by UV photons at 193 nm and thermodynamic data.5 The H(5) → H(2) unimolecular isomerization–dissociation mechanisms of the S0 and S1 states are depicted in Fig. 6b.
The electronic states reported in Table S6† suggest a trend of the CI coefficients for HNO and H2 formation similar to that of NH3O formation. In the S0 state, the reaction is spontaneous because of the increased contributions of Ψ0 along the potential energy curve (C0 = 0.9141, 0.9212, and 0.9493 for structures G6-[1], G6-[2], and G6-[3], respectively). In the S1 state, the contribution of 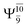 increases along the S1 potential energy curve
increases along the S1 potential energy curve 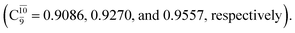
NH and H2O formation
Similar to the HNO and H2 case, the potential energy curves for H(2) → O isomerization shown in Fig. 5c evidence the existence of two possibilities for the formation of NH and H2O. Starting from the N–Hcis dissociated structure (structure E3-[3]§), the H(2) → O isomerization occurs instantaneously in the S1 state (structure E7-[1], RO–H(2) = 1.80 Å). As the O–H(2) distance decreases, the S0 and S1 potential energy curves converge to RO–H(2) = 1.30 Å and reach their minimum at RO–H(2) = 0.97 Å (structure G7-[3]); at 1200 K, ΔGRel in the S1 state is −319 kJ mol−1 (Table S11†). The situation is the same in the S0 state, in which structure G7-[1] spontaneously turns into structure G7-[3]; at 1200 K, ΔGRel = −152 kJ mol−1 (Table S10†). Because the total energies of structures E3-[3]§ and G7-[1] are closer than structures E3-[3]§ and E7-[1], the H(2) → O unimolecular isomerization–dissociation preferentially occurs in the S0 state (Fig. 6c).For H(2) → O isomerization, the CI coefficients listed in Table S7† show the same multiconfigurational character along the potential energy curves of the H(5) → N and H(2) → H(5) isomerization. In the S0 state, the contribution of the electronic ground state increases whereas the contribution of the singly excited state increases in the S1 state.
The interplay between thermal excitations and photoexcitations
The previous sections show in detail the relative Gibbs free energies of the elementary processes and the effects of electronic configuration changes on the potential energy curves. To describe completely the role played by thermal energy in photolytic mechanisms, especially investigating the heat exchange in the endothermic and exothermic processes, the enthalpy changes (ΔH) were calculated in the elementary steps. For the direct photolysis of the N–O and N–H covalent bonds, which involves the formation of the precursors in the S0 state, the linear relationship between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQ-vib(T) and 1/T of eqn (9) was used. For the spontaneous isomerization in the S0 state (channels (5)–(7), negative ΔGRel), the conventional Gibbs free energy change (ΔGRel = ΔHRel − TΔSRel) was used to approximate the enthalpies of the exothermic processes (ΔHRel). Fig. S2a† shows that the linear relationship between ln
kQ-vib(T) and 1/T of eqn (9) was used. For the spontaneous isomerization in the S0 state (channels (5)–(7), negative ΔGRel), the conventional Gibbs free energy change (ΔGRel = ΔHRel − TΔSRel) was used to approximate the enthalpies of the exothermic processes (ΔHRel). Fig. S2a† shows that the linear relationship between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kQ-vib(T) and 1/T is maintained over the entire temperature range. The values of ΔH≠ in Table S8† evidence that, for the N–O and N–Hcis dissociation, the thermal energies required for the formation of the precursors in the S0 state are similar to those required for the formation of the Rydberg orbital (structure G1-[2]≠), being ΔH≠ = 190, 208 and 199 kJ mol−1 with kQ-vib(T) = 7.75 × 104, 8.54 × 103 s−1 and 1.82 × 104, respectively.
kQ-vib(T) and 1/T is maintained over the entire temperature range. The values of ΔH≠ in Table S8† evidence that, for the N–O and N–Hcis dissociation, the thermal energies required for the formation of the precursors in the S0 state are similar to those required for the formation of the Rydberg orbital (structure G1-[2]≠), being ΔH≠ = 190, 208 and 199 kJ mol−1 with kQ-vib(T) = 7.75 × 104, 8.54 × 103 s−1 and 1.82 × 104, respectively.
For the barrierless, direct covalent bond dissociations in the S1 state, the relationship between ΔGRel and T is linear over the entire temperature range (Fig. S2b†). Table S9† reveals that the heat release related to O–H and N–H dissociation in the S1 state is not substantial, compared with that of N–O dissociation (ΔHRel = −3, −9 and −124 kJ mol−1, respectively). Additionally, the exothermic energies of isomerization–dissociation in the S0 state (Table S10†) exceed the thermal energy required for the formation of the precursors, ΔHRel = −219 and −279 kJ mol−1 for channels (5) and (6), respectively. Assuming that the thermal energies generated in the exothermic processes can be transferred to other NH2OH molecules, the exothermic isomerization–dissociation of channel (6), which generates HNO and H2, could generate a relevant excess thermal energy for the formation of the precursors in the S0 state. Thus, the source of thermal energy required to generate the precursors in the S0 state is the formation of HNO and H2. This is supported by the finding that the formation of HNO and H2 is the preferred process in UV experiments at 193 nm, and that HNO is a dominant product in the gas-phase isolated system.18
Conclusion
The photodissociation mechanisms of NH2OH in the lowest singlet-excited state were studied by ab initio calculations in the CASPT2(10,9)/aug-cc-pVDZ framework. This study focused on nonradiative relaxation processes that convert the excited-state molecule to its electronic-ground-state products and on the role played by thermal excitation in photodissociation. All the important equilibrium structures in the S0 and S1 states were characterized, and the potential energy curves for direct covalent bond dissociation and unimolecular isomerization–dissociation were calculated. Additionally, thermodynamic and kinetic data associated with the elementary processes were extracted using the transition state theory.The CASPT2(10,9) geometry optimizations showed that, in the S0 state, the NH2OH equilibrium structure is a 3-D structure with Cs symmetry. An S0 → S1 vertical excitation energy of 6.38 eV (194 nm) was calculated, and NH3O, HNO, and the NH–H2O complex were found to be stable in the S0 and S1 states. Analysis of the CI coefficients of the equilibrium structures revealed that the interference of the primary electronic states with higher excited states is important and that the multiconfigurational character of these structures must be included in ab initio studies. Because all the equilibrium structures and energetics are in good agreement with the available theoretical and experimental data, the use of the CASPT2(10,9) method was proved to be appropriate.
The potential energy curves obtained from the CASPT2(10,9) and relaxed scan methods confirmed that O–H dissociation dominates in the S1 state. Analysis of the CI coefficients of the characteristic structures on the potential energy curves revealed changes in the multiconfigurational character of the pathway upon O–H dissociation. For example, at the inflection point (RO–H(5) = 1.15 Å) of the S1 potential energy curve 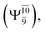 an electronic state associated with excitation of an electron from the lone-pair orbital of the O atom to the Rydberg orbital
an electronic state associated with excitation of an electron from the lone-pair orbital of the O atom to the Rydberg orbital 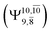 emerges, having its maximum at the intersection of the S0 and S1 states. Therefore, the structure at the inflection point is considered a transition structure, and RO–H(5) = 1.15 Å is considered to be the threshold distance for the development of Rydberg orbitals, which separates the bound and dissociated electronic states (bound-free transition). These conclusions were used as guidelines to discuss the other photodissociation processes.
emerges, having its maximum at the intersection of the S0 and S1 states. Therefore, the structure at the inflection point is considered a transition structure, and RO–H(5) = 1.15 Å is considered to be the threshold distance for the development of Rydberg orbitals, which separates the bound and dissociated electronic states (bound-free transition). These conclusions were used as guidelines to discuss the other photodissociation processes.
Because O–H dissociation is the preferred process in the S1 state, the S1 potential energy curves for the N–O and N–H dissociations were initially constructed by constraining the O–H distance to its equilibrium S0 value. To prevent O–H dissociation, the equilibrium structure in the S0 state must be thermally excited to form appropriate precursors, as suggested by the potential energy curves. Then, the thermally excited precursors are vertically excited to form the transition structures in the S1 state, which then relax nonradiatively along purely repulsive potential energy curves to generate the products in their respective electronic ground states. Although the required thermal energies are relatively high, according to our thermodynamic and kinetic results, the exothermic energy related to the formation of HNO and H2 is at least equally high. Therefore, the thermal excitations in the S0 state determine the rate of N–O and N–H dissociation. The proposed mechanisms, which involve different thermally excited precursors, are supported by experimental observations that show that different photon energies lead to different products in their electronic ground state.
The potential energy curves and thermodynamic results revealed that the unimolecular isomerization–dissociation effectively generates products in their electronic ground state through the direct photolysis of the corresponding covalent bonds. In particular, for the formation of HNO and H2, the potential energy curves suggested that the high quantum yield of photolysis by UV absorption at 193 nm results from a two-step process: first, the O–H bond dissociates; then, isomerization and the formation of H2 in its electronic ground state on a purely repulsive potential curve occur through a strong exothermic process. Overall, the mechanisms proposed in this work emphasize the roles of thermal selectivity and the multiconfigurational character of the associated wavefunctions. Because detailed information on these aspects is limited both theoretically and experimentally, this work provides important insights into the photodissociation of NH2OH. Thus, it can be ground for future theoretical and experimental studies of similar systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Prof. Kritsana Sagarik would like to acknowledge the financial support provided by SUT Research and Development Fund, Project Number: IRD1-102-59-12-13. The financial support provided by the Thailand Research Fund (TRF) (Grant No. MRG6180120) to Dr Jittima Thisuwan is also gratefully acknowledged.References
- J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, John Wiley & Sons, Inc., Hoboken, New Jersey, 3rd edn, 2016 Search PubMed.
- J. Baker, V. Butcher, J. M. Dyke and A. Morris, J. Chem. Soc., Faraday Trans., 1990, 86, 3843–3851 RSC.
- J. Betts and R. A. Back, Can. J. Chem., 1965, 43, 2678–2684 CrossRef CAS.
- L. A. Curtiss, J. Chem. Phys., 1982, 77, 3605 CrossRef CAS.
- K.-H. Gericke, M. Lock, F. Schmidt and F. J. Comes, J. Chem. Phys., 1994, 101, 1988–1995 CrossRef CAS.
- K. Kimura and S. Katsumata, J. Chem. Phys., 1977, 67, 1225–1230 CrossRef CAS.
- D. Luckhaus, J. L. Scott and F. F. Crim, J. Chem. Phys., 1999, 110, 1533–1541 CrossRef CAS.
- U. Bozkaya, J. M. Turney, Y. Yamaguchi and H. F. Shaefer III, J. Chem. Phys., 2012, 136, 164303 CrossRef PubMed.
- I. I.-Burmazović, in The Chemistry and Biology of Nitroxyl (HNO), ed. F. Doctorovich, P. J. Farmer and M. A. Marti, Elsevier, 2017, ch. 5, pp. 67–104 Search PubMed.
- M. Ren, B. Dong and W. Lin, in The Chemistry and Biology of Nitroxyl (HNO), ed. F. Doctorovich, P. J. Farmer and M. A. Marti, Elsevier, 2017, ch. 10, pp. 207–224 Search PubMed.
- R. D. Bach, A. L. Owensby, C. Gonzalez, H. B. Schlegel and J. J. W. McDouall, J. Am. Chem. Soc., 1991, 113, 6001–6011 CrossRef CAS.
- M. Brönstrup, D. Schröder, I. Kretzschmar, C. A. Schalley and H. Schwarz, Eur. J. Inorg. Chem., 1998, 1529–1538 CrossRef.
- A. J. Kirby, J. E. Davies, D. J. Fox, D. R. W. Hodgson, A. E. Goeta, M. F. Lima, J. P. Priebe, J. A. Santaballa and F. Nome, Chem. Commun., 2010, 46, 1302–1304 RSC.
- C. Trindle and D. D. Shillady, J. Am. Chem. Soc., 1973, 95, 703–707 CrossRef CAS.
- V. Staemmler, Acta Phys. Pol., A, 1988, 74, 331 Search PubMed.
- J. A. Miller and C. T. Bowman, Prog. Energy Combust. Sci., 1989, 15, 287–338 CrossRef CAS.
- B. L. Ulich, J. M. Hollis and L. E. Snyder, Astrophys. J., 1977, 217, L105–L108 CrossRef CAS.
- F. W. Dalby, Can. J. Phys., 1958, 36, 1336–1371 CrossRef CAS.
- Y. Zhang, J. Inorg. Biochem., 2013, 118, 191–200 CrossRef CAS PubMed.
- M. D. Bartberger, J. M. Fukuto and K. N. Houk, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 2194–2198 CrossRef CAS PubMed.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251 CrossRef.
- E. Pollak and P. Talkner, Chaos, 2005, 15, 026116 CrossRef PubMed.
- L. González, D. Escudero and L. S.-Andrés, ChemPhysChem, 2012, 13, 28–51 CrossRef PubMed.
- M. Schreiber, M. R. S.-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef PubMed.
- P. Suwannakham, S. Chaiwongwattana and K. Sagarik, RSC Adv., 2018, 8, 36731–36744 RSC.
- H. Hettema and D. R. Yarkony, J. Chem. Phys., 1995, 102, 8431–8439 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz and others, MOLPRO (version 2015.1, a package of ab initio programs), TTI GmbH, Stuttgart, 2015 Search PubMed.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- H.-J. Werner and W. Meyer, J. Chem. Phys., 1980, 73, 2342–2356 CrossRef CAS.
- J. Q. Sun and K. Ruedenberg, J. Chem. Phys., 1994, 101, 2157 CrossRef CAS.
- D. S. Sholl and J. A. Steckel, Density Functional Theory: A Practical Introduction, John Wiley & Sons, Inc., Hoboken, New Jersey, 2009 Search PubMed.
- J. E. House, Principles of Chemical Kinetics, Elsevier, USA, 2nd edn, 2007 Search PubMed.
- E. Wigner, Z. Phys. Chem., 1932, 15, 203–216 Search PubMed.
- E. Wigner, Trans. Faraday Soc., 1938, 34, 29–41 RSC.
- J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed.
- ChemShell, a Computational Chemistry Shell, see http://www.chemshell.org Search PubMed.
- A. G.-Espinoza, J. H.-Cobos and I. O.-Blake, J. Chem. Phys., 2011, 135, 054502 CrossRef PubMed.
- S. Tsunekawa, J. Phys. Soc. Jpn., 1972, 33, 167–174 CrossRef CAS.
- X. Luo, P. R. Fleming, T. A. Seckel and T. R. Rizzo, J. Chem. Phys., 1990, 93, 9194 CrossRef CAS.
- M. Suto and L. C. Lee, J. Chem. Phys., 1983, 78, 4515 CrossRef CAS.
- B. Gelernt, S. V. Filseth and T. Carrington, Chem. Phys. Lett., 1975, 36, 238 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra10956k |
| This journal is © The Royal Society of Chemistry 2020 |