Open Access Article
Open Access ArticleTheoretical design of bis-azole derivatives for energetic compounds†
Keyu Pua,
Linyuan Wang *a,
Jian Liub and
Kai Zhongb
*a,
Jian Liub and
Kai Zhongb
aSchool of Chemistry and Chemical Engineering, Southwest Petroleum University, Chengdu 610500, China. E-mail: vbgr5808062c@163.com
bInstitute of Chemical Materials, CAEP, Mianyang 621999, China
First published on 1st April 2020
Abstract
Bis-azole derivatives are a new class of energetic materials with features that include high nitrogen content, high heat of formation (HOF), high detonation performance and insensitivity to external stimuli. In this paper, 599 new bis-azole compounds were designed in a high-throughput fashion using bis-azole molecules of high density and high thermal decomposition temperature as the basic structure, and high energy groups such as nitro (–NO2) and amino groups (–NH2) as substituents. The molecular geometry optimization and vibration frequency analysis were performed using the DFT-B3LYP/6-311++G(d,p) method. The calculation results show that none of bis-azole derivatives exhibit a virtual frequency. Additionally, the density, heat of formation and characteristic height (h50) of the above compounds were obtained. Detonation performances were predicted by the Kamlet–Jacobs equations, and their structures and performances were studied. Furthermore, correlations between the performance parameters and the parent structure of the molecule, the number of substituting group and configuration were summarized, revealing promising potential candidates for high-energy density materials (HEDMs).
1 Introduction
Energetic materials such as explosives, propellants and pyrotechnics play a vital role in the fields of military, defense, aerospace technology and modern civilization. Recently, novel insensitive HEDMs have become a target for further research and development.1–3 There is a conflict between energy and stability, and the increase in energy is often accompanied by an increase in sensitivity, which poses a challenge for balancing both parameters.4 In recent years, heterocyclic molecules have been introduced into the molecular design due to their advantages of increasing heat resistance and decreasing sensitivity.5 Nanjing University of Science and Technology (NUST) has carried out the molecular design of novel high-energy nitrogen heterocyclic compounds6 with computer technology, which has potential application value in the field of propellants and explosives. The azole ring compounds have become a research hotspot because they have high nitrogen content, high heat of formation, high gas production and produce clean detonation products.7–13 Previously, researchers synthesized various bis-azoles compounds by changing substituents. The synthesis of energetic materials is dangerous, and the characterization is difficult, so theoretical prediction becomes the first choice. This method not only evaluates the performance in advance and reveals the relationship between structures and properties, but also provides guidance for experimental synthesis and reduction of the experimental blindness.14–16In addition to the advantages of traditional azole compounds like high nitrogen content and high heat of formation, the bis-azole compounds also have higher density and lower sensitivity. Compared to traditional nitramines, the bis-azole compounds have more advantages including more convenient control of reaction processes and less environmental impact. Therefore, it is expected to be widely used in production of low-signature propellant, low-smoke fireworks and new explosives.17 In this paper, 599 kinds of nitro-containing compounds were generated by the automatic assembly of the skeleton and functional groups, with each high-energy bis-azole ring as the skeleton, –NH2 as the stabilizing group and –NO2 as the detonating group.18 Compounds were divided into four groups (A–D) according to the skeleton type. The B3LYP/6-311++G(d,p) level of the density functional theory (DFT)19–21 has been applied to study the molecular geometry, density, heat of formation, detonation property and stability of the compounds. Furthermore, the relationship between structure and property was analyzed, and seven compounds meeting the requirements (i.e. high energy and low sensitivity) were selected as potential novel HEDMs.
2 Computational methods
A series of studies by Xiao Heming et al.22–24 on systems containing C, H, O, N and other elements show that the B3LYP method can provide reliable geometric structures and other information in the study of energetic materials. Molecular geometries of the bis-azole derivatives were fully optimized at the B3LYP/6-311++G(d,p) level. The vibration frequency analysis showed that none of the optimized structures exhibited imaginary frequencies, and when all optimized structures corresponded to the local energy minimum points on the respective potential energy surfaces, the stable structures were obtained. DFT combined with the atomization scheme25–28 is used to predict heat of formation, and the principle of the atomization scheme is as follows:| CaHbOcNd(g) → aC(g) + bH(g) + cO(g) + dN(g) | (1) |
That is, the molecule is decomposed into atoms, and the formula for heat of formation ΔH298 at 298 K is
| ΔH298 = ∑ΔHf,p − ∑ΔHf,R = aΔHf,C + bΔHf,H + cΔHf,O + dΔHf,N − ΔHf,CaHbOcNd | (2) |
Additionally,
| ΔH298 = ΔE298 + Δ(pV) = ΔE0 + ΔEZPE + ΔnRT = E0,C + E0,H + E0,O + E0,N − E0,CaHbOcNd − EZPE,CaHbOcNd − ΔET,CaHbOcNd + ΔnRT | (3) |
The characteristic height (h50) can be computed using the following formula, which evaluates the impact sensitivity and stability of energetic compounds,29,30 as suggested by Cao:31
| h50 = 0.1296 + 98.64QNO22 − 0.03405OB100 | (4) |
The following equation was used to calculated OB100:
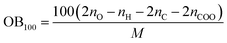 | (5) |
Density directly affects the detonation performance.32 In this paper, the density is calculated by 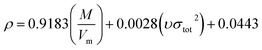 of Politzer's method,33,34 where M is the molecular mass, Vm is the molecular van der Waals volume and υσtot2 reflects the characteristics of the molecules surface electrostatic potentials. Based on the Monte-Carlo method,35,36 Vm is the volume to be defined as the space within a contour of 0.001e bohr−3 (a.u.) density under stable structures. This method for calculating Vm has been successfully applied to the high nitrogen compounds.37 The calculation was performed using the Gaussian 09 and Multiwfn programs.38,39
of Politzer's method,33,34 where M is the molecular mass, Vm is the molecular van der Waals volume and υσtot2 reflects the characteristics of the molecules surface electrostatic potentials. Based on the Monte-Carlo method,35,36 Vm is the volume to be defined as the space within a contour of 0.001e bohr−3 (a.u.) density under stable structures. This method for calculating Vm has been successfully applied to the high nitrogen compounds.37 The calculation was performed using the Gaussian 09 and Multiwfn programs.38,39
Detonation performance is an important indicator to evaluate the quality of energetic materials. For C-, H-, O- and N-series explosives, the widely used semiempirical Kamlet–Jacobs equation40,41 was used to predict the detonation performance:
| D = φ1/2(1.011 + 1.312ρ) | (6) |
φ = N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 1/2Q1/2 1/2Q1/2
| (7) |
| p = 1.558φρ2 | (8) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) is the average molar mass of gaseous detonation products (g mol−1), Q is the detonation chemical energy per gram of explosive (maximum detonation heat per unit mass), J g−1. The term Q = −ΔHf,298, which is the heat of formation. Combined with the heat of formation obtained from the atomization scheme, Q was obtained by using a previously reported method in.23 From the above equation, it can be seen that the impact of the value of Q(−ΔHf,298) on D and p is insignificant, while ρ great influences the estimation of D and p. Previous studies have shown that42–45 the use of the K–J equation to predict detonation performance of high nitrogen compounds is reliable.
is the average molar mass of gaseous detonation products (g mol−1), Q is the detonation chemical energy per gram of explosive (maximum detonation heat per unit mass), J g−1. The term Q = −ΔHf,298, which is the heat of formation. Combined with the heat of formation obtained from the atomization scheme, Q was obtained by using a previously reported method in.23 From the above equation, it can be seen that the impact of the value of Q(−ΔHf,298) on D and p is insignificant, while ρ great influences the estimation of D and p. Previous studies have shown that42–45 the use of the K–J equation to predict detonation performance of high nitrogen compounds is reliable.
All of the above calculation methods and rationales were developed using B3LYP/6-311++G(d,p), and the calculation was performed using the Gaussian 09 quantum chemistry program46 and quantum chemistry Multiwfn program. Additionally, all DFT calculations were performed on the high-throughput computing platform EM-studio1.0 for energetic materials, and the convergence precision is the default value of the program.
3 Results and discussion
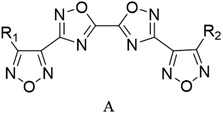
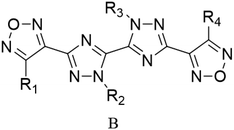
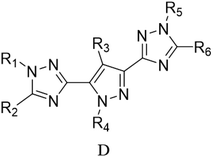
Through the use of a high-throughput computing platform, 599 compounds were designed. The molecular structures of A and C series derivatives are listed in Table 1, and the molecular structures of partial derivatives of B and D series are listed in Table 1, representing and illustrating the structure and performance rules of B and D series. The molecular structures of all designed derivatives of the B and D series are listed (see Tables S1 and S4 in ESI†).| a R1 = H indicates that the R1 substitution site is H, R1,2 = H indicates that R1 and R2 substitution sites are H, and the rest are analogous. | |
|---|---|
 |
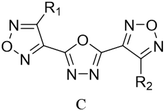 |
| A1: R1 = H, R2 = NO2 | C1: R1 = H, R2 = NO2 |
| A2: R1 = NH2, R2 = NO2 | C2: R1 = NH2, R2 = NO2 |
| A3: R1,2 = NO2 | C3: R1,2 = NO2 |
 |
 |
| B1: R1,2,4 = H, R3 = NO2 | D6: R4,6 = H, R1,2,3 = NH2, R5 = NO2 |
| B2: R1,2,3 = H, R4 = NO2 | D7: R1,3,6 = H, R4,5 = NH2, R2 = NO2 |
| B3: R1,2 = H, R3,4 = NO2 | D8: R1,3 = H, R4,5,6 = NH2, R2 = NO2 |
| B4: R1,3 = H, R2,4 = NO2 | D31: R1,3,5 = H, R2,6 = NH2, R4 = NO2 |
| B5: R1,4 = H, R2,3 = NO2 | D32: R2,3,4,6 = H, R1 = NH2, R5 = NO2 |
| B6: R2,3 = H, R1,4 = NO2 | D33: R1,2,3,4,6 = H, R5 = NO2 |
| B7: R1 = H, R3 = NH2, R2,4 = NO2 | D34: R2,5,6 = H, R1,3 = NH2, R4 = NO2 |
| B8: R2 = H, R1 = NH2, R3,4 = NO2 | D35: R2,3,4 = H, R5,6 = NH2, R1 = NO2 |
| B9: R1 = H, R2 = NH2, R3,4 = NO2 | D120: R2 = H, R1,3,4,5 = NH2, R6 = NO2 |
| B10: R3 = H, R1 = NH2, R2,4 = NO2 | D121: R1 = H, R2,3,4,5 = NH2, R6 = NO2 |
| B11: R1 = H, R4 = NH2, R2,3 = NO2 | D122: R1,2,3,4,5 = NH2, R6 = NO2 |
| B12: R2 = H, R3 = NH2, R1,4 = NO2 | D123: R2,4,6 = H, R1,5 = NH2, R3 = NO2 |
| B13: R2,3 = NH2, R1,4 = NO2 | D124: R2,4 = H, R1,5,6 = NH2, R3 = NO2 |
| B14: R1,3 = NH2, R2,4 = NO2 | D125: R2 = H, R1,4,5,6 = NH2, R3 = NO2 |
| B15: R1,4 = NH2, R2,3 = NO2 | D146: R1,2,4,5 = H, R6 = NH2, R3 = NO2 |
| B16: R1,2 = NH2, R3,4 = NO2 | D147: R1,2,5 = H, R4,6 = NH2, R3 = NO2 |
| B17: R2 = NH2, R1,3,4 = NO2 | D148: R1,4,5,6 = H, R2 = NH2, R3 = NO2 |
| B18: R2 = H, R1,3,4 = NO2 | D152: R2 = H, R1,4,5 = NH2, R3,6 = NO2 |
| B19: R1 = H, R2,3,4 = NO2 | D153: R4 = H, R1,5,6 = NH2, R2,3 = NO2 |
| B20: R1 = NH2, R2,3,4 = NO2 | D154: R4,6 = H, R1,5 = NH2, R2,3 = NO2 |
| B21: R1,2,3,4 = NO2 | D176: R1,4,5 = H, R2,3,6 = NO2 |
| D177: R4,5 = H, R1 = NH2, R2,3,6 = NO2 | |
| D178: R5 = H, R1,4 = NH2, R2,3,6 = NO2 | |
| D183: R5,6 = H, R1,2,3,4 = NO2 | |
| D237: R5 = H, R1,2,3,4,6 = NO2 | |
| D238: R1,2,3,4,5,6 = NO2 | |
3.1 Heats of formation
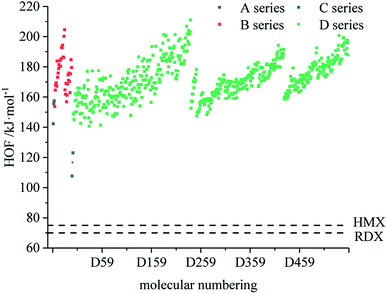
The heat of formation, as the basic thermodynamic property, is an indication of energy level and an important parameter to measure detonation performance. Whether it is to calculate the detonation velocity and detonation pressure of explosives and powders or the specific impulse of propellants, heat of formation occupies a considerable weight in the formula.Fig. 1 compares the heat of formation of the designed 599 derivatives. In the skeleton of the A series, the O on the isofurazan is replaced by N to obtain the skeleton of the B series. Compared with the A series, the heat of formation of the B series is significantly improved, which indicates that the heat of formation increases with the increase of the nitrogen content, and that the skeleton of the B series is energetic and preferable to that of the A series. It is known from Fig. 1 that the heat of formation of all derivatives are higher than that of the traditional energetic materials 1,3,5-trinitro-1,3,5-triazinane (RDX) and 1,3,5,7-tetranitro-1,3,5,7-tetrazocane (HMX). All derivatives exhibit high heat of formation (HOF) values. Therefore, the derivatives can be considered endothermic compounds and possess one of the basic conditions of HEDC. The high HOF values of all derivatives are consistent with previous reports, and high nitrogen heterocyclic energetic compounds have high HOF.47,48 From the perspective of HOF, the application prospects of B and D series are better.
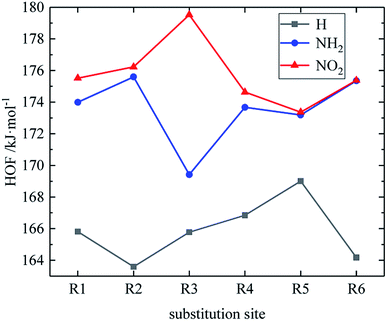
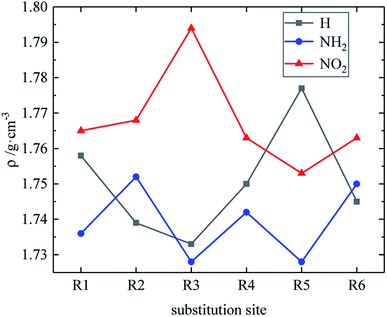
Table 2 shows the heats of formation of partial derivatives, and the heats of formation of all design derivatives of B and D series are presented (see Tables S2 and S5 in ESI†). When the B series substituents are two –NO2 and two –NH2 groups, the HOF of each compound increases in the order of B13 < B14 < B16 < B15. This may be because the reduction of the distance between –NO2 in compounds B13, B14, B16 and B15 leads to the enhancement of steric hindrance effect, thus increasing the HOF of the compound. It indicates that when designing compounds, we can appropriately reduce the distance between –NO2 so as to increase the compound energy. However, when the B series substituents are two –NO2 and one –NH2, the HOF of each compound is: B7 < B8 < B9 < B11 < B10 < B12. Compound B12 has a symmetrical distribution of –NO2 and all the C and N atoms in the molecule are basically on the same plane. The molecule has a stable geometric configuration, so the molecule has larger conjugation and higher HOF. Meanwhile, when the D series contains one –NO2, the derivatives are D1–D151 and D239–D250. In this case, the –NO2 substitution site of the compound with higher HOF is basically on the carbon atom of the diazole ring (R3), especially the compounds D131, D133, D141, D143, D144, D150, and D151 have high HOF. It suggests that we can look for high-energy compounds in D series derivatives with –NO2 at the R3 substitution site. The relationship between the HOF and the substitution site of the D series is shown in Fig. 2. An average HOF of all compounds in the D series that possess an –NO2 group at a certain substitution site (such as R1) is determined, which is the HOF value corresponding to this substitution site (such as R1) on the NO2 line in the figure, and we repeat the above steps for the rest of substitution sites. Similarly, we repeat the above steps to obtain the NH2 line and the H line when the substituents are NH2 and H, as shown in Fig. 2. It is known from the figure that when the D series contains one –NO2 group, –NO2 of compounds with higher HOF is basically substituted at R3, and –NO2 contributes more to the HOF than –NH2. So when designing compounds, we can appropriately introduce multiple –NO2 to improve the HOF of compounds.
| Comp. | HOF | Comp. | HOF | Comp. | HOF | Comp. | HOF | Comp. | HOF |
|---|---|---|---|---|---|---|---|---|---|
| a HOFs (kJ mol−1). | |||||||||
| A1 | 142.2 | B9 | 178.8 | B20 | 200.3 | D34 | 151 | D152 | 184.3 |
| A2 | 155.6 | B10 | 181.5 | B21 | 204.6 | D35 | 155.7 | D153 | 180.1 |
| A3 | 157.4 | B11 | 180.3 | C1 | 107.7 | D120 | 164.9 | D154 | 168.7 |
| B1 | 153.7 | B12 | 184.2 | C2 | 116.7 | D121 | 170.7 | D176 | 169.9 |
| B2 | 164.6 | B13 | 180.3 | C3 | 123.1 | D122 | 177 | D177 | 178.2 |
| B3 | 167.9 | B14 | 185.3 | D6 | 158 | D123 | 157.1 | D178 | 191.1 |
| B4 | 169.4 | B15 | 192.9 | D7 | 150.2 | D124 | 166.1 | D183 | 188.4 |
| B5 | 167.1 | B16 | 192.7 | D8 | 161.4 | D125 | 173.5 | D237 | 203.3 |
| B6 | 183.8 | B17 | 194.3 | D31 | 165 | D146 | 165.9 | D238 | 211.1 |
| B7 | 173.1 | B18 | 186.5 | D32 | 146.2 | D147 | 171.4 | ||
| B8 | 175.9 | B19 | 186.2 | D33 | 140.7 | D148 | 167.7 | ||
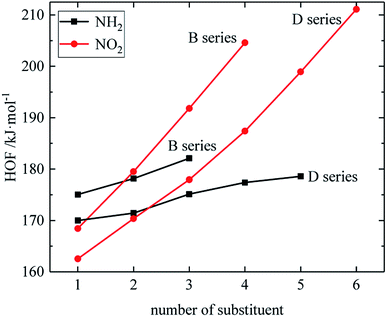
The relationship between the HOF of B and D series and the number of substituents is shown in Fig. 3. The relationship between the contributions of different energetic groups to the HOF is –NO2 > –NH2, and the HOF of B and D series increases as the number of –NH2 or –NO2 increases. It can be seen that in each series of derivatives, the influence of substituents on the HOF of the compounds is consistent. Table 2 also shows that the HOF of A and C series increases with the increase of –NO2 number; among the four series, each compound in which all substituents are –NO2 has the highest HOF in the corresponding respective series of compounds. This is because on the one hand, the introduction of –NO2 increases the energy, and on the other hand, the enhancement of the steric hindrance effect of –NO2 also contributes to the energy increase.
3.2 Sensitivity
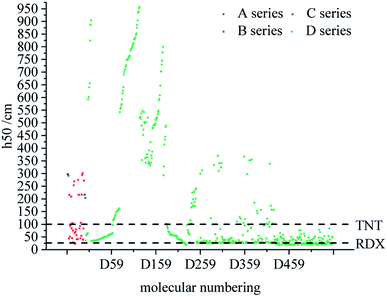
The characteristic height (h50) is the height at which the sample is impacted by a given mass and there is 50% probability of causing an explosion. The h50 has been calculated to reflect the impact sensitivity and stability of the designed compounds in this work. The larger h50, the more stable the compound.Fig. 4 compares the h50 values of all derivatives. Each series has a compound with a higher h50 value than that of TNT (100 cm),49 which indicates that these series have low sensitivity and good stability. The h50 values of all series of derivatives lie in the range of 18–958 cm, which are higher than the h50 value (12 cm)50 of CL-20. Moreover, the h50 value of D series derivatives tends to be higher, indicating that this skeleton of D series may be more stable.
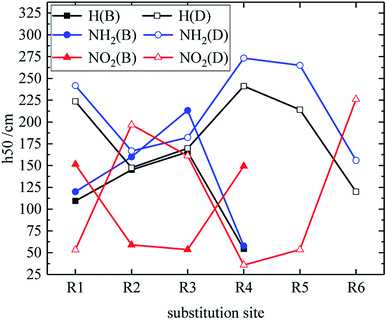
Table 3 shows the h50 values of partial derivatives. The h50 values of all design derivatives of B and D series are presented (see Tables S2 and S5 in ESI†), and the oxygen balance (OB100) and nitro group charge (QNO2) of all derivatives of the B and D series are listed (see Tables S3 and S6 in ESI†). When the B series contains three –NO2, the h50 value of the compound in which substitution sites of –NO2 are adjacent is smaller than that of the isomeride. This behavior can be found in compounds B17 and B20, as well as B18 and B19. Among these compounds, B17 has a higher h50 value than B20 (B17 is more stable than B20), and B18 is less sensitive to external stimuli than B19 because the presence of N–NO2 groups or the decrease of the distance between –NO2 in B19 and B20 increases the sensitivity. When the substituents of the B series are one –NO2 and three H, the h50 value of each compound is: B2 > B1. The compound B2 has a C–NO2 structure, and the compound B1 has an N–NO2 structure. The h50 value of the compound that is substituted at the carbon atom by –NO2 is higher than that of the compound that is substituted at the nitrogen atom by –NO2, so B2 has a higher h50 value and lower sensitivity. Additionally, when the B series contains two –NO2 groups, the h50 value of each compound decreases in the order of B13, B12, B6, B9, B4, B7, B10, B16, B14, B3, B8, B11, B5 and B15, and the number of N–NO2 increases. These results show that the sensitivity increases as the number of N–NO2 groups increases. The h50 values of compounds B6, B12 and B13 are large because the –NO2 distribution of these compounds is symmetrical, so the molecules have stable geometric configurations and low sensitivities. Meanwhile, when the D series contains one –NO2, the derivatives are D1–D151 and D239–D250. The –NO2 of a compound with h50 ≤ 241 cm is substituted on nitrogen (D1–D6, D14–D77 and D239–D250), the –NO2 of a compound with h50 > 241 cm is substituted on carbon (D7–D13, D78–D151). It can be seen that C–NO2 has lower energy and is more stable than N–NO2. This may be because the N–NO2 functional group introduces an N–N bond more than C–NO2, which can effectively increase the energy of the compound and increase the sensitivity of the compound. When the D series contains one –NO2, in compounds with h50 > 241 cm, the h50 value is greater when –NO2 is substituted at the C position of the triazole ring (D7–D13, D78–D122), which may be because –NO2 forms an intramolecular hydrogen bond with H at the N position of the triazole ring, thus reducing the sensitivity of compounds. When the D series contains two –NO2 groups, the derivatives are D152–D175 and D251–D427, and the –NO2 of a compound with h50 ≥ 297 cm is substituted on carbon (D152–D175, D259, D263, D290, D299, D301, D302, D306, D307, D358, D365, D370, D372, D375, D416). It indicates that the h50 value substituted by –NO2 on C atom is higher than the h50 value substituted by –NO2 on N atom. When the D series contains three –NO2 groups, the derivatives are D176–D182 and D428vD558, and the –NO2 of a compound whose h50 value is higher than that of TNT is substituted on carbon (D176–D182). It can be seen that C–NO2 has lower energy and is more stable than N–NO2. The relationship between h50 and the substitution site of the B and D series is shown in Fig. 5. As can be seen from the figure, in series B, when –NO2 is substituted at R1 or R4 (on C atom), the compound has a higher h50 value and lower sensitivity. In the D series, the compound has a higher h50 value and the compound is more stable when –NO2 is substituted at R2 or R3 or R6 (on C atom). These are mutually confirmed with the above laws, and the introduction of –NH2 is more advantageous for the reduction of sensitivity.
| Comp. | h50 | Comp. | h50 | Comp. | h50 | Comp. | h50 | Comp. | h50 |
|---|---|---|---|---|---|---|---|---|---|
| a h50 (cm). | |||||||||
| A1 | 297 | B9 | 105 | B20 | 41 | D34 | 42 | D152 | 478 |
| A2 | 297 | B10 | 75 | B21 | 41 | D35 | 42 | D153 | 482 |
| A3 | 291 | B11 | 28 | C1 | 216 | D120 | 940 | D154 | 490 |
| B1 | 43 | B12 | 253 | C2 | 217 | D121 | 952 | D176 | 293 |
| B2 | 215 | B13 | 269 | C3 | 204 | D122 | 958 | D177 | 328 |
| B3 | 51 | B14 | 66 | D6 | 65 | D123 | 520 | D178 | 414 |
| B4 | 93 | B15 | 23 | D7 | 593 | D124 | 524 | D183 | 102 |
| B5 | 27 | B16 | 70 | D8 | 602 | D125 | 516 | D237 | 116 |
| B6 | 209 | B17 | 79 | D31 | 41 | D146 | 332 | D238 | 104 |
| B7 | 84 | B18 | 57 | D32 | 41 | D147 | 424 | ||
| B8 | 45 | B19 | 40 | D33 | 42 | D148 | 343 | ||
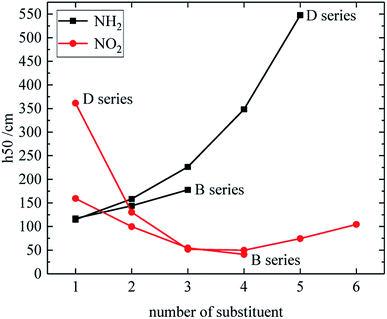
The relationship between the h50 of B and D series and substituent number is shown in Fig. 6, and the effect of different energetic groups on h50 is that –NH2 is more favorable to increase the h50 value, which can reduce the sensitivity, and the h50 value of the B and D series increases as the substituent number of –NH2 increases. The h50 value of the B series decreases as the number of –NO2 groups increases, and the h50 value of the D series decreases first as the number of –NO2 groups increases, and then slightly rises. Table 3 shows that the h50 value of the A and C series decreases as the number of –NO2 increases. In general, the sensitivity of the compound increases with the number of –NO2, because the introduction of –NO2 enhances the steric hindrance effect or increases the energy. It is also found from Fig. 6 that the derivatives of B and D series has high h50 values and low sensitivities when the number of –NO2 is 1. It indicates that when the number of substituents of –NO2 is small, the superconjugation of –NO2 can stabilize the molecular skeleton.
3.3 Predicted density and detonation properties
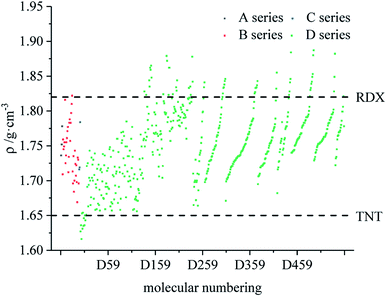
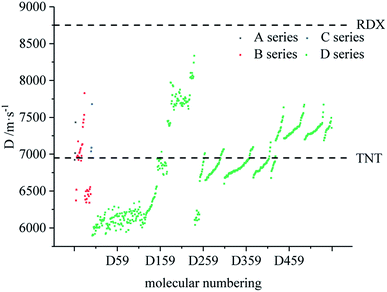
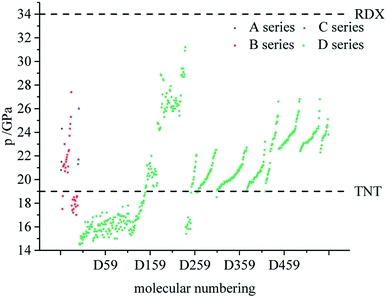
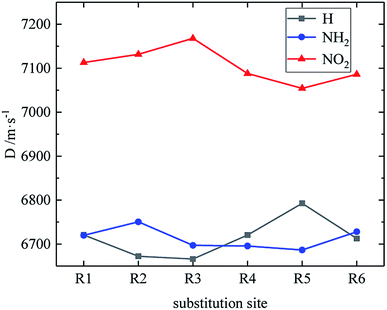
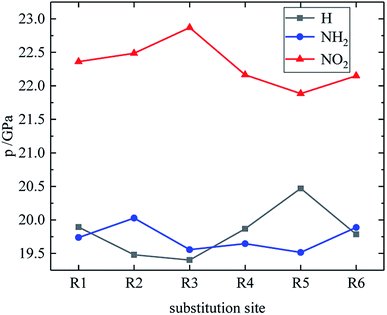
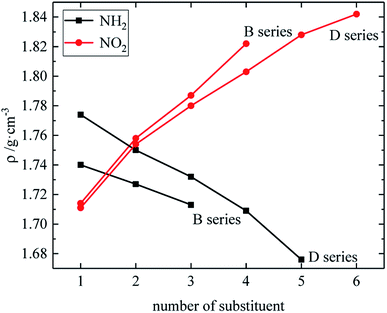
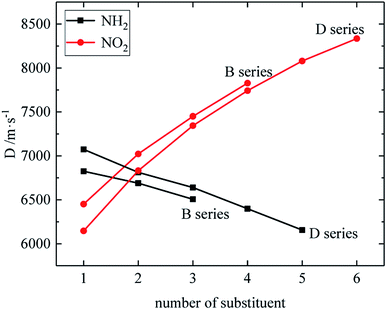
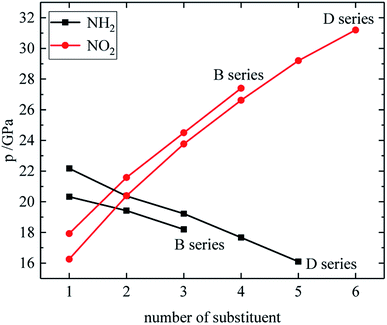
Fig. 7–9 compare the density, detonation velocity and pressure of all derivatives. There are compounds with higher density than that of RDX in the B and D series, and the detonation performance of the D series is closer to RDX. Compared to the A series, the density and detonation performance of the B series are improved, indicating that the skeleton of the B series is better. From the perspective of density and detonation performance, the application prospects of B and D series are better. D230, D233, D237 and D238 have high detonation velocity (8102, 8101, 8242 and 8335 m s−1) because they have a large density and positive HOF. A large amount of heat is released during detonation, and more heat energy is converted into detonation energy, resulting in a high detonation velocity. In each series, the compounds with lower density compared to TNT are mostly planar molecules, while those with higher density compared to RDX exhibit non-planar structures.Table 4 lists the density and detonation parameters of partial derivatives, and the density, detonation velocity and pressure of all derivatives of B and D series are listed (see Tables S2 and S5 in ESI†). When the B series contains three –NO2 groups, the density, detonation velocity and pressure of each compound are: B17 < B18 < B19 < B20. The high density and detonation performance values of B19 and B20 indicate that the group density of N–NO2 is larger, thereby increasing the compound density and detonation performance. When the B series substituents are two –NO2 and two –NH2, the density and detonation performance value of each compound increases in the order of B13, B14, B15 and B16, and the distance between –NO2 decreases in this order. It indicates that the energy of the compound increases with the decrease of the distance between –NO2 in the isomer. When the D series contains one –NO2, the derivatives are D1–D151 and D239–D250, and the density range is 1.616–1.865 g cm−3. The density of the compounds where the substitution site of –NO2 are at the diazole ring is all greater than that of TNT (1.65 g cm−3), including compounds D15–D23, D25, D27–D31, D34, D36, D39, D43, D44, D47, D48, D50–D52, D54, D57, D58 and D123–D151. When the D series contains one –NO2 group, the –NO2 of compounds having a density greater than that of RDX is substituted at R3, and the –NO2 group of compounds having a higher detonation velocity and pressure is also basically substituted at R3, which is the case for compounds D146–D151. In the four series, the compounds whose density is less than or equal to the density of TNT are the D series (D1–D3, D5 and D7–D12), which contain one –NO2 group substituted at the triazole ring. The relationship between density, detonation velocity and detonation pressure of the D series and substitution site is shown in Fig. 10–12: when R3 is –NO2, it contributes the most to the density, detonation velocity and detonation pressure, and it's mutually confirmed with the above-mentioned regular phenomenon. In addition, –NO2 contributes to the density and detonation performance to a greater extent than –NH2.
| Comp. | ρ | D | p | Comp. | ρ | D | p | Comp. | ρ | D | p |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a ρ (g cm−3), D (m s−1), p (GPa). | |||||||||||
| A1 | 1.736 | 6923 | 20.8 | B16 | 1.788 | 7137 | 22.5 | D121 | 1.702 | 6187 | 16.4 |
| A2 | 1.752 | 7015 | 21.5 | B17 | 1.757 | 7370 | 23.7 | D122 | 1.671 | 6138 | 16 |
| A3 | 1.778 | 7432 | 24.3 | B18 | 1.783 | 7429 | 24.3 | D123 | 1.688 | 6065 | 15.7 |
| B1 | 1.709 | 6373 | 17.5 | B19 | 1.797 | 7470 | 24.7 | D124 | 1.686 | 6114 | 15.9 |
| B2 | 1.759 | 6518 | 18.6 | B20 | 1.81 | 7532 | 25.3 | D125 | 1.682 | 6144 | 16.1 |
| B3 | 1.745 | 6957 | 21.1 | B21 | 1.822 | 7827 | 27.4 | D146 | 1.844 | 6421 | 18.6 |
| B4 | 1.749 | 6969 | 21.2 | C1 | 1.716 | 7038 | 21.3 | D147 | 1.835 | 6463 | 18.7 |
| B5 | 1.755 | 6982 | 21.3 | C2 | 1.719 | 7089 | 21.7 | D148 | 1.862 | 6469 | 18.9 |
| B6 | 1.816 | 7174 | 23 | C3 | 1.784 | 7679 | 26 | D152 | 1.779 | 6938 | 21.2 |
| B7 | 1.725 | 6924 | 20.7 | D6 | 1.654 | 6017 | 15.2 | D153 | 1.741 | 6828 | 20.3 |
| B8 | 1.736 | 6960 | 21 | D7 | 1.635 | 5919 | 14.6 | D154 | 1.737 | 6787 | 20 |
| B9 | 1.755 | 7016 | 21.5 | D8 | 1.646 | 6003 | 15.1 | D176 | 1.824 | 7451 | 24.8 |
| B10 | 1.761 | 7034 | 21.7 | D31 | 1.739 | 6210 | 16.8 | D177 | 1.814 | 7442 | 24.7 |
| B11 | 1.771 | 7060 | 21.9 | D32 | 1.658 | 5918 | 14.8 | D178 | 1.811 | 7455 | 24.7 |
| B12 | 1.777 | 7082 | 22.1 | D33 | 1.695 | 5930 | 15 | D183 | 1.879 | 7973 | 28.9 |
| B13 | 1.712 | 6911 | 20.6 | D34 | 1.69 | 6055 | 15.6 | D237 | 1.878 | 8242 | 30.9 |
| B14 | 1.734 | 6977 | 21.1 | D35 | 1.659 | 5991 | 15.1 | D238 | 1.842 | 8335 | 31.2 |
| B15 | 1.783 | 7124 | 22.4 | D120 | 1.656 | 6060 | 15.5 | ||||
The relationship between the density, detonation performance and the substituent number of B and D series is shown in Fig. 13–15. The relationship between the contributions of different energetic groups to the density and detonation performance is –NO2 > –NH2. The density, detonation velocity and pressure of B and D series decrease as the number of –NH2 increases, and increase as the number of –NO2 increases, which supports the viewpoint that the introduction of more –NO2 groups in the molecule can improve the detonation performance. Table 4 shows that the density and detonation performance of A and C series improve as the number of –NO2 increases, and among all derivatives, each compound in which all substituents are –NO2 has the highest density (except D238), detonation velocity and detonation pressure in the corresponding respective series of derivatives.
3.4 Predicted potential HEDM candidates
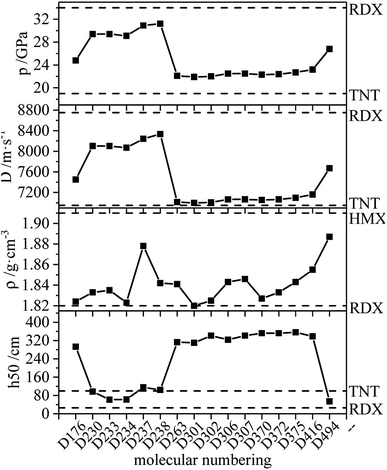
The ideal HEDM candidates should be stable and exhibit effective detonation performance, and of the various factors that constrain each other need to be considered.51 It is generally believed that the promising HEDC meets the following requirements: ρ > 1.9 g cm−3, D > 9.0 km s−1 and p > 40 GPa.52 The HEDM candidates have potential for further development, prompting further investigation into compound synthesis. Compounds meeting the following conditions are selected from each series, and the detonation performance and other parameters are shown in Fig. 16: (1) ρ ≥ ρ (RDX), D > D (TNT), p > p (TNT), −QNO2 ≥ −QNO2 (RDX); (2) ρ ≥ ρ (RDX), D ≥ 8000 m s−1; (3) ρ is the largest.According to the figure, the variation trend of detonation velocity and detonation pressure is the same, while this trend differs from that of density. This indicates that the density is not the only parameter that determines detonation velocity and pressure, and the detonation heat also affects the detonation performance. The density of the compound in the figure is greater than or equal to that of RDX (1.82 g cm−3 (ref. 53)). Also, the unique nitrogen heterocycle of D494 increases the density, and its density is the largest at 1.887 g cm−3, which is close to the density of HMX (1.91 g cm−3 (ref. 53)). D238 has the highest detonation velocity (8335 m s−1) and detonation pressure (31.2 GPa), which are close to RDX (8750 m s−1, 34 GPa (ref. 53)). Meanwhile, the h50 value of D176 is larger than that of TNT, indicating that D176 appears to be insensitive, which is mainly due to the intramolecular hydrogen bond. Calculations revealed that D230, D233, D234, D237 and D238 exhibit high detonation performances and might be HEDM candidates, and the group density of N–NO2 in those molecules is relatively high, which increases the molecular characteristic density and the crystal density of explosives and thus increases the detonation velocity. In addition, the increase in the number of detonating groups, the existence of the unique nitrogen heterocycle structure and the ring tension lead to large detonation velocity, detonation pressure and high energy.
Consequently, based on the results of detonation properties and stability, compounds D176 (1.824 g cm−3, 7451 m s−1, 24.8 GPa, 293 cm), D230 (1.833 g cm−3, 8102 m s−1, 29.4 GPa, 97 cm), D233 (1.835 g cm−3, 8101 m s−1, 29.4 GPa, 62 cm), D234 (1.823 g cm−3, 8068 m s−1, 29.1 GPa, 62 cm), D237 (1.878 g cm−3, 8242 m s−1, 30.9 GPa, 116 cm), D238 (1.842 g cm−3, 8335 m s−1, 31.2 GPa, 104 cm) and D494 (1.887 g cm−3, 7670 m s−1, 26.8 GPa, 54 cm) can be considered as potential HEDM candidates.
4 Conclusions
Based on DFT calculation, the density, heat of formation, detonation velocity, detonation pressure and h50 values of derivatives were compared, and the relationship between structure and performance was studied. The performance parameters are affected by the molecular structure, and the type and number of groups in the structure, the arrangement of the groups and the intramolecular symmetry appear to be influential parameters. The conclusions are as follows: (1) compared with the A series, the B series has higher density, higher heat of formation, better detonation performance and better stability, indicating that the energy improves with the increase of the nitrogen content, and the skeleton of B series is better. (2) The density, heat of formation, detonation velocity and detonation pressure of the compound improve with the increase in the number of the –NO2 group. However, the variation trend of the h50 value is opposite. (3) The density, detonation velocity and detonation pressure of the compound decrease as the number of the –NH2 group increases, while the heat of formation and h50 value increase as the number of the –NH2 group increases, and the growth rate of heat of formation here is less than the growth rate of heat of formation in which the substituent is –NO2. (4) The h50 value indicates that the molecular stability decreases as the number of the –NO2 group increases; however, if the substituent is –NH2, the opposite is true. (5) –NO2 substituents are advantageous for increasing density, heat of formation and detonation properties, while –NH2 substituents are advantageous for increasing stability. (6) The presence of multiple nitrogen–nitro groups (N–NO2) can effectively improve oxygen balance, so these compounds generally have high density and low sensitivity. (7) In terms of detonation performance and stability, compounds D176, D230, D233, D234, D237, D238 and D494 yield promising results and may be considered as potential HEDM candidates.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Project Supported: National Natural Science Foundation of China (No. 51874255).References
- Y. J. Shu and J. C. Huo, Theory of Explosives, Chemical Industry Press, Beijing, 2011, pp. 288–310 Search PubMed.
- X. J. Wang, K. Z. Xu, Q. Sun, B. Z. Wang, C. Zhou and F. L. Zhao, Propellants, Explos., Pyrotech., 2015, 40(1), 9–12 CrossRef CAS.
- P. He, H. Mei and J. Yang, et al., Design and properties of a new family of bridged bis (nitraminotetrazoles) as promising energetic materials, New J. Chem., 2019, 43(10), 4235–4241 RSC.
- G. Y. Hang, W. L. Yu and T. Wang, et al., Theoretical investigations on stabilities, sensitivity, energetic performance and mechanical properties of CL-20/NTO cocrystal explosives by molecular dynamics simulation, Theor. Chem. Acc., 2018, 137(8), 114 Search PubMed.
- X. J. Zhang, Y. C. Li, W. Liu, Y. Z. Yang, L. Peng and S. P. Pang, Chin. J. Energ. Mater., 2012, 20(4), 491–500 Search PubMed.
- X. L. Xia, Molecular designs of new energetic nitrogen-containing heterocycle compounds, Nanjing University of Science & Technology, Nanjing, 2013 Search PubMed.
- Z. M. Li, J. G. Zhang, T. L. Zhang and Y. J. Shu, Prog. Chem., 2010, 22(4), 639–647 Search PubMed.
- Y. N. Li, T. Tang, P. Lian, Y. F. Luo, W. Yang, Y. B. Wang, H. Li, Z. Z. Zhang and B. Z. Wang, Chin. J. Org. Chem., 2012, 32(3), 580–588 CrossRef CAS.
- Q. H. Zhang and J. M. Shreeve, Angew. Chem., Int. Ed., 2013, 52(34), 8792–8794 CrossRef CAS PubMed.
- L. Guanqiong, L. Yuchuan and M. Qiaoli, et al., Research Progress in Synthesis of Nitrogen-Rich Zole-Ring Compounds by Cycloaddition Reaction, Chin. J. Org. Chem., 2010, 30(10), 1431–1440 Search PubMed.
- W. Wang, G. Cheng and H. Xiong, et al., Functionalization of fluorodinitroethylamino derivatives based on azole: a new family of insensitive energetic materials, New J. Chem., 2018, 42(4), 2994–3000 RSC.
- X. C. Huang, Z. J. Wang and T. Guo, et al., Review on Energetic Compounds Based on 1, 2, 4-Oxadiazoles, Chin. J. Energ. Mater., 2017, 25, 603–611 Search PubMed.
- J. L. Zhang, F. Q. Bi and B. Z. Wang, et al., Review on the Aza-polyaromatic Ring Energetic Compounds, Chin. J. Energ. Mater., 2016, 24(8), 810–819 Search PubMed.
- B. M. Rice and J. Hare, Thermochim. Acta, 2002, 384(1), 377–391 CrossRef CAS.
- H. Muthurajan, R. Sivabalan, M. B. Talawar, M. Anniyappan and S. Venugopalan, J. Hazard. Mater., 2006, 133(1—3), 30–45 CrossRef CAS PubMed.
- C. Adachi, T. Tsutsui and S. Saito, Appl. Phys. Lett., 1989, 55(15), 1489–1491 CrossRef CAS.
- H. X. Gao and J. M. Shreeve, Chem. Rev., 2011, 111(11), 7377–7436 CrossRef CAS.
- A. A. Korkin and R. J. Bartlett, J. Am. Chem. Soc., 1996, 118(48), 12244–12245 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136(3B), B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140(4A), A1133–A1138 CrossRef.
- R. G. Parr and W. T. Yang, Density-functional theory of atoms and molecules, Oxford University Press, New York, 1989, pp. 1–333 Search PubMed.
- X. J. Xu, W. H. Zhu and H. M. Xiao, J. Phys. Chem. B, 2007, 111(8), 2090–2097 CrossRef CAS PubMed.
- G. X. Wang, H. M. Xiao, X. H. Ju and X. D. Gong, Propellants, Explos., Pyrotech., 2006, 31(5), 361–368 CrossRef CAS.
- X. J. Xu, H. M. Xiao, X. H. Ju and X. D. Gong, Chin. J. Org. Chem., 2005, 25(5), 536–539 CAS.
- L. M. Qiu, X. D. Gong, J. Zheng and H. M. Xiao, Chin. J. Energ. Mater., 2008, 16(6), 647–651 CAS , 668.
- Y. Zhou, X. P. Long and Y. J. Shu, J. Mol. Model., 2010, 16(5), 1021–1027 CrossRef CAS PubMed.
- Y. Pan, W. H. Zhu and H. M. Xiao, Struct. Chem., 2013, 24(4), 1071–1087 CrossRef CAS.
- F. Wang, G. X. Wang, H. C. Du, J. Y. Zhang and X. D. Gong, J. Phys. Chem. A, 2011, 115(47), 13858–13864 CrossRef CAS PubMed.
- B. M. Rice and E. F. Byrd, J. Mater. Res., 2006, 21, 2444–2452 CrossRef CAS.
- Z. Yu and E. R. Bernstein, J. Phys. Chem. A, 2013, 117, 10889–10902 CrossRef CAS PubMed.
- C. Cao and S. Gao, J. Phys. Chem. B, 2007, 111, 12399–12402 CrossRef CAS PubMed.
- Q. Wu, Q. Li and G. Yan, et al., Molecular design of novel super high energy compounds by incorporating the difluoramino group, N-oxide and different bridge groups into the 1H-tetrazole, J. Fluorine Chem., 2019, 218, 21–26 CrossRef CAS.
- A. Nirwan, A. Devi and V. D. Ghule, Assessment of density prediction methods based on molecular surface electrostatic potential, J. Mol. Model., 2018, 24(7), 166 CrossRef PubMed.
- P. Politzer, J. Martinez and J. S. Murray, et al., An electrostatic interaction correction for improved crystal density prediction, Mol. Phys., 2009, 107(19), 2095–2101 CrossRef CAS.
- L. Qiu, H. M. Xiao, X. H. Ju and X. D. Gong, Acta Chim. Sin., 2005, 63(5), 377–384 CAS.
- M. H. Lin, Computational methods and applications of quantum chemistry, Science Press, Beijing, 2004, pp. 227–233 Search PubMed.
- B. M. Rice, J. J. Hare and E. F. C. Byrd, J. Phys. Chem. A, 2007, 111(42), 10874–10879 CrossRef CAS.
- Sobereva, Use Multiwfn to predict properties such as crystal density, evaporation enthalpy, boiling point, and free energy of dissolution[EB/OL], 2016-6-21, http://sobereva.com/337 Search PubMed.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592 CrossRef CAS.
- J. Y. Zhang, F. Wang and X. D. Gong, Struct. Chem., 2013, 24(4), 1339–1346 CrossRef CAS.
- M. J. Kamlet and S. J. Jacobs, J. Chem. Phys., 1968, 48(1), 23–35 CrossRef CAS.
- T. Wei, W. H. Zhu, X. W. Zhang, Y. F. Li and H. M. Xiao, J. Phys. Chem. A, 2009, 113(33), 9404–9412 CrossRef CAS PubMed.
- T. Wei, W. H. Zhu, J. J. Zhang and H. M. Xiao, J. Hazard. Mater., 2010, 179(1—3), 581–590 CrossRef CAS.
- L. Türker, T. Atalar, S. Gümüş and Y. Çamur, J. Hazard. Mater., 2009, 167(1—3), 440–448 CrossRef PubMed.
- J. C. Gálvez-Ruiz, G. Holl, K. Karaghiosoff, T. M. Klapötke, K. Löhnwitz, P. Mayer, H. Nöth, K. Polborn, C. J. Rohbogner, M. Suter and J. J. Weigand, Inorg. Chem., 2005, 44(12), 4237–4253 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, et al., Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, 2009 Search PubMed.
- M. H. V. Huynh, M. A. Hiskey and C. J. Pollard, Chin. J. Energ. Mater., 2004, 22(4), 217–229 CrossRef CAS.
- M. H. V. Huynh, M. A. Hiskey, J. G. Archuleta, E. L. Roemer and R. Gilardi, Angew. Chem., Int. Ed., 2004, 43(42), 5658–5661 CrossRef CAS PubMed.
- M. Tian, W. J. Chi and Q. S. Li, et al., Theoretical design of highly energetic poly-nitro cage compounds, RSC Adv., 2016, 6(53), 47607–47615 RSC.
- Y. Y. Guo, W. J. Chi and Z. S. Li, et al., Molecular design of N–NO2 substituted cycloalkanes derivatives Cm(N–NO2)m for energetic materials with high detonation performance and low impact sensitivity, RSC Adv., 2015, 5(48), 38048–38055 RSC.
- X. J. Xu, H. M. Xiao, X. D. Gong, X. H. Ju and Z. X. Chen, J. Phys. Chem. A, 2005, 109(49), 11268–11274 CrossRef CAS PubMed.
- L. Qiu, Molecular Design of High Energy Density Materials (HEDM)—Cyclic Nitramines, Nanjing University of Science and Technology, Nanjing, 2007 Search PubMed.
- M. B. Talawar, R. Sivabalan, T. Mukundan, H. Muthurajan, A. K. Sikder, B. R. Gandhe and R. A. Subhananda., J. Hazard. Mater., 2009, 161(2–3), 589–607 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra00385a |
| This journal is © The Royal Society of Chemistry 2020 |