Open Access Article
Open Access ArticleExploring the sub-stoichiometric behavior of plutonium mononitride
Chao Lai a,
Yin Hu*a and
Ruizhi Qiu
a,
Yin Hu*a and
Ruizhi Qiu *b
*b
aScience and Technology on Surface Physics and Chemistry Laboratory, Mianyang 621908, Sichuan, China. E-mail: 860890345@qq.com
bInstitute of Materials, China Academy of Engineering Physics, Mianyang 621907, Sichuan, China. E-mail: qiuruizhi@caep.cn
First published on 30th June 2020
Abstract
The intriguing and controversial sub-stoichiometric behavior of plutonium mononitride is investigated here using first-principles calculations combined with special quasirandom structures. It is found that NaCl-type plutonium mononitride is stable for only stoichiometric levels, and the formation enthalpy of plutonium mononitride is in good agreement with others. By comparing with plutonium monocarbide, the main reason for the absence of sub-stoichiometric behavior is the lower N-2p orbital energy, resulting in less hybridization and weaker Pu–N bonds. The weaker Pu–N bonds cannot support the formation of vacancies.
1 Introduction
Plutonium is one of the essential materials in the field of nuclear energy.1–3 Its compounds, such as carbides and nitrides, are promising fuel materials for generation IV fast breeder reactors because of their high melting point, high fuel density and high thermal conductivity compared with well-established oxide fuels, such as plutonium dioxide.2,4–7 First, nitrides are dominant in terms of energy density over other nuclear materials.8 Secondly, the good compatibility of nitrides with sodium coolants ensures a certain level of safety.8 In addition, the dissolution of nitrides in nitric acid guarantees post-treatment.9 Moreover, similar to uranium nitride, plutonium nitrides may be essential for long-term storage, as nitrides tend to prevent further oxidation of the substrate.10Previous work on plutonium nitrides reported lattice constants,11–13 crystal forms,14 synthesis methods,15,16 and some thermodynamic properties.17–20 Wriedt assessed the phase diagram of Pu–N in 1989, showing that there is only one Pu–N compound, plutonium mononitride (PuN).13 The NaCl-type crystal structure of PuN contains four plutonium and four nitrogen atoms per unit cell. Due to the difficulties of plutonium experiments, a lot of work is theoretical. Atta-Fynn et al. reported the results of electronic, structural and magnetic properties of PuN using the full potential all electron linearized augmented plane wave plus local orbital (FP-LAPW+lo) method.8 Murugan et al. investigated the electronic, structural mechanical and magnetic properties of PuN in three cubic phases, namely, NaCl, CsCl and zinc blende.21 They used the local density approximation (LDA) and generalized gradient approximation (GGA) exchange correlation functional. Analogous to previous work, Wen et al. just evolved the functional using the Heyd–Scuseria–Ernzerhof hybrid functional (HSE).22 Ru-Song Li et al. merged local density approximations with dynamical mean field theory (LDA + DMFT) to research the electronic properties of PuN.23 The structural, magnetic, electronic, dynamical and thermodynamic properties of PuN have been examined by Rong Yang et al. within the frameworks of density functional theory, DFT+U and hybrid DFT.24
Actually, there was still a lack of clarity about the sub-stoichiometric behavior of PuN, which is important for understanding its physical and chemical properties. Previous experimental work about the sub-stoichiometric behavior of PuN was mainly contributed by Ogawa et al. In 1993, Ogawa et al. calculated N/Pu by the vapor pressure data: N/Pu = 0.978 at 2000 K,25 and calculated N/Pu from other data: N/Pu = 0.98 at 1600–2000 K by Kent and Leary25,26 and N/Pu = 0.97 at 2000–2400 K by Alexander.25,27 Ogawa predicted the lower homogeneity range of PuN by measuring the nitrogen vaporization modeled with a sublattice formalism, in which the model gave a significantly wide homogeneity range: the lower phase boundary of the PuN phase lay at N/Pu = 0.89 at 2000 K in 1998.28 Detailed evaluation of boundary positions on Pu-rich and N-rich sides of PuN has not yet been performed, and the composition range of PuN is probably quite narrow. Although carbon and nitrogen are next to each other in the periodic table, plutonium monocarbide (PuC1−x) is significantly sub-stoichiometric even when carbon-saturated, which is different from PuN.29,30 Experimental methods alone are not enough to verify the sub-stoichiometric behavior of PuN and the different sub-stoichiometric behavior of PuN and PuC1−x. To our best knowledge, although extensive research has been carried out on PuN, no single theoretical study exists about the sub-stoichiometric behavior of PuN. Theoretical research may provide a solution, and it is needed to analyze micro-mechanisms. Besides, the recent report of PuC1−x and PuOxC1−x gives us great confidence in using theoretical methods to explore thermodynamic stability.31,32
In this paper, the special quasirandom structure (SQS) will be applied to describe the solid solution sub-stoichiometric PuN.31–38 All SQS’s are calculated by performing first principles calculations within the framework of density functional theory (DFT).39,40 The predicted lattice constants are in good agreement with the experimental results. PuN is compared with PuC in terms of electronic structure and chemical bonding to illustrate the microscopic mechanism.
2 Computational details
Because PuN has quite a narrow composition range, the SQS is only constructed with nine points, from PuN0.75−1.0(Pu32N24 to Pu32N32),31,32,36,41 using a supercell of 64 sites, which is evolved from a NaCl-type structure.14 The local pair and multisite correlation function of the fully disordered system are regulated by Monte Carlo algorithm to generate the SQS configuration.41 The two body, three body and four body correlations are 10 Å, 10 Å, and 8 Å around each atom, respectively.DFT calculations42,43 for the PuN SQS are carried out by the projector augmented wave (PAW) pseudopotential method,42,43 as implemented in the Vienna ab initio simulation package (VASP)42 within the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE)44 to describe the exchange-correlation functional. Plutonium 6s27s26p66d25f4, and nitrogen 2s22p3, are chosen as the valence electrons. The kinetic energy cutoff of plane wave basis is selected as 600 eV. The Brillouin zone is sampled by 5 × 3 × 3 grids according to the Monkhorst–Pack scheme.45 The total energy is relaxed until the convergence is smaller than 10−6 eV for all SQS electronic calculations.
As we know, spin–orbit coupling (SOC) interactions are necessary for certain properties of heavy metal elements with f electrons. However, previous numerical calculations confirmed that the SOC interactions had little affect on the bulk properties of PuN.9,46,47 Therefore, the SOC is neglected here. A Hubbard-like term is added to the Hamiltonian according to Dudarevs DFT+U scheme48 to take into account the strong interactions among 5f electrons, while the U parameter is set as 3.2 eV.49,50 The SQS with low symmetry breaks the degeneracy associated with metastability, so metastable states are unlikely to emerge here.51,52 In addition, the formation energy of PuN is well reproduced by PBE. Thus in this work, first-principles calculations are performed using PBE.
3 Results and discussion
First of all, we should compare the experimental results and previous theoretical work with our calculated lattice parameter in the same scheme. The theoretical equilibrium volume corresponding to the minimum energy is obtained by computing the total energy for various volumes, and then fitting the energy–volume data by the third-order Birch–Murnaghan equation of state.53 The lattice data is estimated by assuming the SQS 64 sites are equivalent to a conventional 2 × 2 × 2 supercell of NaCl-type structure because of the rock salt structure of PuN. The lattice constants of PuN1−x with respect to the nitrogen concentration N/(N + Pu) are plotted in Fig. 1. There is no published experimental or theoretical data about lattice constants of sub-stoichiometric plutonium mononitride. From Fig. 1, a noticeable trend for nitrogen vacancies is when the vacancies decrease and the lattice constants increase, which is consistent with PuC1−x.32 Therefore, this data could be useful for future work.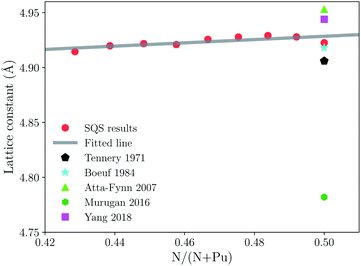 | ||
| Fig. 1 Lattice constants of sub-stoichiometric plutonium mononitride. The red circles, black pentagons, cyan pentagrams, lime triangles, green hexagons, and fuchsia squares, represent the results from our calculations, ref. 12, 11, 8, 21, 24, respectively. | ||
Tennery et al., reported experimental work on the PuN lattice constant which was found to be 4.905 Å at 293 K.12 Boeuf et al., reported that the PuN lattice constant was 4.918 Å at 60 K.11 They were relatively reliable data with similar results to all previous experimental work on PuN lattice constants, which vary because of the effects of impurities, self-irradiation damage, and nitrogen concentration. It should be emphasized here that we should pay attention to the Boeuf’s data because it is the only low temperature data.11 In Fig. 1, the lime triangle, green hexagon, and fuchsia square represent the theoretical data from Atta-Fynn et al.,8 Murugan et al.,21 Rong Yang et al.24 They are 4.953 Å, 4.782 Å, 4.944 Å, respectively, and our calculation is 4.922 Å. Our calculation is a comparative approximation in comparison with the experimental data. Compared to Tennery’s and Boeuf’s experimental lattice values, the errors are 0.016 Å and 0.004 Å, and percentage error is 0.3% and 0.08%, respectively. Such a low error allows us to ensure accuracy and perform further analysis.
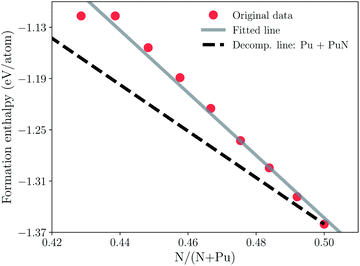
Furthermore, in order to understand the sub-stoichiometric behavior of plutonium mononitride, a convex-hull diagram of PuN is plotted in Fig. 2. The total energy could be obtained from the energy–volume curve fitted by the third-order Birch–Murnaghan equation of state.53 From the conventional definition Ef = (Etot − NPuEPu − NNEN)/(NPu + NN), the formation enthalpy of PuN could be calculated, in which NPu and NN are the numbers of Pu and N atoms in the compounds, and EPu and EN are the computed total energies of δ-Pu and nitrogen, respectively. Note that the unit of formation enthalpy is eV per atom, which is convenient for the plot of the convex hull. In Fig. 2, our calculation data of PuN is −1.360 eV per atom. The Open Quantum Materials Database (OQMD)54,55 data of PuN is −1.370 eV per atom. The data are approximate, and such a low error allows us to ensure accuracy. It can be seen that Ef of PuN is a monotonic function of nitrogen vacancies in the nitrogen concentration range studied in this work. The decomposition line of Pu plus PuN is chosen to determine the thermodynamical stability of N vacancies. Particularly, all the formation enthalpies of SQS’s are above the decomposition, and all the SQS’s except the Pu32N32 are unstable. In other words, the formation of nitrogen vacancies is difficult to form, where one nitrogen vacancy requires approximately 3.375 eV. Thus, plutonium mononitride could hardly show sub-stoichiometric behavior. So far, the sub-stoichiometric behavior of plutonium mononitride has been almost solved.
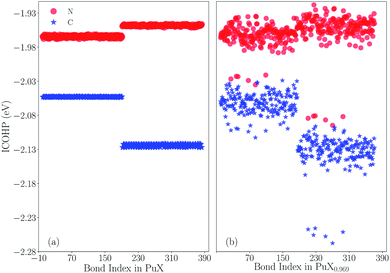
Now, the question about the difference between carbon and nitrogen of plutonium monovalent compounds should be considered. First of all, the crystal orbital Hamilton population (COHP) analysis56–59 is performed to quantitatively distinguish the Pu–X (X = C, N) bonds. Here, the Hamilton matrix element is used to describe the interaction between two orbitals on two adjacent atoms, and the quantitative measure of bonding strength is served by the multiplication with the corresponding density of state (DOS) matrix. The COHP integral value (ICOHP) of each Pu–X bond can be used to measure the bond strength of the Pu–X bond by integrating COHP to the Fermi level. In Fig. 3, the original results of Pu–X bonds for PuX and PuX0.969 (one vacancy) are shown. Note that the lower value of ICOHP indicates the stronger bond. Fig. 3(a) shows that the ICOHP of the spin-up state of Pu–N bonds is −1.964 eV, the corresponding spin-up state of Pu–C bonds is −2.053 eV, the ICOHP of the spin-down state of Pu–N bonds is −1.948 eV, the corresponding spin-down state of Pu–C bonds is −2.124 eV. Here, we know two pieces of basic information: firstly, the Pu–C bond is stronger than the Pu–N bond in general; secondly, for Pu–N bonds, the ICOHP of the spin-up state is lower than the spin-down state, which means the spin-up state provides the major bond contribution, which is in contrast with Pu–C bonds. Fig. 3(b) indicates that if there exists one vacancy, both PuC and PuN have the same quantity of enhanced bonds. Except the enhanced bonds, the rest remains the same as the previous case. The ICOHP of the strengthened Pu–N bonds of the spin-up and spin-down states are −2.021 and −2.082 eV, respectively. The corresponding ICOHP of Pu–C bonds are −2.053 and −2.251 eV. Thus, the difference between the ICOHP of the enhanced bonds and original bonds of PuN are −0.057 eV (spin-up) and −0.134 eV (spin-down), which is almost equal to the PuC, −0.05 eV (spin-up) and −0.127 eV (spin-down). Furthermore, considering the position of the enhanced bonds in PuX, the situation is the same, and all the enhanced bonds are opposite to the vacancy. Therefore, from the enhanced level or the enhanced situation, the vacancy works the same effects at PuC and PuN, that is to say the different stoichiometric behavior of PuC and PuN is not caused by the vacancy. In summary, PuN has no sub-stoichiometric behavior which could be mainly explained as the weaker Pu–N bonds cannot support the formation of vacancies.
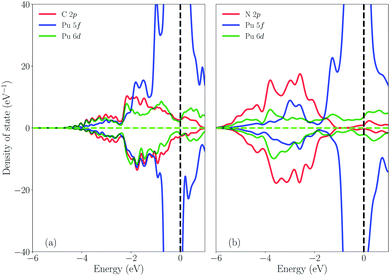
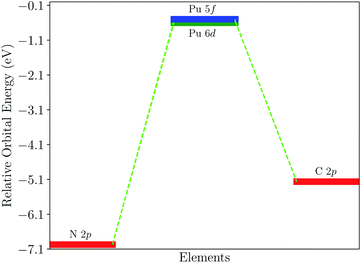
To confirm the above discussion, the density of state (DOS) is plotted in Fig. 4. Fig. 4(a) shows the DOS of PuC and Fig. 4(b) shows the DOS of PuN. From Fig. 4(a), it can be directly observed that the spin-down state of C-2p has more hybridization with the spin-down state of Pu-5f and Pu-6d from the split shape and area of the peak, compared to the spin-up state, which is in good agreement with the ICOHP results of PuC. In comparison, Fig. 4(b) indicates that the spin-up state and the spin-down state are analogous, which also supports the ICOHP results of PuN. Furthermore, PuC hybrids area at −2 eV, but the PuN hybrids are at −3.5 eV; and for the spin-up state, C-2p hybrids with Pu-6d and Pu-5f appear almost simultaneously. However, N-2p is mixed with Pu-6d at first, then Pu-5f, although there are parts that work together, which may result in the spin-up state of ICOHP of PuN being greater than that of PuC. For the spin-down state, C-2p has the stronger hybridization than N-2p with the spin-down state of Pu-5f and Pu-6d from the split shape. In a word, Pu-5f and Pu-6d have more contributions from PuC than PuN. Here, we plot the relative orbital energy for each element found by Johansson et al.60 in Fig. 5. Note that in Fig. 5, these data are calculated from the PBE scheme using Gamma K-points and we underline that it is just a sketch. Johansson emphasized that the degree of mixing between the 3d and 5d states depends on the overlap matrix element and the energy separation between the 3d and 5d levels.60 If the energy distance increases, the degree of mixing will decrease and the opposite holds. Here, the 3d states are replaced by 2p states, and the 5d states are replaced by the 6d and 5f states. If it is just a qualitative analysis, there is almost no problem with this replacement. From Fig. 5, we see the N-2p energy is lower than C-2p, which means that the energy distance of PuN is larger than PuC, corresponding to the same Pu-5f and Pu-6d, and the overlap matrix element of PuN is smaller than PuC. In other words, the Pu–X bonds of PuN are weaker than those of PuC, which is in agreement with Fig. 3 and 4.
4 Conclusions
To summarize, we explore the thermodynamical stability of sub-stoichiometric plutonium mononitrides using first-principles calculations, where the sub-stoichiometric mononitrides are modeled by SQS’s. It is found that plutonium mononitride is unlikely to form vacancies. In contrast, in plutonium monocarbide, the N-2p state energy is lower than the C-2p, corresponding to the same Pu-5f and Pu-6d states, and the overlap matrix element of plutonium mononitride is smaller than that of plutonium monocarbide, which induces weaker bonds in plutonium mononitride. In addition, the spin-up and spin-down state of DOS are discussed, corresponding to the Pu–N and Pu–C bonds. The weaker bonds probably are the main reason for the absence of any sub-stoichiometric behavior for plutonium mononitride.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to acknowledge financial support from the Science Challenge Project of China (Grant No. TZ2016004), the National Natural Science Foundation of China (Grant No. U1630250), and the CAEP project (Grant No. TCGH0708 and YZJJLX2016006).Notes and references
- L. Walters, D. Porter and D. Crawford, Prog. Nucl. Energy, 2002, 40, 513–521 CrossRef CAS.
- D. L. Clark, S. S. Hecker, G. D. Jarvinen and M. P. Neu, The chemistry of the actinide and transactinide elements, Springer, 2008, pp. 813–1264 Search PubMed.
- M. Hori, Proceedings of the 11th Pacific Basin Nuclear Conference, 1998 Search PubMed.
- A. Kudinov, B. Y. Zilberman and N. Goletskii, At. Energy, 2015, 117, 388–393 CrossRef CAS.
- P. Rodriguez, Bull. Mater. Sci., 1999, 22, 215–220 CrossRef CAS.
- D. Srivastava, S. Garg and G. Goswami, J. Nucl. Mater., 1989, 161, 44–56 CrossRef CAS.
- M. Streit and F. Ingold, J. Eur. Ceram. Soc., 2005, 25, 2687–2692 CrossRef CAS.
- R. Atta-Fynn and A. K. Ray, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115101 CrossRef.
- D. Sedmidubskỳ, R. Konings and P. Novak, J. Nucl. Mater., 2005, 344, 40–44 CrossRef.
- K. Liu, L. Luo, L. Luo, Z. Long, Z. Hong, H. Yang and S. Wu, Appl. Surf. Sci., 2013, 280, 268–272 CrossRef CAS.
- A. Boeuf, R. Caciuffo, J. Fournier, L. Manes, J. Rebizant, E. Roudaut and F. Rustichelli, Solid State Commun., 1984, 52, 451–453 CrossRef CAS.
- V. Tennery and E. Bomar, J. Am. Ceram. Soc., 1971, 54, 247–249 CrossRef CAS.
- H. Wriedt, Bull. Alloy Phase Diagrams, 1989, 10, 593–602 CrossRef CAS.
- W. Zachariasen, The Crystal Structure of Plutonium Nitride and Plutonium Carbide, The Transuranium Elements, National Nuclear Energy Series, IV–14B, 1949 Search PubMed.
- Y. Arai, C. Sari and J. Spirlet, J. Nucl. Mater., 1991, 185, 159–166 CrossRef CAS.
- T. Ogawa, Y. Shirasu, K. Minato and H. Serizawa, J. Nucl. Mater., 1997, 247, 151–157 CrossRef CAS.
- U. Benedict, Thermodynamics of nuclear materials 1979, 1980 Search PubMed.
- T. Matsui and R. W. Ohse, High Temp. - High Pressures, 1987, 19, 1–17 CAS.
- R. J. Lemire, et al., Chemical thermodynamics of neptunium and plutonium, Elsevier, 2001, vol. 4 Search PubMed.
- K. E. Spear and J. M. Leitnaker, J. Am. Ceram. Soc., 1968, 51, 706–709 CrossRef CAS.
- A. Murugan, G. S. Priyanga, R. Rajeswarapalanichamy, M. Santhosh and K. Iyakutti, J. Nucl. Mater., 2016, 478, 197–206 CrossRef CAS.
- X.-D. Wen, R. L. Martin, G. E. Scuseria, S. P. Rudin and E. R. Batista, J. Phys. Chem. C, 2013, 117, 13122–13128 CrossRef CAS.
- R.-s. Li, N.-h. Tong, J.-t. Wang, D.-q. Xin and S.-q. Huang, J. Nucl. Mater., 2018, 511, 277–283 CrossRef CAS.
- R. Yang, B. Tang and T. Gao, Acta Phys. Pol., A, 2018, 133, 32–38 CrossRef CAS.
- T. Ogawa, J. Nucl. Mater., 1993, 201, 284–292 CrossRef CAS.
- R. Kent and J. Leary, Mass spectrometric studies of plutonium compounds at high temperatures. IV. The vaporization of PuN, Los Alamos Scientific Lab., N. Mex., Technical Report, 1969 Search PubMed.
- C. A. Alexander, R. B. Clark, O. L. Kruger and J. L. Robbins, Fabrication and High-Temperature Thermodynamic and Transport Properties of Plutonium Mononitride, Plutonium 1975 and Other Actinides, Proc. Conf. in Baden, Baden, 1975, pp. 10–13 Search PubMed.
- T. Ogawa, F. Kobayashi, T. Sato and R. Haire, J. Alloys Compd., 1998, 271, 347–354 CrossRef.
- O. L. Kruger, J. Am. Ceram. Soc., 1963, 46, 80–85 CrossRef CAS.
- S. Rosen, M. Nevitt and A. Mitchell, J. Nucl. Mater., 1963, 10, 90–98 CrossRef CAS.
- R. Qiu, X. Wang, Y. Zhang, B. Ao and K. Liu, J. Phys. Chem. C, 2018, 122, 22821–22828 CrossRef CAS.
- C. Lai, Y. Hu and R. Qiu, Phys. Chem. Chem. Phys., 2020, 22, 9009–9013 RSC.
- A. Zunger, S.-H. Wei, L. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353 CrossRef CAS PubMed.
- E. B. Isaacs and C. Wolverton, Chem. Mater., 2019, 31, 6154–6162 CrossRef CAS.
- I. C. Njifon, M. Bertolus, R. Hayn and M. Freyss, Inorg. Chem., 2018, 57, 10974–10983 CrossRef CAS PubMed.
- P. Ondračka, D. Holec, D. Nečas, E. Kedroňová, S. Elisabeth, A. Goullet and L. Zajíčková, Phys. Rev. B, 2017, 95, 195163 CrossRef.
- W.-J. Yin, Y. Yan and S.-H. Wei, J. Phys. Chem. Lett., 2014, 5, 3625–3631 CrossRef CAS PubMed.
- S.-H. Wei, L. Ferreira, J. E. Bernard and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9622 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- A. Van de Walle, P. Tiwary, M. De Jong, D. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L.-Q. Chen and Z.-K. Liu, Calphad, 2013, 42, 13–18 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- K. O. Obodo and N. Chetty, J. Nucl. Mater., 2013, 442, 235–244 CrossRef CAS.
- Y. Zhang, J. Lan, Z. Zhuo, C. Ge, Z. Zhou, Z. Chai and W. Shi, J. Nucl. Mater., 2019, 516, 264–270 CrossRef CAS.
- S. Dudarev, G. Botton, S. Savrasov, C. Humphreys and A. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- M. Cococcioni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- R. Qiu, B. Ao and L. Huang, Comput. Mater. Sci., 2020, 171, 109270 CrossRef CAS.
- G. Jomard, B. Amadon, F. Bottin and M. Torrent, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075125 CrossRef.
- B. Dorado, B. Amadon, M. Freyss and M. Bertolus, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235125 CrossRef.
- F. Birch, Phys. Rev., 1947, 71, 809 CrossRef CAS.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466 CrossRef CAS PubMed.
- R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- B. Johansson, L. Nordström, O. Eriksson and M. Brooks, Phys. Scr., 1991, 1991, 100 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |