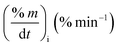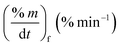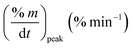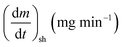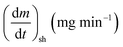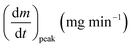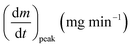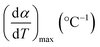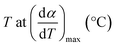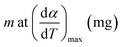Open Access Article
Open Access ArticleThermal pyrolysis and kinetic parameter determination of mango leaves using common and new proposed parallel kinetic models
Saad A. El-Sayed * and
Mohamed E. Mostafa
* and
Mohamed E. Mostafa
Mechanical Power Engineering Department, Faculty of Engineering, Zagazig University, 44519, Zagazig, Egypt. E-mail: shamad53@hotmail.com
First published on 13th May 2020
Abstract
TG/DTG thermal pyrolysis analysis is performed under nitrogen from 100 to 1000 °C at three different heating rates for three types of most famous Egyptian mango leaves to be used as a biomass fuel. Proximate and ultimate analysis, organic composition, metallic components as well as thermal degradation and their characteristic properties are determined and deeply investigated to recognize the possibility to use them as a source of renewable energy. A maximum volatile released method and three isoconversional kinetic models were used to analyze the dependence of the activation energy (Eα) on the degree of conversion. A double parallel random pore model (DRPM), mixed volumetric random pore model (MVRPM) and a new proposed double parallel volumetric model (DVM) were used to investigate the kinetic parameters of the produced volatile and char. Three zones were chosen based on the organic composition and the temperature range of each mango leaf type. The maximum rate loss and second derivative of conversion of volatile matter (α) with temperature are used in the maximum volatile method at peak temperature for determining the kinetic parameters. The three isoconversional kinetic methods give almost closest values of Eav for all sub-zones and especially for a whole volatile zone of Sukari momtaz. The estimated Eav from the isoconversional methods are more dependable than the maximum volatile release method. Compared with previous multireaction models, the new proposed double parallel model can effectively investigate the pyrolysis kinetics of biomass materials.
1. Introduction
Due to the highly growing demand for renewable fuels, there are a wide variety of biomass fuels either being used in pilot scale plants for producing energy or under laboratory research. Most of these fuels fall into one of the following two categories; plant based biomass and animal waste biomass. The increasing availability of biomass fuels along with the recent development of technologies to use them more efficiently with low scale pollutant emissions, makes biomass an increasingly promising fuel choice. Pyrolysis is the decomposition of a compound caused by heat. For most biomass fuels, the pyrolysis process proceeds in two steps; fuel moisture evaporation and release of volatile compounds such as CO, CO2, N2, CxHy, etc.The measured parameters from TG such as mass change, time and temperature recorded during the pyrolysis process can be used to determine the chemical kinetic parameters such as activation energy (E) and pre-exponential factor (A). Thermal Gravimetric Analysis (TGA) is the most common methodology to analyze the pyrolysis kinetics with a heating rate normally lower than 100 °C min−1. As presented in the previous studies, pyrolysis processes with various schemes have been suggested to emulate TGA data to a single heating rate1 or multiple heating rates.2,3
A non-isothermal TGA of oil-palm solid wastes based on the observation of sample mass loss against time or temperature at a specific heating rate is studied by Luangkiattikhun et al.4 TGA provides high precision, fast rate data collection, and high repeatability under well-defined kinetic control region.5 Activation energy for decompositions of hemicellulose and cellulose in EFB and PS by considering different temperature region for first order kinetic reaction was studied by Yang et al.6 Some proposed models suggested that the thermal behavior of the main components and their relative contribution in the initial biomass can present the primary decomposition rates of biomass.7 For lignocellulosic materials, their thermal degradation is contributed to hemicellulose, cellulose and lignin; although, in a few cases, the decomposition of components is involved more than one reaction step, especially hemicellulose and lignin.8 The temperature range of hemicellulose and cellulose decomposition has been studied by Yang et al.9 They estimated this temperature range of decomposition to be about 220–315 °C and 315–400 °C for hemicellulose and cellulose decomposition, respectively, with a maximum mass loss rate at about 268 °C and 355 °C. Also, thermal decomposition of lignin noticed to occur in a wide temperature range from 160 °C to 900 °C, and its maximum mass loss rate is not as clear as in the case of hemicellulose and cellulose. The pyrolysis process of the lignocellulosic biomass can be divided into three main regions: moisture and very light volatiles components removal (<120 °C); degradation of hemicellulose (220–315 °C); lignin and cellulose decomposition (315–400 °C) and lignin degradation (>450 °C).10 In a study was done by Mansaray and Ghaly,11 it was noticed that the loss of lignin typically occurs at a slower rate over a much wider temperature range of 180–900 °C. Also, it was stated that the first three compounds are chemically active and decompose thermo-chemically in the temperature range of 150–500 °C (hemicellulose decomposes predominantly between 150 and 350 °C, cellulose decomposes between 275 and 350 °C and lignin undergoes gradual decomposition between 250 and 500 °C). Tsamba et al.12 investigated the decomposition of lignocellulosic biomass components as hemicellulose, cellulose, and lignin. According to their analysis, decomposition regions of 220–300 °C, 300–340 °C and >340 °C for hemicellulose, cellulose and lignin, respectively.
Development of thermal conversion processes, such as combustion, torrefaction, gasification and pyrolysis, based on these samples, requires a good understanding of their thermal characteristics. A good amount of work has been done in determining these characteristics using different biomass materials under inert (pyrolysis) condition.13 TG method bused as a tool to determine biomass samples proximate analysis data (moisture, ash, volatile matter and fixed carbon contents) just by direct measure of weight changes on each sample's TG chart.14 Combustion of mango wood is investigated by Okoroigwe.15 TGA data can be used to determine the chemical kinetic parameters using different methods. Different thermal analysis methods were adopted to study the chemical kinetics, including isothermal method and non-isothermal methods with single and multiple heating rate. These methods upgraded beginning from non-isothermal single heating rate direct and Coats–Redfern integral methods16 passing by non-isothermal multiple heating rate and model fitting approaches as Friedman, Flynn–Wall–Ozawa (FWO) and Kissinger–Akahira–Sunose method (KAS)17–19 reaching mathematical models that deal with isothermal and non-isothermal conversion. These model fitting methods are also known as isoconversional methods that determine the activation energy independently by solving an unknown reaction mechanism that governs the transformation.20,21 Maximum volatile release method is a new proposed approach that predict the chemical kinetics based on the volatiles peak temperature.22 Other studies employed the parallel models that considers the pyrolysis as numerous independent parallel reactions with different activation energies. The most common approach for these models is the Distributed Activation Energy Model (DAEM) which describes the activation energy distribution of the parallel reactions by a continuous function.23 DAEM is a model-fitting method that simulates mass loss across the overall conversion rate.24,25
The most common and well known traditional mathematical models that provide various formulas for f(α) are the volumetric model (VM) and the random pore model (RPM).26 Most researchers solved these models as one stage27–29 while some applied these models in the modified parallel form that takes into consideration the overlap between the volatiles and produced porous char. Up to date, the previous studies that implemented these modified models for studying the kinetic parameters focused only on both the combustion of raw materials,30–32 combustion of char33,34 and char gasification.27,29,35
In our previously published article,36 the effect of CO2 and H2O on the reactivity and kinetic behavior of rice straw and sawdust raw pellets oxy-steam combustion was investigated using the three parallel models including the DVM model. In the present study, we planned to apply these parallel models to calculate the chemical kinetics for the pyrolysis process. This idea came to us after doing deep literature at this point and found that the researchers who used some of these parallel models applied them for the combustion and gasification processes only and no one applied these models for the pyrolysis process. Up to date, very few studies implemented these models in a modified form for determining kinetic parameters of raw materials either for biomass or coal taking into consideration the simultaneous reactions of volatiles and char combustion and nearly no study handled these models for the pyrolysis process. Thus, in the present study, the two parallel reactions of volatiles and produced porous char will overlap and occur simultaneously during the pyrolysis process.37 Also, not only the lack in models is restricted to the type of solid materials used (i.e. raw material) but also it extends to the application of these models for pyrolysis of raw materials. Through these models, the kinetic parameters of both the volatiles and char can be investigated besides the conversion of these two constituents could be predicted which in turn give a clear picture for what happens during the pyrolysis process. Thus, the new proposed double parallel volumetric model (DVM), double parallel random pore model (DRPM) and mixed volumetric and random pore model (MVRPM) will be applied for the pyrolysis process.
The main purpose of the current study was to investigate the thermal decomposition and determine the kinetic parameters of three types of Egyptian mango leaves. The kinetic parameters for these kinds of leaves not known and didn't carried out before in the literatures to be used as an organic fuel or mix with other organic fuels (Co-firing) on the basis of their thermal decomposition behavior as a biomass fuel. In current work, thermal decomposition behavior was studied as follow: (a) conduct TGA on three types of famous Egyptian mango leaves powder at different heating rates 10, 20, and 30 °C min−1 in a nitrogen atmosphere. (b) Determine the organic and mineral compositions of these types to see their roles in the thermal decomposition behavior of them. (c) Determine the thermal degradation rates, initial degradation temperatures and residual weights for each type with the comparison. (d) Determine the kinetic parameters (activation energy, pre exponential factor and order of reaction) using maximum volatile release method and isoconversional methods. (d) Investigate the kinetic parameters of the volatiles and char reactions for the biomass pyrolysis process using the parallel models DVM, DRPM and MVRPM.
2. Materials and methods
2.1 Mango leaves collection and sample preparation
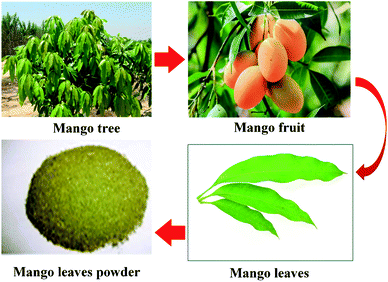
Although mango grows best in tropical region, the areas of high humidity, like coastal areas such as Delta Nile are also considered suitable for mango growing. Egypt produces 232 thousand tons of mangos annually and exports moderate amounts (1500 tons) to 20 countries in the near East and Europe.38 The Ismailia is the most one of the governorates, which cultivates mango trees in Egypt. The soil and climate of Ismailia are especially favorable to the cultivation of Egyptian mango. Mango season in Egypt starts from July till November. Our mango is famous by its fascinating flavor, smell and taste. The mango trees are considered a long-lived type and their leaves are evergreen, alternate, and simple. Egyptian mango leaves dimensions ranges from 15–35 cm long, and 6–16 cm broad and leathery in texture as shown in Fig. 1. The tender leaves of the mango tree are considered useful in treatment, but now we try to use it as a fuel to produce a renewable energy. Leaves of three famous mango types in the Ismailia region (Amber, Sukari momtaz and Barbary) are collected and dried in a shade area (i.e. lab), then it is milled (see Fig. 1) in a milling machine and the collected biomass sample powders were stored in airtight plastic containers until they were needed for the TG analysis.A sieved analysis is done for the three types and the calculated average mean particle diameter of the powdered leaves is 162.5 μm. Sieving process was conducted by the ELE Sieve Shaker (code: 80-0200/0) which is powered by an electromagnetic drive. The unit features a triple Vertical-Lateral-Rotary vibrating action that moves the sample over the sieve producing faster more efficient sieving, while the rapid vertical movements also help keep the apertures from blinding. As standard the shaker includes, timer 0–999 minutes, adjustable vibration intensity and adjustable intermittent or continuous operation. The unit accepts up to ten 200 mm or up to six 300 mm, full height, diameter sieves and lid and receiver. Dimensions of the shaker 380 × 440 × 1085 mm for the length, width and height, respectively. This device is suitable for single phase 220–240 V AC with frequency 50 Hz. The standard procedure that followed when sieving a dry sample using the mechanical sieving technique is the American Society for Testing and Materials (ASTM) C 136.39 These steps were repeated until the end point criteria were met (the mass of the test sieves didn't change by more than 5% of the previous mass on that sieve). This was achieved during this work by observing the change in mass in each sieve in the tested three samples. The total losses must not exceed 2% of the mass of the original test sample according to the standard which is achieved in the present work. In this work, sieving analysis is repeated three times with a fresh sample and continuing the mechanical agitation for 15, 20 and 25 minutes. It is noted that the mass retained on a certain sieve is almost the same in the three times so the proper sieving time is taken the smallest time (i.e. 15 minutes).
2.2 Material characteristics
Three various types of mango leaves were selected for pyrolysis tests. Powder samples of biomass fuels were subjected to proximate, ultimate, fiber, and metallic element analysis. The proximate analysis in this study was done using LECO TGA-701 apparatus and the ultimate analysis is performed using LECO CHNS-932 apparatus. The heating value of the biomass materials was measured by using AC-500 bomb calorimeter. ASTM standard methods for estimating the chemical composition were used to measure the proximate and ultimate composition of the biomass materials. ASTM D3173,40 ASTM D3174,41 ASTM D3175,42 ASTM D3178, ASTM D3178,43 ASTM D3179,44 ASTM D3177 (ref. 45) and ASTM D5865 (ref. 46) methods were followed to measure the moisture, ash, volatiles, carbon. Hydrogen, nitrogen, sulfur and heating value of the materials, respectively. The measurements were performed in triplicate and repeated three times to ensure the repeatability. Proximate and ultimate together with calorific values of the fuels are briefly summarized in Table 1. One can see that the carbon and hydrogen percentage almost the same as other agricultural residues as cotton stalks, sugarcane bagasse, wheat straw, rice straw, etc.1,47 Like other biomass, mango leaves are highly oxygenated (>50% of the matter is oxygen except Barbary leaves). Sulfur content is less than many biomass materials. Ash is high as compared with some other biomass materials such as bagasse, cotton stalk, wheat straw, etc., which means that the investigated material contain high silica judging by our higher percentage ash content.2,3,48 This contributes to some extent in deposition of ash problems such as slagging and fouling. One of the constituents makes a remarkable notice, the nitrogen percentage in Barbary leaf type. The amount of fuel lost during the pyrolysis stage of combustion decreases with decreasing hydrogen to carbon ratio (0.12, 0.125, and 0.12 respectively) and, to a lesser extent, increasing with increasing oxygen to carbon ratio (1.34, 1.3, and 1.1 respectively). Also, these leaves contain almost 4% fat, 78.2% protein and 16.5% carbohydrates. The higher heating values of these materials are quite reasonable like other biomass and can be used as a source of renewable energy.| Material and property | Sukari momtaz | Amber | Barbary |
|---|---|---|---|
| Proximate analysis (weight% on air dry basis) | |||
| Moisture content | 7.68 | 9.52 | 8.61 |
| Ash | 10.45 | 9.57 | 9.77 |
| Volatile matter | 47.17 | 48.41 | 49.92 |
| Fixed carbon | 34.7 | 32.50 | 31.70 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Ultimate analysis (weight% on air dry basis) | |||
| Carbon | 40.01 | 40.80 | 41.59 |
| Hydrogen | 4.92 | 5.11 | 4.97 |
| Oxygen | 53.62 | 52.91 | 46.14 |
| Nitrogen | 1.30 | 1.06 | 7.21 |
| Sulfur | 0.15 | 0.12 | 0.09 |
| Ash | 10.45 | 9.57 | 9.77 |
| Heating value (MJ kg−1) | 16.74 | 16.43 | 16.23 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Fiber fraction | |||
| Hemicelluloses (%) | 6.70 | 8.70 | 7.55 |
| Celluloses (%) | 19.79 | 19.71 | 19.23 |
| Lignin (%) | 11.78 | 11.62 | 12.16 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Metallic elements (ppm) | |||
| Copper | 8.86 | 6.49 | 11.40 |
| Potassium | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167.50 167.50 |
9603.97 | 6451.78 |
| Magnesium | 2875.00 | 2983.16 | 3490.85 |
| Manganese | 37.31 | 44.03 | 46.93 |
| Calcium | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 185.00 185.00 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 022.53 022.53 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 763.74 763.74 |
| Iron | 251.37 | 163.98 | 202.95 |
| Sodium | 3295.00 | 3078.66 | 3446.21 |
| Lead | 0.05 | 0.00 | 1.01 |
The structural main components of any biomass contain cellulose, hemicelluloses, lignin, and many other compounds such as lipids, proteins, simple sugars, starches, water, HC, ash, etc. Their concentrations change based on the type of material and its tissue, growth stages as well as environmental conditions. The structural composition of the three mango leaf types was estimated by the automated fiber analyzer. This method determines Neutral Detergent Fiber, which is the residue remaining after digesting in a detergent solution. The fiber residues are predominantly hemicellulose, cellulose, and lignin as illustrated in Table 1. The three types of mango leaves contain the three components, but the cellulose is the dominant. Because of the skeletal structure of the mango leaves are so weak, so their cellulose constituents do not exceed 20% of the cell wall material. The lignin is considered highly branched in the walls of the cell and usually binds to adjacent cellulose fibers to form a lignocellulosic complex structure. The lignin percentages in leaves are higher than the hemicellulose content and exceed 10%.
Since the metallic elements distribution in the biomass fuels has a remarkable effect on pyrolysis temperature and composition of the pyrolysis process products such as char, tar, and gas, it is very important to determine their concentrations in them. The inherent metallic matter is more intimately distributed throughout the fuel. Biomass materials includes derivatives of some of the alkali and alkaline earth metals such as potassium (K), sodium (Na), sulfur (S), chlorine (Cl), calcium (Ca), magnesium (Mg), iron (Fe) and others are participate in chemical reactions leading to ash fouling and slagging. The principal mechanisms describing these phenomena in biomass combustors are now reasonably well understood as presented in previous studies.2,7–9,49 The metallic elements of the materials were measured by the flame photometer based on the measurement of the emitted light intensity when a metal is introduced into the flame. The wavelength of the color gives information about the element and the color of the flame gives information about the amount of the element present in the sample. The metallic elements of the three mango leaf types are given in Table 1. Potassium and calcium are the main source of alkali in the three mango leave types, which play an important role in the reaction with silica and sulfur to produce alkali silicate and alkali sulfates that leads to a potentially severe ash deposition problem in combustors. Calcium in biomass reacts with sulfur to form sulfates in way to some extent similar to potassium, which also lead to more severe ash deposition problems than potassium due to its high percentage in the material. Sodium and magnesium come after potassium and calcium in this analysis and also they have a role in ash deposition problems. Chlorine is a major factor in ash formation. Sodium concentration is high and causes the problem of ash deposition such sodium sulfate, and sodium chlorine. Chlorine concentration often dictates the amount of alkali vaporized during combustion, as strongly as does the alkali concentration. Iron decrease in concentration, but calcium and magnesium increase in concentration. This is consistent with an occasional principal for increasing ash levels during the combustion.
2.3 Thermal gravimetric analysis (TGA)
The most common technique used to investigate the thermal behaviour and kinetics of fuels is TGA.50 TGA on three types of famous Egyptian mango leaves powder has been conducted at different heating rates 10, 20, and 30 °C min−1 in a nitrogen atmosphere. The experiments were done in a Shimadzu DTG-60H differential thermal gravimetric analyzer with temperature range (ambient to 1000 °C), ±500 mg measurable range (TG), ±1000 μV measurable range (DTA), 0.1 μg weight readability, sample quantity (1 g max. in gross weight) and an inert gas atmosphere is used in this study. Nitrogen flow rate to the thermo-gravimetric analyzer was set at 20 ml min−1. Nearly 9.448, 13.155 and 8.391 mg, 13.325, 9.883 and 8.955 mg and 13.439, 13.325 and 6.29 mg of Sukari momtaz, Amber and Barbary, respectively were used for conducting the TGA experiments at heating rates of 10, 20 and 30 °C min−1. To make sure the reproducibility and accuracy of analysis, each experiment has been repeated three times and the mean value of the recorded data was used for the current analysis.2.4 Chemical kinetic models
The basic first order kinetics model of pyrolysis can be given by
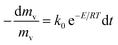 | (1) |
For a single reaction model, different methods are used for the kinetic parameters determination. The following methods are used in this study as follows:
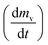 slows and begins to decrease, although the temperature still increasing, creating maximum volatile release rate
slows and begins to decrease, although the temperature still increasing, creating maximum volatile release rate 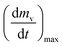 at T = Tmax. Introducing the effect of heat rate (β) and the reaction order, eqn (1) can be rewritten as:22
at T = Tmax. Introducing the effect of heat rate (β) and the reaction order, eqn (1) can be rewritten as:22
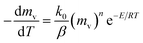 | (2) |
The peaks temperatures can be determining by differentiation of eqn (2) with respect to T, and equating the result to zero 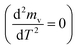 yields:
yields:
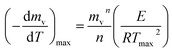 | (3) |
The activation energy values for reaction order different form 1 can be obtained from eqn (3), at peak temperatures and then, k0 can be calculated from eqn (2), at maximum conditions as:
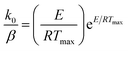 | (4) |
If we consider the degree of conversion of volatile matters (α), is defined as
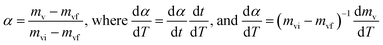 | (5) |
Rearranging eqn (1), based on the degree of conversion (α) and integrating gives the following g(α) function:
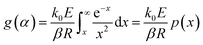 | (6) |
Eqn (6) has no analytical solution, so different approximation methods for the right side of this equation are proposed to solve it. Ozawa, Flynn and Wall (OFW) method55 offered an equation based on Doyle approximation of p(x)56 as follows:
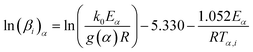 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βi against 1/Tα,i. Finding the slope for different (α) reveals the dependency of (Eα) on (α). Kissinger, Akahira and Sunose (KAS)17 also presented another approximation as follows:
βi against 1/Tα,i. Finding the slope for different (α) reveals the dependency of (Eα) on (α). Kissinger, Akahira and Sunose (KAS)17 also presented another approximation as follows:
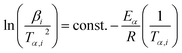 | (8) |
Plot of 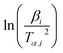 versus
versus 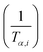 for each (α) gives a straight line with slope of
for each (α) gives a straight line with slope of 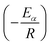 . More accurate approximation of p(x) was suggested by Starink57 as follows:
. More accurate approximation of p(x) was suggested by Starink57 as follows:
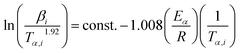 | (9) |
Since there are many data points, it is recommended to do kinetic analysis with a step (Δα) < 0.05 as stated by Okoroigwe.15 In this study, Δα is chosen to be 0.03 to perform analysis. A curve fitting is used to get α at T for all heating rates and for the different zones.
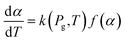 | (10) |
The apparent reaction rate (k) can be expressed based on the temperature according to the Arrhenius equation as follow:
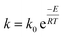 | (11) |
Due to the simultaneous volatile and char decomposition, two distinct conversion fractions (αvol) and (αch) will be resulted for both volatile and char, respectively. As a result of that, each stage will have its own kinetic parameters as activation energy (Evol and Ech) and frequency factor (k0,vol and k0,ch). The conversion of the overall reaction can be expressed by the following relation:
| α = cvolαvol + cchαch | (12) |
The (k) values for the two models (kVM and kRPM) are expressed as 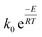 with different values of (k0) and (E) for each model. For non-isothermal TGA, the biomass material is heated at a constant heat rate (β) and the instantaneous temperature (T) is related to the time (t) and the temperature at which heating is started (T0) according to the following relation:
with different values of (k0) and (E) for each model. For non-isothermal TGA, the biomass material is heated at a constant heat rate (β) and the instantaneous temperature (T) is related to the time (t) and the temperature at which heating is started (T0) according to the following relation:
| T = T0 + βt | (13) |
The conversion rate expression for non-isothermal condition for VM and RPM models can be formulated to express the new parallel and mixed models according to eqn (14)–(16). For double parallel volumetric model (DVM), the two stages of volatile and char conversion are expressed by the volumetric model as shown in eqn (14). In the double parallel random pore model (DRPM), the two stages of pyrolysis are expressed by the RPM model as figured in eqn (15). For the mixed volumetric random pore model (MVRPM), the volatile part is expressed by the VM model, while the char part is expressed by RPM model as illustrated in eqn (16).
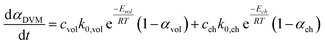 | (14) |
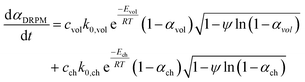 | (15) |
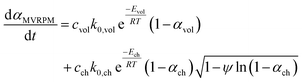 | (16) |
The conversion of overall reaction based on the two traditional models and three modified models was obtained by integrating eqn (14)–(16) as follow:31
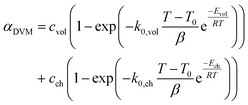 | (17) |
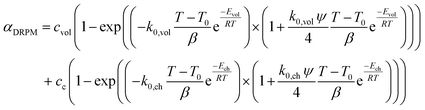 | (18) |
 | (19) |
To estimate the kinetic parameters, the nonlinear least-square fitting method was employed using Excel program by varying all fitting parameters. Constrained generalized reduced gradient (GRG) non-linear solver method was applied to estimate these parameters by considering them as unknowns. Constrains on the range of values were set for the different unknown parameters. Based on the proposed equations for solutions, the estimated values of conversion (αmodel) for the three parallel models were fitted with the experimental conversion values (αexp) that obtained from the TGA data to estimate the values of (k0) and (E) for traditional models and the values of (c), (k0) and (E) for both stages in parallel and mixed models.27 The best fit solution could be reached when the residual sum of squares (RSS) is minimized (see eqn (20)).30
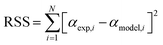 | (20) |
The best way to obtain the structural parameter (ψ) is to fit the equation that relates the reduced time 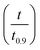 and fractional conversion (α) by regression considering this parameter as unknown.58 Nonlinear least-square method was used to obtain the value of (ψ) by fitting the (αcal) against time with the experimental conversion (αexp) against time at a minimum value of residual sum of squares (RSS). The time that corresponding to 90% conversion of the biomass material is used as the upper limit to eliminate the uncertainty of conversion that occurs near the end of the reaction.59
and fractional conversion (α) by regression considering this parameter as unknown.58 Nonlinear least-square method was used to obtain the value of (ψ) by fitting the (αcal) against time with the experimental conversion (αexp) against time at a minimum value of residual sum of squares (RSS). The time that corresponding to 90% conversion of the biomass material is used as the upper limit to eliminate the uncertainty of conversion that occurs near the end of the reaction.59
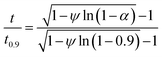 | (21) |
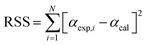 | (22) |
To obtain reliable and accurate kinetic parameters and validate the applied models, both the isoconversional methods and parallel models were solved at three heating rates for each biomass material.
3. Results and discussions
3.1 Thermal degradation characteristics
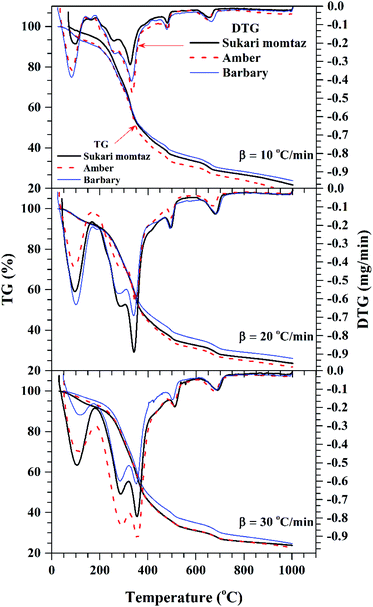
Fig. 2 shows the TG/DTG profiles of the three mango types of heating rates of 10, 20 and 30 °C min−1, respectively. The thermal degradation of the three fiber components; hemicellulose, cellulose, and lignin can be explained based on the mass loss rate and the peak temperatures in each stage as given in Fig. 2 as an example and Table 4.As shown in this figure, the rate of mass loss of moisture and so simple volatiles components is slow and ends almost at temperatures ranged between 160 and 207 °C. Then, the devolatilization process starts and almost ends in the temperature ranged between 700 °C to 750 °C. This figure also shows that all types of mango leaves have five peaks. The first peak lies in the moisture and simple volatile matters region (<200 °C), and this peak exists due to the light volatiles contained in this region. Two peaks exist in the decomposition of the hemicellulosic and cellulose regions (200 °C to 355 °C) and other two peaks in the cellulose-lignin region (355 °C to 750 °C). Tables 2–4 give the most characteristic properties of the three mango leaves taken from the TG/DTG profiles. These properties are important for calculating the kinetic parameters of each type. As we can see that, the shape of the profiles is resembling for the various heating rates and for each type, except for the values of the characteristic properties of each. The detailed of each stage (region) will be explained in the following sections.
| Material | β (°C min−1) | Start of zone | End of zone | Peak in moisture zone | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ti (°C) | Tf (°C) | mloss (%) | tf (min) | tpeak (min) | Tpeak (°C) | mloss (%) | |||||
| Sukari momtaz | 10 | 69.0 | −0.0034 | 207.0 | −0.0109 | 7.66 | 7.55 | −0.0216 | 1.10 | 95.6 | 1.81 |
| 20 | 42.6 | −0.0042 | 168.8 | −0.0138 | 7.65 | 2.83 | −0.0426 | 1.23 | 96.2 | 3.6 | |
| 30 | 30.2 | −0.0031 | 175.7 | −0.0243 | 7.74 | 2.06 | −0.0611 | 1.15 | 105.8 | 3.92 | |
| Amber | 10 | 34.7 | −0.0009 | 191.0 | −0.0069 | 9.47 | 9.85 | −0.0260 | 1.85 | 80.1 | 3.01 |
| 20 | 30.8 | −0.0022 | 198.0 | −0.0155 | 9.48 | 4.26 | −0.0433 | 1.45 | 94.5 | 3.64 | |
| 30 | 51.2 | −0.0061 | 226.0 | −0.0518 | 9.44 | 2.43 | −0.0491 | 0.90 | 110.5 | 3.12 | |
| Barbary | 10 | 24.7 | −0.0004 | 160.5 | −0.0050 | 8.56 | 7.43 | −0.0287 | 2.15 | 82.2 | 3.2 |
| 20 | 24.1 | −0.0014 | 179.3 | −0.0163 | 8.57 | 3.31 | −0.0474 | 1.56 | 101.0 | 3.83 | |
| 30 | 47.4 | −0.0027 | 238.0 | −0.0552 | 8.61 | 2.77 | −0.0382 | 1.05 | 119.0 | 2.39 | |
| Material | β (°C min−1) | Toffset (°C) | TG (%) | m (mg) | M (%) | Ash (%) | VMTG (%) | FCTG (%) |
|---|---|---|---|---|---|---|---|---|
| Sukari momtaz | 10 | 718 | 28 | 9.448 | 7.68 | 10.45 | 64.32 | 17.55 |
| 20 | 750 | 27 | 13.155 | 7.68 | 10.45 | 65.32 | 16.55 | |
| 30 | 760 | 26 | 8.391 | 7.68 | 10.45 | 66.32 | 15.55 | |
| Amber | 10 | 700 | 26 | 13.325 | 9.52 | 9.57 | 64.48 | 16.43 |
| 20 | 710 | 26.5 | 9.883 | 9.52 | 9.57 | 63.98 | 16.93 | |
| 30 | 715 | 26.8 | 8.955 | 9.52 | 9.57 | 63.68 | 17.28 | |
| Barbary | 10 | 700 | 30 | 13.439 | 8.61 | 9.77 | 61.39 | 20.23 |
| 20 | 730 | 30 | 13.325 | 8.61 | 9.77 | 61.39 | 20.23 | |
| 30 | 740 | 29.2 | 6.29 | 8.61 | 9.77 | 62.19 | 19.43 |
The mass loss rate (DTG profiles) gives an indication of reactivity of the materials as shown in Table 4. So for each type, the rate of mass loss (rate of releasing the volatile matters) increases and the time reaching the first peak in the hemicellulose decomposition decreases as β increases. This means that the material becomes more reactive as the heating rate increases.
As stated by Okoroigwe,15 the reactivity is directly proportional to the maximum weight loss rate (dm/dt)max and inversely proportional to its corresponding peak temperature (Tpeak). In current work, (dm/dt)sh and (dm/dt)peak were used to evaluate the reactivity of the hemicellulose and lignocellulose zones, respectively.
According to data presented in Table 4, it is clear that reactivity of all materials at hemicellulosic zone increases with increasing heating rate. This can attributed to the evolving of volatile matter associated with the temperature at which this peak occurs.61 On other hand, reactivity of all materials at the second peak of hemicellulosic zone and all peaks of lignocellulose zone decrease with increasing heating rate. Also, Table 4 shows that at low heating rate (β = 10 °C min−1), the reactivity of Amber is lower than the other types since the time taken to reach the first peak or the second peak in the hemicellulose decomposition is higher than the other types. In general, we can see that Sukari is almost, to some extent, high reactive than the other types. This table also shows that, the most mass loss due to the decomposition of hemicellulosic components is ranged between 160 to 355 °C. This result is in harmony with that stated by Mansaray and Ghaly11 who revealed that, hemicellulose decomposes predominantly between 150 and 350 °C. Regarding lignocellulosic decomposition, the degradation occurs between 355 °C to 505 °C and what can be distinguished as a contribution of lignin decomposition is the last (tail) part of mango leaves decomposition, which also has one peak, because at these temperatures both hemicellulose and cellulose are already decomposed and the lignin decomposition occurs (>505 °C). The maximum decomposition rate occurs at temperatures higher than 650 °C. One can see that the cellulose and lignin maximums overlaps and decomposition of lignin starts with cellulose or maybe with hemicellulose.
The maximum temperature values (maximum mass loss rate) of the hemicellulose, cellulose, lignin decomposition of each type shifts to higher values as β increases for the three types of mango leaves as shown in Table 4. This is in agreement with the results obtained by Deng et al.62 One important thing that, increasing the heat rate from 20 to 30 °C min−1 does not lead to a remarkable change in the overall maximum decomposition temperature. This means that these mango leaves almost do not need a high heating rate for thermal degradation more than done before. The rate of mass loss also showed a lateral shift as the heating rate was increased from 10 to 30 °C min−1. This can be attributed to the effect of the variations in the rate of heat transfer with changing the heating rate and the short exposure time to a particular temperature at higher heating rates, as well as the effect of the kinetics of decomposition.62,63 Actually, the external surface of the biomass particle will be hotter than its core at high heating rates, which in turn lead to reactions occurring inside the particle at lower temperatures. As a result of that, the resultant products will leave and pass through the high-temperature region causing secondary reactions.63 The maximum hemicellulose decomposition rate has almost increased as the heating rate increases. But in the cellulose and lignin the rate fluctuates from increasing to decreasing as the heating rate increases for Sukari momtaz and Barbary.
3.2 Kinetic parameters
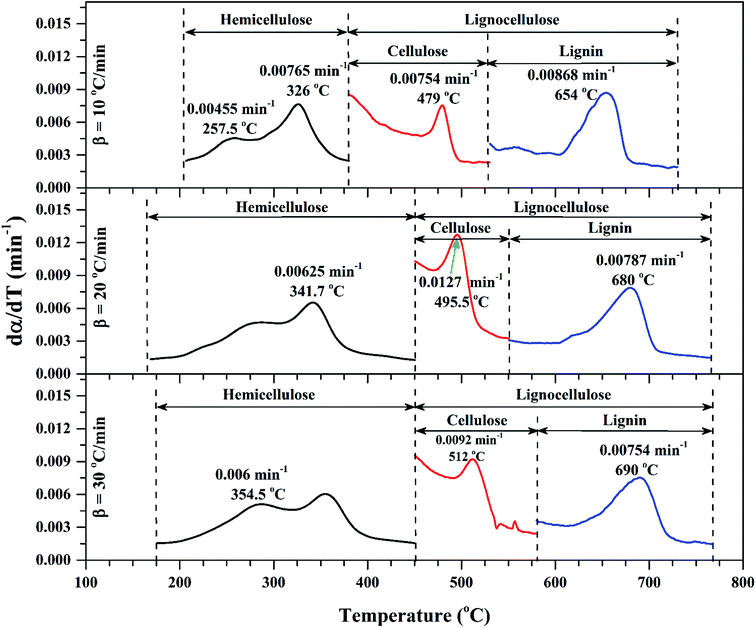 | ||
| Fig. 3 dα/dT vs. T for sub-zones of volatile regions of Sukari momtaz at different heating rates with most important characteristic parameters. | ||
| Zone | β (°C min−1) | mi (mg) | % mloss at peaks (%) | ||||
|---|---|---|---|---|---|---|---|
| Sukari momtaz | Hemicellulose | 10 | 8.68 | 0.0077 | 326 | 5.815 | 33.01 |
| Cellulose | 8.68 | 0.0075 | 479 | 3.595 | 58.58 | ||
| Lignin | 8.68 | 0.0087 | 654 | 2.856 | 67.10 | ||
| Hemicellulose | 20 | 12.07 | 0.0065 | 341.7 | 7.705 | 36.17 | |
| Cellulose | 12.07 | 0.0127 | 495.5 | 4.777 | 60.42 | ||
| Lignin | 12.07 | 0.0079 | 680 | 3.817 | 68.38 | ||
| Hemicellulose | 30 | 7.72 | 0.006 | 354.5 | 4.840 | 37.31 | |
| Cellulose | 7.72 | 0.0092 | 512 | 2.901 | 62.42 | ||
| Lignin | 7.72 | 0.0075 | 690 | 2.321 | 69.93 | ||
| Amber | Hemicellulose | 10 | 12.04 | 0.00775 | 335 | 7.503 | 37.68 |
| Cellulose | 12.04 | 0.00726 | 482.5 | 4.599 | 61.80 | ||
| Lignin | 12.04 | 0.00979 | 647 | 3.777 | 68.63 | ||
| Hemicellulose | 20 | 8.914 | 0.00676 | 348.2 | 5.578 | 37.4 | |
| Cellulose | 8.914 | 0.00656 | 497.1315 | 3.427 | 61.56 | ||
| Lignin | 8.914 | 0.00896 | 668.5 | 2.771 | 68.91 | ||
| Hemicellulose | 30 | 8.03 | 0.00719 | 356.188812 | 5.138 | 36.01 | |
| Cellulose | 8.03 | 0.00670 | 506 | 3.108 | 61.29 | ||
| Lignin | 8.03 | 0.00746 | 677 | 2.510 | 68.75 | ||
| Barbary | Hemicellulose | 10 | 12.28 | 0.00708 | 331.3244 | 8.015 | 34.73 |
| Cellulose | 12.28 | 0.00815 | 478.1192 | 5.424 | 55.83 | ||
| Lignin | 12.28 | 0.00885 | 662.5 | 4.273 | 65.20 | ||
| Hemicellulose | 20 | 12.16 | 0.00605 | 340.5 | 8.069 | 33.64 | |
| Cellulose | 12.16 | 0.00743 | 491.5 | 5.380 | 55.76 | ||
| Lignin | 12.16 | 0.00698 | 683 | 4.253 | 65.03 | ||
| Hemicellulose | 30 | 5.73 | 0.00699 | 352 | 3.848 | 32.85 | |
| Cellulose | 5.73 | 0.00976 | 503 | 2.466 | 56.96 | ||
| Lignin | 5.73 | 0.00795 | 687 | 1.948 | 66.01 |
| Zone | E (kJ mol−1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sukari momtaz | Amber | Barbary | |||||||
| β (°C min−1) | β (°C min−1) | β (°C min−1) | |||||||
| 10 | 20 | 30 | 10 | 20 | 30 | 10 | 20 | 30 | |
| Hemicellulose | 23.74 | 22.70 | 22.50 | 27.26 | 18.22 | 26.03 | 22.12 | 19.16 | 23.00 |
| Cellulose | 59.63 | 111.47 | 88.18 | 64.27 | 61.71 | 61.44 | 58.14 | 54.84 | 77.18 |
| Lignin | 131.34 | 132.94 | 138.84 | 156.53 | 155.69 | 126.02 | 124.37 | 101.89 | 121.93 |
| Etot | 214.71 | 267.11 | 249.52 | 248.06 | 235.61 | 213.49 | 204.62 | 175.89 | 222.11 |
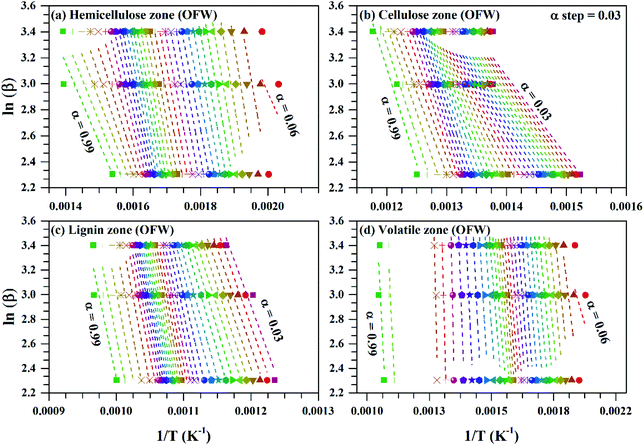 | ||
Fig. 4 ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β vs. 1/T for subzones and whole volatile zone of OFW method for Sukari momtaz mango leaves at different conversion values (α). β vs. 1/T for subzones and whole volatile zone of OFW method for Sukari momtaz mango leaves at different conversion values (α). | ||
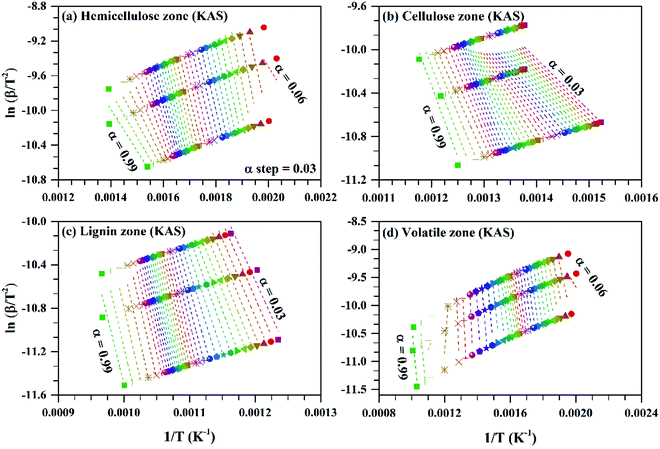 | ||
| Fig. 5 ln(β/T2) vs. 1/T for subzones and whole volatile zone of KAS method for Sukari momtaz mango leaves at different conversion values (α). | ||
The variation of activation energy of the three mango leave types was compared during sub-zones and the whole volatile region in Fig. 6, and from the fitting data of these curves the average values of activation energy can be obtained. Amber type shows more stability and very small fluctuations of activation energy with (α) up to α ≈ 0.7, then deviations becomes larger till the end of conversion. The obtained values of (Eα,av) with their standard deviation and errors are given in Table 7.
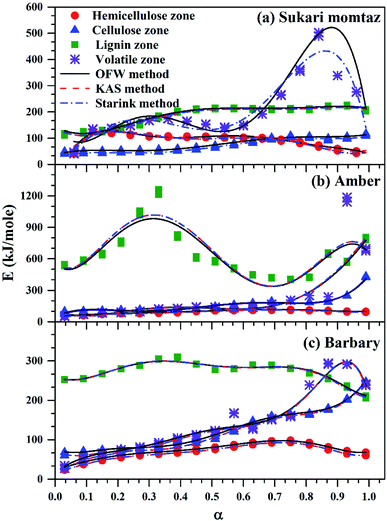 | ||
| Fig. 6 Comparison between OFW, KAS, and Starink methods for volatile sub-zones and completely volatile zone for three types of mango leaves. | ||
| Zones | OFW | KAS | Starink | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Eav (kJ mol−1) | St. Dev. (kJ mol−1) | St. Err. (%) | Eav (kJ mol−1) | St. Dev. (kJ mol−1) | St. Err. (%) | Eav (kJ mol−1) | St. Dev. (kJ mol−1) | St. Err. (%) | |
| Sukari momtaz | |||||||||
| Hemicellulose | 97.33 | 22 | 3.9 | 92.53 | 23.8 | 4.2 | 92.84 | 23.8 | 4.2 |
| Cellulose | 77.59 | 23.6 | 4 | 69.24 | 24.3 | 4.2 | 69.69 | 24.3 | 4.2 |
| Lignin | 190.03 | 37 | 6.4 | 184.59 | 38.2 | 6.6 | 185 | 38.2 | 6.6 |
| Volatile method | 175.6 | 49 | 9.8 | 174.3 | 50 | 10 | 174.6 | 47.7 | 9.7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Amber | |||||||||
| Hemicellulose | 96.29 | 17.8 | 3.1 | 91.54 | 18 | 3.1 | 91.71 | 18.1 | 3.1 |
| Cellulose | 149.36 | 40.5 | 7.2 | 144.99 | 42 | 7.5 | 145.36 | 42 | 7.5 |
| Lignin | 525.12 | 87.4 | 18.2 | 537.26 | 92.3 | 19.2 | 537.40 | 92.2 | 19.2 |
| Volatile method | 133.36 | 48.8 | 9.2 | 130.214 | 50.3 | 9.5 | 130.51 | 50.3 | 9.5 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Barbary | |||||||||
| Hemicellulose | 73.8 | 17.8 | 3.1 | 67.86 | 18.1 | 3.1 | 68.21 | 18.1 | 3.1 |
| Cellulose | 115.25 | 40.7 | 7.4 | 108.95 | 42.7 | 7.7 | 109.36 | 42.7 | 7.7 |
| Lignin | 274.30 | 22.8 | 3.9 | 273.36 | 24.2 | 4.2 | 273.81 | 24.2 | 4.2 |
| Volatile method | 120.34 | 56.3 | 10.4 | 116.26 | 57.8 | 10.7 | 116.46 | 57.9 | 10.7 |
For Sukari momtaz, OFW gives higher values of (Eα,av) than KAS and Starink methods for hemicellulose, cellulose, and lignin zones. KAS and Starink produce almost the same values of (Eα,av). Lignin zone, gives so higher activation energy values, especially for Amber mango type, as compared to the other zones. In general, the three isoconversional methods give almost so closest values of (Eα,av) for all sub-zones and especially for a volatile zone of Sukari momtaz. The same trend can be concluded for the other mango leaves. The most important notice that Barbary mango type shows lower values of (Eα,av) than the other types for hemicellulose, cellulose zones and whole volatile region and the opposite is true for lignin zone. This may be due to differences in organic composition of Barbary type compared with the other two types. One can also see from Table 7, that the arithmetic mean of the activation energy of the three subzones gives a value underestimated that of the whole volatile zone. Also, if we take the total value of the activation energy of the three zones for each mango type gives overestimated the value of activation energy compared with the value of the activation energy of the whole volatile region. The values of the activation energy from the volatile released method are so lower than the values obtained from three isoconversional methods. Because the activation energy, calculated for each sub-zone depends only on the point of maximum release weight and on each heat rate separately. On the other side, the isoconversional methods depend on the function of activation energy on the degree of conversion and from this precise distribution the average of activation energy can be calculated. The obtained kinetic parameters that obtained from the isoconversional methods for the three materials are in a good agreement with that provided previously for other materials have nearly the same chemical composition.48,64,65 For example, the average activation energies of the incense sticks (IS) material that have the same chemical analysis are 190.0 kJ mol−1 for first stage which is compatible with the average values of the hemicellulose and volatiles zones and 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190.0 kJ mol−1 for second stage which is compatible with the average values of the cellulose and lignin zones as presented in Tables 6 and 7.64 Also, the activation energy of the three pseudo-component of sawdust during pyrolysis are 156.25, 162.9 and 301.62 kJ mol−1 for hemicellulose, cellulose and lignin, respectively using KAS method.65 These values follow the same trend observed in Tables 6 and 7 for the three biomass materials with nearly similar values. The activation energies of the pyrolysis process of groundnut shell, cotton husk and municipal solid waste that have nearly the same chemical composition as the studied materials are found to be in the range of 168–218, 187–269 and 150–824 kJ mol−1, respectively.48 These values are close enough to the average values of the kinetic energies for the three mango materials.
190.0 kJ mol−1 for second stage which is compatible with the average values of the cellulose and lignin zones as presented in Tables 6 and 7.64 Also, the activation energy of the three pseudo-component of sawdust during pyrolysis are 156.25, 162.9 and 301.62 kJ mol−1 for hemicellulose, cellulose and lignin, respectively using KAS method.65 These values follow the same trend observed in Tables 6 and 7 for the three biomass materials with nearly similar values. The activation energies of the pyrolysis process of groundnut shell, cotton husk and municipal solid waste that have nearly the same chemical composition as the studied materials are found to be in the range of 168–218, 187–269 and 150–824 kJ mol−1, respectively.48 These values are close enough to the average values of the kinetic energies for the three mango materials.
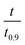 based on the predicted model equation that obtained from correlating αexp with
based on the predicted model equation that obtained from correlating αexp with 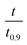 . The values of ψ and the coefficients of the model equations were considered as unknowns.
. The values of ψ and the coefficients of the model equations were considered as unknowns.
| β | Model | Volatiles | Char | ψ | R2 | RSS | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| cvol | Evol (kJ mol−1) | k0,vol (min−1) | cch | Ech (kJ mol−1) | k0,ch (min−1) | |||||
| Parallel and mixed models for Sukari momtaz | ||||||||||
| 10 | DVM | 0.4505 | 49.79 | 936.58 | 0.5495 | 6.93 | 0.067 | — | 0.9992 | 0.438 |
| DRPM | 0.5206 | 28.78 | 7.619 | 0.4794 | 2.62 | 0.018 | 5.06 | 0.9990 | 0.550 | |
| MVRPM | 0.6500 | 31.61 | 23.11 | 0.3500 | 6.40 | 0.024 | 5.06 | 0.9988 | 0.662 | |
| 20 | DVM | 0.7600 | 26.48 | 13.246 | 0.2400 | 22.85 | 0.641 | — | 0.9978 | 0.767 |
| DRPM | 0.4431 | 38.89 | 81.16 | 0.5569 | 1.74 | 0.036 | 5.39 | 0.9993 | 0.213 | |
| MVRPM | 0.6500 | 31.07 | 31.45 | 0.3500 | 4.24 | 0.040 | 5.39 | 0.9982 | 0.587 | |
| 30 | DVM | 0.3821 | 67.10 | 3.87 × 104 | 0.6179 | 9.21 | 0.357 | — | 0.9994 | 0.119 |
| DRPM | 0.4500 | 33.97 | 98.24 | 0.5499 | 3.45 | 0.070 | 5.50 | 0.9993 | 0.136 | |
| MVRPM | 0.6500 | 34.12 | 67.54 | 0.3500 | 4.77 | 0.070 | 5.50 | 0.9986 | 0.311 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Parallel and mixed models for Amber | ||||||||||
| 10 | DVM | 0.7912 | 22.97 | 3.286 | 0.2088 | 37.13 | 0.808 | — | 0.9976 | 1.638 |
| DRPM | 0.4697 | 31.24 | 9.94 | 0.5303 | 0.50 | 0.012 | 5.40 | 0.9988 | 0.737 | |
| MVRPM | 0.6500 | 27.33 | 8.41 | 0.3500 | 4.32 | 0.016 | 5.40 | 0.9978 | 1.513 | |
| 20 | DVM | 0.7970 | 24.96 | 8.76 | 0.2030 | 27.29 | 0.891 | — | 0.9980 | 0.738 |
| DRPM | 0.4651 | 34.60 | 31.62 | 0.5349 | 1.79 | 0.034 | 5.38 | 0.9994 | 0.194 | |
| MVRPM | 0.6500 | 30.45 | 24.91 | 0.3500 | 3.38 | 0.035 | 5.38 | 0.9985 | 0.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517 517 |
|
| 30 | DVM | 0.4365 | 60.00 | 10266 | 0.5635 | 7.98 | 0.276 | — | 0.9996 | 0.075 |
| DRPM | 0.5075 | 34.30 | 41.66 | 0.4924 | 2.67 | 0.059 | 5.51 | 0.9994 | 0.095 | |
| MVRPM | 0.6500 | 36.11 | 106.87 | 0.3500 | 4.54 | 0.065 | 5.51 | 0.9991 | 0.183 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Parallel and mixed models for Barbary | ||||||||||
| 10 | DVM | 0.7636 | 20.99 | 2.339 | 0.2364 | 28.68 | 0.466 | — | 0.9973 | 1.957 |
| DRPM | 0.3865 | 37.06 | 33.57 | 0.6135 | 1.2 | 0.015 | 5.38 | 0.9994 | 0.412 | |
| MVRPM | 0.6500 | 23.51 | 4.014 | 0.3500 | 5.93 | 0.021 | 5.38 | 0.9976 | 1.774 | |
| 20 | DVM | 0.7228 | 25.30 | 10.586 | 0.2772 | 22.95 | 0.656 | — | 0.9989 | 0.738 |
| DRPM | 0.3971 | 39.48 | 94.29 | 0.6029 | 2.38 | 0.038 | 5.19 | 0.9994 | 0.169 | |
| MVRPM | 0.6500 | 27.69 | 16.62 | 0.3500 | 7.03 | 0.054 | 5.19 | 0.9980 | 0.643 | |
| 30 | DVM | 0.4441 | 57.50 | 7458 | 0.5559 | 9.74 | 0.301 | — | 0.9995 | 0.092 |
| DRPM | 0.5170 | 33.48 | 88.80 | 0.4830 | 4.61 | 0.069 | 5.30 | 0.9993 | 0.125 | |
| MVRPM | 0.6500 | 36.85 | 131.13 | 0.3500 | 8.43 | 0.095 | 5.30 | 0.9991 | 0.170 | |
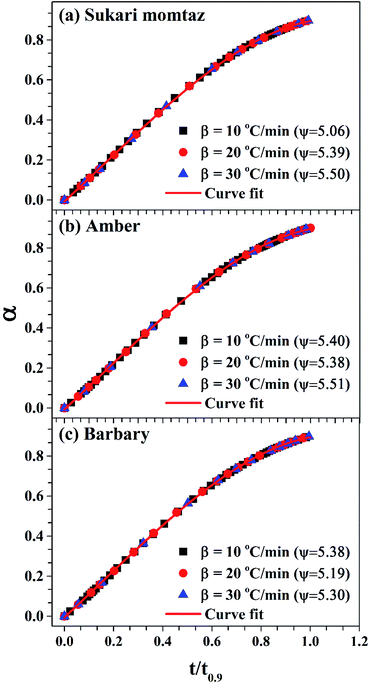 | ||
| Fig. 7 Determination of the structural parameter for the mango materials at different heating rates. | ||
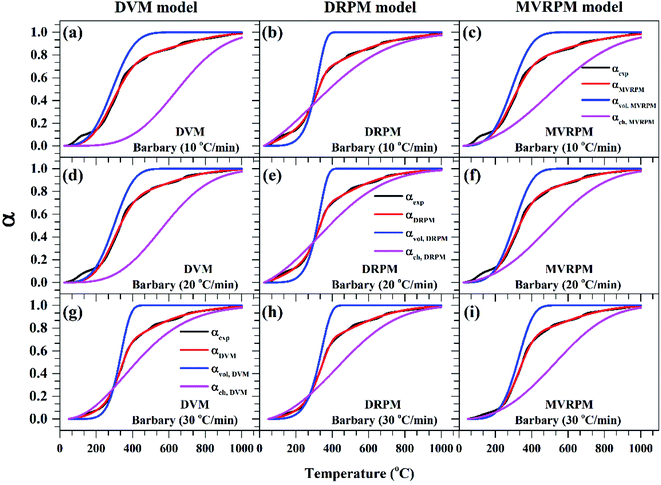
From the kinetic parameters data presented in Table 8, it is clear that the values of activation energies obtained by DRPM model are lower than that obtained by VM model for the three materials at all almost heating rates. That's because the DRPM model focused on the char part which represents the minority constituents of the biomass material, while the DVM model focused on the homogeneous combustion of volatile that accounts the large portion. When the pyrolysis process investigated by using the parallel and mixed model (MVRPM), the kinetic parameters changed and give higher values compared to DRPM.
Table 8 shows that in general the DVM and MVRPM models fit the experimental data better than the DRPM model for all leaf types because it has the highest coefficients of determination R2 and lowest RSS. These results are reasonable because the current study deals with biomass raw material that contains a huge amount of volatile, which reacts homogeneously with less amount of char. This dominant homogeneous reaction is more appropriate for the VM to deal with and the homogeneous and heterogeneous reactions of volatile and char is more suitable to deal with.
Table 8 also shows that (Evol)DRPM < (Evol)MVRPM < (Evol)DVM for heating rates 10 and 30 °C min−1 and the opposite is true for heating rate 20 °C min−1 for Sukari momtaz. For Amber and Barbary types, (Evol)DRMP > (Evol)MVRPM > (Evol)DVM for heating rates 10 and 20 °C min−1 while for heating rate 30 °C min−1, DVM gives higher Evol. On the other side, (Ech)DRPM < (Ech)MVRPM < (Ech)DVM for heating rates 10, 20, and 30 °C min−1 for Sukari momtaz, Amber and Barbary types. (k0,ch)DRPM < (k0,ch)MVRPM < (k0,ch)DVM for all mango leaf types at all heating rates. Table 8 and Fig. 7 also shows that the effect of heating rate on the ψ value of char is small. As the heating rate increases the ψ values increases for all leaves types with some fluctuations at heating rate 20 °C min−1.
It is clear from the obtained results of parallel model solution that the activation energy values of the char reaction are lower than that of the volatiles for the three materials at all heating rates. This could attributed to the lower char content of the biomass material compared with volatiles. Also, the endothermic char oxidation reaction that depends on the energy produced from the volatile reaction.
On the other side, compared with other biomass materials have nearly the same composition, the values of the resulted volatiles and char activation energies are low under the pyrolysis conditions. This result is attributed to the nature of the applied models. As these models were applied for the pyrolysis process, which requires low energy compared with combustion, and considered the volatiles and char reactions as two individual reactions, the resulted activation energy is predicted to be low compared with the total reaction. In the normal case, most models are applied for the global reaction that contains the volatiles and char as one step reaction. This requires more energy especially the complex reaction will appear during the conversion process as a result of the considering the raw material as a bulk fuel. Thus, the obtained activation energy values from DVM, DRPM and MVRPM models are low compared to other models. As the parallel models were applied to the pyrolysis process for the first time in the current study, it was hard to compare the kinetic result with previously obtained data and only presented the reasons of differences in the values. After doing a deep review, a previous study that investigated the kinetics of Botryococcus braunii pyrolysis using commonly used model-free and model-fitting with multiple parallel-reactions.66 Their results showed that the activation energy were in the range of 39.6–64.8 kJ mol−1 and 7.6–64.9 kJ mol−1 for the peak-maximum temperature model and mean mass loss contribution model, respectively. This low activation energy values confirm the credibility of the applied parallel models in the current study.
Fig. 8–10 illustrate the calculated experimental conversion (αexp) and obtained model conversion (αmodel) at different heating rates. At different heating rates, nearly similar volatile conversion profiles were obtained for all materials. It is shown that for Sukari momtaz, αexp and αmodel profiles nearly match with the volatile conversion profiles that obtained from the modified models (MVRPM) at all heating rates that consider both volatile and char together. The αvol,MVRPM profiles at the different heating rates are to some extent far from the experimental conversion, which resulted in lower values of R2. In addition, αch,MVRPM are obvious far from the experimental conversion for heating rates 10 and 20 °C min−1 and this deviation becomes small at heating rate 30 °C min−1. It can be seen that the conversion of volatile is fast and reaches to about 400 to 475 °C where all hemicellulose and most cellulose are decomposed then the rest of cellulose and lignin are so slow decomposed at higher temperature for all models at different heating rates. The deviations between αexp and αmodel (calculated) for char in DVM model are so higher at heating rates 10 and 20 °C min−1 compared to 30 °C min−1 for all leaf types. Also, as shown in Fig. 8–10, the volatile and char conversion profiles of all materials types are far apart from each other which showed that the volatiles aren't embedded deeply with char and their release is easy. It is also clear from Fig. 8–10 that the char conversion is slow and consumes long time depending on the heating rate. On the contrary, the volatile conversions are similar and there is no almost effect of heating rate on them. As the char conversion started during the raw material conversion, the specific surface area of the produced char could be related to the initial specific surface area of raw material and the degree of conversion of the char.54
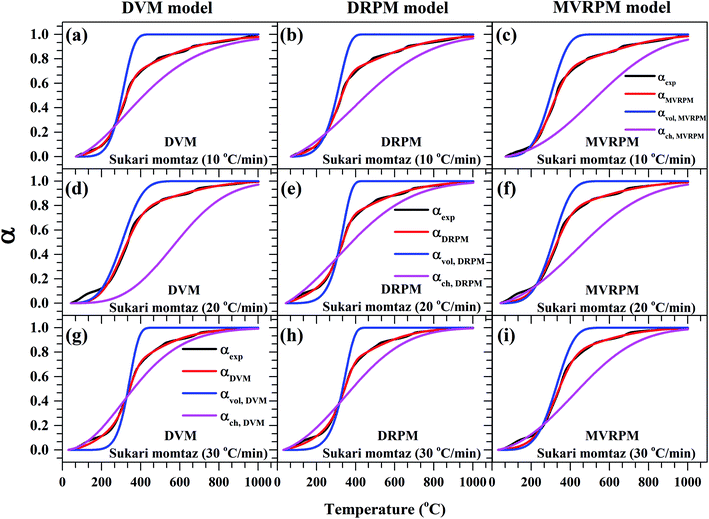 | ||
| Fig. 8 Experimental fractional conversion curves of Sukari momtaz and those calculated from modified parallel and mixed models at different heating rates. | ||
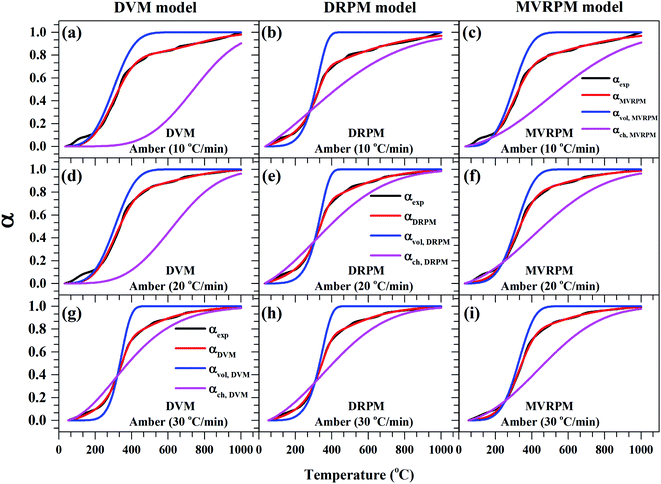 | ||
| Fig. 9 Experimental fractional conversion curves of Amber and those calculated from modified parallel and mixed models at different heating rates. | ||
4. Conclusions
Thermal degradation and kinetic parameters of thermo-chemical conversion of three types of Egyptian mango leaves have been investigated using different models according to thermogravimetric data and the following conclusions are derived as follows:• Sulfur content in the three types of mango leaves is less than many other biomass materials, but the ash content to some extent is higher.
• Since the skeletal structure of these leaves is so weak. So the cellulose constituents do not exceed 20% of the cell wall materials of all types.
• Potassium and calcium are the dominant source of alkali in the three mango leaves types, which play an important role in the reaction with silica and sulfur. This leads to an ash deposition problem in the combustors.
• Amber leaves needs more energy for moisture and light volatile evaporation than the other types at high rate.
• Sukari momtaz type is almost, to some extent, high reactive than the other types because its rate of mass loss increases and the time reaching the peak decreases as the heating rate increases compared to the other types.
• The values of apparent activation energy obtained from the maximum volatile released method are lower than the values of average activation energy obtained by the three isoconversional methods.
• The three isoconversional methods give almost so closest values of average activation energy for all suggested zones and the whole volatile region zone especially for Sukari momtaz type.
• Double parallel random pore model (DRPM), mixed volumetric random pore model (MVRPM) and a new proposed double parallel volumetric model (DVM) produced activation energy values for both volatile and char and their values are underestimated compared with isoconversional kinetic models.
• Compared with previous multi reaction models, the new proposed parallel models can effectively investigate the pyrolysis kinetics of biomass materials.
Nomenclature
| (dmv/dt)max | Maximum volatile release rate, mg s−1 |
| (dm/dt)peak | The overall maximum of the cellulose decomposition rate, mg min−1 |
| (dm/dt−1)sh | The overall maximum of the hemicellulose decomposition rate, mg min−1 |
| dmv/dt | Volatile release rate, mg s−1 |
| dm/dt | Rate of mass loss, mg s−1 |
| αvol | Volatiles conversion fraction, % |
| αch | Char conversion fraction, % |
| Ech | Char activation energy, kJ mol−1 |
| Evol | Volatiles activation energy, kJ mol−1 |
| Pg | Partial pressure of the reactive gas, Pa |
| RDTG,max | Maximum weight loss rate, % °C−1 |
| RM | Reactivity |
| Tf | Final temperature of any zone, K |
| Ti | Initial temperature of any zone, K |
| Tmax | Temperature corresponding to the maximum volatile release rate, K |
| Toffset | The extrapolated offset temperature of the dm/dt curves and this value describes the end of the cellulose decomposition, °C |
| Tonset | The extrapolated onset temperature calculated from the partial peak that results from the decomposition of the hemicellulose component, °C |
| Tpeak | Temperature corresponding to the overall maximum of the cellulose decomposition rate, °C |
| Tsh | Temperature corresponding to the overall maximum of the hemicellulose decomposition rate, °C |
| cch | Mass fraction of char in the biomass material, % |
| cvol | Mass fraction of volatiles in the biomass material, % |
| k0,ch | Char frequency factor, min−1 |
| k0,vol | Volatiles frequency factor, min−1 |
| k0 | Frequency factor, min−1 |
| mf | Final mass of any zone, mg |
| mi | Initial mass of any zone, mg |
| mv | Instantaneous mass of volatiles at any time (t), mg |
| mv | Mass of volatiles at a time (t), mg |
| mvf | Final mass of volatile zone, mg |
| mvi | Initial mass of volatile zone, mg |
| E | Activation energy, kJ mol−1 |
| M | Moisture content, % |
| R | Universal gas constant (8314 J mol−1 K−1) |
| T | Reaction temperature, K |
| f(α) | The change in the physical and chemical characteristics of the fuel sample during the conversion process |
| g(α) | Integral function of conversion |
| k | The apparent reaction rate, min−1 |
| n | Order of reaction |
| p(x) | Reaction model function |
| t | Time, min |
| x | The fraction of a structural quantity, such as a group, a constituent, a broken bond, etc. |
Abbreviations
| DRPM | Double random pore model |
| DVM | Double parallel volumetric model |
| FCTG | Fixed carbon calculated from TGA, % |
| MVRPM | Mixed volumetric random pore model |
| RPM | Random pore model |
| TGA | Thermal gravimetric analysis |
| TPR | Three parallel reaction |
| VM | Volumetric model |
| VMTG | Volatile matter calculated from TGA, % |
Greek symbols
| α | Degree of conversion, % |
| β | Heating rate, °C min−1 |
| ψ | Structural parameter |
Conflicts of interest
There is no conflicts to declare.References
- S. A. El-Sayed and M. E. Mostafa, Pyrolysis characteristics and kinetic parameters determination of biomass fuel powders by differential thermal gravimetric analysis (TGA/DTG), Energy Convers. Manage., 2014, 85, 165–172 CrossRef.
- S. A. El-Sayed and M. E. Mostafa, Kinetic Parameters Determination of Biomass Pyrolysis Fuels Using TGA and DTA Techniques, Waste Biomass Valorization, 2015, 6, 401–415, DOI:10.1007/s12649-015-9354-7.
- S. A. El-Sayed and M. Khairy, Effect of heating rate on the chemical kinetics of different biomass pyrolysis materials, Biofuels, 2015, 6, 157–170, DOI:10.1080/17597269.2015.1065590.
- P. Luangkiattikhun, C. Tangsathitkulchai and M. Tangsathitkulchai, Non-isothermal thermogravimetric analysis of oil-palm solid wastes, Bioresour. Technol., 2008, 99, 986–997, DOI:10.1016/j.biortech.2007.03.001.
- G. Várhegyi, H. Chen and S. Godoy, Thermal decomposition of wheat, oat, barley, and brassica carinata straws. a kinetic study, Energy Fuels, 2009, 23, 646–652, DOI:10.1021/ef800868k.
- H. Yang, R. Yan, T. Chin, D. T. Liang, H. Chen and C. Zheng, Thermogravimetric Analysis–Fourier Transform Infrared Analysis of Palm Oil Waste Pyrolysis, Energy Fuels, 2004, 18, 1814–1821, DOI:10.1021/ef030193m.
- F. J. A. Antunes and J. L. Figueiredo, Pyrolysis kinetics of lignocellulosic materials-three independent reactions model, Fuel, 1999, 78, 349–358, DOI:10.1016/S0016-2361(98)00156-2.
- C. Di Blasi, Modeling chemical and physical processes of wood and biomass pyrolysis, Prog. Energy Combust. Sci., 2008, 34, 47–90, DOI:10.1016/j.pecs.2006.12.001.
- H. Yang, R. Yan, H. Chen, D. H. Lee and C. Zheng, Characteristics of hemicellulose, cellulose and lignin pyrolysis, Fuel, 2007, 86, 1781–1788, DOI:10.1016/j.fuel.2006.12.013.
- X. Zhang, M. Xu, R. Sun and L. Sun, Study on Biomass Pyrolysis Kinetics, J. Eng. Gas Turbines Power, 2006, 128, 493–496, DOI:10.1115/1.2135816.
- K. G. Mansaray and A. E. Ghaly, Determination of reaction kinetics of rice husks in air using thermogravimetric analysis, Energy Sources, 1999, 21, 899–911, DOI:10.1080/00908319950014272.
- A. J. Tsamba, W. Yang and W. Blasiak, Pyrolysis characteristics and global kinetics of coconut and cashew nut shells, Fuel Process. Technol., 2006, 87, 523–530, DOI:10.1016/j.fuproc.2005.12.002.
- L. Wilson, W. Yang, W. Blasiak, G. R. John and C. F. Mhilu, Thermal characterization of tropical biomass feedstocks, Energy Convers. Manage., 2011, 52, 191–198, DOI:10.1016/j.enconman.2010.06.058.
- R. García, C. Pizarro, A. G. Lavín and J. L. Bueno, Biomass proximate analysis using thermogravimetry, Bioresour. Technol., 2013, 139, 1–4, DOI:10.1016/j.biortech.2013.03.197.
- E. Okoroigwe, Combustion Analysis and Devolatilization kinetics of Gmelina, Mango, Neem and Tropical Almond Woods under Oxidative Condition, Int. J. Renew. Energy Res., 2015, 5, 1024–1033 Search PubMed.
- A. W. Coats and J. P. Redfern, Kinetic Parameters from Thermogravimetric Data, Nature, 1964, 201, 68–69 CrossRef CAS , http://www.nature.com/doifinder/10.1038/201068a0, accessed May 28, 2018.
- H. E. Kissinger, Reaction Kinetics in Differential Thermal Analysis, Anal. Chem., 1957, 29, 1702–1706 CrossRef CAS.
- M. Mureddu, F. Dessì, A. Orsini, F. Ferrara and A. Pettinau, Air- and oxygen-blown characterization of coal and biomass by thermogravimetric analysis, Fuel, 2018, 212, 626–637, DOI:10.1016/J.FUEL.2017.10.005.
- J. Hu, Y. Yan, F. Evrendilek, M. Buyukada and J. Liu, Combustion behaviors of three bamboo residues: Gas emission, kinetic, reaction mechanism and optimization patterns, J. Cleaner Prod., 2019, 235, 549–561, DOI:10.1016/J.JCLEPRO.2019.06.324.
- R. G. Mehran Heydari and M. Rahman, Kinetic Study and Thermal Decomposition Behavior of Lignite Coal, Int. J. Chem. Eng., 2015, 9 Search PubMed.
- P. Rantuch and B. Nagypál, Investigation of activation energy of polypropylene composite thermooxidation by model-free methods, Eur. J. Environ. Saf. Sci., 2014, 2, 12–18 CAS.
- W. Chen, K. Annamalai, J. Sun and Y. Chen, Chemical kinetics of bean straw biofuel pyrolysis using maximum volatile release method, Korean J. Chem. Eng., 2016, 33, 2330–2336, DOI:10.1007/s11814-016-0088-4.
- X. Ren, J. Chen, G. Li, Y. Wang, X. Lang and S. Fan, Thermal oxidative degradation kinetics of agricultural residues using distributed activation energy model and global kinetic model, Bioresour. Technol., 2018, 261, 403–411 CrossRef CAS PubMed.
- S. Wang, G. Dai, H. Yang and Z. Luo, Lignocellulosic biomass pyrolysis mechanism: A state-of-the-art review, Prog. Energy Combust. Sci., 2017, 62, 33–86, DOI:10.1016/j.pecs.2017.05.004.
- C. R. Cardoso, M. R. Miranda, K. G. Santos and C. H. Ataíde, Determination of kinetic parameters and analytical pyrolysis of tobacco waste and sorghum bagasse, J. Anal. Appl. Pyrolysis, 2011, 92, 392–400 CrossRef CAS , https://linkinghub.elsevier.com/retrieve/pii/S0165237011001422, accessed March 28, 2020.
- G. Wang, J. Zhang, J. Shao, Z. Liu, H. Wang, X. Li, P. Zhang, W. Geng and G. Zhang, Experimental and modeling studies on CO2 gasification of biomass chars, Energy, 2016, 114, 143–154 CrossRef CAS.
- G. Wang, J. Zhang, J. Shao, K. Li and H. Zuo, Investigation of non-isothermal and isothermal gasification process of coal char using different kinetic model, Int. J. Min. Sci. Technol., 2015, 25, 15–21 CrossRef CAS.
- J. Zhang, G. Wang, J. Shao and H. Zuo, A Modified Random Pore Model for the Kinetics of Char Gasification, Bioresources, 2014, 9, 3497–3507 Search PubMed.
- G. Wang, J. Zhang, X. Hou, J. Shao and W. Geng, Study on CO2 gasification properties and kinetics of biomass chars and anthracite char, Bioresour. Technol., 2015, 177, 66–73 CrossRef CAS PubMed.
- G. Wang, J. Zhang, J. Shao and S. Ren, Characterisation and model fitting kinetic analysis of coal/biomass co-combustion, Thermochim. Acta, 2014, 591, 68–74 CrossRef CAS.
- G. W. Wang, J. L. Zhang, J. G. Shao, Y. K. Jiang, B. Gao, D. Zhao, D. H. Liu, H. Y. Wang, Z. J. Liu and K. X. Jiao, Experiments and kinetic modeling for the oxidative decomposition of herbaceous and wooden residues, BioResources, 2016, 11, 4821–4838 CAS.
- J. Shao, J. Zhang, G. Wang, Z. Wang and H. Guo, Combustion Property and Kinetic Modeling of Pulverized Coal Based on Non-isothermal Thermogravimetric Analysis, J. Iron Steel Res. Int., 2014, 21, 1002–1008 CrossRef CAS.
- M. V. Gil, J. Riaza, L. Álvarez, C. Pevida, J. J. Pis and F. Rubiera, Oxy-fuel combustion kinetics and morphology of coal chars obtained in N2 and CO2 atmospheres in an entrained flow reactor, Appl. Energy, 2012, 91, 67–74 CrossRef CAS.
- M. V Gil, J. Riaza, L. Álvarez, C. Pevida, J. J. Pis and F. Rubiera, Kinetic models for the oxy-fuel combustion of coal and coal/biomass blend chars obtained in N2 and CO2 atmospheres, Energy, 2012, 48, 510–518 CrossRef.
- H.-b. Zuo, W.-w. Geng, J.-l. Zhang and G.-w. Wang, Comparison of kinetic models for isothermal CO2 gasification of coal char–biomass char blended char, Int. J. Miner., Metall. Mater., 2015, 22, 363–370 CrossRef CAS.
- M. E. Mostafa, L. He, J. Xu, S. Hu, Y. Wang, S. Su, X. Hu, S. A. Elsayed and J. Xiang, Investigating the effect of integrated CO2 and H2O on the reactivity and kinetics of biomass pellets oxy-steam combustion using new double parallel volumetric model (DVM), Energy, 2019, 179, 343–357, DOI:10.1016/j.energy.2019.04.206.
- K. Al-Qayim, W. Nimmo, K. Hughes and M. Pourkashanian, Kinetic parameters of the intrinsic reactivity of woody biomass and coal chars via thermogravimetric analysis, Fuel, 2017, 210, 811–825 CrossRef CAS.
- M. A. Nofal and W. M. Haggag, Integrated management of powdery mildew of mango in Egypt, Crop Prot., 2006, 25, 480–486 CrossRef CAS.
- ASTM International – Standards Worldwide, ASTM C136-06, 2006 Search PubMed.
- ASTM D3173, Standard Test Methods for Moisture in the Analysis Sample of Coal and Coke, 2008 Search PubMed.
- ASTM D3174, Standard Test Methods for Ash Analysis of Coal and Coke, 2002 Search PubMed.
- ASTM D3175, Standard Test Methods for Volatile Matter in the Analysis Sample of Coal and Coke, 2007 Search PubMed.
- ASTM D3178, Standard Test Methods for Carbon and Hydrogen in the Analysis Sample of Coal and Coke, 2002 Search PubMed.
- ASTM D3179, Standard Test Methods for Nitrogen in the Analysis Sample of Coal and Coke, 2002 Search PubMed.
- ASTM D3177, Standard Test Methods for Total Sulfur in the Analysis Sample of Coal and Coke, 2002 Search PubMed.
- ASTM D5865, Standard Test Methods for Gross Calorific Value of Coal and Coke, 2010 Search PubMed.
- D. A. Agar, M. Rudolfsson, G. Kalén, M. Campargue, D. Da Silva Perez and S. H. Larsson, A systematic study of ring-die pellet production from forest and agricultural biomass, Fuel Process. Technol., 2018, 180, 47–55 CrossRef CAS.
- A. Bhavanam and R. C. Sastry, Kinetic study of solid waste pyrolysis using distributed activation energy model, Bioresour. Technol., 2015, 178, 126–131 CrossRef CAS PubMed.
- S. G. Viswanath and M. C. Gupta, Estimation of nonisothermal kinetic parameters from a TG curve by the methods of overdetermined system and inflection point, Thermochim. Acta, 1996, 285, 259–267, DOI:10.1016/0040-6031(96)02917-6.
- G. Wang, J. Zhang, J. Shao, Z. Liu, G. Zhang, T. Xu, J. Guo, H. Wang, R. Xu and H. Lin, Thermal behavior and kinetic analysis of co-combustion of waste biomass/low rank coal blends, Energy Convers. Manage., 2016, 124, 414–426 CrossRef CAS.
- P. E. Sánchez-Jiménez, L. A. Pérez-Maqueda, A. Perejón, J. Pascual-Cosp, M. Benítez-Guerrero and J. M. Criado, An improved model for the kinetic description of the thermal degradation of cellulose, Cellulose, 2011, 18, 1487–1498 CrossRef.
- J. Y. Yeo, B. L. F. Chin, J. K. Tan and Y. S. Loh, Comparative studies on the pyrolysis of cellulose, hemicellulose, and lignin based on combined kinetics, J. Energy Inst., 2019, 92, 27–37 CrossRef CAS.
- M. Hu, Z. Chen, S. Wang, D. Guo, C. Ma, Y. Zhou, J. Chen, M. Laghari, S. Fazal, B. Xiao, B. Zhang and S. Ma, Thermogravimetric kinetics of lignocellulosic biomass slow pyrolysis using distributed activation energy model, Fraser-Suzuki deconvolution, and iso-conversional method, Energy Convers. Manage., 2016, 118, 1–11 CrossRef CAS.
- X. Wang, M. Hu, W. Hu, Z. Chen, S. Liu, Z. Hu and B. Xiao, Thermogravimetric kinetic study of agricultural residue biomass pyrolysis based on combined kinetics, Bioresour. Technol., 2016, 219, 510–520 CrossRef CAS PubMed.
- T. Ozawa, A New Method of Analyzing Thermogravimetric Data, Bull. Chem. Soc. Jpn., 1965, 38, 1881–1886 CrossRef CAS.
- C. D. Doyle, Estimating isothermal life from thermogravimetric data, J. Appl. Polym. Sci., 1962, 6, 639–642 CrossRef CAS.
- M. J. Starink, The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods, Thermochim. Acta, 2003, 404, 163–176, DOI:10.1016/S0040-6031(03)00144-8.
- X. Gao, Y. Zhang, B. Li, Y. Zhao and B. Jiang, Determination of the intrinsic reactivities for carbon dioxide gasification of rice husk chars through using random pore model, Bioresour. Technol., 2016, 218, 1073–1081 CrossRef CAS PubMed.
- R. C. Everson, H. W. J. P. Neomagus, R. Kaitano, R. Falcon and V. M. du Cann, Properties of high ash coal-char particles derived from inertinite-rich coal: II. Gasification kinetics with carbon dioxide, Fuel, 2008, 87, 3403–3408 CrossRef CAS.
- A. Matala, C. Lautenberger and S. Hostikka, Generalized direct method for pyrolysis kinetic parameter estimation and comparison to existing methods, J. Fire Sci., 2012, 30, 339–356, DOI:10.1177/0734904112439840.
- H. Haykiri-Açma, Combustion characteristics of different biomass materials, Energy Convers. Manage., 2003, 44, 155–162, DOI:10.1016/S0196-8904(01)00200-X.
- N. Deng, Y. Zhang and Y. Wang, Thermogravimetric analysis and kinetic study on pyrolysis of representative medical waste composition, Waste Manag., 2008, 28, 1572–1580, DOI:10.1016/j.wasman.2007.05.024.
- A. Aboulkas and K. El Harfi, Study of the kinetics and mechanisms of thermal decomposition of Moroccan Tarfaya oil shale and its kerogen, Oil Shale, 2008, 426–443, DOI:10.3176/oil.2008.4.04.
- S. Wen, Y. Yan, J. Liu, M. Buyukada and F. Evrendilek, Pyrolysis performance, kinetic, thermodynamic, product and joint optimization analyses of incense sticks in N2 and CO2 atmospheres, Renewable Energy, 2019, 141, 814–827, DOI:10.1016/j.renene.2019.04.040.
- P. Sharma, O. P. Pandey and P. K. Diwan, Non-isothermal kinetics of pseudo-components of waste biomass, Fuel, 2019, 253, 1149–1161, DOI:10.1016/j.fuel.2019.05.093.
- I. Ali, S. R. Naqvi and A. Bahadar, Kinetic analysis of Botryococcus braunii pyrolysis using model-free and model fitting methods, Fuel, 2018, 214, 369–380, DOI:10.1016/j.fuel.2017.11.046.
| This journal is © The Royal Society of Chemistry 2020 |